Лабораторные работы по физике

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-23.

Изучение основных правил работы с

радиоизмерительными приборами.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: знакомство с основными характеристиками радиоизмерительных приборов, правилами их подключения к измеряемому объекту, методикой проведения измерений и оценкой их погрешностей.

Задание №1: Измерение напряжения сигнала генератора.

Приборы: генератор сигнала Г3, вольтметры В3 и В7.

Экспериментальная часть.

1). Установили на генераторе частоту выходного сигнала f = 5кГц, напряжение U = 2В.

Измерили вольтметром В3 выходное напряжение U_>x>=2В.

Погрешность измерения.

U=U_>x> U=(2  0,4) B.

2). Измерили вольтметром В7 выходное напряжение U_>x>=2,01В.

Погрешность измерения.

U=U_>x> U=(2,01  0,01) B.

Задание №2: Анализ формы и измерение параметров синусоидального сигнала с помощью осциллографа.

Приборы: генератор сигнала Г3, вольтметры В3 и В7, осциллограф С1.

Экспериментальная часть.

1). Установили на генераторе Г3 напряжение U = 2В.

Измерили вольтметром В3 выходное напряжение U_>x>=2В; на вольтметре В7: U_>x>=2В.

Получили на экране осциллографа изображение:

АО=1,4 см, Х = 4 см.

Измерим амплитуду сигнала:

Показания осциллографа совпадают с показаниями вольтметров.

2). Измерили период (Т) и частоту сигнала (f):

Показания осциллографа совпадают со значением на шкале генератора.

Задание №3: Измерение частоты с помощью частотомера и осциллографа.

Приборы: генератор сигнала Г3, вольтметры В3 и В7, осциллограф С1, частотомер Ф.

Экспериментальная часть.

1). Измерили частоту сигнала частотомером:

Погрешность измерения:

Показания генератора: f_>x> = 5кГц.

2). Рассчитаем частоту сигнала по показаниям осциллографа:

Х = 2 см.

Показания всех приборов совпадают.

Задание №4: Измерение фаз двух синусоидальных сигналов с помощью осциллографа.

Приборы: генератор сигнала Г3, осциллограф С1, схема RC.

Экспериментальная часть.

OA = 1,9 см, ОВ = 1,7 см.

Т.к. , а  - разность фаз синусоидальных

сигналов, то

Задание №5: Анализ формы и измерение параметров импульсного сигнала с помощью осциллографа.

Приборы: генератор сигнала Г5, осциллограф С1.

Экспериментальная часть.

1).Установим длительность импульсов  = 500 мкс, частоту повторений f_>П>=490Гц, амплитуду U_>m>=1,32B

2).Получили на экране следующее изображение:

Вычислим амплитуду импульсов:

Полученный результат совпадает с показаниями вольтметра генератора.

Измерим длительность импульсов:

Измерим период и частоту повторений импульсов:

Полученные результаты приблизительно совпадают с показаниями генератора.

Вывод: на этой работе мы ознакомились с основными характеристиками радиоизмерительных приборов, правилами их подключения к измеряемому объекту, методикой проведения измерений и оценкой их погрешностей.

TYPE=RANDOM FORMAT=PAGE>4

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-24.

Экспериментальные исследования электростатических полей с помощью электролитической ванны

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: изучение метода моделирования электростатических полей в электролитической ванне и исследование их характеристик в пространстве между электродами различной формы.

Теоретическая часть.

Электростатическое поле - поле, создаваемое покоящимися электрическими зарядами.

Характеристиками этого поля являются напряженность и потенциал , которые связаны между собой следующим соотношением: .

В декартовой системе координат: , где единичные орты.

Удобной моделью электрического поля является его изображение в виде силовых и эквипотенциальных линий.

Силовая линия - линия, в любой точке которой направление касательной совпадает с направлением вектора напряженности

Эквипотенциальная поверхность - поверхность равного потенциала.

На практике электростатические поля в свободном пространстве создаются заданием на проводниках - электродах электрических потенциалов.

Потенциал в пространстве между проводниками удовлетворяет уравнению Лапласа:.

В декартовой системе координат оператор Лапласа: .

Решение уравнения Лапласа с граничными условиями на проводниках единственно и дает полную информацию о структуре поля.

Экспериментальная часть.

Схема экспериментальной установки.

Методика эксперимента:

В эксперименте используются следующие приборы: генератор сигналов Г3 (I), вольтметр универсальный B7 (2) c зондом (3), электролитическая ванна (4) с набором электродов различной формы (5).

Устанавливаем в ванну с дистилированной водой электроды. Собираем схему, изображенную на РИС. 1. Ставим переключатель П в положение “U”. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f=5 кГц и напряжением U=5 В, затем ставим переключатель П в положение “S”. Далее, помещаем в ванну электроды различной формы ( в зависимости от задания ) и затем, водя по ванне зондом, определяем 4 - эквипотенциальные линии: 1B, 2B, 3B, 4B. И так далее для каждого задания.

Задание №1. Исследование электростатического поля плоского конденсатора.

Таблица 1. Зависимость потенциала  от расстояния.

 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y
0	-11	0	1,38	-5	0	2,88	1	0	4,34	7	0
0,14	-10	0	1,62	-4	0	3,13	2	0	4,57	8	0
0,37	-9	0	1,88	-3	0	3,40	3	0	4,8	9	0
0,62	-8	0	2,14	-2	0	3,65	4	0	4,99	10	0
0,82	-7	0	2,37	-1	0	3,88	5	0	4,99	11	0
0,1	-6	0	2,64	0	0	4,10	6	0

Таблица 2. Эквипотенциальные линии.

 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y
1	-5,7	9	2	-1,6	9	3	2,6	9	4	6,6	9
1	-5,8	6	2	-1,5	6	3	2,5	6	4	6,4	6
1	-5,7	3	2	-1,5	2	3	2,5	3	4	6,5	3
1	-5,7	0	2	-1,5	0	3	2,5	0	4	6,5	0
1	-5,7	-3	2	-1,5	-3	3	2,6	-3	4	6,5	-3
1	-5,7	-6	2	-1,5	-6	3	2,6	-6	4	6,5	-6
1	-5,8	-9	2	-1,5	-9	3	2,6	-9	4	6,5	-9

Обработка результатов измерений.

1). График зависимости .

2). Зависимость .

при x<0

при

при x>x_>2>

3). Погрешность измерения Е:

Е = (Е  Е) = (25  0,15)

4). Силовые и эквипотенциальные линии электростатического поля плоского конденсатора

5). Задача №1.

6). Задача №2.

;

Задание №2. Исследование электростатического поля цилиндрического конденсатора.

Радиусы цилиндров A =3,5 см, В=8,8см

Таблица 3. Зависимость

r),В	r,см	r),В	r,см
0,06	0	2,84	6
0,05	1	3,65	7
0,05	2	4,32	8
0,05	3	4,85	9
0,82	4	4,86	10
1,96	5

Таблица 4. Эквипотенциальные линии.

(x,y)	x	y	(x,y)	x	y	(x,y)	x	y	(x,y)	x	y
1	4	0	2	4,9	0	3	6,2	0	4	7,4	0
1	3,5	2	2	4,6	2	3	5,5	3	4	6,9	3
1	2,6	3	2	3	4	3	3,6	5	4	4,5	6
1	0	3,9	2	0	5	3	0	6,2	4	0	7,6
1	-2,6	3	2	-3,1	4	3	-3,7	5	4	-7	3
1	-3,6	2	2	-4,7	2	3	-5,5	3	4	-4,7	6
1	-4,2	0	2	-5,1	0	3	-6,3	0	4	-7,6	0
1	-3,7	-2	2	-4,8	-2	3	-5,3	-3	4	-6,8	-3
1	-2,9	-3	2	-3,2	-4	3	-3,6	-5	4	-4	-6
1	0	-4	2	0	-5,1	3	0	-6,2	4	0	-7,5
1	2,8	-3	2	-3	-4	3	3,6	-5	4	4,1	-6
1	3,6	-2	2	-4,7	-2	3	5,5	-3	4	7	-3

1). График зависимости r)

2). График зависимости ln r)

3). График зависимости E = E (r).

4). График зависимости E = E (1/r).

5). Эквипотенциальные линии.

6). Расчет линейной плотности  на электроде.

7). Задача №1.

L = 1м

8). Задача №2.

r_>1> = 5см, r_>2> = 8см, l = 0,1м

Задание №3. Исследование электростатического поля вокруг проводников.

Таблица №5.

(x,y)	x	y	(x,y)	x	y	(x,y)	x	y	(x,y)	x	y
1	-3,6	8	2	0,8	8	3	5,9	9	4	7,2	3
1	-3,7	7	2	0,7	7	3	5,7	8	4	5,9	2
1	-3,7	6	2	0,5	6	3	5,2	7	4	5,4	1
1	-4	5	2	0,3	5	3	4,7	6	4	5,2	0
1	-4,7	4	2	0,2	4	3	4,4	5	4	5,4	-1
1	-5	3	2	0,1	3	3	4,1	4	4	6,2	-2
1	-5,2	2	2	0,6	-3	3	3,9	3	4	7,6	-3
1	-5,2	1	2	0,7	-4	3	3,8	2
1	-5	0	2	1	-5	3	4,1	-2
1	-4,9	-1	2	1,2	-6	3	4,4	-3
1	-4,7	-2	2	1,4	-7	3	4,8	-4
1	-4,4	-3	2	1,5	-8	3	5,5	-5
1	-4,2	-4	2	1,6	-9	3	6	-6
1	-4	-5				3	6,7	-7
1	-3,7	-6				3	7,3	-8
1	-3,6	-7				3	7,7	-9

1). Потенциал на электродах: пластинке и втулке постоянен, то есть они являются эквипотенциальными поверхностями. Внутри полости потенциал также постоянен.

Таблица 6.

(x,y)	x	y
1,97	-3	0
1,95	3	0
1,96	2	-1
1,95	-3	-2
1,95	0	0
1,96	-1	0

2). Распределение потенциала вдоль линии, охватывающей пластинку и расположенной на расстоянии

L = 3 мм от её края.

Таблица 7.

(x,y)	x	y
3,05	4	0
1,2	-4,2	0
1,92	0	-2,5
1,99	0	2
1,5	-3	2,1
1,31	-3	-3
2,23	2	-2
2,3	2	15

3). Эквипотенциальные линии.

4). Определение средней напряженности поля в нескольких точках вдоль силовой линии.

а).

б).

в).

5). , .

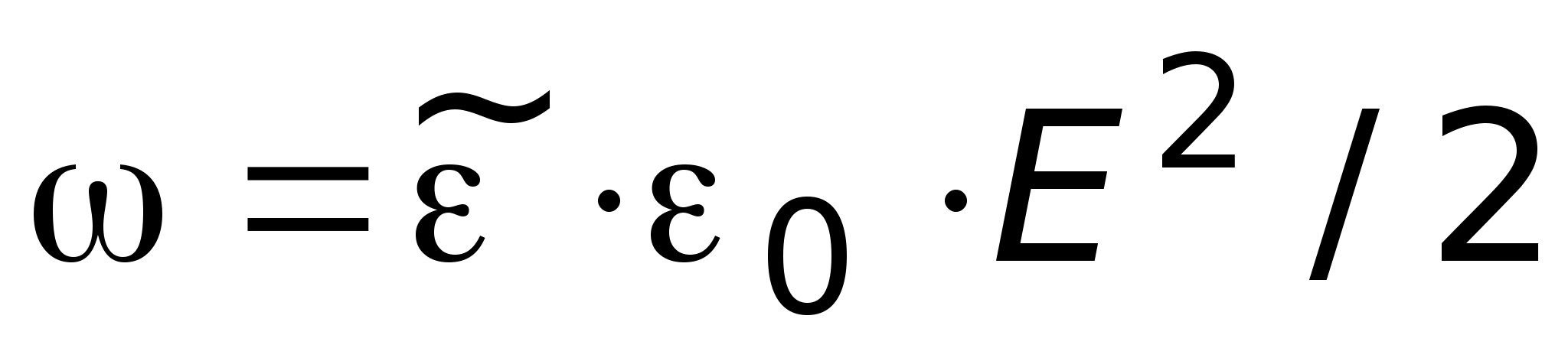Таблица 8.

X, см	y, см	, Кл/м²	E, В/м	, Дж/м³
4	0	3,2410^-9	366,6	5,9510^-7
-4,2	0	2,2110^-9	250	2,7710^-7
0	-5	8,8510^-11	10	4,4310^-10
0	2	1,1810^-10	13,3	7,8210^-10
-3	2,7	1,3310^-9	150	9,9610^-8
-3	-3	1,910^-9	213	2,0010^-7
2	-2	8,2310^-10	93	3,8010^-8
2	1,5	1,0210^-9	116	5,9510^-8

Вывод. В ходе работы получены картины силовых и эквипотенциальных линий плоском и цилиндрическом конденсаторах, а также вокруг проводника, помещенного в электростатическое поле. Установлено, что проводники и полости внутри них в электростатическом поле являются эквипотенциальными поверхностями.

В плоском конденсаторе поле сосредоточено между пластинами, оно является однородным, а потенциал изменяется линейно.

В цилиндрическом конденсаторе поле также сосредоточено между пластинами, его напряженность обратно пропорциональна расстоянию от оси конденсатора до точки измерения. Потенциал изменяется логарифмически.

Поток вектора напряженности поля через коаксиальные с электродами цилиндрические поверхности постоянен, что совпадает с теоретическими предположениями (теорема Гаусса).

TYPE=RANDOM FORMAT=PAGE>11

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике № 2-26.

Исследования магнитных полей в веществе.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: получение зависимостей индукции магнитного поля, намагниченности и магнитной проницаемости ферромагнетика от напряженности магнитного поля; наблюдение петли гистерезиса для различных ферромагнетиков; изучение магнитных цепей.

Практическая ценность работы: экспериментально изучаются важнейшие свойства ферромагнетиков наличных марок: НМ 3000, НМ 600, ППГ (прямоугольная петля гистерезиса).

Теоретическая часть.

Опыт 1. Снятие основной кривой намагничивания (ОКН) ферромагнетика.

Схема экспериментальной установки.

Cобрали цепь по схеме, показанной на РИС. 1. Для этого вольтметры V1 и V2 подключили к клеммам A-B и С-D - на верхней крышке макета соответственно. Переключатель К поставили в позицию 1. При этом исследовали трансформатор, кольцевой сердечник которого выполнен из ферита марки НМ 600, сопротивление R0=1 Ом. Таким образом, показания вольтметров численно равны: V1 - эффективному значению тока, текущего в текущей обмотке исследуемого трансформатора; V2 - эффективному значению ЭДС во вторичной обмотке. С помощью движка потенциометра R установили ток равный 0,5 А и плавно уменьшили его до нуля. Сняли показания вольтметров V1 и V2.

Данные для расчетов:

Используемые формулы:

Таблица № 1. Результаты расчетов.

№	U_>1>, В	_>2>, В	I_>m>, А	_>m>, В	H_>m>,А/м	В_>m>10²,Тл	J_>m>10^-3,А/м	10²
1	0,04	0,01	0,06	0,02	3,75	0,1	0,78	2,1
2	0,10	0,18	0,14	0,25	8,75	1,6	12,77	14,6
3	0,14	0,34	0,20	0,48	12,50	3,1	24,61	19,7
4	0,21	0,73	0,30	1,03	18,75	6,6	52,50	28,0
5	0,29	1,13	0,41	1,60	25,63	10,2	81,25	31,7
6	0,36	1,42	0,51	2,01	31,88	12,8	102,02	32,0
7	0,40	1,57	0,57	2,22	35,63	14,1	112,23	31,5
8	0,48	1,79	0,68	2,53	42,50	16,1	127,93	30,1
9	0,54	1,91	0,76	2,70	47,50	17,2	136,80	28,8
10	0,59	1,99	0,83	2,81	51,86	17,9	142,62	27,5
11	0,65	2,10	0,92	2,97	57,50	18,9	150,08	26,1
12	0,70	2,14	0,99	3,03	61,88	19,3	153,46	24,8
13	0,76	2,22	1,07	3,14	66,88	20,0	159,17	23,8
14	0,84	2,29	1,19	3,24	74,38	20,6	164,38	22,1
15	0,90	2,33	1,27	3,30	79,38	21,0	167,49	21,1
16	0,95	2,36	1,34	3,34	83,75	21,3	169,18	20,2
17	1,00	2,40	1,41	3,39	88,13	21,6	171,85	19,5

Опыт 2. Наблюдение петли гистерезиса.

Для изготовления постоянного магнита лучше использовать ППГ, так как его коэрцитивная сила больше, чем у НМ-3000, а поэтому его сложней размагнитить.

Для изготовления сердечника силового трансформатора лучше взять ферромагнетик с меньшей коэрцитивной силой, чтобы снизить затраты на его перемагничивание.

Опыт 3. Исследование сердечника с зазором.

Графики.

График зависимости В=В(Н) График зависимости =(Н)

График зависимости J=J(H)

Вывод: на этой работе мы получили зависимости индукции магнитного поля, намагниченности и магнитной проницаемости ферромагнетика от напряженности магнитного поля; наблюдали за петлей гистерезиса для различных ферромагнетиков; изучили магнитные цепи.

TYPE=RANDOM FORMAT=PAGE>4

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-27.

Исследование электрических колебаний.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: экспериментальное исследование собственных и вынужденных колебаний тока и напряжения на элементах в колебательном контуре; измерение параметров контура: индуктивности L, сопротивления R, добротности Q; исследование прохождения синусоидального тока через LCR-цепь.

Теоретическая часть.

Рисунок 1.

Уравнение, которому удовлетворяет ток I в колебательном контуре (рис.1) с подключенным к нему генератором синусоидальной ЭДС =_>0>cost имеет вид: (1)

где:

- коэффициент затухания.

- собственная круговая частота, R - сопротивление резистора, L - индуктивность катушки, С - емкость конденсатора, ; _>0>,  - амплитуда и круговая частота синусоидальной ЭДС.

Общее решение неоднородного линейного уравнения (1):

(2)

где: - круговая частота собственных затухающих колебаний тока.

и - начальные амплитуда и фаза собственных колебаний.

I_>0> - амплитуда вынужденных колебаний тока.

 - разность фаз между ЭДС и током.

(3)

(4)

- импеданс цепи.

- индуктивное сопротивление, - емкостное сопротивление.

Собственные колебания:

Если ²<_>0>², то есть R<2, то  - действительная и собственная частота колебаний представляет собой квазипериодический процесс с круговой частотой , , периодом , и затухающей амплитудой (рис 1).

За характерное время ( - время релаксации) амплитуда тока уменьшается в е раз, то есть эти колебания практически затухают.

- добротность контура.

Если ²_>0>², то  - мнимая частота, и колебания представляют собой апериодический процесс.

- критическое сопротивление.

Вынужденные колебания: c течением времени первый член в формуле (2) обращается в ноль и остается только второй, описывающий вынужденные колебания тока в контуре.

- амплитуда вынужденных колебаний напряжения на резисторе R.

При совпадении частоты ЭДС с собственной частотой контура (_>0>), амплитуды колебаний тока и напряжения U_>R0> на резисторе максимальны. Большой селективный отклик колебательной системы на периодическое внешнее воздействие называется резонансом.

Экспериментальная часть.

Результаты эксперимента:

№	f, кГц	_>ЭФ>, мВ	U_>R>_>ЭФ>, мВ	a	b	10^-4	
1	180	200	24	4,0	3,4	1,2	58
2	190	190	32	5,2	4,0	1,7	51
3	195	185	38	6,0	4,3	2,0	48
4	200	180	45	2,8	2,0	2,5	46
5	205	170	54	3,2	2,0	3,2	38
6	210	155	63	3,8	2,0	4,1	32
7	215	142	72	4,2	1,0	5,1	14
8	218	138	75	4,4	0,0	5,4	0
9	220	135	76	4,3	0,5	5,6	6
10	225	140	73	4,2	1,8	5,2	25
11	230	150	65	3,8	2,6	4,3	43
12	235	165	56	3,5	2,6	3,4	48
13	240	175	48	3,0	2,7	2,7	64
14	250	180	36	2,2	2,1	2,0	76
15	260	195	28	1,8	1,7	1,4	90
16	270	200	22	1,6	1,6	1,1	90
17	280	200	18	1,3	1,3	0,9	90
18	290	200	15	1,0	1,0	0,8	90
19	300	205	12	1,0	1,0	0,6	90

Задание 1. Исследование зависимости амплитуды вынужденных колебаний от частоты (резонансная кривая).

Исходные данные:U_>вых>=200 мВ, _>ЭФ>=200 мВ. f[180;300] кГц.

Расчеты необходимых величин:

f _>0>= 220 кГц - частота резонанса.

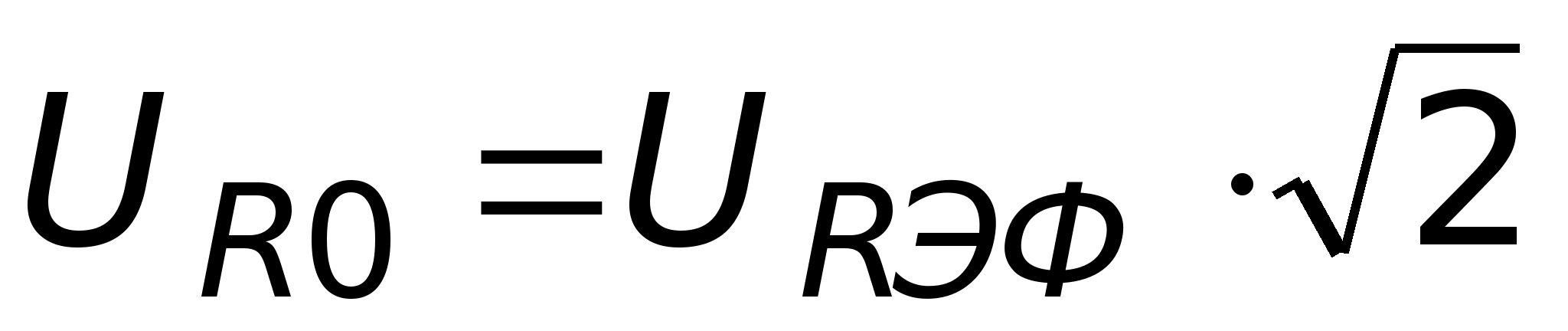
Строим график зависимости

,где _>1> и _>2>- значения частот на уровне

Из экспериментального графика видно, что он по своей форме совпадает с графиком, полученным теоретически из формулы:

Исследование зависимости разности фаз между ЭДС и током в контуре.

Из экспериментального графика =F(f) получаем: f _>0>=218 кГц.

Сравнивая полученные результаты с результатами из предыдущего опыта видно, что различие в величинах _>0> и L незначительны.

Можно сделать вывод, что при резонансной частоте X_>L>X_>C> и величина импеданса цепи минимальна.

Рисунок 2.

Задание 2.Исследование собственных электрических колебаний.

На данном рисунке представлена форма затухающих колебаний напряжения U_>C> на конденсаторе, полученная с помощью осциллографа. Изображение совпадает с теоретическим графиком.

Из графика: Т=22,410^-6с - период колебаний.

=23,810^-6с - время релаксации.

Задание 3. Исследование прохождения синусоидального тока через LCR - цепь

f,кГц	U_>ВЫХЭФ>,10^-3В	U_>0ВЫХ>,10^-3В
150	41	56
160	33	46
170	27	38
180	22	31
190	14	19
200	9	13
205	6	8
210	3	4
215	1	2
218	0	0
220	0	0
225	1	2
230	2	3
235	4	6
240	5	7
250	9	13
260	13	18
270	17	24
280	22	31
290	25	35
300	30	42

Построим график U_>0>_>ВЫХ> =F(f). Резонансная частота из графика равна: f_>0> =220 кГц.

При этом импеданс цепи является бесконечно большим и ток в цепи не протекает.

R=50 Ом, f=2 МГц.

Погрешности измерений.

Задание 1.

1) Погрешность f_>0> : f определяли на частотомере

2) Погрешность L:

3) Погрешность Q:

4) Погрешность R:

_>R> =5% R=3,1Ом

5) Погрешность X_>L>:

6) Погрешность X_>C>:

7) Погрешность :

Вывод: на этой работе мы экспериментально исследовали собственные и вынужденные колебания тока и напряжения на элементах в колебательном контуре; измерили параметры контура: индуктивности L, сопротивления R, добротности Q; исследовали прохождение синусоидального тока через LCR-цепь.

TYPE=RANDOM FORMAT=PAGE>8

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-28.

Экспериментальные исследования электромагнитной индукции.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: экспериментальное исследование зависимости ЭДС индукции от ориентации контура в магнитном поле, измерение взаимной индуктивности двух индуктивно связанных катушек, индуктивности одной из них, исследование зависимости поля от времени в RL-цепи при переходных процессах.

Теоретическая часть.

Схема экспериментальной установки.

Опыт 1. Исследование электромагнитной индукции, взаимоиндукции, самоиндукции.

f=200 Гц, U=8 В - на генераторе, U_>v1>_>>= 8 В - эффективное.

(угол между катушками)=0.

Снимаем значения с L_>1> и L_>2>:

U (L_>1>)=0,19 В, U (L_>2>)=0,04 В, на осциллографе получаем:

Развертка 2 мс/см.

U_>m>=

Гц.

Опыт 2. Исследование зависимости ЭДС индукции (взаимоиндукции) от частоты (скорости) изменения магнитного поля.

F[200, 2000] Гц; f=200 Гц; U_{>эффект}>=8 В.

;

f,Гц	200	400	600	800	1000	1200	1400	1600	1800	2000
_>2>,B	0,04	0,10	0,15	0,20	0,27	0,32	0,37	0,43	0,49	0,54

_>21>(f=400 Гц)=;

Расчет погрешности:

Опыт 3. Исследование зависимости ЭДС индукции от ориентации контура в магнитном поле.

f=2000 Гц; [0;180];  = 15;

	0	15	30	45	60	75	90	105	120	135	150	165	180
_>2>_>(ЭФ),>В	0,55	0,51	0,43	0,33	0,23	0,08	0	0,08	0,20	0,30	0,42	0,50	0,55
_>2>_>(ТЕОР),>В	0,49	0,47	0,42	0,35	0,24	0,12	0	-0,12	-0,24	-0,35	-0,42	-0,47	-0,49

Опыт 4. Исследование зависимости ЭДС самоиндукции от частоты синусоидального сигнала.

f[500;2000] Гц; f=250 Гц, R_>1>=16000 Ом.

f,Гц	500	750	1000	1250	1500	1750	2000
_>1>_>ЭФ>,В	0,50	0,74	0,99	1,22	1,49	1,73	1,98
X_>L>,Ом	707,34	1046,86	1400,53	1725,91	2107,87	2447,39	2801,06

Расчет погрешностей:

Опыт 5. Исследование переходных процессов в LR - цепи.

_>U>=1 мс, f=100 Гц, U_>0>=3 B.

Вывод: Экспериментально исследовали зависимость ЭДС индукции от ориентации контура в магнитном поле, измерили взаимную индуктивность двух индуктивно связанных катушек и нашли индуктивность одной из них. Исследовали зависимость тока от времени в LR-цепи при переходных процессах.

TYPE=RANDOM FORMAT=PAGE>4

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-30.

Экспериментальные исследования диэлектрических

свойств материалов.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: определение диэлектрической проницаемости и поляризационных характеристик различных диэлектриков, изучение электрических свойств полей, в них исследование линейности и дисперсии диэлектрических свойств материалов.

Теоретическая часть:

Схема экспериментальной установки.

В эксперименте используются следующие приборы: два вольтметра PV1 (стрелочный) и PV2 (цифровой), генератор сигналов низкочастотный, макет-схема, на которой установлен резистор R=120 Ом, конденсатор, состоящий из набора пластин различных диэлектриков (толщиной d=2 мм).

Собираем схему, изображенную на РИС. 1. Ставим переключатель SA в положение 1. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f=60 кГц и напряжением U=5 В, затем по вольтметру PV1 установить напряжение U1=5 В. Далее, вращая подвижную пластину, измеряем напряжение U2 для конденсатора без диэлектрика и 4-x конденсаторов с диэлектриками одинаковой толщины. При этом напряжение U1 поддерживаем постоянным.

Напряженность поля между пластинами в вакууме Е_>0> вычисляется по формуле: где При внесении пластины в это поле диэлектрик поляризуется и на его поверхности появляются связанные заряды с поверхностной плотностью . Эти заряды создают в диэлектрике поле , направленное против внешнего поля , и имеет величину: . Результирующее поле: . В электрическом поле вектор поляризации:, где  - диэлектрическая восприимчивость вещества. Связь модуля вектора поляризации с плотностью связанных зарядов: . относительная диэлектрическая проницаемость диэлектрика. Вектор электрической индукции . Этот вектор определяется только свободными зарядами и вычисляется как . В рассматриваемой задаче на поверхности диэлектрика их нет. Вектор D связан с вектором Е следующим соотношением .

Экспериментальная часть:

В данной работе используются формулы: , где S - площадь пластины конденсатора, d - расстояние между ними. Диэлектрическая проницаемость материала: . Для емкости конденсатора имеем: , где U_>1> - напряжение на RC цепи, U_>2> - напряжение на сопротивлении R, f - частота переменного сигнала. В плоском конденсаторе напряженность связана с напряжением U_>1> как:

Опыт №1. Измерение диэлектрической проницаемости и характеристик поляризации материалов.

U_>1>= 5В, R=120Ом, f=60 кГц, d=0,002м.

Материал	U_>2>, мВ
Воздух	40
Стеклотекстолит	97
Фторопласт	61
Гетинакс	89
Оргстекло	76

_>> С_>В>=176 пкФ; С_>СТ>=429 пкФ;

С_>ФП>=270 пкФ; С_>ГН>=393 пкФ; С_>ОС>=336 пкФ;

; ;

Для гетинакса подсчитаем:

;

; ;

;

Расчет погрешностей:

; ; ;

;

(так как ).

;

Опыт № 2. Исследование зависимости  = f(E).

R=120Ом, f=60 кГц, d=0,002м.

U_>1>, В	U_>2>, В (воздух)	U_>2>, В (гетинакс)	С_>0>, пкФ	С, пкФ	Е, В/м	
1	0,009	0,019	200	420	500	2,10
2	0,016	0,036	177	398	1000	2,24
3	0,025	0,052	184	387	1500	2,09
4	0,031	0,070	171	384	2000	2,26
5	0,039	0,086	172	380	2500	2,21

График зависимости  = f(E) - приблизительно прямая, так как диэлектрическая проницаемость не зависит от внешнего поля.

Опыт № 3. Исследование зависимости диэлектрической проницаемости среды от частоты внешнего поля.

U_>1>= 5В, R=120Ом.

f, кГц	U_>2>, В (воздух)	U_>2>, В (гетинакс)	Х_>С>, кОм (гетинакс)	С_>0>, пкФ	С, пкФ	
20	0,015	0,030	20,0	199	398	2,00
40	0,029	0,059	10,2	192	391	2,04
60	0,041	0,089	6,7	181	393	2,07
80	0,051	0,115	5,2	169	381	2,25
100	0,068	0,146	4,1	180	387	2,15
120	0,078	0,171	3,5	172	378	2,18
140	0,090	0,197	3,0	181	373	2,18
160	0,101	0,223	2,7	167	370	2,21
180	0,115	0,254	2,4	169	374	2,21
200	0,125	0,281	2,2	166	372	2,24

По графику зависимости  = F(f) видно, что диэлектрическая проницаемость среды не зависит от частоты внешнего поля. График зависимости Х_>С>=F(1/f) подтверждает, что емкостное сопротивление зависит от 1/f прямо пропорционально.

Опыт № 4. Исследование зависимости емкости конденсатора от угла перекрытия диэлектрика верхней пластиной.

U_>1>= 5В, R=120Ом, f=60 кГц, d=0,002м, r=0,06м, n=18.

,⁰	U_>2>,В	С, пкФ	С_>теор>, пкФ
0	0,039	172	150
10	0,048	212	181
20	0,056	248	212
30	0,063	279	243
40	0,072	318	273
50	0,080	354	304
60	0,089	393	335

Опыт № 5. Измерение толщины диэлектрической прокладки.

U_>1>= 5В, R=120Ом, f=60 кГц.

Схема конденсатора с частичным заполнением диэлектриком.

U_>2>(стеклотекстолит тонкий)=0,051В,

U_>2>(стеклотекстолит толстый)=0,093В,

U_>2>(воздух)=0,039В.

С_>0>=172пкФ - без диэлектрика;

С_>1> = 411пкФ - стеклотекстолит толстый;

С_>1>= 225пкФ - стеклотекстолит тонкий.

; ; ; ;

; ; ;

Вывод: На этой работе мы определили диэлектрическую проницаемость и поляризационные характеристики различных диэлектриков, изучили электрические свойства полей, в них исследовали линейность и дисперсность диэлектрических свойств материалов.

TYPE=RANDOM FORMAT=PAGE>6