Гидрогазодинамика
Министерство образования и науки Украины
Национальная Металлургическая Академия Украины
Кафедра промышленной теплоэнергетики
КУРСОВАЯ РАБОТА
по дисциплине «Гидрогазодинамика»
Разработал студент гр. ПТЭ-02-1 Зеркаль К.Г.
Руководитель работы Мануйленко А.А.
Курсовая работа защищена с оценкой
г. Днепропетровск
2004г.
Задание на курсовую работу
Рассчитать и выбрать оптимальный диаметр трубопровода для транспортировки воды от насоса Н до промышленной установки ПУ. Определить толщину стенок труб, необходимые пьезометрические напоры у насоса и на участках трубопроводов. Построить напорную характеристику трубопровода и график пьезометрических напоров для приведенных условий:
максимальный
часовой расход воды
 ;
;
согласно схеме установки (рис. 1.1.) длины участков трубопровода:
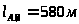
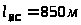

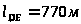
геометрические отметки точек:






местные сопротивления:
-колен с закруглением под
 -
6 шт.
-
6 шт.
-задвижек Дудло: со степенью открытия 5/8 - на участке АВ – 1 шт.,
на участке ВС – 1шт.;
со степенью открытия 7/8 - на участке СD – 1 шт.,
на участке DE – 1 шт.;

Рис. 1.1. Схема водоснабжения ПУ:
Н – насос, ПУ – промышленные установки
Напор у
потребителя, независимый от потерь
напора в трубопроводе ( свободный
напор) -
 ;
;
число часов
работы установки в сутки -
 ;
;
число дней
работы установки в году -
 дней.
дней.
Теоретическая часть
По способам гидравлического расчета трубопроводы делят на две группы: простые и сложные. Простым называют трубопровод, состоящий из одной линии труб, хотя бы и различного диаметра, но с одним же расходом по пути; всякие другие трубопроводы называют сложными.
При гидравлическом расчете трубопровода существенную роль играют местные гидравлические сопротивления. Они вызываются фасонными частями, арматурой и другим оборудованием трубопроводных сетей, которые приводят к изменению величины и направления скорости движения жидкости на отдельных участках трубопровода (при расширении или сужении потока, в результате его поворота, при протекании потока через диафрагмы, задвижки и т.д.), что всегда связано с появлением дополнительных потерь напора. В водопроводных магистральных трубах потери напора на местные сопротивления обычно весьма не велики (не более 10-20% потерь напора на трение).
Основные виды местных потерь напора можно условно разделить на следующие группы:
- потери, связанные с изменением сечения потока;
- потери, вызванные изменением направления потока. Сюда относят различного рода колена, угольники, отводы, используемые на трубопроводах;
- потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы, дроссель-клапаны и т.д.);
- потери, связанные с отделением одной части потока от другой или слиянием двух потоков в один общий. Сюда относятся, например, тройники, крестовины и отверстия в боковых стенках трубопроводов при наличии транзитного расхода.
3. Определение оптимального диаметра трубопровода.
3.1. Для определения оптимального диаметра трубопровода задаемся рядом значений скорости движения жидкости (от 0,5 до 3,5 м/с) и вычисляем расчетные диаметры труб по формуле:
 ,
,

Результаты расчета для всех принятых значений скорости приведены в таблице 3.1.
Таблица 3.1.
Диаметры труб для различных значений скорости движении жидкости
-
Скорость движения
жидкости, м/с
0,5
1,0
1,5
2,0
2,5
3,0
3,5
Диаметр труб,
 ,
м
,
м0,297
0,210
0,172
0,149
0,133
0,121
0,112
3.2. Для каждого расчетного диаметра
труб
 вычисляем приведенные затраты на один
год по формуле:
вычисляем приведенные затраты на один
год по формуле:
 ,
,
где
 - эксплуатационные затраты, включающие
амортизационные отчисления,
- эксплуатационные затраты, включающие
амортизационные отчисления,
стоимость электроэнергии, обслуживания, текущих расходов и др., грн.;
 -
капитальные затраты, грн.;
-
капитальные затраты, грн.;
0,2 – нормативный коэффициент.
Стоимость обслуживания и текущих расходов примерно одинакова для труб разного диаметра. Поэтому эксплутационные затраты принимаем равными сумме амортизационных отчислений и стоимости электроэнергии:
 .
.
Капитальные затраты включают стоимость
труб
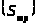 и стоимость монтажа трубопровода
и стоимость монтажа трубопровода
 :
:
 .
.
Примерная цена 1 т труб принимается равной 1300 грн. Тогда стоимость будет равна:
 ,
,
где
 -
масса труб, т.
-
масса труб, т.
Масса труб определяется по формуле:
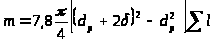 ,
,
где
 -
принятая толщина стенки трубы;
-
принятая толщина стенки трубы;
 - суммарная длина всех участков
трубопровода,
- суммарная длина всех участков
трубопровода,
 ;
;
7,8 – плотность стали, т/ .
.
Стоимость монтажа трубопроводов принимаются равной, примерно 30% стоимости труб:
 ,
грн.
,
грн.
Амортизационные отчисления для каждого значения диаметра трубопровода вычисляются по формуле:
 ,
,
где
 лет – срок службы труб.
лет – срок службы труб.
Стоимость электроэнергии определяется по формуле:
 ,
,
где 0,16 – стоимость 1 кВт·ч электроэнергии, грн.;
 -
мощность потока, кВт.
-
мощность потока, кВт.
Мощность потока вычисляется по формуле:
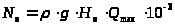 ,
,
где
 -
напор, создаваемый насосом,
-
напор, создаваемый насосом,
 ,
,
 ,
,
где
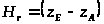 - геометрическая высота,
- геометрическая высота,
 ;
;
 - сопротивление трубопровода,
- сопротивление трубопровода,
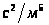 ,
равное
,
равное
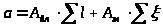 ,
,
где
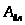 -
удельное сопротивление по длине
трубопровода,
-
удельное сопротивление по длине
трубопровода,
 ;
;
 -
удельное местное сопротивление,
-
удельное местное сопротивление,
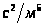 ;
;
 -
сумма коэффициентов местных сопротивлений.
-
сумма коэффициентов местных сопротивлений.
3.3. Расчет численных показателей для
определения приведенных затрат
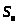 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 ):
):
Определение массы труб в тоннах:
 т.
т.
3.3.2. Определение стоимости труб:
 грн.
грн.
3.3.3. Определение стоимости монтажа трубопровода:
 грн.
грн.
3.3.4. Определение капитальных затрат:
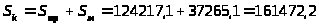 грн.
грн.
3.3.5. Определение амортизационных отчислений:
 грн.
грн.
3.3.6. Определение коэффициента гидравлического трения по формуле Прандтля-Никурадзе:
 ,
,
где
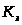 -
эквивалентная шероховатость труб
(принимаем 0,4 мм).
-
эквивалентная шероховатость труб
(принимаем 0,4 мм).
3.3.7. Определение удельного сопротивления по длине:
 .
.
3.3.8. Определение удельного местного сопротивления:
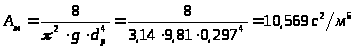 .
.
3.3.9. Определение сопротивления трубопровода:
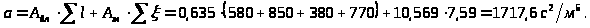

3.3.10. Определение максимального напора, создаваемого насосом:

3.3.11. Определение мощности потока:
 кВт.
кВт.
3.3.12. Определение стоимости электроэнергии:
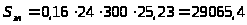 грн.
грн.
2.3.13. Определение эксплуатационных затрат:
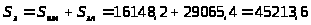 грн.
грн.
3.3.14. Определение приведенных затрат в расчете на год:
 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
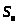 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 ):
):
3.3.1.
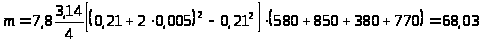 т
т
3.3.2.
 грн.
грн.
3.3.3.
 грн.
грн.
3.3.4.
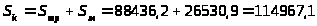 грн.
грн.
3.3.5.
 грн.
грн.
3.3.6.
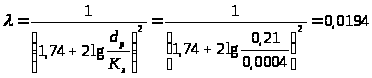
3.3.7.

3.3.8.

3.3.9.

3.3.10.

3.3.11.
 кВт.
кВт.
3.3.12.
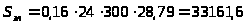 грн.
грн.
3.3.13.
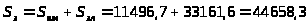 грн.
грн.
3.3.14.
 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
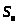 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 )
)
3.3.1.
 т.
т.
3.3.2.
 грн.
грн.
3.3.3.
 грн.
грн.
3.3.4.
 грн.
грн.
3.3.5.
 грн.
грн.
3.3.6.

3.3.7.

3.3.8.

3.3.9.

3.3.10.
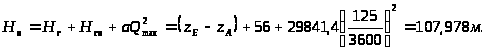
3.3.11.
 кВт
кВт
3.3.12.
 грн.
грн.
3.3.13.
 грн.
грн.
3.3.14.
 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
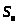 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 ):
):
3.3.1.
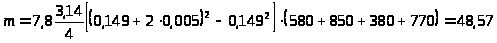 т.
т.
3.3.2.
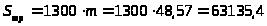 грн.
грн.
3.3.3.
 грн.
грн.
3.3.4.
 грн.
грн.
3.3.5.
 грн.
грн.
3.3.6.

3.3.7.

3.3.8.

3.3.9.

3.3.10.
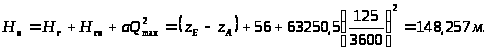
3.3.11.
 кВт
кВт
3.3.12.
 грн.
грн.
3.3.13.
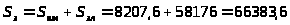 грн.
грн.
3.3.14.
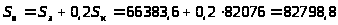 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
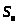 для трубопровода
для трубопровода
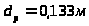 (при скорости движения
(при скорости движения
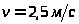 ):
):
3.3.1.
 т.
т.
3.3.2.
 грн.
грн.
3.3.3.
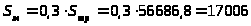 грн.
грн.
3.3.4.
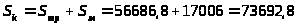 грн.
грн.
3.3.5.
 грн.
грн.
3.3.6.
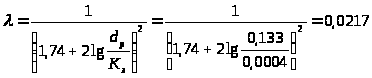
3.3.7.

3.3.8.
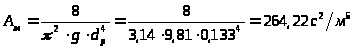
3.3.9.

3.3.10.
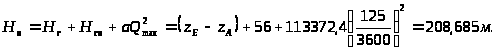
3.3.11.
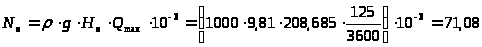 кВт
кВт
3.3.12.
 грн.
грн.
3.3.13.
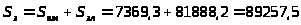 грн.
грн.
3.3.14.
 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
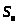 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 ):
):
3.3.1.
 т.
т.
3.3.2.
 грн.
грн.
3.3.3.
 грн.
грн.
3.3.4.
 грн.
грн.
3.3.5.
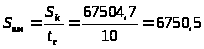 грн.
грн.
3.3.6.

3.3.7.

3.3.8.

3.3.9.
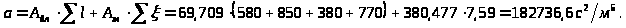
3.3.10.
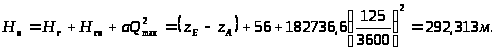
3.3.11.
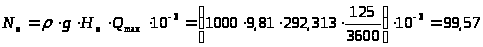 кВт
кВт
3.3.12.
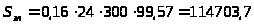 грн.
грн.
3.3.13.
 грн.
грн.
3.3.14.
 грн.
грн.
Расчет численных показателей для
определения приведенных затрат
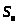 для трубопровода
для трубопровода
 (при скорости движения
(при скорости движения
 ):
):
3.3.1.
 т.
т.
3.3.2.
 грн.
грн.
3.3.3.
 грн.
грн.
3.3.4.
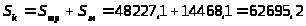 грн.
грн.
3.3.5.
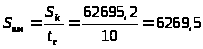 грн.
грн.
3.3.6.

3.3.7.
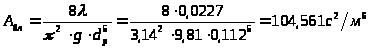
3.3.8.

3.3.9.

3.3.10.

3.3.11.
 кВт
кВт
3.3.12.
 грн.
грн.
3.3.13.
 грн.
грн.
3.3.14.
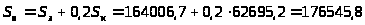 грн.
грн.
Таблица 3.2.
Варианты значений скорости движения жидкости, диаметра
труб и соответствующих им затрат
|
№ ва- риан-та |
Скорость движения жидкости
|
Диаметр труб,
|
Затраты, грн. |
||||
|
|
|
|
|
|
|||
|
1 |
0,5 |
0,297 |
161472 |
16148,2 |
29065,4 |
45213,6 |
77510,0 |
|
2 |
1,0 |
0,210 |
114967 |
11496,7 |
33161,6 |
44658,3 |
67651,8 |
|
3 |
1,5 |
0,172 |
94360 |
9436,0 |
42370,5 |
51806,5 |
70678,6 |
|
4 |
2,0 |
0,149 |
82076 |
8207,6 |
58176,0 |
66383,6 |
82798,8 |
|
5 |
2,5 |
0,133 |
73693 |
7369,3 |
81888,2 |
89257,5 |
103996,0 |
|
6 |
3,0 |
0,121 |
67505 |
6750,5 |
114703,7 |
121454,2 |
134955,1 |
|
7 |
3,5 |
0,112 |
62695 |
6269,5 |
157737,2 |
164006,7 |
176545,8 |
По данным таблицы 3.2. строим графические
зависимости
 ,
,
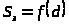 и
и
 ,
которые приведены на рис. 3.1.
,
которые приведены на рис. 3.1.
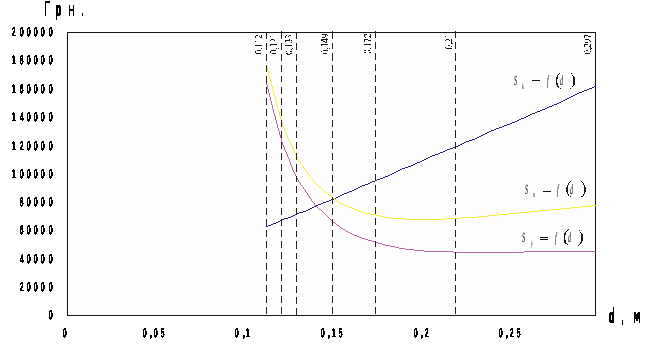
Рис. 3.1. Графическое определение оптимального диаметра трубопровода
Минимальному значению приведенных
затрат
 соответствует оптимальный диаметр
труб. Как видно из графических зависимостей,
оптимальный диаметр трубопровода
находится в пределах
соответствует оптимальный диаметр
труб. Как видно из графических зависимостей,
оптимальный диаметр трубопровода
находится в пределах
 .
.
К установке принимаем стандартный
диаметр, близкий к расчётному диаметру.
Для стальных бесшовных горячедеформированных
труб (ГОСТ 8732-78) ближайший диаметр трубы
(внутренний)
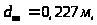
 толщина стенки
толщина стенки


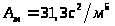 .
.
3.4. Проверка толщины труб по максимальному пьезометрическому напору.
3.4.1. Максимальный пьезометрический напор имеет место в точке А трубопровода и равен:

где
 .
.
3.4.2. Определение сопротивления трубопровода для выбранного стандартного диа- метра труб:

 м в.ст.
м в.ст.
3.4.3. Определение максимального давления в точке А:

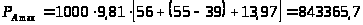
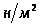 .
.
принимаем
 МПа.
МПа.
3.4.4. Минимально допустимое значение толщины труб определяем по формуле:
 ,
м,
,
м,
где
 -
допустимое напряжение на растяжение
для материала труб, МПа (для стальных
труб
-
допустимое напряжение на растяжение
для материала труб, МПа (для стальных
труб
 =380
МПа);
=380
МПа);

Таким образом, принятые к установке
трубы имеют толщину стенки
 ,
превышающую допустимую
,
превышающую допустимую
 .
.
Определение пьезометрического и полного напоров
в конечных точках трубопровода А и Е
4.1.1. Пьезометрический напор в точке А:

4.1.2.
Полный напор в точке А:
 ,
,
где
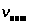 -
оптимальная скорость движения жидкости,
равная
-
оптимальная скорость движения жидкости,
равная


4.1.3. Пьезометрический напор в точке Е равен свободному напору:

4.1.4. Полный напор в точке Е:

По исходным данным геометрических
отметок точек А, В, С, D, Е ( ,
,
 ,
,
 ,
,
 ,
,
 ) и протяженности участков между этими
точками откладываем их значение в
определенном масштабе от плоскости
сравнения (0-0) и строим линию геометрических
напоров. Аналогично, откладывая
значения полных и пьезометрических
напоров в точках А и Е трубопровода и
соединяя их вершины прямыми линиями,
получим линии полного и статического
напоров. Пьезометрические напоры в
точках В, С, D определяются графическим
методом как разность между статическим
и геометрическим напорами в
соответствующих точках. Изменение
напоров по длине трубопроводов
представлено на рис 4.1.
) и протяженности участков между этими
точками откладываем их значение в
определенном масштабе от плоскости
сравнения (0-0) и строим линию геометрических
напоров. Аналогично, откладывая
значения полных и пьезометрических
напоров в точках А и Е трубопровода и
соединяя их вершины прямыми линиями,
получим линии полного и статического
напоров. Пьезометрические напоры в
точках В, С, D определяются графическим
методом как разность между статическим
и геометрическим напорами в
соответствующих точках. Изменение
напоров по длине трубопроводов
представлено на рис 4.1.

Рис. 4.1. График изменения напоров по длине трубопровода
Построение напорной характеристики трубопровода
Уравнение напорной характеристики рассматриваемого трубопровода имеет вид:

где
 - геометрическая высота, м;
- геометрическая высота, м;
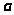 - сопротивление трубопровода,
- сопротивление трубопровода,
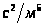 .
.
Задаваясь 5-6 произвольными значениями расхода жидкости Q от 0 до заданного максимального значения, вычисляем Н и строим характеристику трубопровода.
В табл. 5.1. приведены значения Н при различных расходах жидкости.
Таблица 5.1.
|
|
0 |
30 |
50 |
80 |
100 |
125 |
|
|
72,0 |
72,8 |
75,0 |
80,8 |
89,7 |
103,7 |
Напорная характеристика трубопровода представлена на рис 5.1.

Рис 5.1. Напорная характеристика трубопровода
Вывод
При выполнении курсовой работы по выбору
оптимального диаметра трубопровода
для транспортирования воды на основе
гидравлического и технико-экономического
расчетов, построению графика напоров
по длине трубопровода и его напорной
характеристики, был выбран диаметр
(внутренний) равный
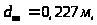
 толщина стенки
толщина стенки


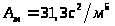 .
При этом проведена проверка принятой
толщины стенок труб по максимальному
напору, который составил
.
При этом проведена проверка принятой
толщины стенок труб по максимальному
напору, который составил
 МПа.
Также определены пьезометрический и
полный напоры в конечных точках
трубопровода А и Е равных:
МПа.
Также определены пьезометрический и
полный напоры в конечных точках
трубопровода А и Е равных:

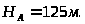 ;
;


7. Литература
|
1. |
Альтщуль А.Д., Животовский Л.С., Иванов Л.П. Гидравлика и аэродинамика. М.: Стройиздат, 1987.- 410 с. |
|
2. |
Чугаев Р.Р. Гидравлика. Л.: Энергоиздат, 1982.- 672с. |
|
3. |
Альтщуль А.Д., Калицун В.И., и др. Примеры расчетов по гидравлике. М.: Стройиздат, 1976.- 256 с. |
|
4. |
Большаков В.А., Константинов Ю.М. и др. Справочник по гидравлике. К.: Вища школа, 1984.-224 с. |
|
5. |
Борисов С.Н., Даточный В.В. Гидравлический расчет газопроводов. М.: Энергия, 1972. |
 ,
,

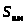


 ,
,

 ,
,