Изучение механизмов металлорежущих станков

Министерство образования РФ

Тверской Государственный Технический Университет

Кафедра "Металлорежущие станки и инструменты"

Изучение механизмов металорежущих станков

Методические указания

к лабораторной работе по курсу "Металорежущие станки"

для студентов специальности 1201- "Технология машиностроения"

Тверь 2001

В методических указаниях к лабораторной работе "Изучение механизмов металлорежущих станков" изложены основные понятия и положения по систематике и функциональному назначению механизмов, входящих в кинематические цепи станков.

Лабораторная работа предназначена для изучения курса "Металлорежущие станки". Методические указания (второе издание) рекомендованы к применению на заседании кафедры "Металлорежущие станки и инструменты" (протокол №2 от 02.11.2000)

Автор: Клюйко Э.В.

СОДЕРЖАНИЕ

Стр.

    1. Цель работы............................................................................................

3

    2. Порядок проведения работы.................................................................

3

    3. Назначение и состав механиз­мов.........................................................

3

    4. Структурные свойства механизмов....................................................

8

    5. Функциональные свойства механизмов .............................................

11

    6. Примеры анализа механизмов..............................................................

13

    7. Индивидуальные задания по анализу механизмов.............................

17

    8. Контрольные вопросы...........................................................................

18

9. Библиографический список .................................................................

18

10. Приложение ............................................... .........................................

19

1. ЦЕЛЬ РАБОТЫ

    Изучить основные свойства передаточных механизмов станков.

    Приобрести определенные навыки в анализе структурных и функциональных свойств механизмов станков.

2. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ

    Ознакомиться с основными свойствими передаточные меха­низмов станков,

    Изучить методику анализа структурных и функциональных свойств механизмов станков.

    По индивидуальному заданию (альбом, макеты механизмов и Приложение на стр 20…22) проанализировать основные свойства и характеристики станочных механизмов.

3. НАЗНАЧЕНИЕ И СОСТАВ МЕХАНИЗМОВ

В металлорежущих станках все многообразие механизмов, пред­назначенных для создания определенных движений, подразделяют на двигательные (приводные), передаточные и исполнительные (формообразующие). Наиболее многочисленные из них передаточные [1,4]. Отличаются они друг от друга по назначению (реверсирующие, суммирующие, корректирующие и др.), по конструкции (шарнирно-рычажные, кулачковые, зубчатые, винтовые и др.) по исполнению опор и зацеплении (передачи скольжения, передачи качения и т.д.).

Механизмы представляют собой (рис. 1) подвижные соединения несколь­ких тел, предназначенных для преобразования движений. Имеется в виду как замена одного вида движения на другое (рис. 1а, 1в), так и передача движения с количественным изменением его параметров (рис. 1г). В качестве основных характеристик движения при настройке механизмов станков, используют пять параметров: траекторию, путь (угловой или линейный), скорость, направление и положение входного или выходного звеньев [2,4].

Передаточные механизмы состоят из звеньев, образующих на стыках между собой кинематические пары (j;k). Звено j или k - это одно ли несколько деталей, жестко (без относительных смещений) связанных между собой. Например, на рис. 1г звено 3 образуют вал и закрепленные на нем шестерни z>4> и z>5>. Звенья могут быть твердыми и деформируемыми, подвижными и неподвижными, ведущими и ведомыми. Основные типы подвижных звеньев, применяемые в станках приведены в таблице 1 и в альбоме ([3], стр.63). Кроме концевых подвижных звеньев в механизмах могут быть промежуточные подвижные звенья и всегда есть одно неподвижное звено, называемое основанием или стойкой. Поэтому можно сказать, что механизм - это многозвенная подвижная передаточная система с одним неподвижным звеном. На рис. 1а показан четырехзвенный (с учетом стойки) механизм привода ползуна 3 долбежного станка. Для компенсации перекосов в шарнирах и смягчения ударной нагрузки в паре (1;2) введена избыточная подвижность (>12>=2 вместо >12>=1). Для придания повышенной жесткости одинаковым рычагам 1 и 3 (рис 1б) к ним в пятизвенном механизме зажимного приспособления присоединен дополнительный шатун 4. На рис 1б показан простейший трехзвенный пространственный механизм с дисковым кулачком 1 и качающимся толкателем 2, применяемый в приводе подачи шпиндельной бабки токарного автомата (кулачок вращается параллельно плоскости yz, а толкатель качается в плоскости ху). Сложный восьмизвенный двухпоточный механизм привода стола продольно-фрезерного станка (рис. 1г) позволяет уменьшить зазоры в косозубых зубчатых передачах и распределить силовую нагрузку между приводными валами 4 и 6 в соответствии с их жесткостью.

Рис.1. Примеры передаточных механизмов:

а) – кривошипно-ползунный механизм с избыточной подвижностью в паре (1;2);

б) – шарнирно рычажный механизм с избыточным звеном 4;

в) – кулачково-рычажный пространственный механизм;

г) – зубчатый замкнутый механизм привода стола

Таблица 1

Основные типы звеньев в механизмах

№

Тип звена

Назначение

Условное обозначение

1

Стойка

(основание)

неподвижное звено

2

Кривошип

вращательное звено

3

Коромысло (рычаг)

качательное звено

4

Кулачок

вращательное или по­ступательное звено с плоским или пространственным криволинейным профилем

5

Шестерня

вращательное звено в виде колеса с зубчатым венцом

6

Рейка

поступательное звено в виде стержня с зубчатой нарезкой

7

Шатун

Звено, совершающее

плоское или пространственное движение

8

Ползун (толкатель)

Звено, совершающее поступательное движение

9

Кулиса

Звено, совершающее любое движение и не­сущее направляющие плоскости для другого звена

10

Винт

(ходовой винт)

Звено в виде вала с винтовой на­резкой для создания вращательного поступательного или винтового движения

11

Гайка

а– простая

б– маточная

в– шариковая

звено, охватывающее в зацеплении ходовой винт для передачи движения

а б в

Кинематическая пара (j;k) представляет собой подвижное соединение двух звеньев j и k. Подвижное соединение может быть выполнено по поверхностям (в низших парах) и по линиям или точкам (в высших парах). Подвижный контакт в парах может поддерживаться геометрическим, силовым или кинематическим замыканием. В первом случае используют ограничение (охват) одних поверхностей другими (рис. 1а, направляющая О для ползуна 3), во втором – применяют пружины (рис 1в), груз или гидроприжим, в третьем – используют дополнительную кинематическую цепь механизмов (рис. 1г). Конструктивно кинематическая пара обычно представляет собой подвижный контакт звеньев в подшипниковых опорах или зацепление этих звеьев. Основные типы пар приведены в таблице 2 (арабскими цифрами в таблице обозначены звенья.)

Основной характеристикой кинематической пары является ее подвижность >jk>, т.е число относительных смещений (линейных или угловых) между звеньями j и k.

Таким образом, передаточный механизм - это совокупность нескольких звеньев, связанных в кинематические пары и предназначенных для преобразования движений одних звеньев (входных) в движения других звеньев (выходных). В таблице 3 приведены основные типы передаточных механизмов общего назначения, применяемые в станках.

Наряду с обычными механическими передачами в металлорежущих станках применяют технологические механизмы, которые являются основными исполнительными механизмами станков и отличаются от передаточных механизмов наличием технологической пары, представляющей собой подвижный контакт инструмента относительно обрабатываемого изделия (табл.2). В технологической паре вместо скольжения или качения создается срезание материала и формообразование изделия. В соответствии с способом обработки технологические пары называют токарными, фрезерными, шлифовальными парами и т.д. На рис.2. приведен пример механизма шлифования с одной шлифовальной парой (2;5)

Рис.2. Механизм врезного шлифования кулачков распредвалов: 1-качающаяся люлька, несущая на себе шпиндель 2 с изделием Д и копиром К;

3-копировальный ролик, установленный на

подшипниках О>1> и контактирующий с копиром;

4-шлифкруг на шпиндельных опорах О>2>> >.> >

Пружина П создает силовой контакт между

копиром и роликом. Ведущим является вращение

шпинделя 2 с изделием и копиром.

Таблица 2

Типы кинематических пар в передаточных механизмах (по ГОСТ 2.770-68 и по рекомендациям ICO ТК/10 ПК4

№

Наименование

Условное изображение

Подвижность, >jk>,

Замыкание

№

Наименование

Условное изображение

Подвижность, >jk>,

Замыкание

1

Ползунная

1

Геометрическое

6

Сферическая
а) обычная


б) с пальцем

3

2

геометри-ческое

2

Вращательная

1

-“-

7

Зубчатая
а) плоская


б) пространственная

2

4 или 5

силовое и геометрическое

3

б) качения

1

-“-

8

Кулачковая
а) плоская

б) пространственная

2

4 или 5

силовое и геометрическое

4

Цилиндри-ческая

2

-“-

9

Технологическая (токарная, фрезерная, шлифовальная и т.д.)
а) с линейным формообразующим контактом

б) с точечным формообразующим контактом

1

2

силовое

5

б) с пальцем

3

2

Силовое

Силовое и геометрическое

4. СТРУКТУРНЫЕ СВОЙСТВА МЕХАНИЗМОВ

4.1. Сложность N механизма. В металлорежущих станках сложные подвижные механические системы, передающие движе­ния от входного звена к выходному (шпиндель, суппорт и т.д.) и образующие последовательные связи между этими звеньями, называют кинематической цепью механизмов Еще более сложными яв­ляются так называемые кинематические группы [2], которые предназначены для создания сложных исполнительных движений и состоящие из нескольких кинематических цепей. Любые кинематические цепи механизмов или их участки, образующие сложные механизмы, могут быть расчленены на простые.

Простой механизм (или передача)- это такой, в котором число звеньев (с учетом неподвижного) равно числу кинематические пар, то есть p = n + 1, где р – число кинематических пар, n – число подвижных звеньев. Графическое изображение основных типов простых механизмов стандартизовано, (см. [3], стр. 65). Каждое звено в простом механизме образует подвижное соединение с двумя другими звеньями. Сложные механизмы содержат несколько простых; в них есть звенья, подвижно связанные более чем с двумя другими звеньями (рис. 3 и 4).

Число N простых механизмов в сложном равно

N = p – n (1)

Если вычисление по формуле (1) дает N = 1, то механизм простой; если N > 1, то механизм сложный; при N < 1 механизм вырождается в жесткую ферму. В числе р кинематических пар в формуле (1) не учитывают избыточные (пассивные) пары, вводимые в механизмы в виде дополнительных опор и зацеплений. Например, в дифференциале(рис.5), такой опорой является пара (2;4) между водилом 2 и ступицей 4 шестерен z>4> и z>8>.

Таким образом, степень сложности механизма определяется в нем числом простых передач.

4.2. Размерность R механизма. Она определяется числом измерений движения звеньев механизма и равна числу независимых уравнений, связывающих параметры движения (положения или скорости или ускорения) всех звеньев механизма. Например, в шарнирном четырехзвеннике А (рис.3) для четырех переменных параметров положения (углы поворота >4>, >5>, >6>, >7>) имеем три независимых уравнения связи, то есть R=3:

1

(2)

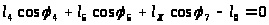) -проекция на ось х

2) 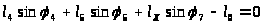-проекция на ось у

3) - сумма внутренних углов 4-звенника

Из примера следует, что размерность простого механизма на единицу меньше числа >> параметров его положения, то есть в большинстве механизмов R = (>>> >– 1). Это обстоятельство позволяет определить R для существующего (известного) механизма без составления вышеуказанных уравнений. Например, для передачи «винт-гайка», R=2, так как параметров положения три: угловое положение винта, линейное положение гайки, а также относительное смещение в зацеплении витков винта и гайки. Для неизвестного (нового) механизма система R вышеуказанных уравнений (2) определяет условия существования механизма и ограничивает число измерений пространства, в котором происходит движение. В общем случае пространство движений – шестимерно. Поэтому размерность R простого механизма определяется зависимостью

R=6 – c>г >(3)

где c>г> – число общих геометрических связей, ограничивающих пространство движений звеньев механизма. Например, для передачи «винт-гайка» c>г>=4 (допускается только две подвижности в механизме: вращение вокруг оси винта и перемещение вдоль этой оси), а для кулачкового механизма (рис. 2 в) величина c>г>=2 (невозможно вращение одного из звеньев вокруг оси y и перемещение перпендикулярно плоскости xy). Так как движения звеньев механизмов не могут иметь более 6-и измерений, то все простые механизмы делят на:

    одномерные, R=1 (приводные электро-, гидро- и пневмодвигатели);

    двухмерные, R=2 (например, трехзвенные клиновые, винтовые и фрикционные механизмы);

    трехмерные, R=3 (все плоские шарнирно-рычажные, кулачковые, зубчатые и поводковые механизмы, а также сферические и зубчато-рычажные механизмы);

    четырехмерные, R=4 (например пространственные рычажно-винтовые и кулачковые механизмы;

    пятимерные, R=5 (например пространственные шарнирно-рычажные, кулачковые и зубчато-рычажные механизмы);

    шестимерные, R=6 (например пространственные шарнирно-рычажные, кулачковые и зубчато-рычажные механизмы)

4.3. Подвижность W механизма. Она определяется числом степеней свободы движений в механизме, т.е. числом независимых движений на разных входных звеньях, передающих их на одно выходное звено механизма. В соответствии с этим механизмы могут быть одноподвижными (подавляющее большинство) и многоподвижными. Примерами последних являются разнообразные суммирующие механизмы станков ([3], стр.79) и промышленные роботы. Подвижность всего механизма зависит от подвижностей отдельных кинематических пар (j;k), определяемых числом возможных перемещений одного звена пары относительно другого. Могут быть одно-, двух-,…, пятиподвижные кинематические пары (табл.2).

В сложном передаточном механизме общая подвижность определяется следующим выражением:

(4)

где - суммарная подвижность всех р кинематических пар механизма, ;

R>> - сумма размерностей N простых механизмов, входящих в состав сложного, R>>= R>1>+ R>2>+…+ R>N>;

>п> – число местных избыточных (пассивных) подвижностей в кинематических парах. Например, лишняя подвижность в паре Р>12> (рис.1а) или «лишнее» вращение ролика 2 (рис.3) на рычажном толкателе 3, не влияют на положение и движение других звеньев механизма. Избыточные подвижности применяют для уменьшения трения, для компенсации перекосов и других погрешностей с целью повышения работоспособности механизмов.

с>к>- число жестких кинематических связей в сложном механизме. К числу кинематических связей относятся как отдельные дополнительные звенья (рычаги, кулачки, шестерни и т.п.), так и цепи дополнительных механизмов, дублирующих или дополняющих работу основных передач. Указанные кинематические связи образуют замкнутые механические контуры (замкнутые механизмы) и способствуют повышению точности, жесткости и других свойств механизмов. Примерами простейших кинематических связей являются дополнительные шатун 4 (рис.1б) и сателлит 7 (рис.5). Пример более сложной кинематической связи показан на рис.1г. Здесь от двигателя М с помощью зубчатой пары z>1>/z>2> на вал 2 передается вращение, которое затем разделяется на два потока передачами z>3>/z>4 >, z>5>/z>6 >и z>7>/z>8 , >z>9>/z>10>, замыкаясь с помощью шестерен z>11 >и z>12> на зубчатой рейке, закрепленной на столе станка. Усилие Q гидроцилиндра или мощной пружины 3 на вал2, благодаря косозубым зацеплениям шестерен, создает дополнительный натяг между боковыми поверхностями зубьев колес z>11>, z>12> с рейкой. В этом механизме n=7, p=14, N=7, с>к>=1 (один замкнутый контур), >п>=0 и W = ( 14 + 7 ) + 1 – 7  3 = 1 (все простые механизмы – трехмерные, R>j>=3).

Подвижность простого механизма в соответствии с (4) равна:

W = >>> >- R>j> - >п> (5)

Здесь с>к>=0, т.к. введение кинематических связей в простой механизм делает его сложным. Например, присоединение дополнительного шатуна 4 (рис. 1б) в шарнирный четырехзвенник добавляет в него две кинематические пары, поэтому N = 6 – 4 = 2 (два подобных четырехзвенника).

5. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА МЕХАНИЗМОВ.

5.1. Трансформизм. Он характеризуется передаточным отношением i>12>, равным производной от параметра положения (>2>, S>2>) выходного звена 2 по параметру положения (>1>, S>1>) входного звена 1 (>j> – угол поворота, S>j> – линейное смещение звена j). Величина i>12 >определяется по формулам:

здесь >1>, >2>, V>1>, V>2> – угловая и линейная скорость звеньев 1 и 2.

Для механизмов, в которых входные и выходные звенья имеют равномерные движения вместо понятия передаточное отношение i>12 >удобнее пользоваться понятием ход S>jk> механизма, под которым понимают угловое (или прямолинейное) перемещение ведомого звена 2 за один оборот (или один мм) перемещения ведущего звена 1. В зависимости от типа передач ход S>12> равен:

Если механизм сложный (кинематическая цепь механизмов с n подвижными звеньями), то передаточное отношение i>1>>n> от звена 1 к звену n равно:

, (6)

то есть передаточное отношение сложного механизма равно произведению передаточных отношений простых механизмов. Соответственно, если перемещения звеньев в механизме определяется с помощью ходов S>jk> простых механизмов, то xод S>1>>n> сложного механизма:

(7)

5.2. Равномерность (линейность) механизма. Это свойство определяется постоянством хода или передаточного отношения в механизме. Если, например, >1> – угол поворота входного звена, >2> – угол поворота выходного звена и >2>=i>12>>1>, где i>12>=const, то механизм линейный; если i>12>const, то механизм неравномерный. Наличие в сложном механизме хотя бы одного простого неравномерного механизма делает весь сложный механизм тоже неравномерным.

В таблице 3 приведены основные типы станочных равномерных механизмов, их ходы S>12> и передаточные отношения i>12>. В примечании к табл.3 указаны расчетные параметры этих механизмов.

Нелинейность движения механизма оценивают коэффициентом неравномерности равным:

, (7)

где D - диапазон скоростей, D = V>max>/V>min> ; V>max>, V>min>> >– скорость (наибольшая и наименьшая) на выходном звене механизма. У равномерных механизмов . Равномерными являются зубчатые, винтовые, фрикционные и некоторые другие механизмы.

5.3. Реверсивность механизма – свойство изменять направление движения на выходном звене при неизменном направлении движения входного звена. Достигается это либо переключением специально вводимых в сложный механизм реверсивных устройств ([3, стр.74]), либо без переключения, так как это свойство органически присуще данному механизму (например, кривошипному или кулачковому). В переключаемых реверсивных механизмах различают два состояния и соответствующие им два передаточных отношения или хода i>P>>1>, i>P>>2 >или S>P>>1>, S>P>>2>, которые обычно одинаковы и постоянны по величине, но отличаются друг от друга знаком. В большинстве шарнирно-рычажных и кулачковых реверсивных механизмах передаточное отношение обычно переменное по знаку и величине.

5.4. Обратимость механизма. Это свойство механизма позволяет передавать движение в обоих направлениях (от звена 1 к звену n и, при необходимости, от звена n к звену 1). Такая особенность механизмов объясняется, в основном, трением в кинематических парах. В необратимых механизмах в результате самоторможения в одной или в нескольких парах движение возможно только в одном направлении. Самотормозящими и, следовательно, необратимыми могут быть винтовые, кулачковые, некоторые зубчатые (например, червячные) и другие передачи скольжения. Напротив, передачи качения являются, как правило несамотормозящими (обратимыми), так как в зацепление между витками (зубцами) звеньев вводят тела качения (шарики или ролики) и коэффициент трения очень мал. Например, в передаче «винт-гайка качения» небольшой нажим (от руки) на гайку вдоль ее оси приводит винт во вращение. Для обратимых механизмов имеет место равенство i>1>>n>=1/i>n>>1> , то есть передаточное отношение (и ход) в механизме от звена 1 к звену n обратно передаточному отношению i>n>>1> (ходу) от звена n к звену 1. Если хотя бы одна кинематическая пара в механизме самотормозящая, то механизм в целом необратимый.

5.5. Регулируемость механизма. Данное свойство определяется возможностью существенного изменения (или небольшой корректировки) какого-либо параметра движения в механизме. Изменяемыми параметрами движения могут быть: длина хода (угловой или линейный путь), скорость (угловая или линейная), направление движения и исходное положение одного из звеньев механизма. Регулировки в механизмах достигаются переключением коробок скоростей и подач, изменением относительного положения или длины одного из звеньев или заменой звеньев (сменных кулачков или шестерен и т.д.), а также введением в механизм специальных корректирующих устройств (см. [3, стр.66,67]).

В общем случае регулируемость механизма по параметру x>j> на выходном звене характеризуется диапазоном D>X> регулирования, D>X>=x>max>/ x>min>, где x>max>> >, x>min> – максимальное и минимальное значения регулируемого параметра. В качестве параметра x>j> обычно выбирают линейную или угловую скорость, угловую частоту (в оборотах в минуту или в двойных ходах в мин), путь (угловой или линейный) и другие характеристики.

6. ПРИМЕРЫ АНАЛИЗА МЕХАНИЗМОВ

6.1. Кулачково-рычажный механизм привода подачи поперечного суппорта токарного станка-автомата.

    Механизм преобразует вращение В>1> сменного кулачка 1 (рис.3) в поступательное движение П>7> суппорта 7. Промежуточные звенья:

2-ролик, 3 и 4– коромысла с зубчатыми секторами, 5- шатун,

6-коромысло с регулируемой длиной l>x> рычага, 7- ползун (суппорт), 0- стойка.

    Число подвижных звеньев n=7; кинематических пар p=11, три из которых двухподвижные (>12>, >34>, >67>). Суммарная подвижность –

>Σ >= 8  1 + 3  2 = 14.

    Простых механизмов в сложном N = 11 – 7 = 4 (кулачково-рычажный с звеньями 0, 1, 2, 3; зубчато-рычажный с звеньями 0, 3, 4; шарнирный 4-звенник с звеньями 0, 4, 5, 6; рычажно-ползунный с звеньями 0, 6, 7). Размерность всех простых механизмов (все они плоские): R>1>=R>2>= R>3>= R>4>= 3

    Общая подвижность механизма по формуле (2) W=14-43-1=1. Здесь >0>=1 – местная подвижность ролика 2 в паре >23> с коромыслом 3.

    Механизм неравномерный, так как содержит шарнирно-рычажные передачи.

    Механизм реверсивный, так как реверсивна кулачковая передача.

    Механизм необратимый, так как необратима кулачково-рычажная передача.

    Механизм регулируемый, так как изменением длины l>x> рычага в коромысле 6 корректируется длина хода Н>х> суппорта 7, а заменой кулачка 1 изменяется длина хода и скорость подачи суппорта.

6.2. Промышленный робот (рис. 4)

    В основании 0 размещен приводной двигательМ>1>, в подвижной стойке 4 установлены двигатели М>2>, М>3 >, а на конце руки 6 закреплен пневмодвигатель ПД, ротор 7 которого непосредственно связан со схватом робота. Остальные звенья: 1-шестерня, 2-поворотная платформа, жестко связанная с шестерней, 3 и 5 –ходовые винты.

    Число подвижных звеньев n=7, кинематических пар Р=10 (одна из них двухподвижная >12>), суммарная их подвижность >>=91+12=11.

    Степень сложности N = 10 – 7 = 3. Промышленный робот содержит 3 простых передаточных механизма: зубчатый с подвижными звеньями 1-2 (R>1>=3) и два винтовых, с подвижными звеньями 3-4 и 5-6 (R>2>=R>3>=2).

    Общая подвижность механизма W = 11 – (3 + 2  2) = 4, то есть робот 4-подвижный: три подвижности (В>2>, П>4>, П>6>) реализуются от двигателей М>1>, М>2>, М>3>, вращающих входные звенья 1,3,5, а одна подвижность (В>7>) осуществляется непосредственно (без передаточного механизма) от неполноповоротного пневмодвигателя ПД.

    Механизм равномерный, нереверсивный, необратимый (содержит винтовые пары скольжения) и регулируемый (направление движения изменяется двигателями, а исходное положение и длина перемещений - путевыми упорами, переключающими двигатели).

Рис. 3 Семизвенный плоский механизм привода подачи суппорта

Рис. 4. Четырехподвижный промышленный робот с

цилиндрической координатной системой

6.3. Суммирующий механизм (рис. 5)

    В этом механизме ведущими являются валы 1 и 3, ведомыми– вал 7. Цепь передач от вала 1 к валу 7 состоит из червячной передачи z>1>/z>2> и планетарной передачи, в которой вал 2 жестко связан с осями сателлитов 5 и 6, образуя так называемое водило. Последнее передает вращение через шестерни 5 и 6 на вал 7. Вторая цепь (от вала 3) состоит из передач z>3>/z>4>, z>8>/z>5>, z>5>/z>7> и дублирующих передач z>8>/z>6>, z>6>/z>7>.

    Число подвижных звеньев n=7, кинематических пар Р=14 (из них шесть пар –двухподвижные, зубчатые); одна пара (2;4) – пассивная поэтому общая подвижность >>=(14–1)+6=19

    Сложность механизма N=13-7=6 (две червячных и четыре конических передачи с размерностями R>j>=3)

    Общая подвижность W=19+1–63=2. Здесь с>к>=1 – один замкнутый контур конических передач.

    Механизм равномерный, нереверсивный, необратимый и нерегулируемый.

Рис. 5. Конический дифференциал: М>1>, М>2 >– электродвигатели соответственно

для ускоренного и рабочего хода, 1– вал с червяком z>1>, 2- вал с закрепленным

на нем водилом В и шестерней z>2>, 3- вал с червяком z>3>, 4- ступица с закрепленными

на ней шестернями z>4> и z>8>, 5 и 6 – сателлиты, свободно насаженные на водило В,

7- выходной вал с шестерней z>7>; пара (2;4) – избыточная, >24>=1.

7. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО АНАЛИЗУ МЕХАНИЗМОВ

7.1. В приложении (стр. 20, 21) предусмотрены задания для 20 вариантов (см. табл. 4). В задании № 1 по схеме механизма необходимо дать его анализ по методике п.7.2. (см. примеры в п.6). В задании 2 предварительно нужно по макету механизма составить его кинематическую схему, учитывая правила изображения звеньев и кинематических пар (табл.1 и 2).

7.2. При анализе свойств механизмов необходимо:

    Разобраться в принципе действия и составных частях механизма.

    Изобразить кинематическую схему механизма, указав в ней все звенья, кинематические пары и их подвижности >jk>. При выполнении задания №3 рекомендуется кроме табл. 1 и 2 использовать условные обозначения механизмов в [3, стр.62-65].

    Дать краткое описание принципа работы механизма с наименованием всех звеньев.

    Проанализировать структуру механизма в следующем порядке

      указать общее число n подвижных звеньев,

      указать общее число р кинематических пар и определить их суммарную подвижность >>,

      по формуле (1) определить степень сложности механизма N и перечислить типы простых механизмов, входящих в состав сложного с указанием их звеньев и размерностей.

      по формуле (4) определить подвижность механизма W и указать его входные и выходные звенья.

    Дать оценку равномерности, реверсивности, обратимости и регулируемости механизмов.

При оценке равномерности движения на макете (задание №2) нужно последовательно, задавая одинаковые перемещения на входном звене, замерить соответствующие перемещения на выходном звене; если примерно одинаковые, то , механизм равномерный, в противном случае неравномерной.

При оценке регулируемости нужно выявить по каким измененным параметрам движения возможна настройка заданного механизма и с помощью каких приемов.

Таблица 4

Индивидуальное задания

№

задания

Варианты

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

1

(табл.5)

Рис.1

Рис.2

Рис.3

Рис.4

Рис.5

Рис.6

Рис.7

Рис.8

Рис.9

Рис.10

Рис.11

Рис.12

Рис.13

Рис.14

Рис.15

Рис.16

Рис.17

Рис.18

Рис.19

Рис.20

2

(макеты)

№1

№2

№3

№4

№5

№6

№7

№8

№9

№10

№11

№12

№13

№14

№15

№16

№17

№18

№19

№20

8.КОНТРОЛЬНЫЕ ВОПРОСЫ

    Понятие о передаточном и технологическом механизмах и их составе.

    Понятие о кинематической паре. Типы пар и их свойства.

    Что такое подвижность механизма? Примеры.

    Размерность механизма. Классификация механизмов по числу измерений. Примеры.

    Какие избыточные («пассивные») элементы вводятся в передаточные механизмы и с какой целью. Примеры.

    Основные особенности простых и сложных механизмов.

    Может ли входное звено быть выходным? В каких механизмах?

    Как оценивается равномерность движения механизма?

    Какие элементы в механизмах регулируются и с какой целью?

    Что такое ход и передаточное отношение механизма? В чем отличие ходов и передаточных отношений простого и сложного механизмов.

    Чему равны передаточное отношение и ход в следующих механизмах: в зубчатой цилиндрической передаче, в червячной передаче, в реечной передаче, в винтовой передаче, в ременной передаче, в цепной передаче?

9. БИБЛИОГРАФИЧЕСКИХ СПИСОК

    Металлорежущие станки /Под ред. Н.С.Ачеркана.-М.:Машиностроение, 1965.

    Федотёнок А.А. Кинематическая структура металлорежущих станков.-М.:Машиностроение, 1970.

    Клюйко Э.В. Кинематика металлорежущих станков.-Калинин:КПИ, 1974.

    Клюйко Э.В., Матвеев А.И. Металлорежущие станки общего назначения.-Тверь:ТГТУ, 1999.

    Клюйко Э.В. Изучение передаточных механизмов металлорежущих станков. Методические указания к лабораторной работе.-Тверь: КПИ, 1991.