Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов

Министерство образования Российской Федерации

Курский государственный технический университет

Кафедра сопротивления материалов и строительной механики

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по выполнению расчетно-графических работ

по сопротивлению материалов

Курск 2003

Составители: Л. Ю. Ступишин, А. В. Масалов

УДК 539.3/8

Рецензент канд. техн. наук., доцент теоретической механики Мищенко В. Я.

Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов/ Курск.гос.техн.ун-т; Сост. Л. Ю. Ступишин, А. В. Масалов. Курск 2003

Излагаются методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов.

Предназначены для студентов технических специальностей.

Ил. 14. Табл. 1

Редактор Т. Н. Иванова

Подписано в печать 16.11.95. Формат 60 х 84 1/16.

Печать офсетная

Усл.печ.л.3,74 Уч.изд.л. 3,96 Тираж 200 экз.

Заказ 464 .Бесплатно

Курский государственный технический университет.

Издательско-полиграфический УСИТР . Курского государственного технического университета. 305035, Курс, ул. 50 лет Октября, 94.

ВВЕДЕНИЕ

Общие замечания

При изучении дисциплин кафедры наибольшие трудности у студентов возникают при решении практических задач.

Вместе с тем именно решение задач в значительной степени способствует развитию инженерного мышления у студентов, приобретению ими необходимых навыков прочности расчетов элементов инженерных конструкций. В настоящей методической разработке подробно рассмотрены решения типовых задач, а также изложены требования по выполнению и оформлению индивидуальных расчетно-графических работ, предусмотренных программками курсов сопротивления материалов, механики деформируемого твердого тела, прикладной и технической механики для студентов дневного обучения всех специальностей.

Основные требования по выполнению расчетно-графических работ

1.2.1 Оформление титульного листа

Все расчетно-графические работы выполняются из стандартных листах бумаги с размерами 210 х 297 мм, окропленных в тетрадь.

Титульный лист (передний лист обложки) оформляется в соответствии с требованиями ЕСКД. Все надписи на титульном листе располагаются в строго определенных местах выполняются чертежным шрифтом. Разрешается выполнять титульный лист в компьютерном варианте.

Рекомендуется следующие номера шрифта для конкретных надписей:

«Министерство образования РФ» – шрифт №7+; в компьютерном варианте шрифт Times 16пт;

«Курский государственный технический университет» - шрифт №5; в компьютерном варианте шрифт Times 14пт;

«Кафедра сопротивления материалов и строительной механики» - шрифт №5; в компьютерном варианте шрифт Times 14пт;

названию расчетно-графической работы – шрифт №10; в компьютерном варианте Times 18пт;

«расчетно-графическая работа №…» - шрифт №7; в компьютерном варианте Times 14пт;

«Выполнил …», «Проверил …» - шрифт №5; в компьютерном варианте Times 14пт;

год выполнения работы – шрифт №5; в компьютерном варианте Times 14пт.

1.2.2. Оформление расчетно-пояснительной записки

Расчетно-пояснительная записка должна быть достаточно краткой, без лишних подробных пояснений и теоретических выводов, имеющихся в учебниках и других учебных пособиях, но не чересчур краткой, содержащей один только формулы и вычисления. В расчетно-пояснительной записке от начала до конца должна четко прослеживаться логическая связь выполняемых операций, а также должны быть отмечены основания для выполнения этих операций. Приведенные в настоящей методической разработке примеры решения отдельных задач могут послужить основой для составления записок.

Формулы, приводимые в записке, должны быть, как правило, записаны сначала в общем виде, а затем уже должна быть произведена подстановка исходных данных и выполнены необходимые вычисления. При подстановке исходных данных нужно внимательно следить за соблюдением одинаковой размерности. После получения значения искомой (промежуточной или окончательной) величины обязательно проставляется ее размерность.

Все записи в расчетно-пояснительной записке ведутся чернилами на одной стороне листа писчей бумаги четкими разборчивым почерком, с расстоянием между строками в 8/12 мм.

На каждой странице оставляются поля: слева шириной 25 мм – для скрепления листов в тетрадь, и справа – 10мм.

Если у автора расчетно-графической работы неразборчивый почерк, то записку он должен выполнять чертежным шрифтом.

Изложение текстового материал записки следует вести от первого лица множественного числа, например: «…определяем…», «…вычисляем…», «…находим…», и т.д., или в безличной форме: «…можно определить…», и т.п., а не «…я определяю…», «…нахожу…», и т.д. Текст всей записки должен быть выдержан в единой стиле; например, если пояснения ведутся в безличной форме, то эта форма должна сохраняться во всей работе.

В конце записки необходимо привести перечень литературы, использованной студентом в процессе выполнения работы, в той последовательности, в какой литературные источники отмечены квадратными скобками в тексте.

В страницы расчетно-графической работы должны быть последовательно пронумерованы в правой верхней части страницы арабскими цифрами с точкой. Нумерация страниц должна быть сквозное от титульного листа до последней страницы, включая чертежи (схемы). На титульном листе, который является первой страницей, номер страницы не ставится, хотя и подразумевается.

1.2.3. Выполнение графической части работы

Графическая часть работы выполняется на бумаге формате А4 (210 х 297 мм) или формата А3 (297 х 480 мм) карандашом или тушью с применением необходимых чертежей инструментов.

В соответствии с заданной схемой по числовым данным варианта вычерчивается в масштабе схема сооружения (расчетная схема, поперечные сечения бруса и т.д.), на которой проставляются исходные данные (размеры) как в буквенных обозначениях, так и в числах, а также наносится заданная нагрузка. Кроме того, все размеры, используемые в расчетах, также должны быть показаны на чертеже. Эпюры внутренних усилий (напряжений, перемещений) должны вычерчиваться строго под расчетной схемой бруса (или рядом с ней). На расчетной схеме должны быть отмечены все сечения, для которых, определяются внутренние усилия; на эпюрах обязательно проставляются значения вычисленных характерных ординат. Для каждой экстремальной точки любой эпюры обязательно определяется ее положение и подсчитывается значение ордината (max или min). Эпюры заштриховываются тонкими линиями (расстояние между линиями 2+3 мм). Перпендикулярно оси элемента конструкции. На заштрихованном поле эпюры проставляется ее знак «+» или «-».

1.2.4. Защита расчетно-графических работ

Каждым студентом все расчетно-графические работы должны выполняться и сдаваться на проверку преподавателю в сроки, предусмотренные графиком работы студентов в текущем семестре. После исправления студентом всех ошибок, отмечен их преподавателем при проверке, каждая расчетно-графическая работа должна быть защищена. При исправлении ошибок из проверенной работы ни в коем случае ничего не выбрасывается. Исправления аккуратно записываются студентом на чистых страницах. На защиту студенты приносят исправленные работы, сдают их преподавателю, получают индивидуальные карточки-задания на решение задачи по соответствующему разделу курса. На решение задачи отводится максимум 30+40 мин. Если студент успешно решил задачу и у преподавателя нет никаких дополнительных замечаний по расчетно-графической работе, то защита считается законченной. После защиты работа остается у преподавателя. Если студентом все работы защищены успешно и в срок, то в конце семестра он автоматически получает зачет по курсу. В случае, когда студент при защите не справляется с решением типовых задач, то преподавателем назначается дополнительная защита (не более двух раз!). Если студентом какие-либо расчетно-графические работы не защищены в течении семестра, то их защита и сдача зачета по курсу производится в зачетное – экзаменационную сессию.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

ПРИМЕР 1

Для изображенного на рис. 1.1. поперечного сечения требуется:

Определить положение центра тяжести сечения;

Определить положение главных центральных осей инерции;

Вычислить величины главных центральных моментов инерции.

Исходные данные:

а = 1,8 м.

РЕШЕНИЕ

1. Определение положения центра тяжести сечения.

Разбиваем сечения на простые фигуры, центры тяжести которых известны

(рис. 1.1.):

полукруг с радиусом R=а;

прямоугольник со сторонами 3/4а*2а;

треугольник с основанием а и высотой а/2.

Определим геометрические характеристики составляющих фигур (У - координата центра тяжести; А – площадь; J. - моменты инерции относительно собственных главных центральных осей).

Изобразим заданные сечения в определенном масштабе и выберем исходные оси (оси, в которых будет определяться центр тяжести). Пример в качестве исходных собственные оси фигуры «2» (рис. 1.2).

Определим координаты центра тяжести всей фигур «с» в выбранной исходной системе координат . Так как ось - ось симметрии всей фигуры, то центр тяжести лежит на оси и Координат равна (рис.1.2):

Откладываем отрезки и и отмечаем центр тяжести С (рис 1.2).

Проверим правильность определения центра тяжести. Статический момент всей фигуры относительно осей, проходящих через центр тяжести, равен нулю.

Определим (рис. 1.2):

Центр тяжести найден верно.

2. Определение положения главных центральных осей.

Заданное сечение имеет ось симметрии Yc. Следовательно, центробежный момент - главные центральные оси.

Вычисление виличины главных центральных моментов инерции .

Смещению центров тяжести С1 , С2, С3 от осей Yc и Zc показано на рис. 1.2. Численные значения приведены выше. Значения моментов инерции составляющих фигур относительно собственных осей приведены в разделе 1.

ПРИМЕР 2

Для изображенного на рис. 2.1. поперечного сечения бруса требуется:

определить положение центра тяжести сечения;

определить положение главных центральных осей инерции;

вычислить величины главных центральных моментов инерции.

Исходные данные:

элемент 1 - [ №20,

элемент 2 – I №20

элемент 3 – прямоугольник

300 х 20 (), мм.

РЕШЕНИЕ

Определение центра тяжести поперечного сечения.

Определим необходимые геометрические характеристики составляющих фигур ( - координата центров тяжести; Ai – площадь; - моменты инерции относительно собственных главных центральных осей). Для прокатных профилей швеллера (I) и двутавра (2) данные взяты из таблиц сортамента прокатной стали.

Изобразим сечение в масштабе, укажем центры тяжести составляющих фигур и переведем главные центральные оси составляющих фигур (рис. 2.2).

За исходные оси (оси, в которых будет определяться центр тяжести) примем главные центральные оси фигуры «2» (рис. 2.2). Определяем координаты Yc и Zc центра тяжести всей фигуры «с» в выбранной исходной системе координат Y2C2Z2. Так как ось У2 – ось симметрии всей фигуры, то центр тяжести лежит на оси Уz и Zc = 0. Координата Ус равна (рис. 2.2).

Откладываем отрезки Ус = - 3,48 и Zc=0 и отмечаем центр тяжести «С» (рис2.2).

Проверка правильности определения центра тяжести проводится аналогично решению примера 1, пункт 1.

Определение положения главных осей.

Заданное сечение имеет ось симметрии Ус. Следовательно, центробежный момент - главные. А так как «С» центр тяжести, то оси Ус и Zc – главные центральные.

Определение величины главных центральных моментов инерции .

Смещение центров тяжести составляющих фигур относительно осей Ус и Zc показано на рис. 2.2:

Значения моментов инерции составляющих фигур относительно собственных главных осей приведены в разделе 1.

ПРИМЕР 3

Для изображенной на рис. 3.1 схема стального бруса требуется:

построить эпюры продольных сил N и нормальных напряжений б, записав в общем виде для каждого участка выражения N и б и указа на эпюрах их значения в характерных сечениях;

установить опасное сечение и записать условие прочности. Определить размеры прямоугольного сечения бруса, приняв h/b=2?0;

найти перемещения сечения 2.

Исходные данные:

Для выполнения числовых расчетов принять: (для студентов строительных специальностей принять R=210МПа)

РЕШЕНИЕ

Изобразим в масштабе расчетную схему бруса (рис. 3.2ба) с учетом знаков исходных данных (если нагрузка задана со знаком минус, то ее на схеме следует направить в противоположную сторону). Построим эпюры N и б, рассматривая каждый участок, начиная со свободного конца. Используя метод сечений, разрежем брус некоторым сечением с ординатой (участок 1-2), изобразим нижнюю часть бруса отдельно, отбросив верхнюю часть и заменив ее действие продольной силой N (рис. 3.2,б).

Запишем уравнение равновесия и найдем силу N:

- уравнение наклонной прямой.

Мысленно выполняя приведенные выше операции метода сечений для каждого участка, запишем выражения для N и б: участок 1-2:

- уравнение наклонной прямой;

- уравнение наклонной прямой при

участок 2-3;

По полученным значениям в масштабе строим эпюру N (рис.3.2, в) и эпюру б (рис.3.2,г).

Сечение будет опасным, если напряженна б будет наибольшим (без учета знака). По эпюре 3.2, г, видно, что опасное сечение 1 или весь участок 3-4, где =2qa/A. Запишем условие прочности:

а) для студентов всех специальностей, кроме строительных:

Принимаем b=0,008м=8мм

h=0,016m=16мм.

б) для студентов строительных специальностей:

Принимаем b=0,010м=10мм

H=0,020m-20mm.

На основании дифференциальных зависимостей при растяжении (сжатии)

которого находим, защемлением.

Найдем перемещение сечения 2, используя эпюру N(рис. 3.1, а; 3.2, в)

(здесь

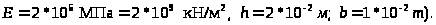
ПРИМЕР 4

Для изображенной на рис. 4.1 схемы стального бруса требуется:

построить эпюры крутящих моментов Т и касательных напряжений , записав в общем виде для каждого участка выражения Т, и указав на эпюрах их значения в характерных сечениях;

установить опасное сечение и записать условие прочности, определить диаметр бруса;

найти угол закручивания сечения 1.

Исходные данные:

Для выполнения числовых расчетов принять:

= 96 МПа; а = 0,5 м;

(для студентов строительных специальностей принять ).

РЕШЕНИЕ

Изобразим в масштабе расчетную схему бруса (рис. 4.2, а) с учетом знаков исходных данных. Построим эпюры Т и , рассмотрев каждый участок, начиная со свободного конца. Используя метод сечений, разрежем брус некоторым сечением с абсциссой (участок 1-2), изобразим правую часть бруса отдельно, отбросив левую часть, заменив действие левой части крутящим моментом Т (рис. 4.2, б).

Запишем уравнение равновесия и найдем момент Т:

Мысленно выполняя приведенные выше операции метода сечений для каждого участка, запишем выражения для Т и :

Участок 1-2

По полученным значениям в масштабе строим эпюру Т (рис. 4.2,в) и (рис. 4.2,г)

Опасным будет сечение, где По эпюре (рис. 4.2,г) видно, что опасным является сечение 3, в котором

Запишем условие прочности:

а) для студентов всех специальностей, кроме строительных:

Принимаем: d= 0,180 м = 150 мм.

б) для студентов строительных специальностей:

Принимаем d=0,135 m = 135 mm.

На основании дифференциальных зависимостей при кручении

определяем, н защемлением.

Найдем угол закручивания сечения 1, используя эпюру Т (рис. 4.2, а).

ПРИМЕР 5

Для изображенной на рис. 5.1. схема стальной балки требуется:

построить эпюры поперечных сил Q (Qy) и изгибающих моментов М (Mz), запасов в общем виде для каждого участка выражения Q и М и указав на эпюрах значения в характерных сечениях;

установить опасное сечение, записать условие прочности и подобрать номер двутавра;

определить прогиб сечения 3 и угол поворота сечения 2.

Исходные данные:

Для выполнения числовых расчетов принять:

(для студентов строительных специальностей принять R=210МПа).

РЕШЕНИЕ

Изобразим в масштабе схему балки (рис. 5.2,ф) с учетом знаков исходных данных.

Расчет двухопорной балки начинаем с определения опорных реакций (для защемленной с одного конца балки реакции обычно не определяются, а построение эпюр Q и М начинается со свободного конца)

Реакции получили со знаком плюс, значит первоначальное направление выбрано верно. Если бы получили одну (или обе) реакцию со знаком минус, то ее (их) следовало бы направить в противоположную сторону.

Проверка:

Следовательно, реакции определены верно и можно приступать и построению эпюр.

Для их построения рассмотрим каждый участок балки и, используя метод сечений (см. пример 3, 4), запишем выражения для Q и М с учетом принятого правила знаков.

Участок 3-1;

Q = -2qx – уравнение наклонной прямой;

- уравнение квадратной параболы;

при

(средняя ордината эл. М)

В масштабе строим эпюры Q и М на участке 3-1 (рис. 5.2, б, 5.2, в). На этом участке эпюра Q знак не меняют, поэтому на эпюре М экстремального значения не будет и ее можно приближенно провести по двум точкам ( Эпюру М принято строить на сжатых волокнах для студентов машиностроительных и технологических специальностей (т.е. отрицательные значения откладываются вниз, положительные – вверх); для студентов строительных специальностей ее принято строить на растянутых волокнах балки (т.е. отрицательные значения откладывается вверх, положительные – вниз (рис. 5.2,г).

Участок 1-4: при

Строим эпюры Q и М на участке 1-4 в выбранном масштабе. На этом участке эпюра Q проходит через нуль, меняя знак, следовательно на эпюре М в этом сечении будет экстремальное значение. Найдем его, приравняв Q на участке 1-4 к нулю (рис. 5.2, г):

Можно продолжать рассмотрение участков балки слева, но расчеты при этом усложняются (в уравнение для Q и М входит много слагаемых). Поэтому далее будем строить эпюры Q и М, рассматривая участки белки справа.

Участок 5-2;

По этим значениям строим эпюры Q и М на участке 5-2.

Участок 2-4;

По этим значениям строим эпюры Q и М на участке 2-4.

2.Опасным будет сечением, где

Из рассмотрения рис. 5.2, в,г видно, что

Запишем условие прочности:

а) для студентов всех специальностей, кроме строительных

По таблице сортимента выбираем двутавр №16, для которого

б) для студентов строительных специальностей:

По таблице сортимента выбираем двутавр №14, для которого

3. Найдем прогиб сечения 3, используя способ перемножения эпюр.

Для этого в направлении предполагаемого перемещения прикладываем единичную силу (рис. 5.2, д). Определяем опорные реакции и стороны единичную эпюру изгибающих моментов

Запишем выражения для изгибающих моментов на участках балки.

Участок 3-1;

Участок 2-1;

По полученным значениям строим эпюру (рис.5.2, е).

Перемножим по формуле Симпсона эпюру М (Мz) на эпюру и найдем искомый прогиб сечения 3:

Знак «минус» показывает, что прогиб сеч. 3 направлен не вниз (как была направлена сила ), а вверх.

Найдем угол поворота сечения 2, используя способ перемножения эпюр. Для этого прикладываем в сечении 2 в предполагаемом направлении его поворота единичную пару сил (рис.5.2, ж.), определяем опорные реакции и строим единичную эпюру изгибающихся моментов (рис. 5.1, з)

Построенная эпюра изображена на рис. 5.2, з. Перемножим по формуле Симпсона эпюру на эпюру М (Мz) и найдем искомый угол поворота сеч. 2:

ПРИМЕР 6 (для студентов строительных специальностей)

Для изображенной на рис. 6.1 схемы рамы (материал-сталь) требуется:

построить эпюры изгибающих моментов М (Мz), поперечных сил Q (Qy) и придельных сил N (Nx) двумя путями:

а) записав в общем виде для каждого участка выражения М, Q, N.

б) построив эпюры М (аналогично п.а. или по значениям М в характерных сечениях), а затем по дифференциальным зависимостям и уравнениям равновесия эпюры Q и N;

2) установить опасное сечение, записать условие прочности и определить

величину безопасности нагрузки;

3) определить горизонтальный прогиб сечения 5 и угол поворота сечения

3 рамы.

Исходные данные:

При выполнении числовых расчетов принять:

Размеры поперечного сечения стержня подбираем из условия его устойчивости в плоскости наименьшей жесткости:

Найдем геометрические характеристики, выразив их через «а»:

Гибкость стержня в плоскости его наименьшей жесткости:

где коэффициент приведения длины (v)M=0,7 при заданных условиях закрепления его концов (рис. 9.1).

Первое приближение: принимаем

Тогда:

Далее найдем:

Из таблицы коэффициентов (имеются в справочниках и пособиях по сопротивлению материалов) по интерполяции находим табличные значения составляющие =102 для стали 3:

при

тогда:

Поскольку (относительная разница между ними составляет:

что больше 5%), то расчет повторяем во втором приближении.

Второе приближение: принимаем

Далее расчет повторяем

Из таблицы:

Окончательно принимаем следующие размеры сечения:

Проверим устойчивость стержня:

Поскольку то критическую силу определяем по формуле Эйлера (если то критическая сила определяется по формуле Ясинского:

Найдем коэффициент запаса устойчивости:

ПРИМЕР 10

Для заданной рамы (рис.10.1) требуется:

установить степень статической неопределимости;

выбрать основную систему и составить канонические уравнения метода сил;

построить эпюры изгибающихся моментов от внешней нагрузки и единичных сил;

вычислить все перемещения, входящие в канонические уравнения;

найти величины лишних неизвестных;

построить окончательные эпюры N, Q и М;

провести деформационную проверку;

подобрать размеры поперечных сечений всех элементов рамы, приняв , поперечное сечение ригеля в форме двутавра, стойки – кольца с соотношением d/D=0,8.

Исходные данные:

РЕШЕНИЕ

По исходным данным строим расчетную схему (рис. 10.2,а).

Устанавливаем степень статистической неопределенности системы:

n=x-y=6-4=2,

где:

x=G-число неизвестных реактивных факторов

( по рис. 10.2,а.);

y=4 – число применимых уравнений равновесия

(- дополнительное уравнение, т.к. в шарнире момент равен нулю по рис. 10.2, а.)

Рассматриваемая рама два раза статистически неопределима.

Выбираем основную систему. Наиболее удобный вариант разрезать ригель по шарниру (рис. 10.2, б.). Приложив к основной системе по направлению отброшенных связей усилия и заданную нагрузку, получим эквивалентную систему (рис.10.2, в.). Запишем канонические уравнения метода сил для этой статически неопределимой системы:

Построим эпюры изгибающих моментов для принятой основной системы:

а) построение эпюры (рис. 10.2, д.) от силы (рис.10.2, г.)-первое единичное состояние.

Так как основная система и нагрузка () симметричны, то эпюра будет симметричной. Поэтому ординаты изгибающих моментов достаточно определить только для элементов одной части рамы (правой или левой) и симметричную отложить их значения на другой.

Вычисляем изгибающие моменты для левой части рамы.

Определяем опорные реакции из уравнения статики:

Построим эпюру :

Участок ШЕ

=0.

Участок ЕА

при

Участок ВА

Построим эпюру на участке ШК, КД, СД аналогично.

По полученным значениям строим эпюру , откладывая ординаты в крайних точках участков со стороны сжатых волокон;

б) построение эпюры (рис.10.2, ж.) от силы (рис. 10.2, е.). Так как основная система симметричная, а нагрузка () – несимметрична, то эпюра также будет несимметричной.