Контрольная по статистике (работа 2)

Задача № 1

Имеются следующие выборочные данные ( выборка 10 % - тная, механическая ) о выпуске продукции и сумме прибыли, млн. руб:

№ предприятия	Выпуск продукции	Прибыль	№ предприятия	Выпуск продукции	Прибыль
1	65	15.7	16	52	14,6
2	78	18	17	62	14,8
3	41	12.1	18	69	16,1
4	54	13.8	19	85	16,7
5	66	15.5	20	70	15,8
6	80	17.9	21	71	16,4
7	45	12.8	22	64	15
8	57	14.2	23	72	16,5
9	67	15.9	24	88	18,5
10	81	17.6	25	73	16,4
11	92	18.2	26	74	16
12	48	13	27	96	19,1
13	59	16.5	28	75	16,3
14	68	16.2	29	101	19,6
15	83	16.7	30	76	17,2

По исходным данным :

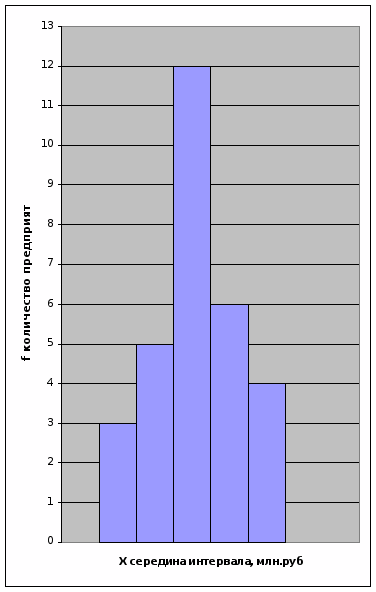
Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте график ряда распределения.

Рассчитайте характеристики ряда распределения предприятий по сумме прибыли : среднюю арифметическую, среднее квадратическое отклонение, дисперсию, коэффициент вариации.

С вероятностью 0,954 определите ошибку выборки для средней суммы прибыли на одно предприятие и границы, в которых будет находиться средняя сумма прибыли одного предприятия в генеральной совокупности.

С вероятностью 0,954 определите ошибку выборки для доли предприятий со средней прибылью свыше 16,6 млн. руб. и границы, в которых будет находиться генеральная доля.

Решение :

1. Сначала определяем длину интервала по формуле :

е=(х_>max> – x_>min>)/k,

где k – число выделенных интервалов.

е=(19,6 – 12,1)/5=1,5 млн.руб.

12,1-13,6; 13,6-15,1; 15,1-16,6; 16,6-18,1; 18,1-19,6.

Распределение предприятий по сумме прибыли.

№ группы	Группировка предприятий по сумме прибыли	№ предприятия	Прибыль
I	12,1-13,6	3	12,1
7	12,8
12	13
II	13,6-15,1	4	13,8
8	14,2
16	14,6
17	14,8
22	15
III	15,1-16,6	1	15,7
5	15,5
9	15,9
13	16,5
14	16,2
18	16,1
20	15,8
21	16,4
23	16,5
25	16,4
26	16
28	16,3
IV	16,6-18,1	2	18
6	17,9
10	17,6
15	16,7
19	16,7
30	17,2
V	18,1 -19,6	11	18,2
24	18,5
27	19,1
29	19,6

Рассчитываем характеристику ряда распределения предприятий по сумме прибыли, для этого составим расчетную таблицу :

Группы предприятий по сумме прибыли; млн.руб	Число предприятий f	Середина интервала Х	xf	X2f
12,1 – 13,6	3	12,9	38,7	499,23
13,6 – 15,1	5	14,4	72	1036,8
15,1 – 16,6	12	15,9	190,8	3033,72
16,6 – 18,1	6	17,4	104,4	1816,56
18,1 – 19,6	4	18,9	75,6	1428,84
	30	------	481,5	7815,15

Средняя арифметическая : =  xf /  f

получаем : = 481,5 : 30 = 16,05 млн.руб.

Среднее квадратическое отклонение :

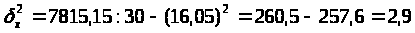
получаем :

О
пределяем среднее квадратическое отклонение для определения коэффициента вариации)

Коэффициент вариации : _>х> = (_>х> * 100%) / x

получаем : _>х> =1,7 * 100% : 16,05 = 10,5%

так как _>х> = 10,5% < 33% то можно сделать вывод, что совокупность однородная, а средняя величина типичная ее характеристика.

О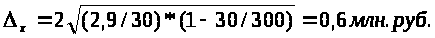
пределяем ошибку выборки (выборка механическая) для средней суммы прибыли на одно предприятие по следующей формуле :

если Р=0,954 то t=2

ошибка выборки для средней суммы прибыли на одно предприятие х = 0,6

С
редняя сумма прибыли будет находиться в границах которые мы находим по формуле :

получаем : 15,45X 

С
вероятностью 0,954 можно утверждать, что средняя сумма прибыли одного предприятия заключается в пределах :

Д
оля предприятий со средней прибылью свыше 16,6 млн.руб. находится в пределах :

В
ыборочная доля составит :

О
шибку выборки определяем по формуле :

,где N – объем генеральной совокупности.

Также объем генеральной совокупности можно определить из условия задачи, так как выборка 10% -тная и в выборку вошло 30 предприятий:

30 предприятий – 10%

Х – 100%

10х=3000

х=300 предприятий, следовательно N=300

п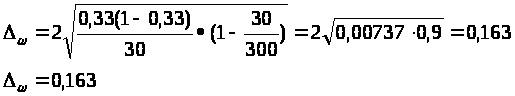
одставляем данные в формулу :

Следовательно с вероятностью 0,954 можно утверждать, что доля предприятий со средней прибылью > 16,6 млн. руб будет находиться в следующих пределах:

33% или 16,7 49,3%

Задача № 2

по данным задачи №1

Методом аналитической группировки установите наличие и характер корреляционной связи между стоимостью произведенной продукции и суммой прибыли на одно предприятие. (результаты оформите рабочей и аналитической таблицами.)

Измерьте тесноту корреляционной связи между стоимостью произведенной продукции и суммой прибыли эмпирическим корреляционным отношением.

Сделайте выводы.

Решение:

П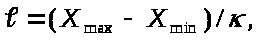
оскольку прибыль предприятия напрямую зависит от объема производимой продукции, то мы обозначим выпуск продукции независимой переменной Х, тогда прибыль зависимой переменной У. Поскольку в каждом отдельном случае рассматривается одно предприятие а на прибыль предприятия, кроме выпуска продукции, может влиять множество факторов в том числе и неучтенных, следовательно можно определенно сказать что связь в данном случае корреляционная. Ее можно выявить при помощи аналитической группировки. Для этого сгруппируем предприятия по выпуску продукции, интервал высчитываем по формуле :

Где К – число выделенных интервалов.

Получаем :

В итоге у нас получаются следующие интервалы :

41 – 53; 53 – 65; 65 – 77; 77 – 89; 89 – 101

Строим рабочую таблицу.

№ группы	Группировка предприятий по объему продукции, млн.руб.	№ предприятия	Выпуск продукции млн.руб Х	Прибыль млн.руб. У	У2
I	41-53	3	41	12,1	146,41
7	45	12,8	163,84
12	48	13	169
16	52	14,6	213,16
		4	186	52,5	692,41
В среднем на 1 предприятие	46,5	13,1
II	53-65	1	65	15.7	264.49
4	54	13.8	190,44
8	57	14.2	201,64
13	59	16.5	272,25
17	62	14.8	219,04
22	64	15	225
		6	361	90	1372,86
В среднем на 1 предприятие	60,1	15
III	65-77	5	66	15,5	240,25
9	67	15,9	252,81
14	68	16,2	262,44
18	69	16,1	259,21
20	70	15,8	249,64
21	71	16,4	268,96
23	72	16,5	272,25
25	73	16,4	268,96
26	74	16	256
28	75	16,3	265,69
30	76	17,2	295,84
		11	781	178,3	2892,05
В среднем на 1 предприятие	71	16,2
IV	77-89	2	78	18	324
6	80	17,9	320,41
10	81	17,6	309,76
15	83	16,7	278,89
19	85	16,7	278,89
24	88	18,5	342,25
		6	495	105,4	1854,2
В среднем на 1 предприятие	82,5	17,6
V	89-101	11	92	18,2	331,24
27	96	19,1	364,81
29	101	19,6	384,16
		3	289	56,9	1080,21
В среднем на 1 предприятие	96,3	18,9
	ИТОГО	2112	483,1
	В среднем	71,28	16,16

Теперь по данным рабочей таблицы строим итоговую аналитическую таблицу:

Группы предприятий по объему продукции, млн.руб	Число пр-тий	Выпуск продукции, млн.руб.	Прибыль, млн.руб
Всего	В среднем на одно пр-тие	Всего	В среднем на одно пр-тие
41-53	4	186	46,5	52,5	13,1
53-65	6	361	60,1	90	15
65-77	11	781	71	178,3	16,2
77,89	6	495	82,5	105,4	17,6
89-101	3	289	96,3	56,9	18,9
	30	2112	356,4	483,1	80,8

По данным аналитической таблицы мы видим, что с приростом объема продукции, средняя прибыль на одно предприятие возрастает. Значит, между исследуемыми признаками существует прямая корреляционная зависимость.

Строим расчетную таблицу :

Группы предприятий по объему продукции, млн.руб	Число пр-тий f>k>	Прибыль, млн.руб	(у>k>-у) 2 f>k>	у2
Всего	В среднем на одно пр-тие Y>k>
41-53	4	52,5	13,1	36	692,41
53-65	6	90	15	7,3	1372,86
65-77	11	178,3	16,2	0,11	2892,05
77,89	6	105,4	17,6	13,5	1854,2
89-101	3	56,9	18,9	23,5	1080,21
	30	483,1	80,8	80,41	7891,73

В
ычисляем коэффициент детерминации по формуле :

Г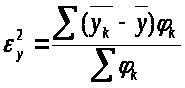
де - межгрупповая дисперсия находящаяся по формуле :

о
бщая дисперсия результативного признака, находится по формуле :

Т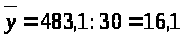еперь находим

Для каждой группы предприятий рассчитаем значение

и вносим в таблицу.

Н
аходим межгрупповую дисперсию :

Для нахождения общей дисперсии, нужно рассчитать :

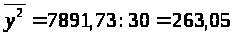где - количество предприятий и

получаем :

Рассчитываем общую дисперсию :

получаем :

Вычисляем коэффициент детерминации :

получаем : , или 70,3 %

Следовательно, на 70,3 % вариация прибыли предприятия зависит от вариации выпуска продукции и на 29,7 % зависит от неучтенных факторов.

Эмпирическое корреляционное отношение составляет :

Это говорит о том, что корреляционная связь играет существенную роль между стоимостью произведенной продукции и суммой прибыли.

Задача № 3

Динамика капитальных вложений характеризуется следующими данными, в сопоставимых ценах, млрд. руб. :

Год. Показатель.	1-й	2-й	3-й	4-й	5-й
Капитальные вложения всего : В том числе	136,95	112,05	84,66	74,7	62,3
производственного назначения	97,35	79,65	60,18	53,10	41,40
непроизводственного назначения	39,6	32,4	24,48	21,6	20,9

Для изучения интенсивности изменения объема капитальных вложений вычислите :

Абсолютные приросты, темпы роста и прироста ( цепные и базисные ) общего объема капитальных вложений. Результаты представьте в таблице.

Для общего объема капитальных вложений, в том числе производственного и непроизводственного назначения :

а) средний уровень ряда динамики;

б) среднегодовой темп роста и прироста.

Осуществите прогноз капитальных вложений на ближайший год с помощью среднего абсолютного прироста и среднего темпа роста.

Определите основную тенденцию развития общего объема капитальных вложений методом аналитического выравнивания, осуществите прогноз на ближайший год.

Изобразите динамику капитальных вложений на графике. Сделайте выводы.

Решение :

Поскольку в данном нам динамическом ряду каждый уровень характеризует явление за определенный отрезок времени, то этот ряд будет интервальным.

Для расчета абсолютного прироста цепной используем формулу :

Д

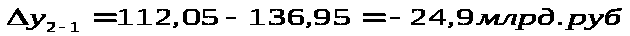
ля расчета базисного прироста используем формулу :

Д

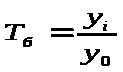
ля расчета


темпа роста цепной используем формулу :

Д




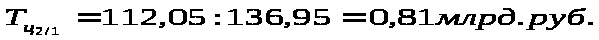
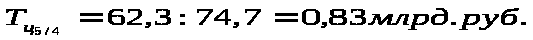
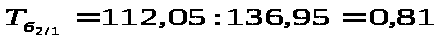
ля расчета темпа роста базисной используем формулу :

Д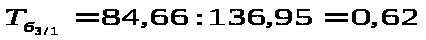



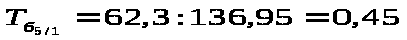
ля расчета темпа прироста цепной используем формулу :

Д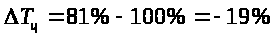





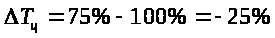
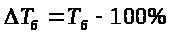
ля расчета темпа прироста базисной используем формулу :

Теперь представим в таблице выше рассчитанные показатели :

Абсолютные приросты, темпы роста и прироста (цепные и базисные) общего объема капитальных вложений.

Показатели Год	у>ц> >млрд.руб>	у>б> >млрд.руб>	Т>ц> >млрд.руб>	Т>б> >млрд.руб>	Т>ц> >%>	Т>б> >%>
1-й	-----	-----	-----	1	-----	-----
2-й	-24,9	-24,9	0,81	0,81	-19%	-19%
3-й	-27,39	-52,29	0,75	0,62	-25%	-38%
4-й	-9,96	-62,25	0,88	0,54	-12%	-46%
5-й	-12,4	-74,65	0,83	0,45	-17%	-55%

По данным таблицы можно сделать вывод, что общий объем капитальных вложений имеет тенденцию к снижению.

а
) Поскольку ряд динамический и интервальный, то для расчета среднего уровня ряда динамики мы будем использовать следующую формулу :

Д


ля общего объема капитальных вложений :

Производственного назначения :

Непроизводственного назначения :

б
) Рассчитываем среднегодовые темп роста и темп прироста по формулам :

С
реднегодовой темп роста :

д
ля общего объема капитальных вложений :

п

роизводственного назначения :

непроизводственного назначения :

Среднегодовой темп прироста :

д
ля общего объема капитальных вложений :

(следовательно в среднем общий объем капитальных вложений за 5 лет снизился на 18%.)

п
роизводственного назначения :

(следовательно в среднем объем капитальных вложений производственного назначения снизился на 20%)

н
епроизводственного назначения :

(следовательно в среднем объем капитальных вложений непроизводственного назначения снизился на 15%)

Д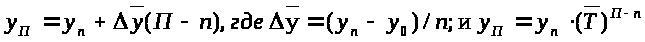
ля расчета прогноза капитальных вложений с помощью среднего абсолютного прироста и среднего темпа роста мы будем использовать следующие формулы :

П


одставив соответствующие значения получим :

Следовательно в ближайший год в среднем общий объем капитальных вложений сократится на 18,66 млрд. руб. и составит сумму от43,6 млрд. руб. до 51 млрд. руб.

4. А теперь мы при помощи метода аналитического выравнивания заменим эмпирический динамический ряд условным теоретическим динамическим рядом, так как он наиболее подходяще выглядит к формулам на основе прямой.

Показатель теоретического ряда рассчитывается при помощи метода наименьших квадратов.

Показатели	1-й	2-й	3-й	4-й	5-й	
Кап. вложения	136,95	112,05	84,66	74,7	62,3	470,66
t	-2	-1	0	1	2	0
y*t	-273,9	-112,05	0	74,7	124,6	-186,65
t2	4	1	0	1	4	10

У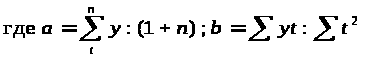
равнение прямой имеет вид : y(t)=a+bt,

а = 470,66 : 5 = 94,1 b = -186,65 : 10 = -18,7

у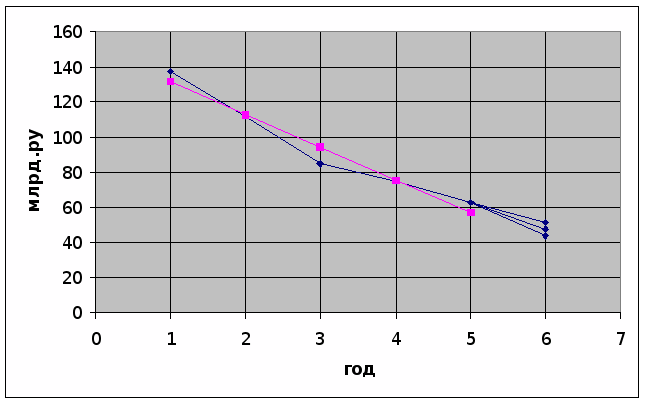
равнение имеет вид : y(t) = 94,1 – 18,7 t

По данным графика можно сделать вывод, что общий объем капиталовложений имеет тенденцию к снижению.

Расчет прогноза проведен с помощью следующих этапов :

значение верхней границы подсчитан по формуле среднего темпа роста.

значение нижней границы выявлено следующим образом : в уравнение прямой y(t) = 94,1 - 18,7t подставили значение t =3 потому что прогноз выполнялся на год вперед, значит t_>усл>= 3

прогнозируемое значение рассчитали по формуле среднего абсолютного прироста.

Задача № 4

Имеются следующие данные по двум предприятиям отрасли :

Предприятие	Реализовано продукции тыс. руб.	Среднесписочная численность рабочих, чел.
1 квартал	2 квартал	1 квартал	2 квартал
I	540	544	100	80
II	450	672	100	120

Определите :

Уровни и динамику производительности труда рабочих каждого предприятия.

Для двух предприятий вместе :

индекс производительности труда переменного состава;

индекс производительности труда фиксированного состава;

индекс влияния структурных изменений в численности рабочих на динамику средней производительности труда;

абсолютное и относительное изменение объема реализации продукции во 2 квартале (на одном из предприятий ) в результате изменения :

численности рабочих;

уровня производительности труда;

двух факторов вместе.

Покажите взаимосвязь между исчисленными показателями.

Решение :

1. Построим расчетную таблицу, где реализованную продукцию в первом квартале обозначим V_>0>, а во втором как V_>1> и среднесписочную численность как S_>0> и S_>1>.

Предприятие	V0=W0*S0 Тыс. руб.	V1=W1*S1 Тыс. руб.	S0 Чел.	S1 Чел.	W0=V0:S0 Руб.	W1=V1:S1 Руб.	Iw=W1:Wo Руб.	W0S0	D0=S0:T0 Чел	D1=S1:T1 Чел	W0D0	W1D1	W0D1
I	540	544	100	80	5,4	6,8	1,3	432	0,5	0,4	2,7	2,72	2,16
II	450	672	100	120	4,5	5,6	1,2	540	0,5	0,6	2,25	3,36	2,7
	990	1216	200	200				972	1	1	4,95	6,08	4,86

2
. (а) Для расчета индекса производительности труда переменного состава и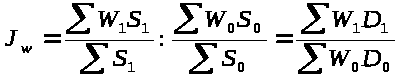
спользуем следующую формулу :

получаем : J_>w>=6,08 : 4,95=1,22

Индекс показывает изменение среднего уровня производительности труда в однородной совокупности под влиянием двух факторов :

изменение качественного показателя W (производительности труда) у отдельных предприятий;

изменение доли, с которой каждое значение W входит в общий объем совокупности.

(
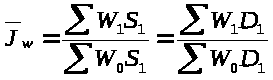
б) Для расчета индекса производительности труда фиксированного состава используем следующую формулу :

получаем :

Индекс показывает изменение среднего уровня только под влиянием изменения индивидуальных значений качественного показателя в постоянной структуре.

(в) Для расчета индекса влияния структурных изменений в численности рабочих на динамику средней производительности труда используем следующую формулу :

получаем : J_>w(d)>=4,86 : 4,95 = 0,98

Р
ассчитанные выше показатели взаимосвязаны между собой количественно, это определяется формулой :

получаем : J_>w>=6,08 : 4,95=1,22

(г) Произошедшее абсолютное и относительное изменение объема продукции во 2-м квартале зависело от следующих факторов :

численность рабочих :

 q(S) = (S_>1>-S_>0>)W_>0>

получаем : q(S) = (80 – 100) * 5,4 = -108

уровень производительности труда :

q(W) = (W_>1>-W_>0>)S_>1>

получаем : q(W) = (6,8 – 5,4) * 80 = 112

обоих факторов вместе :

q = q(S) +q(W)

получаем : q = -108 + 112 =4

Вывод : Поскольку индекс производительности труда переменного состава равен 1,22 или 122%, значит, средняя производительность труда по двум предприятиям возросла на 22%. Индекс производительности труда фиксированного состава равен 1,25 или 125%, значит, средняя производительность труда по двум предприятиям возросла на 25%. Индекс структурных сдвигов равен 0,98 или 98%, значит, средняя производительность труда по двум предприятиям снизилась на 2% за счет изменения структуры.

При условии, что произошедшие изменения производительности труда не сопровождались бы структурными перераспределениями среднесписочной численности рабочих в 1-м и 2-м квартале, то средняя производительность труда по двум предприятиям возросла бы на 25%. Изменение численности рабочих привело к снижению производительности труда на 2%. Но одновременное воздействие двух факторов увеличило среднюю производительность труда по двум предприятиям на 22%.

Задача № 5

Средние запасы материала на предприятии, составившие в первом квартале 200 м², сократились во втором на 30%. При этом, если ранее расход материала в среднем за сутки составлял 40 м²,то теперь он снизился до 32 м².

Определите :

За каждый квартал :

а) коэффициенты оборачиваемости производственных запасов;

б) продолжительность одного оборота в днях;

в) относительные уровни запасов (коэффициенты закрепления)

За второй квартал в сравнении с первым :

а) ускорение (замедление) оборачиваемости запасов в днях;

б) величину среднего запаса высвободившегося (осевшего, закрепившегося) в результате ускорения (замедления) его оборачиваемости.

Решение :

(а) Для расчета коэффициента оборачиваемости производственных запасов

и
спользуем формулу :

Для нахождения средних запасов во втором квартале мы воспользуемся данными задачи :

СЗ_>0 >= 200

i_>сз >=1 - 0,3 = 0,7

СЗ_>1 >= ?

СЗ_>1 >= i_>сз >* СЗ_>0 >=0,7 * 200 = 140 кв.м.

Коэффициент оборачиваемости за I квартал :

40*90=3600 кв.м. – квартальный расход материалов.

К_>обор>= 3600 : 200 = 18 оборотов.

Коэффициент оборачиваемости за II квартал :

32*90=2880 кв.м. – квартальный расход материалов.

= 2880 : 140 = 20,6 оборотов.

(б) Для расчета продолжительности одного оборота в днях используем формулу :

Д = Период : К_>обор>

В 1-ом квартале : Д = 90 : 18 = 5 дней.

Во 2-ом квартале : Д = 90 : 20,6 = 4,37 дней.

(в) Для расчета относительных уровней запасов (коэффициент закрепления) воспользуемся формулой :

К_{>закреп}>= Средние запасы за период : Расход материала за период.

В 1-ом квартале : К_{>закреп}>= 200:3600=0,055 кв.м. запасов на 1 руб расход. матер.

Во 2-ом квартале : К_{>закреп}>= 140:2880=0,0486 кв.м. запасов на 1 руб расход. матер.

2. (а) Для расчета ускорения (замедления) оборачиваемости запасов в днях используем формулу :

Д_>отч.> - Д_>баз.>=если знак « - » то произошло ускорение оборачиваемости.

« + » то произошло замедление оборачиваемости.

Произведем вычисления : 4,37 – 5 = -0,63 дня, следовательно произошло ускорение оборачиваемости.

(


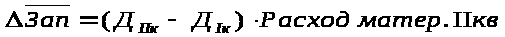
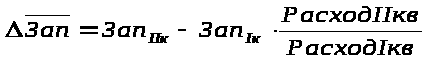
б) Для расчета величины среднего запаса высвободившегося (осевшего, закрепившегося) в результате ускорения (замедления) его оборачиваемости используем следующие формулы :

П


роизведем вычисления :

Аналитическая таблица.

	Средние запасы материала на предпр.	Расход матер. в среднем за сутки.	Коэф. оборач запасов.	Продолж. одного оборота в днях.	Коэф. закр. запасов	Ускор. Или замедл обор вдня	Величина среднего запаса.
I кв.	200	40	18	5	0,055	-0,63	-20 кв.м.
II кв.	140	32	20,6	4,37	0,0486

Вывод : При условии что оборачиваемость производственных запасов не изменится, то во 2-ом квартале расход материалов составит 2880 кв.м., но в следствие того, что оборачиваемость возросла ( 20,6 : 18 = 1,144) на 14,4% то производственных запасов понадобилось на 20 кв.м. меньше.

Список использованной литературы.

« Общая теория статистики » Учебник М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцев. Москва «Инфра-М» 1998г.

« Теория статистики » В.М. Гусаров. Москва «Аудит» « ЮНИТИ» 1998г.

« Теория статистики » Учебник под редакцией профессора Р.А. Шамойловой. Москва «Финансы и статистика» 1998г.

11 / IV / 2000 г.