Электротехника (работа 2)

TYPE=RANDOM FORMAT=PAGE>26

Векторное изображение электрических величин.

При расчёте цепей переменного тока часто приходится производить операции сложения и вычитания токов и напряжений. Когда токи и напряжения заданы аналитически или временными диаграммами, эти операции оказываются весьма громоздкими. Существует метод построения векторных диаграмм, который позволяет значительно упростить действия над синусоидальными величинами. Покажем, что синусоидальная величина может быть изображена вращающимся вектором.

Пусть вектор I_>m> вращается с постоянной угловой частотой против часовой стрелки. Начальное положение вектора I_>m> задано углом (рис.1). Проекция вектора I_>m> на ось y определяется выражением , которое соответствует мгновенному значению переменного тока. Таким образом, временная диаграмма переменного тока является развёрткой по времени вертикальной проекции вектора I_>m>, вращающегося со скоростью .

Изображение синусоидальных величин с помощью векторов даёт возможность наглядно показать начальные фазы этих величин и сдвиг фаз между ними.

На векторных диаграммах длины векторов соответствуют действующим значениям тока, напряжения и ЭДС, так как они пропорциональны амплитудам этих величин.

На рис.2 показаны векторы Е_>1> и Е_>2> с начальными фазами и и сдвигом фаз.

Совокупность нескольких векторов, соответствующих нулевому моменту времени, называют векторной диаграммой. Необходимо иметь в виду, что на векторной диаграмме векторы изображают токи (напряжения) одинаковой частоты.

Министерство образования Российской Федерации

НГАВТ

Реферат

по курсу «Электротехника и основы электроники»

Выполнил:

Студент III курса ОП

Шевченко Т.В.

Вариант №8

Преподаватель:

Горелов В.П.

Томск 2003

TYPE=RANDOM FORMAT=PAGE>10

Логические элементы.

Логические цепочки трудно анализировать в словесной форме. Поэтому, на помощь приходит алгебра логики, основы которой были заложены английским математиком Булем.

В свою очередь, математические построения Буля могут моделироваться с помощью электрических или электронных схем. Эти схемы, широко применяемые в вычислительной технике, и называются логическими элементами. Рассмотрим некоторые из них.

(рис.1)

На рис.1 представлена логическая схема, моделирующая рассуждения, в которые входит слово ИЛИ. Из схемы видно, что сигнал на выходе возникает, если сигнал поступит на первый или на второй вход или на оба входа сразу. Сопротивления предназначены для обеспечения согласованности триггера с выходами схем, к которым он присоединён (источниками сигналов), и входом схемы, которой он выдаёт свой сигнал. Полупроводниковые диоды обеспечивают отсутствие замыкания входов друг на друга.

На рис.2 изображена схема, в которой выходной сигнал появляется только тогда, когда на оба входа одновременно поданы сигналы. Действительно, при отсутствии на входе сигнала ток от источника (+Е) проходит через сопротивление R и одно или оба сопротивления шунтирующие вход. При этом напряжение источника падает на сопротивлении R и напряжение на выходе схемы близко к нулю. Если на входы поступают импульсы, то на входных сопротивлениях появляется падение напряжения определённой полярности. Эти напряжения направлены навстречу ЭДС источника и ток

рис.2

через сопротивление R не проходит, вследствие чего на выходе действует высокое напряжение (U_>вых>=Е).

Схему на рис.1 условно называют квадратом со словом ИЛИ (см. рис.3). Отсутствие сигнала обозначено «0», а наличие – «1». Анализируя состояние схемы при различных комбинациях сигналов на входе, можно составить следующую таблицу:

0+0=0, 0+1=1,

1+0=1, 1+1=1.

Эта таблица совпадает (кроме последней строки) с таблицей сложения двоичных чисел. Поэтому схему ИЛИ называют схемой логического сложения или схемой дизъюнкции.

рис.3

Схему на рис.2 обозначают квадратом с буквой И, так как сигнал на выходе появляется тогда, когда есть сигнал на первом и втором входах. Для неё аналогичным образом можно составить таблицу, отражающую соотношение сигналов на входе и выходе:

0*0=0, 1*0=0,

0*1=0, 1*1=1.

Эта таблица совпадает с таблицей умножения двоичных чисел. Поэтому схему И называют схемой логического умножения или схемой конъюнкции.

В вычислительной технике широко применяют также схему НЕ, у которой сигнал на выходе равен «1», если сигнал на входе равен «0», и, наоборот, на выходе равен «0», если на входе «1». Применяются и некоторые другие логические элементы.

TYPE=RANDOM FORMAT=PAGE>20

Магнитные цепи.

В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т.д.) входят магнитные цепи.

Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и, вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.

В конструктивном отношении магнитные цепи выполняют разветвлёнными и неразветвлёнными, причём применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.

Переменный магнитный поток в катушке с магнитопроводом. Конструкции магнитопроводов и их функциональные назначения в электротехнических устройствах переменного тока весьма разнообразны. Рассмотрим катушки с неразветвлёнными магнитопроводами из ферромагнитного материала.

e=U

e_>l>

Рис.1

У катушки с магнитопроводом, подключенной к источнику синусоидального напряжения _>>(рис.1), переменный ток i в обмотке возбуждает в магнитопроводе переменный магнитный поток Ф, который индуктирует в обмотке ЭДС самоиндукции _>>. Если пренебречь активным сопротивлением обмотки и считать, что все магнитные линии поля катушки замыкаются только по магнитопроводу, то на основании второго закона Кирхгофа для контура, обозначенного на рис.1 пунктиром, получим уравнение:

_>> (1)

или:

_>> (2)

Из этого уравнения найдём закон изменения во времени магнитного потока. Так как:

_>>,

то:

_>>.

Постоянная интегрирования А равна некоторому постоянному магнитному потоку, которого нет в магнитопроводах аппаратов переменного тока в установившемся режиме работы. Следовательно постоянная А = 0 и магнитный поток6

_>>, (3)

где:

_>>, (4)

т.е. при синусоидальном напряжении между выводами катушки магнитный поток в магнитопроводе также синусоидальный.

Так как действующие значения напряжения U между выводами катушки и ЭДС самоиндукции E_>L> (1), то из (4) получим:

_>>. (5)

Последнее соотношение применяют для расчётов ЭДС, индуктируемых в обмотках трансформаторов; поэтому его часто называют уравнением трансформаторной ЭДС.

При определении магнитного потока не учитывались активное сопротивление обмотки и наличие магнитных линий поля катушки, которые частично и полностью замыкаются помимо магнитопровода. Для выявления характера изменения магнитного потока в магнитопроводе во времени это не имеет сколько-нибудь существенного значения. Но при других расчётах активное сопротивление обмотки и магнитные линии поля катушки, которые неполностью замыкаются по магнитопроводу, часто надо учитывать. Соотношения (3; 4; 5) можно рассматривать лишь как ориентировочно связывающие действующие значения напряжения U между выводами катушек и ЭДС самоиндукции E_>L> с амплитудой магнитного потока Ф_>м> в магнитопроводе и числом витков w катушки.

TYPE=RANDOM FORMAT=PAGE>3

Получение однофазного переменного тока. Основные параметры переменного тока.

Переменным называют ток, изменение которого по значению и направлению повторяется через равные промежутки времени.

Рассмотрим принцип действия простейшего генератора переменного тока. Между полюсами электромагнита или постоянного магнита (рис 1) расположен цилиндрический ротор (якорь), набранный из листов электротехнической стали. На роторе укреплена катушка, состоящая из определенного числа витков проволоки. Концы этой катушки соединены с контактными кольцами, которые вращаются вместе с ротором. С контактными кольцами связаны неподвижные контакты (щетки), с помощью которых катушка соединяется с внешней цепью. Воздушный зазор между полюсами и ротором профилируют так, чтобы индукция магнитного поля в нём менялась по синусоидальному закону:

где - угол между плоскостью катушки и нейтральной плоскостью .

Когда ротор вращается в магнитном поле со скоростью в активных сторонах катушки наводится ЭДС индукции

_>>

где _>>- угол между направлени-

ями векторов индукции магнит-

ного поля В и скорости v;

l- длина активных сторон витков катушки.

Магнитное поле в зазоре расположено так, что угол _>>. Таким образом,

_>>_>>

При числе витков _>> число активных сторон катушки равно _>>. Тогда ЭДС катушки: _>>, где _>>- максимальное значение ЭДС.

Таким образом, ЭДС генератора меняется по синусоидальному закону. Если к зажимам генератора подключить нагрузку, то через неё пойдёт ток, который также будет изменяться по синусоидальному закону.

Для количественной характеристики переменного тока служат следующие параметры.

1. Мгновенные значения тока i, напряжения u, ЭДС е - их значения в любой момент времени:_>>; _>>; _>>.

2. Амплитудные значения тока _>>, напряжения _>>, ЭДС _>>- максимальные значения мгновенных величин I, u и e (см рис)

3. Период Т- промежуток времени, в течение которого ток совершает полное колебание и принимает прежнее по величине и знаку мгновенное значение.

4. Угловая скорость характеризует скорость вращения катушки генератора в магнитном поле. На практике для получения нужной частоты при относительно малой угловой скорости генераторы имеют несколько пар полюсов р.

На рисунке показан генератор с двумя парами полюсов, в котором за один оборот катушки ЭДС изменяет положение 4 раза или 2р раз. Введём понятие электрического угла _>эл>: _>эл>=. Тогда скорость определяет электрическую угловую скорость катушки:

_>эл>/(рТ) =р2/(рТ) =2/Т,

где р2 - электрический угол, соответствующий одному обороту катушки в пространстве; рТ – время, соответствующее р периодам тока.

Таким образом, эта формула определяет электрическую частоту вращения.

5. Циклическая частота f – величина, обратная периоду Т, т.е.f=1/T,

и характеризующая число полных колебаний тока за 1с.

Единицей циклической частоты является герц (Гц):

[f]=1/c= Гц.

6. Действующие значения тока I, напряжения U и ЭДС Е. Для измерения переменного тока, напряжения и ЭДС вводят понятие действующего значения. Переменный ток сравнивают с постоянным по тепловому действию. Если положение реостатов подобрано так, что количество теплоты, выделяемой в схемах (см. рис) на резисторе R, оказывается одинаковым, то можно считать, что и токи в схемах одинаковы.

Найдём соотношение между действующим и амплитудным значением тока. Согласно определению, _>>_>->количество теплоты, выделяемое постоянным и переменным токами): ,

где i²Rdt – количество теплоты, выделяемое переменным током за время dt.

Приравняв эти выражения, получим: .

Сократив на общий множитель R и учтя, что ,найдём выражение для действующего значения тока: ,

или после интегрирования:

TYPE=RANDOM FORMAT=PAGE>7

Основные понятия о переходных процессах

в электрических цепях.

Для изучения переходных процессов в любой или сложной цепи необходимо рассмотреть общие сведения о них. В числе таких сведений отметим причины возникновения переходных процессов, основные определения и два закона коммутации, на которых основаны исследования переходных процессов.

Причины возникновения переходных процессов. Электромагнитные процессы, происходящие в электрических цепях при переходе от одного установившегося режима к другому, называют переходными процессами.

Время, в течение которого продолжается переходный процесс в электрической цепи, называют переходным периодом.

Величины токов и напряжений, изменяющиеся в течение переходного периода, называют переходными токами и напряжениями.

Переходные процессы возникают вследствие изменения ЭДС в цепи, напряжения, приложенного к цепи, или в связи с изменением её параметров – сопротивления, индуктивности или ёмкости.

Непосредственными причинами возникновения переходных процессов могут быть: коммутационные изменения режимов, т.е. включения и выключения источников питания, приёмников энергии; короткие замыкания на участках электрических цепей; изменения механической нагрузки электродвигателей и др.

Продолжительность переходных процессов в электрических цепях чаще всего составляет десятые и сотые доли секунды. Однако значения характера их очень важно, так как и за малое время возможно резкие увеличения токов и напряжений, которые могут оказаться опасными для электрических установок.

Соотношение длительностей установившихся и переходных режимов может быть самым различным и зависит от условий эксплуатации и назначения электрических цепей. Одни из них по продолжительности практически всё время работают в установившемся режиме (двигателей с длительной, не меняющейся нагрузкой, лампы электрического освещения), другие, наоборот, непрерывно находятся в переходном режиме (двигатели с повторно-кратковременной нагрузкой, линии связи во время передачи информации и др.).

Первый закон коммутации применяется к цепям, обладающим индуктивностью. Согласно этому закону, ток в индуктивности не может изменяться скачком. Поэтому мгновенное значение тока в ветви с индуктивностью в переходного периода остаётся таким, каким оно было в последний момент предшествующего установившегося режима.

Справедливость первого закона коммутации следует из простых рассуждений, которые изложим применительно к случаю включения катушки индуктивности на

u_>r>

u_>L>

e_>L>

остоянное напряжение U (рис.1)

До замыкания рубильника Р установившийся режим характеризуется тем, что ток в цепи, напряжение активное u_>r>_>> и индуктивное u_>L> равны нулю.

Рис.1

момента замыкания рубильника возникает переходный процесс, в течение которого ток в катушке увеличивается до некоторого значения i = I, изменяются и напряжения u_>r> и u_>L>. Электрическое состоя-

ние цепи по схеме на рис.1 в любой момент переходного периода характеризуется уравнением:

. (1)

Это уравнение выражает баланс напряжений в цепи: часть приложенного к цепи напряжения компенсирует падение напряжения в сопротивлении (ir), а другая часть уравновешивает возникающую при изменении тока ЭДС самоиндукции.

В установившемся режиме при замкнутом рубильнике Р ток в цепи постоянный, т.е. скорость изменения тока равна нулю:, поэтому и индуктивное напряжение u_>L>_>>равно нулю. Напряжение источника полностью приложено к сопротивлению r, и ток в цепи определяется согласно закону Ома:

(2)

Предположим, что переходный период отсутствует и ток в катушке мгновенно (dt=0) от нуля до конечного значения I. Тогда скорость изменения тока должна быть равна бесконечности _>>. Но это противоречит уравнению (1), в котором напряжение источника U- конечная величина. Изменение тока скачком означало бы также, что энергия магнитного поля катушки увеличилась скачком от 0 до _>>. Для мгновенного изменения запаса энергии в магнитном поле цепи требуется источник бесконечно большой мощности _>>, что лишено физического смысла.

Из первого закона коммутации следует, что в начальный момент после замыкания рубильника (при t=0) ток в цепи равен нулю (_>>), падение напряжения в сопротивлении _>>, а индуктивное напряжение равно напряжению источника _>> и цепь как бы разомкнута индуктивностью.

Второй закон коммутации применяется к цепям, обладающим ёмкостью. Согласно этому закону, напряжение на ёмкости не может измениться скачком. Поэтому мгновенное напряжение на ёмкости в первый момент переходного периода остаётся таким, каким оно было в последний момент предшествующего устоявшегося режима.

Рассуждения, подтверждающие второй закон коммутации, проведём применительно к случаю зарядки конденсатора через резистор (включение цепи с r и C на постоянное напряжение, рис.2). До замыкания рубильника Р установившийся режим характеризуется тем, что в цепи, напряжения на резисторе и конденсаторе равны нулю.

U

U_>r>

U_>c>

момента замыкания рубильника возникает переходный процесс, в течение которого напряжение на конденсаторе

увеличивается до напряжения источника U, изменяются ток в цепи и напряжение на резисторе.

Рис.2

лектрическое состояние цепи (рис.2) в любой момент переходного периода характеризуется уравнением, составленным

по второму закону Кирхгофа:

_>>.

Ток в цепи пропорционален скорости изменения напряжения на конденсаторе:

_>>. (3)

Учитывая это, получаем:

_>>. (4)

Приложенное к цепи напряжение делится на две части: одна из них _>> компенсирует падение напряжения в резисторе, а другая (_>>) равна напряжению в конденсаторе.

В установившемся режиме при замкнутом рубильнике Р напряжение на конденсаторе не изменяется , т.е. скорость изменения напряжения на конденсаторе равна нулю:_>>, поэтому и ток в цепи равен нулю: _>>. Напряжение на резисторе равно нулю, и, следовательно, напряжение источника полностью приложено к конденсатору:_>> (т.е. цепь разомкнута конденсатором).

Доказательства существования переходного периода при зарядке конденсатора аналогичны тем, которые ранее были приведены для цепи с катушкой индуктивности.

Предложим, что в момент замыкания рубильника напряжение на конденсаторе изменилось скачком от 0 до U. Такое предположение означает конечное изменение напряжения за время, равное нулю, т.е. _>>, что противоречит уравнению (4), в котором напряжение источника является конечной величиной. Кроме того, при изменении напряжения на конденсаторе скачком энергия электрического поля должна увеличиться мгновенно от 0 до _>>. Для такого скачкообразного изменения энергии требуется источник бесконечно большой мощности, чего не может быть в действительности.

Из второго закона коммутации следует, что начальный момент переходного периода (при t=0) напряжение на конденсаторе равно нулю _>> (конденсатор как бы замкнут накоротко). Напряжение на резисторе равно напряжению источника _>>, а ток в цепи _>>.

Содержание

1. Получение однофазного переменного тока. Основные параметры переменного тока. с. 1

2. Основные понятия о переходных процессах в электрических цепях. с.3

3. Основные логические элементы И, ИЛИ, НЕ и их применение. с.8

4. Триггеры. с.11

5. Трёхфазный ток. с.15

6. Магнитные цепи. с.19

7. Трёхфазные и измерительные трансформаторы. Автотрансформаторы. с.21

КПД трансформатора.

8. Векторное изображение электрических величин. с.25

Список используемой литературы.

1. Касаткин А.С. Немцов М.В.

Электротехника: Учеб. пособие для вузов.-

4-е изд., перераб.- М.: Энергоатомиздат, 1983.-

440с., ил.

2. Евдокимов Ф.Е.

Теоретические основы электротехники.

Изд. 4-е, перераб. и доп. Учебник для энергетич.

и электротехнич. специальностей техникумов.

М. «Высш. Школа», 1975.

496 с. с ил.

3. Данилов И.А., Иванов П.М.

Общая электротехника с основами электроники

Уч. Пособие для студентов неэлектрических

специальностей, средн. специальных уч. Заведений

изд. 3-е.-М.: «Высш. Школа», 1998.

752 с. ил.

4. Китунович Ф.Г.

Электротехника.

3-е изд., переработанное и дополненное.

Минск. «Высш. Школа», 1991.

430 с. ил.

5. Касаткин А.С.

Основы электротехники.

М.-Л., изд-во «Энергия», 1966.

712 с. ил.

TYPE=RANDOM FORMAT=PAGE>25

Трёхфазные и измерительные трансформаторы.

Автотрансформаторы. КПД трансформатора

В линиях электропередачи используют в основном трёхфазные силовые трансформаторы. Магнитопровод трёхфазного трансформатора имеет три стержня, на каждом из которых размещаются две обмотки одной фазы.

Особенностью трёхфазного трансформатора является зависимость коэффициента трансформации линейных напряжений от способа соединения обмоток. Применяются главным образом три способа соединения обмоток трёхфазного трансформатора: соединение первичных и вторичных обмоток звездой (рис а); соединение первичных обмоток звездой, вторичных - треугольником (рис б); соединение первичных обмоток треугольником, вторичных обмоток звездой (рис в).

Способы соединения обмоток трёхфазного трансформатора.

Обозначим отношение чисел витков обмоток одной фазы буквой R,что соответствует коэффициенту трансформации однофазного трансформатора и может быть выражено через отношение фазных напряжений:

R=w_>2/>w_>1>=U_>Ф2>/U_>Ф1>

Обозначим коэффициент трансформации линейных напряжений буквой с:

При соединении обмоток по схеме звезда- звезда

с=U_>Л2>/U_>Л1>=U_>Ф2>/(U_>Ф1>)=R

При соединении обмоток по схеме звезда-треугольник

с= U_>Л2>/U_>Л1=> U_>Ф2>/(U_>Ф1>)=R/

При соединении обмоток по схеме треугольник- звезда

с=U_>Л2>/U_>Л1>=U_>Ф2>/U_>Ф1>=R

Таким образом, при одном и том же числе витков обмоток трансформатора можно в увеличить или уменьшить его коэффициент трансформации, выбирая соответствующую схему соединения обмоток.

Принципиальная схема автотрансформатора изображена на рисунке.

У автотрансформатора часть витков первичной обмотки используется в качестве вторичной обмотки, поэтому помимо магнитной связи имеется электрическая связь между первичной и вторичной цепями. В соответствии с этим энергия из первичной цепи во вторичную передаётся как с помощью магнитного потока, замыкающегося по магнитопроводу, так и непосредственно по проводам.

Поскольку формула трансформаторной ЭДС применима к обмоткам автотрансформатора так же, как и к обмоткам трансформатора, коэффициент трансформации автотрансформатора выражается известными отношениями

R=w_>2>/w_>1>=E_>2>/E_>1>=U_>2>/U_>1>=I_>1>/I_>2>.

Вследствие электрического соединения обмоток через часть витков, принадлежащую одновременно первичной и вторичной цепям, проходят токи I_>1> и I_>2>, которые направлены встречно и при небольшом коэффициенте трансформации мало отличаются друг от друга по значению. Поэтому их разность оказывается небольшой и обмотку w_>2>_>>можно выполнить из тонкого провода.

Автотрансформаторы применяют для пуска мощных двигателей переменного тока, регулирования напряжения в осветительных сетях, а также в других случаях, когда необходимо регулировать напряжение в небольших пределах.

Измерительные трансформаторы напряжения и тока используют для включения измерительных приборов, аппаратуры автоматического регулирования и защиты в высоковольтные цепи.

Измерительные трансформаторы напряжения служат для включения вольтметров и обмоток напряжения измерительных приборов (рис а). Поскольку обмотки имеют большое сопротивление и потребляют маленькую мощность, можно считать, что они работают в режиме холостого хода.

Измерительные трансформаторы тока используют для включения амперметров и токовых катушек измерительных приборов (рис б). Эти катушки имеют очень маленькое сопротивление, поэтому трансформаторы тока практически работают в режиме короткого замыкания.

Результирующий магнитный поток в магнитопроводе трансформатора равен разности магнитных потоков, создаваемых первичной и вторичной обмотками.

КПД трансформатора, как и всякой другой машины, определяется отношением полезной мощности ко всей подведённой. Полезной мощностью для трансформатора является мощность, снимаемая с вторичной обмотки, , а подведённой - мощность , идущая из сети в первичную обмотку. Так как в трансформаторе равен 0,96-099, то непосредственное определение его по формуле не даёт точных результатов из-за того, что ошибка в измерении соизмерима с погрешностью прибора.

Электрические потери в трансформаторе складываются из потерь в меди , вызванных нагреванием проводников обмоток трансформатора, и потерь в стали , вызванных гистерезисом и вихревыми потоками в сердечнике.

В таком случае КПД трансформатора может быть выражен упрощённой формулой

Потери мощности в меди определяются как сумма потерь в первичной и вторичной обмотках: .

Потери мощности в стали определяются величиной и частотой изменения магнитного потока и от нагрузки не зависят.

При работе трансформатора в рабочем режиме. Напряжение на вторичной обмотке считают равным номинальному напряжению , потери в стали постоянными . На практике при работе трансформатора ток во вторичной обмотке не всегда равен номинальному току . Поэтому вводится коэффициент нагрузки и КПД трансформатора определяется по следующей формуле: .

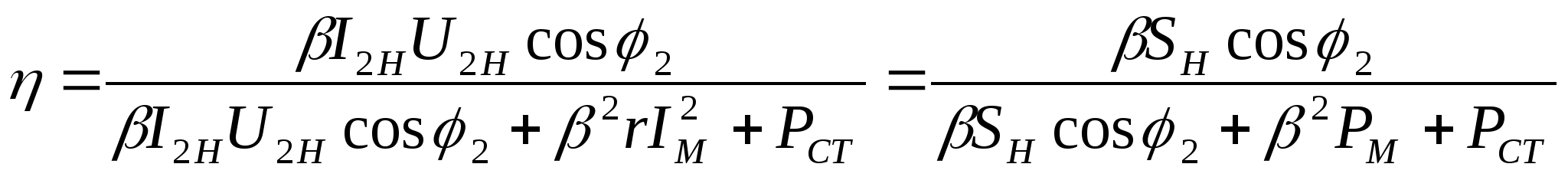Исследовав функцию на максимум, убеждаемся, что максимальный КПД трансформатора получается при равенстве потерь в меди и в стали, т.е. если ,то

Так как обычно , то максимальный КПД трансформатора получается при коэффициенте нагрузки 0,6…0,7, значит,

TYPE=RANDOM FORMAT=PAGE>14

Триггеры.

Триггер- Это схема с двумя устойчивыми состояниями.

На (рис 1) приведена упрощённая схема триггера, собранного на электронных лампах. Так как выходные сигналы таких триггеров имеют вид постоянных по значению напряжений, их называют потенциальными или статическими.

(рис 1)

Триггеры обеспечивают классификацию и запоминание импульсов, поступающих на вход. Если на вход поступает положительный импульс, то на одном из выходов устанавливается высокий потенциал, который сохраняется неограниченно долго, до поступления отрицательного импульса. Потенциал на другом входе в это время равен нулю. При поступлении на вход отрицательного импульса триггер переходит в другое состояние, при котором потенциал на втором выходе возрастает до максимума, а потенциал на первом уменьшается до нуля.

Рассмотрим работу потенциального триггера. Предположим, что входной сигнал отсутствует, а характеристики двух половин схемы абсолютно одинаковые. При подключении напряжения отрицательного смещения U_>см> обе лампы заперты. Если теперь подать анодное напряжение Е_>а>, то на обоих выходах появятся напряжения, равные (U_>вых1>=U_>вых2>=Е_>а>), приложенные через сопротивления R_>oc> к сеткам ламп и компенсирующие напряжение U_>см>. Лампы начнут открываться, чрез них пройдут анодные токи, создавая падение напряжения на R_>a>_>1>и R_>a>_>2>. Выходные напряжения U_>вых1>=Е_>а>-R_>a>_>1>I_>a>_>1> и U_>вых2>=Е_>а>-R_>a>_>21>I_>a>_>2> уменьшатся, их компенсирующее действие ослабнет и U_>см> частично прикроет обе лампы. В результате установится некоторое среднее положение, при котором через лампы проходят равные токи, а равные между собой выходные напряжение меньше анодного напряжения на IR_>a>_>1> и IR_>a>_>1> соответственно.

Такой усреднённый режим неустойчив и в действительности существовать не может, так как предположение об абсолютной симметрии схемы нереально. Пусть по случайным причинам U_>вых1> чуть превысило U_>вых2.> Тогда лампа Л_>2> откроется чуть больше, её анодный ток возрастёт и напряжение U_>вых2.> уменьшится, так как увеличится падение напряжения на R_>a>_>2>. С уменьшением U_>вых2> ослабнет его компенсирующее действие на сетку Л_>1.> Лампа Л_>1> немного прикроется, что приведёт к уменьшению анодного тока I_>a>_>1> и дальнейшему увеличению_>>U_>вых1>. При этом лампа Л_>2> откроется ещё больше и т.д. В конечном счете, в результате лавинообразного процесса лампа Л_>2> откроется полностью(I_>a>_>2>=I_>max>), а лампа Л_>1> полностью закроется (I_>a>_>1>=0). Напряжение U_>вых1> достигнет максимума U_>вых1>=Е_>а>, а U_>вых2> – минимума: U_>вых2>=Е_>а>-R_>a>_>2>I_>a>_>2>.

Мы разделили реальный процесс на логически связанные между собой этапы только для уяснения его сущности. На самом деле все изменения токов и напряжений происходят одновременно, и после включения триггер практически мгновенно устанавливается в одно из устойчивых состояний.

Предположим, что после включения анодного Е_>а> и сеточного U_>см> напряжений триггер установился в состояние, при котором лампа Л_>1> закрыта, U_>вых1> максимально, а лампа Л_>2> открыта и U_>вых2> минимально. Подадим на вход последовательно разнополярные импульсы. При поступлении импульса отрицательной полярности закроется на некоторое время лампа Л_>2>. Этого достаточно, чтобы состояние триггера изменилось, а лампа Л_>2> так и осталась закрытой по окончании импульса. Действительно, как только закроется Л_>2>, напряжение U_>вых2> возрастёт и откроет лампу Л_>1>. При этом U_>вых1> резко уменьшится и перестанет блокировать напряжение отрицательного смещения на лампе Л_>2>, в результате этого лампа Л_>2> будет закрыта уже не напряжением импульса, а напряжением U_>см>. До прихода следующего импульса триггер устойчиво поддерживает минимальное U_>вых1> и максимальное U_>вых2> напряжение. Через некоторое время на вход поступит положительный импульс, который вновь откроет лампу Л_>2>, и триггер перейдёт в первоначальное состояние.

Полная схема потенциального (статического) триггера изображена на рис.2 . Эта схема симметрична, напряжение смещения в ней создаётся ячейкой R_>см> C_>см>, а конденсаторы С, блокирующие сопротивления обратной связи, ускоряют переход триггера из одного состояния в другое. Триггер реагирует только на однополярные импульсы. Полярность импульсов определяется типом транзисторов.

(рис 2)

Динамические триггеры также имеют два состояния. При этом в одном состоянии напряжение на выходе равно нулю, а в другом – вырабатывается непрерывная последовательность импульсов.

Запуск триггера, сопровождаемый его переходом из одного состояния в другое, осуществляется подачей напряжения на базу или коллектор транзистора через специальную схему запуска.

Различают два вида запуска триггера: раздельный и счётный (общий).

При раздельном запуске импульсы на левый и правый транзисторы подаются поочерёдно. Причём используют две серии импульсов, смещённых во времени таким образом, чтобы максимумы импульсов одной серии приходились на интервалы между импульсами другой. Если при раздельном запуске подавать только одну серию однополярных импульсов, то состояние триггера меняться не будет.

При счётном запуске импульс одной серии одновременно подают на оба транзистора. При этом каждый импульс вызывает запуск триггера и переход его из одного состояния в другое.

TYPE=RANDOM FORMAT=PAGE>18

Трёхфазный ток.

Три синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые по фазе на , образуют трёхфазную симметричную систему. Аналогично получаются трёхфазные системы напряжений и токов.

В настоящее время трёхфазные системы получили широкое распространение, что объясняется главным образом следующими причинами: 1) при одинаковых условиях питание трёхфазным током позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными линиями; 2) при прочих равных условиях трёхфазный генератор дешевле, легче и экономичнее, чем три однофазных генератора такой же общей мощности; то же относится к трёхфазным двигателям и трансформаторам; 3) трёхфазная система токов позволяет получить вращающееся магнитное поле с помощью трёх неподвижных катушек, что существенно упрощает производство и эксплуатацию трехфазных двигателей; при равномерной нагрузке трёхфазный генератор создаёт на валу приводного двигателя постоянный момент в отличие от однофазного генератора, у которого мощность и момент на валу пульсируют с двойной частотой тока.

На рис.1 изображена схема простейшего трехфазного генератора, с помощью которой легко пояснить принцип получения трёхфазной ЭДС. В однородном магнитном поле постоянно- го магнита вращаются с постоянной угловой скоростью три рамки, сдвинутые в пространстве одна относительно другой на угол .

В момент времени t=0 рамка AX расположена горизонтально и в ней индуцируется ЭДС .

Точно такая же ЭДС будет индуцироваться и в рамке BY, когда она повернётся на и займёт положение рамки АХ. Следовательно, при t=0 .

Рассуждая аналогичным образом, находим ЭДС в рамке CZ:

На рис.2 представлен график мгновенных значений ЭДС е_>А> ,е_>В> ,е_>С> и векторная диаграмма трехфазной системы ЭДС.

е_>А>

е_>В>

е_>С>

Если к каждой из рамок AX, BY и CZ подсоединить нагрузку (посредством щёток и контактных колец), то в образовавшихся цепях появятся токи.

При симметричной нагрузке, когда все три нагрузочных сопротивления равны по значению и имеют одинаковый характер, синусоиды напряжений и токов изображаются графиками, аналогичными графику ЭДС. При этом начальные фазы токов определяются характером нагрузки, токи I_>A>_>>,I_>B> ,I_>C> равны по амплитуде и сдвинуты по фазе на один относительно другого.

Следует отметить, что в реальном трёхфазном генераторе три неподвижные обмотки размещаются на статоре, а магнитное поле, индукция которого распределена по синусоидальному закону, создаётся вращающимся ротором.

Трёхфазный генератор, соединённый проводами с трёхфазным потребителем, образуют трёхфазную цепь.

В трёхфазной цепи протекает трёхфазная система токов, т.е. синусоидальные токи с тремя различными фазами. Участок цепи, по которому протекает один из токов, называют фазой трёхфазной цепи.

Возможны различные способы соединения обмоток генератора с нагрузкой. В основном обмотки трёхфазного генератора соединяют звездой или треугольником. При этом число соединительных проводов от генератора к нагрузке варьирует от трёх до четырёх.

На электрических схемах трёхфазный генератор принято изображать в виде трёх обмоток, расположенных под углом друг к другу. При соединении звездой (рис.3) концы этих обмоток объединяют в одну точку, которую называют нулевой точкой генератора и обозначают О. Начала обмоток обозначают буквами А, В, С.

При соединении треугольником (рис.4) конец первой обмотки генератора соединяют с началом второй, конец второй – с началом третьей, конец третьей – с началом первой. К точкам А, В, С подсоединяют провода соединительной линии.

Отметим, что при отсутствии нагрузки ток в обмотках такого соединения отсутствует, так как геометрическая ЭДС Е_>А>_>,>_>>Е_>В>_>,> Е_>С> равна нулю.

Рассмотрим соединение генератора с нагрузкой, включенной звездой (рис.5).

_>>

Провод называют нулевым (четырёхпроводная цепь). В соответствии с первым законом Кирхгофа вектор тока в нулевом проводе

I_>0>=I_>A>+I_>B>+I_>C> .

Как отмечалось, при симметричной нагрузке, когда сопротивления Z_>A> ,Z_>B> и Z_>C> равны между собой и имеют одинаковый характер, векторы токов I_>A>_>>,I_>B> ,I_>C> равны по абсолютному значению и образуют трёхлучевую звезду, у которой углы между лучами равны .

Из геометрического построения, показанного на рис.6, следует, что в этом случае векторная сумма токов равна нулю: I_>A>+I_>B>+I_>C>=0.

Таким образом, при симметричной нагрузке нулевой провод не нужен. Получается схема трёхфазной трёхпроводной цепи, изображённая на рис.7.

Площадь поперечного сечения нулевого провода принимают равной половине площади поперечного сечения каждого из остальных трёх проводов (их сечения равны между собой).

Система ЭДС обмоток трёхфазного генератора, работающего в энергосистеме, всегда симметрична: ЭДС поддерживаются строго постоянными по амплитуде и сдвинутыми по фазе на .