Разработка средств оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов
1
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ “ЛЬВОВСКАЯ ПОЛИТЕХНИКА”
Озирковский Леонид Деонисиевич
УДК 621.396.9
РАЗРАБОТКА СРЕДСТВ ОЦЕНКИ ЭФФЕКТИВНОСТИ АЛГОРИТМОВ ПОИСКА И ОБНАРУЖЕНИЯ ЦЕЛЕЙ ПРИЦЕЛЬНЫХ РАДИОЭЛЕКТРОННЫХ КОМПЛЕКСОВ
05.12.17 - Радиотехнические и телевизионные системы
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Львов 2002
Диссертацией есть рукопись.
Работа выполнена в Национальном университете “Львовская политехника” Министерства науки и образования Украины
Научный руководитель: кандидат технических наук, доцент
Волочий Богдан Юрьевич,
Национальный университет “Львовская политехника”, доцент
Официальные оппоненты: доктор технических наук, с.н.с.
Клепфер Евгений Иванович,
Львовский научно-исследовательский радиотехнический институт,
главный научный сотрудник
кандидат технических наук
Лукенюк Адольф Антонович,
Львовский центр института космических исследований Национальной академии наук и Национального космического агентства Украины, заместитель директора
Ведущее учреждение – Национальный технический университет Украины “Киевский политехнический институт” (г. Киев), Министерство образования и науки Украины, кафедра радиотехнических устройств и систем
Защита состоится 30 апреля 2002 г. в 11 часу на заседании специализированного ученого совета Д 35.052.10 в Национальном университете “Львовская политехника ” по адресу: 79013, г. Львов-13,
ул. С. Бандеры, 12.
С диссертацией можно ознакомиться в библиотеке Национального университета “Львовская политехника ” по адресу: 79013, г. Львов-13,
ул. Профессорская, 1.
Автореферат разослан 18 апреля 2002 г.
Ученый секретарь
специализированного ученого совета Романишин Ю.М.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Прицельный радиоэлектронный комплекс (РЭК) предназначен для обнаружения цели по целеуказанию, ее захвата, сопровождения и расчета прогнозируемой траектории движения с передачей соответствующей информации на устройство уничтожения цели. Состав прицельного РЭК формируется так, чтобы обеспечивать выполнение поставленной задачи в условиях воздействия внешних естественных и искусственных помех, при возникновении сбоев и отказов аппаратуры. Поэтому в состав РЭК входят радиоэлектронные системы(РЭС) разных типов.
Последовательность процедур использования информации, которую предоставляют РЭС в процессе выполнения задачи, определяет алгоритм поиска и обнаружения цели (АПОЦ) прицельного РЭК, разработка которого является важной задачей на системотехническом этапе проектирования таких комплексов.
Задачи, которые решаются прицельным РЭК характеризуются жесткими условиями относительно затрат времени на принятие решений оператором. Достичь минимального значения этого времени можно следующими способами:
1) подбором оператора с определенными психофизиологическими возможностями и обеспечением соответствующего уровня его квалификации;
2) привлечением группы операторов и усовершенствованием организации их работы с системами прицельного РЭК;
3) передачей части (или всех) функций оператора информационно-управляющей системе.
Для названных способов формируются варианты АПОЦ прицельного РЭК. Без соответствующих средств задача сравнения вариантов построения АПОЦ на этапе системотехнического проектирования решается качественно, а количественные оценки показателей эффективности АПОЦ и прицельных РЭК в целом определяют на этапе натурных испытаний. Такой подход не обеспечивает решения задачи выбору приемлемых вариантов АПОЦ на этапе системотехнического проектирования и требует большого объема натурных испытаний.
Поэтому актуальной является разработка средств оценки показателей эффективности пригодных для использования на этапе системотехнического проектирования, которые позволят впоследствии уменьшить объем натурных испытаний и соответственно снизить затраты времени и материальных ресурсов. Однако оценка эффективности АПОЦ прицельных РЭК не может быть достоверной без учета показателей надежности аппаратуры. Необходимый уровень показателей надежности РЭС, которые входят в состав комплекса, обеспечивается использованием при их создании соответствующих отказоустойчивых структур.
Связь работы с научными программами, темами. Диссертационная работа выполнялась в рамках приоритетного направления отраслевой программы “Перспективные информационные технологии, приборы комплексной автоматизации, системы связи” в соответствии с планом научно-исследовательских работ кафедры “Теоретическая радиотехника и радиоизмерения” Национального университета “Львовская политехника” на 1992-2000 гг. Диссертационная работа непосредственно связана с госбюджетными научно-исследовательскими работами:
ДБ/51.РЕЗ.94 “Методы и средства автоматизации схемотехническего проектирования отказоустойчивых цифровых устройств”, № гос. регистр.: 0194U029602;
ДБ/Комплекс “Разработка математического обеспечения автоматизированных процедур системотехнического и схемотехническего надежностного проектирования радиоэлектронных устройств и систем”, № гос.регистр.:0196U000186;
ДБ/Синтез “Разработка математического обеспечения процедур оптимального синтеза самоконтролируемых отказоустойчивых и живучих радиоэлектронных средств”, № гос. регистр.: 0198U002382;
ДБ/ЗКМФ “Разработка математического обеспечения компьютерного моделирования функционального и надежностного поведения радиоэлектронных средств”, № гос. регистр.: 0100U000522.
Цель и задачи исследования. Целью работы является разработка математических моделей, методики и программного обеспечения для оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов.
Для достижения цели необходимо решить следующие задачи:
Разработать структурно-автоматную модель алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса.
Разработать марковскую модель алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса.
Разработать логико-вероятностную модель алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса.
Создать методику анализа эффективности вариантов построения алгоритмов поиска и обнаружения целей прицельного радиоэлектронного комплекса.
Для построения математических моделей АПОЦ прицельного РЭК нужно разработать надежностные математические модели отказоустойчивых радиоэлектронных систем с комбинированным структурным резервированием и систем с мажоритарной структурой способной к реконфигурации, которые входят в состав рассматриваемых прицельных радиоэлектронных комплексов.
Провести выбор и выполнить сравнительный анализ методов для построения математических моделей отказоустойчивых систем с учетом эффекта старения и произвольного распределения продолжительности процесса технического обслуживания, надёжностное поведение которых соответствует дискретно-непрерывному случайному процессу.
Разработать методику построения математических моделей отказоустойчивых систем с учётом эффекта старения, надёжностное поведение которых соответствует дискретно-непрерывному случайному процессу.
Объектом исследований являются алгоритмы поиска и обнаружения целей прицельных радиоэлектронных комплексов.
Предмет исследований – показатели эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов (вероятность и среднее время выполнения задачи).
Методы исследований, которые использованы в работе заимствованы из теории радиоэлектронных систем и комплексов, теории моделирования сложных систем, теории марковских случайных процессов, теории надежности.
Научная новизна полученных результатов.
На основании предложенного расширенного описания состояний и установленного перечня определяющих параметров получил дальнейшее развитие метод пространства состояний применительно к построению математических моделей алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов. В модели, построенной усовершенствованным методом, в отличие от существующих, реализовано объединение функционального и надежностного аспектов проектирования алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов.
Получил дальнейшее развитие логико-вероятностный метод построения математических моделей алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов. Предложен способ получения логико-вероятностной модели на основе представления объекта структурно-автоматной моделью.
Разработаны две новые математические модели алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса. Характерной особенностью этих моделей является то, что они формируются на базе единого формализованного представления – структурно-автоматной модели.
Для проектирования отказоустойчивых радиоэлектронных систем с комбинированным структурным резервированием и мажоритарной структурой с реконфигурацией, которые входят в состав прицельных радиоэлектронных комплексов, разработаны новые математические модели. Эти модели, в отличие от существующих, позволяют учесть различные комбинации структурного резервирования, поведение системы при появлении нарушений работоспособности, параметры средств контроля, диагностики и коммутации, вид технического обслуживания, наличие ЗИПа.
Предложен новый метод формализации процедуры перехода от надежностной модели немарковского типа к марковской модели с использованием метода эквивалентной интенсивности потока. Это позволило автоматизировать громоздкую процедуру перехода от немарковской модели к системе дифференционных уравнений Колмогорова-Чепмена.
Практическое значение работы.
Разработанная в работе математическая модель алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса и методика ее построения дает возможность получить значение его показателей эффективности для заданных проектировщиком функциональных и надежностных параметров радиоэлектронных систем при неточностях получения целеуказания, разных уровнях квалификации оператора. Вместе с этим модель разрешает определить влияние на показатели эффективности радиоэлектронных комплексов последовательности использования радиоэлектронных систем при выполнении задачи.
Предложенные математические модели отказоустойчивых структур дают возможность проектировать радиоэлектронные системы, которые предназначены для работы в комплексе, с заданным уровнем надежности. Процесс создания математических моделей и их анализ автоматизирован, для чего разработан специализированный программный пакет.
Для оценки показателей эффективности с учетом процессов старения аппаратуры и произвольного характера процедур технического обслуживания используется разработанная методика построения моделей отказоустойчивых систем, в основу которой положен метод эквивалентной интенсивности потока.
Результаты внедрены во Львовском научно-исследовательском радиотехническом институте:
Методика оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов.
Математические модели отказоустойчивых систем со сложным комбинированным резервированием и систем с мажоритарной структурой способных к реконфигурации.
Методика построения математических моделей отказоустойчивых систем, надежностное поведение которых после появления отказов описывается немарковським дискретно-непрерывным случайным процессом.
Теоретические и практические результаты диссертации использованны:
при выполнении госбюджетных научно-исследовательских работ в лаборатории НДЛ-51 Национального университета “Львовская политехника”;
в учебном процессе у Национального университета “Львовская политехника” в лекционном курсе и практикуме дисциплины “Системотехническое проектирование радиоэлектронных комплексов” ; в дипломном проектировании студентами специальности “Радиоэлектронные устройства, системы и комплексы”.
в учебном процессе колледжа “Западноукраинский коллегиум” в лекционном курсе и практикуме дисциплины “Надежность, контроль и эксплуатация ЭВМ”; в дипломном проектировании студентами специальности “Обслуживание компьютерных и интеллектуальных систем и сетей”.
Личный вклад соискателя. Личный вклад автора в полученных научных результатах состоит в том, что все положения, которые составляют суть диссертации, были сформулированны и решены самостоятельно. В роботах написанных в соавторстве автору диссертации принадлежат: [1] - разработка математической модели алгоритма поиска и обнаружения целей прицельного РЭК: марковской на основе расширенного описания состояния и логико-вероятностной на основе представления объекта структурно-автоматной моделью и определение показателей эффективности алгоритма поиска и обнаружения целей прицельного РЭК; [2] - формирование и исследование моделей вариантов построения радиоэлектронных комплексов с использованием метода логико-вероятностного траекторного моделирования; [4], [10] - сравнительное исследование эффективности и точности метода эквивалентной интенсивности потока, способ формализованного перехода от немарковской модели к системе уравнений Колмогорова-Чепмена; [5] - установлен перечень определяющих параметров радиоэлектронных систем и предложено расширенное описание состояния, [6]- методика оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов; [7], [8] - структурно-автоматные модели двух отказоустойчивых структур; [9]- структурно-автоматная модель радиоэлектронной системы с комбинированным структурным резервирования. [11] - формализованное представление структуры и поведения системы немарковского типа.
Апробация работы. Основные положения и результаты работы докладывались и обсуждались на: международной научно-технической конференции “Современные проблемы автоматизированной разработки и производства радиоэлектронных средств и подготовка инженерных кадров”(г. Львов,1996 г.); 4-й международной научно-технической конференции “Опыт разработки и применение приборо-технологических САПР микроэлектроники”(г. Львов, 1997 г.); 4-й украинской научно-технической конференции “Автоматика-97”(г. Черкассы); международной научно-технической конференции TCSET98 “Современные проблемы средств телекоммуникации, компьютерной инженерии и подготовки специалистов”(г. Львов, 1998 г.); международном симпозиуме “Надежность и качество '99”(г. Пенза, 1999 г.); 3-й международной научно-технической конференции “Математическое моделирование в электротехнике, электронике и электроэнергетике”(Львов, 1999), 15-й открытой научно-технической конференции молодых ученых и специалистов Физико-механического института им. Г.В. Карпенко НАН Украины “КМН-2000” (г. Львов, 2000 г.). Результаты работы обсуждались на научных семинарах кафедры “Теоретическая радиотехника и радиоизмерения” Национального университета “Львовская политехника”, Украинского Львовского института бизнеса и информатики, ОАО “Концерн “Электрон” ОКБ “ТЕКОН”.
Публикации. По теме диссертационной работы опубликованы 11 научных работ, в том числе 4 статьи в профессиональных научных журналах, 7 публикаций в сборниках работ, тезисов и докладов научно-технических конференций.
Структура работы. Диссертация состоит из вступления, четырех разделов, выводов, списка использованных информационных источников и приложений. Диссертация изложена на 216 страницах и включает 125 страниц основного текста, 46 таблиц на 14 страницах, 33 рисунка на 15 страницах, список использованных информационных источников включает 173 наименования на 17 страницах и 4 приложения на 45 страницах.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во вступлении раскрыта сущность научно-практической проблемы создания средств оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов, обоснована актуальность работы, необходимость проведения исследований, сформулирована цель работы, показана научная новизна и практическая ценность полученных результатов, приведены сведения об апробации работы.
В первом разделе проанализирован состав и принципы построения типичных прицельных РЭК, выявлены их особенности. Сформулированы требования к прицельным РЭК и рассмотрены особенности их применения. В результате качественного анализа для проведения исследований сформирован полный набор средств поиска и обнаружения целей прицельных РЭК. Для формирования конкретных вариантов применен подход прототипного проектирования: разрабатываемый вариант может включать как полный так и неполный набор средств, полученный путем исключения из полного набора отдельных РЭС.
Рассмотрена задача выбора показателей эффективности прицельных РЭК. В качестве показателя для количественной оценки эффективности варианта АПОЦ выбрана вероятность выполнения задачи комплексом, а ограничивающим условием – допустимое значение среднего времени выполнения задачи. АПОЦ комплекса является входной информацией для проведения исследований в данной диссертационной работе.
Для решения задач системотехнического этапа проектирования прицельных РЭК необходимо проводить многочисленные исследования и расчеты для оценки показателей эффективности различных вариантов их построения для выбора структуры РЭК и определить необходимые значения параметров для РЭС и АПОЦ с учетом того, что комплексы используются в условиях конфликта.
При построении адекватной математической модели АПОЦ для учета наряду с функциональным аспектом и надежностного, в наборе параметров модели необходимо иметь показатели надежности РЭС. Современные РЭС прицельных РЭК проектируются со свойством отказоустойчивости, которое обеспечивается комбинированным структурным резервированием или использованием мажоритарных структур способных к реконфигурации. В государственных и отраслевых стандартах для таких структур отсутствуют соответствующие математические модели, а поэтому необходимо разработать средства их анализа. Разработанные средства должны учитывать все возможности обеспечения отказоустойчивости таких структур и адекватно отображать их поведение при появлении отказов. Вместе с этим необходимо иметь математические модели отказоустойчивых структур, в которых учитывается эффект старения аппаратных средств и произвольные вероятностные законы распределения для продолжительности процедур технического обслуживания.
При решении проектных задач на этапе системотехнического проектирования РЭК достоверность результатов обеспечивается использованием двух разных методов моделирования объекта проектирования. Указанным выше требованиям отвечают: метод пространства состояний и метод логико-вероятностного траекторного моделирования.
В разделе сформулирован перечень задач, которые решены в данной работе.
Во втором разделе разработаны две математические модели АПОЦ прицельных РЭК и методика для исследования эффективности вариантов этих алгоритмов. Проведена апробация методики на примере конкретного прицельного РЭК.
Первая модель – марковская в виде системы дифференционных уравнений Колмогорова-Чепмена построенная с использованием метода пространства состояний, вторая – логико-вероятностная.
Получение марковской модели в виде системы дифференционных уравнений и логико-вероятностной модели осуществляется с использованием новой технологии, которая предусматривает два этапа: на первом этапе создается программная модель, а на втором этапе с помощью программной модели формируются математические модели.
Первой задачей, решенной в данном разделе есть разработка структурно-автоматной модели (САМ) АПОЦ прицельного РЭК. Эта модель необходима для формализованного представления объекта моделирования, которая разрешает без известных трудностей получить марковскую и логико-вероятностную модели АПОЦ. Для этого разработаны компоненты САМ: вектор состояния и дерево правил модификации.
Вектор состояния (ВС) использован для кодирования пространства состояний, в которых может находиться прицельный РЭК в процессе выполнения задачи. В известных методиках построения марковских моделей РЭК с использованием метода состояний и переходов модель отображает только надежностное поведение РЭК. На основе проведенного анализа функциональной и надежностного поведения прицельного РЭК в процессе поиска и обнаружения цели в работе предложена следующая структура ВС: номер выполняемого операционного блока; номер РЭС, которая служит источником информации; количество повторных обращений к источнику целеуказания; количество градаций порога обнаружения; количество попыток захвата цели; количество зон обнаружения.
В процессе выполнения задачи прицельным РЭК вектор состояния изменяется определенным образом. Для отображения собственно изменений и их последовательности согласно методике автоматизированного построения марковських моделей сформировано дерево правил модификации ВС. Для этого решены следующие подзадачи: установлено множество событий, разработаны правила формирования множества условий, сформированы формулы расчета интенсивностей переходов, разработаны правила формирования формул расчета вероятностей альтернативных переходов, разработаны правила модификации вектора состояния. Полученная САМ в виде ВС и дерево правил модификации разрешают построить программную модель (АПОЦ).
Марковська модель в виде графа состояний и переходов АПОЦ прицельного РЭК формируется из перечня состояний и матрицы интенсивностей переходов, которые получаются в результате компиляции программной модели. На основе полученной матрицы интенсивности переходов с использованием формализованных процедур формируется система дифференционных уравнений Колмогорова-Чепмена. Решение этой системы уравнений дает распределение вероятности пребывания в каждом состоянии, из которых и формируется избранный показатель эффективности, в данном случае вероятность выполнения комплексом поставленной задачи.
Вторая модель АПОЦ комплекса в данной работе построена с использованием логико-вероятностного метода траекторного моделирования. Данный метод разрешает определить значения вероятности и среднего времени выполнения задачи. Оценка вероятности выполнения и времени выполнения задачи АПОЦ осуществляется с помощью транзитивных вероятностей альтернативных переходов p>mn >от m-го блока к n-му. Для этого используется графовая модель АПОЦ, в которой вершины отвечают операционным блокам, а дуги - переходам. Если предоставить каждой дуге значения вероятности перехода по ней p>mn>, то каждому маршруту алгоритма L можно поставить в соответствие вероятность его существования и время прохождения
 , (1)
, (1)
 , (2)
, (2)
где T>Bm> - время выполнения m-го операционного блока, который лежит на данном маршруте.
В свою очередь вероятность> >Р>УВ> и среднее время Т>УВ> выполнение задачи комплексом определяются так:
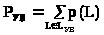 , (3)
, (3)
 , (4)
, (4)
где L>УВ> - множество путей, которые ведут к блоку, фиксирующему выполнение задачи.
В процессе прохождения каждого маршрута “накапливаются“ значение вероятностей и времени согласно формулам (1), (2). В момент достижения операционного блока, который символизирует выполнение задачи, результаты в нем “сбрасываются“ и осуществляется возвращение к последнему разветвлению. В этом операционном блоке результат “накапливается“ в соответствии с формулами (3), (4). После прохождения всех возможных маршрутов L>УВ>, получаем значения вероятности выполнения задачи и среднего времени выполнения задачи при заданных начальных условиях.
На основе созданных САМ, марковской и логико-вероятностной моделей разработана методика исследования эффективности вариантов построения АПОЦ прицельных РЭК и таким образом решена вторая задача. Согласно методике входными данными для построения модели АПОЦ прицельного РЭК являются: состав и структурная схема прицельного РЭК; параметры РЭС, которые входят в состав РЭК; блок-схема АПОЦ комплекса; средние времена и дисперсии выполнения каждого операционного блока АПОЦ; вероятности принятия решения “ДА” и “НЕТ” для каждого блока сравнения АПОЦ. Методика построения моделей и исследование эффективности вариантов построения АПОЦ предусматривает последовательное выполнение следующих пунктов:
Формирование эквивалентного АПОЦ.
Формирование САМ алгоритма поиска и обнаружения целей прицельных РЭК.
Построение ВС.
Формирование множества формальных параметров.
Формирование множества событий.
Формирование множества условий.
Формирование формул расчета интенсивностей переходов.
Формирование формул расчета вероятностей альтернативных переходов.
Формирование правил модификации ВС.
Формирование дерева правил модификации ВС.
Построение марковской модели АПОЦ прицельного РЭК.
Построение логико-вероятностной модели прицельного РЭК.
Разработанная методика апробирована при анализе эффективности варианта построения алгоритма поиска и обнаружения целей прицельного комплекса “АФАЛИНА”. Построено САМ, марковскую модель с ограниченным пространством состояний(далее модель № 1) и логико-вероятностную модель(далее модель № 2) и проведены исследования прицельного РЭК “АФАЛИНА” при различных исходных данных. По результатам исследований дана количественная оценка влияния на показатели эффективности прицельного РЭК следующих факторов: квалификации оператора при введении сообщенных данных и захват целей на экране; количества целей; отказов аппаратных средств; неточности предоставления целеуказания (ЦУ); способа получения ЦУ. Марковская модель имеет 647 состояний и 1805 переходов. На основе полученной модели сформирована система дифференционных уравнений Колмогорова-Чепмена. Процедуры формирования и решения системы дифференционных уравнений автоматизированы. Исходные данные, при которых проведены исследования, представленные в табл.1.
Таблица 1
Исходные данные
-
№
Количество захватываемых целей для РЛС, телевизионно-оптического визира и телевизора.
Время захвата заданного количества целей для РЛС телевизионно-оптического визира и телевизора, с.
Обозначение характеристики на рис.1а, 1б.
1
3;3;3
8;8;8 (квалификация низкая )
P>1>, p>1>
2
3;3;3
4;4;4 (квалификация высокая )
P>2>, p>2>
3
4;4;4
8;8;8 (квалификация низкая )
P>3>, p>3>
4
4;4;4
4;4;4 (квалификация высокая )
P>4>, p>4>
5
5;5;5
8;8;8 (квалификация низкая )
P>5>, p>5>
6
5;5;5
4;4;4 (квалификация высокая )
P>6>, p>6>
В
ероятности
выполнения задачи и время, которое
необходимо оператору для выполнения
задачи от количества целей и от
квалификации оператора, получены с
помощью модели №1 с характеристик
представленых на рис.1а в виде
дифференциального и на рис.1б в виде
интегрального закона распределения
для времени выполнения алгоритма.
Расчитанные средние значения времен
выполнения (Tc>i>)
и вероятностей успешного выполнения
(Рва>i>)
задачи, приведены в табл. 2.
Таблица 2
Средние значения времен выполнения и вероятности выполнения задачи
|
№ |
Обозначение характеристики |
Рва>i> |
Tc>i> |
|
1 |
p>1> |
0,994014 |
34,397196 |
|
2 |
p>2> |
0,994014 |
18,397207 |
|
3 |
p>3> |
0,99302 |
42,397151 |
|
4 |
p>4> |
0,99302 |
22,397204 |
|
5 |
p>5> |
0,992025 |
50,396939 |
|
6 |
p>6> |
0,992027 |
26,397204 |
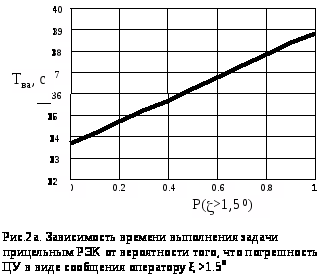
Н
а
рис.2а и рис.2б приведены зависимости
времени выполнения и вероятность
выполнения задачи прицельным РЭК от
вероятности того, что погрешность ЦУ в
виде сообщения оператору >1.50.
М
одель
№1 разрешает получить зависимость
вероятности выполнение задачи комплексом
от уровня надежности аппаратных средств
из которых построен РЭК (рис. 3). С помощью
модели № 2 были проведенные аналогичные
исследования, результаты которых
приведены в табл. 3
На рис.4а и 4б приведены результаты исследования зависимости вероятности выполнение задачи прицельным РЭК в зависимости от выбора РЭС в качестве основного источника информации (модель №1): 1-РЛС, 2-ТОВ, 3-ТПВ, 4-равновероятный выбор РЭС, 5-преимущество РЛС. На рис.5а приведена зависимость вероятности выполнение задача от выбора типа РЭС в качестве источника информации. На рис.5б приведены результаты исследований вероятности выполнение задачи от вероятности обнаружения целей РЛС (эта вероятность изменялась от 0,65 до1).
П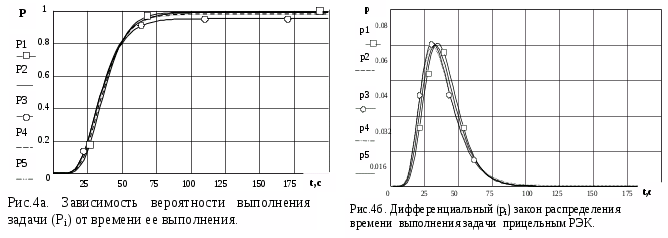
редставленные
результаты иллюстрируют возможности
использования разработанных средств
оценки эффективности АПОЦ прицельных
РЭК в процессе проектирования.
В
практике проектирования РЭС для
прицельных РЭК нашли использования
отказоустойчивые структуры с
комбинированным структурным резервированием
(КСР) и мажоритарные структуры (МС)
способные к реконфигурации. Как показал
информационный поиск, а также анализ
государственных и отраслевых стандартов,
математические модели для таких
отказоустойчивых структур отсутствуют.
В
третьем разделе решается
задача построения математических
моделей для проектирования отказоустойчивых
структур РЭС с комбинированным структурным
резервированием и мажоритарных структур
способных к реконфигурации, в которых
учтены: логика поведения системы после
появления отказа, способность к
реконфигурации, наличие средств контроля
и диагностики (СКД), различные виды
структурного резервирования, средства
коммутации, техническое обслуживание
и ремонт при наличии ограниченного или
неограниченного ЗИПа. В данных моделях
заложено условие об экспоненциальном
характере закона распределения для
интервалов времени пребывания во всех
состояниях, которое разрешает получить
предельные оценки показателей надежности.
Необходимость разработки таких моделей обусловленно потребностью иметь достоверные значения показателей надежности отказоустойчивых РЭС, которые используются для проведения исследований на базе математических моделей АПОЦ прицельных РЭК разработанных в разделе 2. Вместе с этим разработанные модели могут использоваться для проектирования отказоустойчивых структур РЭС.
Поскольку поведение отказоустойчивых систем при появлении нарушений работоспособности представляется соответствующим алгоритмом, то для построения их математических моделей использован подход, примененный в разделе 2 для построения марковских моделей АПОЦ прицельных РЭК. В результате применения такого подхода проектировщик получает модель отказоустойчивой системы в виде системы дифференционных уравнений Колмогорова-Чепмена. Решение этой системы дает вероятности пребывания отказоустойчивой структуры в любом из состояний. С полученных вероятностей формируются показатели надежности проектируемой отказоустойчивой системы.
Первой подзадачей решенной в разделе является разработка универсальной САМ отказоустойчивой системы с комбинированным структурным резервированием (КСР). Типичная система с КСР состоит из N - однотипных модулей основной конфигурации и скользящего резерва. Кроме того предусмотрено применене резервирующих систем, которые осуществляют общее резервирование. Резервирующая система включается в таких случаях: в момент отказа основной конфигурации после исчерпания скользящего резерва; на время подключения модулей скользящего резерва; при отказах комутирующих элементов скользящего резерва. Поскольку в системах с КСР применяют различные виды резервирования одновременно, средства коммутации, средства контроля и диагностики (СКД), различные стратегии технического обслуживания, поэтому в отдельности разработаны модели отказов элементов при разных видах резервирования, в отдельности модели СКД и средств коммутации и из этих моделей построено универсальную модель.
Формирование универсальной САМ системы с комбинированным структурным резервированием обусловило разработку следующих структур данных.
1. Вектор состояния : Компонента ВС V1 отображает текущее количество работоспобных модулей. Начальное значение компоненты V1 равно общему количеству элементов N. Компонента V2 - счетчик восстановлений. Компонента V3 - количество работоспособных резервирующих систем. Компонента V4 равная 1, если на нагрузку работают модули основной конфигурации, и равная 2, если на нагрузку работает одна из резервных систем.
2. Формальные параметры модели: M - количество модулей в минимальной конфигурации системы; F - количество модулей скользящего резерва; N=M+F - общее количество модулей; L - количество резервирующих систем в общем резерве; м - интенсивность отказов одного модуля в основной конфигурации; >ПРС> - интенсивность отказов работающей резервной системы; >НРС> - интенсивность отказов неработающей резервной системы.
Разработанная структурно-автоматная модель представлена таблицей 4.
Таблица 4
Структурно-автоматная модель отказоустойчивой системы с комбинированным структурным резервированием
|
Событие |
Условие |
ФРИП |
ФРИАП |
ПМВС |
Отказ модуля |
V1>=M |
M·г |
1 |
V4=2;V1=V1-1 |
|
Подключение модуля |
(V4=2)and(V1>M) |
1/Т>К> |
P>К> |
V4=1 |
|
(V4=2)and(V1>M) |
1/Т>К> |
1- P>К> |
V2=2 |
|
|
Отказ работающей резервной системы |
V3>0 |
>ПРС> |
1 |
V3=V3-1 |
|
Отказ неработающей резервной системы |
V2>0 |
>НРС> |
1 |
V2=V2-1 |
|
Ремонт резервной системы |
V2<L |
1/T>Р> |
P>Р> |
V2=V2+1 |
|
V2<L |
1/T>Р> |
1- P>Р> |
V2=V2 |
|
|
Ремонт модуля |
V1<N |
1/Tp |
1 |
V1=V1+1 |
|
Критерий отказа (V1<M) and (V2=0) |
Второй подзадачей решенной в разделе является разработка надежностных моделей отказоустойчивых систем с мажоритарной структурой, способных к реконфигурации. Система с МС состоит из 2N+1 однотипных модулей рабочей конфигурации, которые обеспечивают реализацию алгоритма функционирование подсистемы с заданным уровнем качества, и резервной группы - скользящего резерва, который состоит из S модулей. После исчерпания резерва и отказа (2N+1)/2 модулей основной конфигурации предусмотрена реконфигурация МС. Практический интерес представляют два варианта реконфигурации. В первом варианте рабочими остаются два модуля, которые работают в режиме сравнения. Во втором варианте рабочим является один модуль. В обоих вариантах мажоритарный элемент отключается, а высвобожденные после реконфигурации исправные модули переводятся в резерв.
Входными данными для построения структурно-автоматной надежностной модели отказоустойчивых систем с МС являются: количество модулей в рабочей конфигурации до реконфигурации – NP; количество модулей в рабочей конфигурации после реконфигурации - NN; исходное количество модулей в резерве - K; интенсивности отказов модулей рабочей конфигурации (о) и модулей, которые находятся в резерве - (р); показатели качества средств автоматического восстановления работоспобности заданные вероятностями правильного обнаружения, распознавание и локализации отказа (Р>ВРЛ>)> >и> >правильного восстановления работоспособности после отказа (Р>ВП>),> >правильной реконфигурации (Р>РК>), интенсивности восстановления модулей, которые вышли из строя (); вероятности восстановления (ремонта) модуля (P>В>).
Для представления всех возможных состояний подсистемы с обслуживанием кроме компонент V1 и V2, необходимо ввести третью - V3- количество неисправных модулей в рабочей конфигурации и в резерве. Если восстановление ограничено, то нужно ввести в множество формальных параметров максимальное количество восстановлений KV, а в ВС счетчик количества восстановлений - V4:=KV. САМ для этого класса отказоустойчивых систем представлен в табл.6.
Таблица 6.
Структурно-автоматная модель обслуживаемой системы с мажоритарной структурой с непрерывным ограниченным восстановлением
|
События |
Условия |
ФРИП |
ФРИАП |
ПМВС |
|
1 |
2 |
3 |
4 |
5 |
|
Отказ модуля |
V2>0 |
V1*>O> |
Р>ВРЛ>*Р>ВР> |
V2:=V2-1; V3=V3+1 |
|
рабочей конфигурации |
V2=0 and V1>(NP+1)/2 |
V1*>O> |
Р>ВРЛ> |
V1:=V1-1; V3=V3+1 |
|
V2=0 and V1=(NP+1)/2 |
V1*>O> |
Р>ВРЛ>*Р>РК>*Р>ВР> |
V1=NN; V2:=V1-NN-1; V3=V3+1 |
|
|
V2=0 and V1=NN |
V1*>O> |
Р>ВРЛ> |
V1:=V1-1; V3=V3+1 |
|
|
Отказ модуля резервной группы |
V2>0 |
V2*>Р> |
____ |
V2:=V2-1; V3=V3+1 |
|
Восстановление модуля |
V3>0 and V4<KV |
V3* |
P>ВД>* Р>РК> |
V2:=V2+1;V3=V3-1 ;V4:=V4+1 |
|
Критерий отказа: V1>NN. |
Если восстановление модулей неограниченное или ограниченное по вызову, то в таблицах интенсивность восстановления равна 1/(Т>вик>+Т>рем>), где Т>вик >- время необходимое для вызова и прибытия ремонтной бригады, Т>рем> - время проведения ремонта неисправных модулей. САМ необслуженной отказоустойчивой системы с мажоритарной структурой способной к реконфигурации можно получить из модели представленной в табл.6 путем соответствующей настройки.
В связи с тем, что оценка надежности в процессе проектирования должна занимать как можно меньше времени, проектировщику необходим «быстрый» инструмент для расчета показателей надежности. Для этого разработан программный пакет, предназначенный для построения и анализа надежностных математических моделей рассмотреных отказоустойчивых структур.
В разделе 4 решена задача разработки математических моделей отказоустойчивых радиоэлектронных систем, которые бы учитывали эффект старения аппаратуры и реальные законы распределения продолжительности процедур технического обслуживания и ремонта, т.е. надежностное поведение системы, которое описывается немарковським дискретно-непрерывным случайным процессом.
Для уменьшения размерности модели при сохранении достаточно высокой точности расчета показателей показана целесообразность применения метода эквивалентной интенсивности потока (ЭИП). Для этого проведен сравнительный анализ метода ЭИП, метода стадий (фаз Эрланга (ФЭ)) и метода экспоненциальной аппроксимации (ЭА). Модель построена методом стадий служит эталоном. Кривая полученная методом ЭИП дает довольно точную качественную картину в сравнении с методом ЭА. Оценка эффективности метода базируется на сравнении порядков систем дифференционных уравнений, которые формируются при решении тестовой задачи методом ЭИП и методом стадий. С увеличением количества фаз от 3-х к 5-ти порядок системы дифференционных уравнений для метода ЭИП возрос с 41 до 49 , в то время как для метода ФЭ - с 93 до 245. При количественном анализе относительная погрешность метода ЭИП для 3-х фазного моделирующего pН-распределения при t<T>сер.> не превышает 2.5%, а при t>T>сер >не превышает 7%, в то время как относительная погрешность метода ЭА при таких же значениях t достигает 12% и 230% соответственно.
Для практического применения метода ЭИП формализована процедура перехода от немарковской надежностной модели РЭС к системе уравнений Колмогорова-Чепмена с использованием метода ЭИП. Суть метода формализации состоит в отображении не только поведения моделированной системы в виде графа состояний и переходов, но и в одновременном отслеживании протекания вспомогательных процессов. Поэтому осуществлено расширение описание состояния, в котором находится система. Описание состояния системы состоит из двух частей - основной и вспомогательной. В основной части отображена структура моделируемой системы, во вспомогательной части - вспомогательные процессы, которые запускаются в процессе формирования модели и с помощью которых аппроксимируются не экспоненциальные переходы. Перед формированием описания состояния конкретной отказоустойчивой системы нужно определить количество вспомогательных процессов, которые необходимы при моделировании конкретной отказоустойчивой системы.
В отличие от САМ, примененных в разделах 2,3 часть событий касается вспомогательных процессов, а часть - изменения структуры системы, то необходимо множество условий реализации данных событий, которое необходимо проверять перед реализацией каждого события. В результате реализации события происходит первичное изменение состояния или основной, или вспомогательной, части описания состояния моделируемой системы. Если в результате первичного изменения состояния состоялся запуск вспомогательного процесса, то проверяется критерий отказа и рассматривается соответствующее условие реализации события. В случае если в результате первичного изменения состояния состоялось окончание вспомогательного процесса или отказ модуля с распределенной продолжительностью времени безотказной работы, то необходимо рассмотреть множество условий запуска вспомогательных процессов. Если условие запуска выполняется, то необходимо выполнить согласно описанному правилу модификацию основной части ВС и установить направление, интенсивность перехода и вспомогательную часть в описании состояния (осуществить запуск очередного вспомогательного процесса) и установить эквивалентную интенсивность перехода. Правило запуска не допускает одновременного запуска нескольких процессов. Если условие запуска не выполняется, то осуществляется переход к следующему условию реализации события. После исчерпания множества событий процедура построения фазового пространства завершается.
В результате применения такого метода формализации получается граф состояний и переходов моделируемой системы с обозначенными эквивалентными интенсивностями перехода.
На основе формализованного метода перехода от немарковской модели отказоустойчивой РЭС к системе уравнений Колмогорова-Чепмена, разработана методика построения моделей отказоустойчивых систем, надежностное поведение которых отображается немарковським дискретно-непрерывным процессом.
Для программной реализации метода формализации перехода в работе применен усовершенствованный подход построения математических моделей на основе представления САМ в классе Е - сетей Петри.
Методика построения САМ предусматривает выполнение следующей последовательности действий:
Формирование вектора состояния.
Формирование множества формальных параметров.
Формирование цепочек “событие-переход”. Формирование цепочек “условие-переход”.
Формирование формул расчета интенсивностей переходов. Номер формулы отвечает номеру события для которой проводится расчет интенсивности перехода.
Формирование матрицы инцидентности. Матрица инцидентности указывает на то, существует ли связь между определенными двумя цепочками. Элементы матрицы инцидентности могут принимать следующие значения: 0 - если переход входной цепочки не влияет на условие выходной цепочки; 1- если переход входной цепочки влияет на условие выходной цепочки.
Формирование критерия отказа.
Формирование множества формул расчета вероятностей альтернативных переходов.
Построение графа состояний и переходов для моделируемой системы.
Результаты решения ряда задач с использованием разработанной методики показывают принципиальную возможность получения необходимой для потребностей системотехнического проектирования РЭК точности при значительном уменьшении размерности модели и вычислительных затрат на числовой расчет параметров.
В приложениях приведены программная реализация структурно-автоматной модели алгоритма поиска и обнаружения целей прицельным РЭК «Афалина» - марковская модель, программная реализация структурно-автоматной модели алгоритма поиска и обнаружения целей прицельным РЭК «Афалина» - логико-вероятностная модель, вектор состояния и матрица интенсивностей переходов прицельного РЭК «Афалина», акты внедрения результатов диссертационной работы.
ВЫВОДЫ
В диссертационной работе решена задача разработки средств оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов, а именно: созданы математические модели, методики и программные средства для автоматизации процедуры анализа алгоритмов. В рамках данной задачи получены следующие результаты:
В работе получили дальнейшее развитие метод пространства состояний и метод логико-вероятностного траекторного моделирования применительно к построению математических моделей алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов. Усовершенствованные методы, в отличие от существующих, позволяют учесть в моделях как функциональный так и надежностный аспекты проектирования радиоэлектронных комплексов.
В работе решена задача создания программных средств оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов. Созданные средства охватывают функциональный и надежностный аспекты системотехнического проектирования алгоритмов поиска и обнаружения целей и позволяют выполнять сравнительный анализ вариантов построения алгоритмов. Использование этих средств позволяет сократить длительность системотехнического этапа проектирования прицельных радиоэлектронных комплексов.
Разработана методика построения математических моделей алгоритмов поиска и обнаружения целей и исследования их эффективности. Методика формализует процесс получения математической модели для чего предусматривает создание промежуточных моделей, которые трансформируются с одного вида в другой и в конечном счете позволяют сформировать систему дифференционных уравнений Колмогорова-Чепмена. Вместе с марковской моделью формируется логико-вероятностная модель, чем обеспечивается контроль достоверности полученных результатов анализа эффективности алгоритмов поиска и обнаружения целей.
Разработаны новые математические модели отказоустойчивых структур с комбинированным структурным резервированием и мажоритарной структурой способной к реконфигурации, которые применяются при построении радиоэлектронных систем комплекса. Эти модели в отличие от существующих адекватно отображают надежностное поведение системы при появлении отказов, что обеспечивается учетом: параметров средств контроля, диагностики и коммутации, логики использования резерва, стратегии технического обслуживания, наличия ЗИПа. Разработаны программные средства, которые разрешают проектировщику настраивать предложенные структурно-автоматные модели рассмотренных типов отказоустойчивых структур на заданные исходные данные.
Разработан метод формализации перехода от немарковських моделей отказоустойчивых структур к марковським на основе метода эквивалентной интенсивности потока. Автоматизирована громоздкая процедура такого перехода. На основе метода формализации разработана методика построения математических моделей отказоустойчивых структур, надежностное поведение которых отображается немарковським дискретно-непрерывным случайным процессом. Построенные по методике модели разрешают проводить надежностный анализ отказоустойчивых структур с учетом эффектов старения и произвольных законов распределения для продолжительности процедур технического обслуживания.
Результаты разработок приняты к использованию проектировщиками прицельных радиоэлектронных комплексов. Практическая ценность результатов работы состоит в следующем:
Благодаря применению разработанных математических моделей уменьшаются затраты времени на выполнение работ системотехнического этапа проектирования прицельных радиоэлектронных комплексов.
Математические модели алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса дают возможность получить значение его показателей эффективности для заданной логики использования радиоэлектронных систем при определенных проектировщиком функциональных и надежностных параметрах систем, с учетом неточности задания целеуказания и уровня квалификации оператора.
Автоматизирован процесс проектирования радиоэлектронных систем с заданным уровнем надежности в классе отказоустойчивых структур с комбинированным структурным резервированием и мажоритарной структурой способной к реконфигурации благодаря разработке универсальных структурно-автоматных моделей.
Список основных работ опубликованных за темой диссертации
Беляев В.П., Волочий Б.Ю., Грабчак А.В., Миськив М.В., Озирковский Л.Д. Моделирование и оценка эффективности локального радиоэлектронного комплекса // Межведомственный сборник научных работ “Отбор и обработка информации”. - Львов: Изд-во ФМИ НАНУ.-1999.-Вып.13(89) - С.65-70.
Беляев В.П., Волочий Б.Ю., Озирковский Л.Д., Павлив Н.В. Оценка эффективности методов расчета показателей связности в структурном анализе радиоэлектронных комплексов// Межведомственный научно-технич. сборник “Теоретическая электротехника”. - Львов: Изд-во “Світ”.-1998. - Вып. 54. - С.8-14.
Озирковский Л.Д. Надежностные модели систем со сложным комбинированным резервированием и систем с мажоритарной структурой произвольной конфигурации с деградацией // Вестник государственного университета “Львовская политехника” “Радиоэлектроника и телекоммуникации”. - Львов: Изд - во гос. ун - та “Львовская политехника”. - 1999 - № 367 - С. 136-138.
Беляев В.П., Волочий Б.Ю., Озирковский Л.Д. Построение математических моделей поведения радиоэлектронных комплексов по методу эквивалентной интенсивности потока // Вестник государственного университета “Львовская политехника” “Теория и проектирование полупроводниковых и радиоэлектронных устройств”. - Львов: Изд - во гос. ун - та “Львовская политехника”. - 1998 - № 343. - С. 74-77.
Беляев В.П., Волочий Б.Ю., Грабчак А.В., Миськив М.В., Озирковский Л.Д. Оценка эффективности эргатических систем с учетом влияния дестабилизирующих внешних факторов // Тезисы докладов 4-й научно-технической конфер. “Опыт разработки и применения приборо-технологических САПР микроэлектроники”, ч.1 – Львов, 1997.-С.13-14.
Беляев В.П., Волочий Б.Ю., Озирковский Л.Д. Средства автоматизации проектирования алгоритмов функционирования систем управления // Труды 4-й украинской конфер. по автоматическому управлению “АВТОМАТИКА - 97”, т. 2. - Черкассы. - 1997. - С. 37.
Мандзий Б.А., Беляев В.П., Волочий Б.Ю., Озирковский Л.Д. Надежностные модели мажоритарных деградирующих структур и структур со сложным комбинированным резервированием // Труды междунар. симпозиума “Надежность и качество '99”. - Пенза: Изд-во Пенз. гос. техн. ун-та. - 1999. - С. 24-26.
Беляев В.П., Волочий Б.Ю., Озирковский Л.Д. Структурно-автоматные модели двух отказоустойчивых структур радиоэлектронных систем // Тезисы докладов 3-й международной научно - техн. конф. “Математическое моделирование в электротехнике, электронике и электроэнергетике”. - Львов. - 1999. - С. 22.
Озирковский Л.Д., Лемишовская Л.В. Применение комбинированного структурного резервирования в надежностном проектировании отказоустойчивых радиоэлектронных систем // Работы 15-й открытой научно - техн. конф. молодых ученых и специалистов Физико-механического института им. Г.В. Карпенка НАН Украины “КМН-2000”. – Львов: ФМИ. - 2000. - С. 126-127.
Беляев В.П., Озирковский Л.Д., Якубенко У.В. Исследование эффективности и точности анализа отказоустойчивых систем методом эквивалентной интенсивности потока // Труды междунар. научно - техн. конф. “Современные проблемы автоматизированной разработки и производства радиоэлектронных средств и подготовки инженерных кадров”. - Львов. - 1996. - ч. 2. - С. 157.
Беляев В.П., Волочий Б.Ю., Озирковский Л.Д. Построение математических моделей радиоэлектронных комплексов методом эквивалентной интенсивности потока // Работы международной научно-технической конфер. TCSET'98 “Современные проблемы средств телекоммуникации, компьютерной инженерии и подготовки специалистов”. - Львов. - 1998. - С. 26-27.
АННОТАЦИИ
Озирковский Л.Д. Разработка средств оценки эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов. – Рукопись.
Диссертация на соискание научной степени кандидата технических наук по специальности 05.12.17 - радиотехнические и телевизионные системы.
Национальный университет “Львовская политехника”, г.Львов, 2002 г.
Диссертационная работа посвящена постановке и решению научных задач оценки показателей эффективности алгоритмов поиска и обнаружения целей прицельных радиоэлектронных комплексов, а именно созданию средств оценки, пригодных для использования на этапе системотехнического проектирования, которые позволят уменьшить объем натурных испытаний и соответственно снизить затраты времени и материальных ресурсов.
В работе решены следующие задачи. Разработаны структурно-автоматная модель, марковская модель и логико-вероятностная модель алгоритма поиска и обнаружения целей прицельного радиоэлектронного комплекса. Создана методика анализа эффективности вариантов построения алгоритмов поиска и обнаружения целей прицельного радиоэлектронного комплекса. Для получения достоверных показателей надежности для математических моделей алгоритма поиска и обнаружения целей разработаны надежностные математические модели отказоустойчивых радиоэлектронных систем с комбинированным структурным резервированием и систем с мажоритарной структурой способной к реконфигурации, которые входят в состав прицельных радиоэлектронных комплексов. Осуществлен выбор и сравнительный анализ методов для построения математических моделей отказоустойчивых систем с учетом эффекта старения и произвольного распределения продолжительности процедур технического обслуживания.
Полученные результаты внедрены во Львовском научно-исследовательском радиотехническом институте и в учебный процесс подготовки специалистов, будущих проектировщиков радиоэлектронных комплексов и систем.
Ключевые слова: радиоэлектронный комплекс, алгоритм, радиоэлектронная система, системотехническое проектирование, математическая модель, надежность.
Озірковський Л.Д. Розробка засобів оцінки ефективності алгоритмів пошуку і виявлення цілей прицільних радіоелектронних комплексів. – Рукопис.
Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.12.17 - радіотехнічні та телевізійні системи.
Національний університет “Львівська політехніка”, м.Львів, 2002 р.
Дисертаційна робота присвячена постановці та вирішенню наукових задач оцінки показників ефективності алгоритмів пошуку і виявлення цілей прицільних радіоелектронних комплексів, а саме створенню засобів оцінки, придатних для використання на етапі системотехнічного проектування, які дозволять зменшити об’єм натурних випробовувань і відповідно знизити затрати часу та матеріальних ресурсів.
В роботі вирішені наступні задачі. Розроблені структурно-автоматна модель, марковська модель та логіко-імовірнісна модель алгоритму пошуку і виявлення цілей прицільного радіоелектронного комплексу. Створено методику аналізу ефективності варіантів побудови алгоритмів пошуку і виявлення цілей прицільного радіоелектронного комплексу. Для одержання достовірних показників надійності для математичних моделей алгоритму пошуку і виявлення цілей розроблені надійнісні математичні моделі відмовостійких радіоелектронних систем з комбінованим структурним резервуванням та систем з мажоритарною структурою здатною до реконфігурації, які входять в склад прицільних радіоелектронних комплексів. Здійснено вибір і порівняльний аналіз методів для побудови математичних моделей відмовостійких систем з врахуванням ефекту старіння та довільного розподілу тривалості процесу технічного обслуговування.
Отримані результати впроваджено у Львівському науково-дослідному радіотехнічному інституті та в навчальний процес підготовки фахівців, майбутніх проектантів радіоелектронних комплексів та систем.
Ключові слова: радіоелектронний комплекс, алгоритм, радіоелектронна система, системотехнічне проектування, математична модель, надійність.
L. Ozirkovsky. The Development Of Tools For Efficiency Estimation Of Target Search And Detection Algorithms At Radio-Electronics Sighting Complexes .
Thesis devotes to the formulation and solution of scientific problems for the efficiency estimation of target search and detection algorithms at radio-electronics sighting complexes, i.e.: development of estimation tools for system design. These tools will cut down the expenses of time and material resources.
In thesis the following problems are solved. The structurally-automatic model, the Marcov model and logical-probability model of target search and detection algorithms are developed. The technique for efficiency estimation of target search and detection algorithms at radio-electronics sighting complexes are created. For modeling of a target search and detection algorithms at radio-electronics sighting complexes are created models of fault-tolerance systems with combined structural redundancy and with majority structure capable to reconfiguration. Choice and comparative analysis of methods for construction of mathematical models of fault-tolerance systems with taking into account of aging effect and arbitrary process duration distribution of technical service are executed .
Obtained results were implemented in Lviv Radio Engineering Institute and into training process for the experts engaged in the designing of radio-electronics systems and complexes.
Key words: radio-electronics complex, radio-electronics system, algorithm, system design, mathematical model, reliability.
Підписано до друку 21.01.2002 р. Формат 60*84/16
Папір офсетний. Умовн. друк. арк. 0,95.
Друк на різографі. Наклад 100 прим.
Зам. №25. НВП “Компіс”