Определение функций электрической цепи и расчет их частотных зависимостей
Содержание.
1.Введение
2.Анализ нагрузочной цепи
2.1.Выражений входного сопротивления и коэффициента передачи по
напряжению.
2.2.Проверка полученных выражений.
2.3.Определение характера частотных характеристик нагрузочной
цепи.
3.Анализ электрической цепи транзистора с нагрузкой.
3.1.Характер АЧХ и значения ФЧХ коэффициента передачи.
3.2.Составление матрицы проводимостей.
3.3.Получение операторных выражений.
3.4.Проверка выражений для входного сопротивления и коэффициен-
та передачи транзисторя.
3.5.Нормировка элементов цепи и операторных выражений .
3.6.Расчет нулей и полюсов.
3.7.Вычисление АЧХ и ФЧХ на ПНЧ.
3.8.Вычисление АЧХ и ФЧХ на основе опраторных выражений.
3.9.Расчет АЧХ и ФЧХ на ЭВМ.
3.10.Построение частотных характеристик исследуемых фуекций.
3.11.Расчет эквмвалентной модели входного сопротивления.
4.Выводы.
5.Список литературы.
1.Введение.
Для расчета электрических цепей сущетвует много методов.Один из них - матричный метод.
Для его осуществления,строят операторную схему замещения цепи,а затем ,по операторной схеме составляют матрицу проводимости. Из этой матрицы можно получить значения нужные нам операторные выражения (в частности входное сопротивление и коффициент передачи).
При выполнении этого метода могут возникать ошибки,для их устранения используется различные проверки,как в самой матрице,так и полученных операторных выражениях.
При больших степенях в операторных выражениях коэффициенты при максимальной и минимальной очень сильно отличаются.Так как это неудобно,делают нормировку значений элементов.
Результатом иследования электрической эквивалентной цепи транзистора является амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ) исследуемых функций цепи. Использууется так же полюсно-нулевое изображение (ПНИ).
Для проверки полученных данных использовался ЭВМ ' IBM '
2.Анализ нагрузочной цепи.
Нагрузочная цепь является четырехполюсников.

Рис.2.1.Схема нагрузочной цепи.
В расчетах потребуется численные значения элементов цепи.

2.1 Вывод выражений входного сопротивления и коэффициента передачи по напряжения .
Для получения операторных выражений входного сопротивления Z>Вх>(р) и коэффициента передачи по напряжения К>Н>(р) воспользуемся методом преобразований.Для этого изобразим нагрузки в виде ,в которой она представлена на рис.2.2.
В этой цепи
 (2.1)
(2.1)
 (2.2)
(2.2)
 (2.3)
(2.3)
Исходя из схемы на рис.2.2. можно вывести формулу входного сопротивления :
 (2.4)
(2.4)
Теперь, если подставить в формулу (2.4) формулы (2.1), (2.2) и (2.3), то получится выражение входного сопротивления нагрузки :
 (2.5)
(2.5)
А коэффициент передачи имеет вид:
 (2.6)
(2.6)
Подставим в выражение (2.6) формулы (2.1), (2.2) и (2.3):
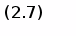

Подставим в выражение численные значения для входного сопротивления :
и для коэффициента передачи:
2.2 Проверка полученных данных
Проверим выражение для входного сопротивления на выполнение условий физической реализуемости.
1) Все коэффициенты являются положительными числами , т.к. значения больше нуля.Это потверждаеся выражение - у него все выражены выражаются положительными числами.
2) Наивысшие степени ,так же как наименьшие , у числителя и знаменателя отличаются на еденицу.
Из этого можно сделать вывод , что выражения не противоречит условиям физической реалиизуемости. Теперь проверим выражение на соответствие порядку цепи. Пусть m-наибольший степень числителя , а n-наибольший степень знаменателя ,тогда верны соотношения :
m=k-
n= где - общее число реактивностей в цепи ;
Кол-во емкостных контуров ,при подключении на вход источника напряжения ,или тока соответственно.
Количество индуктивных сечений ,при подключении на вход источника напряжения ,или тока соответственно. Для цепи ,представленной на рис. по формуле и получается =2 ,а
=3, это соответствует степеням числителя и знаменателя в выраже-
нии для входного сопротивления.
Следушей проверкой будет проверка на соблюдение размерностей в выражении и.Учитывая ,что имеют разиерность в Омах, а - в симмен-
сах, получим :
Полученные размерности сответствуют размерностям истинным. Найдем значения входного сопротивления и коэффициента передачи по формулам, соответственно, при =0 и = ¥.
Проверим полученные значения ,исходя из поведения цепи при пос-
тоянном токе и при бесконечной частоте (при =0 - ток постоянный
-кондесаторы разрываются ,катушки закорачиваются ,а при =оо ток
имеют бесконечную частоту-кондесаторы закорачиваются ,катушки
разрываются).Полученные эквивалентные схемы изображены на рис и
рис .
Эти значения соответсвуют значениям ,полученным из выражений
для входного сопротивления и коэффициента передачи.
2.3 Характера частотных характеристик нагрузочной цепи.
> >

Рис.2.5. АЧХ входного сопротивления Z>Вх.н>(w)
Рис.2.6. ФЧХ входного сопротивления Z>Вх.н>(w)
3.Анализ электрической цепи транзистора с нагрузкой .
На изображена схему транзистора ,включенного по схеме с общей базой с нагрузкой на выходе.

рис. 3.1 Схему транзистора с нагрузкой.
3.1 Характер АЧХ и значения ФЧХ коэффициента передачи.
Значение модуля коэффициента передачи транзистора с нагрузкой можно показть формулой: Так как мы исследуем транзистор до МГц ,то не только зависит от частоты , но крутизна ,а она с увличением частоты убывает.Значит , качественный характер АЧХ коэффициента передачи транзистора похож на АЧХ входного сопротивления нагрузки,однако из-за уменьшения крутизны транзистора при высо ких частотах неровности АЧХ коэффициента передачи менее выражены , чем неровности АЧХ входного сопротивления нагрузки. Цепь транзистора с нагрузкой , включенного по схеме с базой не является инвертирующей , значит , значение ФЧХ коэффициента передачи на постоянном токе не отличаетсяот значения ФЧХ входного сопротивления нагрузки на постоянном токе,то есть.
3.2 Составление матрицы проводимости.
Для схемы ра рис.3.1 составим операторную схему замещения :
Для анализа электрической цепи транзистора с нагрузкой по методу узловых потенциалов составим матрицу проводимости.Матричное уравнение в канонической форме выглядит следущим образом :


где Y-матрица проводимости , U>1> ,U >2 >,U>3 >,U>4>-соответствующие напряжения в узлах 1,2,3,4.
Исходя из схемы на рис. 3.2. составляем матрица проводимости :

Коэффициент передачи цепи по напряжению

Входное сопротивление

Узловое напряжение k-того узла

D -определитель матрицы [Y];
Dik -алгебраическое дополнение элемента y >i k >матрицы [Y];
i - номер узла к которому подключен источник J>i >;
k - номер узла , для которого вычисляется узловое напряжение ;

где D-определитель матрицы [Y];

3.5.Нормировка элементов цепи и операторных выражений
Пронормируем элементы цепи по частоте w>0 >= w>b>> >= 2Pf>b>> >и сопротивлению R>0> =75 Ом. Запишем основные формулы , которые будем использовать при нормировке элементов цепи .

Используя эти формулы пронормируем сопротивления,реактивные элементы цепи и занесем в таблицу .
Таблица 3.1
Нормированные значения цепи элементы.
|
R>Э> |
R>Б> |
R>1> |
R>2> |
С>Э> |
С>К1> |
С>К2> |
С>1> |
С |
L |
Пронормировав значение крутизны управляемого источника тока получим S>H >=
Также сделаем нормировку операторных выражений входного сопротивления () и коэффициента передачи .Учитывая ,что для K>т>(н) (p) b и Z>Вх>(н)> >(p):
> >
3.6 Расчет нулей и полюсов.
Используя ЭВМ получим значения входного сопротивления Z>Вх>(Н)(р) :
Нули :
Полюса :
Для коэффициента передачи транзистора К>Т>(Н)(р) :
Нули :
Полюса :
Подставим нормированные функции входного сопротивления Z>Вх>(Н)(р) и коэффициента передачи транзистора К>Т>(Н)(р) в виде биноминальных произведений :
Карты нулей и полюсов для функций входного сопротивления Z>Вх>(Н)(р) и коэффициента передачи транзистора К>Т>(Н)(р) показаны на рис. и рис. .Из-за большого разброса значений пришлось брать разные масштабы .
5.Вывод
В данной курсовой работе была исследована электрическая схема транзистора с нагрузкой.
Исследуя частотные характеристики цепи получили графики АЧХ и ФЧХ входного сопротивления Z>Вх>(Н)(р) и коэффициента передачи транзистора К>Т>(Н)(р) в диапозоне от 0 до ГГц.
В данной курсовой работе познакомились с матричным методом расчетных цепей.
6.Список литературы
1.Зернов И.В.,Карпов В.Г. "Теория радиотехнических цепей".
Энергия , 1965 г.
2.Попов В.П. "Основы теории цепей".
Высшая школа , 1895 г.