Анализ линейной стационарной цепи
Министерство образования Российской Федерации
Уральский Государственный Технический Университет - УПИ
Кафедра "ТОР"
Курсовая работа
по РТЦС
АНАЛИЗ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ ЦЕПИ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
200800 000000 013 ПЗ
Руководитель: Шилов В.И.
Студент: Черепанов К.А
Группа: Р-307
Екатеринбург
2002
Задание на проектирование
Н
айти
операторный коэффициент передачи цепи
по напряжению и записать его в виде
отношения двух полиномов:
Записать комплексную частотную характеристику цепи K (j ) и соответствующие ей амплитудно-частотную K () и фазочастотную () характеристики.
По найденным аналитическим выражениям рассчитать и построить графики частотных характеристик цепи для двух значений коэффициента усиления ОУ >1> и >2>. Оценить погрешность АЧХ и ФЧХ по формуле.


Определить импульсную h(t) и переходную g(t) характеристики цепи.
Рассчитать и построить графики этих характеристик для двух значений изменяемого параметра >1> и >2>,. В каждом случае оценить постоянную времени >1> и >2 >исследуемой цепи. Постоянная времени цепи равна модулю обратной величины полюса передаточной функции
Используя найденные выше временные характеристики цепи и интеграл наложения, найти реакцию цепи на импульс, изображенный на рис. 2. Параметры входного импульсного сигнала:
Р
ассчитать
и построить импульс на выходе цепи для
двух значений коэффициента усиления
операционного усилителя.
Графики входного и выходных сигналов
совместить на одном
рисунке.
Найти спектральную плотность выходного сигнала S(j), используя спектральный метод анализа. Рассчитать и построить графики модуля и аргумента спектральной плотности для двух значений .
Рассчитать и построить энергетический спектр сигнала на входе и выходе цепи. Графики спектров построить на одном рисунке.
Сравнить спектральные характеристики импульсного сигнала на входе и выходе цепи. Установить характер влияния коэффициента усиления операционного усилителя на свойства выходного сигнала.
Оценить влияние параметров цепи на спектральные и временные характеристики выходного сигнала.
И
сходные
данные:
Рис.1. Общая схема цепи.
Значения параметров элементов цепи вычисляются по формулам
R >k> = (m+1)(n+1)k, Ом, (1)
C = m + n + 2, мкФ, (2)
где k - номер ветви;
m – предпоследняя цифра зачетной книжки;
n – последняя цифра.
|
m=1 |
C = 6 мкФ |
R>2(3) >=24 Ом |
R>3(5) >= 40 Ом |
|
n=3 |
U>m >= 1 B |
R>1(4) >= 32 Ом |
R>4(6) >= 48 Ом |
Коэффициент усиления операционного усилителя (ОУ) является изменяемым параметром и принимает три значения:
>1>=100 ; >2>=100000;
t
СОДЕРЖАНИЕ
Задание на проектирование 2
СОДЕРЖАНИЕ 4
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ, СИМВОЛЫ И СОКРАЩЕНИЯ 5
1.ОПРЕДЕЛЕНИЕ ОПЕРАТОРНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ЦЕПИ ПО НАРЯЖЕНИЮ 6
2. КОМПЛЕКСНО – ЧАСТОТНАЯ ХАРАКТЕРИСТИКА ЦЕПИ 7
3. ГРАФИКИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ 8
4. ПЕРЕХОДНАЯ И ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ЦЕПИ 9
6. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ВРЕМЕНИ ЦЕПИ 12
ВРЕМЕННОЙ МЕТОД АНАЛИЗА 13
7. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ЦЕПИ НА ИМПУЛЬС 13
8. ГРАФИКИ ВХОДНОГО И ВЫХОДНОГО ИМПУЛЬСОВ 14
9. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ВЫХОДНОГО СИГНАЛА 15
10. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА 16
11. Характер влияния коэффициента усиления 17
12. Влияние параметров цепи. 17
ПРИЛОЖЕНИЕ 19
Расчет значений коэффициентов полинома 19
Преобразование Лапласа для нахождения временных характеристик 19
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ, СИМВОЛЫ И СОКРАЩЕНИЯ
С- емкость, Ф
сопротивление, кОм
a,b- коэффициенты полинома
U- напряжение, В
g(t)- переходная характеристика
h(t) - импульсная характеристика
(ω)- фазочастотная характеристика
K(jω)- комплексная частотная характеристика
К(р) - операторный коэффициент передачи цепи по напряжению
К(ω) - амплитудно-частотная характеристика
H(p)- операторная характеристика
L - индуктивность, Гн
р - оператор преобразования Лапласа
t - время, с
- постоянная времени цепи, с
ω- угловая частота, рад/с
x(t)- входной сигнал
s(t) - выходной сигнал
Y- проводимость цепи, См
АЧХ - амплитудно-частотная характеристика
ФЧХ - фазо-частотная характеристика
S>вх>(ω) - спектральная плотность воздействия
S>вых>(ω) - спектральная плотность выходного сигнала
W(ω) - энергетический спектр
Ф(t) – функция Хевисайда (возвращает 0 при t<0, 1 при t0)
∆(t) – функция Дирака (возвращает 0 при t≠0, ∞ при t=0)
1.ОПРЕДЕЛЕНИЕ ОПЕРАТОРНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ЦЕПИ ПО НАРЯЖЕНИЮ

Для
нахождения операторного коэффициента
передачи цепи по напряжению составим
эквивалентную схему замещения
анализируемой цепи, в которой операционный
усилитель заменим простейшей схемой
замещения идеального операционного
усилителя, а идеализированные пассивные
элементы на их операторные схемы
замещения. Для нахождения операторного
коэффициента передачи цепи по напряжению
воспользуемся методом узловых напряжений.
Схема замещения цепи изображена на рис.
3.
Рис. 3. Схема замещения цепи.
Обозначим узловые напряжения в схеме замещения как U>10>, U>20> ,U>30> ,U>40>. Поскольку к узлам 1 и 2 подключены источники, равные соответственно U>10> и U>20> , то узловые уравнения составляются только для узлов 3 и 4. Последние уравнения записываются в канонической форме и имеют вид:

Выразим из второго уравнения системы
 , (3)
, (3)
подставим его в первое и учтем, что
 , (4)
, (4)
В результате получим первое уравнение в следующем виде:
 , (5)
, (5)
Воспользуемся тем, что Y>31>=0 и преобразуем формулу 5
 , (6)
, (6)
Отсюда получается операторный коэффициент передачи цепи по напряжению
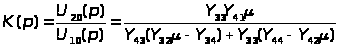 , (7)
, (7)
где K(p)-операторный коэффициент передачи цепи по напряжению.
Подставим в формулу 6 выражения для Y>ji>, получим:
 , (8)
, (8)
где K(p)-операторный коэффициент передачи цепи по напряжению,
p- оператор Лапласа.
Обозначив в формуле 8 за:
 ,
,
Получим операторный коэффициент передачи цепи по напряжению в виде отношения двух полиномов:
 , (9)
, (9)
где K(p)-операторный коэффициент передачи цепи по напряжению
Воспользуемся найденными из формулы 8 коэффициентами и рассчитаем их значения для различных коэффициентов . Расчёт приведён в приложении 1.
По результатам расчётов составим таблицу коэффициентов полиномов.
Таблица 1
|
a>1> |
a>0> |
b>1> |
b>0> |
|
|
>1>=100 |
9,028*10-4 |
4,556 |
-6*10-4 |
-6,667 |
|
>2>=100000 |
0,88 |
4,445*103 |
-0,6 |
-6.667*103 |
2. КОМПЛЕКСНО – ЧАСТОТНАЯ ХАРАКТЕРИСТИКА ЦЕПИ
Заменив p на j, получим комплексный коэффициент передачи цепи по напряжению.
 , (10)
, (10)
где K(j)-комплексный коэффициент передачи цепи по напряжению,
- круговая частота, рад/с.
Для нахождения аналитических выражений для АЧХ и ФЧХ коэффициента передачи цепи по напряжению, преобразуем формулу 10 к показательной форме записи и получаем:
Для амплитудно-частотной характеристики:
 , (11)
, (11)
где K()-амплитудно-частотная характеристика,
- круговая частота, рад/с.
Для фазо-частотной характеристики:
 , (12)
, (12)
где ()-амплитудно-фазовая характеристика,
- круговая частота, рад/с.
3. ГРАФИКИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ
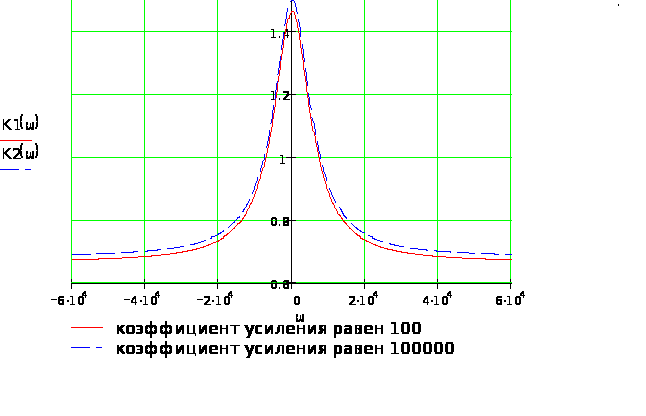
Построим
амплитудно-частотную характеристику
цепи для двух значений коэффициента
усиления.
Рис. 4
Г
рафики
для фазочастотных характеристик для
двух значений коэффициента усиления:
Рис.5.
Погрешность АЧХ

Рис.
4.1.
Погрешность ФЧХ


Рис. 5.1.
4. ПЕРЕХОДНАЯ И ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ЦЕПИ
Для определения переходной и импульсной характеристик цепи с начала найдём их операторные изображения.
Для переходной характеристики цепи:
 , (13)
, (13)
где g(t)- переходная характеристика,
p-оператор Лапласа,
H(p)- операторная характеристика.
Для импульсной характеристики:
 , (14)
, (14)
где h(t)- импульсная характеристика,
p-оператор Лапласа,
H(p)- операторная характеристика.
И
(15)
(16)

спользуя обратное преобразование Лапласа переходим от изображения искомых временных характеристик к оригиналам.
5. ГРАФИКИ ВРЕМЕННЫХ ХАРАКТЕРИСТИК
Воспользуемся формулами (15) и (16), а также значениями коэффициентов, полученных в таб. 1. построим графики импульсной и переходной характеристик для всех значений коэффициентов усиления операционного усилителя.
Переходная характеристика:
Р

ис.
6.
Импульсная характеристика:
Рис. 7.
6. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ВРЕМЕНИ ЦЕПИ
Постоянная времени цепи первого порядка равна модулю обратной величины полюса передаточной функции. Полюсами передаточной функции называется все значения аргумента p=p>oi>, при которых знаменатель передаточной функции обращается в ноль. В формуле 9 приравняем знаменатель функции к нулю, в результате получим:
 , (17)
, (17)
где - постоянная времени цепи, с
Используя формулу 16, рассчитаем значения постоянных времени цепи для всех значений коэффициента усиления операционного усилителя. Расчёт приведён в Приложении 1.
Постоянные времени цепи
Таблица 2
|
, с |
, мкс |
|
|
=100 |
1.982*10-4 |
19,82 |
|
=100000 |
1,98*10-4 |
19,82 |
Временные характеристики исследуемой цепи изображены на рис.6, рис. 7. Частотные характеристики изображены на рис. 4, рис. 5.
ВРЕМЕННОЙ МЕТОД АНАЛИЗА
7. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ЦЕПИ НА ИМПУЛЬС
С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие и в том случае, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией, которая имеет конечное число конечных разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки функции в точках разрыва. Для определения реакции цепи на воздействие импульса изображённого на рис.2 очевидно, что интервал интегрирования необходимо разбить на четыре части ( t(0,t>1>), t(t>1>,t>2>), t(t>2>,t>3>), t>t>3>).
Запишем реакцию на входной импульс:
 , (18)
, (18)
где s(t)-реакция цепи.
П одставив
в формулу 18 исходные данные получим
формулу для нахождения реакции на
входной импульс.
одставив
в формулу 18 исходные данные получим
формулу для нахождения реакции на
входной импульс.
,(19)
где s(t) -реакция цепи,
U>max>-максимальная амплитуда входного сигнала, В,

 - тангенс угла наклона среза.
- тангенс угла наклона среза.
8. ГРАФИКИ ВХОДНОГО И ВЫХОДНОГО ИМПУЛЬСОВ
Построим импульс на выходе цепи для двух значений коэффициента усиления операционного усилителя ( >1> , >2>). Построим графики входного и выходного сигналов друг под другом, выбрав для каждого графика подходящий масштаб.
Р

ис.
8.
Рис. 9.
9. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ВЫХОДНОГО СИГНАЛА
Найдем спектральную плотность выходного сигнала S(jω), используя спектральный метод анализа.
S>вых>(ω)= K(jω)* S>вх>(ω),
где
 ,
,
Рис. 11.
Рис. 10.
Рис. 11.
10. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА

Рис. 12.
Характер влияния коэффициента усиления
В данной курсовой работе был произведён анализ схемы первого порядка, содержащей операционный усилитель. Были получены и рассчитаны АЧХ и ФЧХ исследуемой схемы. По полученному операторному коэффициенту передачи цепи по напряжению можно сделать вывод, что схема не представляет собой ни дифференцирующую, ни интегрирующую цепь первого порядка.
Были получены реакции цепи для двух значений коэффициента усиления операционного усилителя. По результатам анализа можно говорить о том, что изменение значения коэффициента усиления ОУ крайне мало влияет на частотные характеристики цепи и свойства выходного сигнала. Спектральные характеристики выходных сигналов для разных КУ также мало отличаются друг от друга, при увеличении пратически повторяют характеристику импульсного сигнала на входе.
Влияние параметров цепи.
По полученной формуле (8), можно говорить о том, что следующие параметры имеют большое влияние на спектральные и временные характеристики сигнала, а именно:
С – имеет большое воздействие на постоянную времени (17)
R>3,1> – влияет на амплитуду выходного сигнала (чем выше R>3>, тем меньше U)
R>4> – влияет на амплитуду выходного сигнала (чем выше R>4>, тем выше U)
R>2> – влияет на длительность выходного сигнала (чем выше R>2>, тем выше τ)
Подбором вычеперечисленных параметров можно добится требуемой амплитуды и длительности выходного сигнала
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 1988. 536 с.
Попов В.П. Основы теории цепей. М.: Высшая школа, 1985. 496 с.
Радиотехнические цепи и сигналы: Учебное пособие для вузов/ Васильев Д.В., Витоль М.Р., Горшенков Ю.Н. и др.// Под ред. К.М. Самойло. М.: Радио и связь, 1982. 528 с.
ПРИЛОЖЕНИЕ
Расчет значений коэффициентов полинома
Преобразование
Лапласа для нахождения временных
характеристик


Расчёт постоянных
времени цепи 

