6 задач по теории электрических цепей
чЗадание 1


R>2>
R>3>





















İ
R>1>
C
L
Ė




Ů>(10)>
Ů>(20>>)>
Ů>(30)>
Ů>(0)>
(0)
(1)
(2)
(3)






ŮL
ŮR3
ŮR2
ŮR1
ŮC
İ5
I4
İ3
İ2
İ1
Параметры электрической цепи:
R1 = 1.1 кОм L = 0,6 · 10-3 Гн E = 24 В
R2 = 1.8 кОм C = 5.3 · 10-10 Ф I = 29 · 10-3 A
R3 = 1.6 кОм ω = 6.3 · 105 Гц
1). Используя метод узловых напряжений, определить комплексные действующие значения токов ветвей и напряжений на элементах цепи:
Составляем систему уравнений методом узловых напряжений:
Для узла U>(10)> имеем :
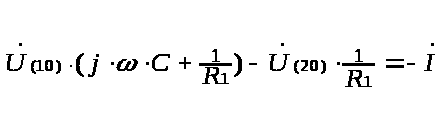
Для узла U>(20>>)> имеем:
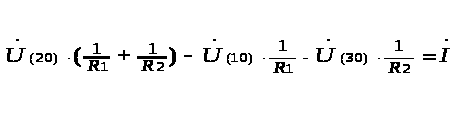
Для узла U>(30)> имеем :
0

Вычисления полученной системы уравнений проводим в программе MATCAD 5.0 имеем :
Ů>(10>>)>
=

Ů>(20)>
=

Ů>(30)>
=

Н
аходим
действующие комплексные значения токов
ветвей (используя программу MATCAD 5.0)
:


Определяем действующие напряжения на єэлементах:
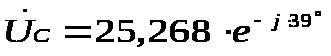

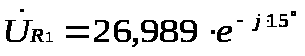

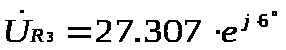

2). Найти комплексное действующее значение тока ветви, отмеченной знаком *, используя метод наложения:
Выключая поочередно источники электрической энергии с учетом того, что ветви содержащие источник тока представляют собой разрыв ветви, а источники напряжения коротко замкнутые ветви имеем:
После исключения источника напряжения составим цепь представленную ниже:


Для полученной схемы составляем уравнения определяющее значение тока İ1.
Имеем:
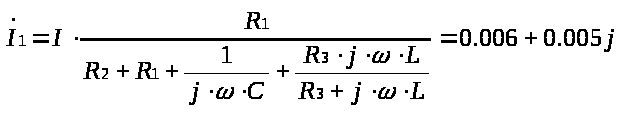
После исключения источника тока имеем следующую схему:
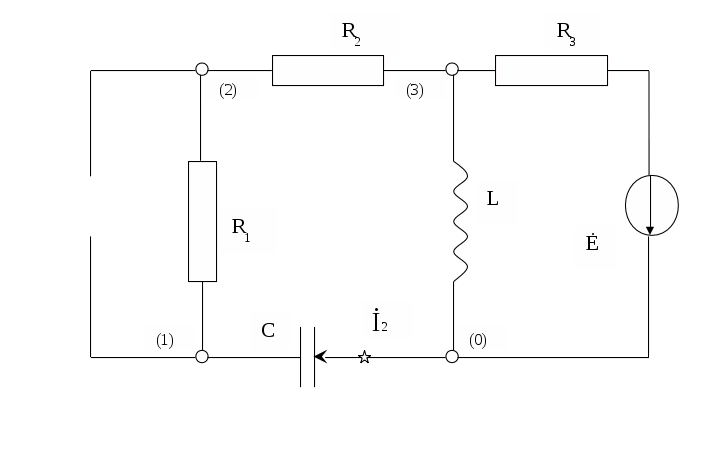

Для полученной схемы определим ток İ 2
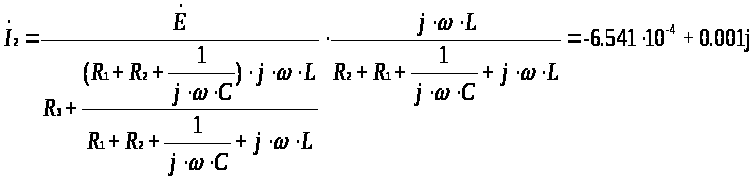
Результирующий ток ветви отмеченной звездочкой найдем как сумму İ1 и İ2 :
İ
ветви
= İ1
+ İ2
= 0,005 + 0,007j=
Топологический граф цепи:



Полная матрица узлов:
|
ветви узлы |
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
-1 |
0 |
0 |
-1 |
-1 |
0 |
|
I |
1 |
-1 |
0 |
0 |
0 |
1 |
|
II |
0 |
1 |
1 |
0 |
0 |
-1 |
|
III |
0 |
0 |
-1 |
1 |
1 |
0 |
Сокращенная матрица узлов
|
ветви узлы |
1 |
2 |
3 |
4 |
5 |
6 |
|
I |
1 |
-1 |
0 |
0 |
0 |
1 |
|
II |
0 |
1 |
1 |
0 |
0 |
-1 |
|
III |
0 |
0 |
-1 |
1 |
1 |
0 |
Сигнальный граф цепи:
ЗАДАНИЕ 2
U3


U4

U5ё
Параметры электрической цепи
С = 1.4 ·10-8Ф Rn = 316,2 Ом
L = 0.001 Гн
R = 3.286 Ом
Рассчитать и построить в функции круговой частоты АЧХ И ФЧХ комплексного коэффициента передачи цепи по напряжению:
Находим комплексный коэффициент передачи по напряжению
Общая формула:
Определяем АЧХ комплексного коэффициента передачи цепи по напряжению:
Строим график (математические действия выполнены в MATCAD 5.0)
Определяем ФЧХ комплексного коэффициента передачи цепи по напряжению, по оси ординат откладываем значение фазы в градусах, по оси обцис значения циклической частоты
Найти комплексное входное сопротивление цепи на частоте источника напряжения:
вх
Комплексное
входное сопротивление равно: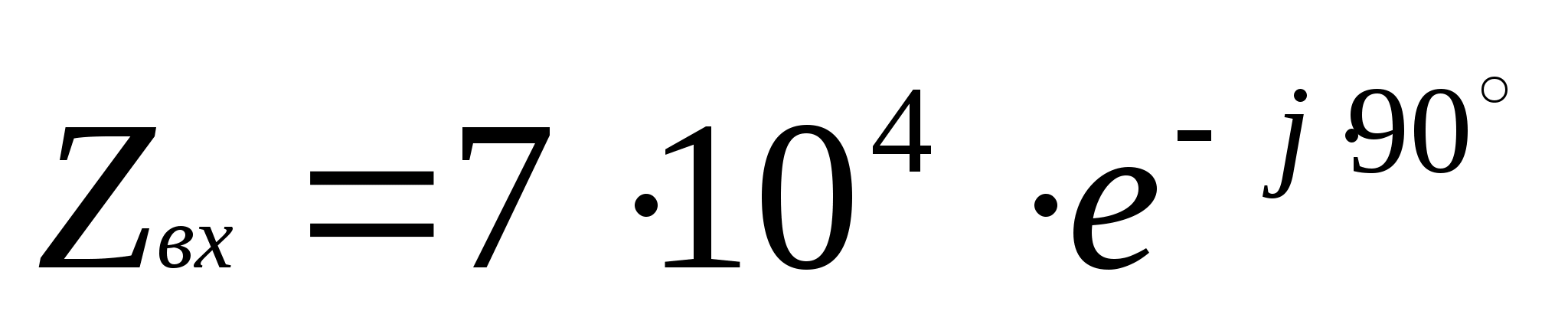
Определяем активную мощность потребляемую сопротивлением Rn:
Pактивная = 8,454·10-13
Задание 3

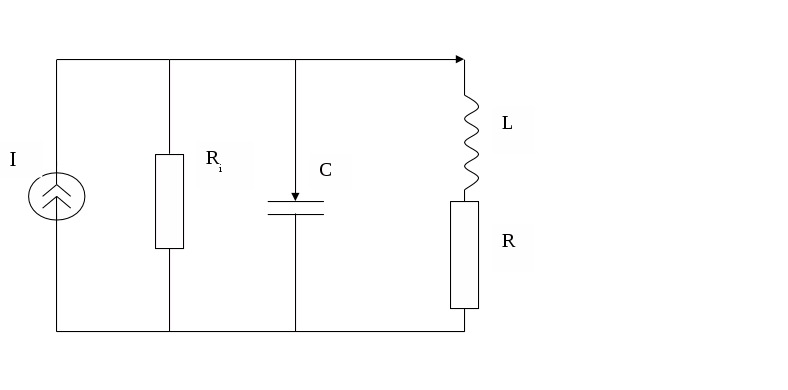
I>LR>
I>C>
Параметры электрической цепи:

L = 1.25·10-4 Гн
С = 0,5·10-9 Ф
R = 45 Ом Rn = R>0>
R>0> = 5,556·103 – 7,133j R>i> = 27780 – 49,665j
определить резонансную частоту, резонансное сопротивление, характеристическое сопротивление, добротность и полосу пропускания контура.
Резонансная частота ω>0> = 3,984·106 (вычисления произведены в MATCAD 5.0)
Резонансное сопротивление:

Характеристическое сопротивление ρ в Омах
Добротность контура

П
олоса
пропускания контура
Резонансная частота цепи
ω>0> = 3,984·106
Резонансное сопротивление цепи
Добротность цепи
Qцепи = 0,09
Полоса пропускания цепи
Р
ассчитать
и построить в функции круговой частоты
модуль полного сопротивления:
Рассчитать и построить в функции круговой частоты активную составляющую полного сопротивления цепи:
Рассчитать и построить в функции круговой частоты реактивную составляющую полного сопротивления цепи:
Рассчитать и построить в функции круговой частоты АЧХ комплексного коэффициента передачи по току в индуктивности:
Р
ассчитать
и построить в функции круговой частоты
ФЧХ комплексного коэффициента передачи
по току в индуктивности:
Рассчитать мгновенное значение напряжение на контуре:
Ucont = 229179·cos(ω>0>t + 90˚)
Рассчитать мгновенное значение полного тока на контуре:
Icont = 57,81cos(ω>0>t + 90˚)
Рассчитать мгновенное значение токов ветвей контура:
I>LR> = 646cos(ω>0>t + 5˚)
I>C >= 456,5cos(ω>0>t - 0,07˚)
Определить коэффициент включения Rn в индуктивную ветвь контура нагрузки с сопротивлением Rn = Ro, при котором полоса пропускания цепи увеличивается на 5%.
C
C
C
Данную схему заменяем на эквивалентную в которой параллельно включенное сопротивление Rn заменяется сопротивлением Rэ включенное последовательно:

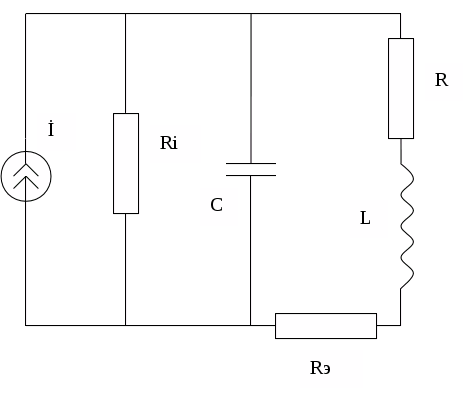
Выполняя математические операции используя программу MATCAD 5.0 находим значение коэффициента включения K>L> :> >
Задание 4


Параметры цепи:
e(t) = 90sinωt = 90cos(ωt - π>/2>)
Q = 85
L = 3.02 · 10-3 Гн
С = 1,76 • 10-9 Ф
Рассчитать параметры и частотные характеристики двух одинаковых связанных колебательных контуров с трансформаторной связью, первый из которых подключен к источнику гармонического напряжения.
определить резонансную частоту и сопротивление потерь R связанных контуров:


2. Рассчитать и построить в функции круговой частоты АЧХ И ФЧХ нормированного тока вторичного контура при трех значениях коэффициента связи Ксв = 0.5Ккр (зеленая кривая на графике), Ксв = Ккр (красная кривая на графике), Ксв = 2Ккр (синяя кривая на графике), где Ккр – критический коэффициент связи.

Ф
ЧХ
нормированного тока вторичного контура
при трех значениях коэффициента связи
Ксв = 0.5Ккр (зеленая кривая на графике),
Ксв = Ккр (красная кривая на графике),
Ксв = 2Ккр (синяя кривая на графике), где
Ккр – критический коэффициент связи.
Г
рафически
определить полосу пропускания связанных
контуров при коэффициенте связи Ксв =
0,5Ккр
Графически определить полосу пропускания связанных контуров при коэффициенте связи Ксв = Ккр
Графически определить полосу пропускания связанных контуров при коэффициенте связи Ксв = 2Ккр, а так же частоты связи.
Задание5
S
R
L

e
Рассчитать переходный процесс в электрической цепи при включении в нее источника напряжения e(t) амплитуда которого равна E = 37 и временной параметр Т = 0,46 мс, сопротивление цепи R = 0.9 кОм, постоянная времени τ = 0.69.
Определить индуктивность цепи, а так же ток и напряжение на элементах цепи
Гн
Так как данная цепь представляет собой последовательное соединение элементов, ток в сопротивлении и индуктивности будет одинаковым следовательно для выражения тока цепи имеем:
Исходное уравнение составленное для баланса напряжений имеет вид:
Заменяя тригонометрическую форму записи напряжения е(t) комплексной формой
Имеем:
Используя преобразования Лапласа заменяем уравнение оригинал его изображением имеем:
Откуда
Используя обратное преобразование Лапласа находим оригинал I(t):
Переходя от комплексной формы записи к тригонометрической имеем
Определяем напряжение на элементах цепи
Задание 6
Параметры четырехполюсника
С = 1.4 ·10-8Ф
L = 0.001 Гн
R = 3.286 Ом
ω = 1000 рад/с
Р
ассчитать
на частоте источника напряжения А
параметры четырехполюсника:
Параметры А11 и А21 рассчитываются в режиме İ 2 = 0

Параметры А12 и А22 рассчитываются в режиме Ŭ 2 = 0


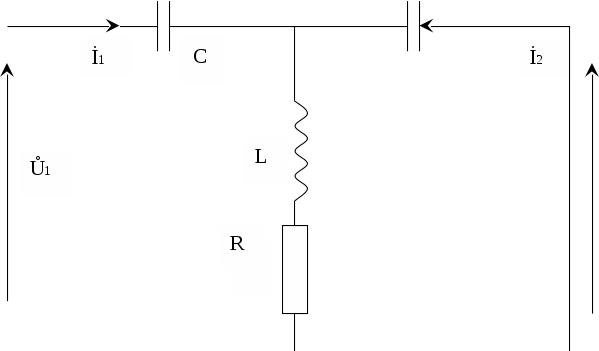
Ů2
И
сходная
матрица А параметров
четырехполюсника:
Оглавление
Задание 1 стр.1-7
Задание 2 стр.8-11
Задание 3 стр.12-18
Задание 4 стр.13-23
Задание 5 стр.14-27
Задание 6 стр.27-30
1









