Механізм приводу поршневого насосу

Курсовий проект

з теорії машин і механізмів

на тему: Механізм приводу поршневого насосу

1. Силове дослідження механізму

Структурний аналіз

Зображуємо структурну схему механізму.

Рис. 1

Номеруємо ланки і позначаємо кінематичні пари.

Складаємо таблицю кінематичних пар.

Таблиця 1. Кінематичнi пари

Назва КП	О	А1	A2	A3,B3	С4
Ланки КП	0-1	1-2	2-3	3-4	4-5
Клас КП	5	5	5	5	5
Вид руху	oб.	oб.	oб.	oб.	пост.

Знаходимо ступінь рухомості за формулою Чебишева:

W = 3n-2p5-p4 = 3∙5-2∙7 = 1

де n – число рухомих ланок;

р5 – число кінематичних пар пятого класу;

р4 – число кінематичних пар четвертого класу.

Ділимо важільний механізм на групи Ассура.

Виділяємо структурну групу з ланок 4 – 5.

Рис.2

1) = 2; p5 = 3;

2) W = 32 – 23 = 0;

Група Асура 2 класа, 2 порядку, 2 виду.

Виділяємо структурну групу з ланок 2 – 3.

1) n = 2; p5 = 3;

2) W = 3∙2 – 2∙3 = 0;

Група Асура 2 класа, 2 порядку, 1 виду.

Рис. 3

Виділяємо механізм першого класу, який складається з ланок 0 – 1.

В загальному, розглянутий механізм другого класу (за класом вищої групи Асура).

1.1 Кінематичне дослідження

Задачами кінематичного дослідження є побудова планів положень механізму, траекторій окремих точок, швидкостей і прискорень ланок механізму. Дані для кінематичного розрахунку ланок механізму.

Розміри ланок важільного механізму :

LOA=0,17 м ; LАВ=1.4 м ; LСD=1,33 м, LО3C=3,2; LО3В=1,6м ;

n-1=1,8; 1=(R2\R1) ·n-1=(157,5/72) ·1,8=3,94 c-1 .

Знаходження масштаба плана побудови:

L = LOA /OA = 0.17/17 = 0.01м/мм .

Побудова плану швидкостей важільного механізму

Для прикладу побудуємо план швидкостей для шостого положення механізму. Рис. 5 (для положення № 6).

Знаходимо швидкість точки А.

VA =LOA w1 = 0,173,94 = 0,67м/с .

В довільному масштабі з довільної точки відкладаємо відрізок Рvа, що зображає швидкість точки А (перпендикулярно до кривошипа ОА в напрямку w1). Знаходимо масштаб побудови плана швидкостей:

v = Vа/(Рva) = 0.67/67 = 0.01 (м/с)/мм .

Для знаходження швидкості точки B запишемо систему векторних рівнянь:

VB = VА + VBA;

VB = VC + VВC .

Точка b буде лежати на перетині лінії, яка проходить через точку a перпендикулярно до ланки OA, з лінією, що проходить через точку Рv перпендикулярно до ланки BC.

Рис. 5

Знаходимо дійсне значення швидкості ланок механізму:

VО3В = (Рvb)v = 13,830,01 =0,14 м/с .

VО3С = (Рvc)v = 27,660,01 =0,28 м/с

VАВ = (ab)v = 74,020,01 =0,74 м/с

VСD = (cd)v = 20,170,01 =0,2 м/с .

VD = (Рvd)v = 37,020,01 =0,37м/с .

Знаходимо кутову швидкість обертання ланки O1A :

w2 = VАB/LВA = 0,74/1,4 = 0,53 рад/с .

Аналогічно знаходимо кутові швидкості ланок ВС і ВD :

w3 = VО3С/LО3С = 0,28/3,2 = 0,09 рад/с .

w4 = VСD/LСD = 0,2 /1,33 = 0,15 рад/с .

Аналогічно будуємо плани швидкостей для інших положень мeханізму.

Будуємо таблицю значень лінійних і кутових швидкостей ланок механізму:

Таблиця 2. Значення лінійних швидкостей ланок механізму

№	VS2,	VS3,В	VS4	VAB	VC	VCD,	VD,
0	0,34	0	0	0,67	0	0	0
1	0,39	0,53	1,44	0,92	1,06	0,91	1,85
2	0,66	0,92	2,31	0,88	1,84	1,42	1,27
3	0,77	0,92	2,25	0,5	1,85	1,38	2,77
4	0,66	0,65	1,5	0,95	1,29	0,03	1,81
5	0,44	0,25	0,56	0,48	0,5	0,36	0,67
6	0,31	0,14	0,31	0,74	0,28	0,2	0,37
7	0,41	0,46	1,05	0,79	0,92	0,67	1,27
8	0,59	0,69	1,63	0,68	1,37	1,01	1,99
9	0,7	0,79	1,95	0,43	1,57	1,19	2,42
10	0,69	0,72	1,87	0,1	1,44	1,15	2,37
11	0,55	0,45	1,24	0,29	0,9	0,79	1,6

Таблиця 3. Значення кутових швидкостейланок механізму

№	W2, c-1	W3, c-1	W4, c-1
0	0,48	0	0
1	0,66	0,33	0,68
2	0,63	0,58	1,07
3	0,36	0,58	1,04
4	0,68	0,4	0,02
5	0,34	0,14	0,27
6	0,53	0,09	0,15
7	0,56	0,29	0,5
8	0,49	0,43	0,76
9	0,31	0,49	0,89
10	0,07	0,45	0,86
11	0,21	0,28	0,59

Побудова плану прискорення важільного механізму Рис. 6 (для положення № 6).

Знаходимо прискорення точки A

aA = w12·lOA = 3,942·0,17 = 2,64 м/с2 .

В довільному масштабі з довільної точки Ра паралельно кривошипу АО в напрямку, який співпадає з напрямком від точки А до т.О (так,як доцентрове прискорення) відкладаємо відрізок Раа, який зображує прискорення точки А.

Знаходимо масштаб плана прискорень:

a = a/(Paa) = 2,64/66 = 0,04(м/с2)/мм

Рис. 6

Для знаходження прискорення точки B, запишемо систему векторних рівнянь:

aB = aA + aBA + aBAn ;

аB = aC + aВCn + aВC .

Для побудови прискорення точки B на плані прискорень виконуємо слідуючі операції :

з точки а відкладаємо відрізок аn2 , що відповідає нормальному рискоренню ланки АВ - aBAn , паралельно АВ в напрмку від В до А, аналогічно з точки Ра відкладаємо відрізок Раn3, паралельно О3В в напрямку від В до О3; він відповідає нормальному прискоренню ланки О3В aО3Bn.

Довжини відрізків, що показують нормальні прискорення aBAn і aО3Bn обчислюємо користуючись такими виразами :

aАВn = VAB2/lAВ = 0,742/1,4 = 0,39 м/с2 ;

аn2 = aАВn /a = 0,39/0,04 = 9,27мм ;

a О3Bn = VBО32/l BО3= 0,142 /1,6 = 0,01 м/с2 ;

Раn3 = a BО3n /a = 0,01/0,04 = 0,25мм ;

Точку b на плані прискорень отримуємо на перетині ліній, що показують тангенціальні прискоренн ланок АВ і О3В, тобто на перетині лінії, що виходить з точки n2 перпендикулрно до АВ і лінії, що виходить з точки n3 перпендикулрнодо О3В. Сполучивши точки a і b отримуємо вектор, що зображає прискорення ланки АВ .

aСDn = VСD2 / lСD = 0,22/1,33 = 0,03 м/с2 ;

аn4 = aСDn /a = 0,03/0,04 = 0,75 мм ;

На лініях, що показують прискорення ланок відкладаємо центри ваги ланок, користуючись такими співвідношеннями :

(AS2) = 0.5 AB

(O3S3) = 0.5 O3C

(CS4) = 0.5 CD

Сполучивши отримані точки з точкою Ра отримуєм вектори, що показують прискорення центрів ваги ланок

Знаходимо дійсні значення прискорень:

Дійсні значення прискорень отримуємо перемноживши довжини відповідних векторів, взятих з креслення, на відповідні масштабні коефіцієнти :

aS2 = (PaS2)a =57,6 ·0,04 =2,3 м/с2

aS3 = (PaS3)a = 68,47·0,04 =2,74 м/с2

aS4 = (PaS4)a = 154,38·0,04 =6,18 м/с2

aS5 = (PaS5)a = 184,16·0,04 =7,37 м/с2

аАВ =(n2b)a= 28,57·0,04 =1,14 м/с2 ;

аO3В=( n3b ) a= 68,47·0,04 =2,74 м/с2 .

аCD=( n4d ) a= 99,95·0,04 =4 м/с2 .

Знаходимо кутову швидкость обертання ланки АB:

2 = аAВ/lAВ = 1,14/1,4 =0,81 рад/с2 .

3 = аO3В/lO3В =2,74/1,6 =1,71 рад/с2 .

4 = аCD/lCD = 4/1,33 =3,01 рад/с2 .

1.2 Діаграми переміщень, швидкостей і прискорень веденої ланки

В правій верхній частині листа 1 викреслюють одну під одною координатні осі всіх трьох графіків.

Масштаб часу визначають за формулою:

n-частота обертання віхдної ланки в об/хв.

L-час одного оберту кривошипу зображуємо відрізком 240 мм.

Масштаби отриманих графіків визначають за формулами:

Масштабний коефіцієнт діаграми переміщення:

Масштабний коефіцієнт діаграми швидкостей:

Де довжина відповідного відрізка(від полюса до початку координат) на діаграмі у мм.

Масштабний коефіцієнт діаграми прискорень:

Де довжина відповідного відрізка(від полюса до початку координат) на діаграмі у мм.

2. Кінематичне дослідження механізму

2.1 Кінетостатичне дослідження механізму

Задачі кінетостатичного дослідження:

а) Знаходження зовнішніх сил, які діють на ланки механізму;

б) знаходження реакцій у кінематичних парах, тобто сил взаємодії ланок;

в) знаходження зрівноважуючої сили або моменту, прикладених до ведучої ланки механізму.

Вихідні дані.

Маса:

m1=(LОАq)=(0,1760)=10,2 кг ;

m2=(LABq)=(1,460)=84 кг ;

m3 ==(LО3Сq)=(3,260)=192 кг ;

m4=(L CD q)=(1,3360)=79,8 кг ;

m5 =9,4кг.

Моменти інерції : 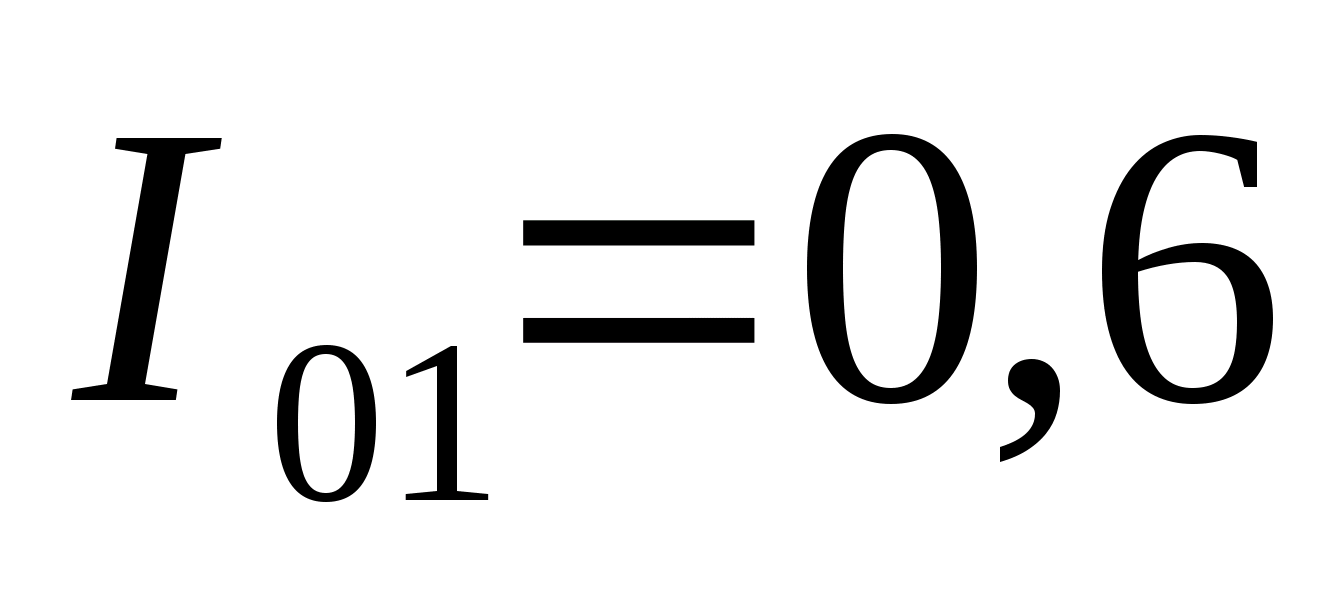кгм2 ;

кгм2 ;

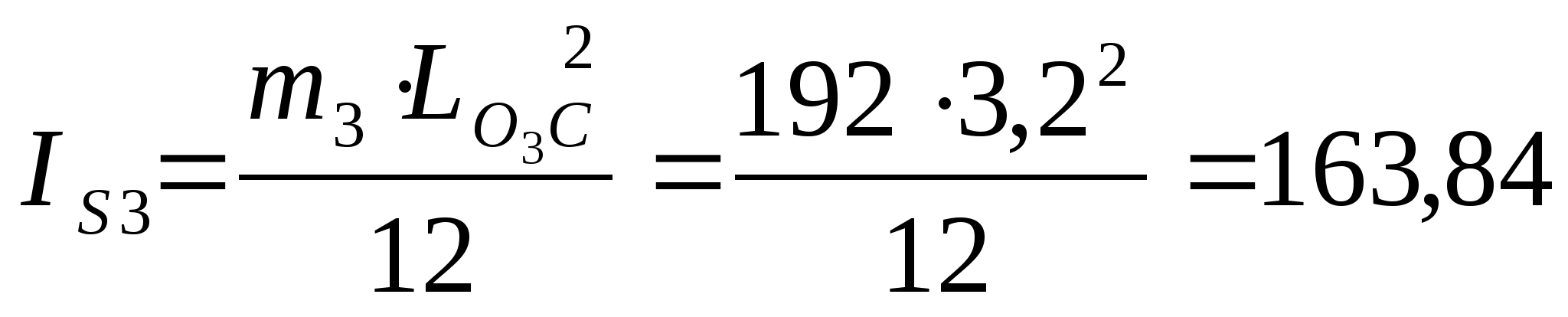кгм2 ;

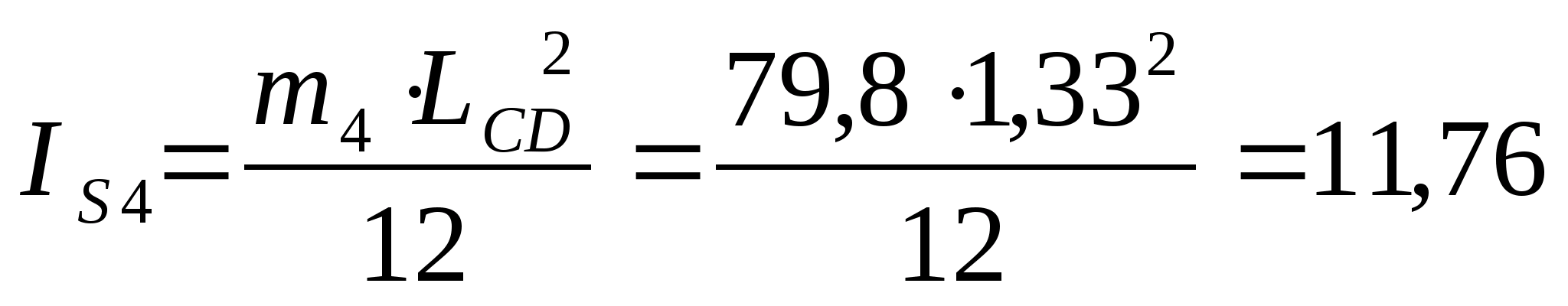кгм2 ;

Визначаємо зовнішні невідомі сили, реакції в кінематичних парах та зрівноважені сили або моменти. Визначаємо сили, що діють на дану групу.

Визначаємо сили тяжіння:

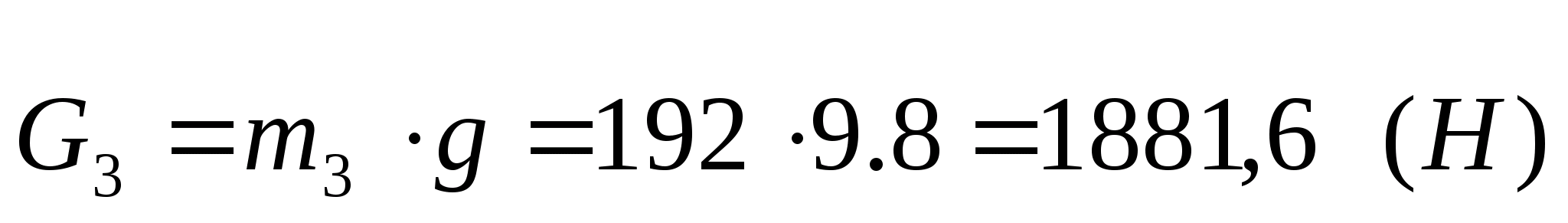
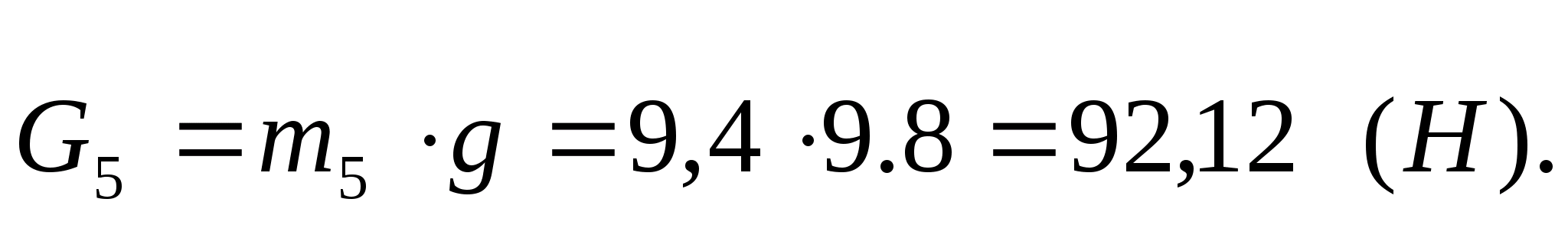
Визначаємо сили інерції і моменти сил інерції.

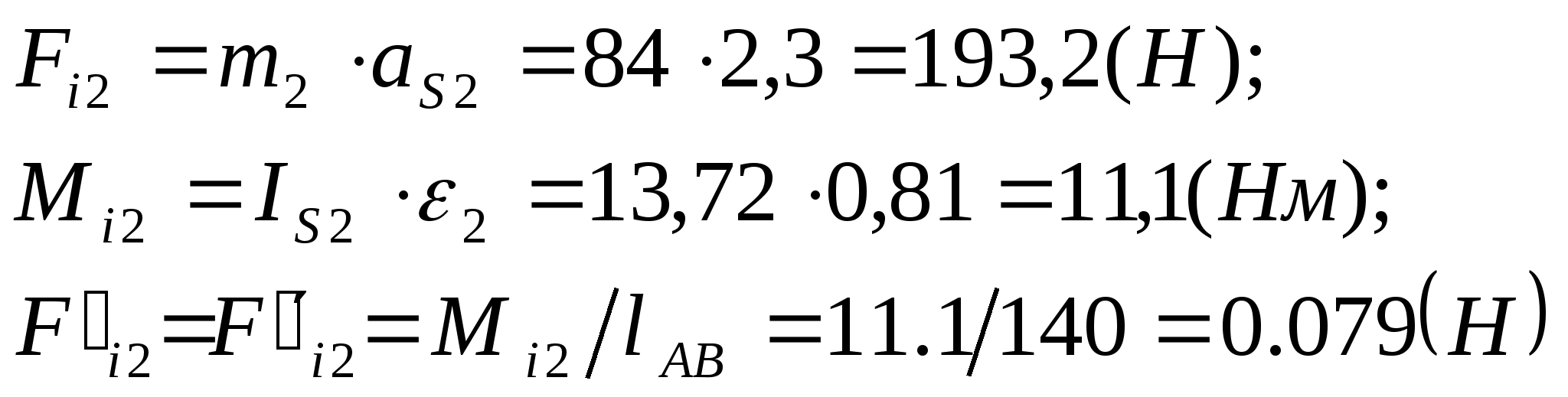
Cила корисного опору.

Fк.о. =5.8кН=5800Н.

Силове дослідження групи 4-5.

Реакції починаємо визначати з тангенціальної складової , складаємо суму моментів .

Записуємо всі моменти, що діють на ланку 4 відносно точки D.

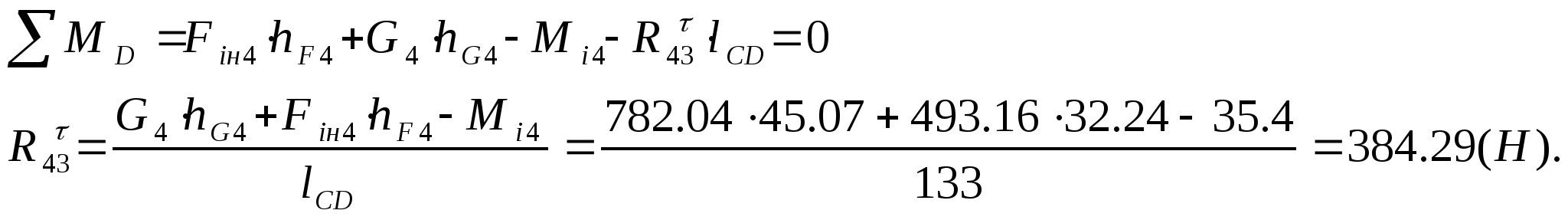
Записуємо всі моменти, що діють на ланку 4 відносно точки C.

Для визначення номінальної складової реакції,запишемо в векторній формі суму всіх сил, що діють на групу Ассура 4-5.

Для визначення невідомої, побудуємо в масштабі силовий багатокутник.

Для побудови силового багатокутника приймаємо масштаб:

З плану сил

Силове дослідження групи Ассура, що складається з ланок 2-3.

Визначаємо реакції з тангіціальної складової і .

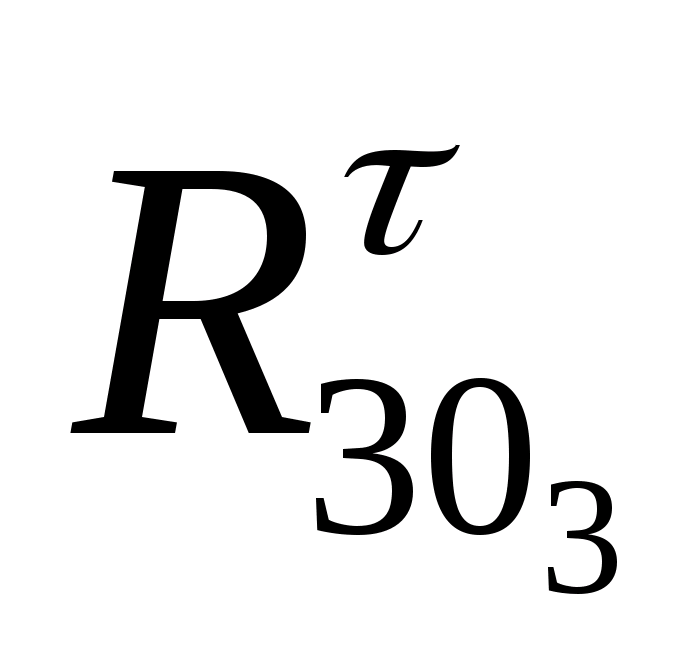Записуємо всі моменти, що діють на ланку 2 відносно точки В.

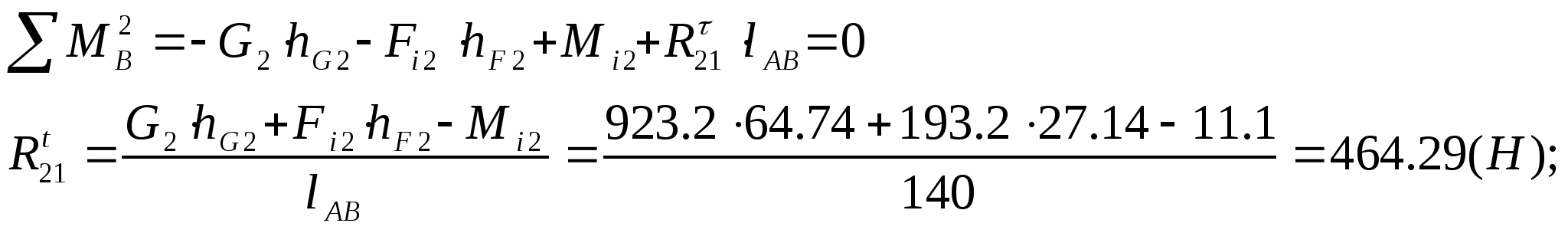
Записуємо всі моменти, що діють на ланку 3 відносно точки В.

Для визначення нормальних складових реакцій і запишемо в векторній формі всі сили, що діють на групу Ассура 2-3.

Для визначення невідомих і побудуємо силовий багатокутника.

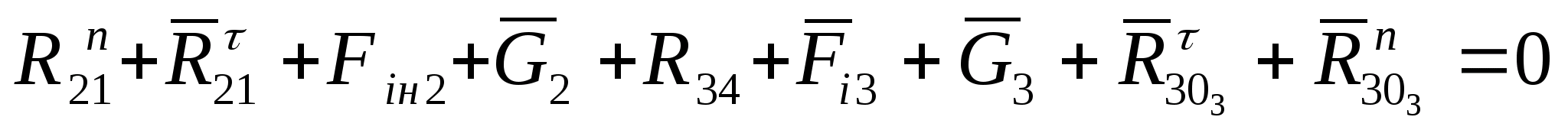
Для побудови силового багатокутника приймаємо масштаб

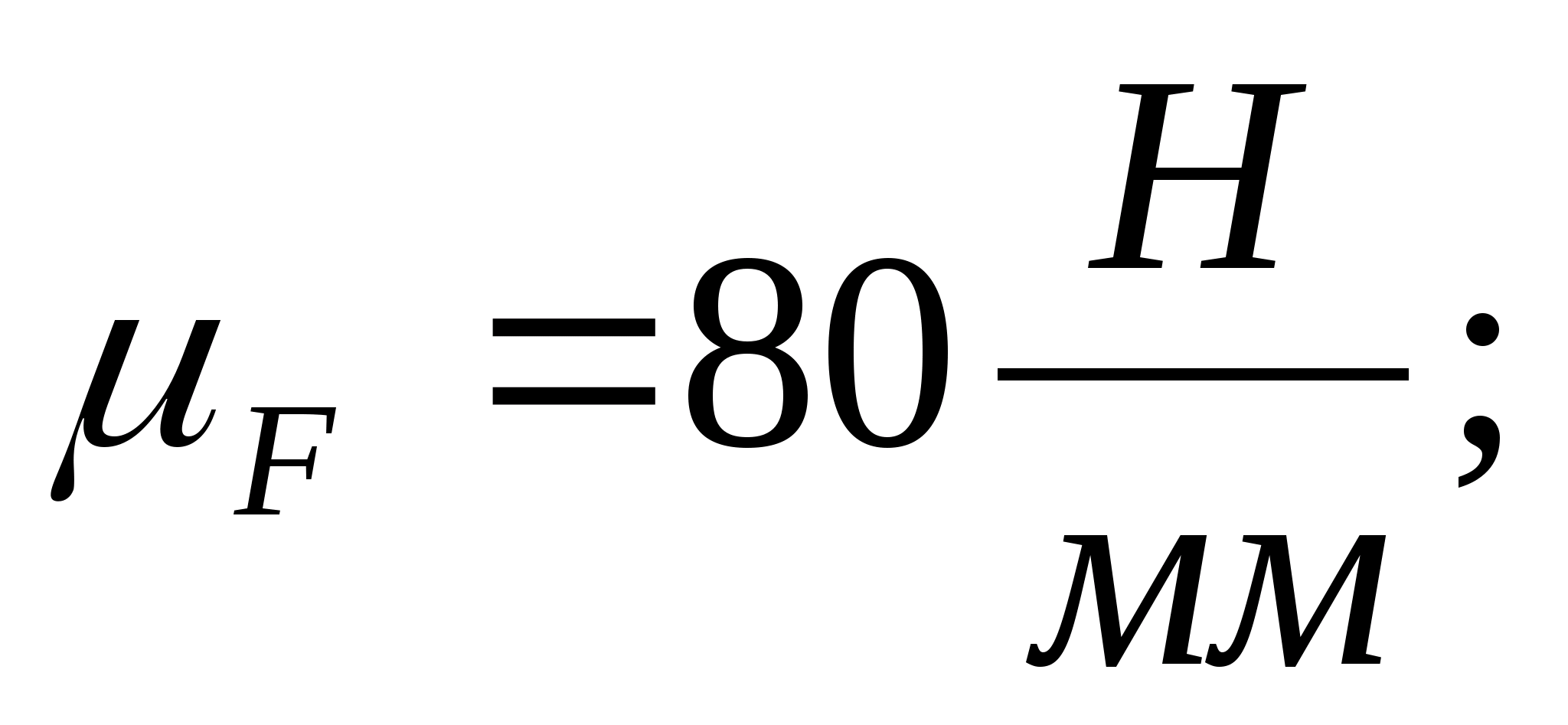
З силового багатокутника отримуємо

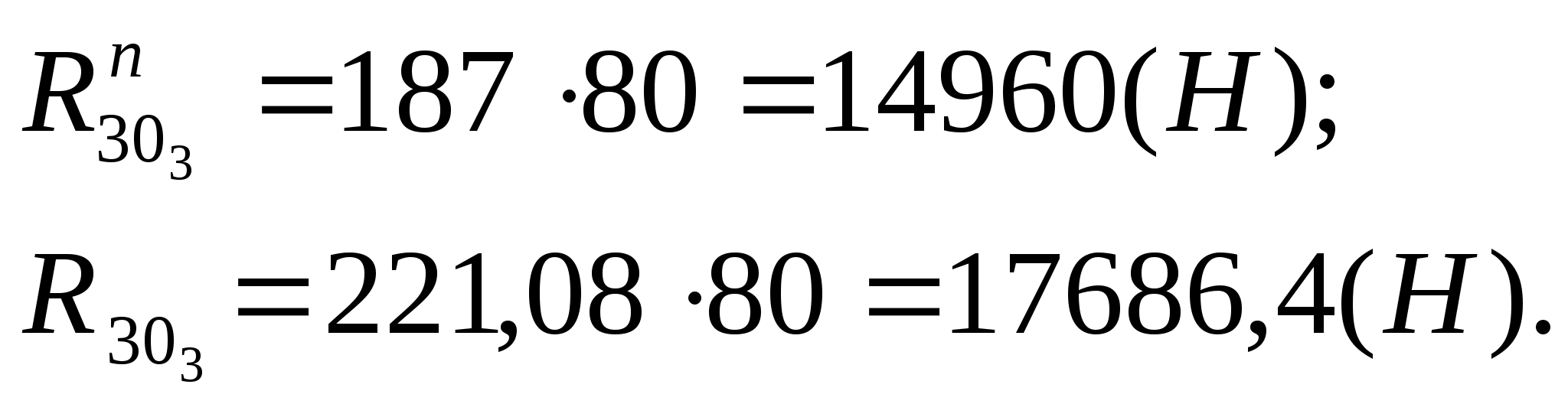
2.2 Силове дослідження механізму 1-го класу

Знайдемо зрівноважену силу.

Оскільки кривошип кріпиться до зубчатого колеса, то знаходиться радіусі зубчатого колеса.

2.3 Визначаємо зрівноважену силу методом важеля Жуковського

Повертаємо план швидкостей на 900, і записуємо суму моментів сил, що діють на важіль Жуковського.

Порівняємо за методом Жуковського і силовим розрахун-ком.

3. Визначення момента інерції маховика

3.1 Побудова графіка залежності МЗР від кута повороту кривошипа φ

Знаходимо для всіх 12 положень за планами швидкостей.

Для розрахунку застосовуємо формулу суми моментів відносно точки 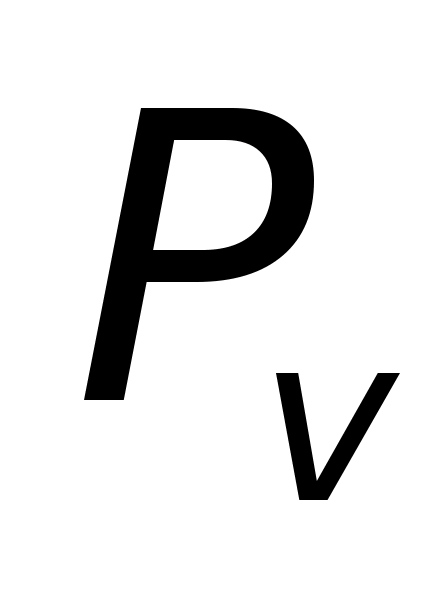. Отримані результати заносимо в таблицю 5.

Приклад: озрахуємо для 2-го положення механізму.

Мзр = FзрlO1A = -6011,010,17 =-1021,87 кHм .

Аналогічні розрахунки проводимо для всіх 12 положень механізму. Результати розрахунків заносимо в таблицю 6.

Таблиця 4.

№п/п	,Н
0	433,54	73,7
1	-3433,17	-583,64
2	-6011,01	-1021,87
3	-6129,83	-1042,07
4	-4373,71	-743,53
5	-1981,93	-336,93
6	3581,18	608,8
7	13483,94	2292,27
8	21487,01	3652,79
9	26338,8	4477,6
10	25788,56	4384,06
11	17501,62	2975,28

Рис. 7

Вихідні дані:

схема механізму без маховика;

маси і моменти інерції ланок:

;; .

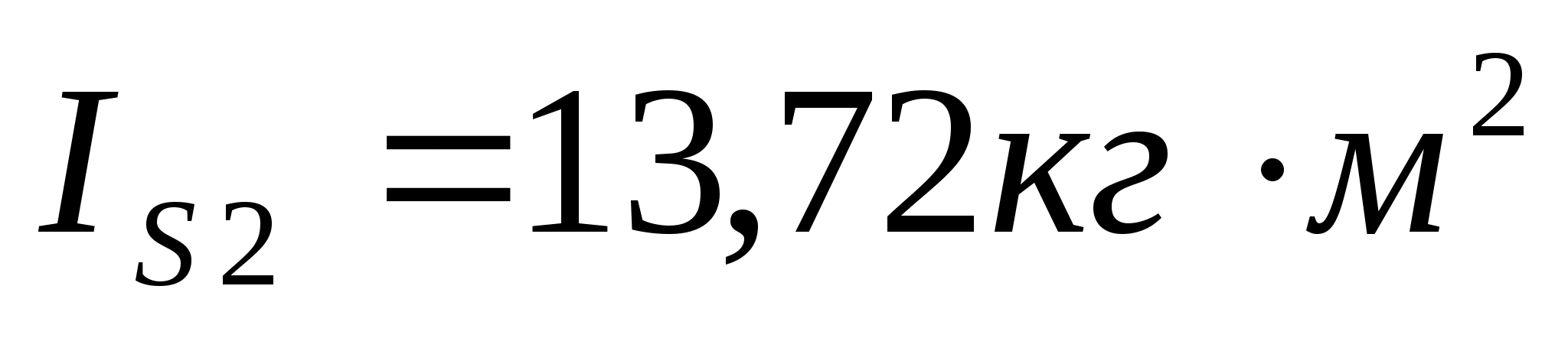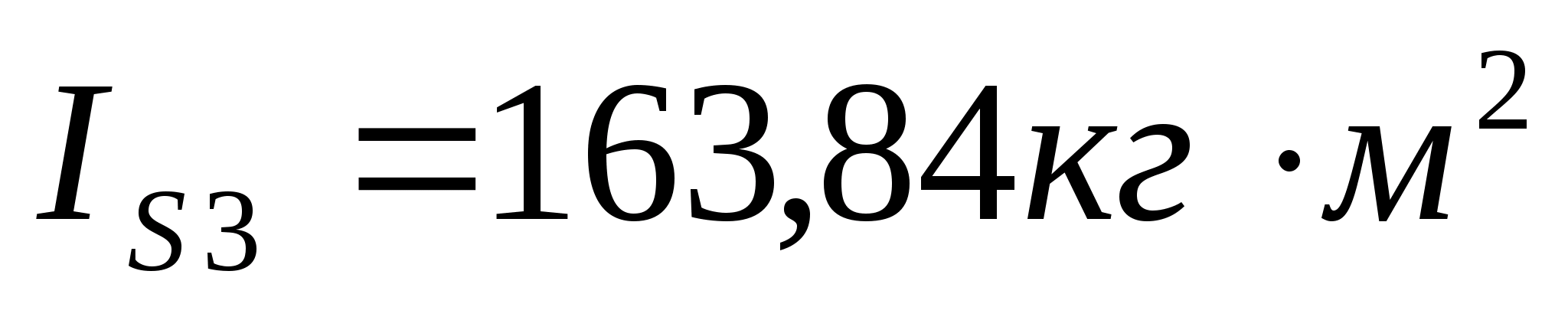середня кутова швидкість ведучої ланки ;

коефіцієнт нерівномірності руху ;

графік зведених моментів сил;

графік зведених моментів інерції.

3.2 Будуємо графік робіт сил опору

Для цього застосуємо метод графічного інтегрування графіка зведених моментів сил.

Послідовність інтегрування:

вибираємо полюс інтегрування Р на відстані Н=50 мм від осі ординат на продовженні вісі абсцис;

будуємо ординату, яка відповідає середині інтервалу 0-1, проектуємо її на вісі ординат і з’єднуємо точку 1’ ординати 01’ з полюсом Р;

теж саме робимо на наступних інтервалах;

з точки 0’ навої осі координат проводимо відрізок на інтервалі 0’1 паралельно променю Р1’ , з кінця отриманого відрізка проводимо відрізок на інтервалі 12 паралельно променю Р2’ і т.д.;

з’єднуємо отримані точки плавною кривою.

Отримана крива О’К є графіком робіт сил опору.

Оскільки за цикл усталеного руху робота рушійних сил дорівнює роботі сил опору, та з’єднавши т.О’ з т.К отримаємо графік робіт рушійних сил.

3.3 Будуємо графік приросту кінетичної енергії

Виконавши алгебраїчне сумування ординат граіфка робіт рушійних сил (беремо зі знаком “+”) та графіка робіт сил корисного опору (беремо зі знаком “-”).

Визначаємо масштабні коефіцієнти побудови графіків:

3.4 Будуємо графік зведених моментів інерції Ізв

Для цього визначаємо зведений момент інерції для 12-ти положень механізму. Оскільки умовою зведення є рівність кінетичних енергій , та

За цією формулою знаходимо зведені моменти інерції в 12-ти положеннях. Результати заносимо в таблицю 3.1.

Розрахуємо зведений момент інерції для 3-го положення механізму.

Значення зведених моментів інерції

Таблиця 5.

№пол.	Ізв, кгм2
0	1,43
1	19,51
2	46,6
3	49,43
4	23,83
5	4,67
6	2,29
7	12,13
8	27,03
9	37,28
10	33,67
11	15,33

За даними Табл.7 будуємо графік зведених моментів інерції, повернений на 900, в масштабі

3.5 Будуємо графік залежості -діаграма Віттенбауера

Для визначення момента інерції маховика необхідно сопчатку визначити максимальний приріст кінетичної енергії 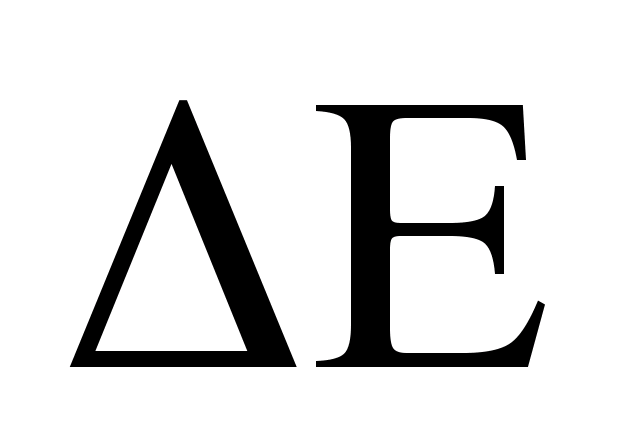, так як.

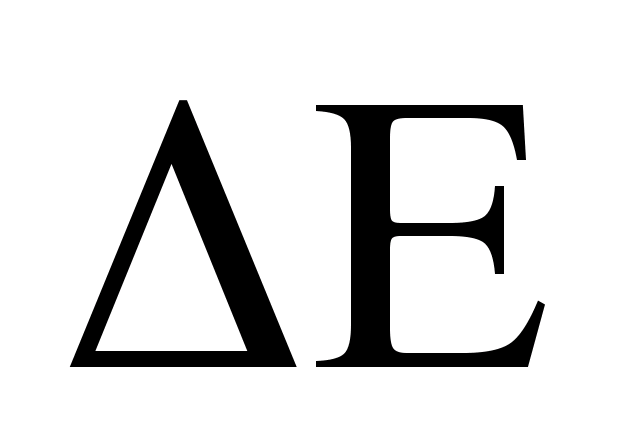визначаємо з діаграми Віттенбауера. Спочатку визначаємо кути, під якими будуть проведені дотичні до діаграми.

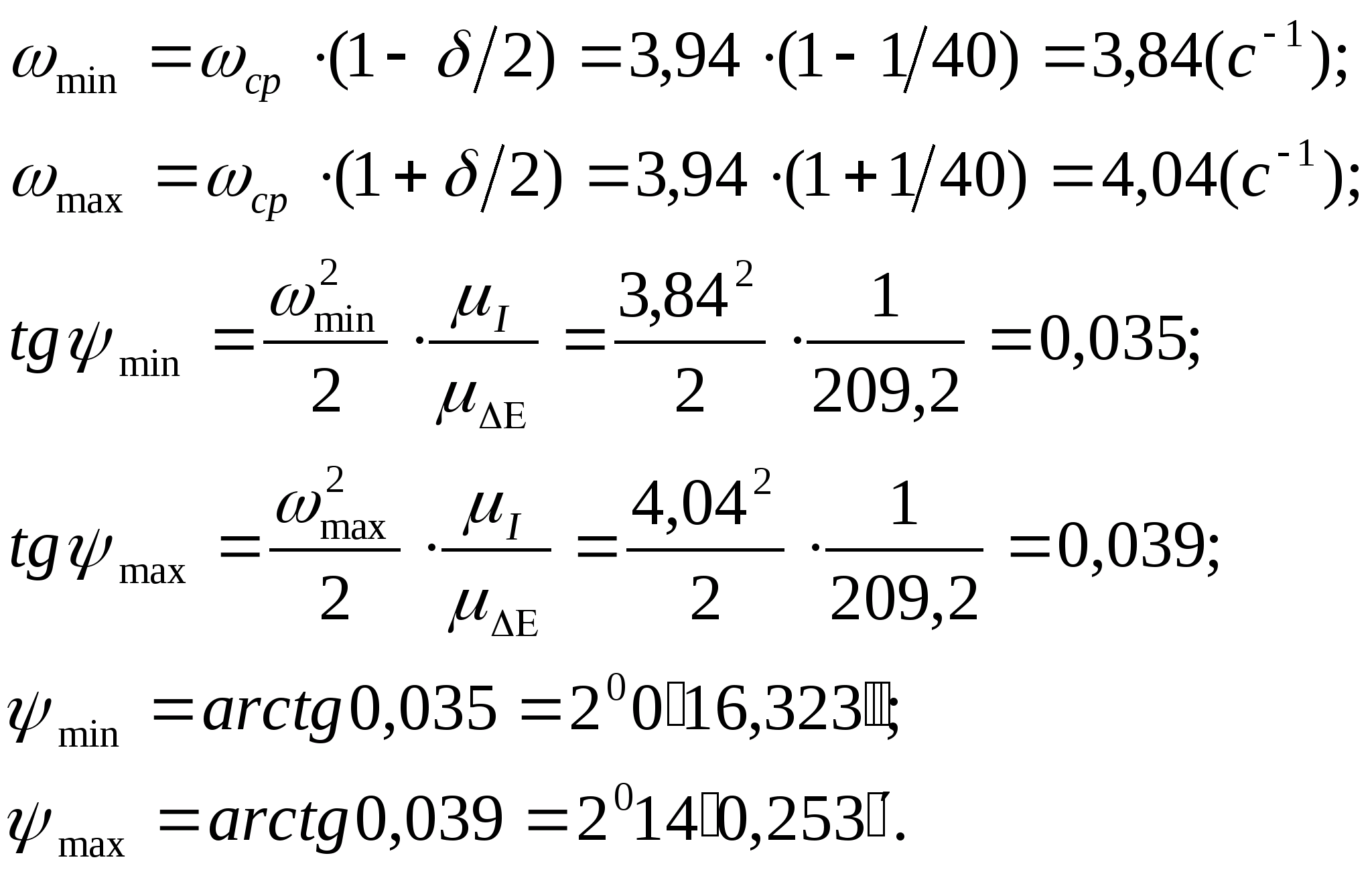
При відомих значеннях , проводимо дотичні до діаграми Віттенбауера. Там де ці лінії перетнуть ординату 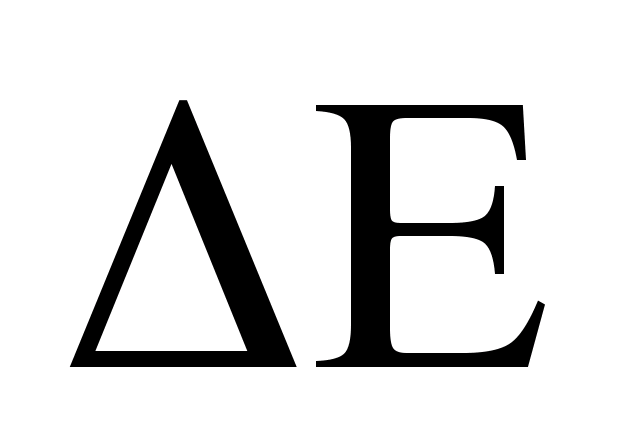, виділяємо відрізок ав.

Визначаємо момент інерції маховика:

.

3.6 Визначаємо геометричні розміри маховика

Оскільки за попередніми розрахунками момент інерції маховика має велике значення і розміри маховика вийдуть великими, доцільно розмістити маховик на валу електродвигуна. Тоді момент інерції маховика буде мати таке значення:

.

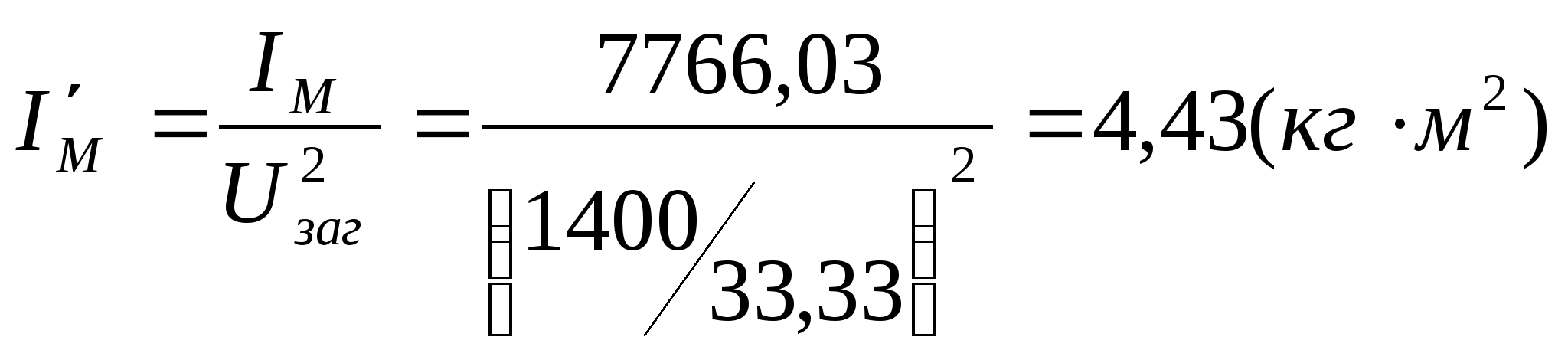Конструктивно приймаємо, що маховик виготовлений в вигдяді диска з масою, зосередженою на ободі, момент інерції якого:

Тоді зовнішній діаметр маховика розраховуємо за формулою:

де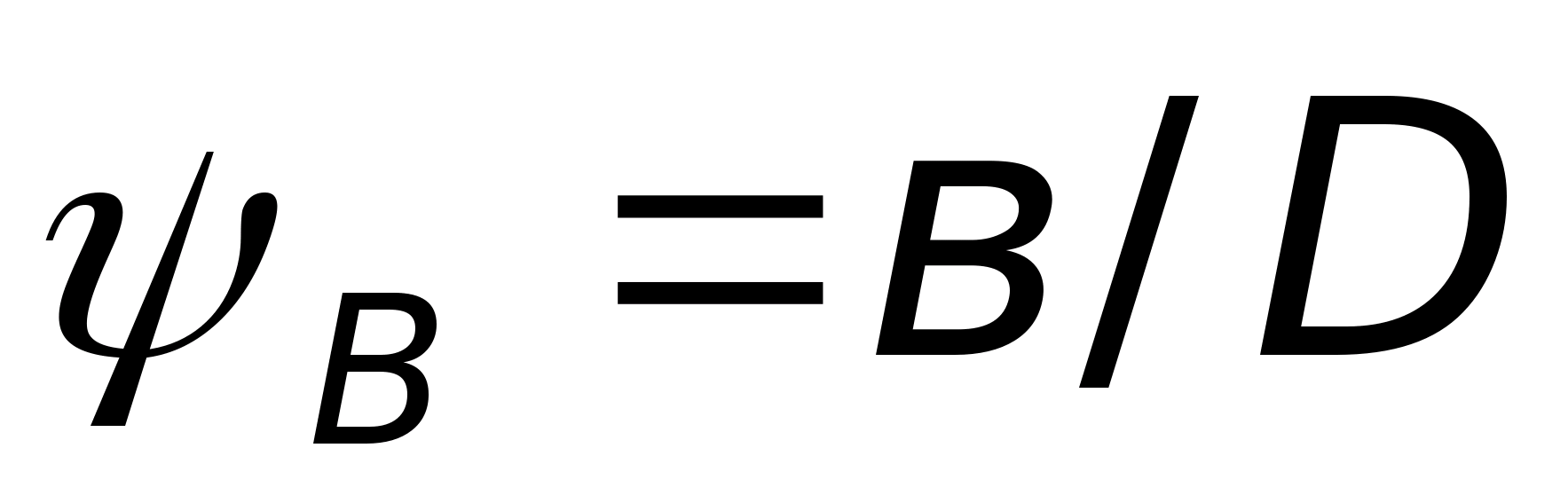- відошення ширини маховика до його діаметра, яке рекомендується приймати в межах (приймаємо 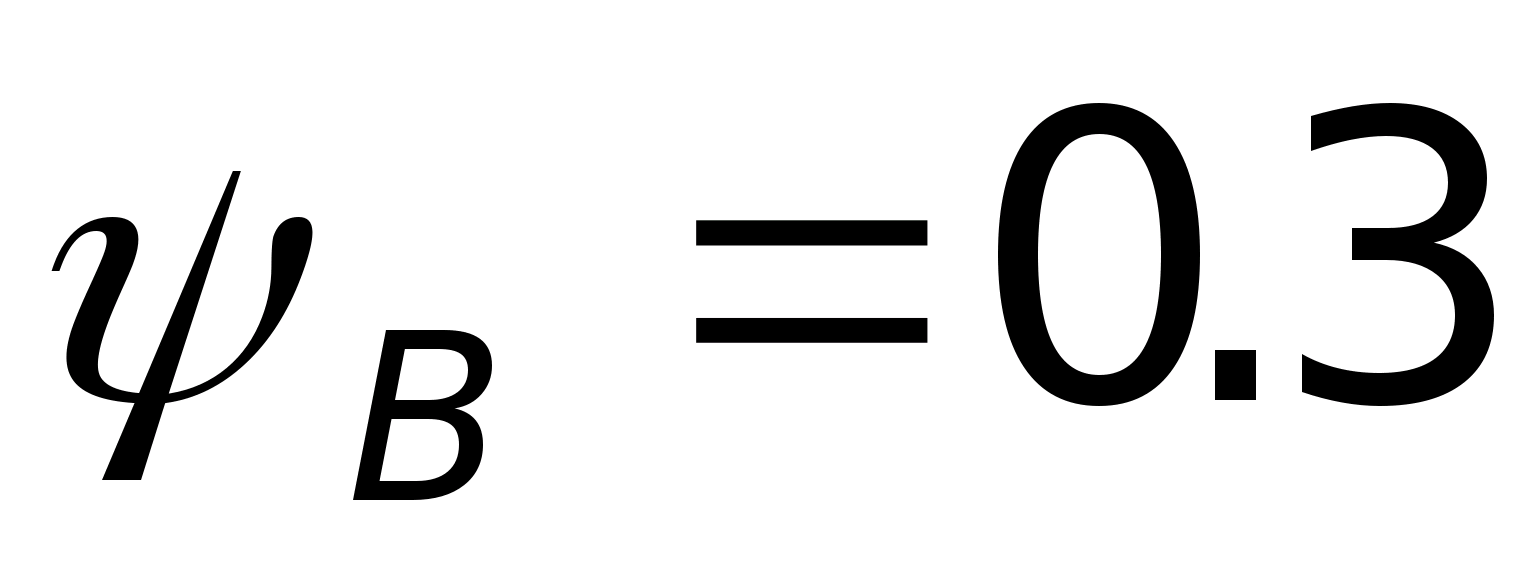); - густина матеріалу (для чавуна ).

Знаходимо внутрішній діаметр кільця:

D1=D·ΨH=0,46·0,8=0,368 м,

де ΨH = D1/D - відношення внутрішнього діаметра кільця до зовнішнього, яке рекомендується приймати в межах ΨH = 0,6...0,8 (в даному випадку приймаємо ΨH = 0,6).

Ширина обода маховика:

Знаходимо масу маховика:

Знаходимо колову швидкість обода маховика:

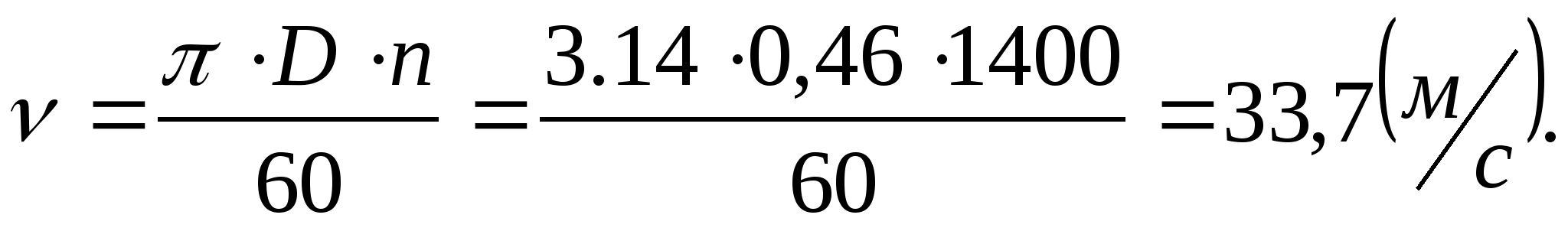
Така швидкість дрпустима для чавунних маховиків (- допустима колова швидкість обода чавунних маховиків).

Рис. 8

4. Синтез кулачкового механізму

Схема механізму

Виконуємо синтез механізму, кінематичний і динамічний аналіз кулачкового механізму з роликовим коромислом за вихідними даними:

Таблиця 6.

-кут відхилення -кут дальнього вистою -кут наближення -кут тиску - хід штовхача -закон руху:

4.1 Будуємо графік кутового переміщення штовхача

Починаємо побудову з графіка аналога прискорень. Далі за методикою інтегруємо графік аналога прискорень і отримуємо криву яка представляє собою графік аналогу швидкостей штовхача. Інтегруючи цей графік, отримаємо криву, яка представляє собою графік кутувого переміщення штовхача.

Визначаємо масштабні коефіцієнти побудови графіків:

Масштабний коефіцієнт осі абсцис діаграм:

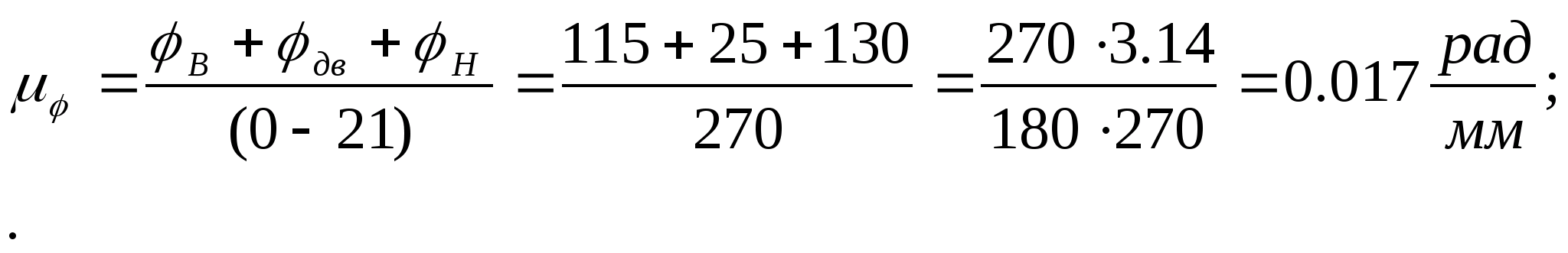
Де -- фазові кути кулачка;

(0-275) – відрізок відповідний суммі цих кутів.

Масштабний коефіцієнт діаграми переміщення:

Де максимальне значення переміщення;

довжина відповідного до відрізка на діаграмі у мм.

Масштабний коефіцієнт діаграми швидкостей:

Де довжина відповідного відрізка(від полюса до початку координат) на діаграмі у мм.

Масштабний коефіцієнт діаграми прискорень:

Де довжина відповідного відрізка(від полюса до початку координат) на діаграмі у мм.

Масштабний коефіцієнт діаграми кутової швидкості:

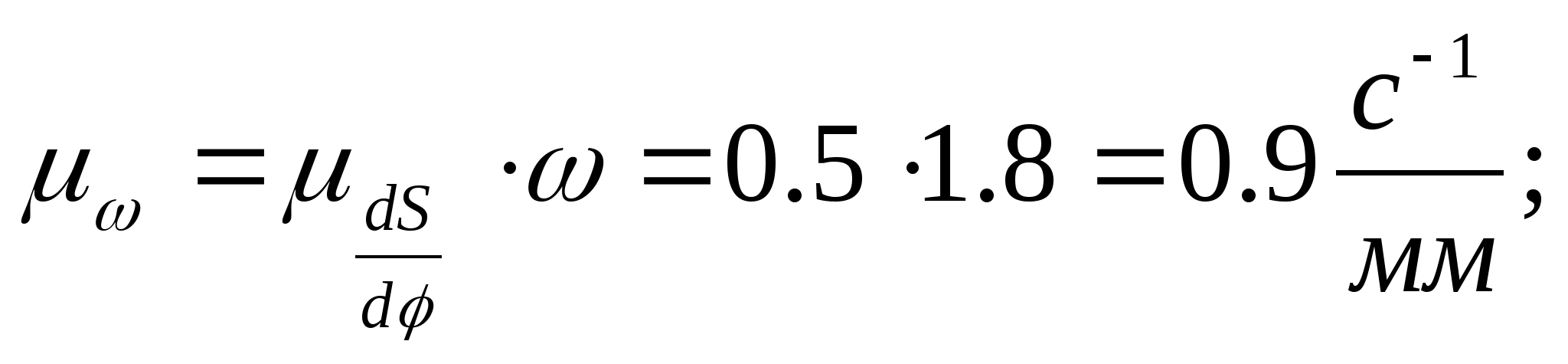
Де 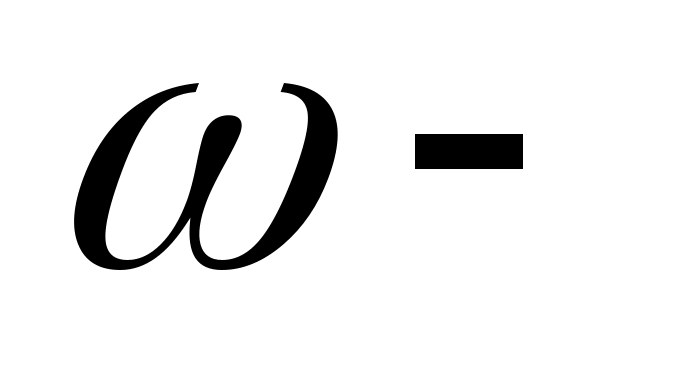кутова швидкість кулачка.

Масштабний коефіцієнт діаграми кутового прискорення:

привід поршневий насос кінетостатичний

4.2 Виконуємо перевірку розрахунків на ЕОМ

Метод базується на графічному способі розвязання умови на базі графіка за цикл. В процесі рішення будують за заданим законом руху штовхача діаграми переміщення і аналогів швидкостей штовхача , а потім шляхом графічного виключення параметра будуюь діаграму , забезпечивши чисельно однакові масштабні коефіцієнти по обох осях.

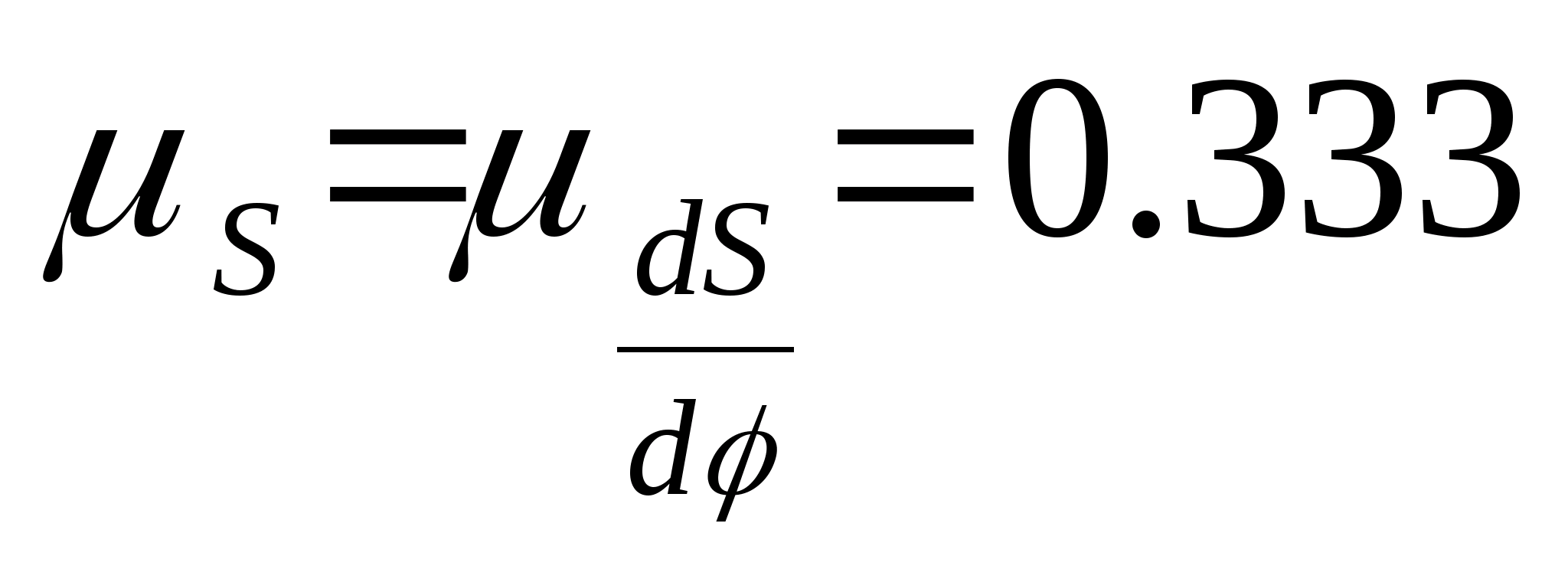
Визначаючи параметри 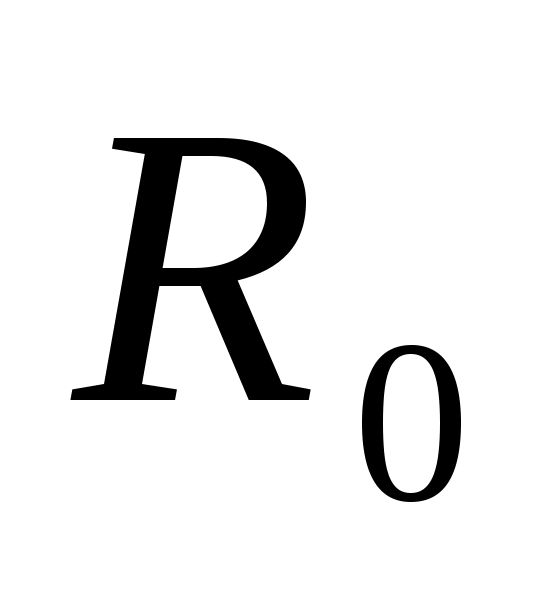і е, слід памятати, що умови обовязково повинна виконуватись тільки при передачі руху від профілю кулачка до штовхача. А тому для кулачкового механізму з силовим замиканням вищої кінематичної пари і обертанні кулачка в напрямку руху годинникової стрілки значення 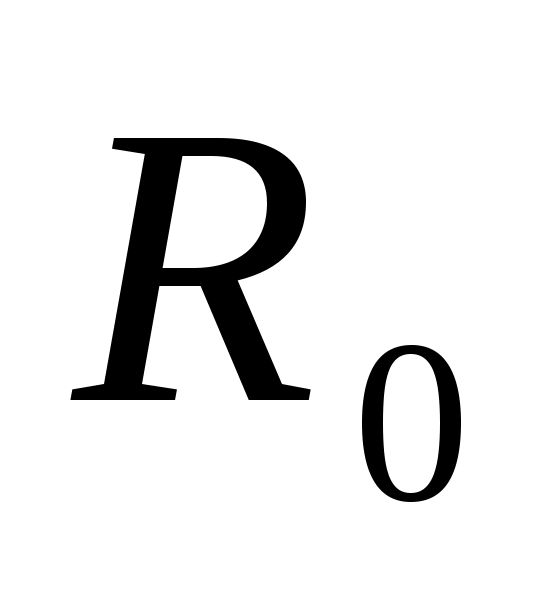і е можуть бути тільки такими, щоб можливе положення осі обертання кулачка на полі діаграми було праворуч від дотичної 1-1 до кривої , проведеної під допустимим кутом передачі тиску до осі на фазі віддалення.

Якщо рух передається від профілю кулачка до штовхача на фазі наближення, то щоб виконувалась умова 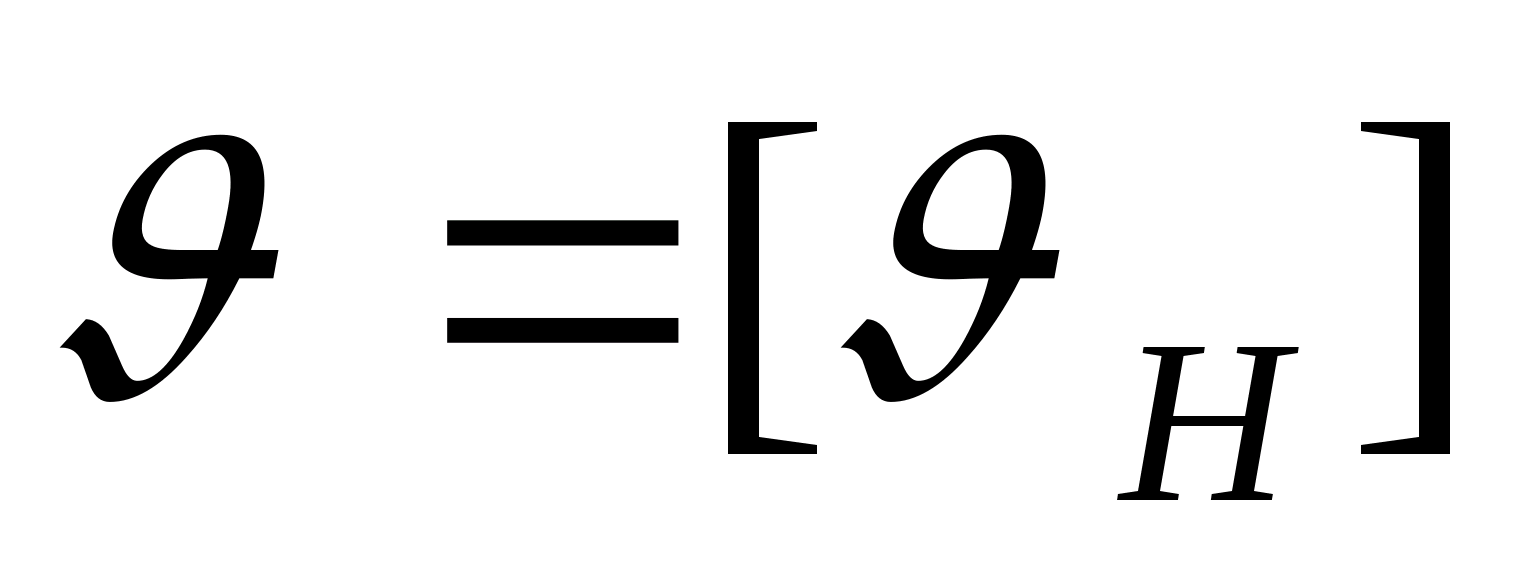, необхідно вісь обертання кулачка наполі діаграми розмістити ліворуч від дотичної 2-2 до кривої , проведеної на фазі наближення під допустимим кутом передачі тиску до осі .

В кулачкових механізмах із геометричним замиканням вищої кінематичної пари повинна виконуватись на фазі віддалення і наближення. Отже, можливе розміщення осі обертання кулачка при геометричному замиканні вищої кінематичної пари буле в заштрихованій зоні. Точка О перетину дотичних 1-1 і 2-2 покаже шукане положення осі обертання кулачка, яке забезпечує найменші розміри кулачка і всього механізму. При розміщенні осі обертання кулачка в точці А одержимо значення 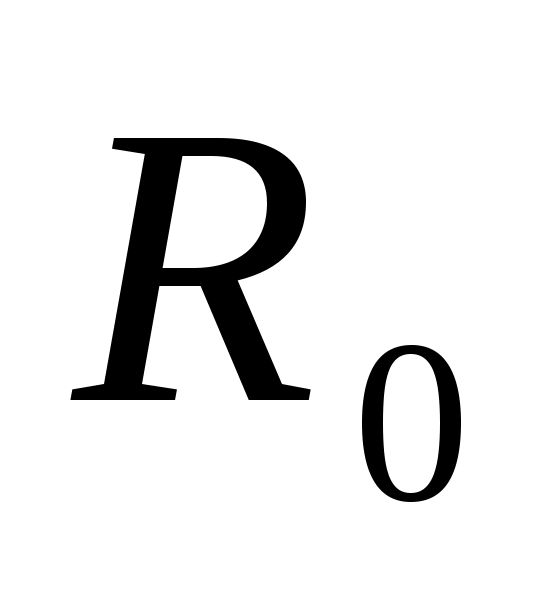і е, які забезпечують виконання умови в будь-якому положенні механізму.

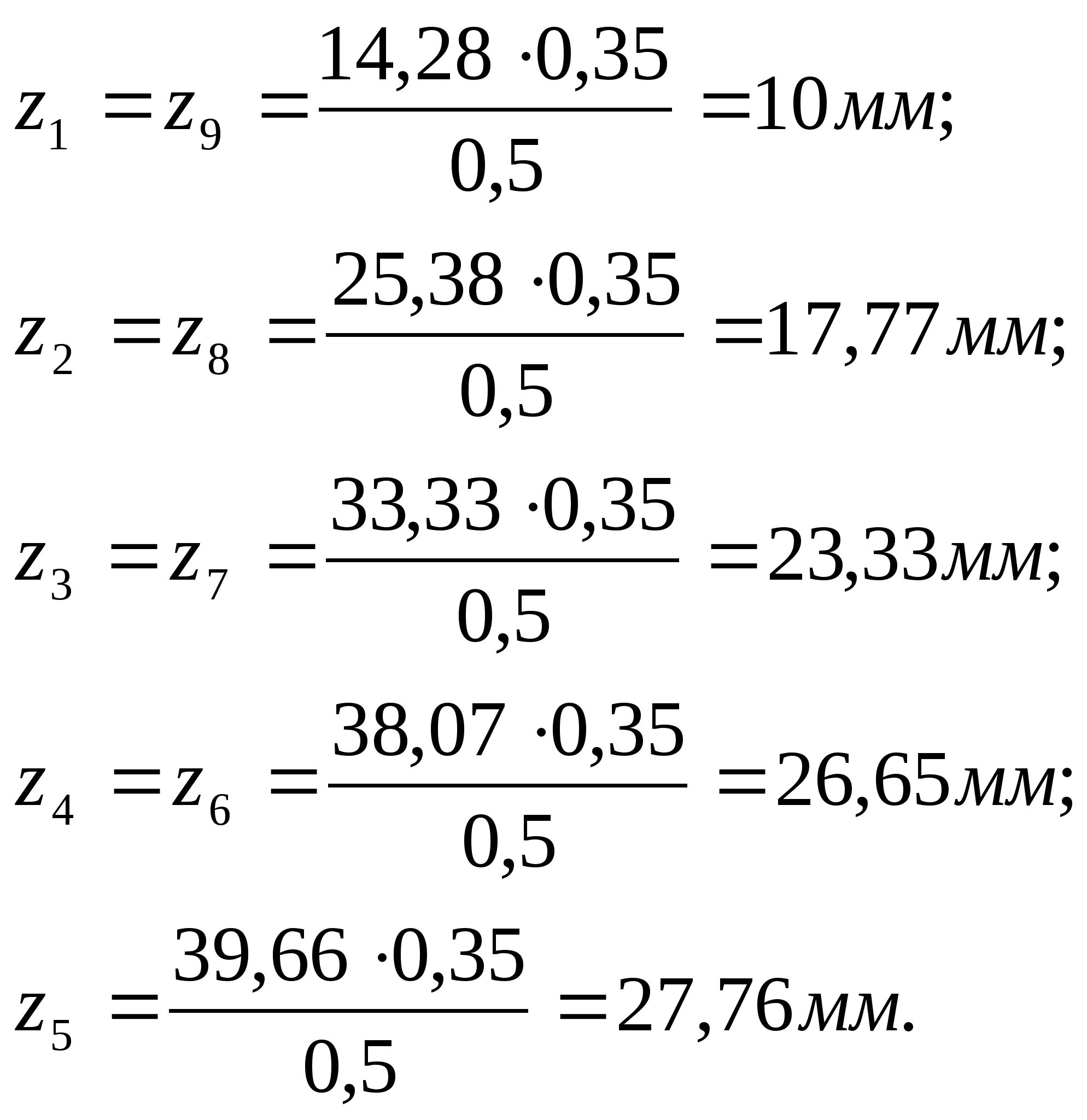
Кінці відрізків z з’єднуємо плавною кривою і отримуємо діаграму залежності .

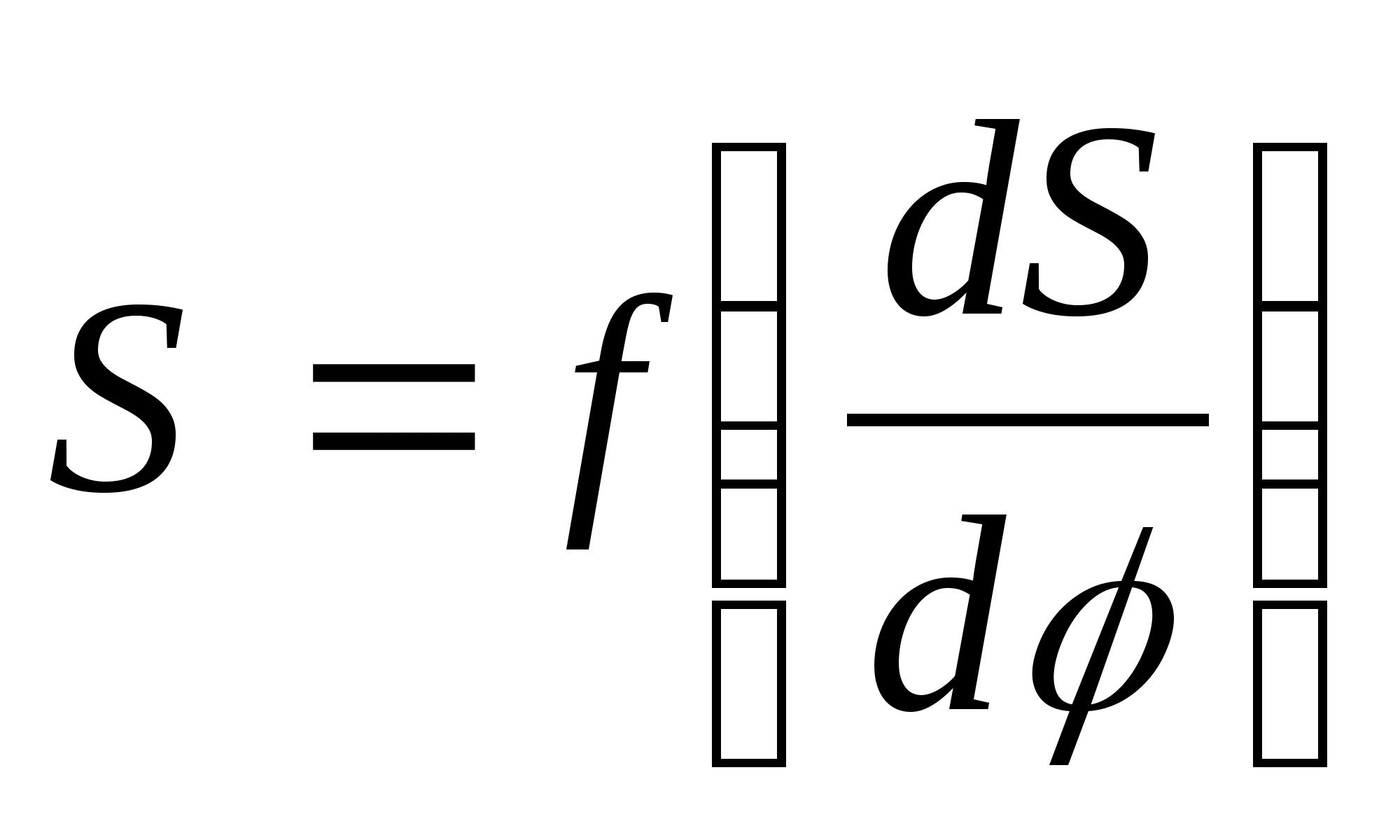До отриманої діаграми проводимо дотичні під кутом тиску , а на їх теретині отримаємо точку 01, яка є центром обертання кулачка з мінімальним радіусом. Центр обертання кулачка можна прийняти в будь-якій точці зони, що утворилась між двома дотичними нижче точки 01.

Приймаємо:

- радіус початковой шайби

4. Побудова профілю кулачка.

Побудова аиконується в масштабі .

Креслимо заданий графік функції руху штовхача, користуючись маштабними коефіцієнтоми по осі ординат і . З одного центра 01 проводимо коло радіусом і коло радіусом і е.

Напродовженні осі абсцис вибираємо довільну точку С що належить штовхачу, і проводимо паралельно до осі ординат лінію руху штовхача, на якій розмічаємо точками 1, 2, 3, ... ,m шлях руху точки С .

З центра О проводимо коло радіусом 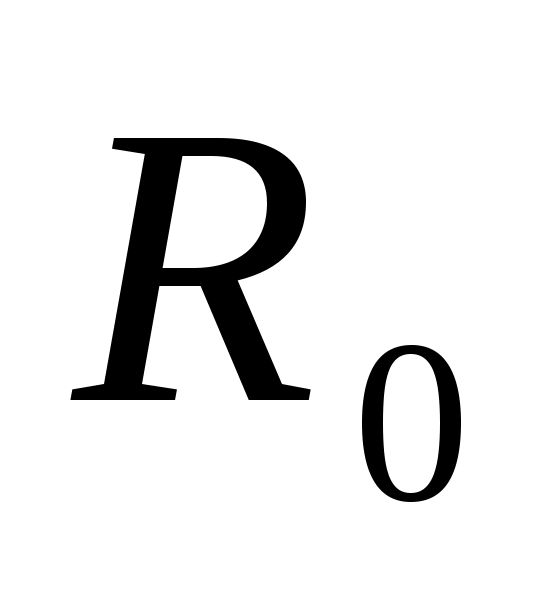. Застосовуючи метод інверсії, у напрямку протилежному напрямку обертаннякулачка від лінії 001 відкладаємо фазові кути .Відкладаємо від прямої ОС в бік, протилежний обертанню кулачка, фазові кути, ділимо кути віддалення і наближенняна десять рівних частин і проводимо промені 0-1, 0-2, ... , 0-10 ., відповідно до положень штовхача.

Перенесимо за допомогою циркуля положення точоки С з розмітки на відповідні напрямні штовхача у відносному русі навколо кулачка і, зєднавши їх плавною кривою, одержимо теоретичний профіль кулачка.

Зточок теоретичного профілю проводимо кола радіусами і будуємо обвідну цих кіл, яка і буде практичним (робочим) профілем кулачка.

Слід зазначити, що в кулачку центрального кулачкового механізму фазові кути і кути відповідних профілів збігаються, а в кулачках позацентрових кулачкових механізмів кути профілів віддалення і наближення залежно від величини і напрямку ексцентриситету можуть бути як більшими, так і меншимивідповідних фазових кутів.

Для побудови практичного профіля кулачка проводимо коло радіусом ролика, яке повторюємо багаторазово, прийнявши за центр лінію теоретичного профілю. Будуємо еквівалентний профіль, який є практичним профілем.

5. Аналітичне визначення радіуса-вектора теоретичного профілю кулачка

Вихідні дані: = 20; =30о (0,524 рад);

R0 = 34мм; =270о (4,7рад);

Вихідні данні: R0 = 34мм, e = 10мм,  в = 115(2рад.),  = 25 (0.35 рад.),

 н = 130 (0.35 рад.) Sm = 20мм, rр = 0 мм

Для даного закону руху коефіцієнти переміщення  і швидкості  вибираємо із таблиці. При

К =  /  в = 100 / 115 = 0,87;  = 0,870;  = 1.8

Переміщення S і аналог швидкості при повороті і кулачка на кут  =100 :

S = ( ∙ Sm) = 0,870 ∙ 20 =17,4мм;

=  ∙ = 1.8∙ = 18мм.

Визначаємо S0, :

S0 = 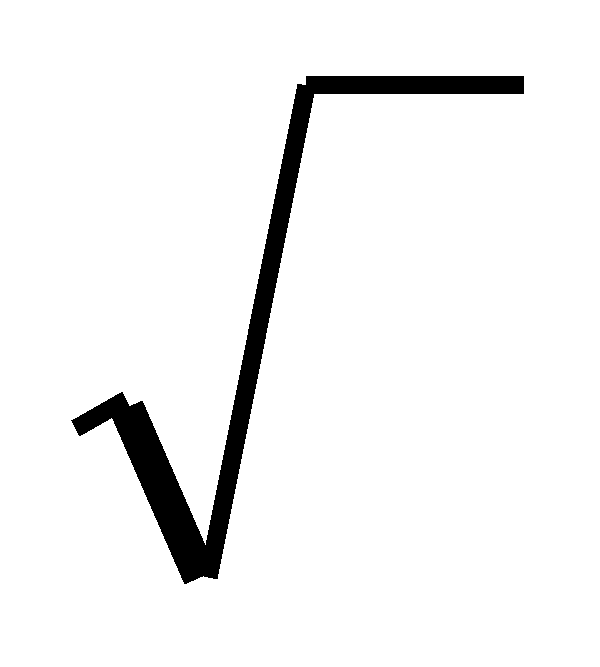R02 – e2 = 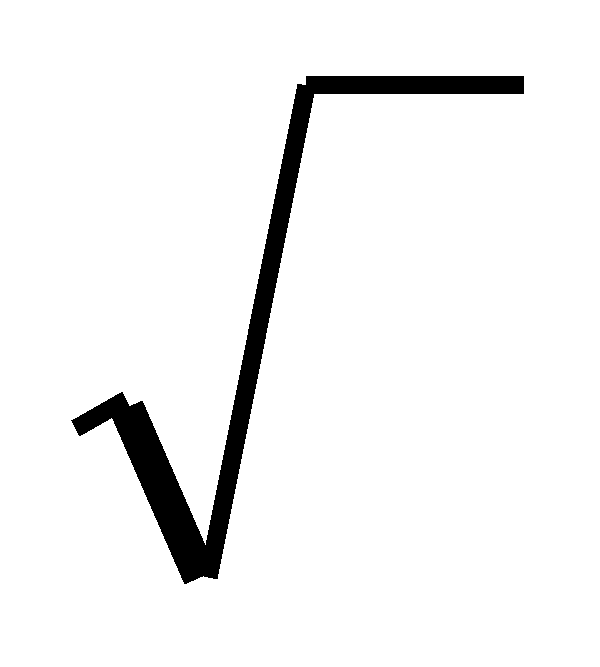342 – 102 =32,5 мм;

tg  = == 0.21;

 = аrctg 0. =124`25,79``.

Визначаємо кут  - кут між радіусом – вектором теоретичного профілю і напрямом рушу штовхача

 = arcsin ( e / r ) = arcsin ( 10 / 34) = 176`16,69``.

Радіус - вектор практичного профілю кулачка буде :

rп = 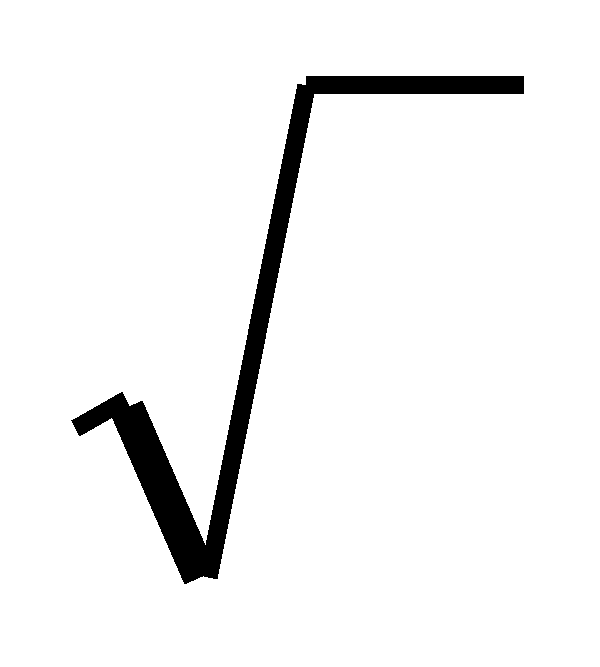r2 + rp2 – 2∙ r ∙rp∙cos ( +  ) =

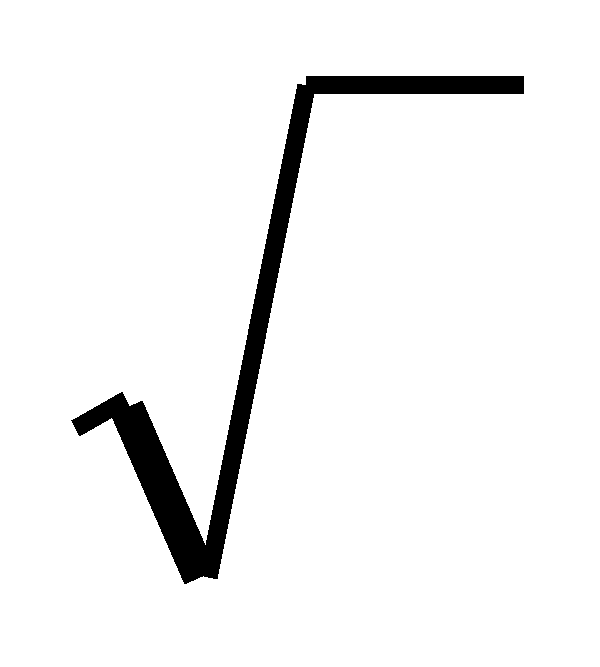342 + 02 – 2∙ 18∙ 0 cos (124`25,79``+ 176`16,69``) = 34мм.

5. Геометричний синтез евольвентного нульового прямозубого зачеплення

Вихідні дані:

мм  модуль;

 число зубців першого колеса;

 число зубців другого колеса;

 коефіцієнт висоти головки зубця;

 коефіцієнт висоти ніжки зубця;

 коефіцієнт радіального зазору;

 коефіцієнт округлення біля ніжки зубця;

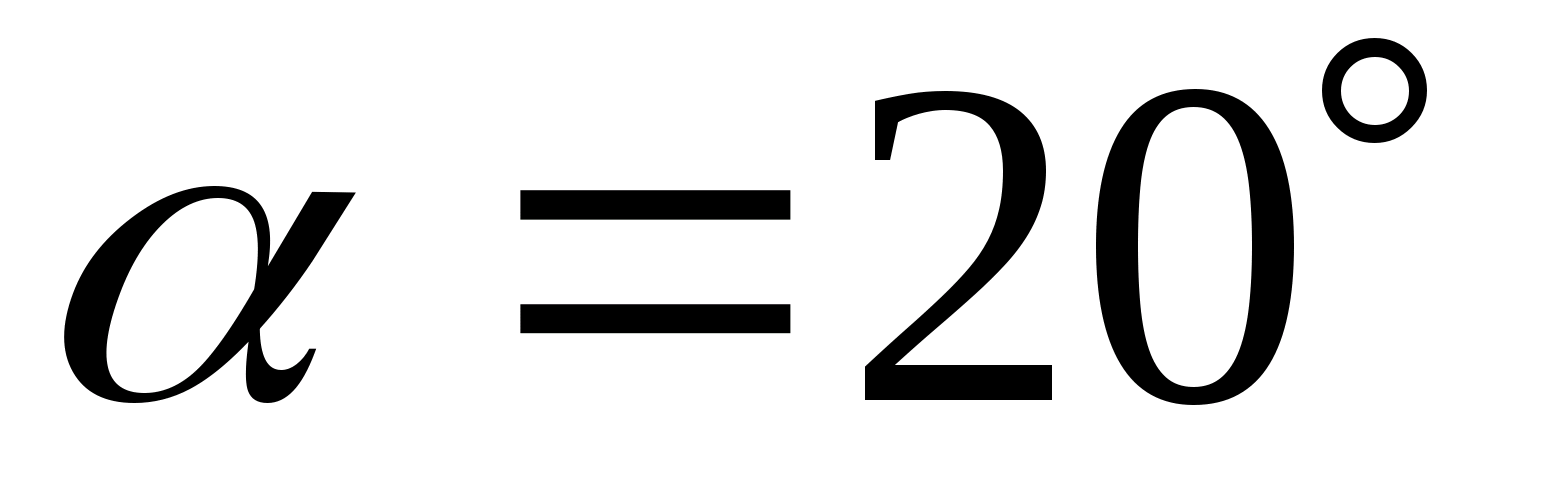 кут профілю.

5.1 Визначення геометричних параметрів зубчастого зачеплення

Визначаємо крок зачеплення

мм.

Визначаємо радіуси ділильних кіл:

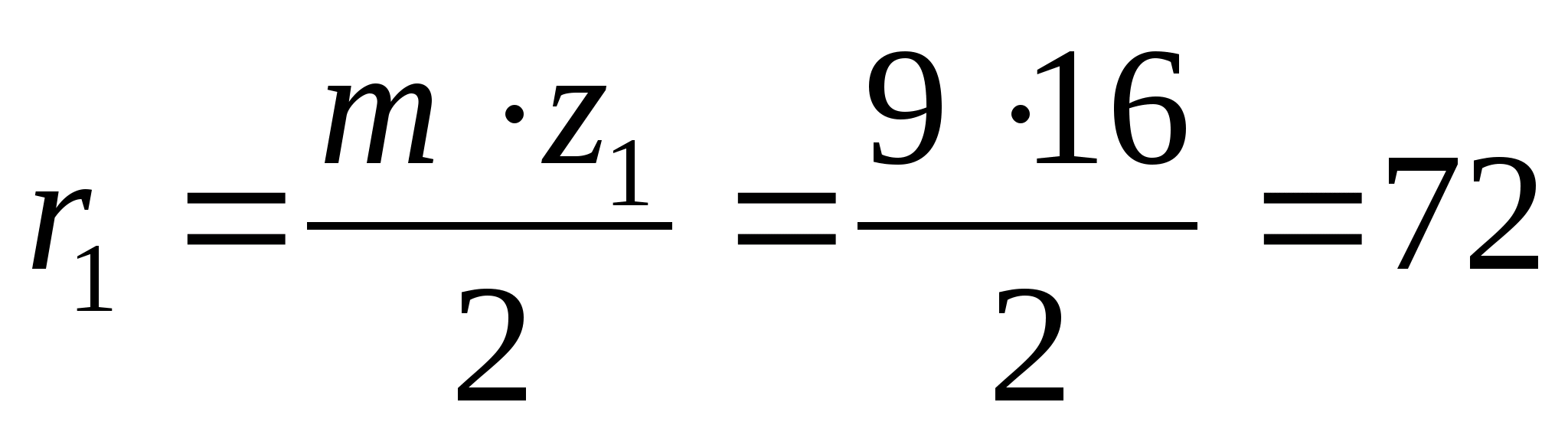мм;

мм.

Визначаємо радіуси основних кіл:

мм;

мм.

Визначаємо товщини зубців:

мм;

мм.

Визначаємо радіуси западин:

мм;

мм.

Визначаємо міжосьову відстань:

мм.

Визначаємо радіуси початкових кіл:

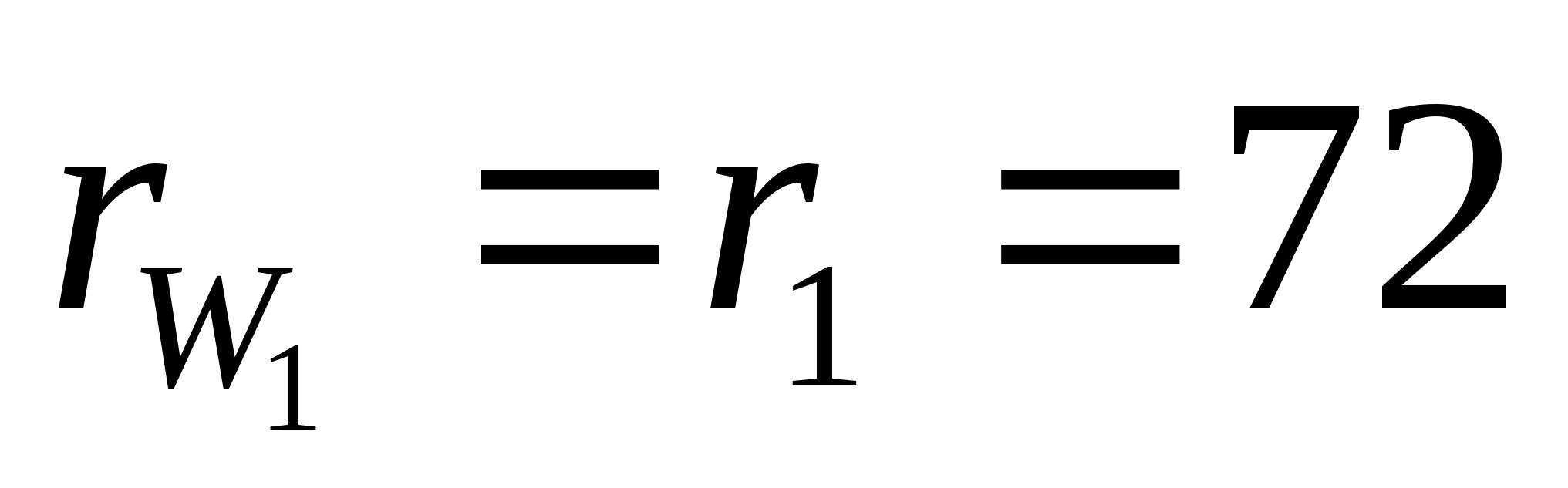мм;

мм.

Визначаємо висоту зубців:

мм.

Визначаємо радіуси вершин зубців:

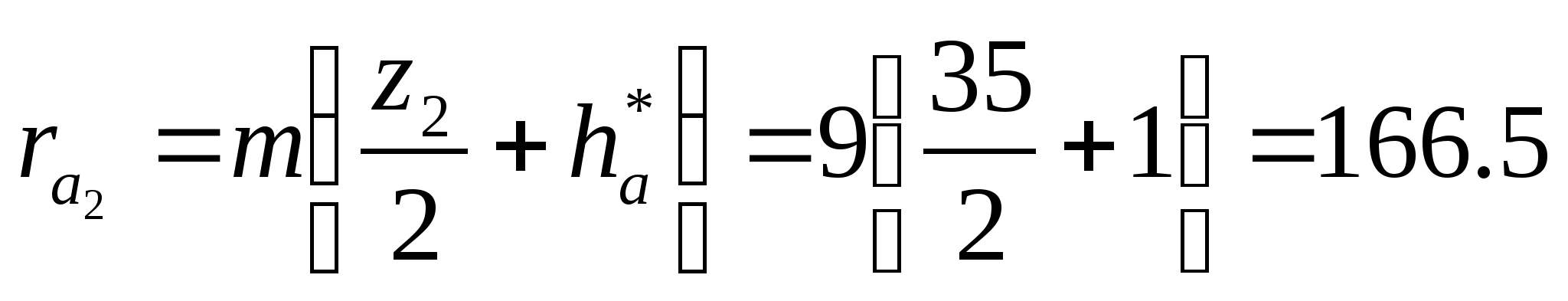мм;

мм.

Виконуємо перевірку розрахунків на ЕОМ

Викреслювання елементів зубчастого зачеплення

Побудову евольвентного зачеплення виконуємо в масштабі М5:1. На лінії центрів коліс від точки Р (полюса зачеплення) відкладаємо радіуси rW1 і rW2 початкових кіл та будуємо ці кола.

Проводимо пряму під кутом 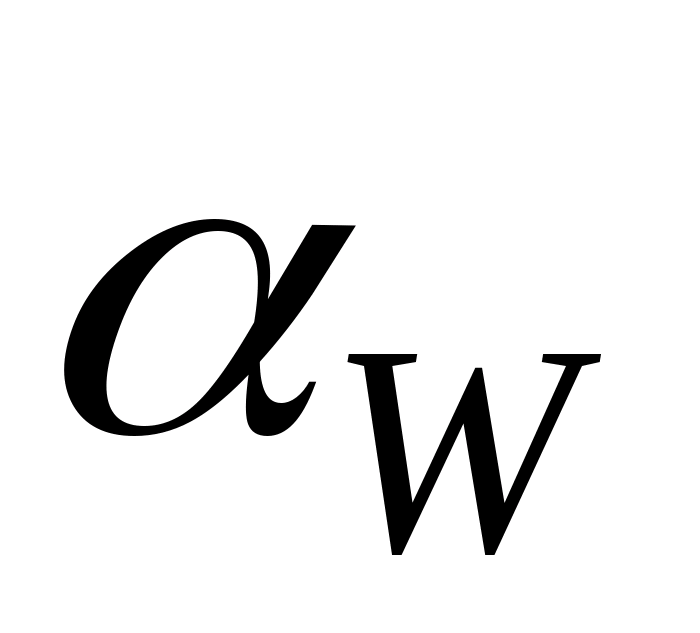, після чого з центрів коліс О1 і О2 відкладаємо перпендикуляри до цієї прямої та . Ці відрізки є радіусами основних кіл 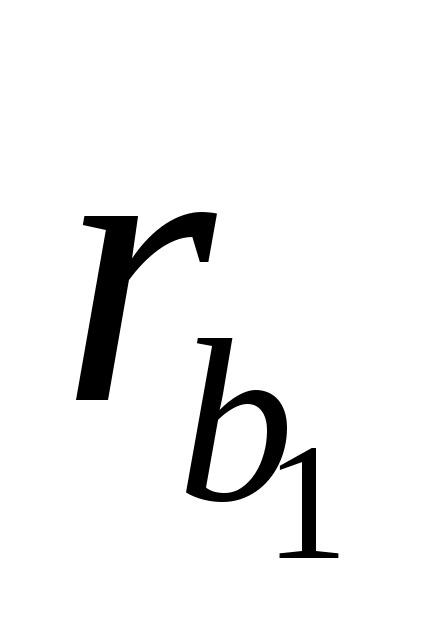і.

Будуємо евольвенти, які описує точка Р прямої 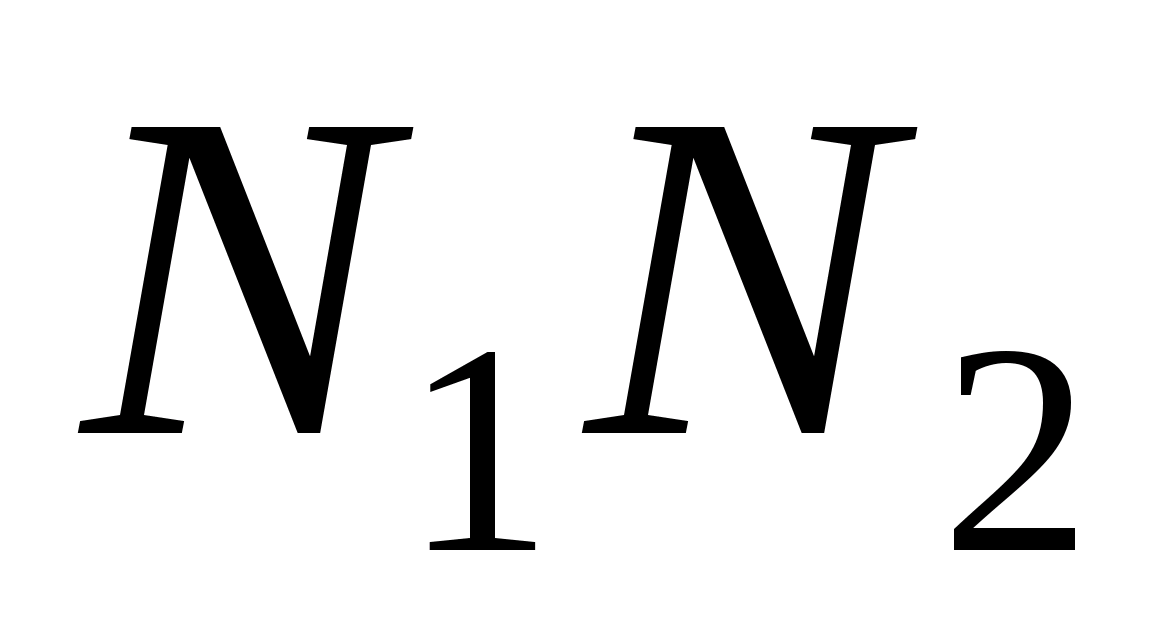при перекочуванні її по основних колах. При побудові евольвенти 1-го колеса ділимо відрізок на чотири рівні частини (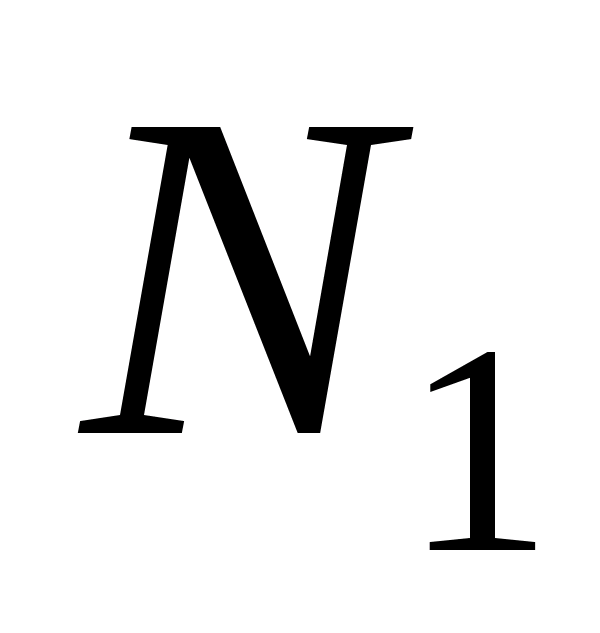3=32=21=P1) і з точки 3 проводимо дугу радіуса 3Р до перетину в точці Р' з основним колом (). Дугу також ділимо на чотири рівні частини (). На прямій за точкою 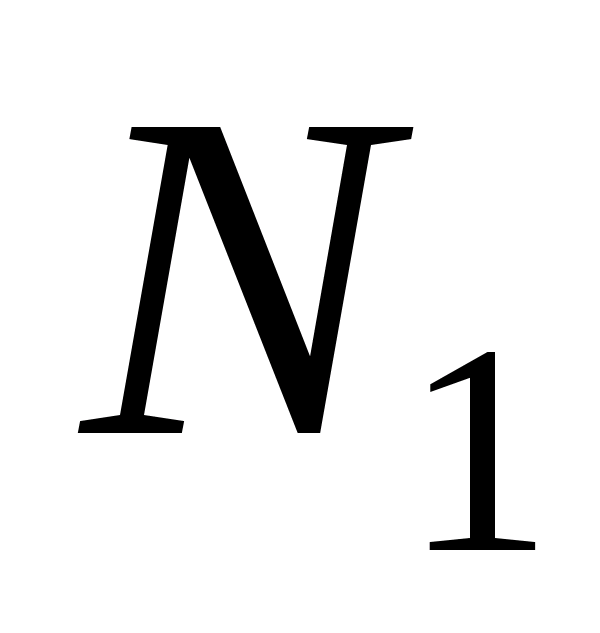відкладаємо відрізки (45=56=…), рівні Р1, а на основному колі  дуги (), рівні дузі . Через точки 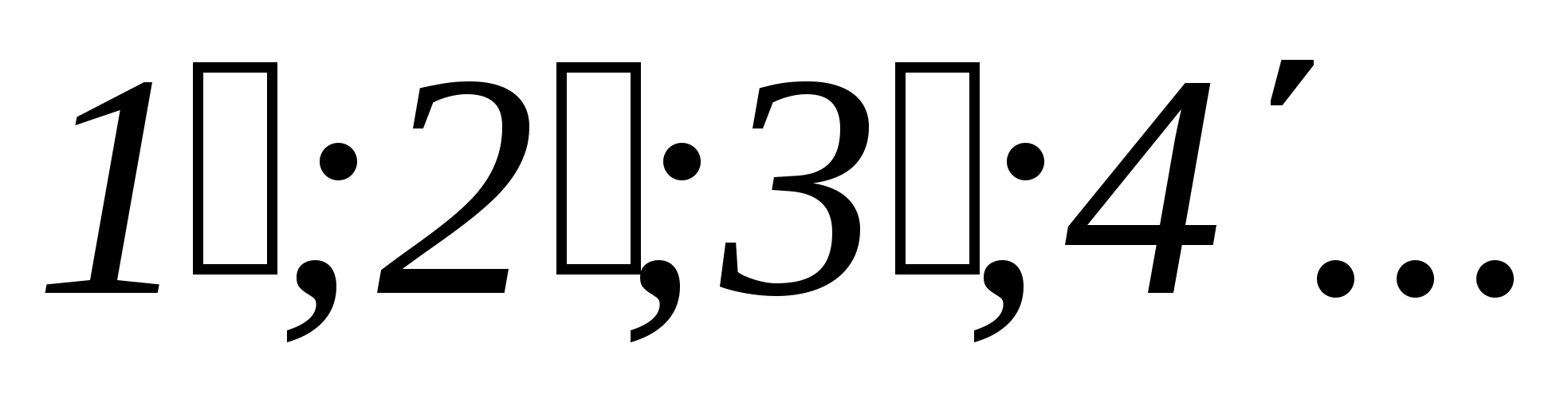проводимо перпендикуляри до відповідних радіусів

На цихперпендикулярах (вони дотикаються до основного кола) відкладаємо відрізки , відповідно рівні відрізкам 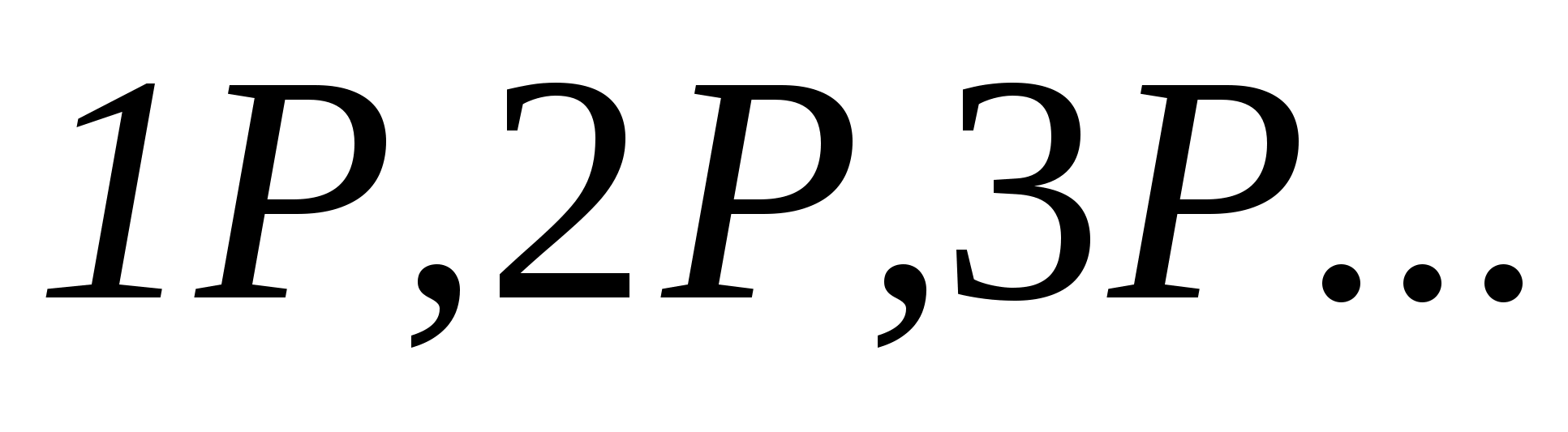З’єднуючи послідовно точки плавною кривою, одержуємо евольвенту для 1-го колеса. Аналогічно будуємо евольвенту для 2-го зубчастого колеса.

Будуємо кола виступів обох коліс 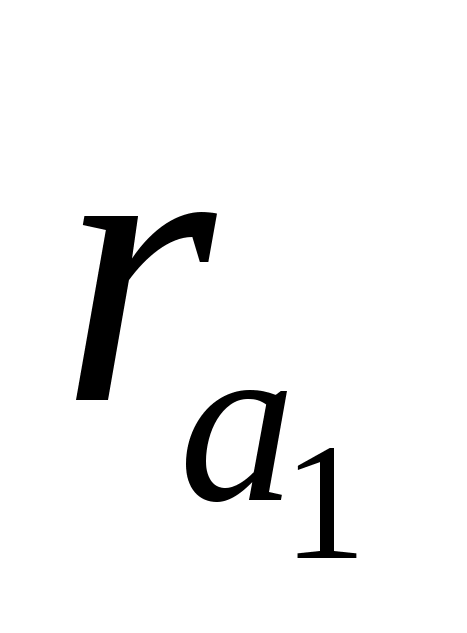і . Знаходимо точки перетину цих кіл з відповідними евольвентами  крайніми точками на профілях головок.

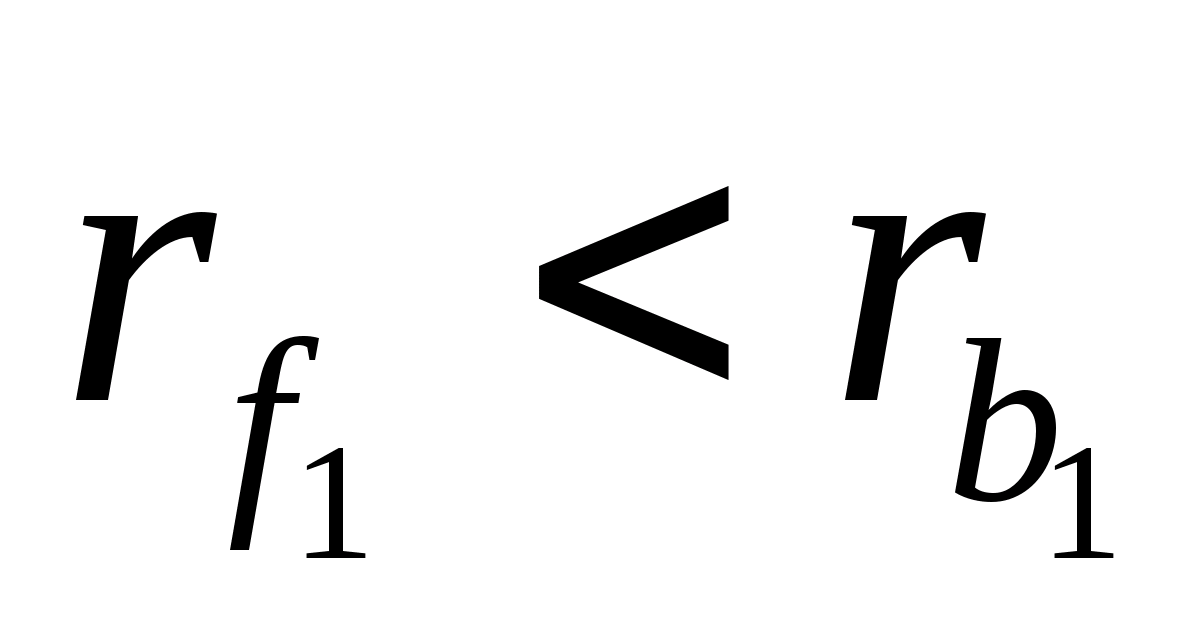Будуємо кола западин обох коліс і . Оскільки , то від основи евольвенти до кола западин проводимо радіальний відрізок, а потім біля основи зубця робимо закруглення радіусом 0,38m. Оскільки , то одержуємо точку перетину кола западин з евольвентою, а потім біля основи робимо закруглення радіусом 0,38m.

Будуємо ділильні кола, одержуємо точку перетину ділильного кола з евольвентою. Від цієї точки відкладаємо вліво дугу, яка рівна половині товщини зубця і через одержану точка проводимо вісь симетрії зубця.

Таким самим способом віддзеркалюємо інші точки евольвенти. В результаті отримуємо зубець колеса, по якому вирізаємо з твердого паперу шаблон, яким користуємося при побудові інших зубців. Аналогічно будуємо зубці 2-го колеса. Обов’язковим є побудова трьох зубців кожного колеса.

Робочі ділянки профілів зубців

Ті ділянки профілів зубців, які беруть участь в зачеплені, називають робочими. Для того щоб знайти ці ділянки потрібно через точку а із центром О1 провести дугу радіусом О1а до перетину в точці А1 з профілем зубця першого колеса і через точку b із центра О2 проводимо дугу радіусом О2b до перетину з профілем зубця другого колеса. Ділянки А1В1 і А2В2 профілів зубців є робочими ділянками профілів. Для позначення на креслені цих ділянок, потрібно провести лінії паралельні А1В1 і А2В2 на відстані 1.5-2 мм і заштрихувати смужки, які отримали. Довжини робочих ділянок не є однакові, оскільки спряжені профілі зубців перекочуються один по одному з проковзуванням.

Дуга зачеплення

Кожну з дуг початкових кіл, які перекочуються одна по одній під час зачеплення однієї пари спряжених профілів, називають дугою зачеплення.

Для її побудови через крайні точки А1 і В1 робочої ділянки першого колеса проводимо по направленню ввігнутості нормалі А1а′ і В1b′ до цього профілю. Знаходимо точки а1 і b1 перетину цих нормалей з початковим колом першого колеса. Дуга а1b1 є дугою зачеплення на початковому колі першого колеса. Аналогічно будуємо дугу зачеплення а2b2 на початковому колі другого колеса.

Довжину k дуги зачеплення визначають за формулою де L – довжина активної частини лінії зачеплення ().

Для визначення дуги зачеплення графічним шляхом потрібно через крайні точки а і b активної лінії зачеплення провести перпендикуляри до неї до перетину в точках а′ і b′ з загальною дотичною до початкових кіл. Відрізок а′b′ рівний довжині k дуги зачеплення.

Визначення якісних показників зачеплення

Коефіцієнти перекриття ε

Коефіцієнтом перекриття називають відношення довжини дуги зачеплення до довжини кроку на основних колах коліс:

Оскільки , то

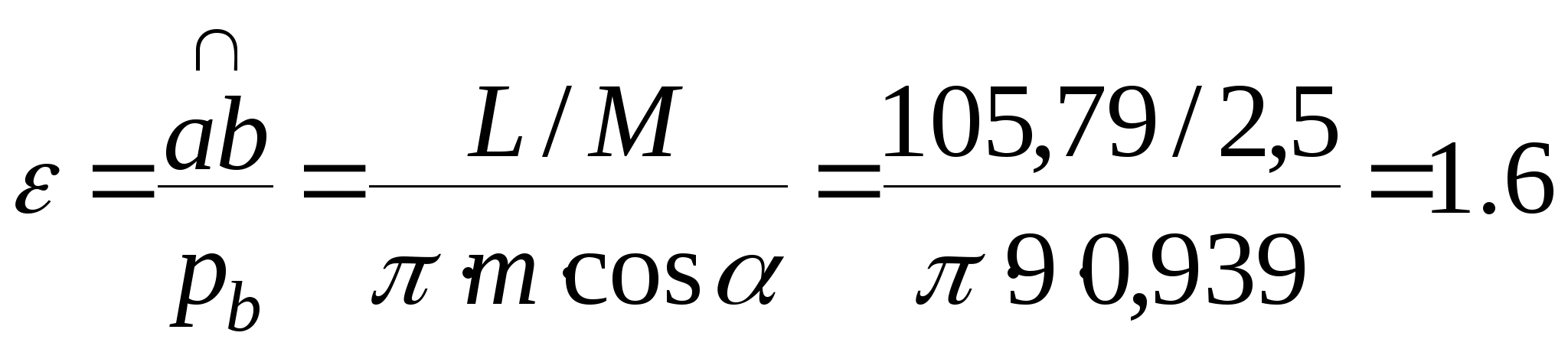
де М – масштаб побудови зачеплення.

Цією формулою зручно користуватись, оскільки зачеплення двох коліс вже викреслено і довжину L() можна виміряти.

Коефіцієнт перекриття не повинен бути більшим двох.

Цією формулою зручно користуватись, так як зачеплення двох коліс вже викреслено і довжину L можна виміряти.

Коефіцієнт перекриття можна визначити також за формулою

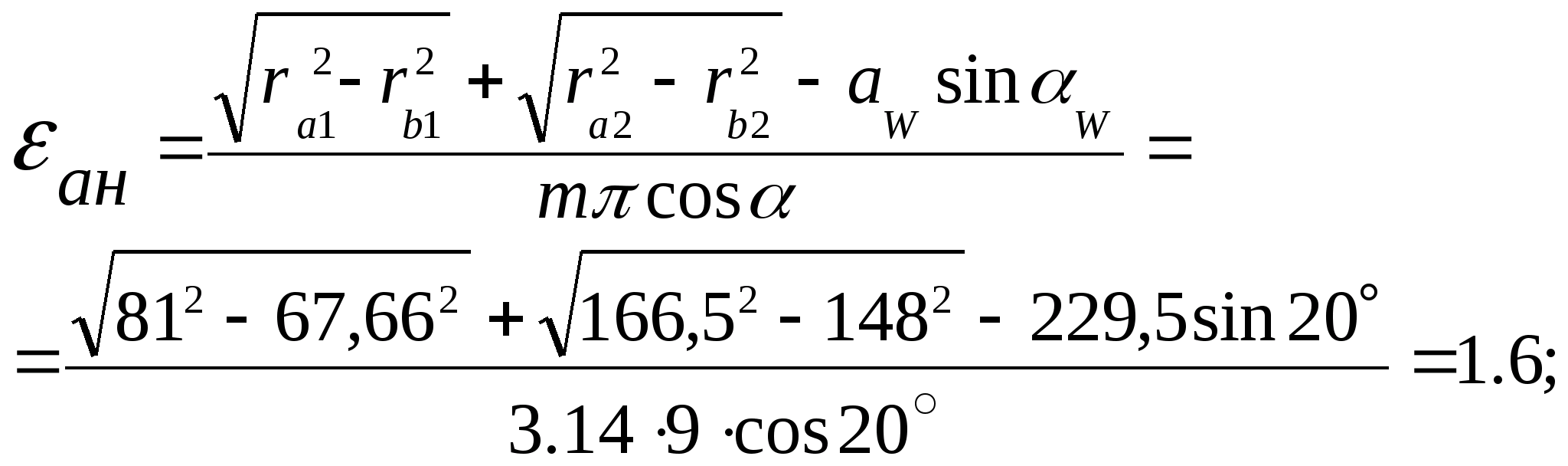
Коефіцієнт перекриття не повинен бути меншим одиниці.

Коефіцієнт відносного ковзання

Характеристикою шкідливого впливу проковзування є коефіцієнти λ1 і λ2 відносного ковзання, які визначаються за формулами

де е = N1N2 – довжина теоретичної лінії зачеплення,

де х – відстань від точки N2 відраховуємо в напрямку до точки N1.

Користуючись цими формулами, складаємо таблицю значень λ1 і λ2. Для прикладу, якщо х =10мм, то

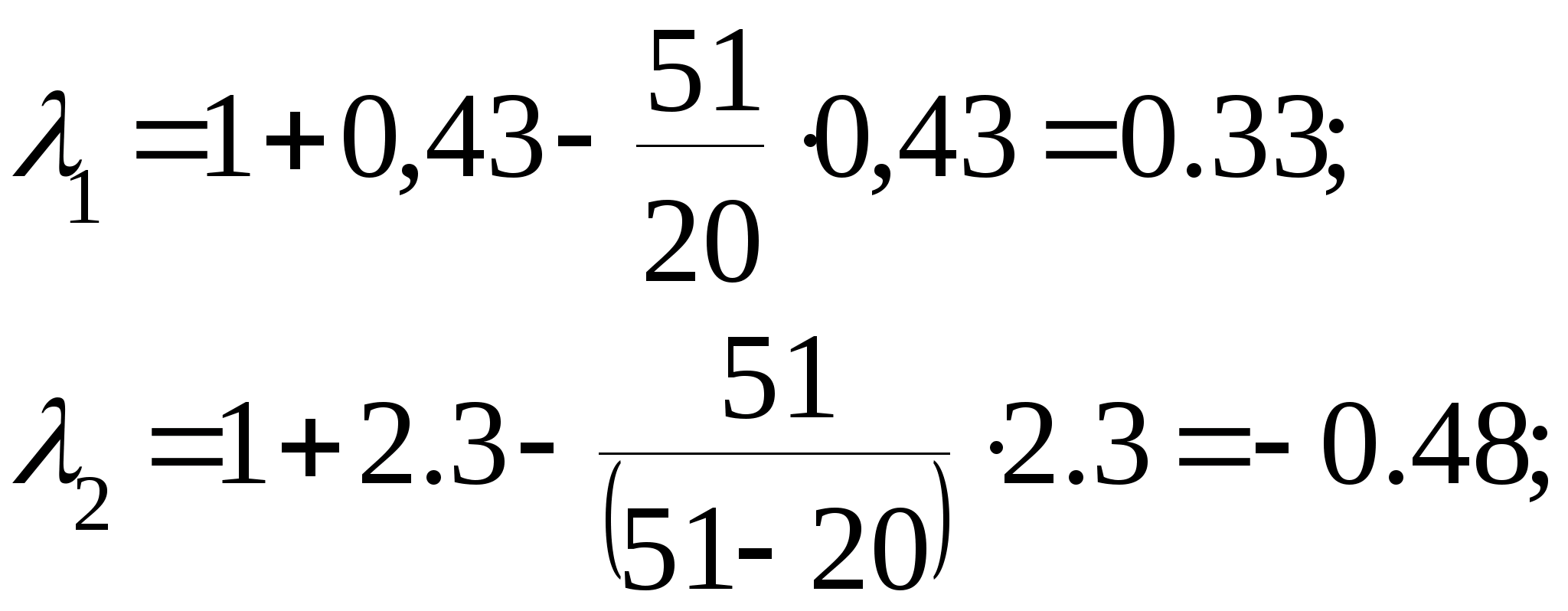
Всі інші значення λ1 і λ2 , можна подати у вигляді таблиці 1.

Таблиця 7. – Значення коефіцієнтів відносного ковзання

х ,мм	0	10	20	Р	30	40	50	60	70	78
λ1	-∞	-2,13	-0,33	0	0,26	0,56	0,74	0,86	0,95	0
λ2	1	0,68	0,24	0	-0,48	-1,32	-2,93	-6,33	-18,25	-∞

Користуючись даними таблиці 1. будуємо діаграми =f(x) і 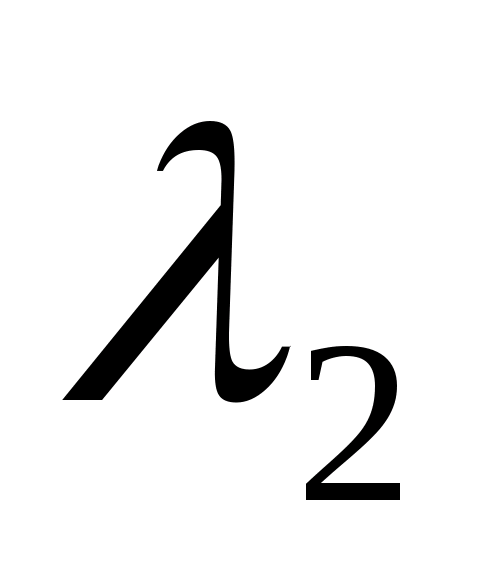=f(x).

1/мм.

Для того щоб виділити ті частини діаграм, які вказують значення λ1 і λ2 для робочих ділянок профілів, потрібно через точки a i b провести перпендикуляри до лінії зачеплення, які відокремлюють на діаграмах шукані ділянки (заштриховані на креслені).

Коефіцієнт питомого тиску

Цей коефіцієнт знаходиться при розрахункові зубців коліс на контактну міцність і визначається за формулою:

,

де m - модуль зачеплення, .

При х = 10мм

Таблиця 8. - Значення коефіцієнтів питомого тиску

х,мм	0	10	20	Р	30	40	50	60	70	78
	-	1,04	0,61	0,54	0,49	0,46	0,5	0,65	1,26	-

Користуючись цими даними будуємо діаграму в масштабі 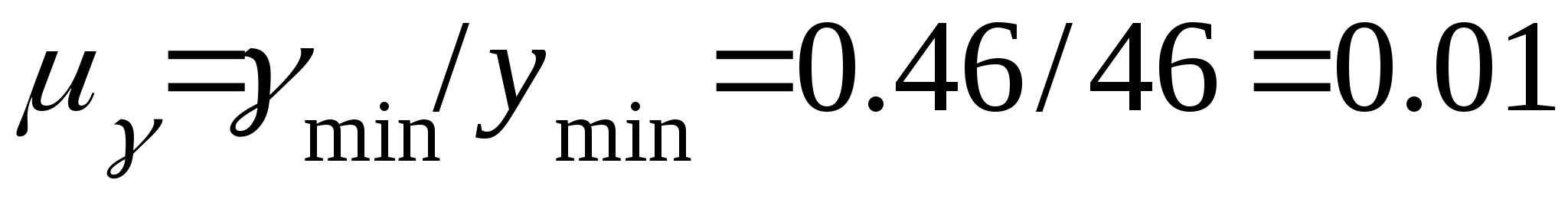1/мм.

Синтез та кінематичний аналіз планетарного механізму

Задача

Виконати синтез планетарної передачі, яка входить до складу приводу (рис.1), за такими вихідним даними:

частота обертання електродвигуна: об/хв;

частота обертання кривошипа робочої машини: 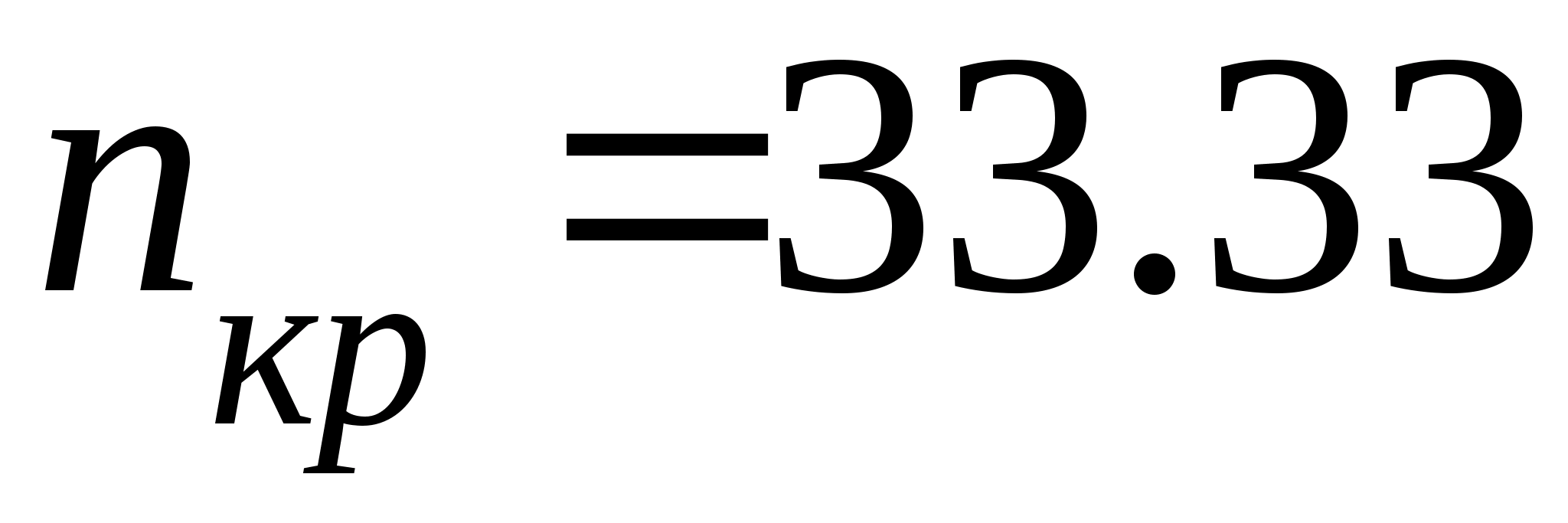об/хв;

кількість зубців коліс: , ;

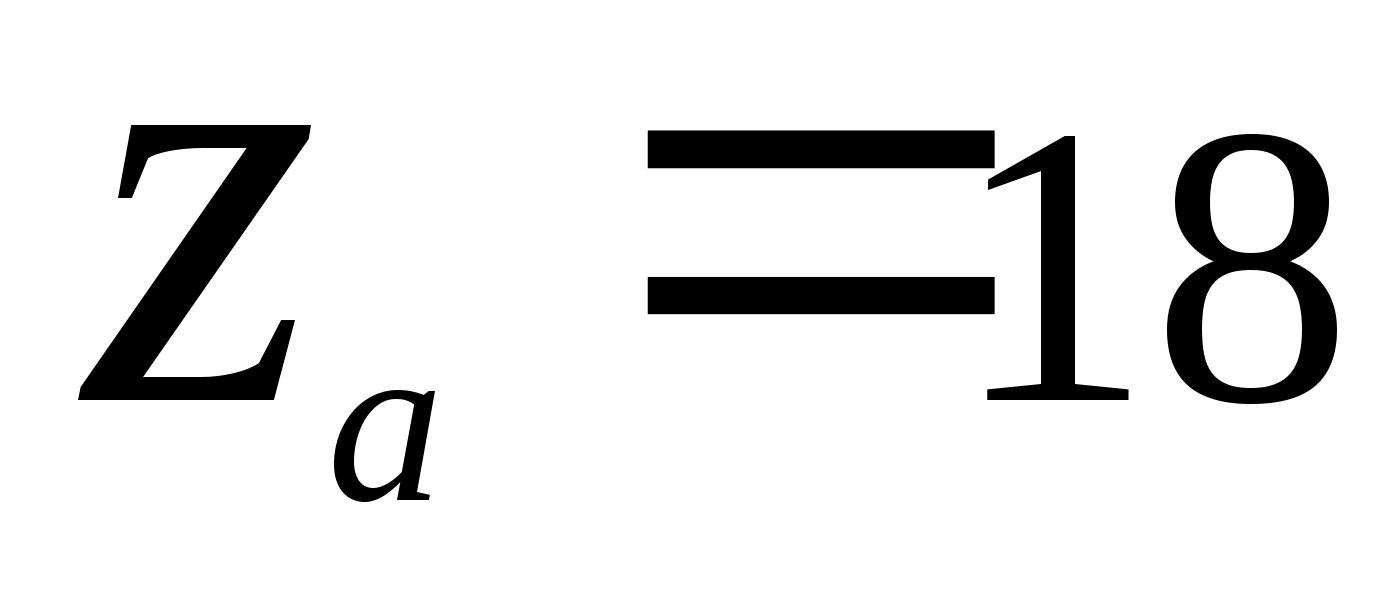модуль планетарного механізму мм.

Визначаємо передаточне відношення планетарного редуктора .

Оскільки передаточне відношення від двигуна до робочої машини

,

.

то

Рисунок 10.-Схема приводу

Безмашинний розрахунок числа зубців планетарного редуктора

Задаються числом зубців малого центрального колеса 1 так, щоб було

Z1  18. При цьому , для забезпечення умови складання Z1 повинно бути кратним числу сателітів . Найбільш вигідне число сателітів n=3 . Тоді , при кратному n значення Z1

З умови забезпечення передаточного відношення визначають число зубів Z2

Великого (короного) центрального колеса:

При цьому значення Z2

Закругляють до числа , кратного числусателітів , і щоб Z2

Задовільняло умові правильності зачеплення .

Де N- ціле число.

де u1H - передаточне відношення редуктора;

p - ціле число повних обертів водила;

З умови співвісності вибирають число зубів сателіта

.

Перевіряємо на умову сусідства.

,

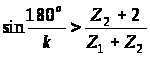де k - кількість сателітів;

сусідства виконується.

Отже, Z1=18, Z2=63, Z3=144.

Синтез планетарного механізму з застосуванням ЕОМ (Додаток Б).

Приймаємо:

- планетарна передача за схемою 1;

- кількість сателітів К =3;

- допустима похибка величини U3H : E = 3%;

- модулі коліс: m1 = m2 = 3 мм;

- зона пошуку Z1 min = 18, Z1 max = 50; Z2 min = 20, Z2max = 60.

Аналіз результатів синтезу на ЕОМ

Прийняті вихідні дані задовольняють декілька варіантів механізмів (див. Додаток Б), серед яких найменші розміри будуть у планетарного редуктора з числами зубців коліс:

Z1 = 18, Z2 = 63, Z3 = 144.

Визначаємо фактичне передаточне відношення:

U1HФ =1-U13H = 1+ z3/z1 = 1+144/18 =9

Кінематичний аналіз планетарного механізму

А. Визначаємо значення абсолютних і відносної 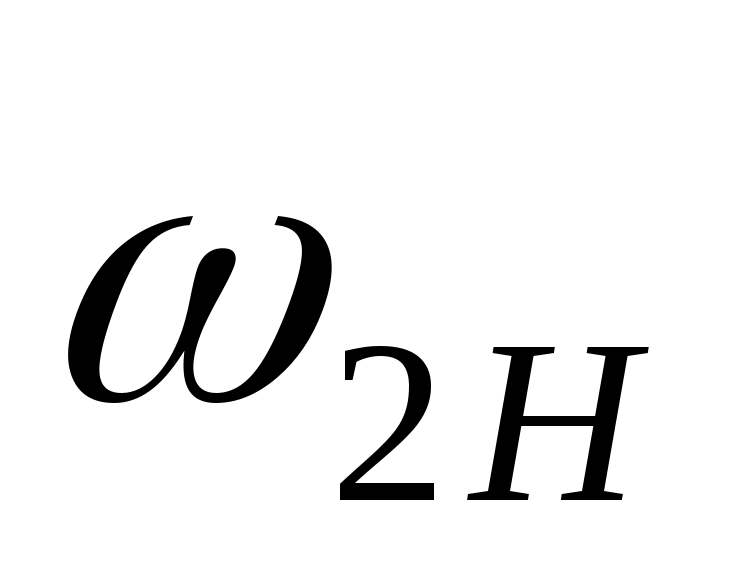кутових швидкостей ланок аналітичним методом:

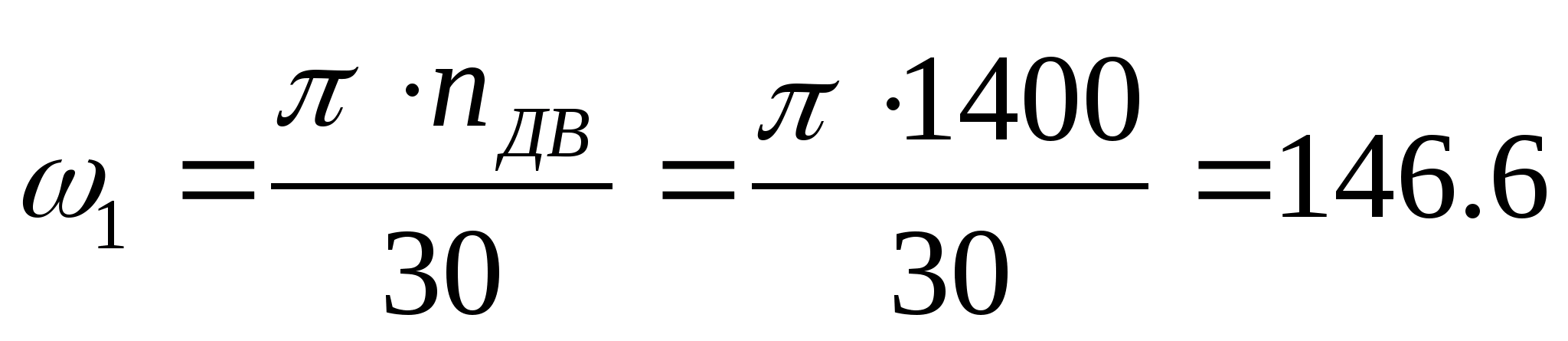рад/с;

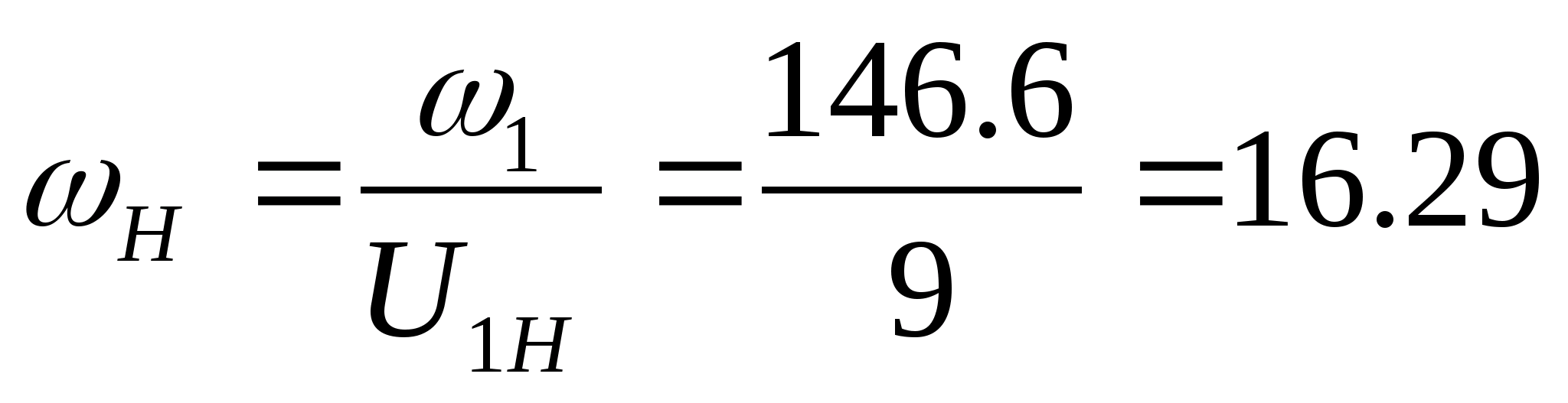рад/с.

Для обчислення скористаємось формулою Вілліса:

, де .

Звідки:

рад/с.

Кутова швидкість блоку сателітів відносно водила:

рад/с.

Б. Графічний метод визначення кутових швидкостей

Визначаємо розміри планетарного механізму:

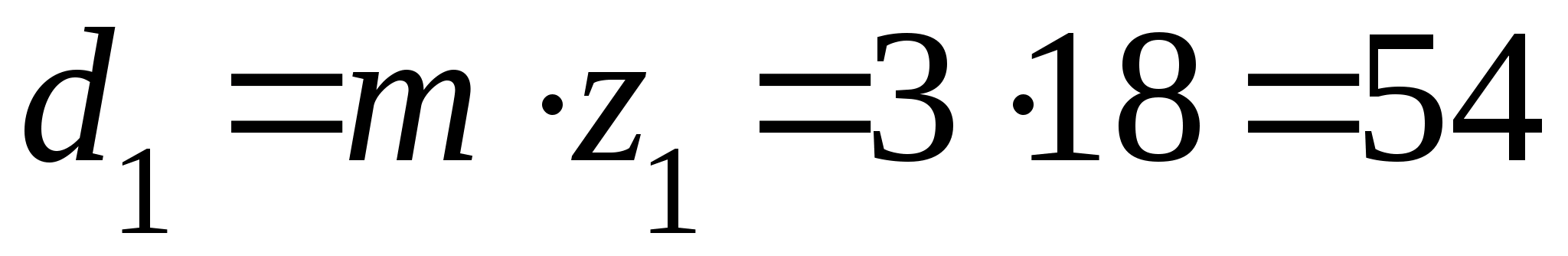мм;

мм;

мм.

Визначаємо коефіцієнт корисної дії (ККД).

При ведучому колесі і U1H > 1 приймаємо ККД пари зубчастих коліс оберненого механізму Тоді

[8]

ККД планетарного механізму визначаємо за формулою [8]

.

Схему механізму викреслюємо з масштабним коефіцієнтом l=r1/L(r1)=0.027/10.8=0.0025 м/мм.

Графічний метод зводиться до побудови трикутника лінійних швидкостей кожного колеса і находження з них ωі.

Колова швидкість колеса Z1:

VА = ω1r1 = 146.60.027=3.96м/с.

Пряма ОА′ утворює з вертикаллю кут 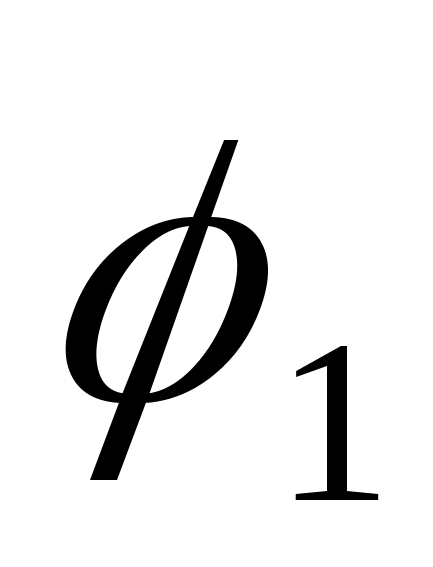і є лінією розподілу швидкостей точок на радіусі колеса 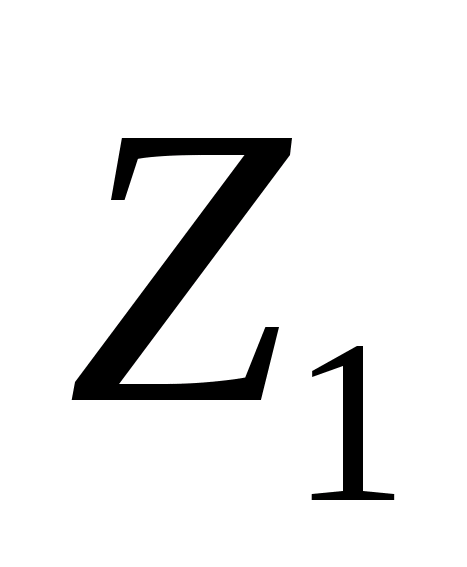. Колесо 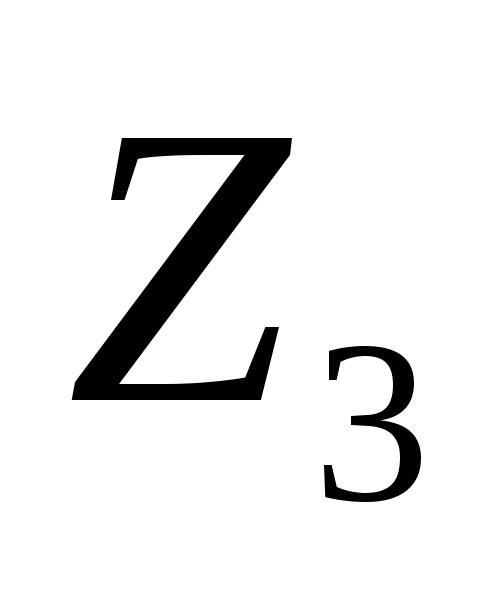є нерухоме, тому через точку O проходить вісь миттєвого обертання блока сателіта з колесом .

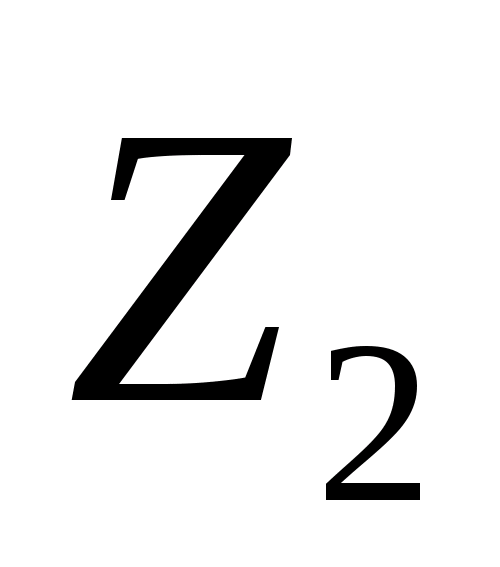На блоці коліс відомі швидкості точок O і B, тому B’A’ є прямою розподілу швидкостей для коліс 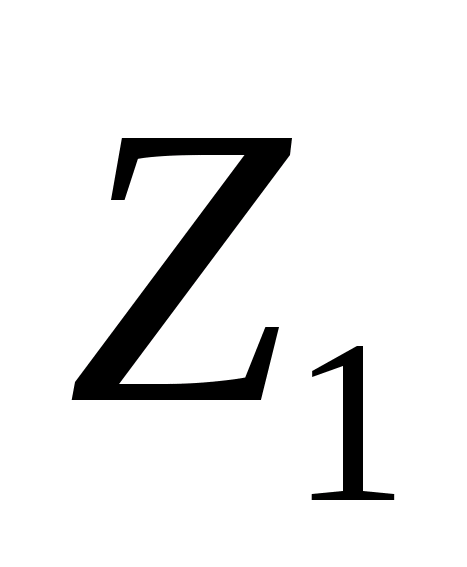і 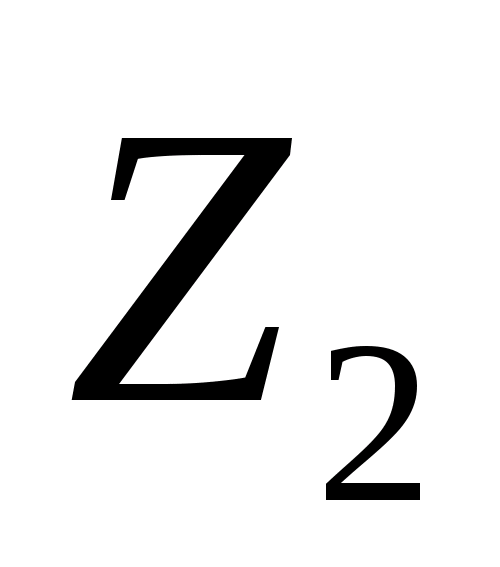, які утворюють кут з вертикаллю. Швидкість осі О2 колеса виражається відрізком BB’. З’єднуючи точку B’ і вісь О, знаходимо пряму розподілу швидкостей для водила Н, яка утворює кут з вертикаллю.

Для отримання наочного уявлення про кутові швидкості коліс планетарного механізму будуємо діаграму кутових швидкостей.

Проводимо довільну горизонтальну лінію. З точки F, яка відкладається на довільній відстані від цієї лінії, під відповідними кутами , , 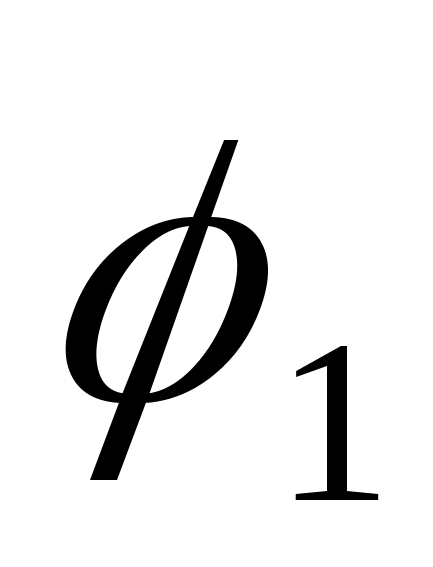до вертикалі, проводимо промені до перетину з цією лінією. Отримуємо точки перетину d, c, b, a, які визначають відрізки dc, cb, ca, довжина яких пропорційна кутовій швидкості відповідних ланок.

Масштаб залежить від довжини відрізка cF.

Довжина вектора (АA′) колової швидкості VA прийнята 60 мм, а відрізок (cF) = 30мм.

Тоді масштабний коефіцієнт:

v = VA / (A′1A1) = 3.96/60=0.066(м/с)/мм.

На кресленні діаграми кутових швидкостей коліс знаходимо масштабний коефіцієнт , що розраховується за формулою:

;

.

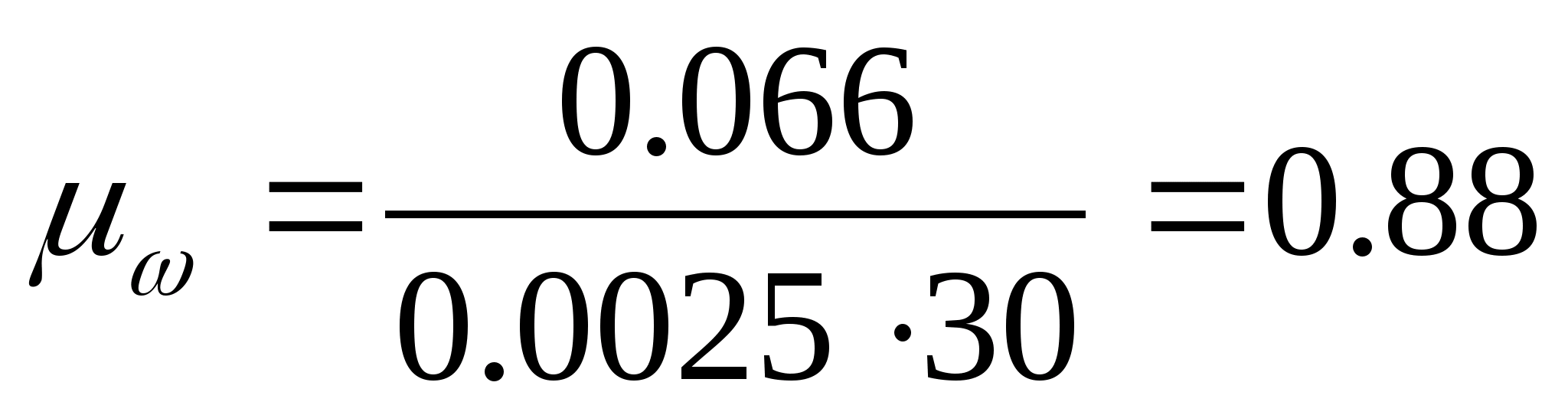
З креслення знаходимо довжини відрізків:

cd =-23.89 мм, ca = 164.01 мм, cb = 18.41 мм.

Визначаємо кутові швидкості всіх ланок графічним методом:

рад/с;

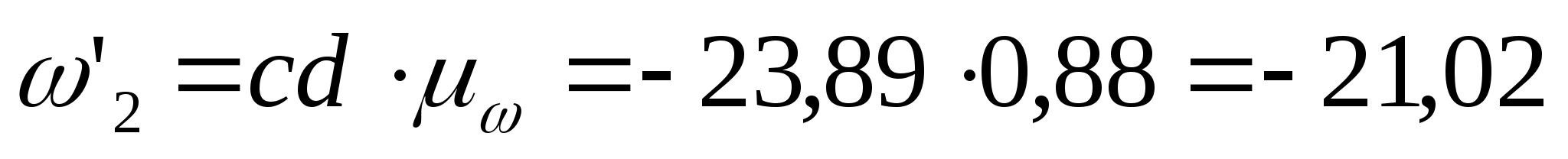рад/с;

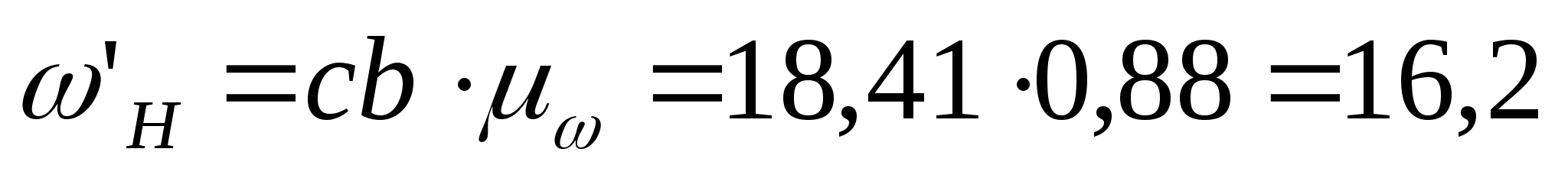рад/с;

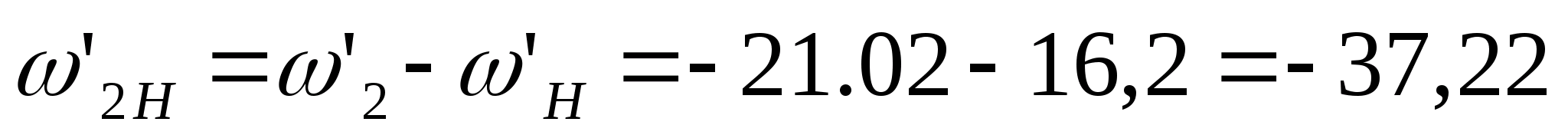рад/с.

6. Визначення похибок при визначенні кутових швидкостей отриманих графічним і аналітичним методами

;

;

;

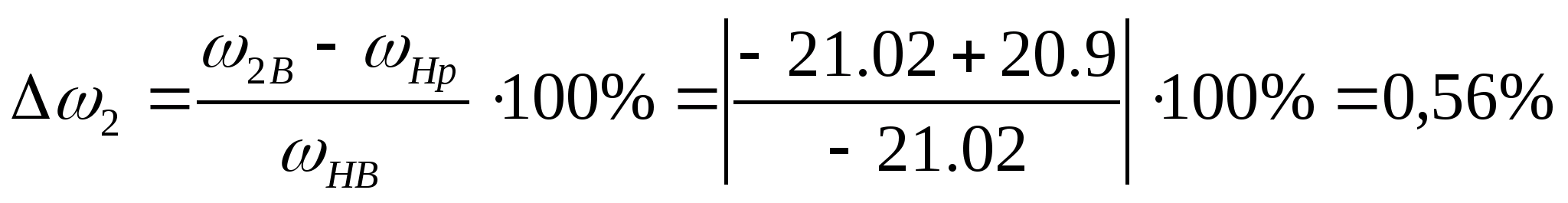Література

1.Артоболевський И.И. Теория механизмов и машин. – М: Наука, 1988. – 640 с.

2.Теория механизмов и машин / Фролов К.В., Попов С.В. Мусатов А.К. и др.; Под ред. К.В.Фролова.–М.: Высш. шк., 1987.–496с.

3.Заблонский К.И., Белоконев И.М., Щекин Б.М. Теория механизмов и машин.–К.: Вища школа, 1989.–370с.

4.Курсовое проектирование по теории механизмов и машин / Кореняко А.С., Кременштейн Л.И., Петровский С.Д. и др.; Под ред. А.С. Кореняко.–К: Вища школа, 1970.–330с.

5. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и машин.–М.: Высш. шк., 1998.–351с.

6. Курсове проектування з теорії механізмів і машин: навчальний посібник / Є.І.Крижанівський, Б.Д.Малько, В.М.Сенчішак та ін.–Івано-Франківськ: 1996.–357с.

7. Теорія механізмів і машин. Механічні передачі: Навч. посібник І.І.Вишенський.–К.: НМКВО, 1992.–356с.

8. Мохнатюк А.І. Синтез кулачкових механізмів на ЕОМ: Навч. посібник.–К.: НМКВО, 1992.–188с.

9. Синтез планетарних передач на ЕОМ. Навчальний посібник до курсового проектування з дисципліни “Теорія механізмів і машин “ / А.І. Мохнатюк.–Вінниця: ВДТУ, 1997.–73с.

10. Кіницький Я.Т. Теорія механізмів і машин. Підручник.–К.: Наукова думка, 2002.–660с.

11. Вірник М.М. Курсове проектування з теорії механізмів і машин.–Вінниця: ВДТУ, 2002.–230с