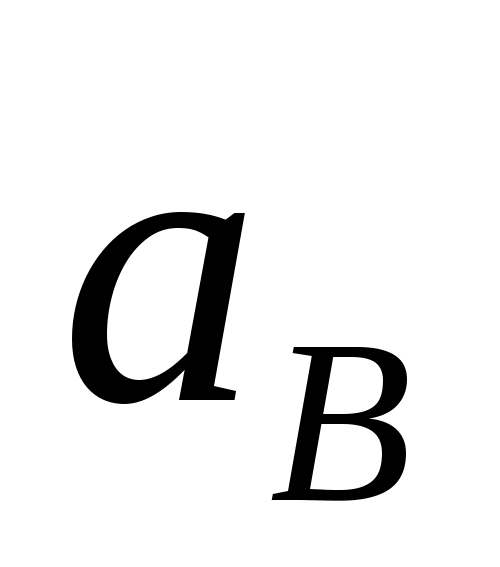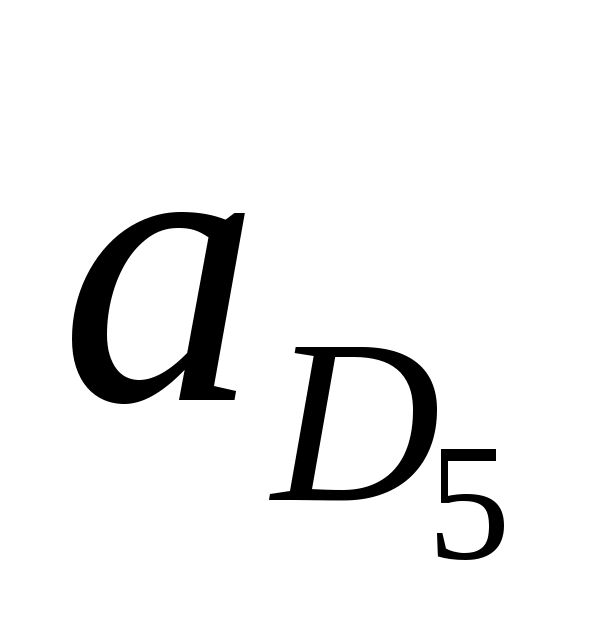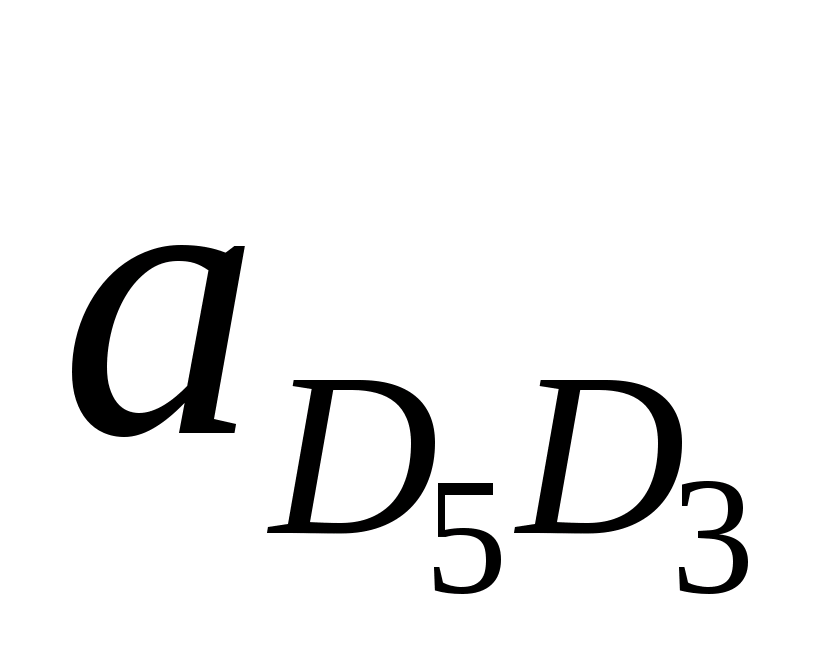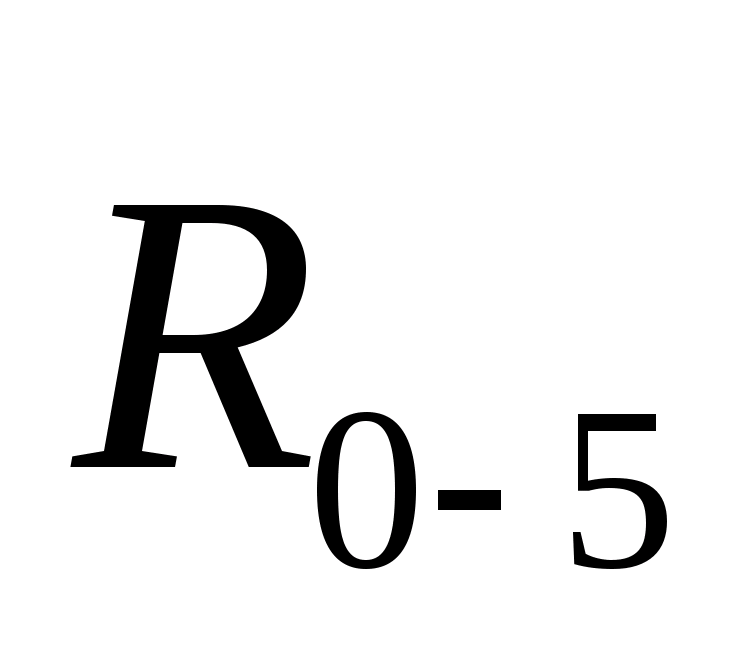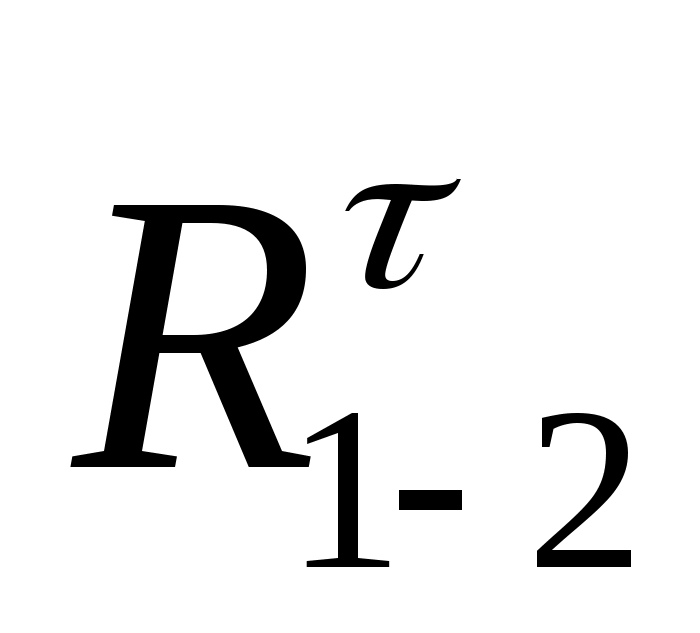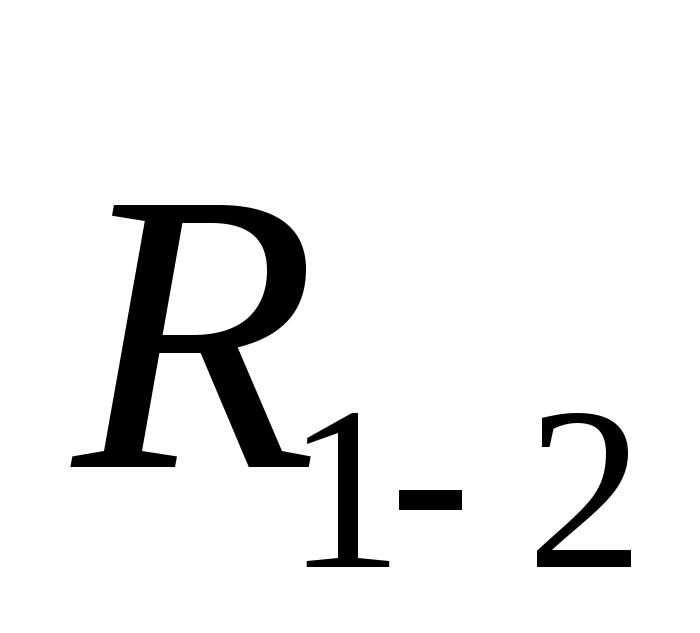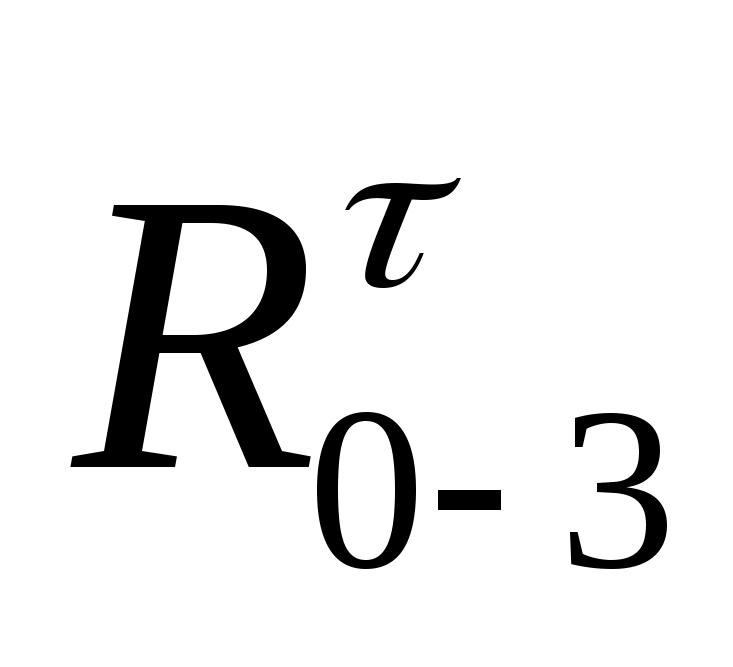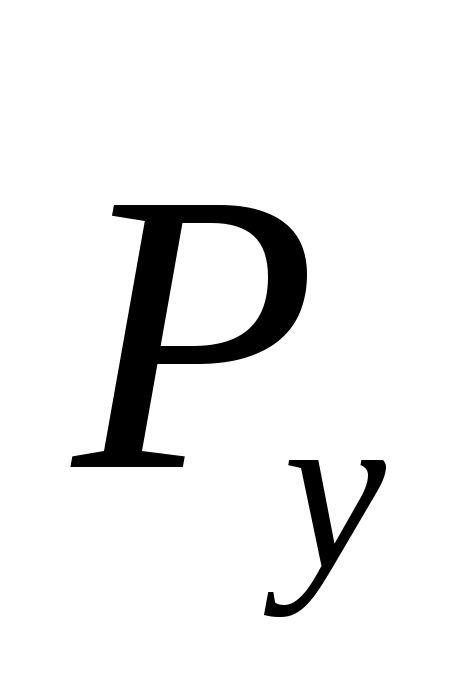Анализ и синтез механизмов технологического оборудования машиностроения
Минобрнауки россии
Пензенская государственная технологическая академия
ПГТА
Факультет «Институт промышленных технологий»
Кафедра теоретической и прикладной механики
Теория механизмов и машин
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту на тему:
Анализ и синтез механизмов технологического оборудования машиностроения
ПГТА 2. 151001. 141-9 ПЗ
Выполнил студент группы 08М1
Хохлов М.А.
Руководитель проекта:
Потемкин А.Н.
2010г.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ
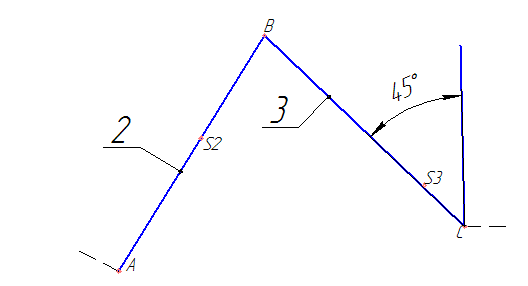
Кинематическая схема механизма представлена на рисунке 1.
Длина кривошипа: OA = 0,05 м;
Длина шатуна: AB = 022 м;
Длина кулисы: ВС = 0,22 м;
OC = 0,31 м;
y = 0,15 м;
Угловая скорость двигателя: ω>d> = 286 рад/с.
Массы звеньев:
m>1> = 12 кг;
m>2> = 15 кг;
m>3> = 19 кг;
m>5> = 21 кг.
Моменты инерции звеньев:

Сила сопротивления Fc=1,4кН.
Числа зубьев зубчатых колес: Z>1>= 12, Z>2>= 30,
модуль зубчатой передачи: m = 3 мм.


Рисунок 1 – Схема механизма
Оглавление
Исходные данные для проектирования
Оглавление
1. Синтез, структурное и кинематическое исследование механизма
Описание схемы механизма
Структурное исследование механизма
1.3 Кинематическое исследование механизма
1.3.1 Построение кинематической схемы механизма
1.3.2 Построение планов скоростей
1.3.3 Определение угловых скоростей звеньев
1.3.4 Построение плана ускорений
1.3.5 Определение угловых ускорений звеньев
2. Силовой (кинетостатический) расчет механизма
2.1 Определение реакций в кинематических парах
2.2 Силовой расчет ведущего звена
2.3 Силовой расчет ведущего звена методом Н.Е. Жуковского
3. Синтез зубчатого зацепления
3.1 Определение геометрических параметров пары цилиндрических прямозубых эвольвентных зубчатых колес
3.2 Построение картины зацепления пары зубчатых колес
4. Синтез кулачкового механизма
Литература
1. Синтез, структурное и кинематическое исследование механизма
Описание схемы механизма
Кинематическая схема механизма представлена на рисунке 1.
Звено 1 совершает полный оборот вокруг оси, проходящей через точку O. Звенья 2 совершает сложные движения в плоскости. Звено 3 совершает качательное движение. Звено 5 совершает поступательное движение.
Структурное исследование механизма
Так как рассматриваемый механизм является плоским механизмом, то степень подвижности определяется по формуле П.Л. Чебышева:

где n – число подвижных звеньев,
 – число кинематических пар
пятого и четвертого классов соответственно.
– число кинематических пар
пятого и четвертого классов соответственно.

В рассматриваемом механизме одно ведущее звено.
Определяем класс и порядок механизма.
В таблице 1 показано разложение механизма на группы Ассура. В таблице 2 приведены обозначения кинематических пар, указаны их вид, порядок и класс.
Таблица 1
|
№ звеньев |
Схема структурной группы и механизма I класса |
Класс |
Порядок |
Вид |
|
5-4 |
|
II |
2 |
4 |
|
3-2 |
|
II |
2 |
1 |
|
0-1 |
|
I |
- |
- |
Таблица 2
|
Обозначение КП |
Звенья, составляющие КП |
Характеристика КП |
|
O |
0-1 |
Вращательная низшая, 5 класс |
|
A |
1-2 |
Вращательная низшая, 5 класс |
|
B |
2-3 |
Вращательная низшая, 5 класс |
|
C |
0-3 |
Вращательная низшая, 5 класс |
|
D>3> |
3-4 |
Вращательная низшая, 5 класс |
|
D>5> |
4-5 |
Поступательная низшая, 5 класс |
|
E |
0-5 |
Поступательная низшая, 5 класс |
Формула строения механизма:
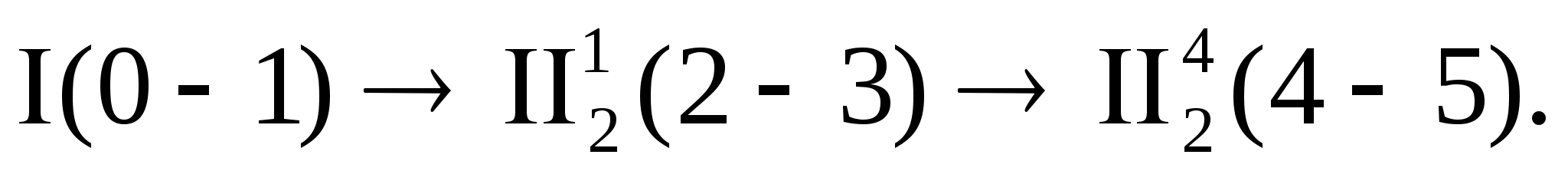
Рассматриваемый механизм является
механизмом
 класса.
класса.
1.3 Кинематическое исследование механизма
1.3.1 Построение кинематической схемы механизма
Масштабный коэффициент кинематической схемы определяется по формуле:

Выполняем построение кинематической схемы механизма в принятом масштабе длин по заданным размерам звеньев и параметров механизма.
Разбиваем траекторию движения кривошипа OA на 12 частей. В качестве нулевого положения механизма (от которого начинается отсчет движения) принимаем одно из крайних положений. С этого положения начинается рабочий ход механизма.
Вычерчиваем траектории движения
центров тяжести звеньев 2 и 4 (точки
 ,
,
 и
и
 )
)
Одно из положений звеньев механизма, положение, для которого выполняется силовой расчет, обводится более яркими линиями.
1.3.2 Построение планов скоростей
Определяем угловую скорость вращения кривошипа:

Определяем скорость точки A кривошипа OA:
 .
.
Вектор скорости точки A перпендикулярен ведущему звену и направлен в сторону его вращения. Откладываем его из полюса в виде отрезка Ра длиной 87.5 мм в масштабе:

Определяем скорости других точек механизма.
Для определения скорости точки B составляем систему векторных уравнений:
 .
.
В этой системе векторных уравнений
известны по модулю и направлению векторы
абсолютных скоростей
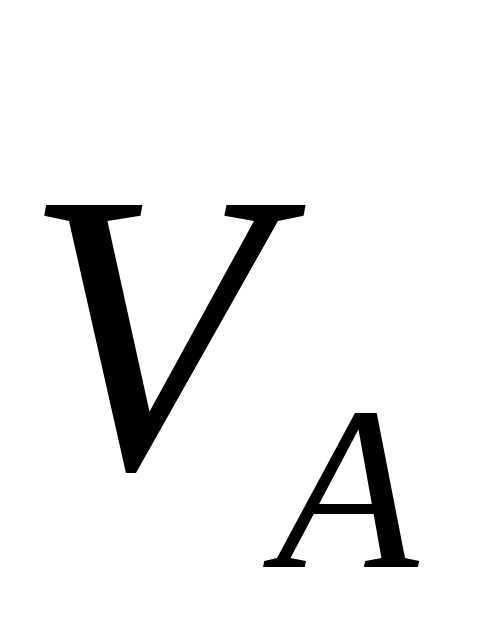 и
и
 (скорость
(скорость
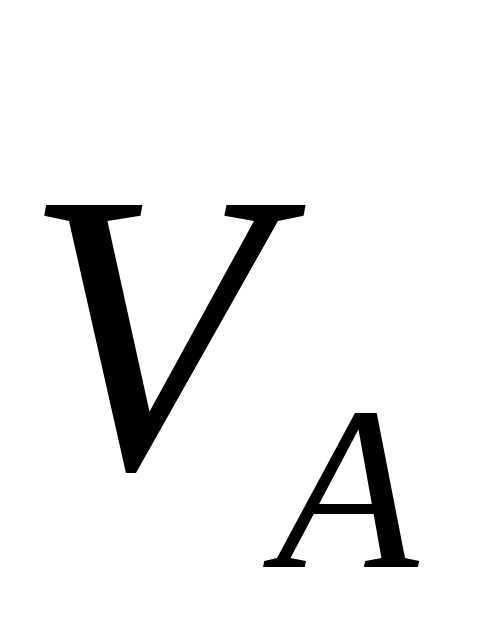 была определена выше, а скорость
была определена выше, а скорость
 равна нулю, т.к. точка принадлежит стойке,
а, следовательно, неподвижна). Векторы
относительных скоростей известны только
по направлению. Вектор скорости
равна нулю, т.к. точка принадлежит стойке,
а, следовательно, неподвижна). Векторы
относительных скоростей известны только
по направлению. Вектор скорости
 направлен перпендикулярно звену AB,
вектор скорости
направлен перпендикулярно звену AB,
вектор скорости
 направлен перпендикулярно звену ВС.
направлен перпендикулярно звену ВС.
Построения выполняем в следующей
последовательности: В соответствии с
первым векторным уравнением проводим
вектор pa
перпендикулярно кривошипу OA
в сторону его вращения. Через конец
этого вектора проводим прямую,
перпендикулярную звену AB
(это линия вектора
 ).
В соответствии со вторым векторным
уравнением вектор
).
В соответствии со вторым векторным
уравнением вектор
 обращается в точку, которую мы и
откладываем в полюсе плана. Из этой
точки, как из конца вектора, проводим
прямую, параллельную направляющей.
Точка пересечения ее с ранее проведенной
прямой дает нам конец вектора абсолютной
скорости точки B
обращается в точку, которую мы и
откладываем в полюсе плана. Из этой
точки, как из конца вектора, проводим
прямую, параллельную направляющей.
Точка пересечения ее с ранее проведенной
прямой дает нам конец вектора абсолютной
скорости точки B
 .
Начало его лежит в полюсе плана скоростей.
.
Начало его лежит в полюсе плана скоростей.
Таким образом, отрезок pb в масштабе определит значение линейной скорости точки B в каждом из положений звеньев механизма.
Аналогично строим план скоростей для точки D>5>. Система векторных уравнений при этом имеет вид:

Скорость точки D>3> определяется из пропорции:
 ,
,
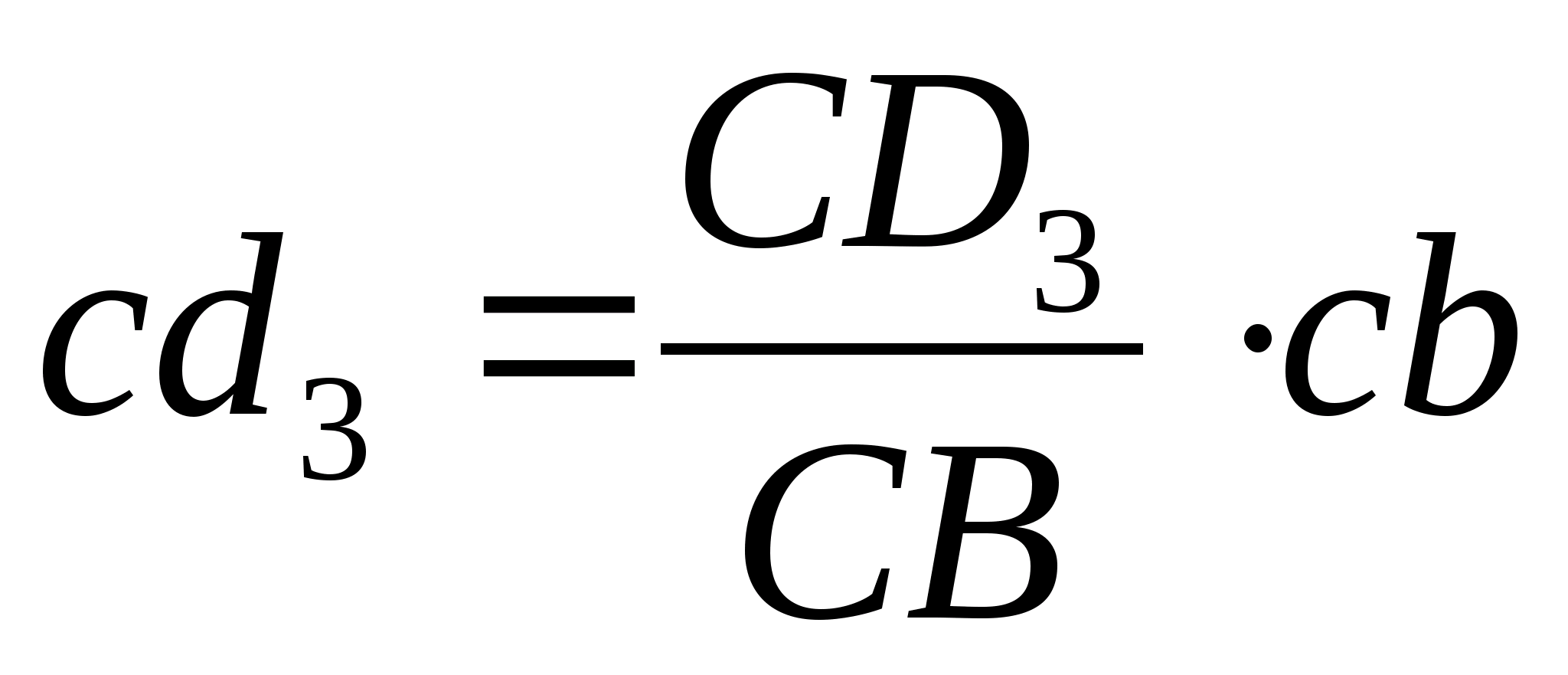
Линейные скорости центров тяжести 2 и 3 звеньев определяются из пропорций:

откуда получаем отрезки
 плана скоростей, которые с учетом
масштаба
плана скоростей, которые с учетом
масштаба
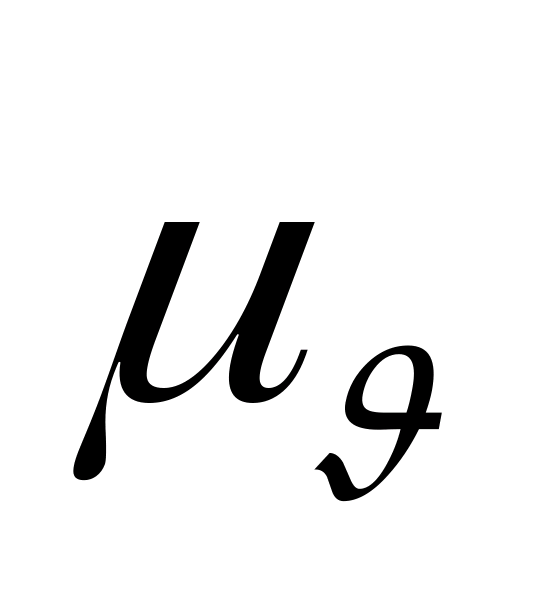 дают значения скоростей центров тяжести.
дают значения скоростей центров тяжести.
Результаты расчетов сводим в таблицу 3.
Таблица 3
|
Номер положения звеньев механизма |
Значение скоростей точек механизма, м/c |
||||||
|
V>B> |
V>BA> |
V>D3> |
V>D5> |
V>D5D3> |
V>S2> |
V>S3> |
|
|
0 |
0 |
1,50 |
1.06 |
1.09 |
0.4 |
||
|
1 |
1.04 |
1.425 |
1,05 |
1,075 |
0,225 |
||
|
3 |
1.475 |
0,21 |
1.04 |
1.025 |
0,2 |
1.03 |
1.475 |
|
5 |
0,66 |
1,41 |
1,06 |
0.9 |
0,26 |
||
|
7 |
0,84 |
1.11 |
1.05 |
1.08 |
0.21 |
||
|
9 |
1,475 |
0,06 |
1.04 |
1.04 |
0,04 |
||
|
11 |
0.9 |
2.2 |
1.375 |
0.01 |
1.375 |
1.3.3 Определение угловых скоростей звеньев
Угловая скорость первого звена была определена выше.
Определяем угловые скорости звеньев AB и CD по формулам:
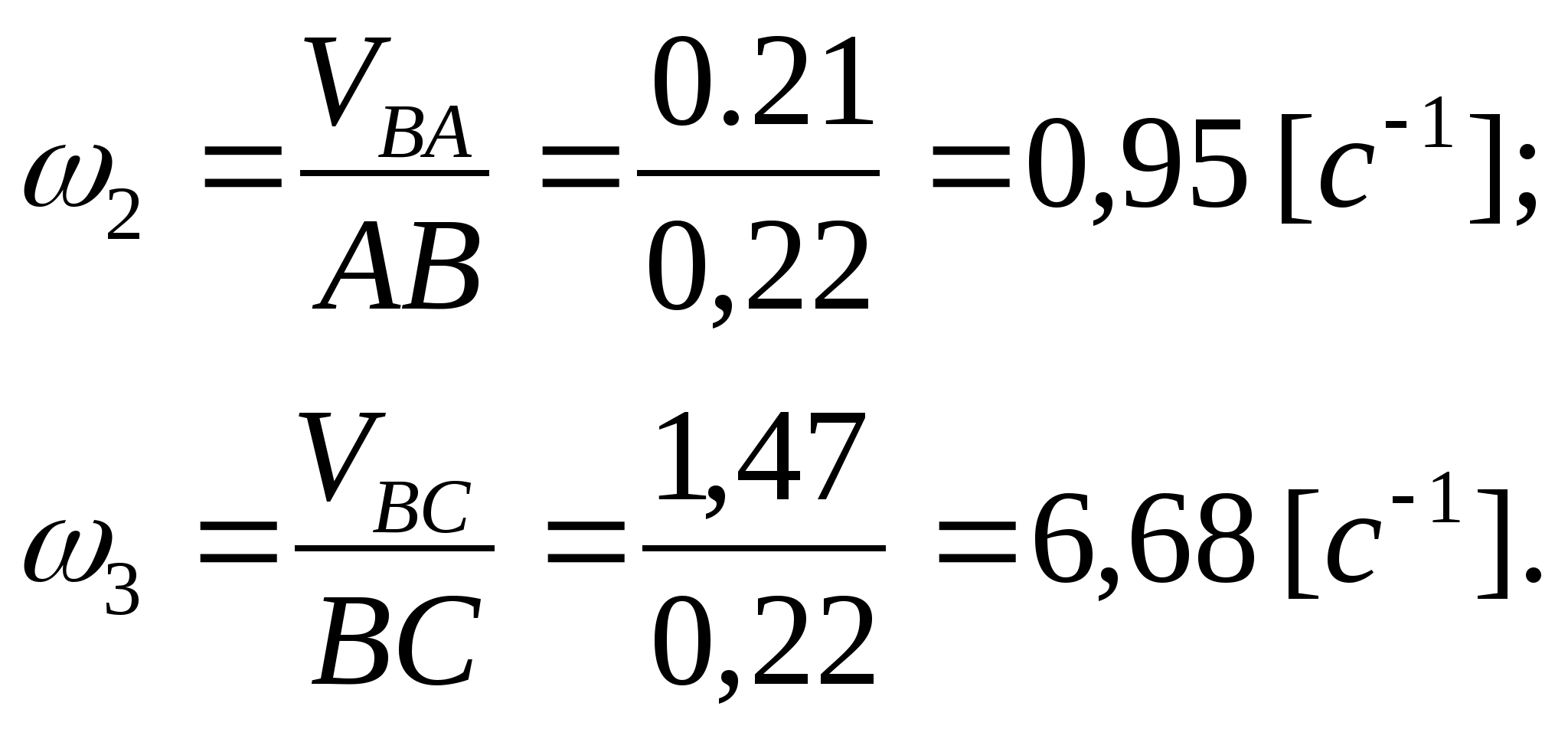
Направление угловых скоростей
 определяются векторами относительных
скоростей
определяются векторами относительных
скоростей
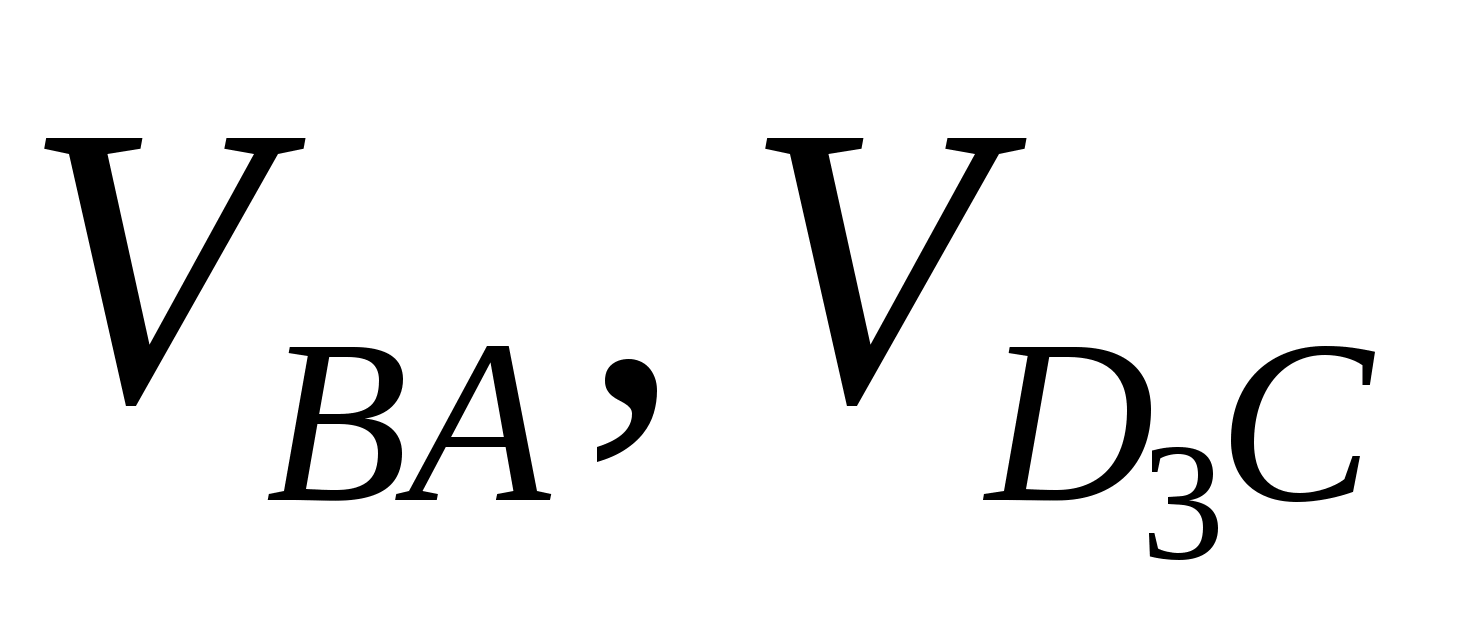 ,
приложенными в соответствующие точки
2 и 3 звеньев.
,
приложенными в соответствующие точки
2 и 3 звеньев.
1.3.4 Построение плана ускорений
Построение плана ускорений выполняем для 3 и 9 положений звеньев механизма.
Ускорение точки A определяется по формуле:

Вектор ускорения точки A
направлен параллельно ведущему звену
1 к центру его вращения, т.к. угловая
скорость
 есть величина постоянная, угловое
ускорение звена 1 равно нулю, тангенциальная
составляющая ускорения равна нулю, и
ускорение
есть величина постоянная, угловое
ускорение звена 1 равно нулю, тангенциальная
составляющая ускорения равна нулю, и
ускорение
 - нормальное ускорение.
- нормальное ускорение.
Масштабный коэффициент для построения плана ускорений определяется по формуле:

Для определения ускорений точек B, C и D составляем системы векторных уравнений:
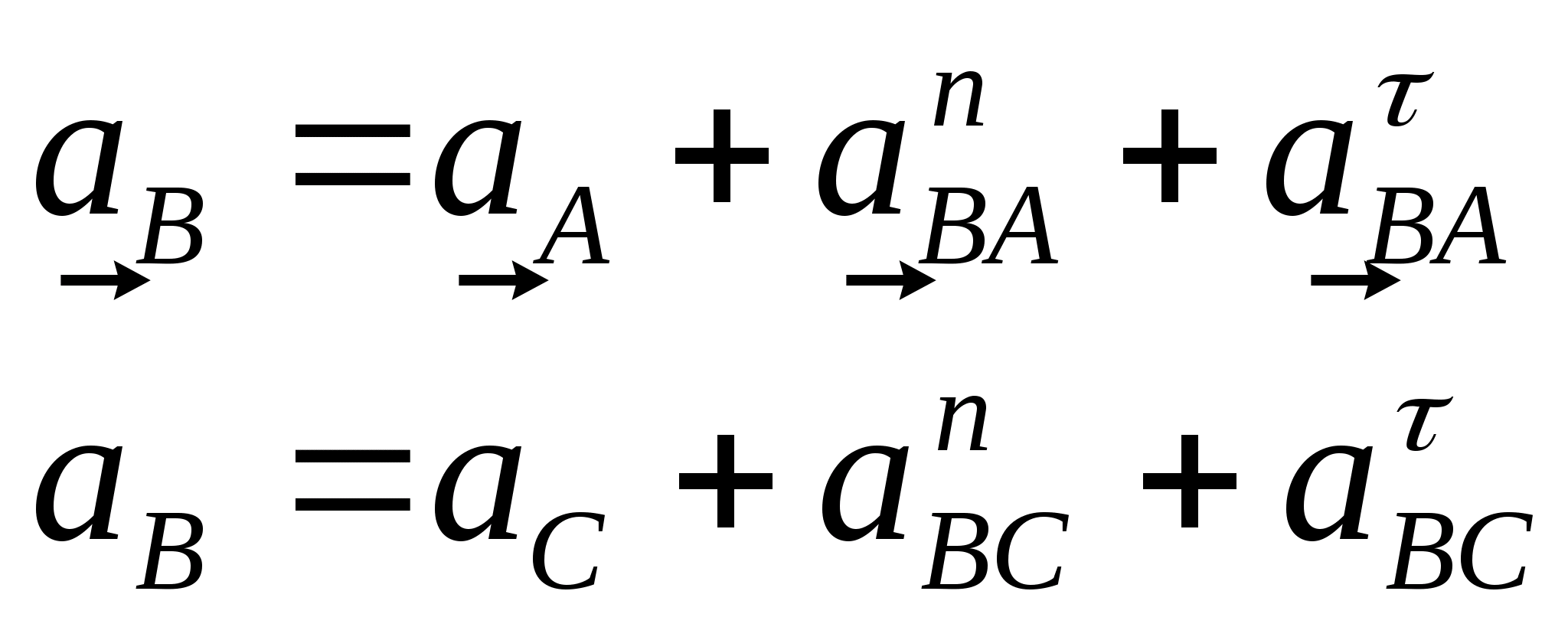
 ,
,
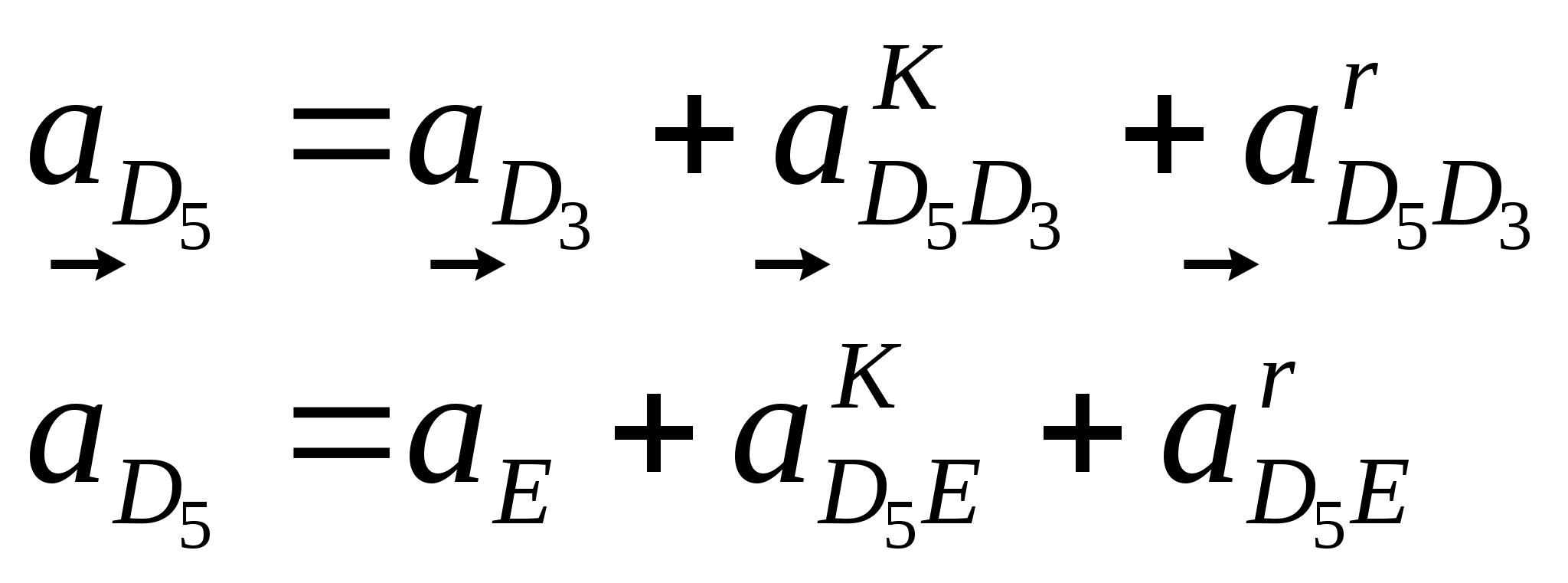
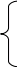 .
.
Рассмотрим вектора в каждой системе уравнений.
Нормальные ускорения определяются по формулам:

Вектор нормального ускорения направлен параллельно соответствующему звену к центру его вращения.
Кориолисово ускорение
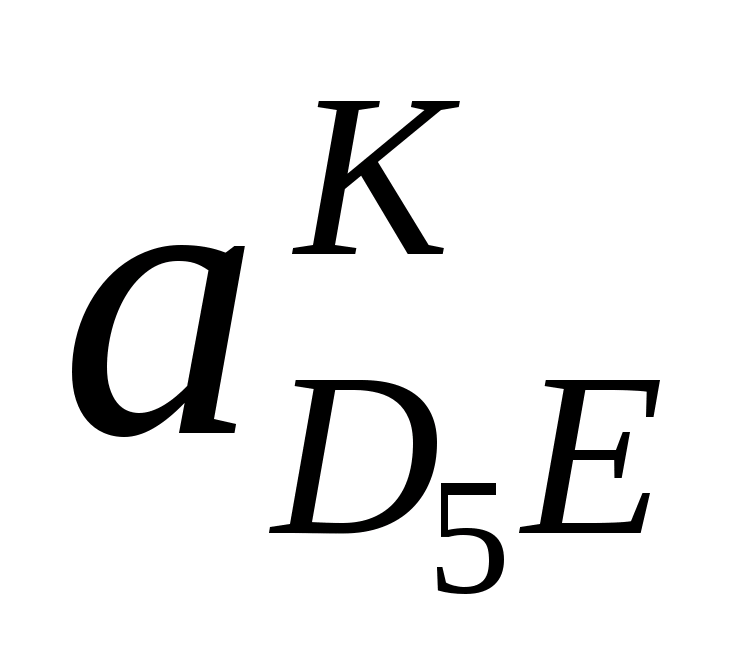 равно нулю, т.к. стойка неподвижна.
Ускорение
равно нулю, т.к. стойка неподвижна.
Ускорение
 также равно нулю, т.к. угловая скорость
направляющей равна нулю.
также равно нулю, т.к. угловая скорость
направляющей равна нулю.
Построение плана ускорений
выполняем в следующей последовательности:
из полюса
 откладываем вектор ускорения точки A
в виде отрезка
откладываем вектор ускорения точки A
в виде отрезка
 длиной 251 мм. Вектор нормального ускорения
длиной 251 мм. Вектор нормального ускорения
 откладываем из конца вектора ускорения
точки A.
Вектор ускорения точки С (оно равно
нулю) откладываем в полюсе. Вектор
нормального ускорения
откладываем из конца вектора ускорения
точки A.
Вектор ускорения точки С (оно равно
нулю) откладываем в полюсе. Вектор
нормального ускорения
 откладываем из полюса как из конца
вектора ускорения точки С. Через концы
векторов ускорений
откладываем из полюса как из конца
вектора ускорения точки С. Через концы
векторов ускорений
 и
и
 проводим направления векторов ускорений
проводим направления векторов ускорений
 и
и
 .
Точка пересечения этих линий даст нам
вектор абсолютного ускорения точки B.
.
Точка пересечения этих линий даст нам
вектор абсолютного ускорения точки B.
Аналогично строим план по второму и третьему уравнениям
Ускорение точки D>3> определяем из пропорции:
 ,
,
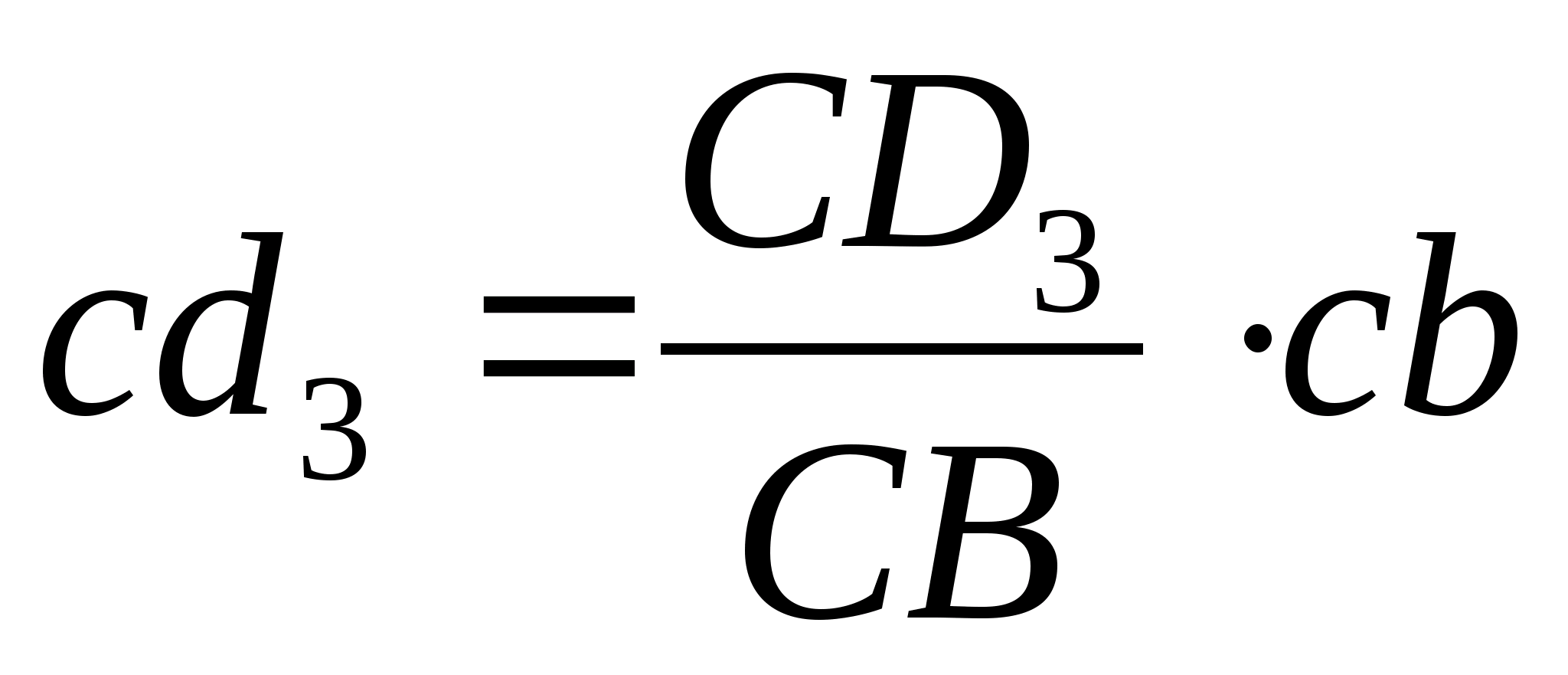 .
.
Результаты расчетов сводим в таблицу 4.
Таблица 4
|
Значение ускорений точек механизма, м/c2 |
|||||||||
|
№ |
|
|
|
|
|
|
|
|
|
|
3 |
15.6 |
10.8 |
6.3 |
54.9 |
55.2 |
12.6 |
6 |
19.5 |
3.3 |
|
9 |
12.6 |
8.7 |
5,1 |
35.7 |
37.6 |
8.7 |
6.9 |
27.3 |
2.7 |
1.3.5 Определение угловых ускорений звеньев
Угловое ускорение первого звена равно нулю, т.к. кривошип вращается равномерно.
Угловые ускорения звеньев AB и CD для третьего положения звеньев механизма определяются по формулам:
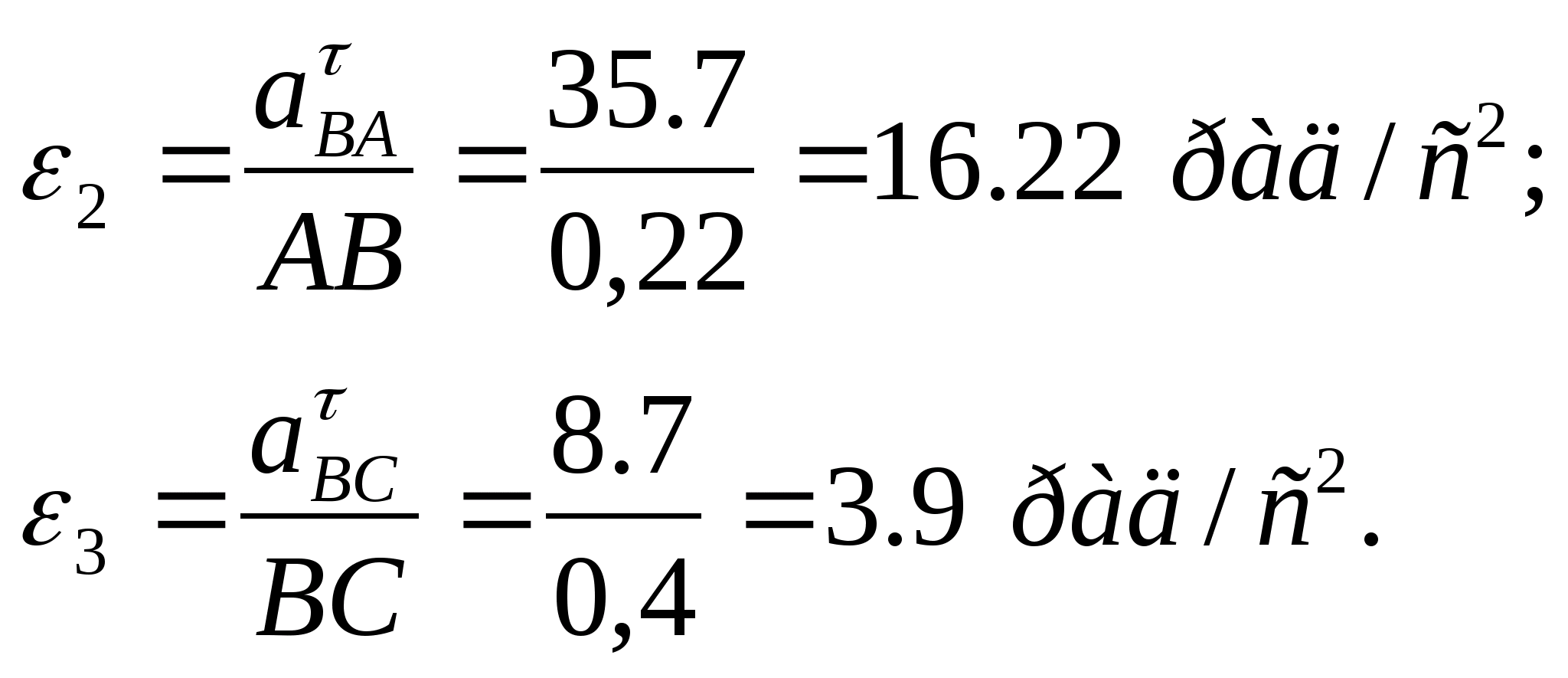
2. Силовой (кинетостатический) расчет механизма
2.1 Определение реакций в кинематических парах
Исследование механизма производим для 3-его положения звеньев механизма. Для этого вычерчиваем кинематическую схему механизма в заданном положении и расчленяем ее на группы Ассура.
Масштабный коэффициент кинематической схемы определяется по формуле:
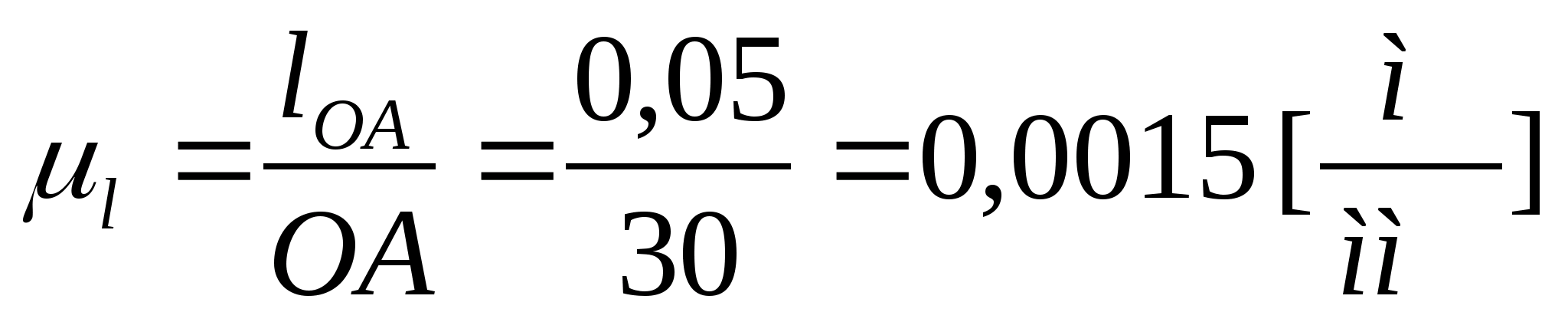
Определяем силы тяжести, действующие на механизм:
G>1>=m>1>*g=117.72 (H)
G>2>=m>2>*g=14712(H)
G>3>=m>3>*g=186.39(H)
G>5>=m>5>*g=206.01(H)
Определяем силы инерции, возникающие при движении звеньев механизма:

Определяем инерционные моменты:

Определяем реакции в кинематических парах Ассура. Начинаем с последней группы, состоящей из звеньев 4 и 5.
Приложив взамен отброшенных звеньев 3 и 0 реакции
 и
и
 ,
,
рассматриваем группу в равновесии под действием сил.
Уравнение равновесия имеет вид:
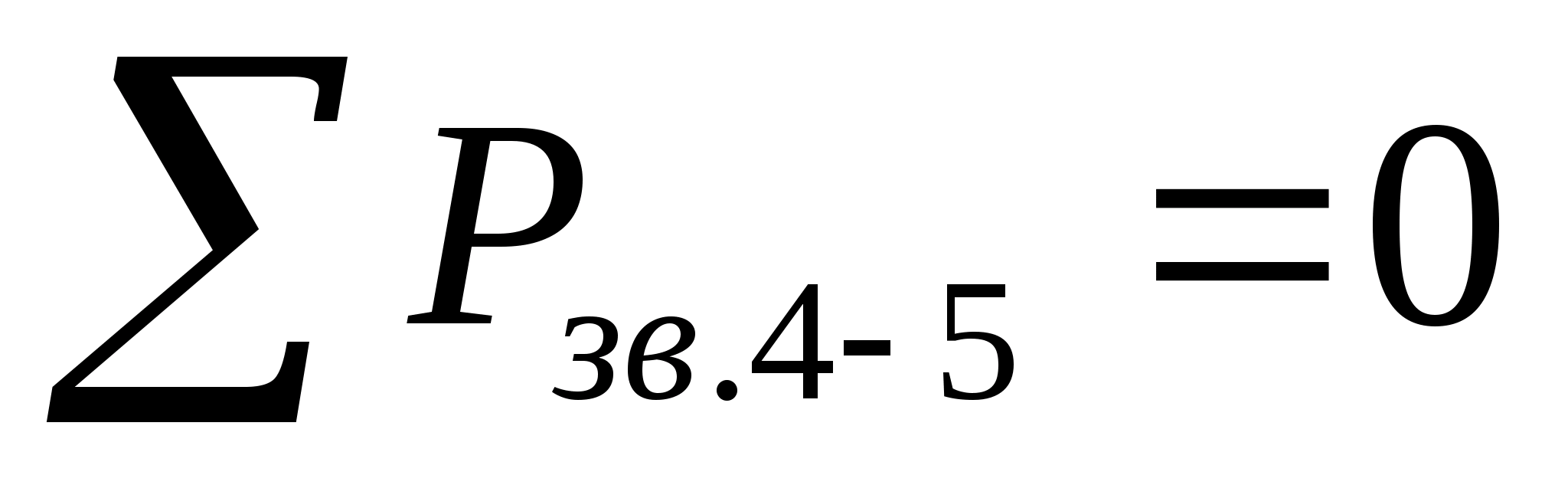 ,
,
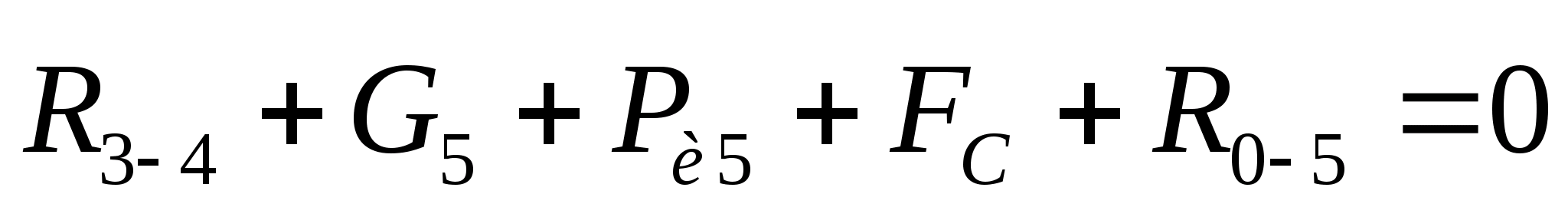
В этом уравнении неизвестные
величины:
 ,
,
 .
.
Строим план сил в масштабе:

Последовательно откладывая
векторы из уравнения равновесия группы,
строим силовой многоугольник, который
замыкаем прямыми линиями в направлениях
векторов
 и
и
 .
.
Полные реакции определяются из плана сил:
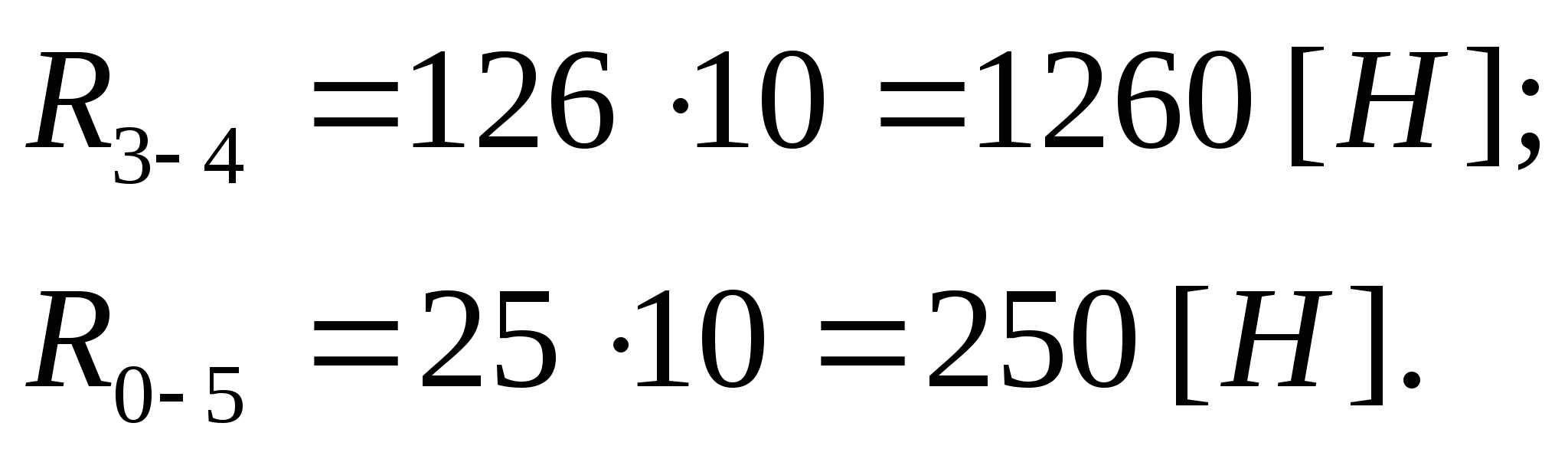
Реакция
 во внутренней кинематической паре
определяется из условия равновесия
звена 4 под действием сил по уравнению:
во внутренней кинематической паре
определяется из условия равновесия
звена 4 под действием сил по уравнению:

Плечо действия силы
 определим из уравнения:
определим из уравнения:

Отсюда
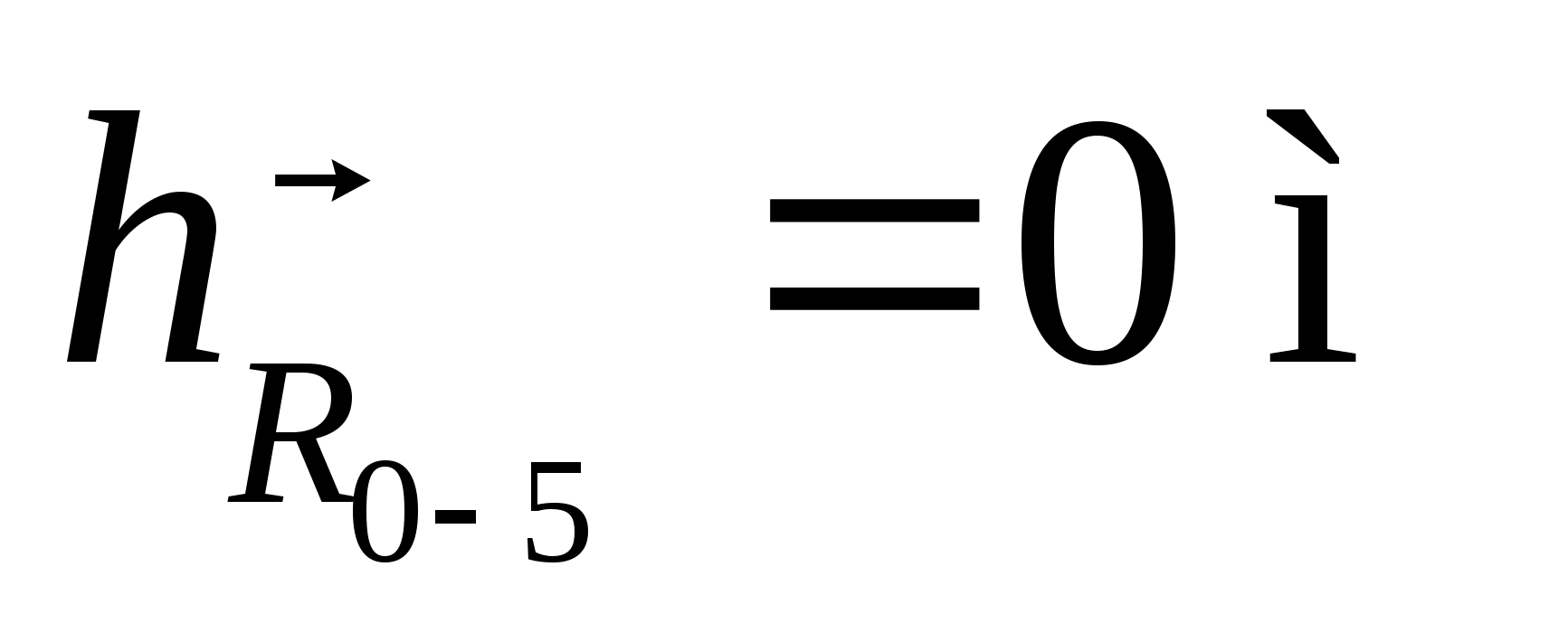
Величины сил, действующих на звенья механизма, а также длины векторов на плане сил, с учетом выбранного масштаба, представлены в таблице 5.
Таблица 5
|
Обозначение силы |
Величина силы, Н |
Длина вектора на плане сил, мм |
Точки на плане сил |
|
|
1210 |
121 |
4-1 |
|
|
250 |
25 |
5-1 |
|
|
190 |
19 |
1-2 |
|
|
1400 |
140 |
3-4 |
|
|
1210 |
121 |
3-7 |
|
|
200 |
20 |
2-3 |
Произведя аналогичные рассуждения и выкладки, определяем реакции в кинематических парах структурной группы Ассура, состоящей из звеньев 2 и 3.
Уравнение равновесия этой группы имеет вид:
 ,
,

Уравнение равновесия звена 2 имеет вид:

Из этого уравнения определяем значение тангенциальной составляющей силы реакции:

Уравнение равновесия звена 3 имеет вид:
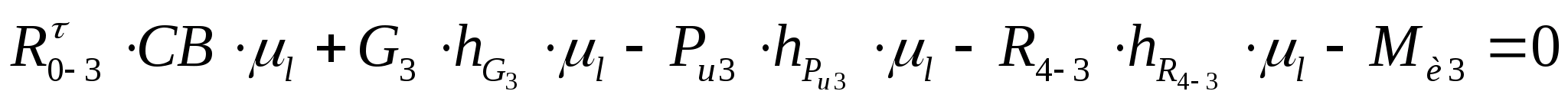
Из этого уравнения определяем значение тангенциальной составляющей силы реакции:

Строим план сил в масштабе:

Из построенного плана сил определяем значения реакций:

G>2>=147.12[H]
G>3>=186.39[H]
P>ин3>=57[H]
Реакцию
 определяем из условия равновесия звена
3 под действием сил по уравнению:
определяем из условия равновесия звена
3 под действием сил по уравнению:
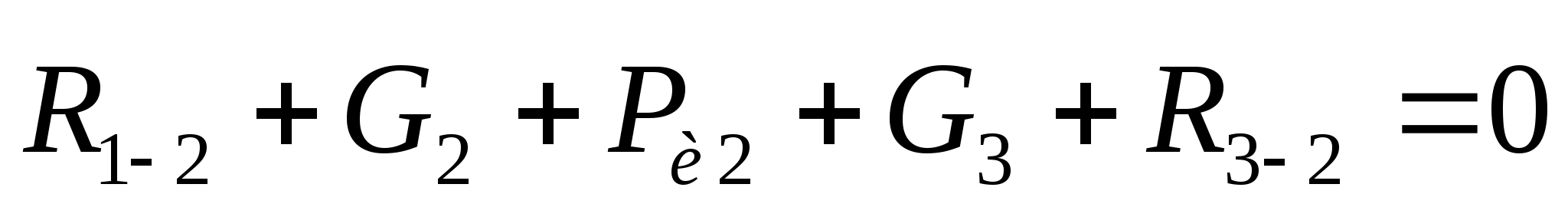
Реакцию
 определяем из плана сил, соединяя точки
9 и 5:
определяем из плана сил, соединяя точки
9 и 5:

Величины сил, действующих на звенья механизма, а также длины векторов на плане сил, с учетом выбранного масштаба, представлены в таблице 6.
Таблица 6
|
Обозначение силы |
Величина силы, Н |
Длина вектора на плане сил, мм |
Точки на плане сил |
|
|
97.5 |
13 |
9-1 |
|
|
202.5 |
27 |
1-2 |
|
|
225 |
30 |
9-2 |
|
|
1170 |
156 |
8-9 |
|
|
382.5 |
51 |
7-8 |
|
|
1230 |
164 |
7-9 |
|
|
300 |
40 |
3-4 |
|
|
52.5 |
7 |
5-6 |
|
|
1260 |
168 |
6-7 |
|
|
390 |
52 |
9-4 |
|
|
142.5 |
19 |
2-3 |
|
|
157.5 |
21 |
4-5 |
2.2 Силовой расчет ведущего звена
Вычерчиваем ведущее звено
механизма в масштабе с соблюдением
заданного положения. Чтобы звено 1
находилось в равновесии, к нему необходимо
приложить уравновешивающую силу
 .
.
Величину уравновешивающей силы
 определяем из условия равновесия звена
1 под действием моментов сил относительно
точки O
по уравнению:
определяем из условия равновесия звена
1 под действием моментов сил относительно
точки O
по уравнению:
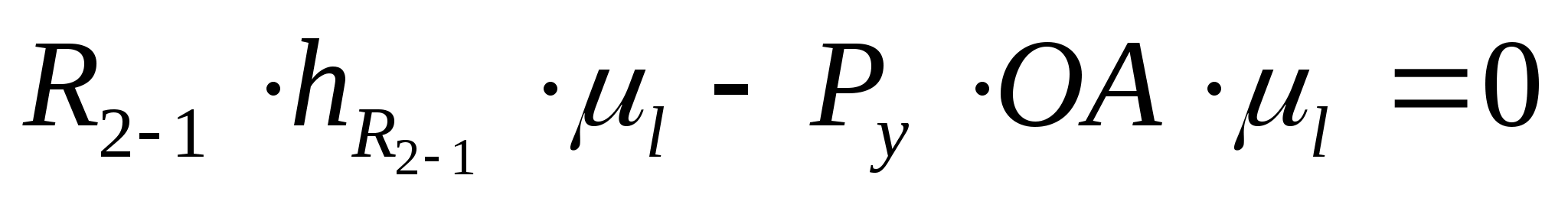

Для нахождения реакции
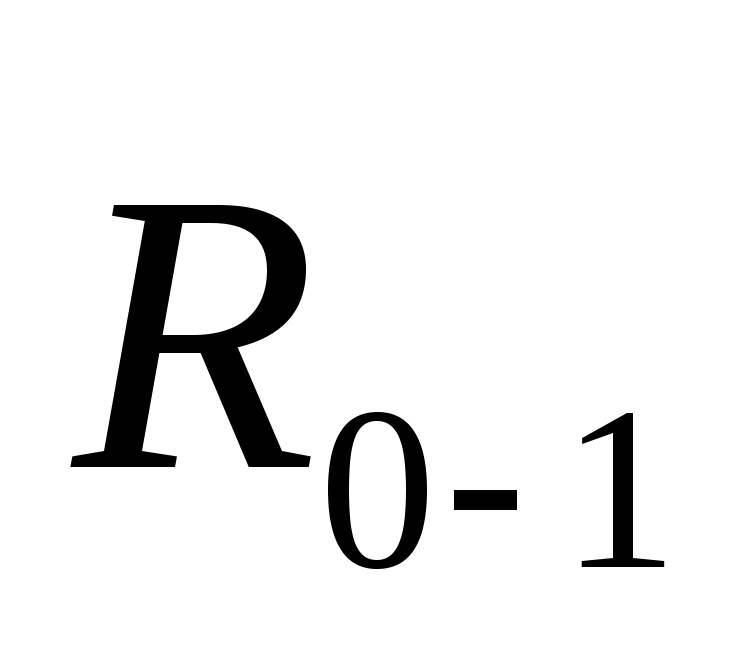 в точке O
рассмотрим равновесие ведущего звена
1 под действием сил по уравнению:
в точке O
рассмотрим равновесие ведущего звена
1 под действием сил по уравнению:

Строим план сил, определяем
величину и направление реакции
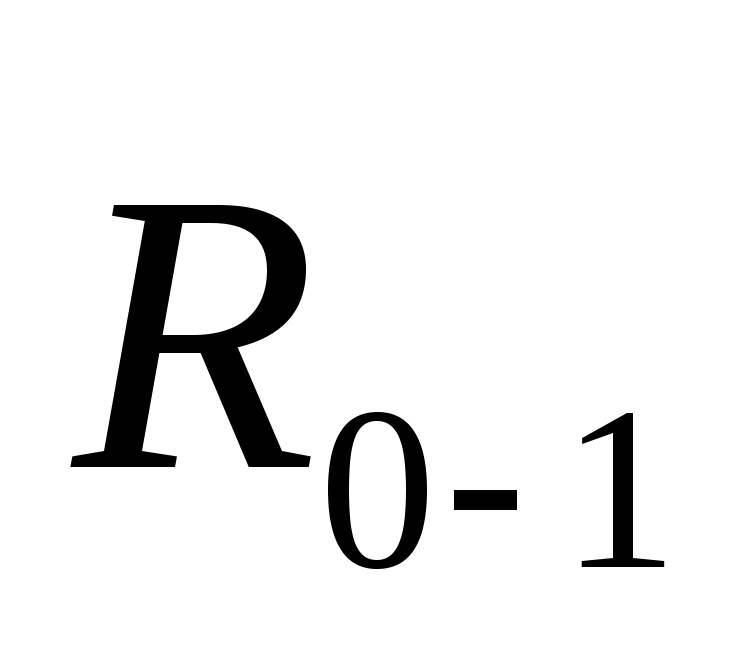 .
.
Масштаб плана сил:

Величины сил, действующих на звенья механизма, а также длины векторов на плане сил, с учетом выбранного масштаба, представлены в таблице 7.
Таблица 7
|
Обозначение силы |
Величина силы, Н |
Длина вектора на плане сил, мм |
Точки на плане сил |
|
|
225 |
150 |
1-2 |
|
|
132 |
88 |
2-3 |
|
|
226 |
178 |
3-4 |
|
G>1> |
117 |
78 |
4-1 |
2.3 Силовой расчет ведущего звена методом Н.Е. Жуковского
Для выполнения силового расчета
ведущего звена методом Н.Е. Жуковского
необходимо построить повернутый на
 относительно
полюса план скоростей для 3-его положения
звеньев механизма.
относительно
полюса план скоростей для 3-его положения
звеньев механизма.
План скоростей строим в масштабе:

Переносим все силы, действующие на звенья механизма, в соответствующие точки повернутого плана скоростей.
Действие моментов
 и
и
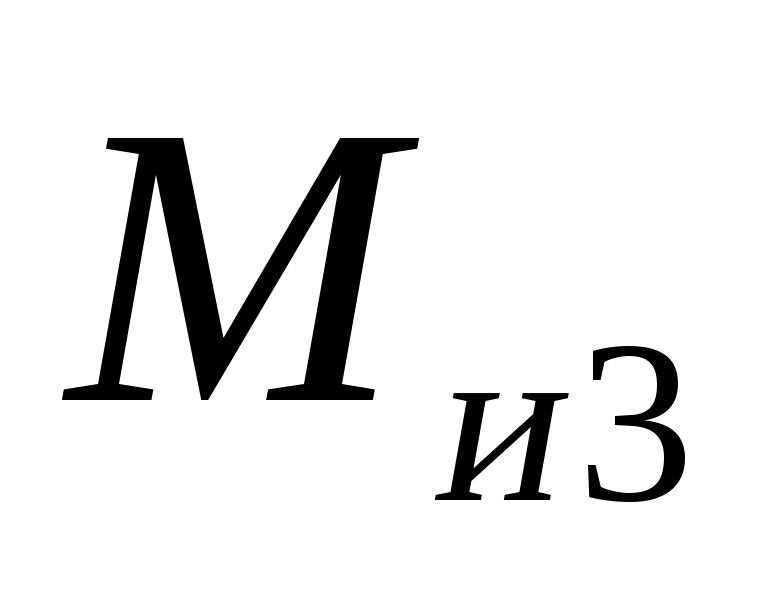 заменяем парами сил:
заменяем парами сил:

Составляем уравнение моментов всех сил, действующих на звенья механизма, относительно полюса плана скоростей:

Откуда
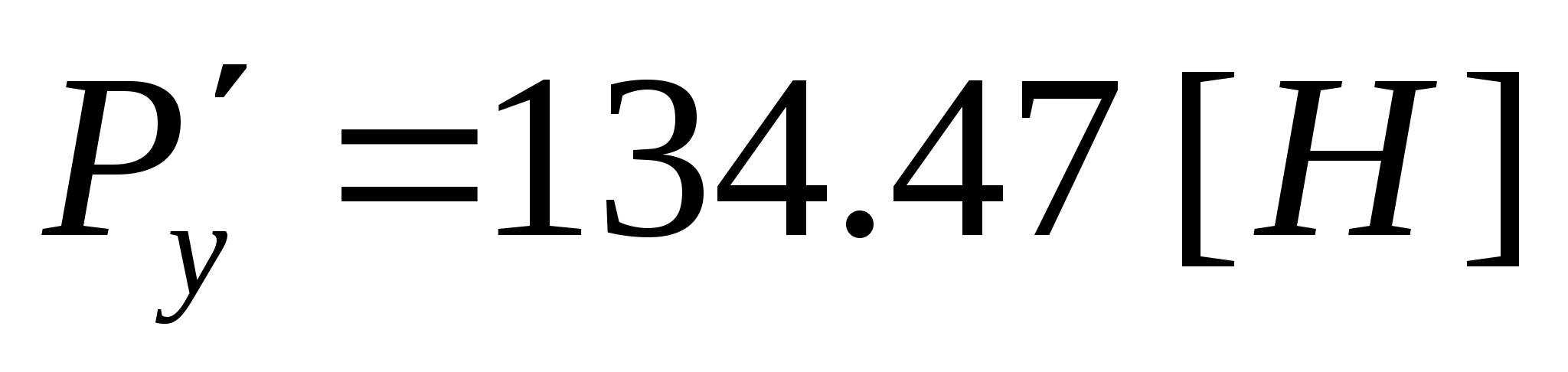
Определим процент ошибки при
подсчете уравновешивающей силы
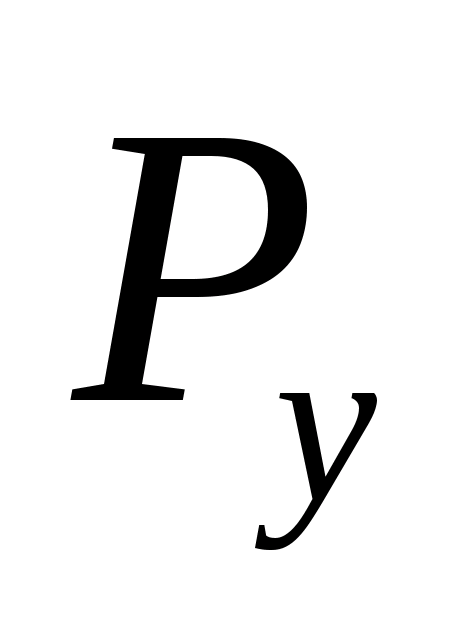 двумя методами:
двумя методами:
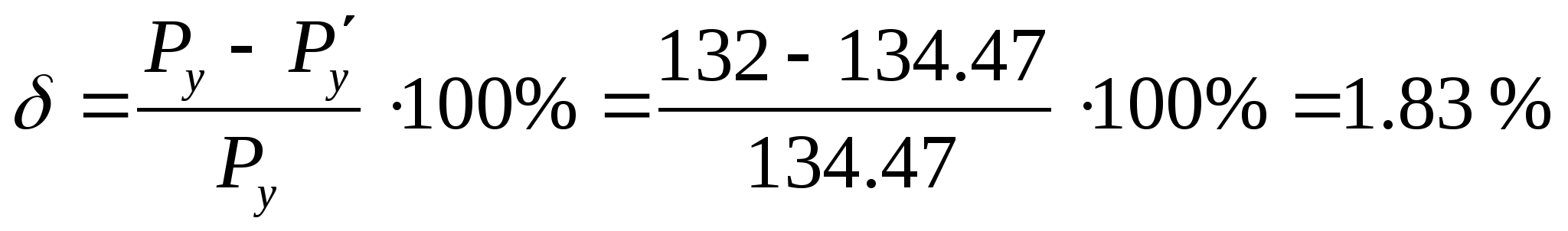
Графическая часть проекта оформляется на листе 2.
кинематический силовой зубчатый кулачковый
3. Синтез зубчатого зацепления
3.1 Определение геометрических параметров пары цилиндрических прямозубых эвольвентных зубчатых колес
Построить схему зацепления пары
зубчатых колес
 .
.
Данные для расчета:
 ,
,
 ,
m = 3 мм.
,
m = 3 мм.
Определяем радиусы делительных окружностей:
 мм
мм
 мм
мм
Определяем радиусы основных окружностей:
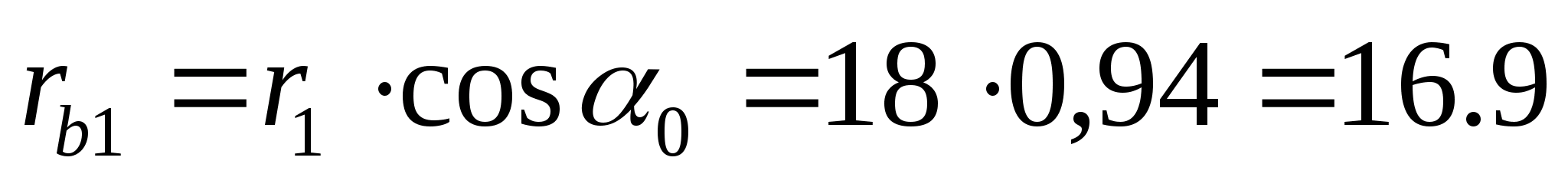 мм
мм
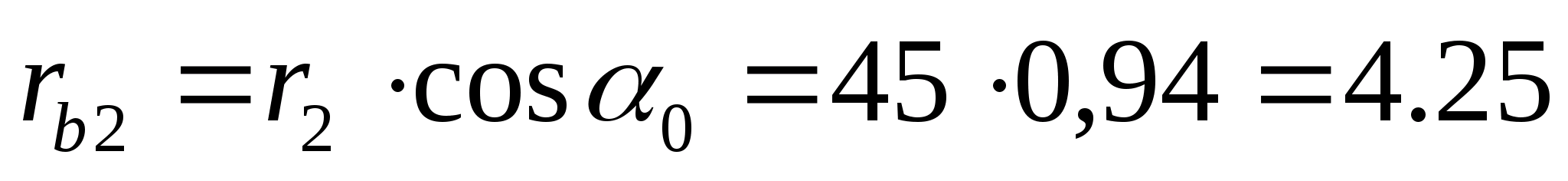 мм
мм
Определяем шаг по делительной окружности:
 мм
мм
Определяем шаг по нормали (шаг по основной окружности):
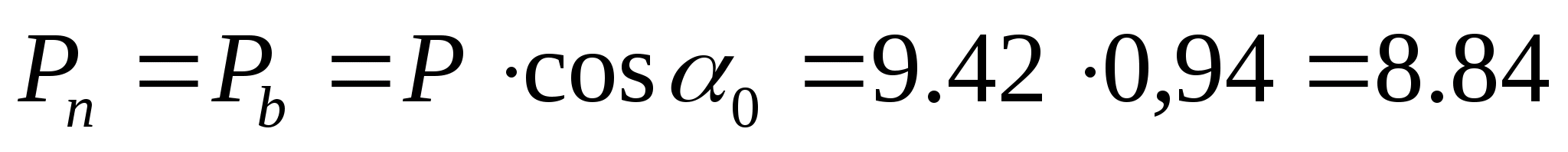 мм
мм
Определяем относительные смещения инструментальной рейки при нарезании зубчатых колес (из условия, что Z>1 >+ Z>2 >< 36):
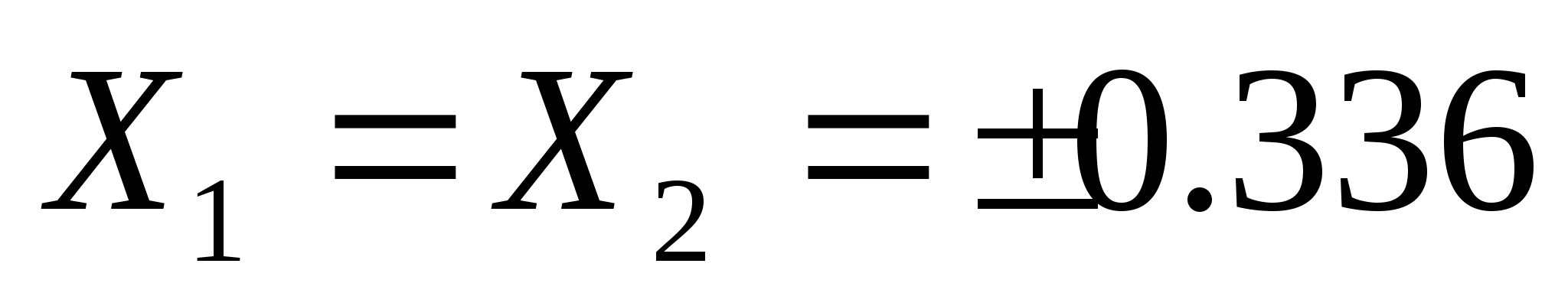
Определяем абсолютные сдвиги:
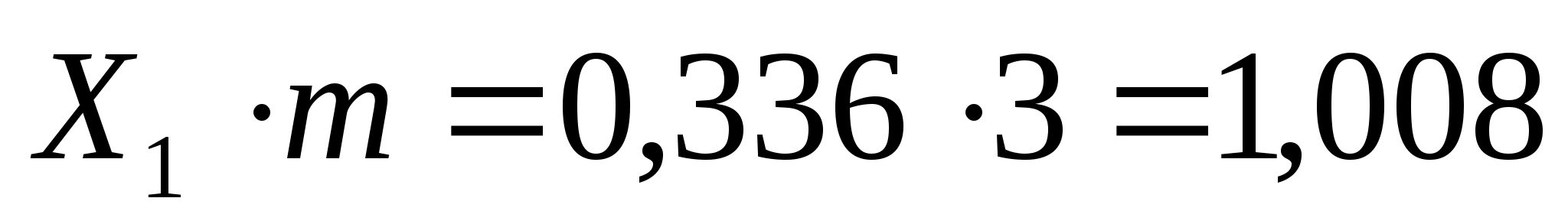 мм
мм
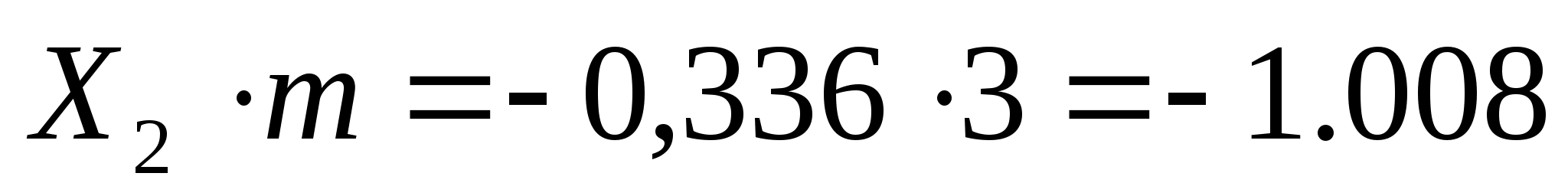 мм
мм
Определяем высоты ножек зубьев:
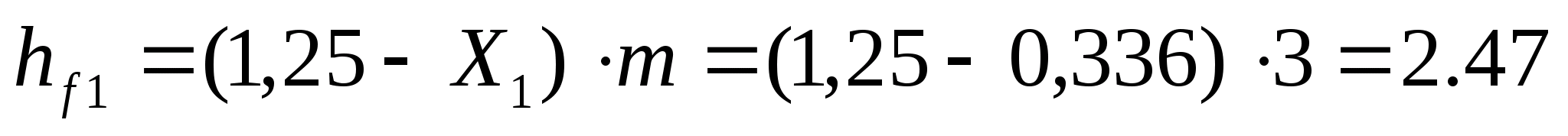 мм
мм
 мм
мм
Определяем толщину зубьев по делительным окружностям:
 мм
мм
 мм
мм
Определяем хорды, соответствующие шагам:
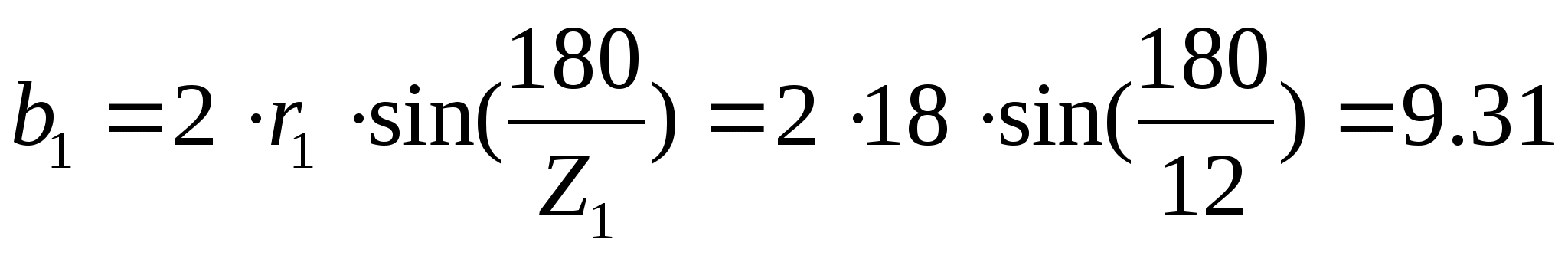 мм
мм
 мм
мм
Определяем угол зацепления в сборке:
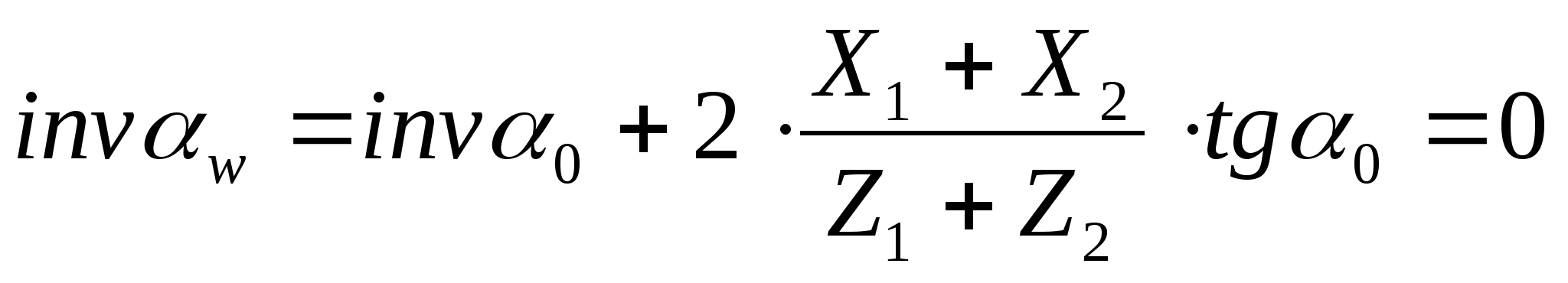

Определяем радиусы начальных окружностей:
 мм
мм
 мм
мм
Определяем межосевое расстояние:
 мм
мм
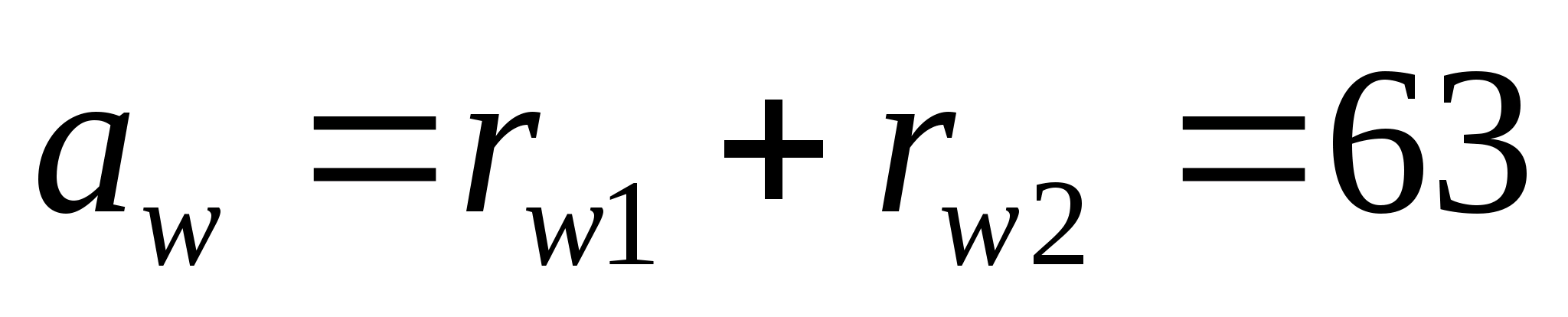 мм
мм
Приращение межосевого расстояния:

Определяем полную высоту зуба:
 мм
мм
Укорочение зуба:
 мм
мм
Определяем высоты головок зубьев:
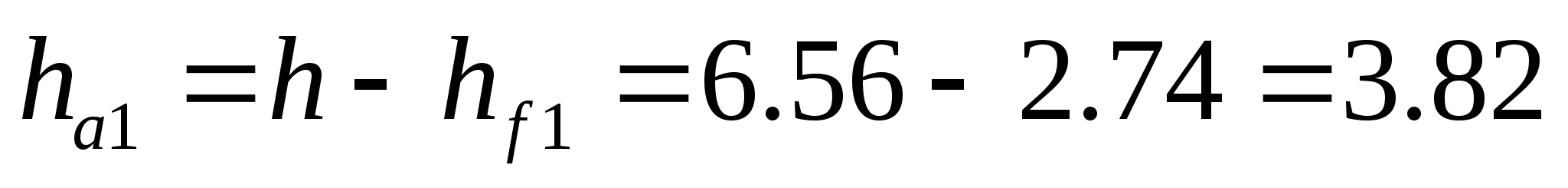 мм
мм
 мм
мм
Определяем радиусы окружностей вершин зубьев:
 мм
мм
 мм
мм
Определяем радиусы окружностей впадин:
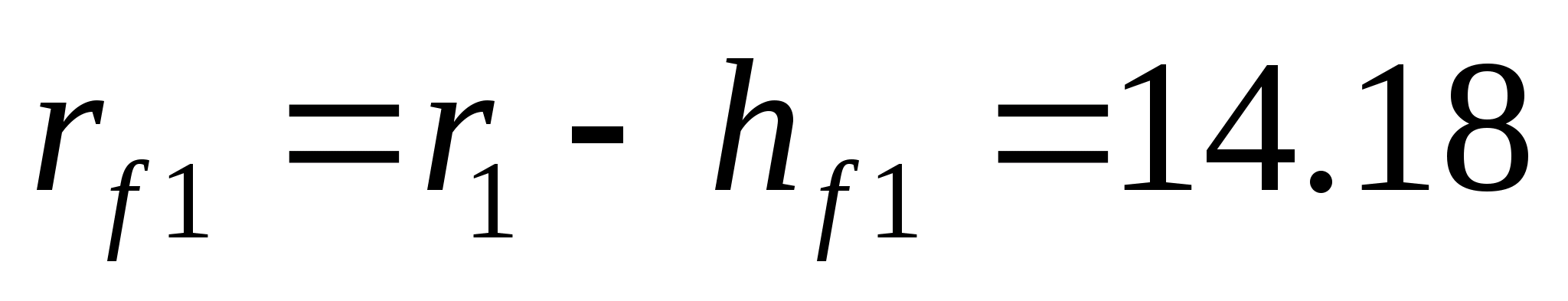 мм
мм
 мм
мм
Определяем коэффициент перекрытия:
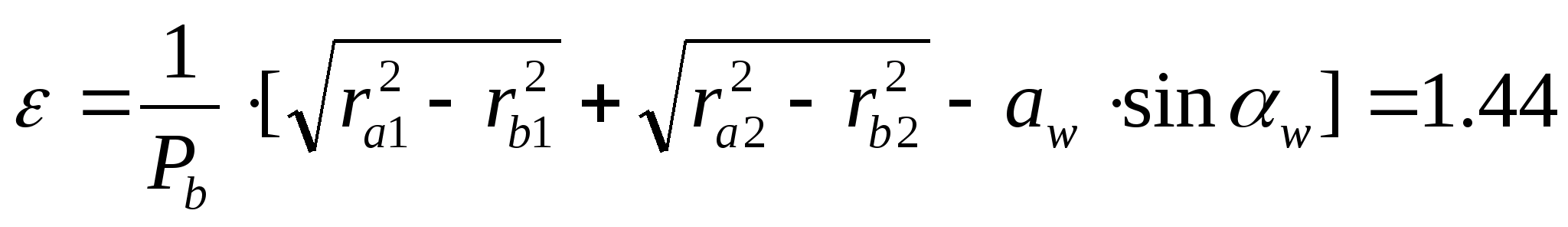
Масштабный коэффициент определяется по формуле:
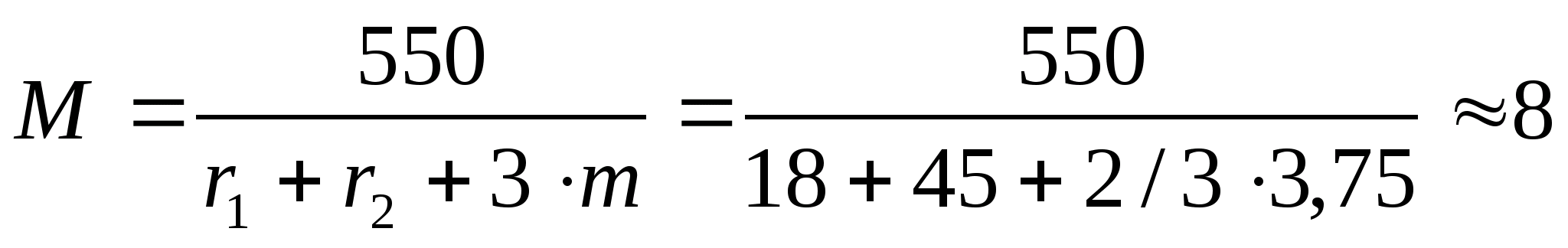
3.2 Построение картины зацепления пары зубчатых колес
Построение эвольвентного
зацепления выполняем в масштабе
 в следующей последовательности:
в следующей последовательности:
Проводим линию центров и
откладываем межосевое расстояние

Из точек О1 и O2
(центры вращения зубчатых колес) проводим
начальные окружности, которые должны
касаться друг друга на линии центров.
Точка касания – полюс зацепления (точка
Р). Через полюс зацепления проводим
общую касательную Т-Т и линию зацепления
N –N
(под углом
 к линии Т-Т).
к линии Т-Т).
Проводим основные окружности
радиусами
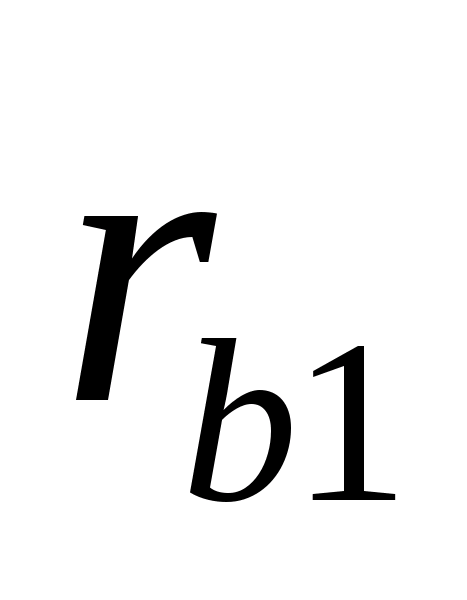 и
и
 ,
а также делительные, вершин и впадин.
Окружности
,
а также делительные, вершин и впадин.
Окружности
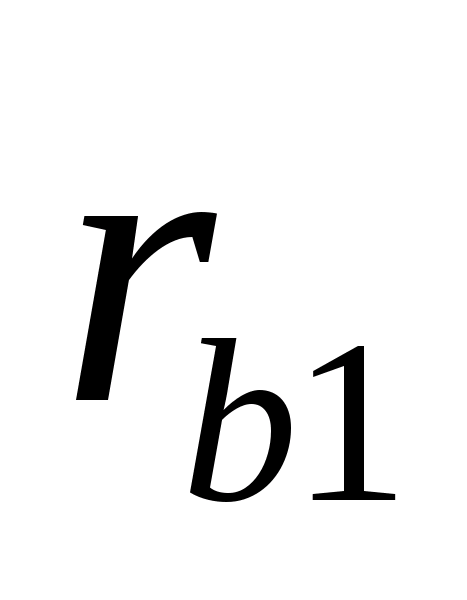 и
и
 должны касаться линии зацепления N-N. Из
центров колес О1 и O2
опускаем на линию зацепления N-N
перпендикуляры. Отрезок KL
– теоретическая линия зацепления.
должны касаться линии зацепления N-N. Из
центров колес О1 и O2
опускаем на линию зацепления N-N
перпендикуляры. Отрезок KL
– теоретическая линия зацепления.
Выполняем построение эвольвентного
профиля зуба. Не эвольвентная часть
зуба (от окружности впадин до основной
окружности) очерчивается сначала по
радиальной, а затем в месте сопряжения
ножки зуба с окружностью впадин делают
небольшое закругление радиусом
 .
.
Точки пересечения окружностей вершин с линией зацепления N-N дадут отрезок MF – практическую линию зацепления. Отложим от левого профиля зуба по делительной окружности расстояние, равное половине толщины зуба и найдем ось симметрии зуба. Проводим ось симметрии зуба и относительно этой оси строим вторую половинку профиля зуба.
Для построения второго и третьего зуба откладываем от оси симметрии первого зуба величину окружного шага по дуге делительной окружности. Выполняем построение второго и третьего зуба на каждом колесе.
Определяем рабочие участки профилей зубьев (показаны штриховкой).
Построение графиков удельного скольжения:
|
λ>1> |
-1.04 |
-0.46 |
0.116 |
0.482 |
|
λ>2> |
1 |
0.1 |
-0.9 |
-5.51 |
Графическая часть проекта оформляется на листе 3
4. Динамический синтез кулачкового механизма
Число оборотов кулачкового вала в минуту

Определяем время одного полного оборота кулачкового вала:
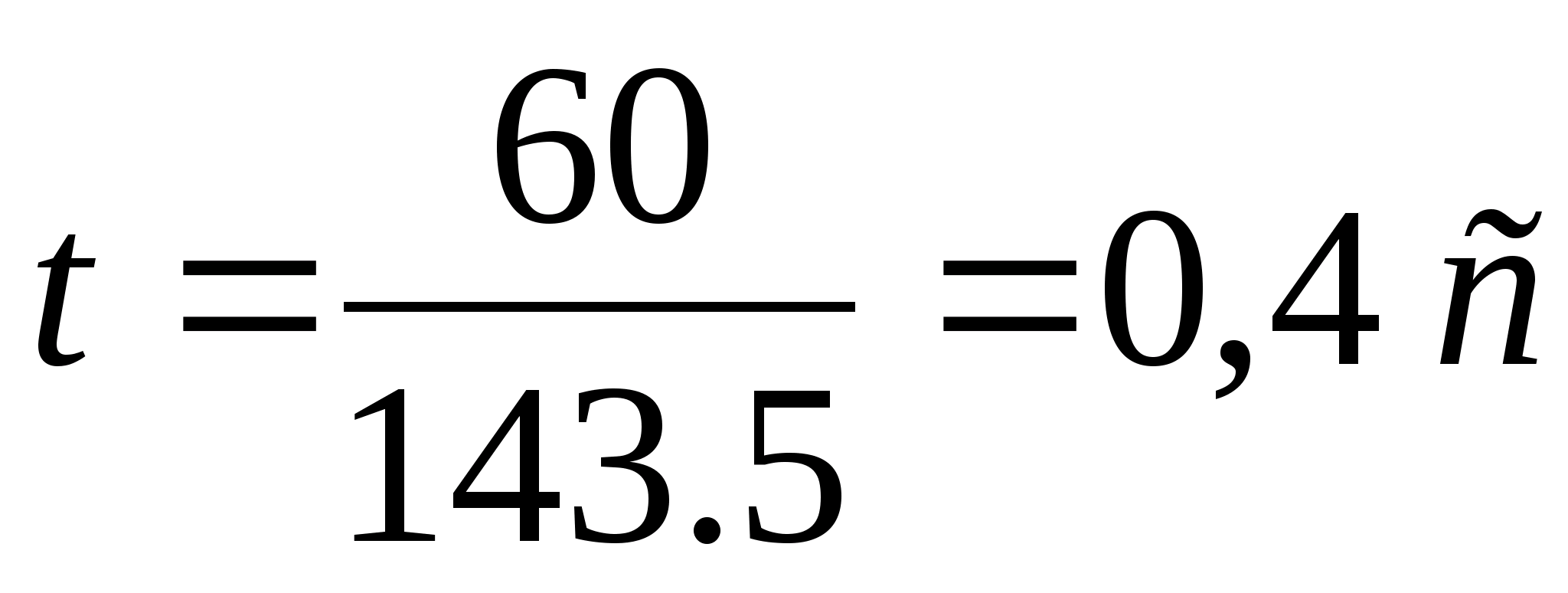
Откладываем на оси абсцисс время одного полного оборота кулачкового вала в виде отрезка длиной 360 мм и определяем масштабы:


Строим график изменения ускорения толкателя. Затем, используя метод графического интегрирования, последовательно строим графики изменения скорости и перемещения толкателя от угла поворота кулачка (
 ).
).
Определяем масштабы диаграмм изменения скорости и перемещения толкателя:
 ,
,
где h – высота подъема толкателя
hmax –
максимальная ордината на графике
перемещений



Определяем величину радиуса
базовой окружности кулачка в зависимости
от значения максимального угла давления
 Справа от диаграмм
Справа от диаграмм
 перпендикулярно
оси
перпендикулярно
оси
 проводим
прямую, на которой откладываем отрезок,
равный по величине ходу толкателя. Делим
его на отрезки, проходимые толкателем
при подъеме и опускании. Через эти точки
перпендикулярно вертикальной оси
проводим линии, на которых откладываем
отрезки определяемые из следующего
соотношения:
проводим
прямую, на которой откладываем отрезок,
равный по величине ходу толкателя. Делим
его на отрезки, проходимые толкателем
при подъеме и опускании. Через эти точки
перпендикулярно вертикальной оси
проводим линии, на которых откладываем
отрезки определяемые из следующего
соотношения:
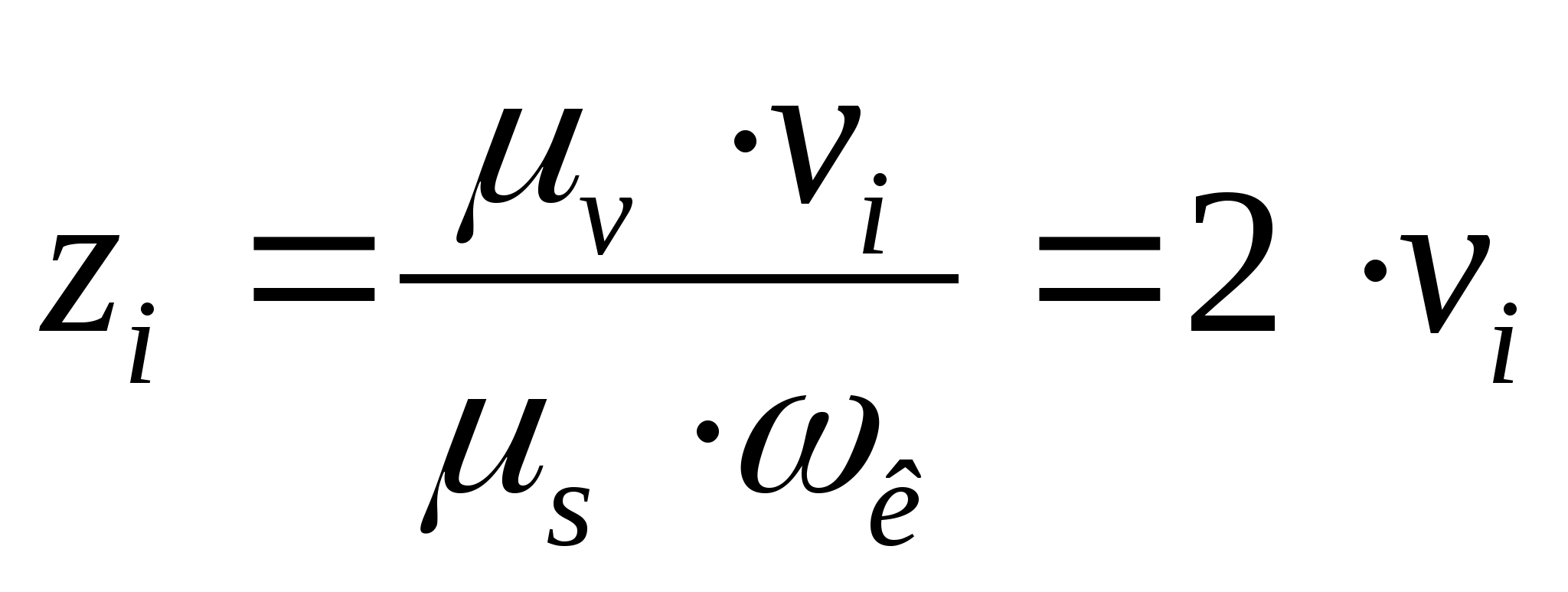
где
 -
ордината, взятая с графика изменения
скорости толкателя
-
ордината, взятая с графика изменения
скорости толкателя
|
Z>0> |
Z>1> |
Z>2> |
Z>3> |
Z>4> |
Z>5> |
Z>6> |
Z>7> |
Z>8> |
|
Z>17> |
Z>16> |
Z>15> |
Z>14> |
Z>13> |
Z>12> |
Z>11> |
Z>10> |
Z>9> |
|
0 |
4.12 |
16.92 |
29.74 |
33.86 |
29.74 |
16.92 |
4.12 |
0 |
Полученные в результате построения
точки соединяем плавной кривой. Под
углом
 к
вертикальной оси проводим две прямые,
касательные к получившейся кривой.
Заштрихованная область между касательными
прямыми – область в которой должен
находиться центр вращения кулачка. С
учетом эксцентриситета принимаем
максимальное значение радиуса
к
вертикальной оси проводим две прямые,
касательные к получившейся кривой.
Заштрихованная область между касательными
прямыми – область в которой должен
находиться центр вращения кулачка. С
учетом эксцентриситета принимаем
максимальное значение радиуса
C учетом масштаба величина радиуса базовой окружности кулачка будет:

Графическая часть проекта оформляется на листе 4.
Литература
Кореняко А.С., Кременштейн Л.И., Петровский С.Д. Курсовое проектирование по теории механизмов и машин. М.–Л: Машиностроение. 1964. – 324 с.
Попов С.А. Курсовое проектирование по теории механизмов и механике машин. М: Высшая школа 1986. – 295 с.