Загальні поняття про якість виробів та основні її показники

Загальні поняття про якість виробів та її основних показників

1. Загальні поняття про якість виробів, показники якості

Якість машин, що виготовляються, має велике народногосподарське значення. Від неї суттєво залежить економічна ефективність використання нової техніки в різних галузях промисловості і народному господарстві.

Якість машин закладається в їх конструкцію при проектно-конструкторських розробках, забезпечується на заданому рівні у виробництві і підтримується протягом певного часу в експлуатації.

За державним стандартом під якістю промислової продукції розуміють сукупність властивостей, що обумовлюють її придатність задовольняти певні потреби у відповідності з її призначенням.

Якість машин характеризується системою показників, на кожен з яких має бути встановлена кількісна величина з допуском на її відхилення, яка б забезпечувала економічність виконання машиною її службового призначення.

Система якісних показників зі встановленими на них кількісними даними і допусками, які описують службове призначення машини, отримали назву технічних умов та норм точності на приймання готової машини.

До найбільш важливих показників якості відносять експлуатаційні показники: технічний рівень машини, її надійність, ергономічність та естетичні характеристики.

Технічний рівень (потужність, ККД, продуктивність, точність роботи, ступінь автоматизації, економічність та ін.) визначає ступінь досконалості машини. Її можна оцінити в абсолютних і відносних одиницях.

Ці показники використовують при порівнянні якості машин, що виготовляються, з кращими вітчизняними та зарубіжними зразками. В деяких випадках застосовують інтегрований (комплексний) показник. Він може, зокрема, відображати відношення загального корисного ефекту від експлуатації машини до сумарних витрат на її створення та експлуатацію.

Технічний рівень машини залежить не тільки від її конструкції, але й від технології її виготовлення.

Надійність є комплексним показником, який включає безвідмовність, довговічність, ремонтопридатність, а також властивість машини зберігати справний і працездатний стан протягом певного проміжку часу. Надійність машини суттєво залежить від технології її виготовлення, яка впливає на естетичні характеристики машини (її загальний вигляд, оформлення), а деякою мірою й на її ергономічні характеристики.

Крім експлуатаційних показників якості машини, надійність оцінюється системою виробничо-технологічних показників, які характеризують ефективність конструктивних рішень з точки зору забезпечення оптимальних затрат праці та коштів на виготовлення виробу, його технічне обслуговування та ремонт. До цих показників відносять: трудомісткість, верстатомісткість, виробничий цикл, конструктивну та технологічну спадкоємність виробу та ін.

Економічні показники якості машини (капіталовкладення у виробництво та експлуатацію машини, собівартість виготовлення машини і собівартість одиниці продукції, що виготовляється машиною) також суттєво залежать від технології виготовлення машини.

Кожен з перелічених основних показників відносно того чи іншого типу машини конкретизується у вигляді цілої системи додаткових якісних і кількісних показників, які характеризують особливості машини даного типу і призначені для виконання даного службового призначення.

Технічними умовами ставиться задача, яку потрібно розв’язати машинобудівному підприємству як в процесі конструювання машини, так і під час її виготовлення. Правильне та чітке формулювання задачі деякою мірою зумовлює успіх найбільш швидкого та економічного її розв’язання.

Отже, розробка якісних і кількісних показників технічних умов є однією з найбільш відповідальних задач, оскільки від її правильного розв’язання залежить якість та економічність виконання машиною службового призначення, швидкість освоєння та економічність виготовлення. На найбільш поширену промислову продукцію технічні умови і стандарти розробляються і затверджуються на державному рівні. Як приклади можна навести стандарти на електродвигуни, автомобілі, верстати, підшипники та ін.

Показником якості машин, досягнення та забезпечення якого викликає найбільші труднощі і затрати в процесі створення і особливо в процесі виготовлення машин, є точність машин. Встановлення необхідної точності та технологічне забезпечення її у виробничих умовах є відповідальною задачею конструктора виробу і технолога.

2. Загальні поняття про точність деталей та точність машин

2.1 Точність деталі

Під точністю деталі розуміють ступінь її наближення до геометрично правильного її прототипу.

Виготовити будь-яку деталь абсолютно точно, тобто у повній відповідності її з геометричним представленням, практично неможливо, тому за міру точності приймають величини відхилень від теоретичних значень. Ці відхилення після їх вимірювання порівнюють з відхиленнями, які допускаються службовим призначенням деталі в машині. Отже, по всіх показниках якості деталі, що характеризують її службове призначення, необхідно встановлювати допустимі відхилення чи допуски.

Допуск – це найбільше значення похибки, при якій деталь ще задовольняє своє службове призначення.

Точність деталі характеризують наступні основні показники:

1. Точність відстані між якими-небудь її двома поверхнями, чи точність розмірів поверхні деталі, що надають їй ті чи інші геометричні форми (наприклад, діаметр і довжина циліндричної поверхні).

Точність повороту (взаємного положення) однієї поверхні відносно іншої, вибраної за базу. Оскільки деталь представляє собою просторове тіло, то точність повороту (відносного положення) однієї поверхні відносно іншої звичайно розглядають в двох перпендикулярних координатних площинах.

Під точністю повороту (взаємного положення) розуміють величину відхилення від потрібного кутового положення однієї поверхні відносно іншої в кожній з двох координатних площин.

3. Точність геометричних форм поверхонь деталі чи правильність геометричних форм. Під цим розуміють найбільше наближення кожної з поверхонь деталі до її геометричного представлення.

З викладеного можна зробити висновок, що деталь вважається точно обробленою (точною), якщо похибка відповідного параметра не перевищує допуск на нього, тобто:

Δ>p>  T>p>; Δ>n>  T>n>; Δ>ф>  T>ф>,

де Δ>p>, Δ>п>, Δ>ф> – фактичне відхилення відповідно розмірів, поворотів (взаємного положення), форми;

T>p>, T>п>, T>ф >– допуски відповідно розмірів, поворотів (взаємного положення), форми.

2.2 Точність машини

Розглянуті вище показники, що характеризують точність деталі, використовуються і для характеристики точності машини. Різниця полягає тільки в тому, що у деталі всі показники точності відносяться до поверхонь однієї даної деталі, у машини ж вони відносяться до виконавчих поверхонь, які належать різним зв’язаним одна з одною деталям машини.

Оскільки виконавчі поверхні машини повинні здійснювати відносний рух, необхідний для виконання її службового призначення, тому одним з основних показників, що характеризує точність машини, є точність відносного руху виконавчих поверхонь.

Під точністю відносного руху приймається максимальне наближення дійсного характеру руху виконавчих поверхонь до теоретичного закону руху, вибраному виходячи із службового призначення машини.

Точність відносного руху характеризується величиною належного відхилення, на яке відповідно з викладеним раніше, повинен встановлюватись (як і на інші показники точності) допуск.

Виходячи з викладеного вище, точність машини характеризується такими основними показниками:

1) точність відносного руху виконавчих поверхонь машини;

2) точність відстаней між виконавчими поверхнями чи замінюючими їх сполученнями та їх розмірів;

3) точністю відносних поворотів виконавчих поверхонь;

4) точністю геометричних форм виконавчих поверхонь (включаючи макрогеометрію та хвилястість);

5) шорсткістю виконавчих поверхонь.

2.3 Встановлення оптимальних допусків

Встановлення заданої точності є відповідальним етапом роботи конструктора. Вона встановлюється на основі аналізу умов роботи машини із врахуванням економіки її виготовлення і наступної експлуатації. Задача розв’язується на базі теоретичних та експериментальних даних із врахуванням досвіду експлуатації машин аналогічного типу.

В залежності від того, які вимоги необхідно витримати, підхід до забезпечення точності може бути різним. У простіших випадках необхідну точність знаходять на основі геометричного аналізу і розрахунку розмірних ланцюгів виробу. Для швидкохідних машин розрахунки потрібно проводити із врахуванням динамічних явищ. Для рухомих з’єднань необхідно врахувати умови змащування контактуючих поверхонь, а для з’єднань з гарантованим натягом обов’язкова перевірка за силами зсуву і моментами. Враховують також теплові явища, вимоги взаємозамінності, якість поверхонь спряжених деталей, умови складання та ремонту, допустиме зношування, яке визначає тривалість роботи машини до ремонту. Проте надто висока точність підвищує витрати при виробництві машин і мало підвищує їх функціональні якості. При жорстких допусках, тобто з підвищенням точності виготовлення машини, зростає трудомісткість та собівартість її виготовлення.

Для кожного конкретного випадку допуски на всі показники якості машини повинні встановлюватись на основі техніко-економічних розрахунків, які повинні мати на увазі досягнення найменших затрат суспільно необхідної праці на вирішення задач, для виконання яких створюється машина.

При цьому не треба забувати, що засоби виробництва безперервно розвиваються і удосконалюються, внаслідок чого, з одного боку, безперервно зростають вимоги до якості машин, а з іншого – створюється можливість забезпечення підвищення якості з найменшими затратами праці і коштів.

Допуски на всі показники точності машини, які встановлені виходячи із її службового призначення, поділяють звичайно на дві складові: першу, яку використовують при виготовленні машини, і другу, яку залишають на зношування машини під час її експлуатації.

Складові допусків, що призначені на виготовлення машини, прийнято називати допусками на приймання готової машини в робочому стані. Ці складові допусків, в свою чергу, також доводиться ділити на декілька нерівних частин, що робиться для компенсації відхилень, які виникають внаслідок:

1) використання наближених, замість точних, законів відносного руху виконавчих поверхонь машини, а також застосування через недостатність знань наближених методів розрахунку;

2) недостатньої жорсткості самих деталей машини, які деформуються як під впливом діючих сил і коливань температури, так і внаслідок перерозподілу внутрішніх напружень;

3) недостатньої жорсткості стиків;

4) похибок регулювання та складання машини і виготовлення її деталей.

Останню частину допусків прийнято називати допусками на приймання готової машини без робочих навантажень. Цю частину також поділяють на: допуски на регулювання та складання машини і на допуски на виготовлення деталей.

Поділ допусків на виготовлення машини між їх складовими також необхідно здійснювати на основі техніко-економічних розрахунків, маючи на увазі найменші витрати суспільно необхідної праці на виготовлення машини.

2.4 Економічна та досяжна точність обробки

Розрізняють економічну та досяжну точність обробки.

Під економічною точністю механічної обробки розуміється середнє значення відхилень деталей від номіналу, що отримують при даному методі обробки за нормальних виробничих умов при найменших затратах.

Під нормальними виробничими умовами розуміють: справне устаткування, застосування необхідного різального і вимірювального інструмента, пристосувань належної якості, відповідність кваліфікації працівника і затрат часу виконуваній роботі.

Поняття економічної точності відносне, оскільки навіть незначна зміна виробничих умов може сильно впливати на неї.

Кожному методу обробки відповідає визначений діапазон квалітетів точності. Для чорнових операцій це, в першу чергу, пов’язано з точністю вихідної заготовки, для чистових – з умовами здійснення обробки.

Точність форми і взаємного розміщення поверхонь суттєво залежить від типу устаткування, на якому обробляються деталі, а також від методу координації інструменту.

Дані з економічної точності обробки при різних її видах наведені в [2, табл.11–13].

У зв’язку з відмінністю розмірів, форми і твердості оброблюваних заготовок, стану верстатів, режимів роботи та інших технологічних факторів таблиці дають середні значення економічної точності обробки.

Точність, яку можна досягти за особливо сприятливих умов для даного виробництва називають досяжною точністю обробки.

Точність необхідно знати технологу, щоб призначити необхідні методи обробки.

В серійному і масовому виробництві застосовують економічну точність, тільки в умовах одиничного виробництва (за відсутності належного устаткування) технолог може орієнтуватись на досяжну точність обробки. Наприклад, в умовах малого підприємства, за відсутності круглошліфувального верстата, можна обробку шийок під підшипники на валу (7 квалітет точності) проектувати на токарному верстаті. В цьому випадку досягнення цього високого кінцевого результату буде забезпечене тільки високою кваліфікацією та старанням робітника.

2.5 Методи досягнення заданої точності розміру деталі

Необхідна точність розміру при обробці деталі може бути досягнута наступними методами.

1. Методом пробних робочих ходів:

– встановити та вивірити заготовку;

– послідовно знімати пробні стружки та замірювати одержані розміри, і так продовжувати до одержання необхідного результату.

Метод трудомісткий, застосовується в одиничному та дрібносерійному виробництвах.

Методом автоматичного одержання заданого розміру.

Суть методу полягає в тому, що партію заготовок обробляють на попередньо настроєному верстаті зі встановленням заготовок у пристроях без вивірення їх положення, а різальний інструмент при налагодженні верстата встановлюють на визначений розмір, який називається настроювальним. Одержання заданого розміру досягають за один робочий хід, тобто при однократній обробці. Цей метод більш продуктивний, ніж метод пробних ходів, але потребує спеціальних пристроїв і більш стабільних за розмірами вихідних заготовок.

Обробку методом автоматичного одержання заданих розмірів широко застосовують в серійному і масовому виробництвах.

В обох розглянутих методах на точність обробки впливають суб’єктивні фактори – кваліфікація робітника: при першому методі цей вплив проявляється на точності встановлення та вивірення заготовки і на точності встановлення інструмента, при другому методі – на точності встановлення інструмента і пристрою в процесі налагодження верстата перед обробкою партії заготовок.

2.6 Точність складання

При складанні машин можуть проявитись похибки взаємного розташування їх елементів, неякісні спряження, а також деформації з’єднуваних деталей. Похибки погіршують функціональні характеристики машин.

Похибки складання викликаються:

1) відхиленнями розмірів, форми і взаємного розташування поверхонь сполучуваних деталей; ці відхилення впливають на зазори і натяги (змінюючи задані посадки), викликають радіальне і торцеве биття при складанні обертаючих частин, неспіввісність та інші похибки взаємного положення елементів машини;

2) неякісною обробкою сполучуваних поверхонь, в результаті чого виникає їх нещільне прилягання, зниження контактної жорсткості стиків і герметичності з’єднань;

3) неточним встановленням та фіксацією елементів машини в процесі її складання;

4) неякісним припасуванням і регулюванням сполучуваних елементів машини;

5) порушенням умов і режимів виконання складальних операцій (нерівномірне затягнення нарізних з’єднань, що викликає перекоси і деформації складуваних елементів, перекоси й деформації при запресуванні та інших видах з’єднань, деформація при закріпленні деталей в складальних пристроях);

6) геометричними неточностями складального обладнання, пристроїв та інструментів;

7) неточним налагодженням складального обладнання;

8) тепловими деформаціями елементів технологічної системи (складальне обладнання – пристрій – інструмент – складуваний об’єкт).

Похибки складання можуть виникати також в результаті деформації сполучуваних деталей від дії залишкових напружень в їх матеріалі. Нетехнологічні конструкції виробів утруднюють отримання заданої точності.

Необхідна точність сполучення деталей при складанні забезпечується методами повної, неповної (часткової) та групової взаємозамінності, а також регулюванням та індивідуальним припасуванням.

При складанні методом повної взаємозамінності відбувається лише з’єднання сполучуваних деталей і частин виробу, що забезпечує організацію потокової роботи, можливість кооперування виробництва, спрощує забезпечення запасними частинами і ремонт машин, що знаходяться в експлуатації.

При складанні методом неповної (часткової) взаємозамінності допуски на розміри сполучуваних деталей беруться більшими, ніж у випадку складання методом повної взаємозамінності. Потрібна точність замикальної ланки досягається не у всіх складуваних об’єктів. В основі методу лежить положення теорії ймовірності, за яким граничні величини ланок розмірного ланцюга зустрічаються рідше, ніж середнє. Тому відсоток виробів, у яких величина замикальної ланки виходить за межі потрібного допуску, незначний.

В тих випадках, коли конструктивні допуски менші за технологічні (економічно доцільні), застосовують метод групової взаємозамінності.

Складання методом регулювання полягає в тому, що потрібна точність замикальної ланки досягається шляхом зміни величини заздалегідь вибраної компенсуючої ланки без зняття з неї шару матеріалу.

Деталі, шляхом зміни положення яких досягається потрібна точність замикальної ланки, отримали назву рухомих компенсаторів (рис. 1).

Рис. 1. Схема досягнення точності замикальної ланки методом регулювання з використанням рухомого компенсатора

Спеціальні деталі належних розмірів чи з потрібним відносним поворотом їх поверхонь (з потрібними кутовими відхиленнями), що вводяться в розмірний ланцюг з тією ж метою, називають нерухомими компенсаторами (рис. 2).

Складання методом індивідуального припасування полягає в тому, що задану точність сполучення досягають шляхом індивідуального припасування однієї зі сполучуваних деталей до іншої.

Припасування виконують обпилюванням, шабренням, притиранням, а також спільною обробкою сполучуваних поверхонь (розточування чи розвертання отворів для забезпечення їх співвісності).

Вибір того чи іншого методу забезпечення точності визначається аналізом розмірних ланцюгів виробу, що складається. Ця задача розв’язується конструктором. В кресленнях виробу повинен бути відображений і прийнятий метод його складання.

Рис. Схема досягнення точності методом регулювання з використанням нерухомого компенсатора

Розмірні ланцюги, в залежності від методу складання, розраховують двома методами, а саме: методом максимуму-мінімуму та ймовірнісним методом. Обидва методи розрахунку розмірних ланцюгів з розв’язанням прямих і обернених задач наведені у державному стандарті.

3. Контроль якості машин

3.1 Поняття про контроль точності машин та їх вузлів

Контроль, якому піддаються кожен вузол і кожна машина, має за мету перевірити відповідність форми, відносного положення і переміщення їх виконавчих поверхонь встановленим нормам.

Ефективність будь-якого контролю тим вища, чим ближчі результати вимірювань параметрів, що контролюються, до їх дійсних значень.

Ступінь наближення виміряного значення до дійсного залежить від наступних факторів:

– розкриття суті параметра, що контролюється, і явищ, що породжують виникнення похибок;

– правильності виявлення взаємозв’язку різних параметрів та вміння відокремити параметр, що контролюється;

– правильності вибору чи розробки засобів контролю;

– техніки здійснення контролю.

Правильна і чітка термінологія розкриває суть параметра, що контролюється. Основні терміни, що характеризують відхилення форми, відносне положення і переміщення поверхонь деталей, встановлені державними стандартами.

Проте, для успішного здійснення контролю ще недостатньо розуміти суть параметра, що контролюється. Необхідно бачити і враховувати взаємозв’язок параметра, що контролюється, з іншими параметрами, що впливають на точність машини. Наприклад, точність визначення відстані між двома плоскими поверхнями деталі залежить від точності повороту (взаємного положення) і форми цих поверхонь. Тому, в першу чергу, необхідно контролювати форму, потім – поворот, і в останню чергу – відстань між плоскими поверхнями.

Згідно визначення державного стандарту, радіальне биття є результатом спільного прояву відхилення від циліндричності поверхні та неспівпадання осі поверхні, що контролюється, з віссю обертання деталі. Це неспівпадання складається з відносного зміщення і повороту осей 1 і 2 у просторі (рис. 3). Тому робити висновок про радіальне биття будь-якої поверхні деталі можна не взагалі, а лише відносно до перерізу, в якому здійснюється контроль.

Рис. 3. Неспіввісність шийок вала у двох координатних площинах

Щоб отримати при контролі найбільш повне уявлення про значення параметра, що контролюється, необхідно виключити, наскільки це можливо, вплив похибок взаємозв’язаних з ним параметрів. Наприклад, співвісність переднього і заднього центрів токарного верстата звичайно перевіряють за допомогою оправки, закріпленої в центрах. Переміщуючи вздовж по оправці розташовані в двох координатних площинах і встановлені на супорті індикатори, роблять висновки про величину і напрямок відхилення від співвісності центрів (рис. 4, а). Але аналогічні покази можуть дати індикатори за наявності повороту осі оправки відносно напрямних станини при абсолютній співвісності центрів (рис. 4, б). Тому, перш ніж приступати до перевірки співпадання осей центрів у передній і задній бабках токарного верстата, необхідно забезпечити паралельність осей отворів під центри в шпинделі і пінолі в більш жорстких межах у порівнянні з допустимим відхиленням від співвісності центрів.

Контроль деяких параметрів потребує матеріалізації геометричних представлень (наприклад, відстань між осями двох отворів, відхилення від площинності поверхні деталі).

а) б)

Рис. 4. Перевірка співвісності центрів токарного верстата за допомогою оправки l – довжина вимірювання; γ – різниця показів індикаторів

Геометричні представлення матеріалізують за допомогою спеціальних деталей або пристосувань (оправки, контрольні плити тощо).

Оскільки все це пов’язано із введенням у вимірювальні розмірні ланцюги додаткових ланок, які мають похибки, то велике значення має власна точність всіх деталей і пристосувань, що використовують при перевірках, а також точність їх встановлення. За цих умов вважається допустимою похибка розпізнання параметра, що контролюється, яка не перевищує 10…20 % його поля допуску.

3.2 Випробовування машин

Метою випробовування машин є перевірка правильності роботи і взаємодії всіх механізмів машини, перевірка її потужності, продуктивності та точності. Таким чином, випробовування машини є перевіркою якості машини, одержаної в результаті всього виробничого процесу її виготовлення.

В залежності від виду, призначення та масштабу випуску машини проходять випробування на холостому ходу (перевірка роботи механізмів і паспортних даних) і в роботі під навантаженням, а також випробовування на продуктивність, жорсткість, потужність та точність.

Випробовування на холостому ходу. При цьому випробовуванні перевіряють всі включення і переключення органів керування та механізмів машини, правильність їх взаємодії та надійність блокування, безвідмовність дії та точність роботи автоматичних пристосувань. Разом з тим перевіряють додержання норм правильності роботи підшипників, зубчастих коліс.

Випробовування машин під навантаженням повинні виявити якість її роботи у виробничих умовах, близьких до умов експлуатації. Під навантаженням на певних режимах, що встановлюються технічними умовами або правилами, випробовують всі машини.

Випробовуванню на продуктивність піддають звичайно не всі машини, а лише машини спеціального призначення та дослідні зразки. В процесі випробовування виявляють, чи відповідає продуктивність виготовленої машини вимогам замовлення, чи має машина потрібну швидкість.

Випробовування на жорсткість. На жорсткість випробовують головним чином верстати. В наш час норми жорсткості та методи випробовування широкого кола верстатів стандартизовані.

Випробовування на потужність. Цим випробовуванням піддають всі машини при одиничному виробництві і всі або вибірково машини, виготовлені серійно. Не випробовують на потужність машини простої конструкції, а також машини, що заздалегідь мають великий запас потужності.

Мета випробовування машини на потужність – визначити її коефіцієнт корисної дії при максимально допустимому навантаженні. Навантаження машині створюють за допомогою спеціальних гальмівних пристосувань, які відтворюють максимальні сили, що виникають при експлуатації машини.

Випробовування на точність. На точність випробовують звичайно машини, які виробляють, сортують та контролюють продукцію (верстати, преси та ін.). Контроль машин на точність повинен дати заключну оцінку якості машини, її спроможності виробляти продукцію потрібної якості. Тому оцінку точності машини при проведенні випробовувань дають за результатами досягнення нею точності виконання роботи.

Для машин поширених типів (токарні, фрезерні та інші верстати) порядок проведення випробовувань на точність, зразки деталей, що виготовляються, і точність обробки зразків регламентовані державними стандартами.

Для оригінальних машин програму і режими випробовувань розробляють в залежності від їх призначення, конструкції та потрібної точності.

4. Розсіювання характеристик якості

При розгляді цього пункту і далі прийняті наступні позначення:

X – ім’я випадкової величини;

– середньоарифметичне значення X;

x – можливі значення випадкової величини X;

x>j> – поточне значення незгрупованих значень X;

x>i> – середина інтервалу (за наявності згрупованих даних);

N – генеральна сукупність спостережень (вимірювань);

n – обсяг вибірки (число деталей у вибірці);

m>i> – частота (кількість деталей, що мають однакове значення вимірюваного параметра);

– частість;

f – число інтервалів;

Y – значення ординати теоретичної кривої розсіяння (Y = m>1> – частота, що відповідає x);

S – емпіричне середнє квадратичне відхилення випадкової величини;

 – середнє квадратичне відхилення випадкової величини;

2 – дисперсія випадкової величини;

e – основа натурального логарифму e = 2,7128;

 = 3,14.

Випадкова величина (випадкова похибка) – це змінна величина, яка в результаті досліджень (випробовувань) може прийняти те чи інше значення в межах певного інтервалу (на певний момент її значення і напрямок невідомі).

Систематична постійна похибка – це така похибка, значення і напрямок якої можна визначити вимірюванням. Систематична змінна похибка – це похибка, значення і напрямок якої можна визначити за законом згідно з яким вона змінюється.

4.1 Загальні поняття про розсіювання характеристик якості виробів

При протіканні будь-якого технологічного процесу на нього впливає велика кількість різноманітних факторів. Наприклад, при обробці заготовок на верстаті беруть участь верстат, пристрій для встановлення та закріплення заготовки і різального інструмента, самі оброблювані заготовки, робітник, середовище тощо.

В силу ряду причин всі ці фактори безперервно змінюються, в результаті чого виникають випадкові похибки які змінюють і всі показники кінцевого результату технологічного процесу.

Тому незважаючи на те, що вироби виготовлені за допомогою одного й того ж технологічного процесу, всі вони відрізняються один від одного і від розрахункового прототипу по всіх характеристиках якості. Це явище одержало назву розсіяння характеристик якості виробів.

Сукупність значень істинних розмірів заготовок, оброблених за незмінних умов і розташованих у зростаючому порядку із вказанням частоти повторення цих розмірів, називається розподілом розмірів заготовок.

За різних умов обробки заготовок розсіяння їх істинних розмірів підкоряється різним математичним законам.

В технології машинобудування велике практичне значення мають наступні закони: нормального розподілу (закон Гаусса); рівної ймовірності; трикутника (Сімпсона); ексцентриситету (Релея) і функції розподілу, що представляють собою композиції цих законів.

4.2 Закон нормального розподілу (Закон Гаусса)

Експериментально встановлено, що у більшості випадків при стійкому процесі механічної обробки заготовок на налагоджених верстатах з точністю 8–10 квалітетів і грубіше та за відсутності змінюваних в часі систематичних похибок точність обробки підкоряється закону нормального розподілу, який зображується кривою Гаусса, рівняння якої має вигляд:

.

Графічно закон нормального розподілу (закон Гаусса) зображується у вигляді кривої горбоподібного типу (рис. 5), гілки якої входять у + ∞ та – ∞, асимптотично наближуючись до осі абсцис.

Рис. 5. Крива нормального розподілу (закон Гаусса)

Закон нормального розподілу характеризується двома параметрами:  і . Параметр  є мірою розсіювання випадкової величини Х. Зі збільшенням  крива розподілу стає більш пологою, а її гілки розсовуються ширше, зі зменшенням  крива нормального розподілу робиться більш витягнутою, а її гілки зближуються (рис. 6).

 приблизно, за результатами вимірювань, розраховується за формулою:

.(2)

Рис. 6. Вплив середнього квадратичного відхилення на форму кривої нормального розподілу

Параметр є мірою положення кривої нормального розподілу відносно осі ординат. Зі збільшенням криві розподілу зсуваються вправо, зі зменшенням – вліво (рис. 7).

Рис. 7. Вплив на положення кривої розподілу відносно початку координат

визначається за формулою:

,

або при розподілі згрупованих даних за f-інтервалами:

.(3)

Оскільки гілки кривої нормального розподілу прямують до нескінченності, то поле розсіяння випадкової величини Х дорівнює нескінченності. З віддаленням значень х від ймовірність отриманих результатів їх зменшується і доходить до надто малих значень. При малих ймовірностях подія здійснюється рідко і, отже, значеннями х можна знехтувати. Тому для практичного використання кривої нормального розподілу її абсцису виражають через  і обмежують поле розсіяння значень х межами х ± t, тобто практичне поле розсіяння випадкової величини приймають рівним (рис. 5):

,(4)

де – нормований параметр розподілу.(5)

Значення t вибирається в залежності від прийнятої ймовірності Р знаходження значень x в межах поля розсіяння Δ>p> та ймовірності q = 1 – p виходу значень x за межі Δ>p> Вибір значень t провадять за відповідними таблицями, які додаються до курсу математичної статистики.

Найчастіше приймають t = 3. Цьому значенню відповідає ймовірність Р = 0,9973 і q = 0,0027. Отже, при t = 3,99,73 % всіх можливих значень х буде лежати в межах поля розсіювання, рівного Δ>p> = 6, і тільки 0,27 % значень вийде за його межі. Цей відсоток настільки малий, що значеннями , які виходять за межі Δ>p> = 6, можна знехтувати і практично вважати, що всі значення лежать в межах поля розсіювання.

Часто на практиці спочатку будують емпіричну криву розподілу, де емпіричне середнє квадратичне відхилення визначається за формулою (2), а потім визначається  за формулою:

 = γS,(6)

де γ – коефіцієнт, який враховує похибку визначення  при малих розмірах партії вимірюваних заготовок.

Таблиця 1 Поправковий коефіцієнт γ [3]

N

25

30

40

50

60

70

75

80

90

100

200

γ

1,4

1,39

1,33

1,3

1,26

1,24

1,25

1,22

1,21

1,2

1,15

Нормальний закон розподілу спостерігається в тих випадках, коли досліджувана випадкова величина є результатом дії великої кількості різних факторів, причому всі фактори за інтенсивністю свого впливу діють однаково. Цьому закону підкоряється велика кількість безперервних величин: розміри деталей, оброблених на настроєних верстатах; маса заготовок і деталей машин; твердість та інші механічні властивості матеріалу; висота мікронерівностей на оброблених поверхнях; похибки вимірювань та деякі інші величини. У всіх перелічених випадках доводиться спостерігати невеликі відхилення від нормального закону.

4.3 Побудова кривої нормального розподілу

деталь машина обробка точність

1. Береться поточна вибірка із партії заготовок, оброблених підряд одна за одною за одних і тих же умов обробки на одному й тому ж верстаті. Для отримання достовірних результатів обсяг вибірки повинен бути в межах 1000  n  50.

Вимірюють всі заготовки за потрібним параметром інструментом зі шкалою з мінімальною ціною поділки. Ціну поділки вимірювального інструменту вибирають з умови:

де Т – допуск вимірюваного параметра.

За результатами вимірювань визначається різниця між найбільшим і найменшим розмірами, тобто:

w>p> = x>max> – x>min>.

3. Отримані значення параметра заготовок вибірки розбивають на f інтервалів. Ширина d інтервалу повинна не менше ніж у два рази перевищувати ціну поділки вимірювального інструменту (приладу): d  2с; d = Δ>p>/f.

Число інтервалів визначається за таблицею:

n

20–40

40–60

60–100

100

100–160

160–250

f

6

7

8

10

11

12

або за формулою:

f = 1 + 3,322 lg n.

4. Для кожного інтервалу розраховують частоту m>i> та частість m>i>/n і заносять їх у табл.

Таблиця 2 Розподіл розмірів заготовок

Інтервал, мм

Частота

Частість

20,00–20,05

20,05–20,10

20,10–20,15

20,15–20,20

20,20–20,25

20,25–20,30

20,30–20,35

2

11

19

28

22

15

3

0,02

0,11

0,19

0,28

0,22

0,15

0,03

Всього

n = ∑m = 100

∑m/n = 1

5. За даними табл. 2 будується графік (рис. 8). По осі абсцис відкладають інтервали розмірів у відповідністю з табл. , а по осі ординат – відповідні їм частоти m>i> або частості m>i>/n.

Рис. 8. Розподіл виміряних розмірів заготовок

В результаті побудови отримується ступінчаста лінія І, яка називається гістограмою розподілу. Якщо послідовно з’єднати між собою точки, що відповідають середині кожного інтервалу, то створюється ламана крива, яка називається емпіричною кривою розподілу, або полігоном розподілу. При значній кількості виміряних заготовок і великій кількості інтервалів розмірів ламана емпірична крива наближається за формою до плавної кривої, яка називається кривою розподілу.

За формою емпіричної кривої приймають гіпотезу про теоретичний закон розподілу досліджуваного параметра.

6. За прийнятою гіпотезою визначають основні параметри емпіричного розподілу.

7. На основі емпіричного розподілу та його параметрів порівнюють емпіричний розподіл з теоретичним, тобто визначають теоретичні частоти і будують теоретичну криву.

Приблизно можна вважати, що:

,(7)

де – теоретична частота;

d – ширина (ціна) інтервалу;

n – число вимірювань (число деталей у вибірці).

З рівняння (7) маємо:

.(8)

Якщо у вираз (8) підставити нормований параметр розподілу , то отримаємо:

.

Позначимо і враховуючи, що  = S, формула (8) набуде вигляду:

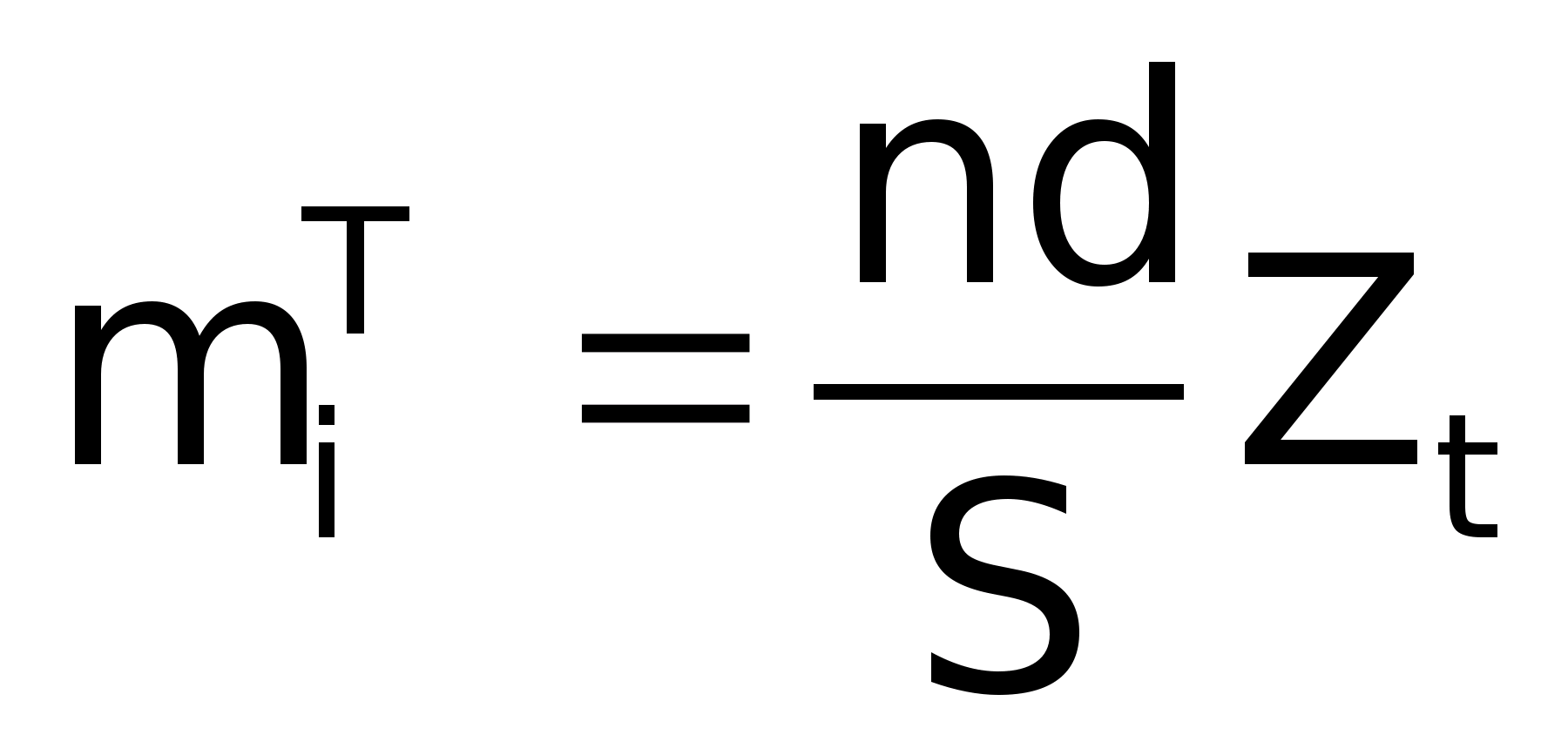.(9)

Величина Z>t> обчислена для різних значень t і наведена в [7, додаток 1].

Значення t для кожного інтервалу розмірів знаходять за формулою:

,(10)

де x>i> – середина і-го інтервалу.

Таким чином, для підрахунку теоретичних частот необхідно для кожного інтервалу розмірів за формулою (10) визначити значення t [7, додаток 1],визначити Z>t> і потім скористатись формулою (9).

Необхідно відмітити, що теоретична крива нормального розподілу може бути побудована за характерними точками. Координати характерних точок кривої нормального розподілу наведені в табл. 3.

Таблиця 3 Характерні точки кривої нормального розподілу

Характерна точка

Абсциса

Ордината

Вершина кривої

Х

Точка перегину

XS

Характерна точка

Х2S

Характерна точка

X3S

Далі потрібно перевірити відповідність емпіричного розподілу теоретичному нормальному.

8. Перевірка відповідності емпіричного розподілу теоретичному нормальному.

Для перевірки відповідності емпіричного розподілу теоретичному існує ряд критеріїв, з яких найбільше практичне застосування мають критерій λ А.Н. Колмогорова і критерій χ2 Пірсона.

Розглянемо розподіл за критерієм χ

,(11)

де f – число розрядів (інтервалів);

m>i>, – відповідно емпірична і теоретична частоти і-го інтервалу значень X.

Для зручності обчислення χ2 доцільно використовувати табл. 4.

Таблиця 4 Дані для розрахунку χ2

Інтервали розмірів

від

до

1

2

3

4

5

6

7

При визначенні критерію необхідно, щоб частота була не менше 5. Якщо в будь-якому інтервалі частота буде менше п’яти, то необхідно цей інтервал об’єднати з сусіднім.

Потім необхідно знайти число К за формулою:

К = m – p – 1,

де р – число параметрів теоретичного розподілу (для нормального розподілу р = 2):

К = m – 2 – 1 = m – 3.

За таблицею [7, додатку Б], за знайденими значеннями χ2 і К визначається ймовірність p(χ2). Якщо буде виконуватись нерівність p(χ2) > 0,05, то можна вважати, що емпіричний розподіл відповідає теоретичному (нормальному) і можна використовувати його закономірності для аналізу точності обробки.

4.4 Інші закони розподілу

Закон рівної ймовірності

Якщо розсіювання розмірів залежить тільки від змінних систематичних похибок (наприклад, від зношування різального інструменту), то розподіл дійсних розмірів партії оброблених заготовок підкоряється закону рівної ймовірності.

При сталому процесі різання зношування різального інструмента відбувається за законом прямої лінії. Отже, за цим законом буде відбуватись і зміна розмірів заготовки (рис. 9, а). А це означає, що в будь-який проміжок часу ми будемо мати однакову (постійну) кількість заготовок, тобто щільність ймовірності (x) = const, і розподіл щільності ймовірності графічно буде зображуватись у вигляді прямокутника з основою ав і висотою (x) = const (рис. 9, б).

При інтервалі зміни випадкової величини X від а до в:

,

тобто ймовірність того, що випадкова величина X при дослідженнях буде приймати значення в інтервалі від a до в, дорівнює площі під диференціальною кривою розподілу. У відповідності з рисунком 9, б ця площа представляє собою прямокутник з основою ав і висотою (x). Отже:

(в – а)(х) = 1.

Рис. 9. Розподіл розмірів оброблених заготовок за законом рівної імовірності

Звідси рівняння диференціальної функції розподілу чи щільності ймовірності буде мати вигляд:

(12)

Закон рівної ймовірності має два параметри: і σ2, які згідно з формулами:[7, (4), (8)].

,

будуть дорівнювати:

;(13)

;(14)

,(15)

де – зміна розміру оброблюваної заготовки.

Фактичне поле розсіяння з формули (15) дорівнює:

.(16)

Закон рівної ймовірності розповсюджується на розподіл розмірів заготовок підвищеної точності (56 квалітет і вище) при їх обробці за методом пробних ходів. Через складність отримання розмірів дуже високої точності ймовірність попадання розміру заготовки у вузькі границі допуску за середнім, найбільшим чи найменшим його значенням стає однаковою.

Закон трикутника (закон Сімпсона)

У тому випадку, коли розмір х інтенсивно зростає на початку різання (інтенсивне зношування інструмента, його припрацювання), потім його ріст сповільнюється (сталий період зношування інструмента) і знову збільшується (в кінці стійкості різального інструменту), що показано на рис. 10, а, крива розподілу розмірів, яка показана на рис. 10, б, відповідає закону трикутника (закону Сімпсона), який представляє собою поєднання двох незалежних випадкових величин, розподілу розмірів яких підлягає закону рівної ймовірності.

Р

а)

б

ис. 10. Розподіл за законом трикутника

Закон застосовується при обробці заготовок з точністю 7-го, 8-го, а в деяких випадках і 6-го квалітетів поля розсіювання:

.(17)

Закон ексцентриситету (закон Релея)

Закон розподілу ексцентриситету чи закон Релея має місце при відхиленнях ексцентриситету осей чи биття поверхонь деталей, які є безперервними випадковими величинами. Ці похибки є додатними величинами, вони змінюються від нуля до певного значення. Крива розподілу ексцентриситетів R ступінчастих циліндричних деталей показана на рис. 11, б. Вона має несиметричну форму, деталей з нульовим ексцентриситетом немає, більша частина деталей має середній ексцентриситет, деталей з великим ексцентриситетом мало.

Рис. 11. Утворення ексцентриситету (радіуса-вектора) втулки 1 при її обробці на циліндричній оправці 2 при різниці зазору між оправкою та отвором втулки (а) і функція y = f(R) розподілу розмірів за законом Релея (б)

Закону ексцентриситету (закону Релея) підкоряється також розподіл значень непаралельності та не перпендикулярності двох поверхонь, різностінність порожнистих деталей (при нефіксованій площині вимірювання).

Цей закон одно параметричний, і рівняння його розподілу має вигляд:

,(18)

де R – змінна величина ексцентриситету чи биття:

;

x і y – координати точки кінця R (рис. 11, а, в).

 – середнє квадратичне відхилення значень координат x і y, які мають однаковий розподіл за нормальним законом. Тому  = >x> = >y> (а розподіл R – не є нормальним).

Зв’язок між >R>, і σ виражається наступними залежностями:

;(19)

.(20)

Фактичне поле розсіювання значень змінної величини радіуса-вектора R (ексцентриситету, різностінності, непаралельності тощо) знаходять з виразів:

Δ>p> = 5,252>R>;(21)

Δ>p> = 3,44.(22)

Функція розподілу a(t)

У більшості випадків механічної обробки заготовок на настроєних верстатах на точність їх розмірів одночасно впливає велика кількість близьких за величиною і незалежних одна від одної випадкових причин, які обумовлюють розподіл розмірів за законом Гаусса, і змінних систематичних похибок, що виникають внаслідок рівномірного зношування різального інструменту, які визначають розподіл за законом рівної ймовірності або іншим (наприклад, степеневим) законом.

У подібних випадках зміна досліджуваної величини X>t> залежить від часу і сама функція може бути подана в загальному вигляді на деякий момент часу t виразом:

,(23)

де y>i> – незалежні або слабо залежні випадкові величини;

C>t> – сума значень постійно діючих факторів, яка відповідає моменту часу t.

Композиція законів Гаусса і рівної ймовірності створює криві розподілу різної форми, які залежать від ступеня дії на кінцевий розподіл кожної зі складових законів. Для розрахунків точної обробки заготовок при подібній композиції законів розподілу зручно користуватись розробленою професором Н.А. Бородачовим функцією розподілу a(t).

Функція a(t) формується законом Гаусса з його параметрами  і , які залежать від точності виду обробки і технологічної системи, і законом рівної ймовірності з параметрами:

,

на величину поля розсіювання якого впливає швидкість та тривалість процесу (у випадку зношування інструменту ℓ визначається питомим зношуванням і тривалістю різання).

Таким чином, функція a(t) відображає не тільки точність, але і тривалість процесу обробки.

Функцію a(t) можна розглядати як результат рівномірного зміщення в часі вершини кривої Гаусса із середнім квадратичним σ на величину параметра 2ℓ кривої розподілу закону рівної ймовірності. На рис. 12 показано криву a(t), яка для деякого моменту часу t виражається формулою:

,(24)

де σ – середнє квадратичне відхилення закону нормального розподілу, який визначає функцію a(t);

a>0 >– середнє арифметичне значення розміру у початковий момент часу.

Рис. 1 Крива функції а(t)

Форма кривої розподілу функції a(t) залежить від параметра λ>a>, який визначається за формулою:

.(25)

Лінійну функцію a(t) можна подати у вигляді:

.(26)

Середнє арифметичне значення розміру функції дорівнює:

,(27)

а середнє квадратичне відхилення >a> функції a(t):

.(28)

На рис. 13 подано сім’ю нормованих кривих розподілу лінійної функції a(t) при різних значеннях λ>a>.

Рис. 13. Сім’я нормованих кривих розподілу лінійної функції a(t) при різних значеннях λ>а>

Усі криві симетричні, мають плоскі вершини і змінюють свій вигляд від кривої 1 нормального розподілу Гаусса (при ℓ  0 і λ>a>= 0) до прямокутника 2 розподілу рівної ймовірності при λ>a >=  і   0.

Поле розсіювання Δ>p> розмірів при функції розподілу a(t) залежить від параметра λ>a> наступним чином:

λ>a>

3

6

10

24

Δ>p>

4,74σ>a>

4,14σ>a>

3,76σ>a>

3,56σ>a>

При виконанні технологічних процесів доводиться зустрічатись також зі зміною величин випадкових факторів, коли питома вага деяких із них за окремі проміжки часу підсилюється, починає домінувати над іншими, наприклад, збільшення коливання величини припуску на обробку через включення в партію заготовок, одержаних із значними коливаннями припуску внаслідок похибок початкових заготовок. При цьому форма кривої розподілу не змінюється, але змінюється величина поля розсіювання.

4.5 Композиції законів розподілу і підсумовування похибок

При обробці заготовок на точність їх розмірів часто одночасно діють різні фактори, які викликають появу як випадкових похибок, створюваних за різними законами, так і систематичних або змінних систематичних похибок. У подібних випадках закон розподілу розмірів оброблюваних заготовок представляє собою композицію декількох законів розподілу.

Систематичний постійний фактор (похибка) на форму кривої розподілу не впливає, зсуває центр групування відносно середини поля допуску або відносно розрахункового настроювального розміру на свою величину, в бік свого знака (рис. 14, б, в). Прикладом може бути розвертання отворів у однієї половини партії заготовок розверткою діаметром 20 мм, у другої – діаметром 20,08 мм (Δ>сист.> = ±0,08 мм). Аналогічна ситуація буде при двох різних настроюваннях технологічної системи. У таких випадках поле сумарного розсіювання розмірів заготовок визначається з виразу:

Δ>р> = 6 + Δ>сист>.(29)

Якщо при цьому крива розсіювання будується за значеннями вимірювань без врахування систематичної похибки (наприклад, коли вимірюється вся партія заготовок, оброблених з декількох настроювань), форма загальної кривої розсіювання викривлюється і відрізняється від форми кривої Гаусса (крива має декілька вершин різної висоти відповідно до числа настроювань та кількості заготовок, оброблених з кожного настроювання (рис. 14, в, г)).

При обчисленні сумарної похибки обробки систематичні похибки складаються алгебраїчно, тобто із врахуванням їх знаків. Внаслідок цього результат підсумовування може показати не тільки збільшення, але й зменшення загальної похибки у зв’язку з взаємною компенсацією впливу складових похибок. Наприклад, подовження різця у зв’язку з його нагріванням, що зменшує діаметр обточуваного вала, може скомпенсувати вплив зношування різця, що викликає збільшення діаметра обробки.

Систематична похибка із випадковою похибкою складається арифметично у відповідності з формулою (29).

Випадкові похибки, які не підкоряються закону Гаусса, за відсутності домінуючої похибки підсумовуються геометрично, тобто:

,(30)

де Δ>1>, Δ>2>,…,Δ>n> – поля розсіювання випадкових похибок, що підсумовуються;

K>1>, K>2>,…,K>n> – коефіцієнти відносного розсіювання випадкових величин.

Рис. 14. Зміна форми сумарної кривої розсіювання під впливом систематичної похибки при обробці декількох партій заготовок з піднастроюванням верстата

Коефіцієнт відносного розсіювання K>i> показує, у скільки разів відрізняється фактичне розсіяння значень і-ої похибки від величини розсіяння цієї похибки при її нормальному розподілі з тим же значенням.

Для закону нормального розподілу К = 1, для закону Сімпсона К = 1,2, для закону рівної ймовірності К = 1,73.

В теорії ймовірності встановлено, що за відсутності домінуючих похибок, розсіювання сумарної похибки підкоряється закону Гаусса незалежно від законів розподілу складових похибок.

Коли всі похибки, що підсумовуються, підкоряються закону Гаусса (K>1> = K>2>= … = 1,0), поле розсіювання сумарної похибки дорівнює:

.(31)

У звичайних умовах обробки на налагоджених верстатах і за відсутності помітного впливу зношування інструменту розподіл більшості складових похибок підкоряється закону Гаусса і можна було б прийняти К = 1,0. Проте, для того щоб врахувати можливий на практиці відхід розподілу окремих складових від закону Гаусса, в розрахунках за формулою (31) часто приймають (для створення деякої гарантії точності) значення К = 1,2, що відповідає розподілу за законом Сімпсона, тобто:

.(32)

Використана література

1. Балакшин Б.С. Основы технологии машиностроения. – М.: М., 1969. – 559 с.

Бондаренко С.Г. Розмірні розрахунки механоскладального виробництва. – К. 1993. – 544 с.

3. Маталин А.А. Технология машиностроения. – Л. – М., 1985. – 496 с.

4. Методичні вказівки і завдання для індивідуальної роботи з основ технології машинобудування під контролем викладача. – ЧІТІ, 1993.

5. Основы технологии машиностроения / Под ред. В.С Корсакова. – М.М., 1977. – 416 с.

6. Руденко П.А. Теоретические основы технологии машиностроения: Конспект лекций. – Чернигов, 1986. – 258 с.

7. Солонин И.С. Математическая статистика в технологии машиностроения. – М.М., 197 – 216 с.

8. Технология машиностроения (специальная часть). / А.А. Гусев, Е.Р. Ковальчук., И.М. Колесов и др. – М.М., 1986. – 480 с.