Освоение метода гистограмм в металлообработке

Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего профессионального образования "Уральский федеральный университет имени первого Президента России Б.Н.Ельцина"

Кафедра "Металлорежущие станки и инструменты"

Курсовая работа

по дисциплине

Статистические методы контроля и управления качеством

Руководитель

С.И. Фоминых

Исполнитель

Студент гр.МЗ-65024

Ю.А.Недотко

Верхняя Салда

2010

Условие задачи

Из партии заготовок, обработанных на станке-полуавтомате в течение рабочей смены и представленных на контроль, взята большая случайная выборка объема в N=100 единиц продукции. Заготовки проконтролированы шкальным измерительным инструментом с ценой деления шкалы dи = 2мкм по размеру Аном = 40 мкм с допуском T = 100мкм и предельными отклонениями TB = 100 мкм ТH = 0 мкм. Полученные в результате измерений значения реализаций проверяемого показателя качества (отклонения от номинального размера Аном в мкм) приведены в таблице контрольного листка.

Отклонения от номинального размера Аном в мкм
80	80	66	54	76	72	72	74	64	56
70	74	72	72	88	88	58	84	56	88
72	88	58	84	66	78	72	72	62	76
72	74	78	60	64	80	62	88	70	78
68	72	62	88	58	70	68	62	56	48
90	62	82	64	66	64	52	42	52	58
54	86	88	56	64	82	80	66	90	74
62	52	70	80	84	68	66	50	78	72
78	52	100	82	62	96	48	74	78	92
62	74	80	66	68	88	56	74	72	70

Требуется:

Выполнить анализ полученных данных, используя метод гистограмм. Обработку данных провести в следующей последовательности:

• составить таблицу выборочного распределения,

• вычислить выборочные оценки среднего и стандартного отклонения,

• проверить гипотезу нормальности выборочного распределения по критерию Пирсона,

• определить характеристики поля рассеяния показателя качества,

• построить на одном графике и в одном масштабе гистограмму выборочного распределения и теоретическую кривую нормального распределения,

• привести схему распределения поля рассеяния относительно поля допуска,

• проверить условия обеспечения качества соответствия,

• вычислить индексы возможностей, оценить уровень несоответствий,

• сформулировать и обосновать выводы и предложения.

Цели анализа:

• статистическая оценка возможностей процесса,

• оценка их соответствия заданным требованиям по качеству – цели и допустимым отклонениям,

• оценка уровня несоответствий,

• выработка рекомендаций по улучшению.

заготовка деталь гистограмма качество

Обработка исходных данных

1. Составляем таблицу выборочного распределения

Ширина интервала расчетная:

Ширина интервала принятая:

При dи= 2 мкмhx = 8

Начало 1-го интервала таблицы распределения:

X1н = 42-8/2= 38 мкм

Таблица эмпирического (опытного) распределения показателя качества

Интервалы Xj от до	Подсчет частот	ƒi
38 - 46	/	1
46 - 54	///////	7
54 - 62	////////////	12
62 - 70	///////////////////////	23
70 - 78	/////////////////////////	25
78 - 86	//////////////////	18
86 - 94	///////////	11
94 - 102	//	2
Σ		100

2. Вычисляем выборочные оценки среднего и стандартного отклонения

Вспомогательная таблица для вычисления 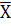и x

Интервалы Xj от до	Xi	ƒi	yi	yi ƒi	ƒi
38 - 46	42	1	-7	-7	49
46 - 54	50	7	-6	-42	252
54 - 62	58	12	-5	-60	300
62 - 70	66	23	-4	-92	368
70 - 78	74	25	-3	-75	225
78 - 86	82	18	-2	-36	72
86 - 94	90	11	-1	-11	11
94 - 102	98*	2	0	0	0
Σ		100		-323	1277

= 8*=8* = 12,23мкм

3. Проверяем гипотезу нормальности выборочного распределения по критерию Пирсона

Гипотеза принимается, если расчетное значение

Критические значения имеют следующую величину при β1=5%:

k	1	2	3*	4	5	6	7	8	9
	3,8	6,0	7,8*	9,5	11,1	12,6	14,1	15,5	16,9

Расчет теоретических частот для нормального закона распределения выполняем по формуле

где - нормированный параметр для заданного интервала с серединой Xi,

– нормированная плотность нормального распределения (определяется по таблице в зависимости от параметра zi).

Вспомогательная таблица для проверки гипотезы о модели выборочного распределения

№ п/п	Xi	zi	φ(zi)	ƒiT	ƒi
1	42	2,47	0,0303	1,98	8,56	1	8	0,04
2	50	1,81	0,1006	6,58	7
3	58	1,16	0,2323	15,20		12		0,70
4	66	0,50	0,3637	23,80	23	0,03
5	74	0,15	0,3918	25,63	25	0,02
6	82	0,80	0,2874	18,80	18	0,03
7	90	1,50	0,1456	9,52	12,42	11	14	0,20
8	98	2,11	0,0441	2,90	2

Решение о принятии гипотезы нормальности распределения: К=m-3=3 условие выполнено

4. Определяем границы и величину поля рассеяния показателя качества

Анализ результатов и выработка рекомендаций

1. Конкретизируем цели в области качества

Цель:

Предельные отклонения от цели: ± T/2 = 50 мкм

2. Строим на одном графике и в одном масштабе гистограмму выборочного распределения, теоретическую кривую нормального распределения, наносим среднее значение и границы поля рассеяния, границы поля допуска и цель по качеству.

3. Проверяем условия обеспечения качества соответствия

73,44<100условие выполняется

108,85>100условие не выполняется

35,41>0условие выполняется

Выводы: смещение поля рассеяния в минус за Тв приводит к появлению некоторого процента дефектных изделий.

4. Вычисляем индексы возможностей и оцениваем уровни несоответствий

Индекс пригодности:

Решение

Минимальный уровень несоответствий: Qmin = 1-2Ф(3Сp)=1-2*0,4999=0,0002%

Индексы реализаций возможностей:

Выводы: так как , то процесс не пригоден для реализации заданных требований.

Q+ = 0,5-Ф(3СpB)=0,5-0,4918=0,01%

Q- = 0,5-Ф(3СpH)=0,5-0,4999=0,0001%

Общий уровень несоответствий: Q = Q+ +Q- =0,01+0,0001=0,01%

5. Общие выводы и предложения по улучшению

Точность достаточная, но имеется смещение поля в минус за границу допуска, уровень дефектности составляет 0,01%. Соотношения величины и расположения поля рассеяния ωx относительно допуска T, полученные на основе зрительного восприятия проверяются по количественным условиям обеспечения точности ωx ≤ T, т.е. процесс является пригодным для обеспечения заданных требований.