Определение аналитической зависимости сопротивления металла пластической деформации для стали 30ХГСА
Overview
KtKe
Ku
множествен_регрессия
линейн
сравнительная таблица
Лист2
Лист1
Лист3
Sheet 1: Kt
| исходные данные | данные, полученные в результате парного регрессионного анализа |
|||||||||||||
| t, С | Кt | Кt = -2,8261Ln(t) + 20,524 | ||||||||||||
| 900 | 1,30 | t, С | Кt | |||||||||||
| 925 | 1,23 | 900 | 1,30 | |||||||||||
| 950 | 1,15 | 925 | 1,22 | |||||||||||
| 975 | 1,07 | 950 | 1,15 | |||||||||||
| 1000 | 1,00 | 975 | 1,07 | |||||||||||
| 1025 | 0,93 | 1000 | 1,00 | |||||||||||
| 1050 | 0,85 | 1025 | 0,93 | |||||||||||
| 1075 | 0,79 | 1050 | 0,86 | |||||||||||
| 1100 | 0,74 | 1075 | 0,80 | |||||||||||
| 1125 | 0,68 | 1100 | 0,73 | |||||||||||
| n= | 10 | 1125 | 0,67 | |||||||||||
| Y cp= | 0,97 | 0,97 | ||||||||||||
| 1012,50 | уравнение регрессии | R2 | k | Fp | F0,95 | |||||||||
| 1 | Кt = -0,0028*t + 3,8065 | 0,9963 | 2 | 2154,162 | 5,318 | |||||||||
| 2 | Кt = -2,8261Ln(t) + 20,524 | 0,9987 | 2 | 6145,846 | 5,318 | |||||||||
| 3 | Кt = 0,000002*t2 - 0,0077x + 6,2793 | 0,9993 | 3 | 4996,500 | 4,737 | |||||||||
| 4 | Кt = 6*109*t-2,9378 | 0,995 | 2 | 1592,000 | 5,318 | |||||||||
| 5 | Кt = 18,259e-0,0029t | 0,9982 | 2 | 4436,444 | 5,318 | |||||||||
| Наилучшим отображением связи между Кт и t является логарифмическая функция | ||||||||||||||
| Kt = -2,8261Ln(t) + 20,524 , так как для данной аппроксимации различие между | ||||||||||||||
| рассчетным числом Фишера Fp и табличным F0,95 является наибольшим | ||||||||||||||
| АППРОКСИМАЦИЯ | ||||||||||||||
| Y=b0+b1*X^m | ||||||||||||||
| Y'=Y | X'=X^m | m= | 0,5 | σв | ei | Ei | ||||||||
| 1,30 | 30,00 | b0' | b1' | 1,294 | 0,01 | 0,33 | ||||||||
| 1,23 | 30,41 | 6,63 | -0,18 | 1,221 | 0,01 | 0,26 | ||||||||
| 1,15 | 30,82 | b0 | b1 | 1,148 | 0,00 | 0,18 | ||||||||
| 1,07 | 31,22 | 6,63 | -0,18 | 1,076 | -0,01 | 0,10 | ||||||||
| 1,00 | 31,62 | 1,005 | -0,01 | 0,03 | ||||||||||
| 0,93 | 32,02 | 0,936 | -0,01 | -0,04 | ||||||||||
| 0,85 | 32,40 | 0,867 | -0,02 | -0,12 | ||||||||||
| 0,79 | 32,79 | 0,798 | -0,01 | -0,18 | ||||||||||
| 0,74 | 33,17 | 0,731 | 0,01 | -0,23 | ||||||||||
| 0,68 | 33,54 | 0,664 | 0,02 | -0,29 | ||||||||||
| 0,00 | 0,41 | |||||||||||||
| Результат "корреляция" | ||||||||||||||
| t, С | Кt | |||||||||||||
| t, С | 1 | -0,99816 | ||||||||||||
| Кt | -0,99816 | 1 | ||||||||||||
| Матрица корреляции r(Y,Xj) | ||||||||||||||
| t, С | Кt | |||||||||||||
| t, С | 1 | -0,99816 | ||||||||||||
| Кt | -0,99816 | 1 | ||||||||||||
| Оценивание значимости | ||||||||||||||
| коэффициентов корреляции | ||||||||||||||
| n | 10 | |||||||||||||
| m | 2 | |||||||||||||
| a | 0,95 | |||||||||||||
| t(a:n-2) | 2,3060 | |||||||||||||
| t(Т,Kt) | 46,5527 | ДА |
Sheet 2: Ke
| исходные данные | данные, полученные в результате парного регрессионного анализа |
|||||||||||||
| ε, % | Кε | Kε = 0,5186*ε0,2857 | ||||||||||||
| 5 | 0,82 | ε, % | Кε | |||||||||||
| 7,5 | 0,92 | 5 | 0,82 | |||||||||||
| 10 | 1,00 | 7,5 | 0,92 | |||||||||||
| 12,5 | 1,07 | 10 | 1,00 | |||||||||||
| 15 | 1,13 | 12,5 | 1,07 | |||||||||||
| 17,5 | 1,18 | 15 | 1,12 | |||||||||||
| 20 | 1,22 | 17,5 | 1,17 | |||||||||||
| 22,5 | 1,26 | 20 | 1,22 | |||||||||||
| 25 | 1,30 | 22,5 | 1,26 | |||||||||||
| 27,5 | 1,33 | 25 | 1,30 | |||||||||||
| n= | 10,00 | 27,5 | 1,34 | |||||||||||
| 16,25 | 1,12 | 1,12 | ||||||||||||
| уравнение регрессии | R2 | k | Fp | F0,95 | ||||||||||
| 1 | Kε = 0,0219*ε + 0,7665 | 0,9672 | 2 | 235,902 | 5,318 | |||||||||
| 2 | Kε = 0,304Ln(ε) + 0,3123 | 0,9967 | 2 | 2416,242 | 5,318 | |||||||||
| 3 | Kε = -0,0006*ε2 + 0,022ε + 0,6338 | 0,9985 | 3 | 2329,833 | 4,737 | |||||||||
| 4 | Kε = 0,5186*ε0,2857 | 0,9996 | 2 | 19992,000 | 5,318 | |||||||||
| 5 | Kε = 0,799e0,020ε | 0,9388 | 2 | 122,719 | 5,318 | |||||||||
| Наилучшим отображением связи между Кε и ε является степенная функция | ||||||||||||||
| Kε = 0,5186*ε0,2857, так как для данной аппроксимации различие между | ||||||||||||||
| рассчетным числом Фишера Fp и табличным F0,95 является наибольшим | ||||||||||||||
| АППРОКСИМАЦИЯ | ||||||||||||||
| Y=b0+b1*X^m | ||||||||||||||
| Y'=Y | X'=X^m | m= | 0,5 | σв | ei | Ei | ||||||||
| 0,82 | 2,24 | b0' | b1' | 0,838 | -0,02 | -0,30 | ||||||||
| 0,92 | 2,74 | 0,46 | 0,17 | 0,923 | 0,00 | -0,20 | ||||||||
| 1,00 | 3,16 | b0 | b1 | 0,995 | 0,00 | -0,12 | ||||||||
| 1,07 | 3,54 | 0,46 | 0,17 | 1,058 | 0,01 | -0,05 | ||||||||
| 1,13 | 3,87 | 1,115 | 0,01 | 0,01 | ||||||||||
| 1,18 | 4,18 | 1,168 | 0,01 | 0,06 | ||||||||||
| 1,22 | 4,47 | 1,217 | 0,00 | 0,10 | ||||||||||
| 1,26 | 4,74 | 1,262 | 0,00 | 0,14 | ||||||||||
| 1,30 | 5,00 | 1,306 | -0,01 | 0,18 | ||||||||||
| 1,33 | 5,24 | 1,347 | -0,02 | 0,21 | ||||||||||
| 0,00 | 0,26 | |||||||||||||
| Результат "корреляция" | ||||||||||||||
| ?, % | К? | |||||||||||||
| ?, % | 1 | 0,983456 | ||||||||||||
| К? | 0,983456 | 1 | ||||||||||||
| Матрица корреляции r(Y,Xj) | ||||||||||||||
| ε, % | Кε | |||||||||||||
| ε, % | 1 | 0,983456 | ||||||||||||
| Кε | 0,9834557433 | 1 | ||||||||||||
| Оценивание значимости | ||||||||||||||
| коэффициентов корреляции | ||||||||||||||
| n | 10 | |||||||||||||
| m | 2 | |||||||||||||
| a | 0,95 | |||||||||||||
| t(a:n-2) | 2,3060 | |||||||||||||
| t(ε,Kε) | 15,3555 | ДА |
Sheet 3: Ku
| исходные данные | данные, полученные в результате парного регрессионного анализа |
||||||||||||||||||||||
| U, c-1 | Кu | Ku = 0,1253Ln(U) + 0,7081 | |||||||||||||||||||||
| 1 | 0,71 | U, c-1 | Кu | ||||||||||||||||||||
| 2 | 0,80 | 1 | 0,71 | ||||||||||||||||||||
| 4 | 0,88 | 2 | 0,79 | ||||||||||||||||||||
| 6 | 0,92 | 4 | 0,88 | ||||||||||||||||||||
| 8 | 0,98 | 6 | 0,93 | ||||||||||||||||||||
| 10 | 1,00 | 8 | 0,97 | ||||||||||||||||||||
| 20 | 1,07 | 10 | 1,00 | ||||||||||||||||||||
| 30 | 1,12 | 20 | 1,08 | ||||||||||||||||||||
| 40 | 1,18 | 30 | 1,13 | ||||||||||||||||||||
| 50 | 1,21 | 40 | 1,17 | ||||||||||||||||||||
| n= | 10,00 | 50 | 1,20 | ||||||||||||||||||||
| 17,10 | 0,99 | 0,99 | |||||||||||||||||||||
| уравнение регрессии | R2 | k | Fp | F0,95 | |||||||||||||||||||
| 1 | Ku = 0,0086U + 0,8404 | 0,8274 | 2 | 38,350 | 5,318 | ||||||||||||||||||
| 2 | Ku = 0,1253Ln(U) + 0,7081 | 0,9960 | 2 | 1992,000 | 5,318 | ||||||||||||||||||
| 3 | Ku = -0,0002*U2 + 0,0202*U + 0,7777 | 0,9246 | 3 | 42,919 | 4,737 | ||||||||||||||||||
| 4 | Ku = 0,7268*U0,1317 | 0,9930 | 2 | 1134,857 | 5,318 | ||||||||||||||||||
| 5 | Ku = 0,8401*e0,0087U | 0,7648 | 2 | 26,014 | 5,318 | ||||||||||||||||||
| Наилучшим отображением связи между Кu и U является степенная функция | |||||||||||||||||||||||
| Ku = 0,7392*U0,125 , так как для данной аппроксимации различие между | |||||||||||||||||||||||
| рассчетным числом Фишера Fp и табличным F0,95 является наибольшим | |||||||||||||||||||||||
| АППРОКСИМАЦИЯ | |||||||||||||||||||||||
| Y=b0+b1*X^m | |||||||||||||||||||||||
| Y'=Y | X'=X^m | m= | 0,5 | σв | ei | Ei | |||||||||||||||||
| 0,71 | 1,00 | b0' | b1' | 0,790 | -0,08 | -0,28 | |||||||||||||||||
| 0,80 | 1,41 | 0,72 | 0,08 | 0,821 | -0,02 | -0,19 | |||||||||||||||||
| 0,88 | 2,00 | b0 | b1 | 0,865 | 0,01 | -0,11 | |||||||||||||||||
| 0,92 | 2,45 | 0,72 | 0,08 | 0,899 | 0,02 | -0,07 | |||||||||||||||||
| 0,98 | 2,83 | 0,928 | 0,05 | -0,01 | |||||||||||||||||||
| 1,00 | 3,16 | 0,953 | 0,05 | 0,01 | |||||||||||||||||||
| 1,07 | 4,47 | 1,051 | 0,02 | 0,08 | |||||||||||||||||||
| 1,12 | 5,48 | 1,126 | -0,01 | 0,13 | |||||||||||||||||||
| 1,18 | 6,32 | 1,190 | -0,01 | 0,19 | |||||||||||||||||||
| 1,21 | 7,07 | 1,246 | -0,04 | 0,22 | |||||||||||||||||||
| 0,01 | 0,24 | ||||||||||||||||||||||
| Результат "корреляция" | |||||||||||||||||||||||
| U, c-1 | Кu | ||||||||||||||||||||||
| U, c-1 | 1 | 0,909605 | |||||||||||||||||||||
| Кu | 0,909605 | 1 | |||||||||||||||||||||
| Матрица корреляции r(Y,Xj) | |||||||||||||||||||||||
| t, С | Кt | ||||||||||||||||||||||
| t, С | 1 | 0,9096048228 | |||||||||||||||||||||
| Кt | 0,9096048228 | 1 | |||||||||||||||||||||
| Оценивание значимости | |||||||||||||||||||||||
| коэффициентов корреляции | |||||||||||||||||||||||
| n | 10 | ||||||||||||||||||||||
| m | 2 | ||||||||||||||||||||||
| a | 0,95 | ||||||||||||||||||||||
| t(a:n-2) | 2,3060 | ||||||||||||||||||||||
| t(U,Ku) | 6,1923 | ДА |
Sheet 4: множествен_регрессия
| исходные данные | σ0= | 105 | МПа | УРАВНЕНИЕ РЕГРЕССИИ | |||||||||||||||||||||
| σт= 390,20 - 0,33*T +2,21*E +0,98*U | |||||||||||||||||||||||||
| Т, С | E, % | U, c-1 | σт=σ0*Kt*Ke*Ku | ЗНАЧИМОСТЬ КОЭФФИЦИЕНТОВ | |||||||||||||||||||||
| 1012,50 | 5,0 | 17,10 | 82,77 | t[0,05;n - k] | b0 | Значим | |||||||||||||||||||
| 1012,50 | 7,5 | 17,10 | 92,87 | ВЫВОД ИТОГОВ | 2,0518 | b1 | Значим | ВЫВОД ИТОГОВ | |||||||||||||||||
| 1012,50 | 10,0 | 17,10 | 100,94 | b2 | Значим | АВТОКОРРЕЛЯЦИЯ | |||||||||||||||||||
| 1012,50 | 12,5 | 17,10 | 108,01 | Регрессионная статистика | b3 | Значим | ОСТАТКОВ | Регрессионная статистика | |||||||||||||||||
| 1012,50 | 15,0 | 17,10 | 114,06 | Множественный R | 0,97 | НАДЕЖНОСТЬ АППРОКСИМАЦИИ | DW | 0,8232707587 | Множественный R | 0,9706544469 | |||||||||||||||
| 1012,50 | 17,5 | 17,10 | 119,11 | R-квадрат | 0,94 | F[0,05;k-1n-k] | Аппроксимация | Отсутствует | R-квадрат | 0,9421700552 | |||||||||||||||
| 1012,50 | 20,0 | 17,10 | 123,15 | Нормированный R-квадрат | 0,94 | 3,3541 | надежная | Нормированный R-квадрат | 0,9354973693 | ||||||||||||||||
| 1012,50 | 22,5 | 17,10 | 127,19 | Стандартная ошибка | 5,00 | Стандартная ошибка | 5,0041856283 | ||||||||||||||||||
| 1012,50 | 25,0 | 17,10 | 131,22 | Наблюдения | 30,00 | Наблюдения | 30 | ||||||||||||||||||
| 1012,50 | 27,5 | 17,10 | 134,25 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 1 | 81,54 | Дисперсионный анализ | Дисперсионный анализ | ||||||||||||||||||||
| 1012,50 | 16,25 | 2 | 91,88 | df | SS | MS | F | Значимость F | df | SS | MS | F | Значимость F | ||||||||||||
| 1012,50 | 16,25 | 4 | 101,07 | Регрессия | 3,00 | 10607,59 | 3535,86 | 141,20 | 3,29338179484332E-016 | Регрессия | 3 | 10607,5891430598 | 3535,8630476866 | 141,1980219824 | 3,29338179484332E-016 | ||||||||||
| 1012,50 | 16,25 | 6 | 105,66 | Остаток | 26,00 | 651,09 | 25,04 | Остаток | 26 | 651,0887188726 | 25,0418738028 | ||||||||||||||
| 1012,50 | 16,25 | 8 | 112,55 | Итого | 29,00 | 11258,68 | Итого | 29 | 11258,6778619325 | ||||||||||||||||
| 1012,50 | 16,25 | 10 | 114,85 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 20 | 122,89 | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | ||||||
| 1012,50 | 16,25 | 30 | 128,63 | Y-пересечение | 390,20 | 22,68 | 17,21 | 0,00 | 343,58 | 436,81 | 343,58 | 436,81 | Y-пересечение | 390,1957386164 | 22,6771324929 | 17,2065731299 | 9,96716311639728E-016 | 343,5822256504 | 436,8092515824 | 343,5822256504 | 436,8092515824 | ||||
| 1012,50 | 16,25 | 40 | 135,52 | Т, С | -0,33 | 0,02 | -14,77 | 0,00 | -0,37 | -0,28 | -0,37 | -0,28 | Т, С | -0,3255877556 | 0,0220377082 | -14,7741204559 | 3,67384588470762E-014 | -0,3708869131 | -0,280288598 | -0,3708869131 | -0,280288598 | ||||
| 1012,50 | 16,25 | 50 | 138,97 | E, % | 2,21 | 0,22 | 10,05 | 0,00 | 1,76 | 2,67 | 1,76 | 2,67 | E, % | 2,2145731745 | 0,220377082 | 10,0490175936 | 1,91463925779587E-010 | 1,7615815993 | 2,6675647498 | 1,7615815993 | 2,6675647498 | ||||
| 900 | 16,25 | 17,10 | 151,30 | U, c-1 | 0,98 | 0,10 | 10,21 | 0,00 | 0,79 | 1,18 | 0,79 | 1,18 | U, c-1 | 0,9842818758 | 0,0963609315 | 10,2145325936 | 1,36016522445278E-010 | 0,7862091462 | 1,1823546053 | 0,7862091462 | 1,1823546053 | ||||
| 925 | 16,25 | 17,10 | 143,15 | ||||||||||||||||||||||
| 950 | 16,25 | 17,10 | 133,84 | ||||||||||||||||||||||
| 975 | 16,25 | 17,10 | 124,53 | ||||||||||||||||||||||
| 1000 | 16,25 | 17,10 | 116,38 | ВЫВОД ОСТАТКА | ВЫВОД ОСТАТКА | ||||||||||||||||||||
| 1025 | 16,25 | 17,10 | 108,24 | ||||||||||||||||||||||
| 1050 | 16,25 | 17,10 | 98,92 | Наблюдение | Предсказанное σт=σ0*Kt*Ke*Ku | Остатки | (ei - ei -1)2 | Наблюдение | Предсказанное σт=σ0*Kt*Ke*Ku | Остатки | Стандартные остатки | ||||||||||||||
| 1075 | 16,25 | 17,10 | 91,94 | 1 | 88,44 | -5,67 | 32,16 | 1 | 88,4422220564 | -5,6710202564 | -1,1968510695 | ||||||||||||||
| 1100 | 16,25 | 17,10 | 86,12 | 2 | 93,98 | -1,11 | 20,77 | 2 | 93,9786549927 | -1,1134041927 | -0,2349804689 | ||||||||||||||
| 1125 | 16,25 | 17,10 | 79,14 | 3 | 99,52 | 1,43 | 6,45 | 3 | 99,5150879291 | 1,4254020709 | 0,3008266442 | ||||||||||||||
| 4 | 105,05 | 2,95 | 2,34 | 4 | 105,0515208655 | 2,9548034345 | 0,6236020136 | ||||||||||||||||||
| 5 | 110,59 | 3,47 | 0,27 | 5 | 110,5879538018 | 3,4747998982 | 0,7333456391 | ||||||||||||||||||
| 6 | 116,12 | 2,99 | 0,24 | 6 | 116,1243867382 | 2,9853914618 | 0,6300575209 | ||||||||||||||||||
| 7 | 121,66 | 1,49 | 2,25 | 7 | 121,6608196745 | 1,4865781255 | 0,313737659 | ||||||||||||||||||
| 8 | 127,20 | -0,01 | 2,25 | 8 | 127,1972526109 | -0,0122352109 | -0,002582203 | ||||||||||||||||||
| 9 | 132,73 | -1,51 | 2,25 | 9 | 132,7336855473 | -1,5110485473 | -0,3189020649 | ||||||||||||||||||
| 10 | 138,27 | -4,02 | 6,29 | 10 | 138,2701184836 | -4,0192667836 | -0,8482536706 | ||||||||||||||||||
| 11 | 97,51 | -15,97 | 142,73 | 11 | 97,5092320703 | -15,9662929703 | -3,3696361419 | ||||||||||||||||||
| 12 | 98,49 | -6,61 | 87,46 | 12 | 98,4935139461 | -6,6141459461 | -1,3958947934 | ||||||||||||||||||
| 13 | 100,46 | 0,61 | 52,12 | 13 | 100,4620776976 | 0,6052271024 | 0,127731285 | ||||||||||||||||||
| 14 | 102,43 | 3,23 | 6,89 | 14 | 102,4306414491 | 3,2306317509 | 0,6818147161 | ||||||||||||||||||
| 15 | 104,40 | 8,15 | 24,23 | 15 | 104,3992052006 | 8,1530205994 | 1,7206694709 | ||||||||||||||||||
| 16 | 106,37 | 8,48 | 0,11 | 16 | 106,3677689521 | 8,4814410479 | 1,7899815783 | ||||||||||||||||||
| 17 | 116,21 | 6,68 | 3,25 | 17 | 116,2105877097 | 6,6780669903 | 1,4093851297 | ||||||||||||||||||
| 18 | 126,05 | 2,58 | 16,81 | 18 | 126,0534064673 | 2,5777087327 | 0,5440173574 | ||||||||||||||||||
| 19 | 135,90 | -0,37 | 8,71 | 19 | 135,8962252248 | -0,3741574248 | -0,078964753 | ||||||||||||||||||
| 20 | 145,74 | -6,77 | 40,93 | 20 | 145,7390439824 | -6,7714998824 | -1,429103849 | ||||||||||||||||||
| 21 | 149,98 | 1,31 | 65,34 | 21 | 149,9847927709 | 1,3119437291 | 0,2768816164 | ||||||||||||||||||
| 22 | 141,85 | 1,30 | 0,00 | 22 | 141,8450988818 | 1,3048902682 | 0,2753930056 | ||||||||||||||||||
| 23 | 133,71 | 0,13 | 1,37 | 23 | 133,7054049927 | 0,1340157573 | 0,028283606 | ||||||||||||||||||
| 24 | 125,57 | -1,04 | 1,37 | 24 | 125,5657111036 | -1,0368587536 | -0,2188257936 | ||||||||||||||||||
| 25 | 117,43 | -1,04 | 0,00 | 25 | 117,4260172145 | -1,0439122145 | -0,2203144045 | ||||||||||||||||||
| 26 | 109,29 | -1,05 | 0,00 | 26 | 109,2863233255 | -1,0509656755 | -0,2218030153 | ||||||||||||||||||
| 27 | 101,15 | -2,22 | 1,37 | 27 | 101,1466294364 | -2,2218401864 | -0,4689124149 | ||||||||||||||||||
| 28 | 93,01 | -1,07 | 1,34 | 28 | 93,0069355473 | -1,0650725973 | -0,224780237 | ||||||||||||||||||
| 29 | 84,87 | 1,26 | 5,39 | 29 | 84,8672416582 | 1,2555160418 | 0,2649727297 | ||||||||||||||||||
| 30 | 76,73 | 2,41 | 1,34 | 30 | 76,7275477691 | 2,4122836309 | 0,5091049076 |
Sheet 5: линейн
| № п/п | Т, С | E, % | U, c-1 | σт=σо.д.*kt*ku*ke | РЕЗУЛЬТАТЫ ЛИНЕЙН() | ОСТАТКИ | |||||
| 1 | 1012,5 | 5 | 17,1 | 82,771 | y^ | e | (ei-ei-1) | ||||
| 2 | 1012,5 | 7,5 | 17,1 | 92,865 | 0,9843 | 2,2146 | -0,3256 | 390,1957 | 88,4 | -5,6710 | - |
| 3 | 1012,5 | 10 | 17,1 | 100,940 | 0,0964 | 0,2204 | 0,0220 | 22,6771 | 94,0 | -1,1134 | 20,77 |
| 4 | 1012,5 | 12,5 | 17,1 | 108,006 | 0,9422 | 5,0042 | #N/A | #N/A | 99,5 | 1,4254 | 6,45 |
| 5 | 1012,5 | 15 | 17,1 | 114,063 | 141,1980 | 26 | #N/A | #N/A | 105,1 | 2,9548 | 2,34 |
| 6 | 1012,5 | 17,5 | 17,1 | 119,110 | 10607,5891 | 651,0887 | #N/A | #N/A | 110,6 | 3,4748 | 0,27 |
| 7 | 1012,5 | 20 | 17,1 | 123,147 | РЕГРЕССИОННАЯ СТАТИСТИКА | 116,1 | 2,9854 | 0,24 | |||
| 8 | 1012,5 | 22,5 | 17,1 | 127,185 | R² | Se | n-k | 121,7 | 1,4866 | 2,25 | |
| 9 | 1012,5 | 25 | 17,1 | 131,223 | 0,9421700552 | 5,0041856283 | 26 | 651,0887188726 | 127,2 | -0,0122 | 2,25 |
| 10 | 1012,5 | 27,5 | 17,1 | 134,251 | ∑E² | ∑e² | Fp | 132,7 | -1,5110 | 2,25 | |
| 1 | 1012,5 | 16,25 | 1 | 81,543 | 10607,5891430598 | 651,0887188726 | 141,1980219824 | 10607,5891430598 | 138,3 | -4,0193 | 6,29 |
| 2 | 1012,5 | 16,25 | 2 | 91,879 | ТАБЛИЧНЫЕ ЗНАЧЕНИЯ | 97,5 | -15,9663 | 142,73 | |||
| 3 | 1012,5 | 16,25 | 4 | 101,067 | P,% | t[0,05;n-k] | F[0,05;k-1;n-k] | 98,5 | -6,6141 | 87,46 | |
| 4 | 1012,5 | 16,25 | 6 | 105,661 | 95,00 | 2,0555 | 3,3690 | 100,5 | 0,6052 | 52,12 | |
| 5 | 1012,5 | 16,25 | 8 | 112,552 | ОЦЕНИВАНИЕ КОЭФФИЦИЕНТОВ | 102,4 | 3,2306 | 6,89 | |||
| 6 | 1012,5 | 16,25 | 10 | 114,849 | b2 | b1 | b0 | 104,4 | 8,1530 | 24,23 | |
| 7 | 1012,5 | 16,25 | 20 | 122,889 | 0,9843 | 2,2146 | -0,3256 | 390,1957 | 106,4 | 8,4814 | 0,11 |
| 8 | 1012,5 | 16,25 | 30 | 128,631 | Sb2 | Sb1 | Sb0 | 116,2 | 6,6781 | 3,25 | |
| 9 | 1012,5 | 16,25 | 40 | 135,522 | 0,0964 | 0,2204 | 0,0220 | 22,6771 | 126,1 | 2,5777 | 16,81 |
| 10 | 1012,5 | 16,25 | 50 | 138,968 | tb2 | tb1 | tb0 | 135,9 | -0,3742 | 8,71 | |
| 1 | 900 | 16,25 | 17,1 | 151,297 | 10,2145 | 10,0490 | -14,7741 | 17,2066 | 145,7 | -6,7715 | 40,93 |
| 2 | 925 | 16,25 | 17,1 | 143,150 | ЗНАЧИМ | ЗНАЧИМ | ЗНАЧИМ | ЗНАЧИМ | 150,0 | 1,3119 | 65,34 |
| 3 | 950 | 16,25 | 17,1 | 133,839 | УРАВНЕНИЕ РЕГРЕССИИ | 141,8 | 1,3049 | 0,00 | |||
| 4 | 975 | 16,25 | 17,1 | 124,529 | σт= 390,20 - 0,33*T +2,21*E +0,98*U | 133,7 | 0,1340 | 1,37 | |||
| 5 | 1000 | 16,25 | 17,1 | 116,382 | ОЦЕНКА АППРОКСИМАЦИИ | 125,6 | -1,0369 | 1,37 | |||
| 6 | 1025 | 16,25 | 17,1 | 108,235 | Аппроксимация надежная | 117,4 | -1,0439 | 0,00 | |||
| 7 | 1050 | 16,25 | 17,1 | 98,925 | АВТОКОРРЕЛЯЦИЯ ОСТАТКОВ | 109,3 | -1,0510 | 0,00 | |||
| 8 | 1075 | 16,25 | 17,1 | 91,942 | DW | 0,77469 | 101,1 | -2,2218 | 1,37 | ||
| 9 | 1100 | 16,25 | 17,1 | 86,123 | СУЩЕСТВУЕТ | 93,0 | -1,0651 | 1,34 | |||
| 10 | 1125 | 16,25 | 17,1 | 79,140 | 84,9 | 1,2555 | 5,39 | ||||
| D | 88,7684 | 76,7 | 2,4123 | 1,34 | |||||||
| 0,53 |
Sheet 6: сравнительная таблица
| σ0= | 105 | Сравнительная таблица | ||||||||||
| № п/п | Т, С | E, % | U, c-1 | σT1 | σT2 | Расхождение % | σT3 | Расхождение % | σT4 | |||
| 1 | 1012,5 | 5,0 | 17,1 | 82,77 | 82,90 | 0,16 | 88,44 | 6,41 | 77,42 | 6,91 | 390,20 | |
| 2 | 1012,5 | 7,5 | 17,1 | 92,87 | 93,08 | 0,23 | 93,98 | 1,18 | 83,03 | 11,85 | -0,33 | |
| 3 | 1012,5 | 10,0 | 17,1 | 100,94 | 101,06 | 0,12 | 99,52 | 1,43 | 88,64 | 13,88 | 2,21 | |
| 4 | 1012,5 | 12,5 | 17,1 | 108,01 | 107,71 | 0,28 | 105,05 | 2,81 | 94,25 | 14,59 | 0,98 | |
| 5 | 1012,5 | 15,0 | 17,1 | 114,06 | 113,47 | 0,52 | 110,59 | 3,14 | 99,86 | 14,22 | ||
| 6 | 1012,5 | 17,5 | 17,1 | 119,11 | 118,58 | 0,45 | 116,12 | 2,57 | 105,47 | 12,93 | ||
| 7 | 1012,5 | 20,0 | 17,1 | 123,15 | 123,19 | 0,03 | 121,66 | 1,22 | 111,08 | 10,86 | ||
| 8 | 1012,5 | 22,5 | 17,1 | 127,19 | 127,40 | 0,17 | 127,20 | 0,01 | 116,70 | 8,99 | ||
| 9 | 1012,5 | 25,0 | 17,1 | 131,22 | 131,30 | 0,06 | 132,73 | 1,14 | 122,31 | 7,29 | ||
| 10 | 1012,5 | 27,5 | 17,1 | 134,25 | 134,92 | 0,50 | 138,27 | 2,91 | 127,92 | 4,95 | ||
| 11 | 1012,5 | 16 | 1 | 81,54 | 81,34 | 0,25 | 97,51 | 16,37 | 85,28 | 4,38 | ||
| 12 | 1012,5 | 16 | 2 | 91,88 | 91,31 | 0,62 | 98,49 | 6,72 | 86,36 | 6,39 | ||
| 13 | 1012,5 | 16 | 4 | 101,07 | 101,29 | 0,22 | 100,46 | 0,60 | 88,52 | 14,17 | ||
| 14 | 1012,5 | 16 | 6 | 105,66 | 107,12 | 1,37 | 102,43 | 3,15 | 90,68 | 16,52 | ||
| 15 | 1012,5 | 16 | 8 | 112,55 | 111,26 | 1,16 | 104,40 | 7,81 | 92,84 | 21,23 | ||
| 16 | 1012,5 | 16 | 10 | 114,85 | 114,48 | 0,33 | 106,37 | 7,97 | 95,00 | 20,89 | ||
| 17 | 1012,5 | 16 | 20 | 122,89 | 124,45 | 1,26 | 116,21 | 5,75 | 105,80 | 16,15 | ||
| 18 | 1012,5 | 16 | 30 | 128,63 | 130,29 | 1,27 | 126,05 | 2,04 | 116,60 | 10,32 | ||
| 19 | 1012,5 | 16 | 40 | 135,52 | 134,43 | 0,81 | 135,90 | 0,28 | 127,40 | 6,38 | ||
| 20 | 1012,5 | 16 | 50 | 138,97 | 137,64 | 0,96 | 145,74 | 4,65 | 138,20 | 0,56 | ||
| 21 | 900 | 16 | 17,1 | 151,30 | 151,27 | 0,02 | 149,98 | 0,87 | 137,43 | 10,09 | ||
| 22 | 925 | 16 | 17,1 | 143,15 | 142,26 | 0,63 | 141,85 | 0,92 | 129,70 | 10,37 | ||
| 23 | 950 | 16 | 17,1 | 133,84 | 133,49 | 0,26 | 133,71 | 0,10 | 121,98 | 9,72 | ||
| 24 | 975 | 16 | 17,1 | 124,53 | 124,94 | 0,33 | 125,57 | 0,83 | 114,25 | 8,99 | ||
| 25 | 1000 | 16 | 17,1 | 116,38 | 116,62 | 0,20 | 117,43 | 0,89 | 106,53 | 9,25 | ||
| 26 | 1025 | 16 | 17,1 | 108,24 | 108,49 | 0,24 | 109,29 | 0,96 | 98,81 | 9,54 | ||
| 27 | 1050 | 16 | 17,1 | 98,92 | 100,57 | 1,63 | 101,15 | 2,20 | 91,08 | 8,61 | ||
| 28 | 1075 | 16 | 17,1 | 91,94 | 92,83 | 0,96 | 93,01 | 1,15 | 83,36 | 10,30 | ||
| 29 | 1100 | 16 | 17,1 | 86,12 | 85,27 | 1,00 | 84,87 | 1,48 | 75,63 | 13,87 | ||
| 30 | 1125 | 16 | 17,1 | 79,14 | 77,88 | 1,62 | 76,73 | 3,14 | 67,91 | 16,54 | ||
| Средняя ошибка | 0,59 | 3,02 | 11,03 | |||||||||
Sheet 7: Лист2
| исходные данные | σ0= | 105 | МПа | ||||||||||||||||
| σт= 390,20 - 0,33*T +2,21*E +0,98*U | |||||||||||||||||||
| Т, С | E, % | U, c-1 | σт=σ0*Kt*Ke*Ku | при 1000 | при 1180 | 900,00 | 1125,00 | ||||||||||||
| 1012,5 | 5 | 17,1 | 79,47 | Т, С | E, % | U, c-1 | σт | Т, С | σт | U, c-1 | Т=900 | Т=1125 | |||||||
| 1012,5 | 7,5 | 17,1 | 89,16 | 390,20 | 900 | 16,25 | 1 | 134,14 | 1125 | 60,88 | 1 | 134,14 | 60,88 | ||||||
| 1012,5 | 10 | 17,1 | 96,92 | -0,33 | 900 | 16,25 | 2 | 135,12 | 1125 | 61,86 | 2 | 135,12 | 61,86 | ||||||
| 1012,5 | 12,5 | 17,1 | 103,70 | 2,21 | 900 | 16,25 | 4 | 137,09 | 1125 | 63,83 | 4 | 137,09 | 63,83 | ||||||
| 1012,5 | 15 | 17,1 | 109,51 | 0,98 | 900 | 16,25 | 6 | 139,06 | 1125 | 65,80 | 6 | 139,06 | 65,80 | ||||||
| 1012,5 | 17,5 | 17,1 | 114,36 | 900 | 16,25 | 8 | 141,03 | 1125 | 67,77 | 8 | 141,03 | 67,77 | |||||||
| 1012,5 | 20 | 17,1 | 118,24 | 900 | 16,25 | 10 | 143,00 | 1125 | 69,74 | 10 | 143,00 | 69,74 | |||||||
| 1012,5 | 22,5 | 17,1 | 122,11 | 900 | 16,25 | 20 | 152,84 | 1125 | 79,58 | 20 | 152,84 | 79,58 | |||||||
| 1012,5 | 25 | 17,1 | 125,99 | 900 | 16,25 | 30 | 162,68 | 1125 | 89,42 | 30 | 162,68 | 89,42 | |||||||
| 1012,5 | 27,5 | 17,1 | 128,90 | 900 | 16,25 | 40 | 172,52 | 1125 | 99,27 | 40 | 172,52 | 99,27 | |||||||
| 1012,5 | 16,25 | 1 | 79,47 | 900 | 16,25 | 50 | 182,37 | 1125 | 109,11 | 50 | 182,37 | 109,11 | |||||||
| 1012,5 | 16,25 | 2 | 89,54 | ||||||||||||||||
| 1012,5 | 16,25 | 4 | 98,50 | ||||||||||||||||
| 1012,5 | 16,25 | 6 | 102,98 | при 6 | при 24 | 0 | 5,00 | 27,50 | |||||||||||
| 1012,5 | 16,25 | 8 | 109,69 | Е | Т | U | σт | Е | σт | Т | ε=5 % | ε=27,5 % | |||||||
| 1012,5 | 16,25 | 10 | 111,93 | 5 | 900 | 17,1 | 125,07 | 27,5 | 174,90 | 900 | 125,07 | 174,90 | |||||||
| 1012,5 | 16,25 | 20 | 119,77 | 5 | 925 | 17,1 | 116,93 | 27,5 | 166,76 | 925 | 116,93 | 166,76 | |||||||
| 1012,5 | 16,25 | 30 | 125,36 | 5 | 950 | 17,1 | 108,79 | 27,5 | 158,62 | 950 | 108,79 | 158,62 | |||||||
| 1012,5 | 16,25 | 40 | 132,08 | 5 | 975 | 17,1 | 100,65 | 27,5 | 150,48 | 975 | 100,65 | 150,48 | |||||||
| 1012,5 | 16,25 | 50 | 135,44 | 5 | 1000 | 17,1 | 92,51 | 27,5 | 142,34 | 1000 | 92,51 | 142,34 | |||||||
| 900 | 16,25 | 17,1 | 79,47 | 5 | 1025 | 17,1 | 84,37 | 27,5 | 134,20 | 1025 | 84,37 | 134,20 | |||||||
| 925 | 16,25 | 17,1 | 75,19 | 5 | 1050 | 17,1 | 76,23 | 27,5 | 126,06 | 1050 | 76,23 | 126,06 | |||||||
| 950 | 16,25 | 17,1 | 70,30 | 5 | 1075 | 17,1 | 68,09 | 27,5 | 117,92 | 1075 | 68,09 | 117,92 | |||||||
| 975 | 16,25 | 17,1 | 65,41 | 5 | 1100 | 17,1 | 59,95 | 27,5 | 109,78 | 1100 | 59,95 | 109,78 | |||||||
| 1000 | 16,25 | 17,1 | 61,13 | 5 | 1125 | 17,1 | 51,81 | 27,5 | 101,64 | 1125 | 51,81 | 101,64 | |||||||
| 1025 | 16,25 | 17,1 | 56,85 | ||||||||||||||||
| 1050 | 16,25 | 17,1 | 51,96 | ||||||||||||||||
| 1075 | 16,25 | 17,1 | 48,29 | при 2 | при 60 | 0 | 1,00 | 50,00 | |||||||||||
| 1100 | 16,25 | 17,1 | 45,24 | U | Т | E | σт | U | σт | E | U=1 | U=50 | |||||||
| 1125 | 16,25 | 17,1 | 41,57 | 1 | 1012,5 | 5 | 72,60 | 50 | 120,83 | 5 | 72,60 | 120,83 | |||||||
| 1 | 1012,5 | 7,5 | 78,13 | 50 | 126,36 | 7,5 | 78,13 | 126,36 | |||||||||||
| 1 | 1012,5 | 10 | 83,67 | 50 | 131,90 | 10 | 83,67 | 131,90 | |||||||||||
| 1 | 1012,5 | 12,5 | 89,20 | 50 | 137,43 | 12,5 | 89,20 | 137,43 | |||||||||||
| 1 | 1012,5 | 15 | 94,74 | 50 | 142,97 | 15 | 94,74 | 142,97 | |||||||||||
| 1 | 1012,5 | 17,5 | 100,28 | 50 | 148,51 | 17,5 | 100,28 | 148,51 | |||||||||||
| 1 | 1012,5 | 20 | 105,81 | 50 | 154,04 | 20 | 105,81 | 154,04 | |||||||||||
| 1 | 1012,5 | 22,5 | 111,35 | 50 | 159,58 | 22,5 | 111,35 | 159,58 | |||||||||||
| 1 | 1012,5 | 25 | 116,89 | 50 | 165,12 | 25 | 116,89 | 165,12 | |||||||||||
| 1 | 1012,5 | 27,5 | 122,42 | 50 | 170,65 | 27,5 | 122,42 | 170,65 | |||||||||||
Sheet 8: Лист1
| Марка стали (сплава) | σо.д.,МПа |
| 08 кп | 84 |
| 3 | 86 |
| 6 | 92 |
| 20 | 85 |
| 25 | 86 |
| 45 н.р. | 87 |
| 40 | 88 |
| 45 | 88 |
| 40Х | 92 |
| 45Х н.р. | 89 |
| 45ХН н.р. | 95 |
| 18ХГТ н.р. | 95 |
| 30ХГСА | 105 |
| 4Х13 | 109 |
| У8 | 90 |
| ШХ15 | 95 |
| 15ХСНД | 97 |
| 14ГН | 99 |
| 60С2 | 114 |
| 1Х13 | 124 |
| Х18Н12М2Т | 147 |
| Р18 | 159 |
| Х17Н2 | 112 |
| 18ХНВА | 115 |
| ХН78Т (ЭИ435) | 196 |
| ХН75МБТЮ (ЭИ602) | 222 |
| ВЖ98 | 250 |
| ХН70Ю (ЭИ652) | 266 |
| ЭИ661 | 330 |
| Молибдено- марганцовистая | 110 |
| Хромомолибденовая | 115 |
| Кремниймарганцовистая | 120 |
| Хромоникель- молибденовая | 120 |
| 12ХНЗА | 100 |
| 20ХГНР н.р. | 100 |
| Х18Н9Т | 122 |
Sheet 9: Лист3
| факторы | -1 | ОУ | +1 | ∆Х | № | Х0 | Х1 | Х2 | Х3 | У1 | У2 | У3 | у | S2 | S | d max | τ | yэi | |||||||
| Т, С | E, % | U, c-1 | σт | Х1- температура t, С | 900 | 1012,5 | 1125 | 112,5 | 1 | 1 | -1 | -1 | -1 | 79,5 | 79,4 | 78,2 | 79,0 | 0,3 | 0,58 | 0,5 | 0,790 | ошибки нет | 92,36 | ||
| 1012,50 | 5 | 17,10 | 77,42 | Х2 - степень деформации ε, % | 5 | 16,25 | 27,5 | 11,25 | 2 | 1 | 1 | -1 | -1 | 41,6 | 40,9 | 38,5 | 40,3 | 1,7 | 1,31 | 1,3 | 0,959 | ошибки нет | 19,92 | ||
| 1012,50 | 7,5 | 17,10 | 83,03 | Х3 - скорость деформации u, с-1 | 1 | 25,5 | 50 | 24,5 | 3 | 1 | -1 | 1 | -1 | 128,9 | 129,2 | 131,2 | 129,8 | 1,1 | 1,03 | 1,4 | 1,405 | ошибки нет | 138,36 | ||
| 1012,50 | 10 | 17,10 | 88,64 | σ0= | 105 | МПа | 4 | 1 | 1 | 1 | -1 | 67,4 | 66,5 | 68,5 | 67,5 | 0,7 | 0,82 | 1,0 | 1,256 | ошибки нет | 70,70 | ||||
| 1012,50 | 12,5 | 17,10 | 94,25 | 5 | 1 | -1 | -1 | 1 | 135,4 | 134,3 | 139,5 | 136,4 | 5,0 | 2,23 | 3,1 | 1,384 | ошибки нет | 143,20 | |||||||
| 1012,50 | 15 | 17,10 | 99,86 | 390,20 | 6 | 1 | 1 | -1 | 1 | 70,8 | 69,1 | 71,5 | 70,5 | 1,0 | 0,99 | 1,0 | 1,012 | ошибки нет | 75,54 | ||||||
| 1012,50 | 17,5 | 17,10 | 105,47 | -0,33 | 7 | 1 | -1 | 1 | 1 | 219,7 | 218,6 | 215,5 | 217,9 | 3,1 | 1,77 | 1,7 | 0,987 | ошибки нет | 193,98 | ||||||
| 1012,50 | 20 | 17,10 | 111,08 | 2,21 | 8 | 1 | 1 | 1 | 1 | 114,9 | 112,5 | 115,2 | 114,2 | 1,4 | 1,19 | 1,0 | 0,828 | ошибки нет | 126,33 | ||||||
| 1012,50 | 22,5 | 17,10 | 116,70 | 0,98 | |||||||||||||||||||||
| 1012,50 | 25 | 17,10 | 122,31 | ||||||||||||||||||||||
| 1012,50 | 27,5 | 17,10 | 127,92 | число Стьюдента | 12,706 | 1,410 | S2max | 5,0 | |||||||||||||||||
| 1012,50 | 16,25 | 1 | 85,28 | [0,05;2] | 4,30 | S2min | 0,3 | ||||||||||||||||||
| 1012,50 | 16,25 | 2 | 86,36 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 4 | 88,52 | число фишера | Fрасч= | 14,878 | |||||||||||||||||||
| 1012,50 | 16,25 | 6 | 90,68 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 8 | 92,84 | Fтабл | 19,00 | ||||||||||||||||||||
| 1012,50 | 16,25 | 10 | 95,00 | 6,59 | |||||||||||||||||||||
| 1012,50 | 16,25 | 20 | 105,80 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 30 | 116,60 | однородность дисперсии | однородна | ||||||||||||||||||||
| 1012,50 | 16,25 | 40 | 127,40 | ||||||||||||||||||||||
| 1012,50 | 16,25 | 50 | 138,20 | Дисперсия воспроизводимости | 1,78 | ||||||||||||||||||||
| 900 | 16,25 | 17,10 | 137,43 | ||||||||||||||||||||||
| 925 | 16,25 | 17,10 | 129,70 | определение коэф регрессии | b0= | 106,95 | 111,74 | ||||||||||||||||||
| 950 | 16,25 | 17,10 | 121,98 | b1= | -33,83 | -34,76 | |||||||||||||||||||
| 975 | 16,25 | 17,10 | 114,25 | b2= | 25,39 | 25,25 | |||||||||||||||||||
| 1000 | 16,25 | 17,10 | 106,53 | b3= | 27,81 | 26,46 | |||||||||||||||||||
| 1025 | 16,25 | 17,10 | 98,81 | ||||||||||||||||||||||
| 1050 | 16,25 | 17,10 | 91,08 | ||||||||||||||||||||||
| 1075 | 16,25 | 17,10 | 83,36 | проверка значимости коэф регр | 0,22 | ||||||||||||||||||||
| 1100 | 16,25 | 17,10 | 75,63 | ||||||||||||||||||||||
| 1125 | 16,25 | 17,10 | 67,91 | tb0= | 226,60 | значим | |||||||||||||||||||
| tb1= | 71,67 | значим | |||||||||||||||||||||||
| tb2= | 53,80 | значим | |||||||||||||||||||||||
| tb3= | 58,92 | значим | |||||||||||||||||||||||
| проверка адекватность модели | S2Е | 7982,75 | Fр | 21,7257865853 | модель адекватна | ||||||||||||||||||||
| S2e | 367,43 |
Министерство образования и науки Российской Федерации
ГОУ ВПО Магнитогорский Государственный Технический Университет
им. Г. И. Носова
Кафедра обработки металлов давлением
Курсовая работа
На тему
«Определение аналитической зависимости сопротивления металла пластической деформации для стали 30ХГСА»
По дисциплине
«Организация и планирование эксперимента»
г. Магнитогорск 2009г.
Задание
На основании базисного значения пластичности меди (σ >о.д> =105 МПа для стали 30ХГСА) с использованием графиков термомеханических коэффициентов Кt, Ке, Кu, составить аналитическую зависимость, позволяющую определить сопротивление деформации (σ>т>) при горячей прокатке непосредственно от величин температуры, скорости и степени деформации для стали 30ХГСА.
Введение
Моделирование представляет собой метод исследования свойств определенного объекта (оригинала) посредством изучения свойств другого объекта (модели). В данной работе мы моделируем зависимость сопротивления металла пластической деформации от трех факторов. Согласно классификации видов моделирования, эту работу можно отнести к гибридному моделированию (включающему аналоговое и цифровое).
Для научного анализа процессов обработки металлов давлением широко применяют математическую и прикладную теории пластичности. Физические явления, происходящие при ОМД, описываются системой дифференциальных уравнений, которые содержат значительное число переменных.
Метод моделирования позволяет на высоком научном уровне проводить экспериментальные исследования физических процессов. Этим методом можно на модели, уменьшенной или увеличенной по сравнению с оригиналом, проводить качественное или количественное изучение протекающих в реальности процессов, что не всегда доступно для детального исследования, а в ряде случаев, когда, например, создается новый процесс или оборудование, вообще невозможно.
При разработке технологических процессов обработки металлов давлением и проектировании оборудования необходимо знать полное усилие Р, которое нужно приложить к деформируемому телу для преодоления сопротивления последнего пластической деформации и трения на поверхности контакта с инструментом. По величине Р определяют характеристики необходимого для деформации оборудования – усилие пресса, мощность двигателя прокатного стана и др.
Из существующих методов определения «мгновенного» предела текучести (сопротивления металла деформации) чаще всего используют метод термомеханических коэффициентов, как наиболее простой и доступный, позволяющий в тоже время с достаточной для практики точностью вычислить σт при заданных температуре, степени и скорости деформации.
σт=σ>0.д.>*Kt*K ε *Ku (1)
где σ>0.д >– базисное значение сопротивления деформации;
Kt – температурный коэффициент;
Kε – степенной коэффициент;
Ku – скоростной коэффициент.
Графики зависимости коэффициентов Kt, Kε и Ku от температуры, степени деформации и скорости деформации приведены в справочниках.
Задачей регрессионного анализа ставится нахождение зависимости отклика от фактора, то есть термомеханического коэффициента от его аргумента.
П.Л.Клименко путем аппроксимации обобщенных кривых изменения k>t>, k>> и k>u> вывел формулы зависимости коэффициентов от температуры, степени и скорости деформации:
(2)
для
(3)
для
(4)
для
с-1 (5)
для
с-1,
(6)
Нам надлежит найти похожие уравнения зависимостей Kt=f(t), Kε=f(ε) и Ku=f(u), используя метод парного регрессионного анализа. Парный регрессионный анализ – это метод математической статистики, который позволяет найти отображение (модель, аппроксимацию) стохастической зависимости между откликом У и фактором Х.
В случае стохастической зависимости при определенном значении Хi фактора Х может наблюдаться множество значений отклика У. В производственных условиях фактор является переменной величиной, но при проведении регрессионного анализа полагают, что его значение хi неслучайно.
Учитывая возможные отклонения, модель связи некоторого значения отклика с соответствующим значением фактора может быть представлена в виде двух составляющих
yi=φ(xi)+εi (7)
где φ(xi) – систематическая (объясненная) составляющая; она обусловлена существованием связи между откликом и фактором;
εi – случайная составляющая; она обусловлена разнообразными возмущениями и вызывает отклонение уi от соответствующих реальной зависимости.
Относительно εi делают следующие предположения:
- это нормально распределенная случайная переменная.
- μ(εi)=0 (математическое ожидание случайной составляющей равно нулю).
- σ(εi)=const (дисперсия случайной составляющей постоянна).
- в различных наблюдениях значения εi не зависят друг от друга.
Задача определения вида уравнения регрессии состоит в нахождении систематической составляющей φ(xi).
Из различных уравнений регрессии наилучшим считают то, которое обеспечивает минимум дисперсии фактических (полученных экспериментально) значений отклика относительно линии регрессии. Эту дисперсию называют остаточной дисперсией относительно регрессии и находят по формуле
(8)
Объясненная дисперсия характеризует рассеяние уi, обусловленное зависимостью отклика от фактора; ее находят по формуле
(9)
После расчетов проверяют соответствие полученного уравнения опытным данным по критерию Фишера
(10)
где a- уровень значимости;
k- число наблюдений.
Если это условие выполняется, то объясненная дисперсия существенно больше остаточной. Это означает, что между откликом и фактором существует взаимосвязь, которую с вероятностью a допустимо аппроксимировать рассматриваемым уравнением регрессии.
Проведя парный регрессионный анализ, находим значения термомеханических коэффициентов по полученным уравнениям и подставляем их в уравнение (1). Таким образом находим сопротивление металла деформации вторым методом (первый раз σт находили, используя графики).
Множественный регрессионный анализ – это метод математической статистики, позволяющий найти наиболее точное и достоверное отображение (модель, аппроксимацию) стохастической зависимости между откликом Y и факторами Х>1>, Х>2>, …,Х>j>,X>m>.
Связь отклика с некоторым комплексом факторов также можно представить в виде объясненной и случайной составляющих.
Коэффициенты регрессии b>j> являются случайными величинами с математическими ожиданиями β>j> и дисперсиями, которым соответствуют стандартные отклонения S>bj>. Значение b>j >признается статистически значимым, если выполняется условие
(11)
где t>bj> и t[a;n-k] – расчетное и табличное число Стьюдента.
Если условие (11) не выполняется, то влияние фактора Х>j> на отклик несущественное, и его надо исключить из дальнейших расчетов.
Статистическая надежность выбранного уравнения регрессии проверяется также по критерию Фишера (уравнение (10).
После проведения множественного регрессионного анализа получаем уравнение вида
σт = f (t, U, ε), (12)
Находим при помощи полученного уравнения сопротивления металла деформации третьим способом.
Затем сравниваем результаты всех трех подходов к определению σ>т> и выбираем наилучший результат, у которого меньше средняя ошибка.
Краткая характеристика стали 30ХГСА
Из стали 30ХГСА изготовляют различные улучшаемые детали: валы, оси, зубчатые колеса, фланцы, корпуса обшивки, лопатки компрессорных машин, работающие при температуре до 200°С, рычаги, толкатели, ответственные сварные конструкции, работающие при знакопеременных нагрузках, крепежные детали, работающие при низких температурах. Склонна к отпускной способности, флокеночувствительна
Таблица 1 – Химический состав стали 30ХГСА,(%).
|
С |
Si |
Mn |
S |
P |
Cr |
Ni |
Cu |
|
0,3 |
0,9-1,2 |
0,8-1,1 |
0,025 |
0,025 |
0,8-1,1 |
0,3 |
0,3 |
Исходные данные
Данные с исходных графиков приведены в таблице 2.
Таблица 2 – Исходные данные данные.
|
Число наблюю-дений |
t,ºC |
Kt |
ε,% |
Kε |
u, c-1 |
Ku |
|
1 |
900 |
1,30 |
5 |
0,82 |
1 |
0,71 |
|
2 |
925 |
1,23 |
7,5 |
0,92 |
2 |
0,80 |
|
3 |
950 |
1,15 |
10 |
1,00 |
4 |
0,88 |
|
4 |
975 |
1,07 |
12,5 |
1,07 |
6 |
0,92 |
|
5 |
1000 |
1,00 |
15 |
1,13 |
8 |
0,98 |
|
6 |
1025 |
0,93 |
17,5 |
1,18 |
10 |
1,00 |
|
7 |
1050 |
0,85 |
20 |
1,22 |
20 |
1,07 |
|
8 |
1075 |
0,79 |
22,5 |
1,26 |
30 |
1,12 |
|
9 |
1100 |
0,74 |
25 |
1,30 |
40 |
1,18 |
|
10 |
1125 |
0,68 |
27,5 |
1,33 |
50 |
1,21 |
|
среднее |
1012,5 |
0,97 |
16,25 |
1,12 |
17,1 |
0,99 |
Определение уравнений зависимости термомеханических коэффициентов от их физических величин
Проведем парный регрессионный анализ. Рассмотрим по 5 уравнений для каждой зависимости. Расчеты удобно проводить в среде электронных таблиц MS Excel. Результаты оценки пяти уравнений представлены в таблицах 3-5. В таблицах жирной строкой выделено то уравнение, которое является наилучшей аппроксимацией исследуемой зависимости. Для температурного коэффициента это логарифмическая зависимость, для коэффициента деформации - степенная зависимость, для скоростного коэффициента – логарифмическая зависимость. При выборе уравнения ориентировались на критерий Фишера F>расч> принимающий максимальное значение, а также условие F>расч>>F>табл>.
Графики выбранных уравнений приведены на рисунках 1-3 . На рисунках точками изображены значения, полученные по исходным графикам зависимостей термомеханических коэффициентов от их физических величин. Сплошными линиями показаны графики полученных уравнений аппроксимации.
Таблица 3 – Уравнения зависимости Кt от t
|
функция |
Уравнение регрессии |
R2 |
k |
Fp |
F>0,95> |
|
|
Линейная |
1 |
Кt = -0,0028*t + 3,8065 |
0,9963 |
2 |
2154,162 |
5,318 |
|
Логарифмическая |
2 |
Кt = -2,8261Ln(t) + 20,524 |
0,9987 |
2 |
6145,846 |
5,318 |
|
Полином 2 степ |
3 |
Кt = 0,000002*t2 - 0,0077x + 6,2793 |
0,9993 |
3 |
4996,500 |
4,737 |
|
Степенная |
4 |
Кt = 6*109*t-2,9378 |
0,995 |
2 |
1592,000 |
5,318 |
|
экспоненциальная |
5 |
Кt = 18,259e-0,0029t |
0,9982 |
2 |
4436,444 |
5,318 |
Таблица 4 – Уравнения зависимости Кε от ε
|
функция |
Уравнение регрессии |
R2 |
k |
Fp |
F>0,95> |
|
|
Линейная |
1 |
Kε = 0,0219*ε + 0,7665 |
0,9672 |
2 |
235,902 |
5,318 |
|
Логарифмическая |
2 |
Kε = 0,304Ln(ε) + 0,3123 |
0,9967 |
2 |
2416,242 |
5,318 |
|
Полином 2 степ |
3 |
Kε = -0,0006*ε2 + 0,022ε + 0,6338 |
0,9985 |
3 |
2329,833 |
4,737 |
|
Степенная |
4 |
Kε = 0,5186*ε0,2857 |
0,9996 |
2 |
19992,000 |
5,318 |
|
экспоненциальная |
5 |
Kε = 0,799e0,020ε |
0,9388 |
2 |
122,719 |
5,318 |
Таблица 5 – Уравнения зависимости Кu от U
|
функция |
Уравнение регрессии |
R2 |
k |
Fp |
F>0,95> |
|
|
Линейная |
1 |
Ku = 0,0086U + 0,8404 |
0,8274 |
2 |
38,350 |
5,318 |
|
Логарифмическая |
2 |
Ku = 0,1253Ln(U) + 0,7081 |
0,9960 |
2 |
1992,000 |
5,318 |
|
Полином 2 степ |
3 |
Ku = -0,0002*U2 + 0,0202*U + 0,7777 |
0,9246 |
3 |
42,919 |
4,737 |
|
Степенная |
4 |
Ku = 0,7268*U0,1317 |
0,9930 |
2 |
1134,857 |
5,318 |
|
экспоненциальная |
5 |
Ku = 0,8401*e0,0087U |
0,7648 |
2 |
26,014 |
5,318 |
Рисунок 1. Температурный коэффициент для стали 30ХГСА
Рисунок 2. Степенной коэффициент для стали 30ХГСА
Рисунок 3. Скоростной коэффициент для стали 30ХГСА
По данным, полученным в результате парного анализа (таблица 6) строим графики (рисунки 4-6).
Таблица 6 – Данные полученные в результате парного регрессионного анализа
-
Число наблюдений
t,ºC
Kt
ε,%
Kε
u, c-1
Ku
1
900
1,30
5
0,82
1
0,71
2
925
1,22
7,5
0,92
2
0,79
3
950
1,15
10
1,00
4
0,88
4
975
1,07
12,5
1,07
6
0,93
5
1000
1,00
15
1,12
8
0,97
6
1025
0,93
17,5
1,17
10
1,00
7
1050
0,86
20
1,22
20
1,08
8
1075
0,80
22,5
1,26
30
1,13
9
1100
0,73
25
1,30
40
1,17
10
1125
0,67
27,5
1,34
50
1,20
Рисунок 4. Температурный коэффициент для стали 30ХГСА
Рисунок 5. Степенной коэффициент для стали 30ХГСА
Рисунок 6. Скоростной коэффициент для стали 30ХГСА
Определение уравнения зависимости сопротивления деформации непосредственно от физических величин
Для проведения множественного регрессионного анализа нужно подготовить таблицу исходных данных, в которой каждому значению σ>т> (отклику) соответствует набор из трех значений параметров: температуры, скорости деформации и степени деформации. При формировании таблицы нужно два из трех факторов оставлять неизменными, а третий должен меняться. Так следует смоделировать три опыта, в которых по очереди меняются значения температуры, степени деформации и скорости. Исходные данные для множественного регрессионного анализа приведены в таблице 7.
Таблица 7 – Исходные данные для составления уравнения σт = f (t, U, ε)
|
σт=σ>0>*Kt*Ke*Ku |
Т, С |
E, % |
U, c-1 |
|
82,77 |
1012,5 |
5,0 |
17,1 |
|
92,87 |
7,5 |
||
|
100,94 |
10,0 |
||
|
108,01 |
12,5 |
||
|
114,06 |
15,0 |
||
|
119,11 |
17,5 |
||
|
123,15 |
20,0 |
||
|
127,19 |
22,5 |
||
|
131,22 |
25,0 |
||
|
134,25 |
27,5 |
||
|
81,54 |
16,25 |
1 |
|
|
91,88 |
2 |
||
|
101,07 |
4 |
||
|
105,66 |
6 |
||
|
112,55 |
8 |
||
|
114,85 |
10 |
||
|
122,89 |
20 |
||
|
128,63 |
30 |
||
|
135,52 |
40 |
||
|
138,97 |
50 |
||
|
151,30 |
900 |
17,1 |
|
|
143,15 |
925 |
||
|
133,84 |
950 |
||
|
124,53 |
975 |
||
|
116,38 |
1000 |
||
|
108,24 |
1025 |
||
|
98,92 |
1050 |
||
|
91,94 |
1075 |
||
|
86,12 |
1100 |
||
|
79,14 |
1125 |
По подготовленной таблице в MS Excel с помощью функции «Регрессия» из пакета анализа данных проводим множественный регрессионный анализ.
В результате получаем уравнение σ>т>= 390,20 - 0,33*T +2,21*E +0,98*U
Для выяснения статистической значимости коэффициентов уравнения сравниваем рассчитанные коэффициенты Стьюдента с табличными для числа наблюдений 10 и уравнения с четырьмя коэффициентами и доверительной вероятностью 95%. Коэффициенты Стьюдента, рассчитанные для коэффициентов t, ε , u оказались больше табличного коэффициента Стьюдента, то есть, статистически значимыми.
Для выяснения надежности аппроксимации полученным уравнением сравниваем рассчитанное число Фишера с табличным для степеней свободы (10-4=6) и доверительной вероятностью 95%. Рассчитанный критерий Фишера оказался больше табличного, значит, уравнение достоверно отражает исследуемую зависимость. Лист MS Excel с расчетом представлен на рисунке 7.
Рисунок
7 – Лист МS
Excel
Для построения графика полученного уравнения с двумя неизвестными на плоскости нужно, чтобы один из факторов принимал два экстремальных значения, а второй непрерывно изменялся. Тогда графически это уравнение можно представить как область в координатах «изменяющийся параметр – предел текучести». Такие графики для полученного уравнения представлены на рисунках 8-10.
Рисунок 5. Зависимость сопротивления металла деформации от скорости деформации
Рисунок 6. Зависимость сопротивления металла деформации от температуры деформации
Рисунок 7. Зависимость сопротивления металла деформации от степени деформации
Планирование полного факторного эксперимента
Необходимо отыскать по экспериментальным данным уравнение, связывающее предел текучести сплава 30ХГСА со степенью деформации, скоростью деформации и температурой, путем постановки полного факторного эксперимента. Зададим параметры, влияющие на предел текучести, а также определим основной уровень (ОУ), интервалы варьирования (∆Х), а также верхний и нижний уровни факторов (-1/+1).
Таблица 8 – Факторы, влияющие на предел текучести
-
факторы
-1
ОУ
+1
∆Х
Х>1>- температура t, С
900
1012,5
1125
112,5
Х>2> - степень деформации ε, %
5
16,25
27,5
11,25
Х>3> - скорость деформации u, с-1
1
25,5
50
24,5
Введем фиктивную переменную Х>0>, всегда принимающую значение +1. Примем количество параллельных опытов равным 3 (таблица 9)
Таблица 9 – Матрица планирования эксперимента
-
№
Х>0>
Х>1>
Х>2>
Х>3>
У>1>
У>2>
У>3>
уS2
1
+1
-1
-1
-1
79,5
79,4
78,2
79,0
0,3
2
+1
+1
-1
-1
41,6
40,9
38,5
40,3
1,7
3
+1
-1
+1
-1
128,9
129,2
131,2
129,8
1,1
4
+1
+1
+1
-1
67,4
66,5
68,5
67,5
0,7
5
+1
-1
-1
+1
135,4
134,3
139,5
136,4
5,0
6
+1
+1
-1
+1
70,8
69,1
71,5
70,5
1,0
7
+1
-1
+1
+1
219,7
218,6
215,5
217,9
3,1
8
+1
+1
+1
+1
114,9
112,5
119,2
115,5
7,6
Оценка дисперсий среднего арифметического в каждой строке матрицы
Определим среднее значение параметра оптимизации для первой строки матрицы планирования
Результаты расчета У>i> для каждой строки приведены выше в матрице планирования эксперимента.
Далее определяем дисперсию параметра оптимизации в каждой строке матрицы планирования. Для первой строки уравнение запишется как
Исключение ошибок в параллельных опытах
Находим статистики S, d>max> и τ>max> для каждой строки матрицы планирования. Для первой строки
=0,5
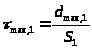=0,790
Далее определяем табличное значение τ[0,05;n-2] =1,410. Принимая во внимание, что τ>max>>,1>=0,790< τ[0,05;n-2] =1,410 считаем, что опыт не содержит грубых ошибок.
Проверка однородности дисперсий с помощью критерия Фишера
Экспериментальные значения дисперсии в матрице планирования эксперимента составляют: S2>max>=5,0; S2>min>=0,3
Определим число Фишера и сравним его с табличным значением:
=
14,88
F>табл>=[0,05;2;2]=19,00
Так как расчетное значение числа Фишера меньше табличного (F>расч><F>табл>), считаем, что дисперсии однородны.
Расчет дисперсии воспроизводимости
Определим дисперсию воспроизводимости:
Определение коэффициентов регрессии
Определяем значения коэффициентов уравнения регрессии. Свободному члену в уравнении математической модели соответствует коэффициент при фиктивной переменной Х>0>:
b>0 >= (79,0+40,3+129,8+67,5+136,4+70,5+217,9+114,2)/8=106,95
Аналогично находятся значения остальных коэффициентов регрессии:
b>1>=(-1*79,0+1*40,3-1*129,8+1*67,5-1*136,4+1*70,5-1*217,9+114,2)/8= -33,83
b>2>= 25,39; b>3>=27,81
Проверка значимости коэффициентов регрессии
Для проверки значимости коэффициентов необходимо найти дисперсию коэффициентов регрессии по формуле
=1,78/8=0,22
Далее, для каждого коэффициента определяем расчетное число Стьюдента
t>b>>0>=
Табличное число Стьюдента при t[0,05;2]=4,30. Так как t>b>>0>=226,69>t[0.05;2]=2,78, коэффициент b>0> является значимым. Аналогичным образом поступаем с другими коэффициентами t>b>>1>=71,67; t>b>>2>=53,80; t>b>>3>=58,92. Таким образом, коэффициенты являются значимыми и уравнение модели примет вид
УЭ=106,95-33,83Х>1>+25,39Х>2>+27,81Х>3>
Проверка адекватности модели
По полученному выше уравнению модели рассчитаем значения параметра оптимизации для каждой строки матрицы планирования. Рассчитаем величину объясненной дисперсии, величина которой составляет:
=
= ((79,0-106,95)2 + (40,3-106,95)2 + (129,8-106,95)2 + (67,5-106,95)2 + (136,4-106,95)2 +
+(70,5-106,95)2 + (217,9-106,95)2 +(114,2-106,95)2)/3=7982,75
Используя средние фактические значения параметра оптимизации и полученные по уравнению модели определяем величину остаточной дисперсии
((79,0-87,24)2+(40,3-19,92)2+(129,8-138,36)2+(67,5-71,04)2+(136,4-143,2)2+(70,5-75,88)2+
+(217,9-194,32)2+(114,2-126,33)2)/4=367,43
Находим число Фишера (Fp) и сравниваем его с табличным значением F>табл>[0,05;f>E>;f>e>],
где f>E>> >=k-1 числа степеней свободы объясненной дисперсии; f>e>=N-k числа степеней свободы остаточной дисперсии;
F>табл>[0,05;3;4]=6,59
=7982,75/367,43=21,72;
F>p>>F>табл>, то есть созданная математическая модель адекватно описывает изменение предела текучести сплава 30ХГСА в зависимости от температуры, степени и скорости деформации.
Таким образом, путем постановки полного факторного эксперимента было найдено уравнение, связывающее предел текучести сплава 30ХГСА с температурой, степенью и скоростью деформации. Значимые коэффициенты регрессии равны:
b>0>= 106,95; b>1>= -33,83; b>2>= 25,39; b>3>=27,81
Наибольшим по модулю является коэффициент b>1>= -33,83, соответствующий температуре прокатки. Это означает, что наиболее интенсивно на предел текучести сплава 30ХГСА является температура прокатки.
Уравнение математической модели имеет вид:
Сравнительная таблица
Построим сравнительную таблицу, позволяющую сопоставить сходимость результатов определения сопротивления металла деформации методом термомеханических коэффициентов (1), применением уравнений, полученных после проведения парного регрессионного анализа (2), использованием уравнения, полученного множественным регрессионным анализом (3) и использованием уравнения, полученного с применением планирования факторного эксперимента(4).
Таблица 3.1 – Сравнение результатов
|
№ п/п |
Т, С |
E, % |
U, c-1 |
σ>т1> |
σ>т2> |
Расхождение % |
σ>т3> |
Расхождение % |
σ>т4> |
Расхождение % |
|
1 |
1012,5 |
7,5 |
17,1 |
92,87 |
93,08 |
0,23 |
93,98 |
1,18 |
83,03 |
11,85 |
|
2 |
1012,5 |
10,0 |
17,1 |
100,94 |
101,06 |
0,12 |
99,52 |
1,43 |
88,64 |
13,88 |
|
3 |
1012,5 |
12,5 |
17,1 |
108,01 |
107,71 |
0,28 |
105,05 |
2,81 |
94,25 |
14,59 |
|
4 |
1012,5 |
15,0 |
17,1 |
114,06 |
113,47 |
0,52 |
110,59 |
3,14 |
99,86 |
14,22 |
|
5 |
1012,5 |
17,5 |
17,1 |
119,11 |
118,58 |
0,45 |
116,12 |
2,57 |
105,47 |
12,93 |
|
6 |
1012,5 |
20,0 |
17,1 |
123,15 |
123,19 |
0,03 |
121,66 |
1,22 |
111,08 |
10,86 |
|
7 |
1012,5 |
22,5 |
17,1 |
127,19 |
127,40 |
0,17 |
127,20 |
0,01 |
116,70 |
8,99 |
|
8 |
1012,5 |
25,0 |
17,1 |
131,22 |
131,30 |
0,06 |
132,73 |
1,14 |
122,31 |
7,29 |
|
9 |
1012,5 |
27,5 |
17,1 |
134,25 |
134,92 |
0,50 |
138,27 |
2,91 |
127,92 |
4,95 |
|
10 |
1012,5 |
16 |
1 |
81,54 |
81,34 |
0,25 |
97,51 |
16,37 |
85,28 |
4,38 |
|
11 |
1012,5 |
16 |
2 |
91,88 |
91,31 |
0,62 |
98,49 |
6,72 |
86,36 |
6,39 |
|
12 |
1012,5 |
16 |
4 |
101,07 |
101,29 |
0,22 |
100,46 |
0,60 |
88,52 |
14,17 |
|
13 |
1012,5 |
16 |
6 |
105,66 |
107,12 |
1,37 |
102,43 |
3,15 |
90,68 |
16,52 |
|
14 |
1012,5 |
16 |
8 |
112,55 |
111,26 |
1,16 |
104,40 |
7,81 |
92,84 |
21,23 |
|
15 |
1012,5 |
16 |
10 |
114,85 |
114,48 |
0,33 |
106,37 |
7,97 |
95,00 |
20,89 |
|
16 |
1012,5 |
16 |
20 |
122,89 |
124,45 |
1,26 |
116,21 |
5,75 |
105,80 |
16,15 |
|
17 |
1012,5 |
16 |
30 |
128,63 |
130,29 |
1,27 |
126,05 |
2,04 |
116,60 |
10,32 |
|
18 |
1012,5 |
16 |
40 |
135,52 |
134,43 |
0,81 |
135,90 |
0,28 |
127,40 |
6,38 |
|
19 |
1012,5 |
16 |
50 |
138,97 |
137,64 |
0,96 |
145,74 |
4,65 |
138,20 |
0,56 |
|
20 |
900 |
16 |
17,1 |
151,30 |
151,27 |
0,02 |
149,98 |
0,87 |
137,43 |
10,09 |
|
21 |
925 |
16 |
17,1 |
143,15 |
142,26 |
0,63 |
141,85 |
0,92 |
129,70 |
10,37 |
|
22 |
950 |
16 |
17,1 |
133,84 |
133,49 |
0,26 |
133,71 |
0,10 |
121,98 |
9,72 |
|
23 |
975 |
16 |
17,1 |
124,53 |
124,94 |
0,33 |
125,57 |
0,83 |
114,25 |
8,99 |
|
24 |
1000 |
16 |
17,1 |
116,38 |
116,62 |
0,20 |
117,43 |
0,89 |
106,53 |
9,25 |
|
25 |
1025 |
16 |
17,1 |
108,24 |
108,49 |
0,24 |
109,29 |
0,96 |
98,81 |
9,54 |
|
26 |
1050 |
16 |
17,1 |
98,92 |
100,57 |
1,63 |
101,15 |
2,20 |
91,08 |
8,61 |
|
27 |
1075 |
16 |
17,1 |
91,94 |
92,83 |
0,96 |
93,01 |
1,15 |
83,36 |
10,30 |
|
28 |
1100 |
16 |
17,1 |
86,12 |
85,27 |
1,00 |
84,87 |
1,48 |
75,63 |
13,87 |
|
29 |
1125 |
16 |
17,1 |
79,14 |
77,88 |
1,62 |
76,73 |
3,14 |
67,91 |
16,54 |
|
30 |
1012,5 |
7,5 |
17,1 |
92,87 |
93,08 |
0,23 |
93,98 |
1,18 |
83,03 |
11,85 |
|
Средняя ошибка |
0,59 |
3,02 |
11,03 |
Заключение
По величине средней ошибки можно судить о возможности применения каждого из методов в инженерных расчетах и на действующих станках. При использовании метода парного регрессионного анализа средняя ошибка составила 0,59 %. При расчетах методом множественного регрессионного анализа средняя ошибка составила 3,02%. При расчетах с применением планирования факторного эксперимента средняя ошибка составила 11,03%
Значит, первый вариант дает более точные результаты.
Список использованной литературы
Третьяков А.В., Зюзин В.И. Механические свойства металлов и сплавов при обработке металлов давлением. Справочник. М. Металлургия. 1973. 224с.
Веников В.А., Веников Г.В. Теория подобия и моделирования. Учебник для вузов. М. Высш.шк. 1984. 439с.
Моллер А.Б. Методические указания для выполнения курсовой работы по дисциплине «Теория подобия и физическое моделирование». Магнитогорск: МГТУ, 2000.
Моллер А.Б., Синицкий О.В., Назаров Д.В.Моделирование процессов ОМД с применением планирования факторного эксперимента. Методические указания для самостоятельной работы, практических занятий и выполнения расчетно-графических работ по дисциплине «Планирование и организация эксперимента». Магнитогорск: МГТУ, 2008.
Румянцев М.И. Методические указания к лабораторной работе по дисциплине «Обработка и анализ числовой информации». Магнитогорск: МГТУ, 2003.