Методы кинематического исследования механизмов
Задачи ТММ. Основные понятия и определение машин, механизмов, звеньев и кинематических пар
Машина – устройство, совершающее механическое движение для преобразования энергии с целью получения народно-хозяйственного эффекта. Система тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел, называется механизмом. По функциональному назначению механизмы делятся на: 1) механизмы двигателей и преобразователей;
2) передаточные механизмы;
3) исполнительные механизмы;
4) механизмы управления, контроля и регулирования; 5) механизмы подачи, транспортировки, питания и сортировки обрабатываемых средств и объектов; 6) механизмы автоматического счета, взвешивания и упаковки готовой продукции. Теория механизмов есть наука, изучающая строение, кинематику и динамику механизмов в связи с их анализом и синтезом. Задачи ТММ делятся на две группы: 1) структурный и кинематический анализ; 2) динамический анализ механизмов; 3) синтез механизмов. Твердые тела, из которых образуется механизм, называют звеньями. Звено – это одна деталь, либо совокупность нескольких деталей. Кривошип – звено, вращающееся на полный оборот вокруг неподвижной оси, при неполном обороте – коромыслом. Звено, совершающее возвратно- поступательное движение по неподвижной оси – ползуном. Звено, связывающие два подвижных звена называется шатуном. Неподвижное звено называют стойкой. Кулисой называется звено, совершающее возвратно-поступательное или вращательное движение по подвижной оси. Кинематической парой называют подвижное соединение двух соприкасающихся звеньев. Совокупность поверхностей, линий и точек звена, входящих в соприкосновение с другим звеном пары, называют элементом пары. Систему звеньев, образующих между собой кинематические пары, называют кинематической цепью. Таким образом, механизм – кинематическая цепь, в состав которой входит неподвижное звено.
Классификация кинематических пар по характеру сопряжения звеньев и по числу относительных подвижностей звеньев
Кинематические пары делятся на низшие и высшие. Кинематическая пара называется высшей, если элементы звеньев соприкасаются по линиям или в точках, и низшей, если только по поверхности. Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение их звеньев. Число условий связи, наложенных на относительное движение каждого звена кинематической пары, может располагаться в пределах от 1 до 5. Следовательно, число степеней свободы H звена кинематической пары в относительном движении может быть выражено зависимостью H = 6 – S.
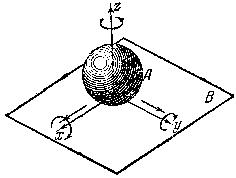
пяти подвижная КП
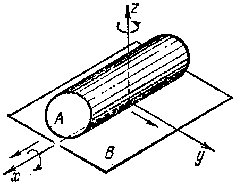
четырех подвижная КП
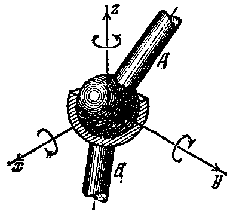
трех подвижная КП
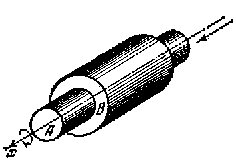
двух подвижная вращательная КП

одно подвижные КП
Все кинематические цепи в свою очередь делятся на замкнутые и незамкнутые. Замкнутой кинематической цепью называется кинематическая цепь, каждое звено которой входит по крайней мере в две кинематические пары. Незамкнутой кинематической цепью называется кинематическая цепь, в которой есть звенья, входящие только в одну кинематическую пару.
Группы Ассура. Определение числа степеней свободы плоских и пространственных механизмов и анализ структуры плоских рычажных механизмов
Группой Ассура набор звеньев механизма, которые не вносят подвижности в механизм (суммарная степень подвижности равно 0) и не распадаются на более простые цепи, обладающие также нулевой степенью подвижности. Образование любого плоского механизма может быть представлено как последовательное присоединение групп, удовлетворяющих условию 3n–2p>1>–p>2> = 0 (n – число подвижных звеньев цепи, p>1,2> – число кинематических пар, соответственно одно или двух подвижных). Отсюда следует, что условие, которому должны удовлетворяться группы, в состав которых входят только одноподвижные пары, можно записать так: 3n–2p>1> = 0, следовательно, p>1> = 3n/2 – условие существования группы Ассура. Все входящие в состав плоского механизма высшие кинематические одноподвижные и двухподвижные пары могут быть заменены кинематическими цепями, образованными только одноподвижными парами.
Группой Ассура первого вида называется группа состоящая из 3-х кинематических пар, в которой элементы 2-х звеньев остаются свободными.
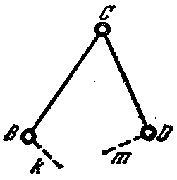
Вторым видом является тот, при котором поступательной парой заменена одна из крайних вращательных пар.
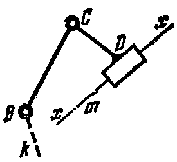
В третьем виде поступательной парой заменена средняя вращательная пара.
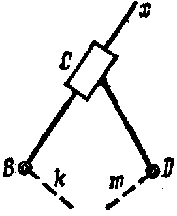
В четвертом виде две крайние вращательные пары заменены двумя поступательными парами.
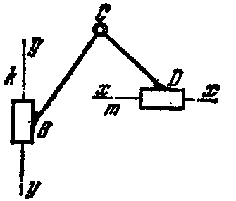
В пятом виде поступательными парами заменены крайняя и средняя вращательные пары.
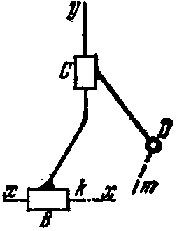
Под степенью подвижности кинематической цепи понимается ее наибольшее число степеней свободы относительно условно неподвижной стойки.
Для плоских механизмов, звенья которых движутся в плоскостях, параллельных между собой, число степеней свободы определяется по формуле Чебышева: W = 3n – 2p>1> – p>2>. Данная формула является структурной формулой плоских механизмов.
Пассивные связи и избыточные подвижности
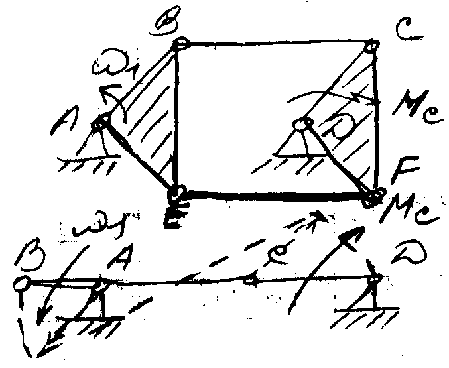
M>C>–момент сопротивления движению. Переход механизма из одной сборки в другую (механизм неправильно спроектирован). Усовершенствованный механизм с дополнительными звеньями не меняет сборки при работе.
W = 3n–2p>1 >=34–26 = 0. Это говорит о том, что механизм не вращается. Но на самом деле он вращается, но есть пассивная связь EF, не добавляющая степеней свободы механизму.
Аналитический метод кинематического исследования механизмов. Аналоги скоростей и ускорений
Кинематическое исследование механизма, т.е. изучение движения звеньев механизма без учета сил, обусловливающих это движение, состоит в основном в решении трех следующих задач:
1) определение перемещений звеньев и траекторий, описываемых точками звеньев; 2) определение скоростей отдельных точек звеньев и угловых скоростей звеньев; 3) определение ускорений отдельных точек звеньев и угловых ускорений звеньев. В аналитической форме функция перемещений, скоростей или ускорений задаются в виде функции, связывающей перемещение или угол поворота ведущего звена со временем, в зависимости от того, какую пару образует ведущее звено. Рассмотрим Группу Ассура 3-го вида:
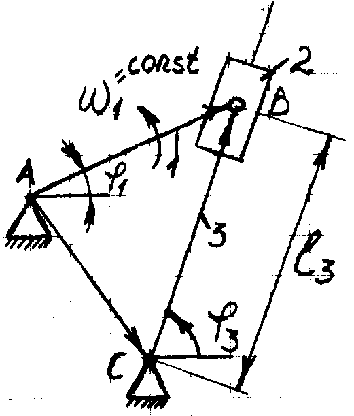
Используется метод замкнутых векторных контуров.
1)AB =AC + CB,
С>х> +ℓ>3>cos>3> = B>x>
C>y>+ℓ>3>sin>3> = B>y>
ℓ>3> =[(B>x>–C>x>)2+(B>y>–C>y>)2], >3> = arctg[B>y>–C>y>)/(B>x>–C>x>)],
откуда B>x>=ℓ>AB>cos>1>,
B>y> = ℓ>AB>sin>1>.
2)Угловая скорость >k> этого звена может быть представлена так: >3> = d>3>/dt – угловая скорость, >3>= d>3>/d – безразмерная угловая скорость звена 3, называемая аналогом угловой скорости.
3)Угловое ускорение определяется формулой >k> = d>k>/dt, тогда d2>3>/d>1>2 = >3> называется аналогом углового ускорения. Скорость поступательного движения какого-либо звена равна V = dS/dt , величина
dS/dt=dS/dd/dt,
где dS/dt – аналог скорости, имеющий размерность длины. Т.е V = S (уравнение связи), где S–аналог скорости звена. Продифференцировав это выражение по времени, получаем
a>m> = dV/dt = d(S)/dt = dS/dt + Sd/dt = 2S + S.
Величина a = S=d2S/d>2> есть аналог ускорения, имеющий также размерность длины.
Графический метод кинематического анализа плоских рычажных механизмов. Два метода разложения движения. Построение планов скоростей и ускорений. Теорема о подобии
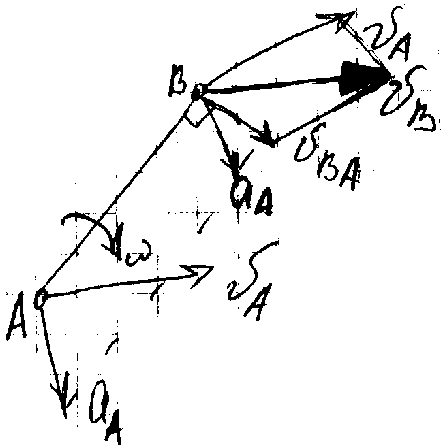
1-й способ разложения движения (применяется когда известно движение одной точки звена и требуется определить движение другой точки того же звена):
V>B> = V>A>+V>BA>,
где V>A>–переносная скорость, V>BA> – относительная скорость (скорость точки В по отношению к точке А),
a>B> = a>A> + a>BA>n + a>BA>,
где a>A> – переносное ускорение, a>BA>n и a>BA> – относительные ускорения. 2-й способ (применяется когда известно движение звена и надо определить движение второго звена и эти два звена образуют поступательную пару):
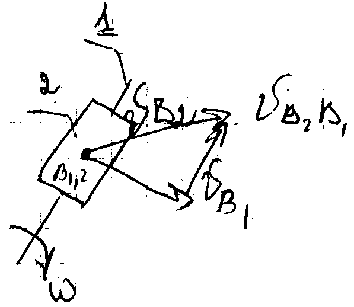
Точки B>2> и B>1> совпадают, V>B>>2> = V>B>>1> + V>B>>2>>B>>1>, где V>B>>1>– переносная (вращательная) скорость, V>B>>2>>B>>1>– относительная скорость (поступательная); a>B>>2>=a>B>>1> + a>B>>2>>B>>1>k + a>B>>2>>B>>1>r, a>B>>1>– переносное ускорение, a>B>>2>>B>>1>k (поворотное) и a>B>>2>>B>>1>r(реактивное)– относительные.
Теорема о подобии (применяется для точек одного звена, когда известны скорости, ускорения двух точек этого звена): относительные скорости и ускорения точек одного и того же звена образуют на планах скоростей и ускорений фигуры, подобные одноименной фигуре на схеме механизма. Эти фигуры сходственно расположены, т.е. при чтении буквенных обозначений их вершин в одинаковом направлении буквы следуют в одинаковом порядке.
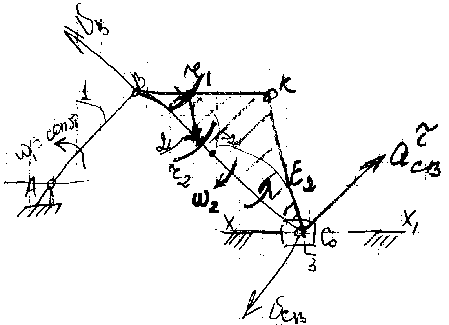
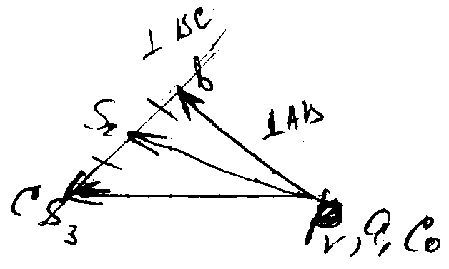
Построение плана скоростей: P>V>> >- полюс плана скоростей ( в этой точке скорость равна 0), V>B>>1> = >1>ℓ>AB> [м/с], 1 = 2n/60 =n/30, >V> = V>B>/(p>V>b) – масштабный коэффициент скорости,
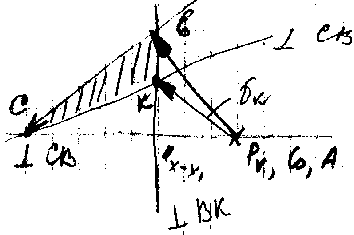
V>C> = V>B> + V>CB> (CB)
V>CB> = V>C0> (=0)+V>CDC0> ( x-x>1>),
>2> = V>CB>/ℓ>CB> = (cb)>V>/ℓ>CB>, VC = (P>V>c)>V>.
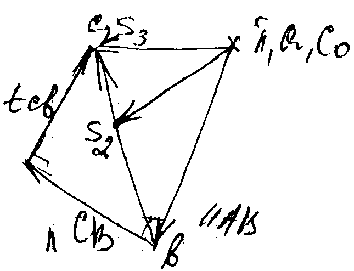
Построение плана ускорений: a>B> = a>B>n = >1>ℓ>AB> [м/с2]. = P>V> – полюс плана ускорений,
>a> = a>B>n/(b>1>) [м/(с2мм)].
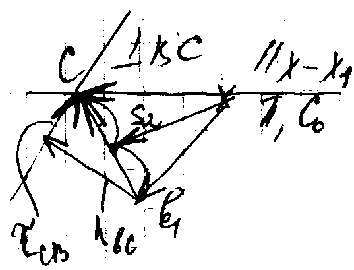
a>C >= a>B> + a>CB>n + a>CB>
a>C3> = a>C0> + a>C3C0>K(=0)+ a>C3C0>,
aK = 2V>отн>>пер >– Кориолисово ускорение, a>CB>n=>2>2ℓ>B>>С> = V>BC>/ℓ>CB> =
= (bc>V>)2/ℓ>BC>, n>BC> = a>BC>n/>a>, >i> = a>i>/ℓ>i>,
>2> = a>CB> /ℓ>CB> = (>CB>)>a>/ℓ>CB>.
Силовой расчет. Задачи и методы, допущения
Кинетостика – задача силового расчета (на основе обыкновенных уравнений равновесия твердых тел.). Перед кинетостатикой ставится две задачи: 1) определение усилий к кинематических парах; 2) определение уравновешивающей силы (F>ур>). Силовой раcчет провидится по методу Даламбера (если ко всем внешним действующим на звено механизма силам присоединить силы инерции, то под действием всех этих сил можно звено рассматривать условно находящимся в равновесии, F>i>=0): F>xi>=0, F>yi> = 0, F>zi> = 0, силы трения при этом не учитываются.
Условие статической определимости системы
3n=2p>1>+p>2> – усилие статической определимости, число усилий = число неизвестных. Чаще 3n = 2p>1>, т.к. p>2> = 0, условие существований групп Ассура (W=3n–2p>1> = 0).
Определение сил инерции и моментов от сил инерции
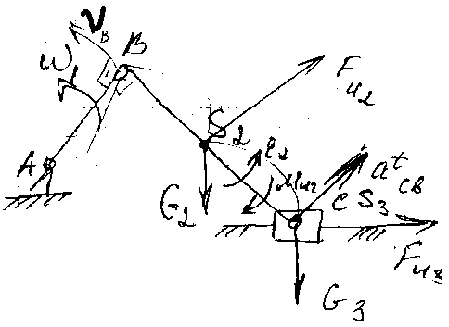
S>2> – центр масс 2-го звена
F>И2>= –m>2>a>S>>2> = – m>2>(nS>2>)>a>> >, M>И2>
(момент от силы инерции)= –J>S>>2>E>2> = –J>S>>2>(t>cb>)>a>/
/ℓ>CB>, F>И>>3> = –m>3>a>S3> = –m>3>(S>3>)>a> = 0.
Силовой расчет первой группы Ассура
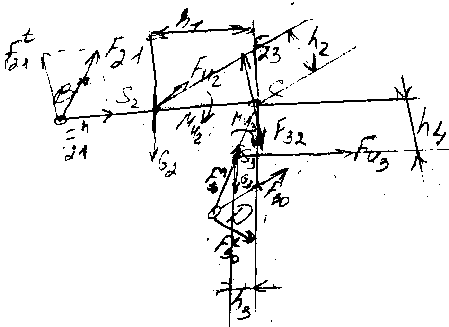
F>30> – сила в точке D со стороны отброшенной опоры 0; F>21> – сила, действующая со стороны первого (отброшенного) звена на второе. Разложим силы F>21> и F>30> – на второе путем проецирования их на соответствующие звенья 2 и 3. 1)F>21>, M>C> =0 (равновесие 2-го звена):
F>21> (BC)>ℓ>–G>2>h>1>>ℓ>+F>И>>2>h>2>>ℓ >+ M>И>>2>=0,
F>21>=(G>2>h>1>>ℓ>–F>И>>2>h>2>>ℓ>–M>И>>2>)/[(BC)>ℓ>].
2)F>30>, M>C>=0 (равновесие 3-го звена):
F>30>(CD)>ℓ >+ G>2>h>3>>ℓ >+ F>И3>h>4>>ℓ >– M>И3>=0,
F>30>=[–G>2>h>3>>ℓ >– F>4>h>4>>ℓ >+ M>И3>] / [(CD)>ℓ>].
3)F>21>n, F>30>n, F=0 (равновесие звена 2 и 3):
F>21>n+F>21>+G>2>+F>И2>+G>3>+F>И3>+F>30>+F>30>n = 0.
Величины искомых сил известны, но не известны их направления.
4)F>23>, F=0 (равновесие звена 2 и 3):
F>21>n + F>21> + G>2 >+ F>23>=0.
Далее определяем значение уравновешивающей силы на начальном звене:

F>10> – сила со стороны отброшенной опоры 0 на звено 1.
5) F>ур>, M>A> = 0: F>ур>(АВ)>ℓ>–F>12>h>1>>ℓ> = 0, т.к. на звене формально нет момента, то >ℓ> можно не писать, т.е получим F>ур>(АВ) – F>12>h>1>=0
6) F>10>, F = 0: F>ур>+F>12>+F>10> = 0
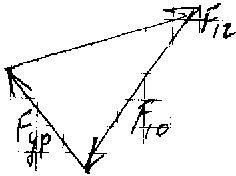
Рисуем все известные силы последовательно, учитывая величины и направления. Т.к. F=0, то соединив конец вектора силы F>12> и начало F>ур> получим искомую силу F>10>.
Силовой расчет группы Ассура 2-го вида
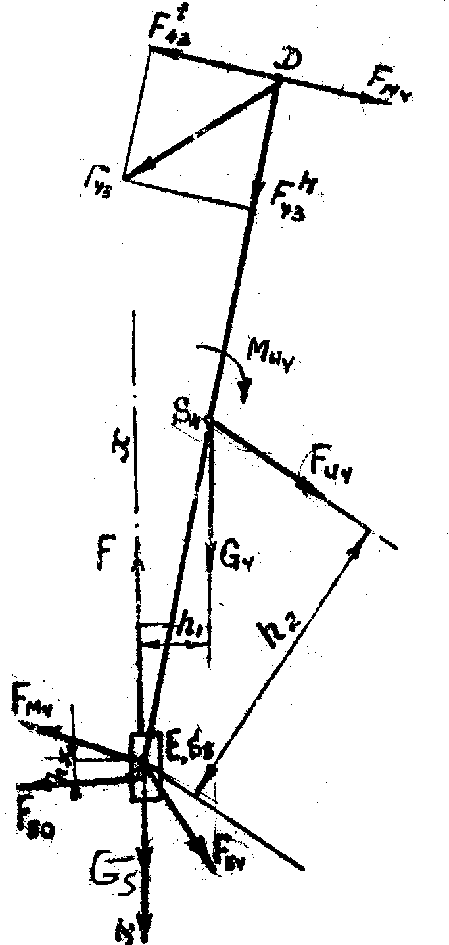
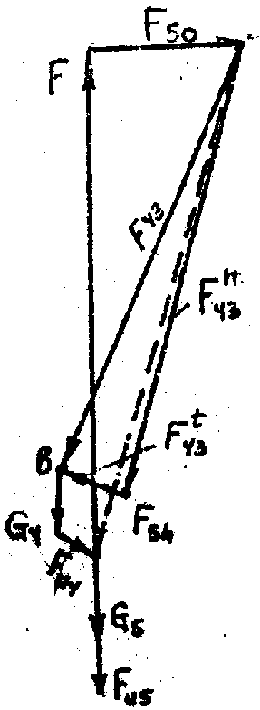
F>43> – сила, действующая со стороны третьего (отброшенного) звена на четвертое.
1) F>43>t, M>E> = 0 (равновесие звена 4): F>43>t(DE)>ℓ>–G>4>h>1>>ℓ>–F>И4>h>2>>ℓ>–M>И4>=0
F>43>t=(G>4>h>1>>ℓ>+F>И>>4>h>2>>ℓ>+М>И>>4>)/(DE)>ℓ>
2) F>50>,F>43>n, F = 0 (равновесие звена 4):
F>43>n + F>43>t + G>4 >+ F>И>>4 >+ G>5 >+ F>И>>5 >+ F + F>50>=0
3) F>54>, F = 0 (равновесие звена 5):
G>5 >+ F>И>>5 >+ F + F>50 >+ F>54>=0.
4) h>x>, M>E>=0 (равновесие звена5): F>50>h>x>>ℓ>=0, h>x>=0.
Силовой расчет группы Ассура 3-го вида
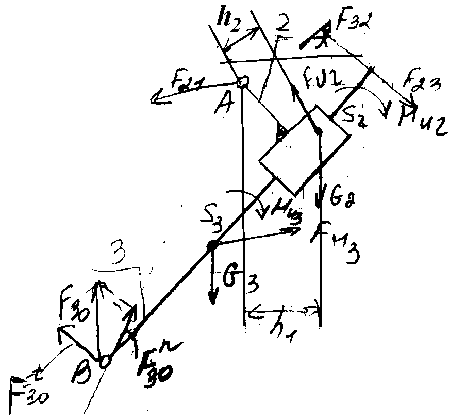
1)F>30>, M>A>=0 (равновесие звена 2 и 3)
2)F>30>n, F32, F=0 (равновесие звена 3):
F>30>n + F>20>n +G>3> +F>И>>3> + F>32>= 0
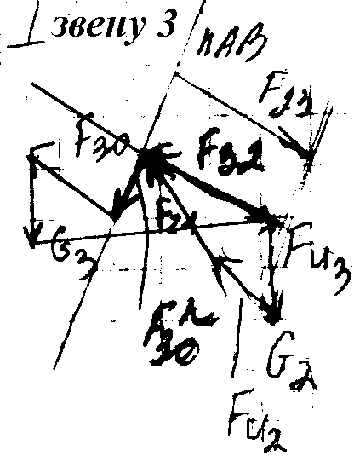
3) F>21>, F=0 (равновесие звена 3):
F>23 >+ G>2 >+ F>И>>2> + F>21>=0
4)h>X>, M>A>=0 (равновесие звена 2):
F>23>h>x>>ℓ >+ M>И2 >+ G>2>h>1>>ℓ >– F>И2>h>2>>ℓ >=0,
h>x>> >= [–М>И2> – G>2>h>1>>ℓ >+ F>И2>h>2>>ℓ>] / (F>23>>ℓ>)
Силовой расчет группы Ассура 4-го вида

1)F>21> и F>34>, F=0 (равновесие звеньев 2 и 3):
F>21> + G>2 >+ F>И>>2 >+ G>3 >+ F>И>>3 >+ F>34>=0
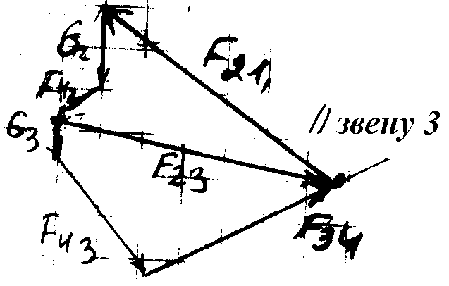
2)F>23>, F=0 (равновесие звеньев 2 (3)):
F>21>+G>2>+F>И>>2>+F>23>=0
3)h>x>>1>, M>B>=0 (равновесие звена 2):
F>21>h>x>>1>–G>2>h>1>+F>И2>h>2>=0, h>x>>1>=(G>2>h>1>–F>И2>h>2>)/F>21>
4)h>x>>2>, M>B>=0 (равновесие звена 3):
F>34>h>x2>–G>3>h>3>+F>И3>h>4>=0
Силовой расчет группы Ассура 5-го вида
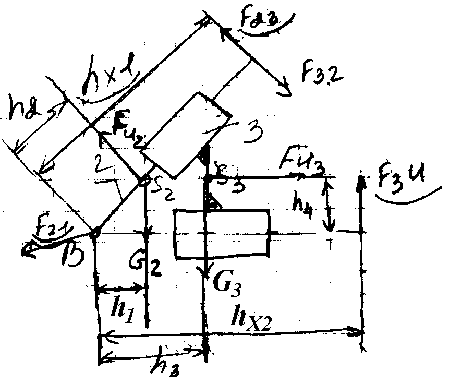
1)F>32> и F>34>, F=0 (равновесие звена 3):
F>34 >+ G>3 >+ F>И3 >+ F>34 >= 0
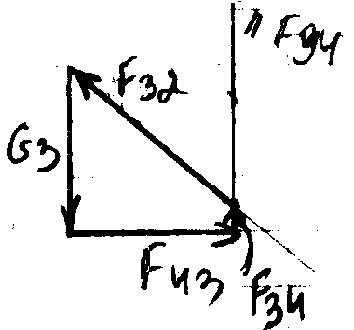
2)F>21>, F=0 (равновесие звена 2):
F>23 >+ G>2 >+ F>И2 >+ F>21 >= 0
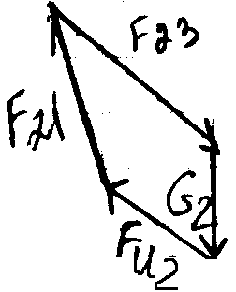
3)h>x>>1>, M>B>=0 (равновесие звена 2):
F>23>h>x>>1>–G>2>h>1>+F>И2>h>2>=0, h>x>>1>=G>2>h>1>+F>И2>h>2>=0
4)h>X>>2>, M>B>=0 (равновесие 2 и 3):
F>34>h>X2>–G>3>h>3>–F>И3>h>4>–G>2>h>1>+F>И2>h>2>=0
h>X2>=(G>3>h>3>+F>И3>h>4>+G>2>h>1>–F>И2>h>2>)/F>34>.
Силовой расчет с учетом сил трения
Если учитывают силы трения, то сначала расчет производится без учета трения, а во втором расчете рассчитывают эти силы трения.
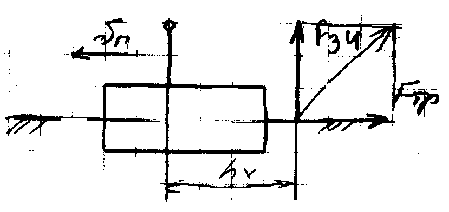
F>тр>=F>34>f,
где f – коэффициент трения
Определение уравновешивающей силы
Уравновешивающая сила определяется по рычагу Жуковского. Рычагом Жуковского называется повернутый на 90 план скоростей (желательно против направления вращения начального звена), к которому прикладывают все силы, действующие на механизм без изменения их направления и ищется равновесие этого рычага по принципу Лагранжа (для равновесия твердого тела необходимо, чтобы сумма работ равнялась нулю), т.е.
F>i>S>Di>cos(F>i>, S>Di>) = 0, F>i>dS>Di>cos(F>i>,dS>Di>)=0, точка D – точка, лежащая на звене к которой приложена сила F. Разделим все на dt:
F>i>V>Di>cos(F>i>, V>Di>) = 0
Для равновесия твердых тел необходимо и достаточно, чтобы мощность всех действующих на систему сил равнялась нулю. P = F>2>V>S2>cos = F>2>(P>V>S>2>)>V>cos .
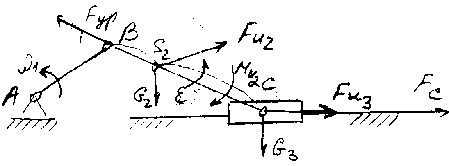
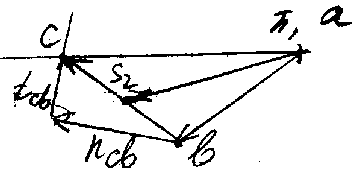
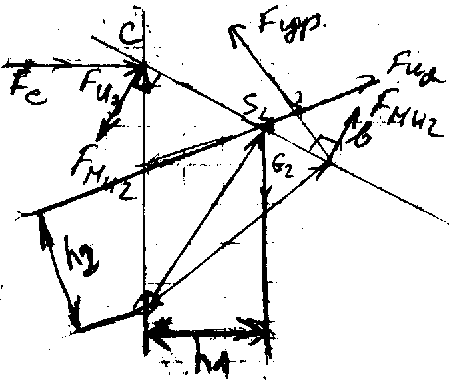
План ускорений
План скоростей
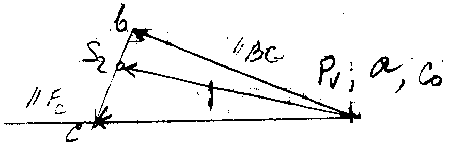
Рычаг Жуковского
M>И2> = F>МИ2> ℓ>BC>, F>M>>И2> = M>И2>/ℓ>BC>,
Момент на рычаге Жуковского:
>V>(F>ур>(ab) +F>M>>И2>(bc)–G>2>h>1>–F>И2>h>2>–(F>C>+F>И3>)p>V>c)=0,
F>ур>= (–F>МИ2>bc+G>2>h>1>+F>И2>h>2 >+(F>C>+F>И3>)p>V>c)/ab
Уравновешивание рычажных механизмов
Метод замещающих масс:
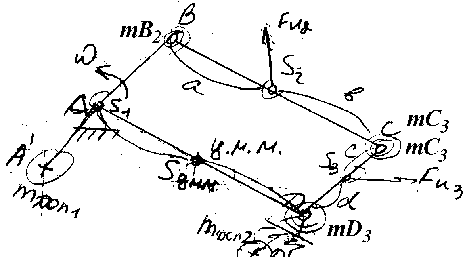
Сместим центр масс звена АВ в точку А путем некоторого противовеса у точки А. Тоже самое проделываем для звена CD.
1)m>1> + m>2>+ m>3> + m>4> = M
2) m>i>x>i>> >= 0
3) m>i>y>i> = 0
Выше написанное является условием смещения центра масс.
4) m>i>(x>i>2+y>i>2)=J>s>
Для второго звена: m>B>>2>a = m>C>>2>b –статические моменты,
m>B>>2>(a+b) = m>C>>2>b, m>C>>2> = mb/(a+b), m>C>>2>=m>2>a/(a+b).
Для третьего звена:
m>C3> = m>3>d/(c+d), m>D3> = m>3>c/(c+d)
Рассмотрим равновесие первого звена:
m>B2>AB = m>доп>>1>AA, m>доп>>1>=m>B2>AB/AA, (m>C2>+m>C3>)CD = m>доп>>2>DD, m>доп>>2> = (m>С>>2>+m>С>>3>)CD/DD, (m>B2>+m>доп>>1>)AS>цмм> = (m>C2>+m>C3>+m>D>+m>доп>>2>)DS>цмм>, m>>>A>AD = (m>>>A>+m>>>D>)SD, SD = ADM>>>A>/(m>>>A>+m>>>D>)
Уравнение удовлетворяет трем условиям: сумма по оси x и y = 0, сумма всех масс = общей массе.
Уравновешивание роторных систем
При наличии неуравновешенности вращающихся звеньев возникают значительные по величине и меняющиеся по направлению центробежные силы инерции. Они отрицательно влияют на опоры, являясь источником вибраций, вызывают изгиб ротора. При статической неуравновешенности ротора необходимо сместить центр масс в начало координат. Силы инерции при этом будут следующие –m>r>2ℓ=Fц, ℓ–искомое расстояние, F>ц> – центробежная сила.

Вводим соответствующую корректировочную массу (m>k>):
m>1>r>1>2+m>2>r>2>2+m>3>r>3>2+m>k>r>k>2=0,
где r>i>– расстояние от оси вращения до массы.
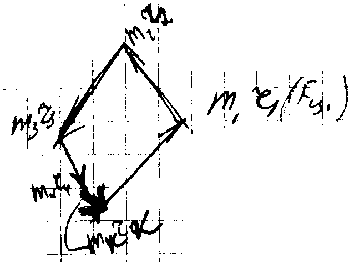
В этом роторе главный вектор дисбалансов равен нулю. При моментной неуравновешенности ротора (главная центральная ось инерции ротора не параллельна оси ротора, но пересекает ее в центре масс ротора) вычисляется главный момент дисбалансов ротора M>D> = m>i>[ℓ>i> e>i>], где e>i> –эксцентриситеты – радиус-векторы центров заданных масс относительно оси ротора. Вводим две дополнительных плоскости и подбираем уравновешивающую массу в каждой плоскости.
Определение КПД механизмов. Мгновенный и цикловой КПД. КПД последовательных и параллельных соединений механизмов
Силы, действующие на механизм могут быть движущими и силами сопротивления. Движущие силы – это такие силы, которые осуществляют положительную работу (угол между направлением звена и направлением силы <90). Силы сопротивления можно разделить на две категории: 1)силы полезного сопротивления (F>пс>) – это те силы, которые надо преодолевать при полезной работе 2)силы вредного сопротивления (силы трения) F>вс> = F>тр> , т.к. они рассеивают энергию. КПД – это мера эффективности механизма, определяемая отношением полезной работы к подведенной при его работе (полной), т.е. =A>пс >(полезного сопротивления)/A>дв> (движущие силы), т.к.
A>дс>=А>сп>+А>св>, то =(А>дс>–А>св>)/А>дс> = 1–А>св>/А>дс> = 1–,
где – коэффициент потерь. При циклические движении механизма за один оборот повторяются технические и кинематические характеристики. –цикловой КПД. Мгновенный КПД равен отношению мгновенных мощностей и этот КПД меняет в течении цикла свои значения: =P>пс>/P>дв>. При последовательно соединенных механизмах общий КПД равен произведению КПД всех механизмов и применение механизма с низким КПД не выгодно. При параллельном соединении механизмов
A>i>=A>дс>>i>>i>, = A>i>/A>дс>=>i>>i>,
при этом один из механизмов будет с малым КПД.
Динамическое исследование механизмов
Определение истинного движения начального звена механизма с учетом всех сил, действующих на механизм.
Основная задача: >1>=>1>(), вспомогательная задача:
=(>max>–>min>)/>ср> > []
mx=F>x>, my=F>y>, J=M
J>пр>>ср>2/2=T>> =(m>i>V>Si>2/2+J>Si>>i>2/2),
M>пр>– приведенный момент, J>пр> – приведенный момент инерции, Т – кинетическая энергия.
J>пр>= 2/>ср>2 (m>i>V>Si>2/2 + J>Si>>i>2/2), J>пр>=(m>i>(V>Si>> >/>ср>)2+J>Si>(>i>> >/)2), V=S – скорость с аналогом скорости,
A=S2 – ускорение с аналогом ускорения. Определим момент сил, действующих на звено приведения:
M>пр>>ср>=(F>i>V>Si>(cos)+M>i>>i>), М>пр>=1/>ср>(F>i>V>Si>(cos)+M>i>>i>)= (F>i>V>Si>cos />ср>+M>i>(>i>/>ср>).
Определение момента инерции маховика методом профессора Мерцалова
T>MM>+T>>–T>0>=A,
где T>MM>– кинетическая энергия массовых масс, равная
T>MM>=T>max>–T>ЗВ>>const>,
где T>max>– кинетическая энергия маховика, T>ЗВ>>const> – кинетическая энергия звеньевых констант.
T>MM>=(>A>+T>0>–T>>)>max> (при >max>)–(A+T>0>–T>>)>min> (при >min>). Т.к. Т>0> =const, то: J>MM>/2(2>max>–2>min>)=(A–T>>)>max>–(A–T>>)>min>, J>MM>/2(>max>+>min>)(>max>–>min>)= (A–T>>)>max>–(A–T>>)>min>, J>MM>2>ср>[] =(A–T>>)>max>–(A–T>>)>min>, JMM = [(A–T>>)>max>–(A–T>>)>min>] / []>ср>2, J>max> = J>MM >–J>ЗВ>>const>.
Этот момент считается приблизительно, т.к. мы среднее значение определяем грубо (не точно) – по графику.
Определение момента инерции маховика методом Виттенбауэра (метод энергомасс)
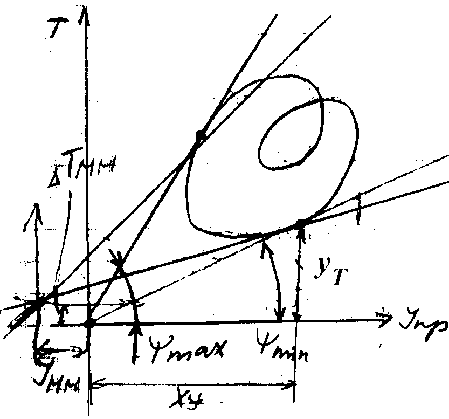
Tg >min>=y>T>/x>y>, т.к. T=y>T>>T>, а J>пр>=х>y>>y>, то tg>min> =(T/>T>)/(J>пр>/>y>)=T>y>/(J>пр>>Т>).
Перенеся масштабные коэффициенты в левую часть получим:
tg >T>/>y>=T/J>пр> = J>пр>(2>min>/2)/J>пр> = >min>2/2, т.е. 2>min>=2>T>/>y> tg>min> (1).
По этому графику можно определять момент инерции маховика:
>ср>=(>max>+>min>)/2 (2), =(>max>–>min>)/>ср> (3).
Из формулы (3) получаем >max>=>ср>+>min>. Из формулы (2) получаем: >min>=2>ср>–>max>. Подставив >max> в это выражение получаем:
>max> = >ср>+2>ср>+>max>, = >ср>(1+/2)
>min> = >ср>(1–/2).
Подставив полученное в выражение (1), получим:
>max>2=>ср>2(1++2/4) ср(1+), 2>min> = >ср>2(1–+2/4)2>ср>(1–), т.к. –
малая величина, то 2/4 будет еще меньше, следовательно, ей можно пренебречь, тогда:
>ср>2(1+)=2>T>/>y> tg>max>
2>ср>(1–)=2>T>/>y> tg>min>.
Типы и виды механизмов с высшими кинематическими парами
Среди механизмов с высшими кинематическими парами наибольшее распространение получили зубчатые, кулачковые, фрикционные, мальтийские и храповые механизмы.
В зубчатых передачах различают внешнее, внутренне и реечное зацепление. В зависимости от расположения осей могут быть с параллельными осями (цилиндрические), с пересекающимися осями (конические) и со скрещивающимися осями или гиперболоидные передачи (винтовые, червячные).
В кулачковых механизмах высшая пара образована звеньями, называемыми кулачок и толкатель (звено 1 и 2). Замыкание силовое, с помощью пружины. Форма входного звена – кулачка определяет закон движения выходного звена – толкателя.
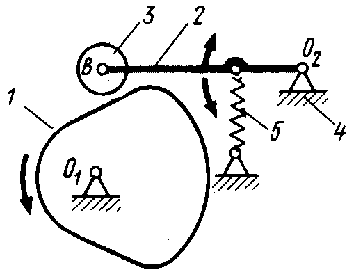
В фрикционном механизме передача вращательного движения осуществляется посредством трения между звеньями, образующими высшую кинематическую пару. Простой фрикционный механизм состоит из двух вращающихся круглых цилиндров 1,2 и стойки 3. Силовое замыкание высшей пары осуществляется пружинами. При постоянной угловой скорости диска 1 посредством перемещения колеса 2 вдоль своей оси можно плавно изменять его угловую скорость и даже направление вращения.
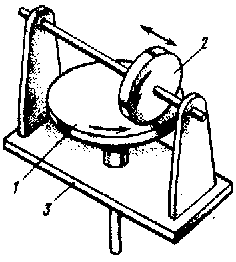
Мальтийский механизм преобразует непрерывное вращение входного звена – кривошипа 1 в прерывистое вращение выходного звена – креста 2. Механизм имеет стойку 3 и высшую пару, образованную цевкой В кривошипа и пазом креста.
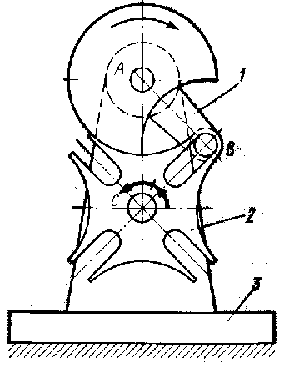
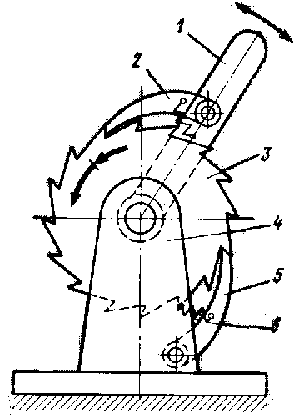
Храповой механизм с ведущей собачкой и стойкой 4 служит для преобразования возвратно-вращательного движения коромысла 1 с собачкой 2 в прерывистое вращательное движение храпового колеса 3. Собачка 5 с пружиной 6 не дает колесу вращаться в обратную сторону. Высшая КП здесь образована собачкой и храповым колесом.
Эвольвента и ее свойства. Свойства эвольвентного зацепления. Основная теорема зацепления. Зубчатые механизмы

Эвольвента – это траектория некоторой фиксированной точки прямой, катящейся без скольжения по окружности. Окружность, по которой без скольжения катится эвольвента называется основной. Основные свойства эвольвенты: 1)нормаль любой точки эвольвенты касается основной окружности, т.е. явл. производящей прямой; 2)отрезок производящей прямой от точки эвольвенты до точки касания равен радиусу кривизны; 3)эвольвента не бывает внутри основной окружности.
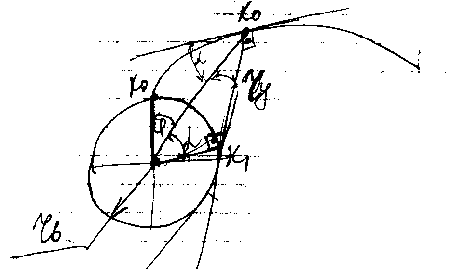
k>1>– точка касания, – угол профиля
k>0>k>1>=k>1>k>0>, r>b>(+)=r>b>tg, =tg–, inv=tg– – уравнение эвольвенты, r>y>cos=r>b>, r>y>=r>b>/cos. Основная теорема зацепления (т. Виллиса): >1>/>2>=p>2>p / p>1>p

V>k1>=V>k1>cos>1> = r>1>>1>cos>1>
V>k2>=V>k2>cos>2> = r>2>>2>cos>2>
O>1>L>1>>1> = O>2>L>2>>2>, >1>/>2> = O>2>L>2> / O>1>L>1>.
Теорема: нормаль в точке касания в высшей кинематической паре делит межосевое расстояние (O>1>O>2>) на части обратно пропорциональные угловым скоростям. Основные свойства эвольвентного зацепления: 1)Эвольвентное зацепление обеспечивает постоянство передаточных отношений:
>1>/>2>=O>2>p/O>1>p = rw>2>/rw>1>=rb>2>/rb>1>.
2)Прямая N>1>N>2> является общей касательной точка соприкосновение зубьев всегда лежит на ней и тогда она называется прямой зацепления, >w> – угол зацепления, который всегда равен 20. 3) Если одно из колес будет увеличиваться в размерах, то профиль зуба будет прямой), то она превратится в в зубчатую рейку и будет перемещаться поступательно.
Элементы геометрии прямозубых зубчатых колес. Угловой шаг, окружный шаг, модуль, окружности: основная, делительная, впадин и вершин зубьев
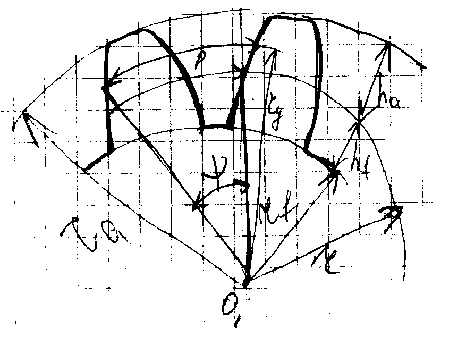
p–окружной шаг, p>y> – шаг по промежуточному радиусу, r>a> – радиус окружности внешних зубьев, r>f> – радиус окружности впадин между зубьями, r – радиус делительной окружности, r>y> – радиус промежуточной окружности,
h>a> – высота головки зуба (часть зуба выше делительной окружности), h>f> –высота ножки зуба (ниже делительной окружности), = 2/z – угловой шаг, где z – число зубьев, p = r = r2/z, p>y> = r>y> =r>y>2/z, pz – длина делительной окружности, d – диаметр делительной окружности pz=d, откуда
d=zp/= zm,
где m – модуль.
d>a> = d+2h>a>, d>f> = d+2h>f>, h>a>=h>a>*m=m,
где h>a>*–коэффициент высоты головки зуба, равный 1.
h>f>> >=(h>a>*+c*)m, где c*–коэффициент стандартного радиального зазора, равный 0,25. d>a>=d+2m=m(z+2),
d>f>=d–2m = d–2(1,25m) = m(z–2,5).
r>b> –радиус основной окружности = rcos, =20.
Методы нарезания зубчатых колес
Зубчатые колеса изготавливаются двумя методами: 1) метод копирования. Состоит в том, что по чертежам тщательно изготавливается дисковая фреза. Режущая кромка фрезы имеет очертание впадины между зубьями. Вращаясь, фреза перемещается в направлении боковой образующей зуба. За каждый ход фрезы вдоль оси колеса получается нарезанной одна впадина. По прохождении всей впадины фреза возвращается в исходное положение. После этого нарезаемое колесо поворачивается на величину угла =2/z, где z–число зубьев нарезаемого колеса и процесс повторяется. 2) метод огибания и метод обкатки. Этот метод заключается в том, режущему инструменту и заготовке сообщают то относительное движение, которое имели бы 2 зубчатых колеса, находящихся в правильном зацеплении. В таком случае режущий инструмент должен представлять собой также зубчатое колесо. Такое колесо инструмент носит название долбяк, который совершает поступательное движение параллельно оси х-х нарезаемого колеса. Одновременно долбяку и колесу сообщается вращательное движение с соотношением угловых скоростей, как если бы долбяк и колесо находятся в зацеплении. Практически долбление происходит последовательно этап за этапом, а не непрерывно: долбяк движется вверх и вниз, поворачивается нарезаемое колесо и т.д. Тогда профиль нарезаемого колеса получается как огибающая всех положений режущей кромки долбяка, т.е. инструмент как бы обкатывает нарезаемое колесо (позволяет вырезать колеса с внутренним зацеплением). Первый метод более простой, второй требует специального дорогостоящего оборудования и является более точным.
Нарезание производящей рейкой без смещения. Геометрический расчет таких колес
Так как для любого колеса может быть спроектирована сопряженная с колесом рейка, то вместо колеса-инструмента в качестве использована рейка. Рейка совершает в вертикальном направлении возвратно-поступательное движение, параллельное оси нарезаемого колеса. Заготовка имеет двойное движение в горизонтальной плоскости. Вращаясь вокруг оси, она одновременно перемещается вдоль рейки. Таким образом, заготовка осуществляет движение колеса относительно рейки, и профили зубьев нарезаемого колеса получаются процессом обкатывания. Геометрический расчет зубчатых колес без смещения:
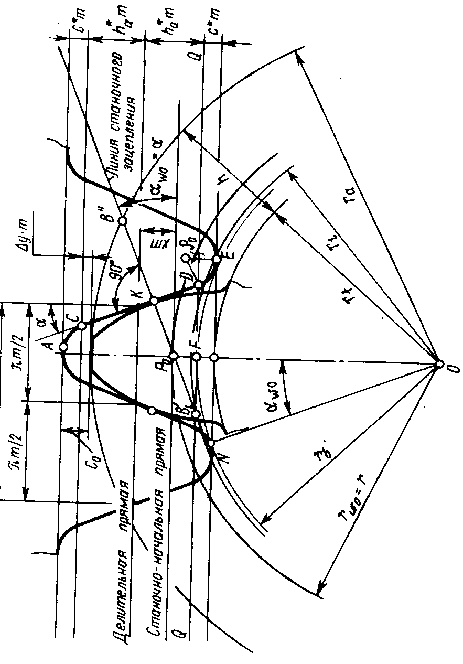
Делительная прямая делит шаг рейки пополам. Шаг рейки равен p=m, h>a>*–коэффициент высоты зуба, c* – коэффициент радиального зазора. h>a> = h>a>*m, c = c*m, m –стандартный модуль. h>a> – высота головки зуба,
h>a>=(h>a>*+X–y)m – для случая со смещением, X – коэффициент смещения, y– коэффициент уравнительного смещения, h>f> – высота ножки зуба. h>f> = (h>a>*–X+C*)m – для случая со смещением, d>a> – окружности вершин зубьев, d>a> =d+2h>a>=mz+2(h>a>*+X–y)m, d>f>–диаметр окружности впадин зубьев, d>f> = d–2h>f>= mz-2(h>a>*–X + C*)m, d– диаметр делительной окружности.
Минимальное число зубьев шестерни без подрезания. Основные причины введения смещения при нарезании зубчатых колес
PBPN, PBsin=h>a>*m, PB=h>a>*m/sin, PN = mz/2sin, h>a>*m/sinmz/2sin, Z>min> =2h>a>*/sin2=21/sin220= 17,09717
Причины введения смещения инструментальной рейки при нарезании зубчатых колес следующие: 1) устранение подрезания (подрезание уменьшает эвольвентную часть профиля зуба и ослабляет его опасное сечение; 2) увеличение прочности зуба; 3) вписывание в заданные межосевые расстояния.
Определение минимального коэф-та смещения. Два вида геометрического расчета зубчатых колес при смещении (дано: 1)z>1>, z>2>, m, α, x>1>, x>2>; 2)z>1>, z>2>, m, α, α>W>)
PBPN, PBsin=(h>a>*–X)m, PB=mz/2 sin, (h>a>*–X)m/sinmz/2 sin,
h>a>*–z/2 sin2 X, X>min>=h>a>*[1–z/ (2h>a>*/
/sin2)]. Минимальное число зубьев , своб. от подрезания равно 17, , X>min> = h>a>*(z>min>–z)/z>min>, т.к. h>a>*=1, то X>min>=(z>min>-z)/z>min> = (17-z)/17.
Расчет зубчатых колес
1) α>W> – угол зацепления, α – угол рейки. inv α>W >= inv α + 2x>Σ>tgα/(z>1>+z>2>), inv α>W >= tg α>W >– α>W >(инвалюта). a>W> – межосевое расстояние при смещении, a – межосевое расстояние без смещения. a>W>=acosα/cosα>W>, a=r>1>+ r>2>, r>1> – радиус делительной окружности шестерни, r>2> – радиус делительной окружности зубчатого колеса. a=r>1>+r>2>=(m/2)(z>1>+z>2>). y – коэф-т воспринимаемого смещения. ym=α>W>-a, y=(α>W>-a)/m. Δy – коэф-т уравнительного смещения.
½mz>1>+½mz>2>+ym=½mz>1>+(h>a>*+x>1>+y)m+ ½mz>2>–(h>a>*–x>2>+c*)m+c*m
a>W>=r>1>+r>2>+ym, a>W>=r>1a>+r>f2>+c*m,
сократив одинаковые выражения в левой и правой частях уравнения и разделив все на m, получим: y=x>1>+x>2>-Δy x>1>+x>2>=x>Σ> – суммарный коэф-т смещения,
Δy= x>Σ>–y
2) a>W >= a∙cosα/cosα>W>,
α>W >= arccos(a∙cosα/a>W>),
inv α>W >= inv α + 2x>Σ>tgα/(z>1>+z>2>)
x>Σ>=(invα>W >– invα)(z>1>+z>2>)/2tgα
y=(α>W>-a)/m. Δy= x>Σ>–y
Коэф-т перекрытия. Определение его графическим и аналитическим методами
Коэф-т перекрытия определяет плавность работы зубчатой передачи и показывает среднее значение числа пар сопряжения зубьев, находящихся в сопряжении. Такие качества передачи обеспечиваются перекрытием работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепления еще до того, как предшествующая пара выйдет из зацепления.> >E=B>1>B>2>/πmcosα, πm – шаг по делительной окружности, πmcosα – шаг по основной окружности, B>1>B>2> – часть линии зацепления ограничительной окружности вершин зубьев шестерни зубчатого колеса, которая называется активной частью линии зацепления.
Аналитический метод. B>1>B>2>=B>1>P+PB>2>=B>1>N>1>–PN>1>+BN>2>–PN>2>=√(r2>a1>–r2>b1>)+√(r2>a2>–r2>b2>)–N>1>N>2>,
N>1>N>2>= r>W1>sinα>W>+r>W2>sinα>W>=a>W>sinα>W>
r>W>>1>, r>W>>2> – радиусы начальных окруж.
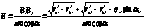
E > 0 должно быть всегда. Для обычных передач Е ≈ 1,3. Чем больше число зубьев, тем больше Е.
Графический метод
О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового зацепления – это угол поворота колеса от положения зубьев при входе в зацепление. Следовательно,
Е = >а1>/>1>,
где >1>=2/z>1>– угловой шаг.
Если Е<1, то непрерывности зацепления зубьев не будет.
Виды смещений. Основной вид смещения при нарезании, уравнительное и воспринимаемое смещения
1) смещение равно 0

2) Начальная прямая, которая катится без скольжения в процессе нарезания зубчатых колес Х>m>>1 это случай положительного смещения.

3) X>m><0 – случай отрицательного смещения.
начальная прямая

x>Σ> – суммарный коэф-т смещения x>1>+x>2>=x>Σ>, y – коэф-т воспринимаемого смещения, Δy – коэф-т уравнительного смещения.
Δy= x>Σ>–y
Передаточное отношение одно- и многоступенчатых зубчатых передач с неподвижными осями вращения
Одноступенчатая передача с внешним зацеплением. Особенность: меняет знаки.
u>12>=±ω>1>/ω>2>, ω>1>=v>k>/r>1>, ω>2>=v>k>/r>2>.
Одноступенчатая зубчатая передача с внутренним зацеплением. Особенность: не меняет знаки.
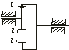
Подставим ω>1 >и ω>2> в формулу для передаточного отношения u>12>:
u>12>=±r>2>/r>1>=±z>2>/z>1>.
Многоступенчатая зубчатая передача с неподвижными осями (односторонние зубчатые передачи соединены последовательно:
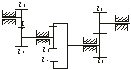
u>16 >= u>12 >∙ u>34 >∙ u>56 >= (-1)ω>1>/ω>2 >∙ ω>3>/ω>4 >∙ (-1)ω>5>/ω>6 >= ω>1>/ω>2 >∙ ω>3>/ω>4 >∙ ω>5>/ω>6 >= (-1) z>2>/z>1 >∙ z>4>/z>3 >∙ (-1) z>6>/z>5>
Передаточное отношение многоступенчатой зубчатой передачи = передаточному отношению входному колесу от выходного колеса.
z>2>∙z>4>∙z>6> - произведение числа зубьев ведомых колес.
z>1>∙z>3>∙z>5> - произведение числа зубьев ведущих колес. Тогда
U>вх/вых> = Пz>ведомых колес>/Пz>ведущих колес> (-1)k,
где k – число внешних зацеплений.
Определение передаточного отношения планетарного механизма аналитическим методом (методом обращения движения)
Если одно из центральных колес многоступенчатого зубчатого механизма неподвижно, то она называется планетарным механизмом.
Число степеней свободы W=3n-2p>1>-
-2p>2>=3∙3-2∙3-2=1
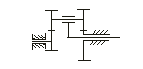
Планетарный механизм, имеющий неподвижное звено всегда можно превратить в дифференциал, и наоборот. Это и есть свойство обратимости планетарных механизмов. Основная идея метода Виллиса (метода обращения движения): берем центральное звено планетарного механизма и даем ему дополнительное вращение равное скорости вращения водила, но направленное в противоположную сторону. Тогда водило становится неподвижным звеном и механизм из планетарного превращается в зубчатый механизм с неподвижными осями колес (обращенный механизм), состоящий из нескольких последовательных соединенных пар зубчатых колес.
|
Движение |
Z>1> |
в |
Z>4> |
|
действит. |
Ω>1> |
ω>в> |
0 |
|
Дополнит |
-ω>в> |
-ω>в> |
-ω>в> |
|
суммарное |
ω>1>-ω>в> |
0 |
-ω>в> |
Передаточное отношение обращенного механизма имеет вид:
u>14>(в)=(ω>1>-ω>в>)/(-ω>в>)=(-1)2z>2>z>4>/z>1>z>3>
u>1в>(4)=ω>1>/ω>в>=1-u>14>(в)
u>1в> - передаточное отношение планетарного механизма.
u>в1>(4)=1/u>1в>(4)=1/1-u>14>(в)
Передаточное отношение от четвертого колеса к водилу, если первое колесо остановлено:
u>4в>(1)=1-u>41>(в)
u>в4>(1)=1/u>4в>(1)=1/1-u>41>(в)
u>1в>(4)=1/1-u>14>(в)=1-z>2>z>4>/z>1>z>3>=1-99∙101/100∙100=0,0001
u>в1>(4)=1/u>1в>(4)=10000
Т.е. при одном обороте водила колесо повернется на 0,0001.
Передаточное отношение планетарного механизма по методу баланса мощностей в балансу моментов
u>1в> - ?
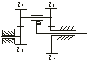
u>1>>в>=1-u>14>(в)=1-(-1)2z>2>z>4>/z>1>z>3>=1-r>2>r>4>/r>1>r>3>
⌠M>1>ω>1>+M>в>ω>в>=0
│M>1>+M>в>+M>4>=0
ω>1>/ω>в>=-M>в>/M>1>=(M>1>+M>4>)/M>1>=1+M>4>/M>1>
M>1>=F>12>∙r>1>, M>4>= -F>43>∙r>4>, F>34>∙r>3>=F>21>∙r>2>,
F>34>= F>21>∙ r>2>/r>3>, F>43>= -F>34>= -F>21>∙ r>2>/r>3>,
u>1в>=ω>1>/ω>в>=1+M>4>/M>1>=1-F>12>∙r>2>∙r>4>/F>12>∙r>1>∙r>3>=1-r>2>r>4>/r>1>r>3>
Передаточное отношение планетарных механизмов графическим методом
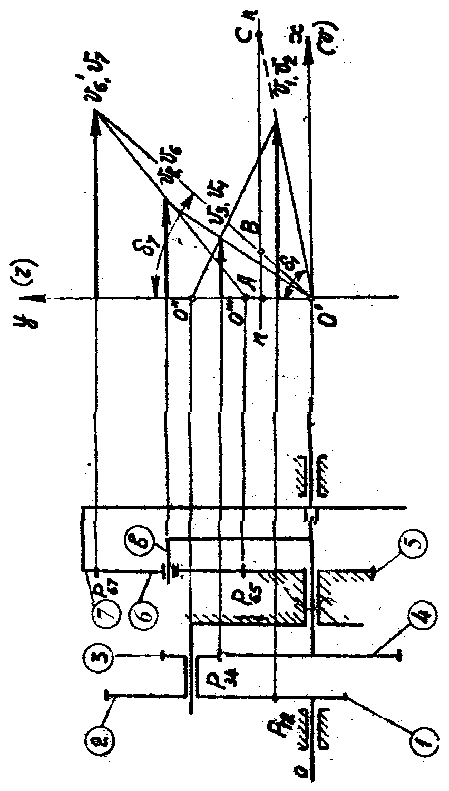
Особенности определения передаточного отношения дифференциальных механизмов с замыкающей кинематической цепью аналитическим и графическим методами
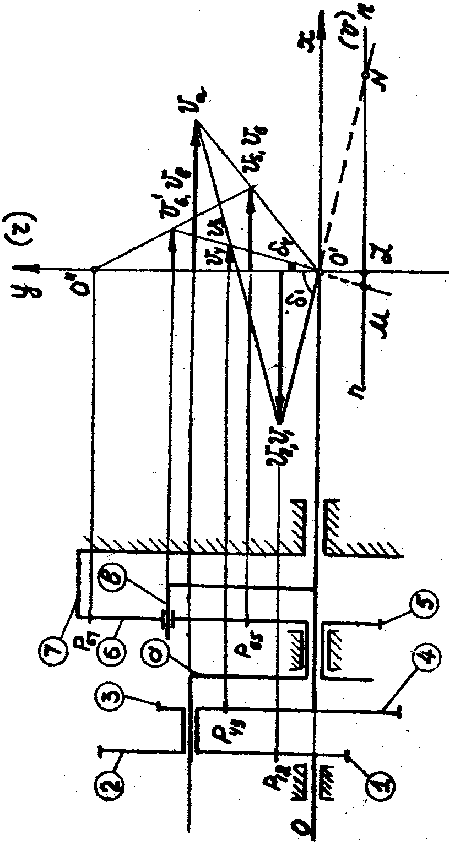
Механизм имеет два водила «a», «в» содержит 2 планетарных механизма. Т.к. оба центральных колеса могут вращаться, заключаем, что левая часть заданного механизма, состоящая из водила «а», сателлита 2-3 и центральных колес 1,4 является дифференциалом (два колеса могут вращаться). Данный механизм является замкнутым, т.к. в выделенном дифференциале водило «а» и колесо 4 соединены между собой зубчатой передачей. Замыкающая цепь содержит водило «в», на котором установлен сателлит. Поскольку центральное колесо 7 здесь неподвижно, то замыкающая цепь (колеса 5 и 7, водило «в» и сателлит 6) представляет собой простой планетарный механизм. Рассмотрим дифференциал (1,2-3, «а», 4) отдельно. Воспользуемся методом Виллиса, т.е. остановим водило, преобразуем дифференциал в приведенный зубчатый механизм.
|
Движение |
а |
1 |
4 |
|
действит. |
ω>а> |
>1> |
>4> |
|
дополнит. |
-ω>а> |
-ω>а> |
-ω>а> |
|
суммарное |
0 |
>1>(а)= =>1>–>а> |
ω>4>(а)= =>4>–>а> |
Далее, для приведенного механизма составляем отношение угловых скоростей центральных колес и выражаем его через радиусы:
i>14>(a)=>1>(a)/>4>(a)=(>1>–>a>)/(>4>–>a>)=(r>2>r>4>)/(r>1>r>3>)
После этого рассматриваем отдельно замыкающую цепь. Поскольку она выполнена в виде простого планетарного механизма, то и здесь применяем метод Виллиса:
-
Движение
в
5
7
действит.
ω>в>
>5>
>7 >=0
дополнит
-ω>в>
-ω>в>
-ω>в>
суммарное
0
>5>(в)= >5>–>в>
ω>7>(в)= –>в>
i>57>=>5>(в)/>7>(в)=(>5>–>в>)/(–>в>) = –r>7>/r>5>.
С целью определения искомого передаточного отношения решаем полученные уравнения совместно:
(1-е): (>1>–>5>)/(>4>–>5>) = r>2>r>4>/(r>1>r>3>),
(2-е): 1–>5>/>4>= –r>7>/r>5>.
Из 2-го уравнения >5>=>4>(1+r>7>/r>5>). Подставив это значение в 1-е уравнение, получим: [>1>–>4>(1+r>7>/r>5>)] /
/ [>4>–>4>(1+r>7>/r>5>) = (r>2>r>4>)/(r>1>r>3>), сократив на >4>, получим: [(>1>/>4>) – (1+r>5>/r>7>)] /
/ [1–(1+r>7>/r>5>)]=r>2>r>4>/(r>1>r>3>). Отсюда i>14>=>1>/>4>=1+r>7>/r>5>–(r>2>r>4>r>7>)/(r>1>r>3>r>5>).
Дифференциал автомобиля и его кинематика
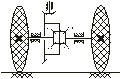
(ω>1>-ω>в>)/(ω>4>-ω>в>)=1, ω>1>-ω>в>= - (ω>4>-ω>в>)
(ω>1>+ω>4>)/ω>2>=ω>в>
Имитация движения автомобиля на повороте:
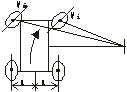
Ω=v>Л>/(R+a)= v>П>/(R–a)
ω>Л>/(R+a)=ω>П>/(R–a)
ω>Л>/ω>П>=(R+a)/R–a)
Кулачковые механизмы. Назначение и виды кулачковых механизмов
Кулачковые механизмы преобразуют вращательное движение начального звена (кулачка) в возвратно-поступательное движение выходного звена (толкателя). При этом форма кулачка определяет закон движения толкателя. Кулачковые механизмы бывают следующих видов:
1) Плоский кулачок с качающимся толкателем. 1-кулачок, 2-толкатель, 3-ролик, 4-силовой элемент (пружина).
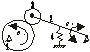
2)Плоский кулачок с поступательно перемещающимся толкателем.
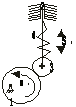
3)Пространственный кулачок.
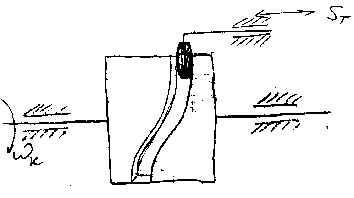
Основные этапы проектирования кулачкового механизма
1)Выбор схемы кулачкового механизма, 2)Определение закона движения толкателя, 3)Выбор основных размеров кулачкового механизма, 4)Профилирование кулачка.
v>T>=S>T>∙ω>K>,
где S>T> – аналог скорости толкателя,
dS/dφ>k>, a>T>≈S>T>∙ω>K>2, a>T>=S>T>∙ω>K>+S>T>∙E>K>, S>T>=d S>T>/dφ>k>≈ ∆S>T>/∆φ= S>T>/∆φ
при Δφ→0, S>T>→ ∞, что соответствует жесткому удару (скачкообразно изменяется аналог скорости толкателя S>T>)
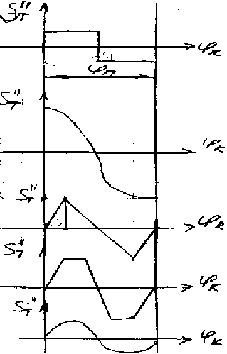
>П> – фаза подъема толкателя. 1– жесткий удар, 2–мягкий удар (скорость толкателя нарастает быстрее), 3, 4, 5– безударное движение.
Графические методы определения закона движения толкателя
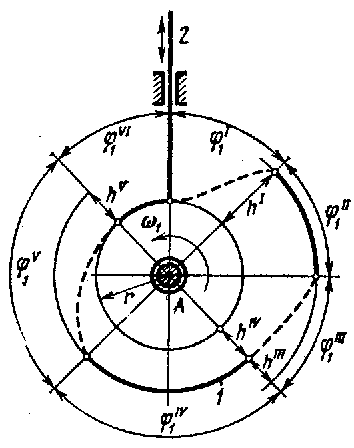
Схема механизмам поступательно движущимся толкателем
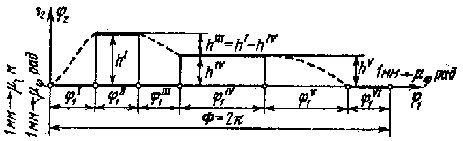
Закон движения ведомого звена (толкателя)
Определение минимальных размеров кулачка
Режим самозаклинивания толкателя – когда толкатель не может передвигаться. r>0> – минимальный радиус. Для кулачков с поступательным движением толкателя угол давления (α) не более 300. Для кулачков с качающимся толкателем угол давления (α) допускается до 450.
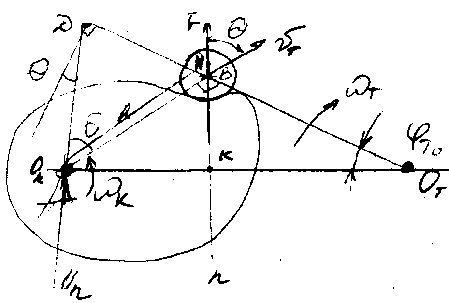
По основной теореме зацепления:
>K>/>T>=KO>T>/O>K>K = ℓ>T>/DB
(по подобию треугольников),
DB = ℓ>T>>T>/>K>, S>K> = V>T>. tg=DN/NO>K> = [(ℓ>T>+S>T>)–acos>T>]/[asin], –угол зацепления.
asin>T> tg + acosT = (ℓ>T>+S>T>), a=(ℓ>T>+S>T>)/ (sinT tg + cos>T>)
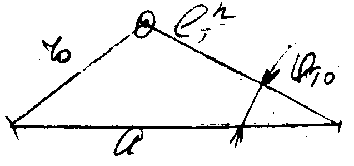
r>0> = (a2+ℓ>T>2–2aℓ>T>cos>T0>)
Определение действительного профиля кулачка
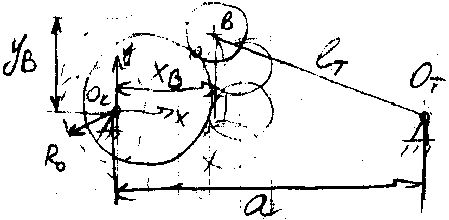
⌠x>B>=a-e>T>cosφ>T>(φ>K>)
│y>B>=e>T>sinφ>T>(φ>K>)
(x-x>B>)2+(y-y>B>)2=r2
-2(x-x>B>)∙dx>B>/dφ>K>–2(y-y>B>)∙dy>B>/dφ>K>=0
(x-x>B>)= -(y-y>B>)(dy>B>/dφ>K>)/(dx>B>/dφ>K>)
(y-y>B>)2 ∙[(dy>B>/dφ>K>)/(dx>B>/dφ>K>)]2+(y-y>B>)2=r2,
(y – y>B>)2 = r2 (dx>B>/d>K>)2 / [(dx>B>/d>K>)2 + (dy>B>/d>K>)2], y = y>B > r (dx>B>/d>K>) / [(dx>B>/d>K>)2 + (dy>B>/d>K>)2]
x = x>B> r (dy>B>/d>K>) / [(dx>B>/d>K>)2 + (dy>B>/d>K>)2]