Типи передач

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

УЖГОРОДСЬКИЙ НАЦІОНАЛЬНИЙУНІВЕРСИТЕТ

КАФЕДРА ПРИЛАДОБУДУВАННЯ

РОЗРАХУНКОВА РОБОТА №2

З дисципліни: OPKEP

Інженерно-технічний факультет

Група НАЕПС – 3

Студент Фучко О.П

Шифр - 67

Ужгород - 2008

Зміст

Вступ

1. Плоско пасова передача

1.1 Загальні відомості

1.2 Ремені і шківи

1.3. Кінематичні параметри

1.3.2 Геометричні параметри

1.3.2 Геометричні параметри

2 Пружини

2.1. Призначення та конструкції пружин

2.2 Розрахунок гвинтових циліндричних пружин

2.2.1 Розрахунок гвинтових циліндричних пружин розтягу та стиску

2.2.2 Розрахунок гвинтових циліндричних пружин кручення

3.1 Загальні положення

3.2 Основні схеми кулачкових механізмів

3.3 Основні параметри кулачкових механізмів

3.4 Побудова графіка переміщень штовхальника при заданому профілі кулачка

3.5 Поняття про кут тиску

3.5.1 Виведення формули для кута тиску в кулачковому механізмі

3.5.2 Поняття про відрізок кінематичних відношень

3.6 Синтез (проектування) кулачкових механізмів по заданому закону руху штовхальника

3.6.1 Побудова закону руху осі штовхальника

3.6.2 Визначення мінімального радіуса кулачкової шайби по відомому закону руху штовхальника

3.6.3 Побудова профілю кулачка

Вступ

На сучасному етапі науково-технічного прогресу приладобудування займає дуже важливу позицію. Повсякденне життя людини неможливо уявити без використання усілякого роду приладів. Вони застосовуються у всіх галузях народного господарства. Отже приладобудування є однією з провідних галузей інженерії.

Вагома роль успіху при створенні нової техніки вирішується тим, як підготовлений інженер. А саме: як він використовує набуті знання при розв’язку поставлених задач.

Створення нових приладів потребує глибоких навичок та практичного досвіду. Найважливіша задача при створенні нового приладу в тому, щоб при заданих вхідних параметрах отримати необхідні вихідні, застосовуючи такі елементи які б забезпечували всі необхідні вимоги по міцності, пластичності, довговічності та надійності, а також по технологічності та економічності.

Розробка елементів, які б забезпечували ці параметри, пов′язана із тривалими розрахунками, що значно ускладнює процес створення нових розробок. Для прискорення розрахунків застосовують різні системи автоматичного проектування, однією з них є комп′ютерна програма APM WinMashine, яка дозволяє проводити розрахунок практично усіх механічних частин приладів. Ця програма була використана при виконанні даної курсової роботи.

1. ПЛОСКОПАСОВА ПЕРЕДАЧА

1.1. Загальні відомості

Пасова передача відноситься до передач тертям з гнучким зв'язком. Вона складається з двох або декількох шківів, що охоплюються гнучким ременем, надітим на шківи з натягом (рис. 1.1).

Рис. 1.1 Пасова передача

Передаточне відношення даного типу передач знаходяться в межах i = 4... 10, і лише при дуже малому передавальному моменті його збільшують до 15... 16.

До переваг ремінних передач відносяться хороші амортизуючі і демпфуючі властивості, безшумність, здатність служити запобіжною ланкою при випадкових перевантаженнях, простота конструкції, знижені вимоги до точності виготовлення і монтажу, менша початкова вартість, можливість передавати обертання при великих міжосьових відстанях і можливість здійснення безступінчатого регулювання швидкості.

У порівнянні із зубчатими, ремінні передачі мають наступні недоліки: великі габаритні розміри, менший ККД, меншу довговічність, великі експлуатаційні витрати і непостійність передавального відношення із-за наявності ковзання ременя по шківу.

Однією з переваг ремінних передач є універсальність в розташуванні осей валів.

Так, в ремінній передачі компресора є два шківи: обертання і передача корисного навантаження здійснюються від ведучого шківа, пов'язаного з двигуном, на ведений, пов'язаного з робочим органом. Привід вентилятора і генератора у автомобільних двигунів включає трьохшківну передачу.

Для забезпечення необхідної сили тертя між ременем і шківами, ремінь повинен бути натягнутий. Натягнення ременя - основна умова роботи пасових передач. Його може бути створено:

— за рахунок пружності ременя укороченням його при зшиванні (рис. 1.2, а);

— пересуванням одного валу (рис. 1.2, б);

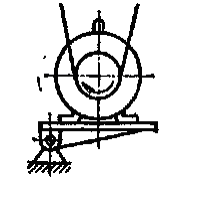
—автоматично, масою системи, що коливається (рис.1.2,в);

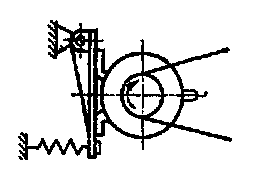
—силою пружини, що діє на систему (рис. 1.2, г);

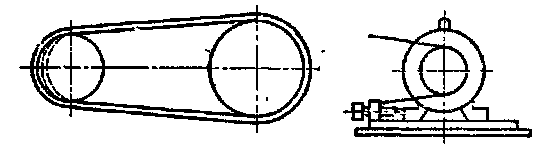
а) б)

в) г)

Рис. 1.2 Види пасових передач

Величину натягу при першому способі важко контролювати. Як правило, натяг виявляється більшим за необхідний. При другому способі натягнення встановлюється по найбільшому навантаженню, і воно постійне. Оскільки на практиці більшість передач працюють із змінним режимом навантаження, то ремені з постійним попереднім натягом у період недовантажень виявляються натягнутими більше, ніж необхідно для передачі корисного навантаження, що негативно позначається на довговічності паса. Залежно від виду ременя розрізняють передачі плоскоремінні, клиноремінні, поліклинові і круглоремінні (рис. 1.3, а...г).

а) б) в) г)

Рис. 1.3 Типи пасів

Плоскоремінна передача. У цій передачі корисне навантаження передається за рахунок сил тертя між внутрішньою поверхнею ременя і поверхнею шківа (рис. 1.3, а). Сила тертя розосереджена по всій ширині ременя, що забезпечує рівномірне навантаження всіх його елементів. Ремінь - найбільш тонкий і гнучкий елемент прямокутного перетину. Передача допускає застосування шківів найменших діаметрів. У порівнянні з іншими механічними передачами, плоскоремінна передача забезпечує найбільш спокійний хід без вібрації. Ця перевага робить її у ряді випадків незамінною, особливо в точних верстатах.

Клиноремінная і поліклинова передачі. У цих передачах корисне навантаження передається за рахунок сил тертя між бічними поверхнями паса трапецієдального перетину і канавок шківа (рис. 1.3, б). Через заклинюючу дію клиноремінна передача в порівнянні з плоскоремінною володіє більшою тяговою здатністю. Внаслідок цього при однаковій передаваній потужності вона вимагає меншого натягнення, створює менший тиск на вали і опори, допускає малі кути охопленя на шківах і тому застосовується при великих передавальних числах і менших міжосьових відстанях. Клиноремінна передача краще пристосована для безступінчатого регулювання швидкості, для чого шківи виконують у вигляді розсувних дисків.

До недоліків клиноремінної передачі відноситься менший ККД передачі внаслідок великих втрат на вигин ременя і можливу непостійність розмірів перетину ременя по його довжині. При необхідності застосування в передачі декількох ременів і неминучого розкиду їх розмірів і пружних властивостей з'являються відмінності в передавальних відносинах окремих струмків і в натягові ременів. Це викликає нерівномірне навантаження ременів і знижує їх довговічність.

Ці недоліки усунені в поліклінової передачі, в якій, так само як в клиноремінній передачі, корисне навантаження передається за рахунок сил тертя між бічними поверхнями ребер клиновидної форми і канавок шківа (рис. 1.3, в).

Ремені поліклинової передачі поєднують переваги клинових ременів (підвищене зчеплення з шківами) і гнучкість, характерну для плоских ременів, що дозволяє використовувати поліклинові паси на шківах малого діаметру. Поліклинова передача рекомендується для приводів, що не допускають вібрації. Працює при швидкості до 50 м/с, передавальне число до 12.

Круглоремінна передача. Передача корисного навантаження здійснюється за рахунок сил тертя між внутрішньою поверхнею круглої форми паса і канавки шківа (рис. 1.3, г). Широко використовується в поліграфічних і побутових машинах, у верстатах, годинниковій промисловості і приладах. Застосовують шкіряні, бавовняні, капронові і прогумовані ремені. Ремені випускають діаметром від 2 до 20 мм..

1.2. Ремені і шківи

Ремінь є найважливішим елементом передачі, що визначає її працездатність. До ременя пред'являються наступні основні вимоги: висока тягова здатність, тобто надійність зчеплення з шківом, достатня міцність, довговічність і зносостійкість, невисока вартість.

У плоскоремінній передачі застосовують два види ременів: звичайні - з кутовою швидкістю v = 25...30 м/с і швидкохідні - v > 30 м/с.

До звичайних відносяться ремені прогумовані, шкіряні, бавовняні і шерстяні. Випускають їх рулонами. Кінці ременів потрібної довжини зшивають різними методами. Місце зшивання важче і володіє меншою гнучкістю, ніж сам пас. Це викликає удари при проходженні по шківах, вібрацію і різко скорочує термін служби.

Найбільш поширені, прогумовані ремені, нормуються по ГОСТ 23831-79. Вони складаються з декількох шарів тканини на синтетичній основі з гумовими прошарками і обкладинками, завулканізованими в одне ціле. Ширина ременів b = 20...500 мм, товщина б = З...13,5 мм. Ремені випускають трьох типів: А - нарізні, з гумовими прошарками між всіма прокладками і з кромками, захищеними водотривким складом ;

Б - пошарово загорнені як з гумовими прошарками, так і без них;

В - спірально загорнені без гумових прошарків.

Шкіряні ремені (ГССТ 18697-73) відрізняються високою тяговою здатністю і допускають найбільші перевантаження. Унаслідок високої вартості їх застосування обмежене.

Швидкохідні ремені виготовляють з капрону або нейлону з фрикційним покриттям з синтетичних смол або шкіри. Завдяки високій міцності цих матеріалів, ремені являючись набагато тоншими і легшими, допускають значно великі натягнення. Виконують їх нескінченними або кінцевими із зварюванням кінців так, що місце з'єднання не відрізняється від цілого ременя, чим забезпечується найбільш спокійна робота передачі. Швидкохідні ремені допускають швидкість до 100 м/с. Якнайкращі експлуатаційні показники мають нейлонові ремені. Для клиноремінної передачі застосовують прогумовані нескінченні ремені двох конструкцій: з несучим елементом з декількох шарів тканини 1 (рис. 1.4, а) або з шаром шнура 2, навитого по спіралі, завулканізованих у резину 3 (рис. 1.4, б). Ремені можуть мати тканинну обгортку поверхні 4, а також можуть бути 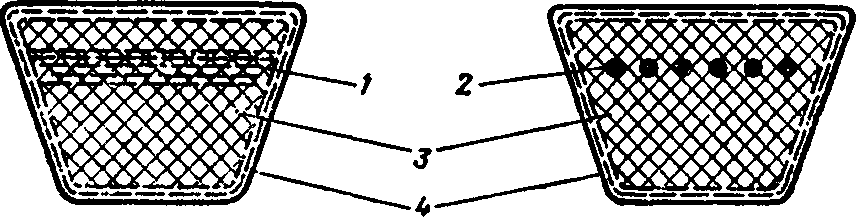виконані без неї.

а) б)

Рис. 1.4 Структура пасів

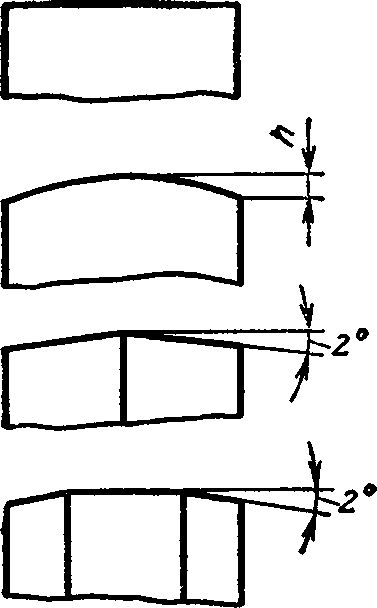
Рис. 1.5 Шківи для плоских ременів

Для плоских ременів форма поверхні шківа гладка циліндрична. Для попередження спаду плоского ременя з шківів один з них (бажано більший) виконують з опуклим ободом, описаним по дузі, або циліндровим з двосторонньою конусністю (рис. 1.5).

Шорсткість робочої поверхні обода повинна бути не більше Ra = 2,5 мкм; у шківів для швидкохідних передач ця поверхня полірується. При швидкості v > 40 м/с із-за повітряного клину, що утворюється між шківом і набігаючою гілкою ременя, знижується зчеплення між взаємодіючими поверхнями і падає несуча здатність передачі. Для попередження цього явища на шківах передбачають кільцеві канавки. При швидкості v≥ 5 м/с шківи необхідно статично балансувати. Шківи швидкохідних передач необхідно піддавати динамічному балансуванню. Основні розміри шківів - діаметр d, ширина В і стріла опуклості h регламентовані ГОСТ 17383-73*.

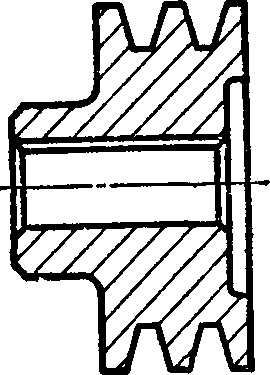
Для клинових ременів (рис. 1.6) робочою поверхнею є бічні сторони клинової канавки в ободі шківа. Робоча поверхня канавок шківа має шорсткість Ra = 2,5 мкм; її бажано полірувати. Шківи повинні бути добре збалансовані. Розміри і число канавок визначаються профілем ременя і числом ременів. Ремінь при вигині на шківі деформується, і кут його перетину зменшується тим більше, чим менше діаметр шківа. Для кращого прилягання бічних поверхонь ременя до канавок шківа кут канавки φ слід вибирати залежно від розрахункового діаметру шківа.

Для поліклинових ременів робочою поверхнею є бічні сторони клинових канавок в ободі шківа. Кут клину канавок шківа φ = 40˚ незалежно від діаметру шківа.

Для круглих ременів профіль канавок вибирають напівкруглим з радіусом, рівним радіусу ременя.

Рис. 1.6 Шків для клинових ременів

Шківи виконують з чавуну СЧ 15 - при v ≤ 30 м/с, модифікованого чавуну і сталі 25Л - при v ≤ 45 м/с, алюмінієвих сплавів - при v ≤ 80 м/с, з легованої сталі - при v ≤ 100 м/с, зварними з прокату і штампованих елементів - при v ≤ 60 м/с, а також із пластмас і дерева.

1.3 Основи розрахунку пасових передач

Теоретичні основи розрахунку являються загальними для всіх типів ременів. Основними критеріями працездатності ременних передач є: тягова здатність, яка визначається силою тертя між та шківом, довговічність ременя, яка в умовах нормальної експлуатації обмежується розрухою ременя від втоми. На сьогоднішній день основними розрахунками ременних передач є розрахунки по тяговій здатності. Довговічність ременя збільшують при розрахунку шляхом вибору основних параметрів передачі в співвідношенні з рекомендаціями, виробленими на практиці.

1.3.1. Кінематичні параметри. Окружні швидкості на шківах

v1 = d1 n1 / 60 ; v2 = d2 n2 / 60. (1.1)

Враховуючи жорстке ковзання ременя, можна записати v1 < v2 чи

v2 = v1 (1—ε). (1.2)

де ε – коефіцієнт ковзання. При цьому передаточне відношення

i = n1 / n2 = v1 d1 = d2 / [ d1 (1—ε) ]. (1.3)

В подальшому показано, що величина ε залежить від навантаження, тому в ременній передачі передаточне відношення не завжди є постійним. При нормальних робочих нагрузках ε ≈ 0,01…0,02. Найбільше значення ε дозволяє наближено приймати:

i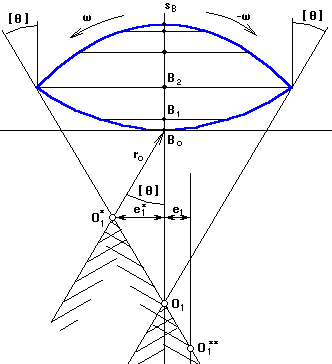 ≈ d2 / d1. (1.4)

1.3.2 Геометричні параметри

Н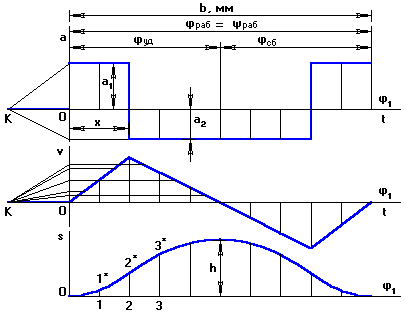а рис1.7, а – міжосьова відстань; β – кут між гілками ременя; α – кут обхвату ременем малого шківа. При геометричному розрахунку відомими зазвичай є d1, d2 і а, які визначають кут  і довжину ременя l. В результаті витяжки і провисання ременя значення α і l не являються точними і визначаються приблизно так:

α = 180°— β ; sin (β/2) = (d2— d1) / (2a) (1.5)

Враховуючи, що β/2 практично не перевищує 15°, приблизно приймаємо значення синуса рівним аргументу і запишемо

β = (d2 — d1) / а рад ≈ 57 ( — d1) / а° (1.6)

Довжина ременя вираховується як сума прямолінійних ділянок і дуг обхвату:

l ≈ 2a + 0,5 (d2 + d1) / (4а) (1.7)

Рис. 1.7 Геометричні параметри передачі

1.3.3 Сили та силові залежності

Н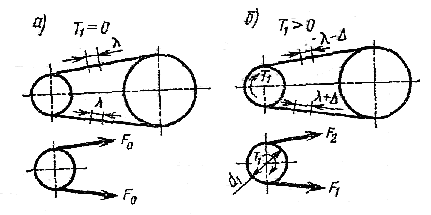
а рис.1.8 показане навантаження гілок ременя у двох випадках: Т1 = 0 (рис.1.8,а) і Т1 > 0 (рис.1.8,б). Тут позначено Fo – початковий натяг ременя ; F1 і F2 –натяг ведучої та веденої гілок в навантаженій передачі; Ft = 2 T1 / d1 – окружна сила передачі.

Рис. 1.8 Сили та силові залежності

За умовою рівноваги шківа маємо:

T1 = 0,5 d1 (F1 – F2) (1.8)

або

F1 – F2 = Ft (1.9)

Зв’язок між Fo, F1 та F2 можна встановити на основі наступних роздумів.

Геометрична довжина ременя не залежить від навантаження [див. формулу (1.7)] і залишається незмінною як в ненавантаженій, так і в навантаженій передачі. З цього випливає, що додаткова витяжка ведучої гілки компенсується рівним скороченням веденої гілки (рис.1.8). Запишемо:

F1 = Fo + ∆F , F2 = Fo – ∆F (1.10)

або

F1 + F2 = 2Fo (1.11)

Із рівнянь (1.10) і (1.11) випливає:

F1 = Fo + Ft / 2 , F2 = Fo – Ft / 2 (1.12)

Отримали систему двох рівнянь з трьома невідомими Fo, F1 та F2. Ці рівняння встановлюють змінення натягу ведучої чи веденої гілок в залежності від навантаження Ft, але не дозволяють передавати це навантаження чи тягову передачу, яка зв’зана з величиною сили тертя між ременем і шківом. Така залежність встановлена Ейлером.

2 ПРУЖИНИ

2.1 Призначення та конструкції пружин

Пружні елементи, або пружини, належать до розповсюджених деталей, що використовуються в різних машинах, механізмах та при­ладах. Вони виконують інколи дуже відповідальні та складні функції.

Пружні властивості пружин дають змогу використовувати їх у та­ких випадках:

а) для створення потрібних постійних зусиль (у натискних та натяжних пристроях передач тертям, муфтах, гальмах, клапанах);

б) для акумулювання механічної енергії попереднім деформуван­ням пружин (пружинні двигуни приладів часу та інші пристрої);

в) для віброізоляції та амортизації ударів за рахунок пружних характеристик відповідним чином підібраних пружин (у транс­портних засобах, опорних пристроях чутливих елементів приладів та ін.);

г) для вимірювання сил, що здійснюється фіксацією пружних де­формацій пружин (динамометри та інші вимірювальні прилади).

Усі пружини за видом навантаження поділяють на пружини роз­тягу, стиску, кручення (рис.2.1).

Р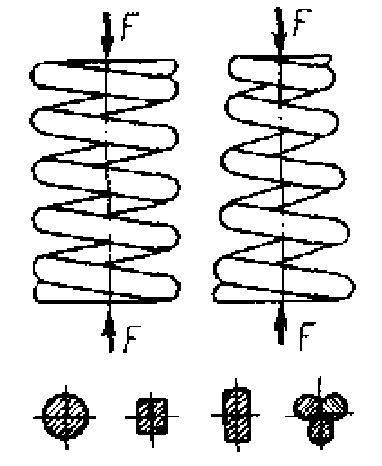


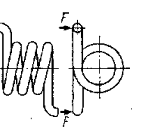
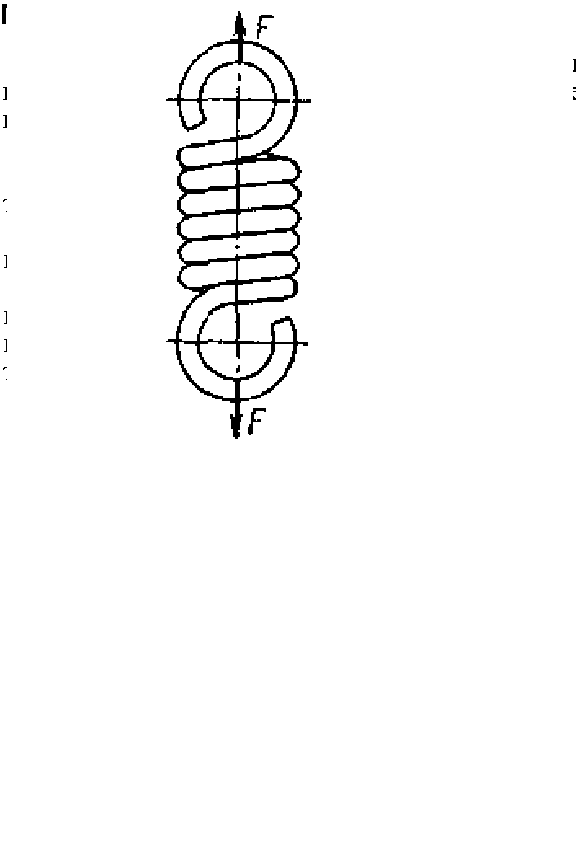
ис. 2.1 Види пружніх елементів

У приладобудуванні найрозповсюдженішими є гвинтові пружини розтягу, стиску та кручення, виконані із дроту круглого або іншого перерізу. Гвинтова пружина розтягу виготовляється зі щільним навиванням витків, до того ж крайні витки плавно перехо­дять у спеціальні вушка, які зручні для закріплювання пружини.

Гвинтові пружини стиску бувають циліндричної та конічної фор­ми. Конічна форма забезпечує пружині змінну жорсткість при дефор­муванні. В таких пружинах стиску робочі витки не дотикаються між собою, а лише крайні витки виконуються зі щільною навивкою для надання пружині плоских опорних торців. Гвинтові пружини стиску найчастіше виготовляють із дроту круглого перерізу, а при великих стискаючих силах застосовують пружини з квадратним або прямокут­ним перерізом витків. З метою підвищення податливості в умовах об­межених габаритних розмірів використовують багатожильні гвинто­ві пружини стиску.

2. Розрахунок гвинтових циліндричних пружин

1. Розрахунок гвинтових циліндричних пружин розтягу та стиску

Гвинтові циліндричні пружини розтягу та стиску мають такі основ­ні геометричні параметри (рис. 2.2 а, б):

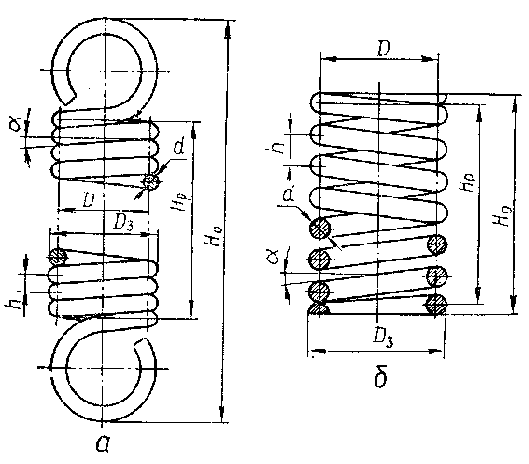
Рис. 2.2 Гвинтові циліндричні пружини розтягу та стиску

d— діаметр витків (дроту) пружини;

D— середній діаметр пружини;

D_>з> = D + d — зовнішній діаметр пружини;

С = D/d — індекс пружини;

h — крок витків у ненавантаженій пружині (h = d — для пру­жини розтягу, рис.2.2, a);

α — кут підйому витків (tg α = h/(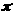D);

H_>0> — довжина (висота) ненавантаженої пружини;

H_>p> — довжина робочої частини ненавантаженої пружини;

і = Н_>р>/h — кількість робочих витків;

L — довжина дроту для виготовлення пружини.

Податливість циліндричних пружин пропорційна їхньому індек­су С. Для збільшення податливості індекс С беруть якомога більшим; практичне застосування мають пружини з індексом С = 4...12. За­лежно від діаметра витків рекомендують такі значення індексу C цилінд­ричних пружин:

Таблиця 2.1 Рекомендовані значення індексу С.

d, мм	<2‚5	3—5	6—12
С	5—12	4—10	4—9

Збільшуючи індекс пружини певної жорсткості, можна зменшити довжину пружини через збільшення її діаметра, а зменшуючи індекс, можна зменшити діаметр через збільшення довжини пружини.

Для розрахунку на міц­ність розглянемо силові фактори, що діють у пере­різі витка, навантаженого силою F пружини (рис. 2.3).

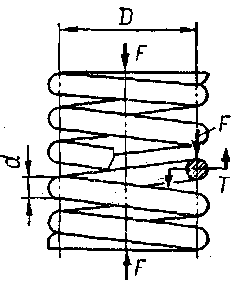
Рис. 2.3 Навантаження витків пружини стиску.

За умовою рівноваги ниж­ньої частини пружини виз­начаємо, що у довільному перерізі витка діють крутний момент Т = 0‚5FD та поперечна сила F, які спри­чинюють відповідно кручен­ня та зріз витка. Нехтую­чи кутом підйому витків α, який для більшості пружин менший ніж 10—12°, а також напруженнями зрізу від поперечної сили, на­пруження кручення витків визначають за виразом:

τ = TK/W_>P> = 8FD/(πd³ ), (2.1)

де K — коефіцієнт, що враховує кривину витків; W_>p> = πd³/16 — полярний момент опору перерізу витка. Коефіцієнт K беруть залежно від індексу С пружини із співвідношення

K=1 + 1‚4/С. (2.2)

Умову міцності витків пружини на основі ви­разу (2.2) записують у вигляді

τ = 8FDК/(πd³) < [τ]. (2.3)

Потрібний діаметр дроту пружини із умови (2.3) визначають за формулою

. (2.4)

Якщо в умові (2.3) врахувати, що D/d = С, то формулу для визна­чення діаметра дроту пружини можна записати у вигляді

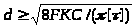(2.5)

Добуте значення d округлюють до значення у стандартному ряду діаметрів дроту для виготовлення пружин.

Діаметр дроту пружини дає змогу визначити середній та зовнішній

діаметри пружини:

D = Сd; D_>3> = D + d.

Осьову пружну деформацію пружини (розтяг або стиск) під дією навантаження F можна дістати як добуток кута закручування витків θ пружини та середнього радіуса пружини 0‚5D:

λ =0‚5Dθ = 0‚5DТπDі/(GI_>р>) = 0,25FπD³i/(GI_>p>),

де і — кількість робочих витків пружини; G — модуль пружності при зсуві матеріалу пружини (для сталі G = 8 10⁴ МПа); I_>p> = πd⁴/32 — полярний момент інерції перерізу витка пружини.

Виражаючи I_>p> через d та враховуючи, що D/d = С, вираз для осьо­вої пружної деформації пружини можна записати у вигляді

λ = 8FD³i/(Gd⁴) = 8FС³i/(Gd). (2.6)

Відношення навантаження F до осьової пружної деформації λ пру­жини називається жорсткістю k пружини. Із виразу (2.6)

k = Gd⁴/(8D³і) = Gd/(8С³i). (2.7)

Вираз (2.6) дає змогу визначити потрібну кількість робочих вит­ків пружини, якщо відоме значення λ:

і = Gd⁴λ/(8FD³) = Gdλ/(8FС³). (2.8)

Щ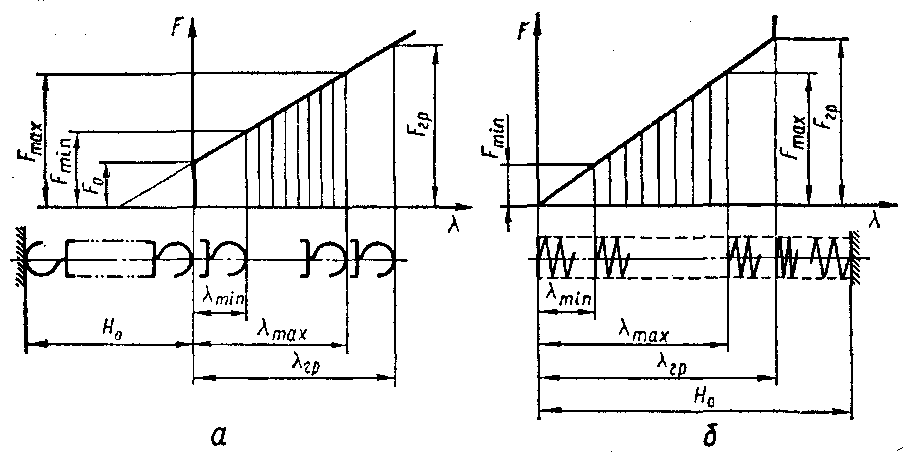
об правильно розрахувати та підібрати пружину, треба знати її робочу характеристику (рис.2.4 а, б), на якій повинні бути зазна­чені: λ_>mіn>, λ_>mах> — відповідно мінімальна та максимальна розрахунко­ві деформації пружини; F_>min>, F_>max>, F_>гp> — відповідно мінімальне і мак­симальне розрахункові навантаження та граничне навантаження на пружину (при посадці витків у пружинах стиску і за міцністю витків у пружинах розтягу).

Рис. 2.4 Робочі характеристики пружин розтягу та стиску

Для пружин розтягу (рис.2.2, а), виготовлених із щільним (за­критим) навиванням витків, початковий натяг (притискання сусідніх витків)

F_>0> =(0,2...0,3)F_>гp>. Граничне навантаження для пружин роз­тягу та стиску беруть F_>гp> = (1,1... 1,2) F_>max>.

Подальший розрахунок пружини розтягу полягає у визначенні з умови міцності діаметра дроту d за максимальним навантаженням F_>mах> і середнього D та зовнішнього D_>з> діа­метрів пружини. Потім знаходять потрібну кількість робочих витків і за формулою (2.8), беручи максимальне розрахункове навантажен­ня F_>mах> та деформацію λ_>mах >.

Решту розмірів пружин обчислюють за такими формулами:

1. Для пружин розтягу

довжина робочої частини ненавантаженої пружини (див. рис.2.2.а) H_>p> = іd повна кількість витків І_>0> = І + (1...2);

довжина ненавантаженої пружини H_>0> = і_>0>d + 2h_>в>,

де h_>в> =(0.5...1)D — висота одного вушка; довжина пружини при максимальному розрахунковому навантажені F _>mах>

H=H_>0> + λ_>max> = H_>0> + (F_>max> - F_>0>)/k = H_>0> + 8С³ і(F_>max> – F_>0>)/(Gd);

довжина дроту для виготовлення пружини

L = πDi/соsα + 2l_>в>,

де l_>в> — довжина дроту для одного вушка.

2. Для пружин стиску

загальна кількість витків і_>0> = i + (1,5...2), де кількість крайніх щільно навитих витків становить 1,5—2;

мінімальний зазор між витками при максимальному розрахунковому навантаженні F_>max> — ∆ = (0,1...0,2) λ_>max>/i, крок витків ненавантаженої пружини h = λ_>max>/i + d + ∆;

довжина пружини, стиснутої до дотику витків, H_>гp> = (i_>0> — 0,5) d; довжина ненавантаженої пружини H_>0> = H_>гp> + і (h — d); довжина дроту для виготовлення пружини L = πDі_>0>/cos α.

При великій кількості витків довгі пружини стиску під наванта­женням можуть втрачати поздовжню стійкість. Тому рекомендують при H_>0>/D > 3 встановлювати пружини стиску на оправках або у від­повідних трубках.

2.2.2 Розрахунок гвинтових циліндричних пружин кручення

При навантаженні циліндричної пружини кру­чення зовнішнім моментом М = Fа (рис. 2.5) у поперечних пере­різах витків утворюється такий же момент М, вектор якого напрмле­ний уздовж осі пружини.

Р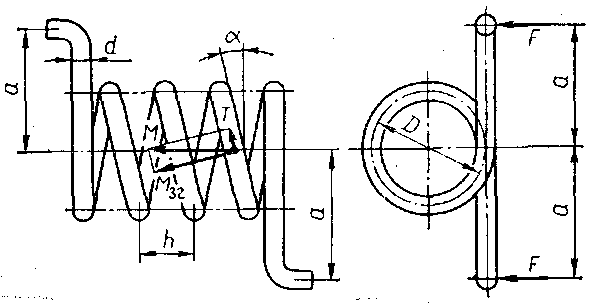
ис. 2.5 Гвинтова циліндрична пружина кручення

Якщо розкласти момент М на складові вздовж витка та перпендикулярно до витка, то в поперечному перерізі витка будемо мати крутний Т = М sіn α і згинальний M_>зг> = М соs α моменти. Оскільки кут підйому витків α < 10°, скручуванням вит­ків можна знехтувати (Т ≈ 0), а розрахунок витків на міцність ви­конати тільки на згин за згинальним моментом M_>зг> = М = Fа.

Напруження згину для витків циліндричної пружини кручення визначають за виразом

σ = M_>aг>K'/W_>0> = З2МК'/(πd³) (2.9)

де K' = (С — 0‚25)/(С — 1) — коефіцієнт кривини витків, що зале­жить від індексу пружини С = D/d; W_>0> = πd³/32 — осьовий момент опору перерізу витка (дроту пружини) діаметром d.

На основі виразу (2.9) умову міцності витків на згин записують у вигляді

σ = З2МК'/(πd³) < [σ]. (2.10)

При проектувальному розрахунку пружини кручення діаметр витків (або дроту) визначають за формулою, що випливає із умови (2.10),

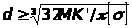(2.11)

Крок витків пружини кручення беруть h = d + (0,2...0,5) мм. Кут закручування пружини під дією моменту М визначають за фор­мулою

φ = МπDі/(ЕІ), (2.12)

де i — кількість робочих витків пружини; Е — модуль пружності ма­теріалу; I=πd/64 — осьовий момент інерції перерізу витка.

3 КУЛАЧКОВІ МЕХАНІЗМИ

3.1 Загальні положення

Кулачковим називається механізм, що містить дві основних ланки: кулачок і штовхальник, що утворюють вищу кінематичну пару.

Кулачкові механізми знайшли широке застосування в системах газорозподілу ДВЗ, у системах керування електричних ланцюгів, у вагонах метрополітену (контролери).

Достоїнства кулачкових механізмів:

1.можливість відтворення практично будь-якого закону руху вихідної ланки;

2.мала кількість деталей (кулачок і штовхальник), що дозволяє просто виготовляти й обслуговувати.

Недолік:

Наявність вищої кінематичної пари, у якій можуть виникати підвищені питомі тиски, що може привести до руйнування поверхні кулачка.

1 – кулачок

2 – штовхач

3 – ролик

4 – пружина

5 – контакти

Поверхня кулачка, з яким взаємодіє штовхальник - робочий (дійсний) профіль кулачка.

Поверхня, що проходить через точку В віддалена від дійсного профілю на відстані радіуса ролика - теоретичний профіль (рис. 3.1).

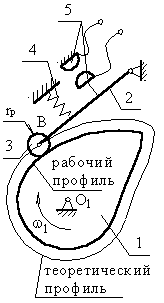
Рис. 3.1 Профіль кулачка

3.2 Основні схеми кулачкових механізмів

Кулачковий механізм із поступально рухаючим штовхальником.

а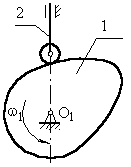
) з центральним штовхальником (вісь штовхальника проходить через вісь обертання кулачка),(рис.3.2)

Рис. 3.2 Кулачковий механізм із центральним штовхальником

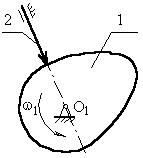
б) з позавісним штовхальником (рис. 3.3). Позавісність ліва, тому що вісь штовхальника проходить праворуч осі обертання кулачка, е – ексцентриситет.

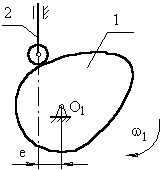
Рис.3.3 Кулачковий механізм із позавісним штовхальником

Кулачковий механізм із поступально рухаючимся товхальником (рис. 3.4), ланка 2 (штовхальник) робить зворотньо-обертовий рух з центром обертання в точці О2.

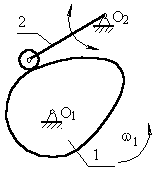
Рис. 3.4 Кулачковий механізм із поступально рухаючимся товхальником

3.3 Основні параметри кулачкових механізмів

У процесі роботи штовхальник робить 3 рухи (рис. 3.5):

1. поступально вгору - у цьому випадку штовхальник взаємодіє з ділянкою 01;

2. стоїть на місці (вистій) - контакт із ділянкою 12.

Тут постійний радіус кривизни.

3. штовхальник опускається (зближення) - контакт із ділянкою 23.

У першій фазі підйому штовхальника (фаза видалення) на профілі кулачка відповідає кут ψ_>удал>;

у фазі вистою – ψ_>выс>;

у фазі зближення – ψ_>сб>.ψ_>удал> + ψ_>выс> + ψ_>сб> = ψ_>раб> – робочий кут профілю кулачка

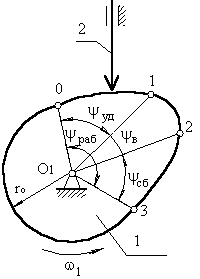
а)

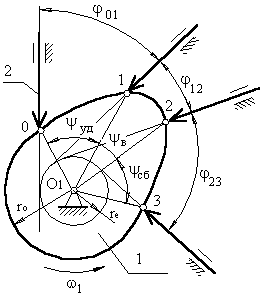
б)

Рис.3.5 Основні параметри кулачкових механізмів

Кут профілю кулачка можна показати тільки на кулачку. Кут повороту кулачка, що відповідає вище зазначеним фазам переміщення штовхальника, визначають, використовуючи метод повернення руху, відповідно до якого, всій системі, включаючи стійку, уявно повідомляють рух з кутовою швидкістю (ω_>1>).Тоді в зверненому русі кулачок стає нерухомим: ω*_>1> = ω_>1> + (–ω_>1>) = 0, а вісь штовхальника разом зі стійкою будуть переміщатися в напрямку (–ω_>1>). І кут повороту кулачка, що відповідає тій чи іншій фазі руху, визначається по куту повороту осі штовхальника в зверненому русі на відповідній ділянці. Вісь штовхальника в зверненому русі в будь-якому положенні буде стосуватися окружності радіуса r_>е>.

Поворот кулачка на ділянці:

01 – φ_>01 >12 – φ_>12 >23 – φ_>23>

робочий кут повороту кулачка φ_>раб>:

φ_>раб> = φ_>01> + φ_>12> + φ_>23>

(уб) (выс) (сб)

Завжди незалежно від схеми механізму φ_>раб> = ψ_>раб>, а

φ_>уд> ≠ ψ_>уд>, φ_>выс> ≠ ψ_>выс>, φ_>сб> ≠ ψ_>сб>,

для всіх схем, крім кулачкового механізму з центральним штовхальником.

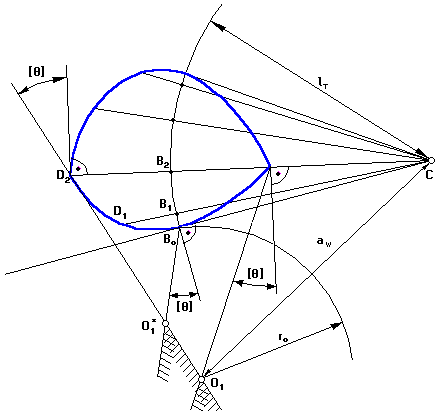
3.4 Побудова графіка переміщень штовхальника при заданому профілі кулачка

Переміщення відраховуються від початкової окружності радіуса r_>o>.

Точка В належить штовхальнику, що повертається навколо осі С, т.В переміщається по дузі окружності радіусом r = l_>т>. З точки 1 проводимо окружність r = lт до перетинання з окружністю, радіус якої дорівнює відстані між тО_>1> і тС: r = a_>w>. Точка перетину т.С_>1> – положення осі обертання штовхальника в зверненому русі, коли штовхальник контактує з поверхнею кулачка в точці 1. З т.С_>1> проводимо дугу окружності r = l_>т >до перетину з початковою окружністю. Тоді переміщення точки В буде рівним довжині дуги

11*. На ділянці 12 штовхальник не переміщається. На ділянці 23 переміщення точки В шукається аналогічно переміщенню на ділянці 01.

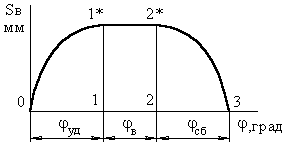
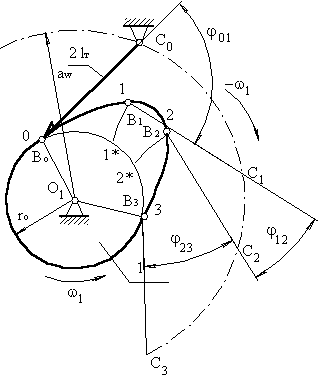
Рис.3.6 Графік переміщень штовхальника при заданому профілі кулачка

3.5 Поняття про кут тиску

Кут тиску - кут між вектором лінійної швидкості вихідної ланки (штовхальника) і реакцією, що діє з ведучої ланки (кулачка) на вихідну ланку. Ця реакція без обліку сил тертя спрямована по загальній нормалі до взаємодіючих поверхонь. Кут тиску визначається експериментально. Для кулачкового механізму з поступально рухаючимся штовхальником припустимий кут тиску дорівнює: [θ] = 25º÷35º.

Для кулачкового механізму з хитним штовхальником припустимий кут тиску дорівнює: [θ] = 35º÷40º.

Реакцію можна розкласти на дві складов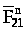і:

і .

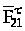Якщо, при дії яких-небуть причин, кут тиску буде збільшуватися, то 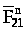буде зменшуватися, а 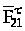– збільшуватися.

При досягненні кутів більше припустимого, можливий перекіс осі штовхальника в направляючій (рис. 3.7).

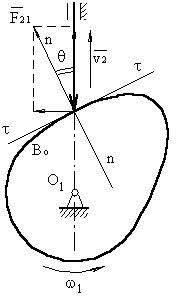
Рис.3.7 Кут тиску

3.5.1 Виведення формули для кута тиску в кулачковому механізмі.

З трикутника ΔКВР (рис.3.8):

(1)

КР = О_>1>Р – О_>1>К = О_>1> – е

КВ = s_>o> + s_>B>

(2)

Трикутник ΔО_>1>ВР подібний трикутнику ΔАВС. Тоді

­ 

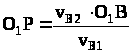
v_>B1>= ω_>1>·O_>1>B

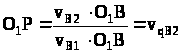
Підставимо це рівняння в (2):

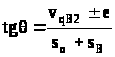
Знак “ – ” – для правої позавісності;

знак “ + ” – для лівої позавісності.

Кут тиску в кулачковому механізмі залежить від розмірів кулачкової шайби: чим вона більше, тим кут тиску менше.

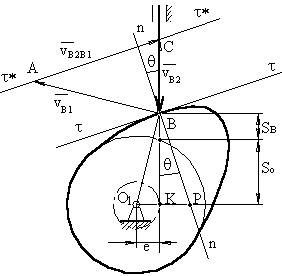
Рис. 3.8 Кут тиску в кулачковому механізмі

3.5.2 Поняття про відрізок кінематичних відношень

Якщо з точки В для якогось поточного положення штовхальника проведемо лінію, рівнобіжну О_>1>Р, а із центра – || nn, то при їхньому перетині одержимо точку D:

BD = O_>1>P = v_>B>_>2> / v_>B>_>1> =v_>qB>_>2>

З (рис. 3.9) випливає, що переміщення точки В штовхальника і, знайшовши максимальний відрізок кінематичного відношення, можна визначити положення центра обертання кулачка, відклавши зовнішнім чином від точки D припустимий кут тиску.

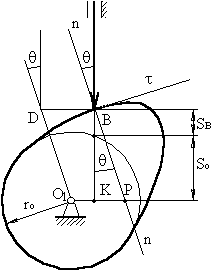
Рис. 3.9 Кінематичні відношення

3.6 Синтез (проектування) кулачкових механізмів по заданому закону руху штовхальника

Під синтезом кулачкового механізму будемо розуміти побудову профілю кулачка, у кожній точці якого кут тиску не перевищував би припустимого, а розміри самого профілю були б мінімальні.

Дана задача розв’язується в 3 етапи:

1. Будується графік заданого закону руху (як правило графік прискорення точки В штовхальника як функція кута положення – a_>B >= f(φ_>1>), або графік лінійної швидкості точки В – v_>B>= f(φ_>1>)). Потрібно побудувати графік переміщення точки В як функцію від кута повороту кулачка s_>B>= f(φ_>1>).

2. Визначення мінімального розміру кулачкової шайби за умови, що кут тиску в будь-якій точці профілю не перевищує припустимого.

Побудова профілю кулачка.

3.6.1 Побудова закону руху осі штовхальника

Дано: Треба побудувати:

Вигляд графіка a_>B >= f(φ_>1>), 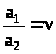графіки a_>B >= f(φ_>1>)

максимальний хід v_>B>= f(φ_>1>)

штовхальника h_>т >s_>B>= f(φ_>1>)

Рис.3.10

b – база графіка (скільки відводиться на графік по осі φ_>1­>).

Порядок побудови:

1. Довільно вибирається база графіка.

2. Рахуємо масштаб по осі φ_>1>:

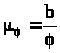, мм/град

3. Якщо заданий симетричний вид графіка, тоді:

φ_>уд> = φ_>сб>  b_>уд> = b_>сб>

У загальному випадку закон руху може бути несиметричним.

4. Задамося довільним чином а_>1>= 40 ÷ 50 мм. Тоді

а_>2>= а_>1>/ν

Виникає питання: яким повинна бути відстань х ?

Його знаходять з умови рівності площ під, і над віссю φ_>1>.

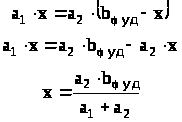
Чому треба витримувати рівність площ?

Фізичний зміст площі під кривою швидкості на ділянці φ_>уд> - максимальне видалення (переміщення т.В штовхальника). Якщо площі не будуть рівновеликими, то штовхальник, піднявшись на одну величину, опуститься на іншу.

Побудувавши графік прискорення, будуємо графік швидкості методом графічного інтегрування, вибравши відрізок інтегрування ОК_>1>. Інтегруючи графік швидкості (з відрізком інтегрування ОК_>2>, звичайно ОК_>1>=ОК_>2>), одержуємо графік переміщення т.В штовхальника. Отриману ламану лінію заміняють плавною кривою. Розрахунок масштабу:

(уS_>В>)_>max> на графіку переміщень виходить автоматично, і його величина залежить від відрізка ОК_>2>. Тоді, знаючи хід штовхальника, масштаб переміщення буде:

μ=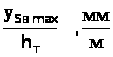

Потім у першому наближенні приймаємо, що кулачок обертається рівномірно, тоді кут повороту кулачка пропорційний часу повороту, і осі φ і t збігаються, але кожна вісь має свій масштаб.

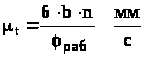
де b – в [мм]; частота обертання кулачка n – [об/мин]; φ_>раб> – [град].

Масштаб швидкості :

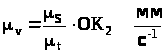
Масштаб прискорення:

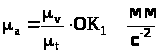
3.6.2 Визначення мінімального радіуса кулачкової шайби по відомому закону руху штовхальника

а) для кулачка з поступально рухаючимся штовхальником:

Дано: s_>B>=f(φ_>1>); v_>B>= f(φ_>1>); [θ]

Визначити: r_{>o min}> за умови, що кут тиску в будь-якій точці профілю кулачка не перевищує припустимий.

Порядок побудови графіка кінематичних відношень:

1. проводиться вертикальна вісь s_>B>,мм уздовж якої від довільно обраної точки В_>о> (початок відліку) відкладаються відрізки переміщення т.В, узяті з графіка s_>B>=f(φ_>1>). Масштаб по осі μ_>s*> переміщень може дорівнювати масштабу графіка переміщень μ_>s>.

2. у кожній з отриманих точок визначають відрізки кінематичних відношень, полічені в масштабі μ_>s*>, і відкладають їх під кутом 90º по напрямку обертання кулачка.

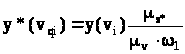мм

Там, де відрізок має максимальне значення, відновлюється перпендикуляр, і під кутом [θ] проводиться промінь.

Якщо враховувати реверс, то другий промінь проводять під кутом [θ] через відрізок кінематичних відношень, відкладений під кутом 90º у напрямку реверса і маючи максимальне значення. Якщо реверс не враховувати, другий промінь проводять через т.Во під кутом [θ]. Якщо допускається позавісність, то вона буде рівна е_>1>*. Якщо позавісність дорівнює нулю, то центр кулачка буде в т.О_>1>:

r_>o> = O_>1>B_>o>

Якщо позавісність задана в технічному завданні, наприклад ліва, то проводять пряму, рівнобіжну прямої О_>1>В_>о> і віддалена від неї на відстані, рівній величині позавісності е_>1>, з урахуванням масштабу μ_>s*>. У підсумку одержують точку О_>1>**.(рис.3.11).

Рис.3.11

б) для кулачка з хитним штовхальником:

Порядок побудови: У довільному місці вибирається точка С_>о>, з якої радіусом, рівним довжині штовхальника, проводять дугу окружності. По хордах відкладають переміщення т.В. Отримані точки послідовно з'єднують з т.С_>о>.

1. На цих прямих і на їхньому продовженні відкладаються відрізки кінематичних відношень, полічені в масштабі μ_>s*> по вищенаведеній формулі. Там, де відрізок має максимальне значення, відновлюється перпендикуляр, і під кутом [θ] проводиться промінь.

2. Якщо враховувати реверс, то другий промінь проводять під кутом [θ] через відрізок кінематичних відншень, відкладений під кутом 90º по напрямку реверса і який має максимальне значення. Центр кулачка буде в т.О_>1>*:

r_>o> = O_>1>Bo

Якщо реверс не враховувати, то другий промінь проводять через т. Во під кутом [θ]. Центр кулачка буде в т.О_>1>*: r_>o> = O_>1>*Bo (рис.3.12).

Рис.3.12

3.6.3 Побудова профілю кулачка

а) з поступально рухаючимся штовхальником (рис. 3.13.а):

Дано: r_{>o min}>, позавісність ліва е, φ_>раб> = ψ_>раб>, ω_>к>=ω_>1>, s_>B> = f(φ_>1>)

Потрібно побудувати профіль кулачка.

У зверненому русі кулачок обертається з кутовою швидкістю, рівною

ω_>1> + (–ω_>1>) = 0.

Порядок побудови:

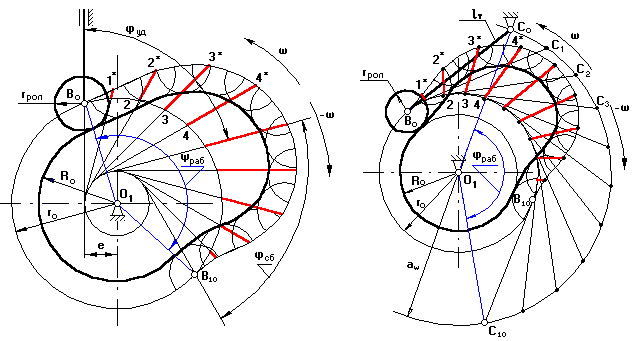
На окружності, радіусом r =r_>o> , проведеній в масштабі μ_>l>, з лівої сторони від осі О_>1> на відстані е вибирається точка В_>о> (перетинання осі штовхальника, що відстає на величину е від точки О_>1>, з окружністю r_{>o min}>). Точку В_>о> з'єднують з центром О_>1>. Від отриманого променя В_>о>О_>1> у напрямку (–ω_>1>) відкладають кут φ_>раб>=ψ_>раб >і проводять промінь О_>1>В_>10>. Отримана дуга В_>о>В_>10> ділится на 10 рівних частин. В кожній із позицій 1,2… проводиться положення осі штовхальника в зверненому русі, при цьому вісь штовхальника, переміщаючи в напрямку (–ω_>1>), буде увесь час торкатися окружності радіуса е, проведеної з центра О_>1> з урахуванням масштабу μ_>l>. В кожній із позицій від точок 1,2,3… відкладають переміщення т.В штовхальника уздовж осі штовхальника, узяті з графіка переміщень з урахуванням співвідношення масштабів μ_>l> і μ_>s>. Отримані крапки 1*,2*,3*… з'єднують плавною кривою й одержують центровий чи теоретичний профіль. Для побудови робочого профілю необхідно знати радіус ролика штовхальника. Якщо він не заданий, то його вибирають з конструктивних розумінь:

r_>p>=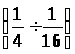r_{>o min}>

Крім того, радіус ролика повинен бути таким, щоб при побудові профілю кулачка не було загострення у вершині кулачка. Вибравши радіус ролика, з будь-яких точок теоретичного профілю кулачка (чим частіше, тим краще) проводять дуги окружності r=r_>p> внутрішнім чином. Провівши огинаючу до дуг, одержують робочий профіль кулачка. Якщо потрібно побудувати профіль кулачка з поступально рухаючимся штовхальником і позавісністю е=0, тоді порядок побудови профілю буде таким же, тільки вісь штовхальника буде проходити через центр обертання кулачка О_>1>.

рис. 3.13.а рис. 3.13.б

б) с хитним штовхальником (рис. 3.13.б):

Дано:

r_{>o min}>, l_>т>, φ_>раб> = ψ_>раб>, ω_>к>=ω_>1>, s_>B> = f(φ_>1>),a_>w >(з креслення для визначення r_{>o мin}>)

Потрібно побудувати профіль кулачка.

Порядок побудови:

У масштабі μ_>l> проводяться окружності радіусами r_>o> і a_>w>. У довільному місці окружності з r = a_>w> виберемо т.С_>0>. З'Єднаємо точку С_>0> з точкою О_>1>. Від отриманого променя в напрямку (–ω_>1>) відкладемо кут φ_>раб> = ψ_>раб>, одержимо точку С_>10>. Дугу С_>0>С_>10> розділимо на 10 рівних частин (одержимо точки С_>1>,С_>2>,С_>3>…– положення осі штовхальника в зверненому русі). З отриманих точок проводимо окружності радіусом l_>т> до перетинання з окружністю радіуса r_{>o_min}>. З отриманих точок 1,2,3... по хордах відповідних дуг відкладають переміщення т.В штовхальника, узятих із графіка переміщення з урахуванням масштабу μ_>l>. Отримані точки 1*,2*,3*… з'єднують плавною кривою - теоретичний профіль кулачка. Радіусом ролика проводять дуги в середину і будують огинаюючу лінію. Це і є дійсний профіль кулачка.