Проектирование и исследование механизмов упаковочного автомата
Проектирование и исследование механизмов упаковочного автомата
Автомат предназначен для горизонтального и вертикального перемещения упаковочных изделий в автоматизированном технологическом комплексе. Коленчатый вал I приводится в движение от электродвигателя 13 через муфту 14, планетарный редуктор 15, прямозубую передачу (число зубьев колёс z>16>, z>17>) и цепную передачу 7, передаточное число которой равно единице. На коленчатом валу 1 установлен маховик 18. Рычажный шестизвенный кулисный механизм, предназначенный для горизонтального перемещения изделия И, состоит из кривошипа (коленчатого вала) 1, шатуна (кулисного камня) 2, кулисы 3, шатуна 4, и ползуна 6. При рабочем ходе механизма преодолевается сила трения F>5>>T>, между ползуном 5, перемещающим изделие И, и направляющими стойки 6 Во время вспомогательного хода (в.х.) ползуна 5 происходит вертикальное перемещение изделия И при помощи ползуна 12 на величину H>L>. Ползун 12 через шатун 11 связан с толкателем 10 кулачкового механизма, состоящего из кулачка 8 и роликового толкателя 10. Допустимый угол давления в кулачковом механизме = 30. Закон изменения ускорения толкателя в зависимости от угла поворота кулачка показан на рис. 126в.
Исходные данные
|
№ п/п |
Наименование параметра |
Обозначения |
Единица СИ |
Числовое значение |
|
1 |
Ход ползуна 5 |
H>5> |
м |
0,5 |
|
2 |
Ход ползуна 12 |
H>L> |
м |
0,05 |
|
3 |
Частота вращения кривошипа 1 |
n>1> |
1/с |
0,3 |
|
4 |
Коэффициент неравномерности вращения кривошипа 1 |
|
- |
1/24 |
|
5 |
Коэффициент изменения средней скорости ползуна 5 |
K>V> |
- |
1,6 |
|
6 |
Отношение смещения e направляющей ползуна 5 к длине кривошипа 1 |
>e>=e/l>1> |
- |
1.15 |
|
7 |
Отношение длины шатуна 4 к длине кулисы 3 |
>43>=l>4>/l>3> |
- |
0,25 |
|
8 |
Длина ползуна 5 в долях от его хода |
>5>=l>5>/H>5> |
- |
4 |
|
9 |
Длина ползуна 12 в долях от его хода |
>12>=l>12>/H>L> |
- |
2,5 |
|
10 |
Масса единицы длины ползуна 5 |
M>l>>5>/l>5> |
Кг/м |
16 |
|
11 |
Масса единицы длины кулисы 3 |
M>l>>3>/l>3> |
Кг/м |
6 |
|
12 |
Масса единицы длины ползуна 12 |
M>l>>12> |
Кг/м |
11 |
|
13 |
Масса изделия И |
m>И> |
кг |
20 |
|
14 |
Коэффициент трения в направляющих ползуна 5 |
f>T56> |
- |
0,24 |
|
15 |
Момент инерции кривошипа (коленчатого вала) |
I>1A> |
Кг*м2 |
0.06 |
|
16 |
Угловая координата (для силового расчёта механизма) |
>1> |
град |
120 |
|
17 |
Число зубьев зубчатых колёс |
Z>16>; Z>17> |
- |
12;18 |
|
18 |
Модуль зубчатых колёс |
m |
мм |
4 |
|
19 |
Передаточное отношение редуктора 17 |
u |
- |
55 |
|
20 |
Длина толкателя FM кулачкового механизма. |
l>fm> |
м |
0,35 |
Лист 1. Проектирование эвольвентой зубчатой передачи.
1.1. Исходные данные и постановка задачи:
Число зубьев:
 .
.
Модуль:
 мм.
мм.
Угол главного профиля:
 .
.
Угол наклона зубьев:
 .
.
Коэффициент радиального
зазора:
 .
.
Коэффициент высоты зуба:
 .
.
Постановка задачи:
Рассчитать эвольвентную зубчатую передачу для коэффициентов
 ,
,
 .
.Обосновать выбор коэффициентов
 ,
,
 .
.Вычертить эвольвентное зубчатое зацепление и вычертить станочное зубчатое зацепление для
 и
и
 .
.
1.2. Алгоритм расчёта передачи:
При расчете необходимо придерживаться следующего порядка:
Определить
 по формуле
по формуле

Проверить заданные коэффициенты смещения.
Найти угол зацепления по

где
 и
и
 .
Угол
.
Угол
 находится
по
находится
по
 в таблице эвольвентных функций.
в таблице эвольвентных функций.
Определить коэффициент воспринимаемого смещения
 .
.
Подсчитать коэффициенты уравнительного смещения

Коэффициенты уравнительного смещения при реечном исходном контуре – всегда величина положительная.
Вычислить радиусы делительных окружностей

Определить радиусы основных окружностей

Определить радиусы начальных окружностей

Найти межосевое расстояние

Проверить
 по формуле
по формуле

Определить радиусы окружностей вершин

Определить радиусы окружностей впадин

Найти высоту зуба

Проверить сделанный расчет по формулам

Определить толщину зубьев по дуге делительной окружности

Определить толщину зубьев по окружности вершин
 ,
,
где
 и
и
 определяются по соответствующим углам
определяются по соответствующим углам
 и
и
 в таблице эвольвентных функций, а углы
– по косинусам
в таблице эвольвентных функций, а углы
– по косинусам

Сделать проверку на отсутствие заострения зуба, вычислив толщину зуба по окружности вершин

Определить коэффициент перекрытия для прямозубой передачи

Проверить достаточность полученного коэффициента перекрытия
 ,
,
где

Расчет выполнен на ПЭВМ, результаты расчета отражены в приложении.
1.3. Выбор коэффициента
смещения
 .
.
Условие отсутствия подреза:
 ,
,
 .
.
 ,
,

Условие отсутствия заострения:
 .
.

Достаточность коэффициента перекрытия:
 .
.

Равномерный износ:
 .
.

1.4. Построение эвольвентного зубчатого зацепления
По вычисленным параметрам проектируемая зубчатая передача строится следующим образом:
Выбираем масштаб
 ,
где O>1>O>2>
– межосевое расстояние на чертеже
,
где O>1>O>2>
– межосевое расстояние на чертеже

Откладывается межосевое расстояние
 и проводятся окружности: начальные
и проводятся окружности: начальные
 ,
,
 ;
делительные
;
делительные
 ,
,
 и основные
и основные
 ,
,
 ;
окружности вершин
;
окружности вершин
 ,
,
 и впадин
и впадин
 ,
,
 .
Начальные окружности должны касаться
в полюсе зацепления. Расстояние между
делительными окружностями по осевой
линии равно величине воспринимаемого
смещения
.
Начальные окружности должны касаться
в полюсе зацепления. Расстояние между
делительными окружностями по осевой
линии равно величине воспринимаемого
смещения
 .
Расстояние между окружностями вершин
одного колеса и впадин другого, измеренное
также по осевой линии, должно быть равно
величине радиального зазора
.
Расстояние между окружностями вершин
одного колеса и впадин другого, измеренное
также по осевой линии, должно быть равно
величине радиального зазора
 .
.Через полюс зацепления, касательно к основным окружностям колёс, проводиться линия зацепления колес. Точки касания
 и
и
 называются предельными точками линии
зацепления. Линия зацепления образует
с перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления
называются предельными точками линии
зацепления. Линия зацепления образует
с перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления
 .
.
Буквами
 и
и
 отмечается активная линия зацепления.
Точка
отмечается активная линия зацепления.
Точка
 является точкой пересечения окружности
вершин второго колеса с линией зацепления
и называется точкой начала зацепления,
а точка
является точкой пересечения окружности
вершин второго колеса с линией зацепления
и называется точкой начала зацепления,
а точка
 является точкой пересечения окружности
вершин первого колеса с линией зацепления
и называется точкой конца зацепления.
является точкой пересечения окружности
вершин первого колеса с линией зацепления
и называется точкой конца зацепления.
Построение эвольвенты:
1. На основной окружности обоих колес откладывают от 10 до 20 одинаковых по длине отрезков, длину выбирают из промежутка от 10 до 20 мм.
2. Из получившихся точек проводятся касательные к основной окружности и на касательных откладываются отрезки длины, равной длине дуги окружности от первой касательной к текущей. Соединив точки, получаем эвольвенту.
3. По делительной окружности
откладывается половина толщины зуба
 ,
из центра через получившуюся точку
проводится прямая, получается ось
симметрии зуба.
,
из центра через получившуюся точку
проводится прямая, получается ось
симметрии зуба.
4. Через линию пересечения эвольвенты и основной окружности проводим прямую параллельную оси зуба и сопрягаем её окружностью равной 0,4m с окружностью впадин.
5. Обводим контур зуба и
отражаем его симметрично относительно
оси зуба. Полученную заготовку поворачиваем
на угловой шаг
 .
.
Аналогичные построения выполняем для другого колеса.
Выполним графическую проверку коэффициента перекрытия:
Графическое определение коэффициента перекрытия
 ,
,

 ,
,
где
 - коэффициент перекрытия
- коэффициент перекрытия
 - коэффициент перекрытия
полученный построением,
- коэффициент перекрытия
полученный построением,
 - линия зацепления, мм
- линия зацепления, мм
 - шаг по основной окружности,
мм.
- шаг по основной окружности,
мм.
1.5. Построение станочного зацепления.
Откладываем от делительной окружности выбранное смещение
 и проводим делительную прямую исходного
производящего контура реечного
инструмента.
и проводим делительную прямую исходного
производящего контура реечного
инструмента.На расстоянии
 вверх
и вниз от делительной прямой проводим
прямые граничных точек, а на расстоянии
вверх
и вниз от делительной прямой проводим
прямые граничных точек, а на расстоянии
 -
прямые вершин и впадин.
-
прямые вершин и впадин.Станочно-начальную прямую проводим касательно к делительной окружности в точке Р (полюс станочного зацепления). Проводим линию станочного зацепления NР через полюс станочного зацепления Р касательно к основной окружности в точке N.
Строим исходный производящий контур реечного инструмента так, чтобы ось симметрии впадины совпадала с вертикалью. Для этого от точки пересечения вертикали с делительной прямой откладываем влево по горизонтали отрезок в 0.25 шага, равный
 и через конец его перпендикулярно линии
зацепления NР>0>
проводим наклонную прямую, которая
образует угол
с вертикалью. Эта прямая является
прямолинейной частью профиля зуба
исходного производящего контура
инструмента.
и через конец его перпендикулярно линии
зацепления NР>0>
проводим наклонную прямую, которая
образует угол
с вертикалью. Эта прямая является
прямолинейной частью профиля зуба
исходного производящего контура
инструмента.Закругленный участок профиля строим как сопряжение прямолинейной части контура с прямой вершин или с прямой впадин окружностью радиусом >f>> >= 0.4m = 1.6. Симметрично относительно вертикали (линия симметрии впадин) cтроим профиль второго зуба исходного производящего контура, прямолинейный участок которого перпендикулярен к другой возможной линии зацепления: РK'. Расстояние между одноименными профилями зубьев исходного контура равно шагу
 мм.
мм.
1.6. Выводы
Произведен расчет эвольвентного зубчатого зацепления, выбран коэффициент смещения
 0.6,
X>2
>= 0.5, удовлетворяющий
качественным показателям передачи и
обеспечивающий отсутствие подреза и
заострения.
0.6,
X>2
>= 0.5, удовлетворяющий
качественным показателям передачи и
обеспечивающий отсутствие подреза и
заострения.Построено эвольвентное зацепление в
 .
Графически проверен коэффициент
перекрытия
.
Графически проверен коэффициент
перекрытия
 ,
погрешность
,
погрешность
 .
.Построено станочное зацепление.
Лист2:Синтез планетарного редуктора
Исходные данные:
Схема механизма – двухрядный планетарный редуктор со смешанным зацеплением.
все колеса имеют одинаковый модуль
 мм;
мм;передаточное отношение планетарного редуктора
 11;
11;число сателлитов планетарного редуктора
 ;
;
Постановка задачи:
Подобрать числа зубьев, удовлетворяющие всем условиям для многосателлитных планетарных редукторов.
Начертить схему редуктора в масштабе, в 2-х проекциях.
Построить диаграммы распределения для угловых и линейных скоростей, оценив погрешность передаточного отношения.
Основные условия проектирования многосателлитного планетарного редуктора
Формула Виллиса.
 =1
+
=1
+
 .
.
Условие соосности: r>1> + r>2> = r>4> – r>3.>
Условие сборки:
 ,
,
где К – число сателлитов,
Р – целое число полных оборотов водила,
N – любое отвлеченное целое число.
Условие соседства:
 .
.
Подбор чисел зубьев планетарного редуктора
Анализируем условие сборки
 ,
,
получаем:

Z>1> должно быть кратно 3.
U>1-H>
= 1-U>1-4>
=1 +

10=

Z>1>=A(D-C)q=4q
Z>1>=B(D-C)q=8q
Z>1>=C(A+B)q=3q
Z>1>=D(A+B)q=15q
q=9, Z>1>=36; Z>1>=72; Z>1>=27; Z>1>=135;
Проверяем условие соседства:



0,86 > 0.68
проверяем условие сборки
 ,
при любом целом
,
при любом целом
 –
–
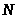 целое число.
целое число.
Графическая проверка передаточного отношения
Расчет радиусов колес планетарного редуктора:
 ,
,
где
 - радиус iого
колеса редуктора,
- радиус iого
колеса редуктора,
 - модуль.
- модуль.
 18
мм
18
мм
 =
36 мм
=
36 мм
 13.5
мм
13.5
мм
 =
67.5 мм
=
67.5 мм
Построение схемы планетарного редуктора в масштабе
 .
.Построение диаграммы распределения линейных скоростей

Выберем масштаб линейной скорости


Для построения распределения линейных скоростей на схеме редуктора отметим характерные точки: центра колёс и точки зацепления, вынесем их на вертикальную ось радиусов.
Откладываем отрезок СС’. Строим линию распределения скоростей блока сателлитов – BA’. Строим OА’ - линия распределения скоростей 1 звена.
Строим отрезок AA’
выражающий в масштабе
 скорость точки A.
Отрезок OC’
- линия распределения скоростей водила.
скорость точки A.
Отрезок OC’
- линия распределения скоростей водила.
 =11,
=11,


Построение диаграммы распределения угловых скоростей
Выберем масштаб угловой скорости:

Для построения плана
угловых скоростей проводим горизонтальную
линию угловых скоростей. На ней откладываем
отрезок OA>B>
в масштабе
 =4
=4
 .
.
Через точку A>B> проводим линию, параллельную линии ОА>В >с диаграммы линейных скоростей. Точка пересечения с вертикальной осью, проходящей через т.О, является полюсом Р.
Проводим из полюса лучи,
параллельные линиям распределения
скоростей до пересечения с осью. Отрезки
OA>B>,
OC’,
ОА’ выражают в масштабе
 угловые скорости водила, блока сателлитов
и первого звена соответственно.
угловые скорости водила, блока сателлитов
и первого звена соответственно.
Вычислим передаточное отношение построенного планетарного редуктора:

 .
.
Выводы
В результате расчета подобраны числа зубьев колес планетарного редуктора Z>1>=36; Z>1>=72; Z>1>=27; Z>1>=135, удовлетворяющие условиям сборки, соосности и соседства.
Был начерчен планетарный
редуктор в масштабе, в 2-х проекциях в
 .
.
Передаточное отношение
проверено графически
 .
.
Лист 3. Динамическое исследование основного механизма.
3.1. Исходные данные и постановка задачи:
|
№ п/п |
Наименование параметра |
Обозначения |
Единица СИ |
Числовое значение |
|
1 |
Ход ползуна 5 |
H>5> |
м |
0,5 |
|
2 |
Частота вращения кривошипа 1 |
n>1> |
1/с |
0,3 |
|
3 |
Коэффициент неравномерности вращения кривошипа 1 |
|
- |
1/24 |
|
4 |
Коэффициент изменения средней скорости ползуна 5 |
K>V> |
- |
1,6 |
|
5 |
Отношение смещения e направляющей ползуна 5 к длине кривошипа 1 |
>e>=e/l>1> |
- |
1.15 |
|
6 |
Отношение длины шатуна 4 к длине кулисы 3 |
>43>=l>4>/l>3> |
- |
0,25 |
|
7 |
Длина ползуна 5 в долях от его хода |
>5>=l>5>/H>5> |
- |
4 |
|
8 |
Масса единицы длины ползуна 5 |
M>l>>5>/l>5> |
Кг/м |
16 |
|
9 |
Масса единицы длины кулисы 3 |
M>l>>3>/l>3> |
Кг/м |
6 |
|
10 |
Масса изделия И |
m>И> |
кг |
20 |
|
11 |
Коэффициент трения в направляющих ползуна 5 |
f>T>>56> |
- |
0,24 |
|
12 |
Момент инерции кривошипа (коленчатого вала) |
I>1A> |
Кг*м2 |
0.06 |
Постановка задачи:
Провести геометрический синтез механизма.
Создать динамическую модель машинного агрегата
Определить движущий момент, необходимый при установившемся режиме на холостом ходу.
Получить закон движения главного вала машины
Рассчитать маховик.
3.2. Геометрический синтез механизма
1)

2)
3) ,
учитывая, что
,
учитывая, что
 и
и
 получаем:
получаем:
 =
=
4)

5)

6)

Для построения механизма
выбираем масштаб
 .
Произвольно выбираем место расположения
шарнира A,
проводим через точку A
вертикальную прямую. Кроме того, проводим
из т. A
окружность радиусом АB.
Разобьем окружность через равные углы
на 12 частей
.
Произвольно выбираем место расположения
шарнира A,
проводим через точку A
вертикальную прямую. Кроме того, проводим
из т. A
окружность радиусом АB.
Разобьем окружность через равные углы
на 12 частей
 .
Строим механизм в 12 положениях (0-11) и в
двух крайних положениях (2’,10’).
.
Строим механизм в 12 положениях (0-11) и в
двух крайних положениях (2’,10’).
3.3. Создание динамической модели
Для того чтобы упростить
определение закона движения сложной
системы, реальный механизм заменяют
динамической моделью. Модель представляет
собой стойку и вращающееся звено,
называемое звеном приведения, инерционность
которого определяется суммарным
приведенным моментом инерции
 .
На звено приведения действует суммарный
приведенный момент сил
.
На звено приведения действует суммарный
приведенный момент сил
 .
Параметры динамической модели
.
Параметры динамической модели
 и
и
 определяют так, чтобы законы движения
звена приведения динамической модели
и движения начального звена реального
механизма совпадали:
определяют так, чтобы законы движения
звена приведения динамической модели
и движения начального звена реального
механизма совпадали:
 ;
;
 .
.
В качестве начального
звена механизма выбран кривошип 1. Таким
образом, обобщенная координата для
механизма
 .
.
 и
и
 определяются методом приведения сил и
масс.
определяются методом приведения сил и
масс.
3.3.1 Определение суммарного приведенного момента
Метод приведения сил основан на равенстве элементарных работ и мгновенных мощностей приведенного момента, приложенного к модели, и реальных сил – к реальному механизму.
Для модели мощность
 ,
где
,
где
 ,
а для реального механизма
,
а для реального механизма
 ,
где
,
где
 - проекции на вертикаль скорости центра
масс
- проекции на вертикаль скорости центра
масс
 -го
звена.
-го
звена.
N>мод>=N>мех>
>  >
>
>  >
>


3.3.2 Определение суммарного приведенного момента инерции
Метод приведения масс и моментов инерции основан на равенстве кинетической энергии звена приведения динамической модели и кинетической энергии реального механизма в каждый момент времени.
T>мод>=T>мех>
>  >
>
>  >
>
 ,
,
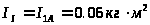

3.4 Передаточные функции
Определение передаточных функций
Передаточные функции определяются из построения планов скоростей.
План скоростей:
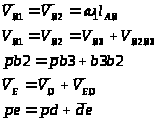
План скоростей построим
в вынужденном масштабе. Выберем величину
отрезка
 с плана скоростей равную отрезку ОА
на плане механизма.
с плана скоростей равную отрезку ОА
на плане механизма.
Так как
 ,
то
,
то
 .
Таким образом масштаб построения планов
скоростей определяется по следующей
формуле:
.
Таким образом масштаб построения планов
скоростей определяется по следующей
формуле:
 и
и

Скорость центров тяжести второго звена S>3> определятся методом подобия
 .
.
При построении плана скоростей скорость точки B1 будет направлена перпендикулярно звену АB, относительная скорость точки В2> >будет направлена по> >3 звену, скорость переносного движения точки В2 будет направлена перпендикулярно звену СВ, также направлена и скорость точки D. Скорость точки Е направлена по оси OX
Определение
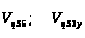


Таким образом, для
нахождения передаточной функции
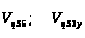 >
>для каждого положения
механизма достаточно замерить величину
отрезка
>
>для каждого положения
механизма достаточно замерить величину
отрезка
 с плана скоростей, переводя через масштаб
с плана скоростей, переводя через масштаб
 ,
получим
,
получим
 в м. (результаты в Таблицу 4)
в м. (результаты в Таблицу 4)
Определение
передаточных функций
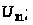

Для плана скоростей в
каждом положении механизма замеряем
отрезок
 ,
и делим его на длину звена СВ.
(результаты см. Таблицу 4)
,
и делим его на длину звена СВ.
(результаты см. Таблицу 4)
Таблица 4
Значения передаточных функций.
|
Передаточная функция |
Положения механизма |
|||||||||||||
|
0 |
1 |
2 |
2' |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10' |
10 |
11 |
|
|
|
-0.387 |
-0.242 |
-0.049 |
0 |
0.077 |
0.139 |
0.172 |
0.185 |
0.176 |
0.14 |
0.062 |
0 |
-0.042 |
-0.242 |
|
|
0.549 |
0.355 |
0.067 |
0 |
0.112 |
0.205 |
0.249 |
0.262 |
0.249 |
0.205 |
0.112 |
0 |
0.067 |
0.355 |
3.5 Построение графика приведенного момента сил полезного сопротивления
Рассчитаем силы полезного сопротивления:
На рабочем ходу: звено 5
двигается вместе с изделием, значит

На холостом ходу:

Рассчитаем
 для положения 1:
для положения 1:

Остальные значения
 запишем в таблицу 5
запишем в таблицу 5
Таблица 5
Значения приведённых моментов.
|
Приведённый момент |
Положения механизма |
|||||||||||||
|
0 |
1 |
2 |
2' |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10' |
10 |
11 |
|
|
|
-29.749 |
-18.572 |
-3.76 |
0 |
-9.593 |
-17.427 |
-21.414 |
-23.033 |
-21.998 |
-17.429 |
-7.79 |
0 |
-3.235 |
-18.618 |

Далее строим график
изменения момента

Выбираем масштаб

Вычислим масштаб
 :
:

3.6 Построение графика работ.
Проинтегрируем график
 и получим график
и получим график
 .
Его масштаб определяется по формуле:
.
Его масштаб определяется по формуле:
 ,
,
где
 - масштаб работы,
- масштаб работы,
 и
и
 –
масштабы по осям координат графика
приведенного движущего момента,
–
масштабы по осям координат графика
приведенного движущего момента,
 - отрезок интегрирования.
- отрезок интегрирования.
В данном случае приведенный
момент
 равен действительному моменту
равен действительному моменту
 ,
т. к. последний приложен к входящему
звену и в первом приближении его можно
считать постоянным. Однако величина
,
т. к. последний приложен к входящему
звену и в первом приближении его можно
считать постоянным. Однако величина
 определяется из условия, что
определяется из условия, что
 .
Конечная ордината графика
.
Конечная ордината графика
 должна быть равна
должна быть равна
 для установившегося режима движения и
с учетом того, что
для установившегося режима движения и
с учетом того, что
 ,
строится график
,
строится график
 в виде наклонной прямой линии. Дальнейшим
графическим дифференцированием графика
в виде наклонной прямой линии. Дальнейшим
графическим дифференцированием графика
 определяем величину
определяем величину
 .
.
 ,
с другой стороны:
,
с другой стороны:

Погрешность:

Сложим график работ
движущей силы
 за цикл и работы сил сопротивления
за цикл и работы сил сопротивления
 за цикл, получим график суммарной работы.
за цикл, получим график суммарной работы.
3.7 Определение приведенного
момента инерции второй группы звеньев
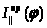
Подсчитаем значение
 для механизма в положении 0:
для механизма в положении 0:

Значения
 для всех остальных положений механизма
сведем в таблицу 6:
для всех остальных положений механизма
сведем в таблицу 6:
Таблица 6
Значения моментов инерции.
|
Момент инерции |
Положения механизма |
|||||||||||||
|
0 |
1 |
2 |
2' |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
10' |
11 |
|
|
I3 |
0.21 |
0.087 |
0.003 |
0 |
0.009 |
0.029 |
0.043 |
0.048 |
0.043 |
0.029 |
0.009 |
0.003 |
0 |
0.087 |
|
I5 |
5.102 |
1.988 |
0.082 |
0 |
0.2 |
0.663 |
1.001 |
1.158 |
1.056 |
0.663 |
0.132 |
0.06 |
0 |
1.998 |
|
I_IIгр |
5.312 |
2.076 |
0.085 |
0 |
0.21 |
0.692 |
1.044 |
1.206 |
1.099 |
0.692 |
0.141 |
0.063 |
0 |
2.086 |
По данным таблицы строим
график
 в масштабе
в масштабе
 :
:

График
 может быть приближенно принят за график
кинетической энергии второй группы
звеньев
может быть приближенно принят за график
кинетической энергии второй группы
звеньев
 .
Действительно:
.
Действительно:
 .
.
Закон изменения
 еще не известен. Поэтому для определения
еще не известен. Поэтому для определения
 приближенно принимаем
приближенно принимаем
 ,
что возможно, т.к. величина коэффициента
неравномерности
,
что возможно, т.к. величина коэффициента
неравномерности
 величина малая и, тогда величину
величина малая и, тогда величину
 можно считать пропорциональной
можно считать пропорциональной
 ,
а построенную кривую можно принять за
приближенную кривую
,
а построенную кривую можно принять за
приближенную кривую
 .
Масштаб графика
.
Масштаб графика
 :
:

3.8 Построение приближенного
графика
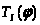
Известно, что
 .
С другой стороны
.
С другой стороны
 ,
т.е. кинетическая энергия механизма
отличается от
,
т.е. кинетическая энергия механизма
отличается от
 на некоторую постоянную величину
на некоторую постоянную величину
 .
Поэтому ранее построенный график
.
Поэтому ранее построенный график
 можно
принять за график
можно
принять за график
 относительно
оси
относительно
оси
 ,
отстоящей от оси
,
отстоящей от оси
 на величину
на величину
 .
следовательно для построения кривой
.
следовательно для построения кривой
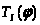 необходимо из ординат кривой
необходимо из ординат кривой
 в каждом положении механизма вычесть
ординаты графика
в каждом положении механизма вычесть
ординаты графика
 ,
взятые в масштабе
,
взятые в масштабе
 ,
в каком построена кривая
,
в каком построена кривая
 :
:
 .
.
Полученная кривая
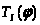 приближенная,
т.к. построена вычитанием из точной
кривой
приближенная,
т.к. построена вычитанием из точной
кривой
 приближенных значений
приближенных значений
 .
.
На кривой
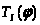 находят
находят
 и
и
 ,
и определяют максимальное изменение
кинетической энергии I
группы звеньев за период одного цикла:
,
и определяют максимальное изменение
кинетической энергии I
группы звеньев за период одного цикла:
 ,
откуда
,
откуда

3.9 Определение закона движения начального звена механизма
Максимальному значению
 соответствует
соответствует
 ,
а
,
а
 соответствует
соответствует
 ,
т.к.
,
т.к.
 .
Поэтому
.
Поэтому
 будет соответствовать
будет соответствовать
 в масштабе
в масштабе
 .
Чтобы определить график
.
Чтобы определить график
 ,
необходимо найти положение оси абсцисс
,
необходимо найти положение оси абсцисс
 .
Для этого через середину отрезка
.
Для этого через середину отрезка
 , проводят линию, которая является
средней угловой скоростью
, проводят линию, которая является
средней угловой скоростью
 .
Рассчитаем графическую величину
.
Рассчитаем графическую величину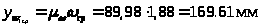 .
Определим коэффициент неравномерности
вращения :
.
Определим коэффициент неравномерности
вращения :
Определим погрешность
3.10 Геометрический расчет маховика.
Определим момент инерции дополнительной маховой массы





предположим что
 ,
тогда
,
тогда
 м
м

Чертим маховик в масштабе

Вывод:
Провели геометрический синтез механизма, определили:






Создали динамическую модель, с параметрами:




Подобраны размеры маховика:



Создан закон движения ω(φ)
Определим угловую скорость и ускорение, при φ=60О:
ω1= ωср+Δy/μω=1.88+1.018 /89.98= 1,891 c-1
ε1= ω1*tgψ*μφ/μω=1.891*tg(18.63)*19.1/89.98= 0,135c-2


