Основы робототехники

Промышленный робот - автоматическая машина, состоящая из манипулятора и устройства программного управления его движением, предназначенная для замены человека при выполнении основных и вспомогательных операций в производственных процессах.

Манипулятор - совокупность пространственного рычажного механизма и системы приводов, осуществляющая под управлением программируемого автоматического устройства или человека-оператора действия (манипуляции), аналогичные действиям руки человека.

Назначение и область применения

Промышленные роботы предназначены для замены человека при выполнении основных и вспомогательных технологических операций в процессе промышленного производства. При этом решается важная социальная задача - освобождения человека от работ, связанных с опасностями для здоровья или с тяжелым физическим трудом, а также от простых монотонных операций, не требующих высокой квалификации. Гибкие автоматизированные производства, создаваемые на базе промышленных роботов, позволяют решать задачи автоматизации на предприятиях с широкой номенклатурой продукции при мелкосерийном и штучном производстве. Копирующие манипуляторы, управляемые человеком-оператором, необходимы при выполнении различных работ с радиоактивными материалами. Кроме того, эти устройства незаменимы при выполнении работ в космосе, под водой, в химически активных средах. Таким образом, промышленные роботы и копирующие манипуляторы являются важными составными частями современного промышленного производства. Также они используются в лесной промышленности для погрузки и разгрузки пачек деревьев.

Основные понятия и определения. Структура манипуляторов

Формула строения - математическая запись структурной схемы манипулятора, содержащая информацию о числе его подвижностей, виде кинематических пар и их ориентации относительно осей базовой системы координат (системы, связанной с неподвижным звеном).

Движения, которые обеспечиваются манипулятором, делятся на:

    глобальные (для роботов с подвижным основанием) - движения стойки манипулятора, которые существенно превышают размеры механизма;

    региональные (транспортные) - движения, обеспечиваемые первыми тремя звеньями манипулятора или его "рукой", величина которых сопоставима с размерами механизма;

    локальные (ориентирующие) - движения, обеспечиваемые звеньями манипулятора, которые образуют его "кисть", величина которых значительно меньше размеров механизма.

В соответствии с этой классификацией движений, в манипуляторе можно выделить два участка кинематической цепи с различными функциями: механизм руки и механизм кисти. Под "рукой" понимают ту часть манипулятора, которая обеспечивает перемещение центра захвата - точки М (региональные движения захвата); под "кистью" - те звенья и пары, которые обеспечивают ориентацию захвата (локальные движения захвата).

Рассмотрим структурную схему антропоморфного манипулятора, то есть схему которая в первом приближении соответствует механизму руки человека (рис.1)

Рисунок 1. Схема манипулятора.

Этот механизм состоит из трех подвижных звеньев и трех кинематических пар: двух трехподвижных сферических А>3сф> и С>3сф> и одной одноподвижной вращательной В>1в>.

Рабочее пространство манипулятора - часть пространства, ограниченная поверхностями огибающими к множеству возможных положений его звеньев.

Зона обслуживания манипулятора - часть пространства соответствующая множеству возможных положений центра схвата манипулятора. Зона обслуживания является важной характеристикой манипулятора. Она определяется структурой и системой координат руки манипулятора, а также конструктивными ограничениями наложенными относительные перемещения звеньев в КП.

Подвижность манипулятора W - число независимых обобщенных координат однозначно определяющее положение захвата в пространстве:

или для незамкнутых кинематических цепей:

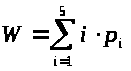
Маневренность манипулятора М - подвижность манипулятора при зафиксированном (неподвижном) захвате:

Структура кинематической цепи манипулятора должна обеспечивать требуемое перемещение объекта в пространстве с заданной ориентацией. Для этого необходимо, чтобы схват манипулятора имел возможность выпонять движения минимум по шести координатам: трем линейным и трем угловым. Рассмотрим на объекте манипулирования точку М, которая совпадает с центром схвата. Положение объекта в неподвижной (базовой) системе координат 0x>0>y>0>z>0> определяется радиусом-вектором точки М и ориентацией единичного вектора с началом в этой точке. В математике положение точки в пространстве задается в одной из трех систем координат:

    прямоугольной декартовой с координатами x>M>, y>M>, z>M>;

    цилиндрической с координатами rs>M>, j >M>, z>M>;

    сферической с координатами r>M>, j >M>, q >M>.

Ориентация объекта в пространстве задается углами a, b и g, которые вектор ориентации образует с осями базовой системы координат. На рис. 2 дана схема шести подвижного манипулятора с вращательными кинематическими парами с координатами объекта манипулирования.

Рисунок 2. Схема шести подвижного манипулятора с вращательными кинематическими парами с координатами объекта манипулирования.

При структурном синтезе механизма манипулятора необходимо учитывать следующее:

    кинематические пары манипуляторов снабжаются приводами, включающими двигатели и тормозные устройства, поэтому в схемах манипуляторов обычно используются одноподвижные кинематические пары: вращательные или поступательные;

    необходимо обеспечить не только заданную подвижность свата манипулятора, но и такую ориентацию осей кинематических пар, которая обеспечивала необходимую форму зоны обслуживания, а также простоту и удобство программирования его движений;

    при выборе ориентации кинематических пар необходимо учитывать расположение приводов (на основании или на подвижных звеньях), а также способ уравновешивания сил веса звеньев.

Задачи механики манипуляторов

К основным задачам механики манипуляторов можно отнести:

    разработку методов синтеза и анализа исполнительных механизмов (включая механизмы приводов);

    программирование движения манипулятора;

    расчет управляющих усилий и реакций в КП;

    уравновешивание механизмов манипуляторов;

    другие задачи.

Эти задачи решаются на базе общих методов исследования структуры, геометрии, кинематики и динамики систем с пространственными многоподвижными механизмами. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). При определении функций положения механизма, в прямой задаче находят закон изменения абсолютных координат выходного звена по заданным законам изменения относительных или абсолютных координат звеньев. В обратной - по заданному закону движения схвата находят законы изменения координат звеньев, обычно, линейных или угловых перемещений в приводах. Решение обратной задачи или задачи синтеза более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное. В обратной задаче кинематики по требуемому закону изменения скоростей и ускорений выходного звена определяются соответствующие законы изменения скоростей и ускорений в приводах манипулятора. Обратная задача динамики заключается в определении закона изменения управляющих сил и моментов в приводах, обеспечивающих заданный закон движения выходного звена.

Кинематический анализ механизма манипулятора

Первая и основная задача кинематики - определение функции положения. Для пространственных механизмов наиболее эффективными методами решения этой задачи являются векторный метод и метод преобразования координат. При решении прямой задачи о положении захвата манипулятора обычно используют метод преобразования координат. Из множества методов преобразования координат [ 1, 2 ] , которые отличаются друг от друга правилами выбора осей локальных систем координат, для манипуляторов обычно используется метод Денавита и Хартенберга.

Опишем два вида матриц:

    матрицы М, определяющие отношение между системами координат соседних звеньев;

    матрицы Т, определяющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.

Воспользуемся однородными координатами трехмерного проективного пространства РR3, в которых движение евклидова пространства R3 можно представить линейным преобразованием:


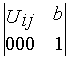
где: М>ij> - матрица 4x4 вида

Это преобразование эквивалентно преобразованию в эвклидовом пространстве где .То есть преобра-зованию, которое включает поворот, определяемый матрицей U>ij> размерностью 3х3, и параллельный перенос, задаваемый вектором размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:

x = x'/t', y = y'/t', z = z'/t'.

Обычно принимают t'=1. У матрицы поворота U>ij> элементами u>ij> являются направляющие косинусы углов между новой осью i и старой осью j. Вектор - трехмерный вектор, определяющий положение начала новой системы координат i в старой системе j. Выбор расположения осей должен соответствовать решаемой задаче. При решении задачи о положениях необходимо: в прямой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной - заданное положение выходного звена представить как функцию перемещений в приводах. Выбор расположения и ориентации локальных систем координат должен обеспечивать выполнение этих задач. При использовании метода Денавита и Хартенберга оси координат располагаются по следующим правилам:

    Для звена i ось z>i> направляется по оси кинематической пары, образуемой им со звеном (i+1). Начало координат размещают в геометрическом центре этой пары.

    Ось x>i> направляется по общему перпендикуляру к осям z>i-1>> >и z>i> с направлением от z>i-1>> >к z>i>. Если оси z>i-1>> >и z>i> совпадают, то x>i> перпендикулярна к ним и направлена произвольно. Если они пересекаются в центре кинематической пары, то начало координат располагается в точке пересечения, а ось x>i> направляется по правилу векторного произведения (кратчайший поворот оси z>i> до совмещения с z>i-1>> >при наблюдении с конца x>i> должен происходить против часовой стрелки).

    Ось y>i> направляется так, чтобы система координат была правой.

В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат Mx>n>y>n>z>n> по отношению к неподвижной или базовой системе координат Kx>0>y>0>z>0>. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i-1. Согласно принятому методу, каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (рис. 3):

    поворот i-ой системы вокруг оси x>i> на угол -q>i> до параллельности осей z>i> и z>i-1 >(положительное направление поворота при наблюдении с конца вектора x>i> против часовой стрелки);

    перенос вдоль оси x>i> на величину -a>i> до совмещения начала системы координат O>i> с точкой пересечения осей x>i> и z>i-1 >(отсчет по оси xi от точки пересечения оси x>i >и оси z>i-1>);

Рисунок 3. Схема манипулятора перехода из звена i в i-1.

    перенос вдоль оси z>i-1> на величину -s>i>, после которого начало системы координат O>i> оказывается в начале координат O>i-1> системы (i-1) (отсчитывается по оси z>i-1> от ее начала координат O>i-1> до точки ее пересечения с осью x>i>);

    поворот вокруг оси z>i-1> на угол -ji, до тех пор пока ось x>i> не станет параллельной оси x>i-1> (положительное направление поворота при наблюдении с конца вектора z>i-1> против часовой стрелки).

Необходимо отметить, что знак угла поворота не имеет значения, так как в матрицах перехода используются направляющие косинусы (четные функции). Целесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой (i-1). Перемещения начала координат определяются как координаты начала старой системы O>i> в новой O>i-1>.

В манипуляторах обычно используются одноподвижные кинематические пары или вращательные, или поступательные. Оба относительных движения как вращательное, так и поступательное, реализуются в цилиндрических парах. Поэтому при общем представлении механизма используются (рис. 3) цилиндрические пары.

Матрицы перехода их системы O>i> в систему O>i-1 >можно записать так:


где:

- матрица поворота вокруг

оси x>i> на угол -q>i>,


-матрица переноса вдоль оси x>i> на -a>i>,


-матрица переноса вдоль оси z>i-1>> >на -s>i>,


- матрица поворота вокруг оси z>i-1 >на уг угол -j>i>.

В этих матрицах переменные s>i> и j>i> соответствуют относительным перемещениям звеньев в кинематических парах и являются обобщенными координатами манипулятора, определяющими конфигурацию механизма в рассматриваемом положении. Переменные a>i> и q>i> определяются конструктивным исполнением звеньев манипулятора, в процессе движения они остаются неизменными.

Положение некоторой произвольной точки М в системе координат звена i определяется вектором r>Mi>>, >а в системе координат звена (i-1) - вектором r>Mi-1>. Эти радиусы связаны между собой через матрицу преобразования координат М>i> следующим уравнением:

где:

M>i> - матрица перехода из i-ой системы координат в (i - 1)-ю.

Точность манипуляторов ПР

Точность манипуляторов определяется погрешностями позиционирования характеристической точки захвата (точка М) и погрешностями угловой ориентации захвата. Погрешности позиционирования определяются технологическими отклонениями размеров звеньев манипулятора, зазорами в кинематических парах манипулятора и механизмов приводов, деформациями (упругими и температурными) звеньев, а также погрешностями системы управления и датчиков обратной связи. В паспортных данных манипуляторов указывается максимально допустимое отклонение центра захвата манипулятора точки М от ее номинального расположения на множестве возможных конфигураций механизма. В результате погрешностей точка М описывает в пространстве некоторый эллипсоид, который называется эллипсоидом отклонений (рис. 4).

Рисунок 4. Схема манипулятора в пространстве.