Кольцевой индукционный датчик угла
Министерство образования и науки РФ
Федеральное агентство по образованию
ГОУ ВПО
Саратовский государственный технический университет
Кафедра «Приборостроение»
Кольцевой индукционный датчик угла
Пояснительная записка к курсовой работе по дисциплине
«Электрические измерения»
Выполнила:
студентка группы ПБС-32
Боровкова Т.М.
Проверил: доц. каф. ПБС
Ледовской В.И.
Саратов 2006
Реферат
Пояснительная записка содержит 46 с., 15 рисунков. Приложение содержит графический материал, в сумме составляющий один формат А1.
Ключевые слова: кольцевой индукционный датчик угла, вращающийся трансформатор, статор, ротор, магнитопровод, обмотки.
В данной пояснительной записке к курсовой работе по дисциплине «Электрические измерения» рассматривается такая разновидность датчиков угла, как кольцевые индукционные датчики угла (КИДУ). Описана конструкция КИДУ, принцип действия, включая уравнения э.д.с., основные типы погрешностей, присущих данному типу датчиков угла. Приведен расчет основных геометрических и электрические параметры КИДУ, на основе которого выполнены сборочный и рабочие чертежи деталей.
В процессе выполнения курсовой работы использовались современные программные средства, такие как САПР «Компас 3D 8», векторный графический редактор «Corel Draw 12», среда математического моделирования «MatLab 7» и п.р.
Содержание
Введение
1. Конструкция кольцевых датчиков угла
2. Конструкция двухполюсного КИДУ
3. Принцип действия КИДУ
3.1 Уравнения э. д. с.
3.2 Параметры КИДУ
4. Погрешности КИДУ
4.1 Классификация погрешностей
5. Расчет КИДУ
5.1 Выбор геометрии магнитопровода
5.2 Расчет обмоток и параметров КИДУ
6. КИДУ со скосом пазов
Заключение
Список использованных источников
Введение
Для определения углового положения гироскопа и передачи этих данных в систему управления гироприбором необходимо преобразовывать угол поворота кардановых колец в другую физическую величину, более удобную для дистанционной передачи и дальнейшего использования [1]. Устройства, выполняющие такого рода преобразование, называются датчиками угла.
К датчикам угла, применяемым в гироприборах, предъявляются следующие требования [1]:
момент, прикладываемый со стороны датчика к гироскопу,должен быть минимальным;
характеристика
датчика должна быть линейной
 ,
где
U>вых>
–
напряжение, снимаемое с датчика;
– угол поворота ротора; k>д>
–
коэффициент пропорциональности, который
называется крутизной характеристики
датчика;
,
где
U>вых>
–
напряжение, снимаемое с датчика;
– угол поворота ротора; k>д>
–
коэффициент пропорциональности, который
называется крутизной характеристики
датчика;
порог чувствительности должен быть минимальным, с тем чтобы обеспечить фиксирование достаточно малых углов поворота гироскопа;
масса и габариты подвижных частей датчика должны быть также минимальны, с тем чтобы не увеличивать трение в опорах гироприбора;
мощность сигнала, снимаемого с датчика, должна быть максимально большой; это позволяет в ряде случаев не прибегать к усилению сигнала, что упрощает общую схему;
характеристика датчика должна быть стабильной и не зависимой от условий работы прибора;
остаточный сигнал датчика и шумы должны быть минимальными; в выходном напряжении датчиков, работающих на переменном токе, не должно быть высших гармоник, помех и остаточных э. д. с, сдвинутых по фазе на 90° относительно полезного сигнала.
Перечисленные требования иногда оказываются противоречивыми; так, например, увеличение выходной мощности приводит к увеличению момента, создаваемого датчиком. Решение вопроса о том, какое из перечисленных требований является основным, зависит от типа гироскопической системы, ее назначения и требуемой точности.
В качестве датчиков угла могут применяться различного типа устройства: потенциометрические, индукционные, емкостные, фотоэлектрические, пневматические, электромашинные и т. п. В настоящем курсовой работе рассматриваются кольцевые индукционные датчики угла (КИДУ).
Основными достоинствами КИДУ являются [1]:
отсутствие механического контакта между подвижной и неподвижной частями датчика, вследствие чего при работе датчика не возникают моменты сил сухого трения;
возможность обеспечения большого рабочего угла;
достаточно высокая разрешающая способность;
простота конструкции датчика, обусловливающая высокую надежность работы и малую стоимость;
удобство компоновки в приборе вследствие симметричности конструкции;
возможность использования в различных режимах работы.
Основными недостатками КИДУ являются:
наличие остаточного сигнала и сравнительно большого обратного момента;
небольшая мощность выходного сигнала, что требует применения усилителя;
зависимость выходного сигнала от нестабильности напряженияи частоты питания;
необходимость специальных токоподводов для обеспечения безмоментной электрической связи обмоток ротора с другими электроэлементами, расположенными на неподвижной части гироприбора;
сравнительно большая масса и габариты.
Вследствие указанных недостатков КИДУ в настоящее время не удовлетворяют жестким требованиям, предъявляемым к датчикам углов для прецизионных гироприборов. Поэтому в качестве линейных датчиков углов КИДУ применяются только в гироприборах средней и низкой точности.
1. Конструкция кольцевых датчиков угла
Кольцевые датчики угла представляют собой поворотные трансформаторы плоского типа с переменным коэффициентом трансформации, который изменяется в зависимости от относительного углового положения ротора и статора датчика [2]. Основными величинами, характеризующими работу датчика угла, являются:
1) потребляемые мощность и ток при номинальных значениях напряжения возбуждения и частоты сети;
рабочий диапазон угла поворота;
крутизна выходной характеристики;
степень линейности выходного напряжения в зависимости от угла поворота ротора;
симметрия выходного напряжения в зависимости от изменения знака угла;
остаточная э.д.с. в нулевом положении;
выходное сопротивление датчика;
значение реактивного момента,
По принципу изменения коэффициента взаимоиндукции между первичной и вторичной обмотками кольцевые датчики делятся на три типа:
датчики со сосредоточенными или распределенными обмотками на статоре и роторе;
датчики с короткозамкнутой обмоткой на роторе;
датчики без обмотки на роторе.
Рассмотрим кратко особенности каждого из этих типов кольцевых датчиков угла.
1. Кольцевые датчики угла с обмотками на статоре и роторе. В настоящее время этот тип кольцевого датчика является наиболее распространенным в гироскопических приборах. Магнитопровод датчика состоит из двух колец (рисунок 1.1), в пазы которых уложены по две электрически взаимно перпендикулярные сосредоточенные или распределенные обмотки. С целью исключения влияния эксцентриситета на работу датчика угла обмотки выполняются многополюсными. Для уменьшения реактивных моментов производится скос пазов внешнего и внутреннего магнитопроводов на одно зубцовое деление. У большинства датчиков угла коэффициенты взаимоиндукции между обмотками статора и ротора изменяются по синусоидальному закону от электрического угла поворота ротора а>э> = ра. В этом случае удовлетворительная линейность выходной характеристики (до 1%) достигается в диапазоне изменения угла поворота ротора ±15°.

Рисунок 1.1 Принципиальная схема кольцевого датчика угла.
Принципиально для работы датчика угла достаточно по одной обмотке на статоре и роторе. Применение двух электрически взаимно перпендикулярных обмоток на статоре и роторе позволяет датчик сделать более универсальным и использовать его для синхронной передачи угла.
2. Датчики с короткозамкнутой обмоткой на роторе. Недостатком датчиков, имеющих первичную или вторичную обмотку на роторе, является необходимость осуществления токоподвода к ротору. Это увеличивает момент, необходимый для поворота ротора, что приводит к снижению точности датчика и уменьшению надежности его работы. Чтобы исключить этот недостаток ротор выполняют с короткозамкнутой обмоткой, а статор – с двумя сдвинутыми на 90° обмотками. Одна из обмоток статора – обмотка возбуждения, а другая – выходная обмотка. Выходная э. д. с. датчика создается поперечной составляющей магнитного потока ротора.

Рисунок 1.2 Датчик угла с короткозамкнутым витком на роторе

Рисунок 1.3 Датчик углас явнополюсным ротором
Датчик с короткозамкнутой обмоткой на роторе имеет сравнительно простую конструкцию, однако наличие на роторе контура с током приводит к появлению момента обратного воздействия, который превышает соответствующую величину момента для датчиков угла с обмотками на роторе и статоре.
3) Датчики угла без обмоток на роторе. Принципиальная схема датчика приведена на рисунке 1.3. На статоре датчика укладываются две обмотки (обычно распределенные), оси которых смещены на 90 электрических градусов. Одна из обмоток – обмотка возбуждения, другая – выходная. Ротор явнополюсный и имеет такое же число пар полюсов, как и обмотка статора. При совпадении осей полюсов с осями обмоток э.д.с. на выходной обмотке датчика равна нулю. Э.д.с. достигает максимального значения, когда этот угол составляет 45 электрических градусов.
Недостатки датчиков этого типа – наличие реактивного момента и большая степень нелинейности в зависимости выходной э.д.с. от угла поворота ротора.
Указанные недостатки можно устранить за счет применения явнополюсной конструкции статора и ротора и дифференциальной схемы включения обмоток.
Далее будем рассматривать кольцевой индукционный датчик угла с обмотками на статоре и роторе. В соответствии с техническим заданием КИДУ является двухполюсным с двумя взаимно перпендикулярными обмотками на статоре и роторе.
2. Конструкция двухполюсного КИДУ
Двухполюсные КИДУ выполняются как неявнополюсные электрические машины [1], имеющие равномерно распределенные пазы на статоре и роторе (рисунок 2.1). Пакеты статора и ротора набираются из листовой электротехнической стали или пермаллоя. Для получения однородных магнитных свойств применяется веерная сборка листов и скос паза ротора на одно зубцовое деление. В пазы статора и ротора укладываются по две взаимно перпендикулярные обмотки; закон распределения витков по пазам подбирается таким образом, чтобы коэффициент взаимоиндукции между обмотками статора и ротора изменялся по синусоидальному (косинусоидальному) закону от угла поворота ротора. Напряжение к обмоткам ротора подводится (снимается) с помощью контактных колец и щеток или с помощью контактных пружин; во втором случае угол поворота ротора ограничен.
На рисунке 2.1. обозначены:
1 – пакет статора; 2 – пакет ротора; 3 – корпус; 4 – крышки; 5 – подшипники; 6 – контактные кольца.

Рисунок 2.1 Принципиальная конструктивная схема КИДУ.
3. Принцип действия КИДУ
Датчик угла преобразует угол поворота в два переменных напряжения, амплитуды которых пропорциональны соответственно sin и cos.

Рисунок 3.1 Электрическая схема

Рисунок 3.2 К принципу работы
Наиболее просто это преобразование реализуется с помощью двухполюсного четырехобмоточного ВТ.. Схема включения приведена на рисунок 3.1. Здесь f – обмотка возбуждения (field winding); k – квадратурная обмотка (killer winding); a – косинусная обмотка; б – синусная обмотка.
При рассмотрении основных режимов работы ВТ примем следующие допущения [3]:
коэффициенты взаимоиндукции между обмотками статора и ротора изменяются по синусоидальному (косинусоидальному) закону;
обмотки на статоре (роторе) электрически перпендикулярны;
потери в стали пренебрежимо малы;
собственные параметры обмоток статора и ротора попарноодинаковы и постоянны.
Такой ВТ называется идеализированным.
Наиболее простым является режим холостого хода Z>на>=Z>нб>=. При включении обмотки возбуждения в сеть переменного тока в расточке машины образуется переменный продольный магнитный поток Ф, ось которого совпадает с осью обмотки возбуждения. Этот поток индуктирует (рисунок 3.2):
э. д. с. в обмотке возбуждения
 ; (3.1)
; (3.1)
э. д. с. в косинусной и синусной обмотках
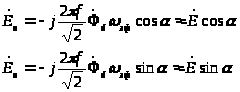 (3.2)
(3.2)
Здесь
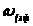 и
и
 – эффективные значения витков обмотки
возбуждения и вторичных обмоток; Е
–
действующее значение вторичной э. д. с,
когда оси обмоток совпадают (
= 0).
– эффективные значения витков обмотки
возбуждения и вторичных обмоток; Е
–
действующее значение вторичной э. д. с,
когда оси обмоток совпадают (
= 0).
Отношение
 называется
коэффициентом трансформации.
называется
коэффициентом трансформации.
Уравнение э. д. с. для обмотки возбуждения имеет вид
 . (3.3)
. (3.3)
Этому уравнению соответствует схема замещения, приведенная на рисунке 3.3. Вторичная обмотка показана для случая, когда ее ось совпадает с осью обмотки возбуждения.
Отношение
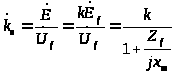 (3.4)
(3.4)
называется коэффициентом передачи по напряжению
Э.д.с.
квадратурной обмотки
 в
режиме холостого хода у идеализированного
ВТ
равна
нулю. При нагрузке вторичных обмоток
ВТ
различными
сопротивлениями
в
режиме холостого хода у идеализированного
ВТ
равна
нулю. При нагрузке вторичных обмоток
ВТ
различными
сопротивлениями
 электромагнитные
процессы существенно усложняются. Во
вторичных обмотках а
и
b
появляются
токи
электромагнитные
процессы существенно усложняются. Во
вторичных обмотках а
и
b
появляются
токи
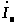 и
и
 ,
которые совместно с токами в обмотке
возбуждения создают намагничивающие
силы по продольной оси:
,
которые совместно с токами в обмотке
возбуждения создают намагничивающие
силы по продольной оси:
 (3.5)
(3.5)
по перечной оси
 (3.6)
(3.6)
Этим
намагничивающим силам будут соответствовать
продольный и поперечный магнитные
потоки
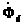 и
и
 можно представить себе как совокупность
двух однофазных трехобмоточных
трансформаторов, соединенных по схеме
рисунка 3.3.
можно представить себе как совокупность
двух однофазных трехобмоточных
трансформаторов, соединенных по схеме
рисунка 3.3.
Магнитный
поток
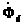 ,
если
пренебречь падением напряжения на
собственном сопротивлении обмотки
возбуждения, остается постоянным и его
можно найти из следующего уравнения
,
если
пренебречь падением напряжения на
собственном сопротивлении обмотки
возбуждения, остается постоянным и его
можно найти из следующего уравнения
 . (3.7)
. (3.7)
Поперечный
поток
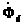 создается
н. с. вторичных обмоток и его величина
в общем случае зависит от угла поворота
ротора
создается
н. с. вторичных обмоток и его величина
в общем случае зависит от угла поворота
ротора
 (3.8)
(3.8)
Этот поток будет индуктировать во вторичных обмотках добавочную э.д.с, что приведет к искажению синусоидальной зависимости вторичных напряжений от угла поворота ротора . При замкнутой накоротко квадратурной обмотке этот поток демпфируется и выходные напряжения сохраняют синусоидальную зависимость от угла поворота ротора при любых сопротивлениях нагрузки. В этом случае говорят, что выполнено первичное симметрирование.

Рисунок 3.3 Схема замещения двух обмоточного КИДУ.
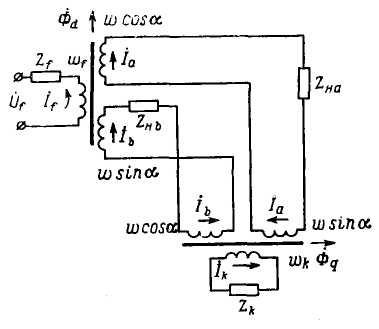
Рисунок 3.4 Приведение КИДУ к двум одно фазным трансформаторам.
Поперечный
поток
 ,
равен также нулю, если
,
равен также нулю, если
 . (3.9)
. (3.9)
Токи
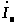 и
и
 равны
равны
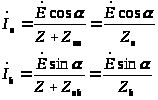 (3.10)
(3.10)
где Z – собственное сопротивление вторичной обмотки.
Подставляя
эти выражения в формулу (3.9), получим
 .
При
этом условии, называемом условием
вторичного симметрирования, вторичное
напряжение изменяется по синусоидальному
закону от угла поворота ротора.
.
При
этом условии, называемом условием
вторичного симметрирования, вторичное
напряжение изменяется по синусоидальному
закону от угла поворота ротора.
3.1 Уравнения э. д. с.
Будем считать, что параметры обмоток не приведены к обмотке возбуждения. В этом случае в индуктивное сопротивление взаимоиндукции должен войти коэффициент трансформации. В матричном виде уравнения э.д.с. имеют вид:
 , (3.11)
, (3.11)
где Z>f>,
Z>k>
–
собственные сопротивления обмоток
возбуждения и квадратурной, включая
сопротивление источника питания и
симметрирующее сопротивление; k
–
коэффициент трансформации; х>т>
–
индуктивное сопротивление взаимоиндукции
обмотки возбуждения;
 и
и
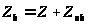 –
сопротивления косинусной и синусной
обмоток, включая сопротивление нагрузки.
Решая уравнения (3.11) относительно токов,
получим
–
сопротивления косинусной и синусной
обмоток, включая сопротивление нагрузки.
Решая уравнения (3.11) относительно токов,
получим
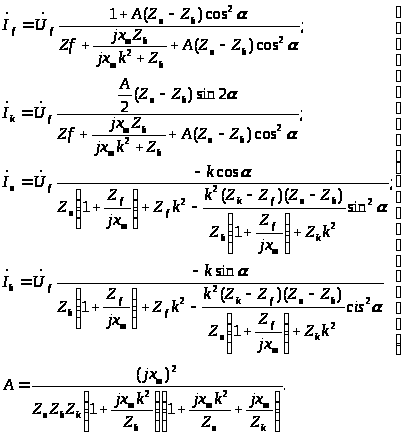 (3.12)
(3.12)
Из полученных
выражений следует, что выходные напряжения
ВТ
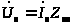 и
и
 изменяются по косинусоидальному и
синусоидальному законам от угла поворота
ротора а при выполнении одного из
следующих условий:
изменяются по косинусоидальному и
синусоидальному законам от угла поворота
ротора а при выполнении одного из
следующих условий:
 –
условия первичного симметрирования;
–
условия первичного симметрирования;
 – условия вторичного симметрирования.
– условия вторичного симметрирования.
Из первой
формулы (3.12) следует, что потребляемый
ток и входное сопротивление не зависят
от угла ,
если
 ,
т.
е. выполнено вторичное симметрирование.
Точно также можно показать, что выходное
сопротивление вторичных обмоток не
зависит от угла ,
если выполнено первичное симметрирование.
Точность вторичного симметрирования
(а при питании со стороны вторичных
обмоток – и первичного симметрирования)
можно оценить по э. д. с. квадратурной
обмотки, которая определяется по формуле
,
т.
е. выполнено вторичное симметрирование.
Точно также можно показать, что выходное
сопротивление вторичных обмоток не
зависит от угла ,
если выполнено первичное симметрирование.
Точность вторичного симметрирования
(а при питании со стороны вторичных
обмоток – и первичного симметрирования)
можно оценить по э. д. с. квадратурной
обмотки, которая определяется по формуле
 при
при
 .
Подставляя сюда значение
.
Подставляя сюда значение
 из () и полагая, что
из () и полагая, что
 получим:
получим:
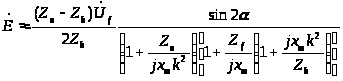 (3.13)
(3.13)
Для анализа работы КИДУ в некоторых схемах целесообразно в уравнениях (3.12) исключить токи статора. Уравнения э.д.с. примут вид:
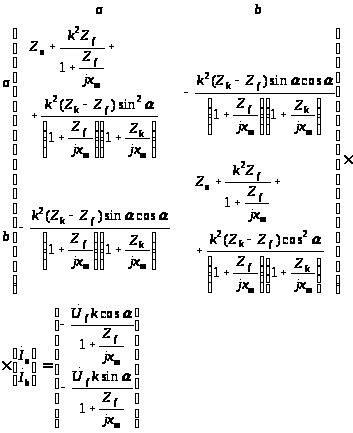 (3.14)
(3.14)
Из этих
уравнений следует, что при соблюдении
условия первичного симметрирования
 выходные обмотки ВТ
можно
рассматривать как две независимые
обмотки с выходным сопротивлением
выходные обмотки ВТ
можно
рассматривать как две независимые
обмотки с выходным сопротивлением
 (3.15)
(3.15)
и э.д.с. (рисунок 3.5):
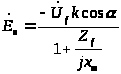 ;
;
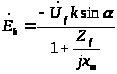 (3.16)
(3.16)

Рисунок 3.5 Схема КИДУ с исключенными обмотками возбуждения и квадратурной обмоткой
3.2 Параметры КИДУ
КИДУ
характеризуется
рядом величин, определяющих возможность
его применения в той или иной схеме и
точность работы. К величинам первой
группы относятся:
 –
номинальное напряжение возбуждения; f
– частота сети; k
–
коэффициент трансформации или коэффициент
передачи по напряжению
–
номинальное напряжение возбуждения; f
– частота сети; k
–
коэффициент трансформации или коэффициент
передачи по напряжению
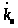 ;
;
 –
входное и выходное сопротивления;
–
входное и выходное сопротивления;
 – угол сдвига фазы между вторичной э.
д. с. и приложенным напряжением.
– угол сдвига фазы между вторичной э.
д. с. и приложенным напряжением.
Их схемы замещения, приведенной на рисунке 3.3, получаем:
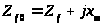 – сопротивление холостого
хода;
– сопротивление холостого
хода;
 – сопротивление
короткого замыкания;
– сопротивление
короткого замыкания;
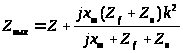 – входное
сопротивление при некотором сопротивлении
нагрузки;
– входное
сопротивление при некотором сопротивлении
нагрузки;
 – угол сдвига фазы между
вторичной э.д.с. и приложенным напряжением,
где Z>н>
– сопротивление источника.
– угол сдвига фазы между
вторичной э.д.с. и приложенным напряжением,
где Z>н>
– сопротивление источника.
Имея эти параметры, нетрудно определить любые электромагнитные величины, характеризующие работу КИДУ в схеме: потребляемые ток и мощность, выходное напряжение, оптимальную нагрузку и т.п.
Наиболее важными являются величины второй группы, характеризующие точность; они определяют, насколько реальная машина отличается от идеализированной. К этим величинам относятся:
1. Относительная амплитудная ошибка в синусоидальной зависимости вторичной э.д.с. от угла поворота ротора; она выражается в процентах или угловых минутах:
 , (3.17)
, (3.17)
где
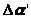 максимальная угловая ошибка в минутах
максимальная угловая ошибка в минутах
По амплитудной относительной ошибке, выраженной в %, определяются классы точности: 0,01; 0,02; 0,05; 0,1; 0,2;0,3.
2. Асимметрия нулевых точек, характеризующая неперпендикулярность обмоток статора и ротора КИДУ. Для ее определения КИДУ поочередно возбуждается со стороны первичных обмоток, и затем определяются угловые положения ротора, при которых э.д.с. вторичных обмоток равна нулю. Отклонение этих угловых положений от углов, кратных 90о, представляет собой асимметрию нулевых точек КИДУ.
Из () следует,
что для данного класса точности
максимальное значение асимметрии
 в угловых минутах не должно превосходить
в угловых минутах не должно превосходить
 , (3.18)
, (3.18)
где — относительная амплитудная ошибка в процентах.
3. Остаточная э.д.с в нулевых точках (е>ос>, %). Вследствие электрической и магнитной асимметрии магнитопровода от различных'технологических причин при однофазном питании КИДУ образуется эллиптическое вращающееся магнитное поле, которое индуктирует во вторичных обмотках э.д.с, сдвинутую по фазе на некоторый угол по отношению к э.д.с. от основного магнитного потока. Эта добавочная э.д.с. Может быть разложена на две составляющие (рисунок 3.6): совпадающую по фазе с основной э.д.с. и квадратурную э.д.с. Совпадающая по фазе э.д.с. компенсируется поворотом ротора, что обусловливает асимметрию нулевых точек. Квадратурная э.д.с. не может быть скомпенсирована, она представляет собой остаточную э.д.с, которая состоит из э.д.с. основной частоты и э.д.с. высших гармоник, появляющихся от нелинейности кривой намагничивания магнитопровода.
На работу КИДУ в компенсационных схемах главное влияние оказывает остаточная э.д.с. основной частоты. Ее величина не должна превосходить половины полезного сигнала, соответствующего максимальной угловой ошибке.
4. Э.д.с. квадратурной обмотки (e>k>, %). В идеальном КИДУ взаимоиндукция между перпендикулярными обмотками статора (ротора) должна отсутствовать. В действительности, вследствие различного рода технологических погрешностей коэффициент взаимоиндукции между обмотками не равен нулю, что приводит к появлению э.д.с. на одной обмотке при включении в сеть другой. Эту э.д.с. называют э.д.с. квадратурной обмотки. Она состоит из основной гармоники, имеющей частоту сети, и высших временных гармоник. Э.д.с. квадратурной обмотки зависит от углового положения ротора и содержит постоянную составляющую, не зависящую от углового положения ротора, переменную составляющую, изменяющуюся с двойной периодичностью от угла поворота ротора, и зубцовые гармоники (рисунок 3.7).

Рисунок 3.6 Векторная диаграмма остаточной э. д. с.

Рисунок 3.7 Зависимость э. д. с. квадратурной обмотки от угла по ворота ротора
Кривая э. д. с. квадратурной обмотки является весьма полезной при анализе качества изготовления магнитопровода КИДУ. Обычно для КИДУ как электрической машины задается максимальное значение э. д. с. квадратурной обмотки, выраженное в процентах от напряжения возбуждения
 . (3.19)
. (3.19)
5. Относительная разница (в %) коэффициентов передачи по напряжению косинусной и синусной обмоток
 . (3.20)
. (3.20)
Вследствие разницы в числе витков вторичных обмоток коэффициенты передачи по напряжению могут несколько отличаться. Это отклонение для данного класса точности не должно превосходить относительной амплитудной ошибки воспроизведения синусоидальной зависимости.
4. Погрешности КИДУ
4.1 Классификация погрешностей
Всем описывающим электроэлементам присущи погрешности, которые по физическим причинам можно разделить на четыре основные группы:
погрешности, вытекающие из принципа работы датчика;
погрешности от конструктивных ограничений;
технологические погрешности;
погрешности, вызванные влиянием внешней среды.Первая группа погрешностей, вытекающих из принципа действия, свойственна счетно-решающим электроэлементам, которые предназначены для решения тех или иных функциональных зависимостей.
С этой точки зрения датчики угла являются списывающими элементами, работа которых заключается в преобразовании углового перемещения ротора в пропорциональный ему электрический сигнал. Для выше рассмотренных типов датчиков погрешности, вызывающие нарушение этой пропорциональности, которая чаще всего выражается линейным законом, не связаны с принципом работы датчиков, а являются следствием влияния причин последующих групп. Поэтому остановимся именно на последних трех группах причин, вызывающих погрешности датчиков.
Конструктивные погрешности. Наличие магнитопровода статора и ротора в датчиках угла, как и во всех электрических машинах и аппаратах, приводит к искажению идеальной кривой намагничивания. Нелинейность кривой намагничивания обусловливает нелинейный характер изменения величины выходного напряжения от угла поворота ротора. Кроме того с нелинейностью кривой намагничивания связано появление высших временных гармоник в намагничивающем токе. Рассмотренные типы датчиков являются дифференциальными только по отношению к основной и нечетным гармоникам выходного напряжения. Поэтому нелинейность кривой намагничивания, приводит к. увеличению остаточного напряжения датчиков за счет присутствия в нем четных гармоник.
Следует отметить, что все явления, связанные с искажением кривой намагничивания, в датчиках рамочного типа проявляются в значительно меньшей степени, чем в других датчиках. Это объясняется наличием в датчиках рамочного типа значительного по величине воздушного зазора, представляющего собой большое линейное магнитное сопротивление, по сравнению с которым нелинейное сопротивление стального участка магнитной цепи составляет незначительную величину.
Специфическая конфигурация магнитопровода, а также наличие воздушного зазора обусловливают наличие в датчике значительных полей рассеяния. Распределение и расчет этих полей представляет известные трудности. Асимметрия, вводимая полями рассеяния в общую картину поля датчика, вызывает появление асимметрии и нелинейности выходного напряжения датчика при повороте ротора.
Технологические погрешности. Значения допусков на отдельные детали и несовершенство технологии изготовления и сборки датчиков определяют наличие целого ряда погрешностей датчиков угла.
Необходимым условием при установке в гироскопе датчика угла с перемещающимся ротором является требование равномерности воздушного зазора между статором и ротором. Это объясняется тем, что при неравномерном воздушном зазоре магнитные проводимости под крайними пальцами различаются, что приводит к появлению значительного по величине выходного напряжения в нулевом положении ротора датчика. В некоторых конструкциях гироскопов выходное напряжение может быть уменьшено с помощью поворота статора датчика и подключения фазирующего сопротивления или за счет использования компенсирующих устройств. Однако, несмотря на это, неравномерный воздушный зазор приводит к искажению характеристики выходного напряжения датчика, делая ее несимметричной.
Аналогичное влияние, но в несколько меньшей степени, оказывает магнитная асимметрия магнитопроводов обоих типов датчиков. Эта асимметрия вызывается двумя причинами:
различной величиной магнитной проводимости пластин магнитопровода вдоль и поперек направления проката;
наличием контуров электрической проводимости в магнитопроводе, возникающих при механической обработке пакетов магнитопровода, вследствие замыкания пластин между собой, недостаточной изоляции между пластинами и т. п.
Короткозамкнутые контуры в магнитопроводе датчика, а также короткозамкнутые витки в выходных катушках приводят к фазовому сдвигу потока, пронизывающего эти контуры, следствием чего является дополнительный фазовый сдвиг между напряжениями в левой и правой половине выходной обмотки.
Отличие угла сдвига фазы между напряжениями выходных катушек от 180° приводит к появлению значительного остаточного напряжения, для устранения которого необходимо использовать один из выше рассмотренных методов и которое приводит к дополнительному увеличению несимметричности характеристики выходного напряжения датчиков. Большое влияние на точность датчика рамочного типа оказывает качество намотки рамки – двух встречно включенных катушек, перемещающихся в воздушном зазоре. Несимметричное выполнение этих катушек приводит к тому, что при повороте рамки изменение потокосцепления с каждой катушкой неодинаково, поэтому нелинейность и несимметричность характеристики выходного напряжения такого датчика существенно увеличиваются.
Этим объясняется более высокая (по сравнению с датчикам рамочного типа) точность датчиков с перемещающимся ротором для которых равномерная намотка выходных катушек не представляет больших трудностей.
При сборке двухкоординатных датчиков угла предъявляются высокие требования к запрессовке пакетов магнитопроводов дл каждой координаты, которые должны быть сдвинуты один относительно другого на 90°. Отклонение от этого угла приводит к созданию электрического сигнала по обеим координатам приводит к смещению ротора в направлении оси одной из координат. Сигнал по второй координате дает ложный угол.
Погрешности, вызванные влиянием внешней среды. При работе датчиков угла в гироскопе на точность их работы оказывают существенное влияние температурные воздействия, а также наличие внешних электромагнитных полей.
Теплоизлучение других элементов гироскопического прибор может привести к принудительному нагреву датчика угла. В это случае решающее значение имеет правильный выбор конструкционных материалов датчика, так как различные коэффициенты линейного расширения деталей датчика могут привести к нарушению первоначально установленной величины и равномерности во; душного зазора, а следовательно, к смещению электрического нуля датчика и искажению характеристики выходного напряжения.
При изготовлении материала магнитопровода датчика из ферритов в результате нагрева происходит значительное ухудшению магнитных свойств последних, что непосредственно привода к ухудшению параметров датчиков.
В рассматриваемых датчиках при нулевом положении ротор воздействие внешнего электромагнитного поля приводит к увеличению остаточного напряжения за счет четных гармоник э. д. с складывающихся в дифференциальных выходных обмотках.
5. Расчет КИДУ
Согласно техническому заданию, имеем следующие исходные данные для расчета КИДУ:
наружный диаметр корпуса D>k >= 32 мм;
внутренний диаметр ДУ D>ac> = 12 мм.
длина корпуса ДУ l>k> = 14 мм.
крутизна датчика k>ду>=6,00 в/град;
напряжение возбуждения U>1> = 36 В;
номинальная частота f = 400 Гц;
диаметр проволоки обмотки статора не более 0,08 мм.
Методика расчета изложена в [2] и [4].
5.1 Выбор геометрии магнитопровода
Определяем максимально допустимые значения индукции в магнитопроводе и плотности тока в обмотках при холостом ходе:
 (5.1)
(5.1)
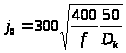 (5.2)
(5.2)
 =0,5625
Тл.
=0,5625
Тл.
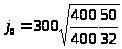 =375
а/см2
=375
а/см2
Материал для высечки в соответствии с [4] выберем 50Н ГОСТ 10394-74.
2. Определяем отношение «теоретических» площадей пазов статора и ротора:
 (5.3)
(5.3)
где
 – коэффициент нагрузки, принимается
равным 2 [4],
– коэффициент нагрузки, принимается
равным 2 [4],
 =0,22,
=0,22,
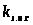 =0,32:
=0,32:
 =1,375
=1,375
3. Определяем приведенный воздушный зазор:
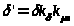 (5.4)
(5.4)
где
 = 0,1 мм – величина воздушного зазора;
= 0,1 мм – величина воздушного зазора;
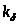 = 1,02;
= 1,02;
 =
1,003 ([4] и п.8).
=
1,003 ([4] и п.8).
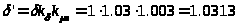 мм.
мм.
4. Приняв D>н> = 30 мм, находим отношение:
 (5.5)
(5.5)
где
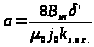 (5.6)
(5.6)
 см2
см2
5. По
известным
 и
и
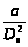 с помощью графиков, приведенных на
рисунке 5-7 [4], определяем:
с помощью графиков, приведенных на
рисунке 5-7 [4], определяем:
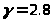 ;
;

6. Находим основные величины, характеризующие геометрию пластин статора и ротора (см. рисунки 5.1 и 5.2):

Рисунок 5.1 Основные геометрические параметры пластин статора

Рисунок 5.2 Основные геометрические параметры пластин ротора
 (5.7)
(5.7)
 (5.8)
(5.8)
 (5.9)
(5.9)
 (5.10)
(5.10)
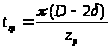 (5.11)
(5.11)
 (5.12)
(5.12)
После расчета получаем:
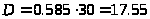 мм,
мм,
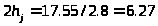 мм,
мм,
 мм,
мм,
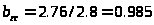 мм,
мм,
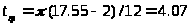 мм,
мм,
 мм.
мм.
Дополнительные параметры геометрии пластин ротора и статора [2]:
 (5.13)
(5.13)
Принимаем
 мм
[4], число пазов статора и ротора
соответственно (по [4]):
мм
[4], число пазов статора и ротора
соответственно (по [4]):
 .
.
 (5.14)
(5.14)
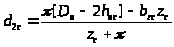 (5.15)
(5.15)
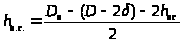 (5.16)
(5.16)
 (5.17)
(5.17)
 (5.18)
(5.18)
 (5.19)
(5.19)
 (5.20)
(5.20)
 (5.21)
(5.21)
 (5.22)
(5.22)
 (5.23)
(5.23)
 мм,
мм,
 мм,
мм,
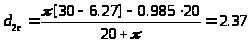 мм,
мм,
 мм,
мм,
 мм,
мм,
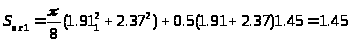 мм2.
мм2.
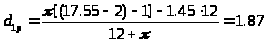 мм,
мм,
 мм,
мм,
 мм
мм
Поскольку
величина получилась отрицательной
уменьшим значение
 до 4 мм, а для обеспечения внутреннего
размера 12
применим переходную деталь типа ось.
до 4 мм, а для обеспечения внутреннего
размера 12
применим переходную деталь типа ось.
 мм,
мм,
 мм,
мм,
 мм,
мм,
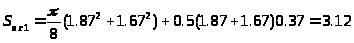 мм2.
мм2.
7. Толщина пластин высечки:
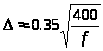 (5.24)
(5.24)
 мм.
мм.
Длина пакета статора:
 . (5.25)
. (5.25)
 мм.
мм.
8. Определяем
коэффициенты
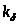 и
и

 (5.26)
(5.26)
где
 (5.27)
(5.27)
По [4] принимаем
 мм.
мм.

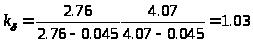
9. Находим
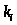 :
:
 (5.28)
(5.28)
По [4] принимаем
 Ом.
Ом.

5.2 Расчет обмоток и параметров КИДУ
1. Определяем относительные значения параметров обмотки возбуждения (таблицы 3-2 и 3-3 [4]):
 (5.29)
(5.29)
 (5.30)
(5.30)
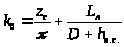 (5.31)
(5.31)
 (толщину магнитопровода
(толщину магнитопровода
 выбираем равной 4 мм.)
выбираем равной 4 мм.)
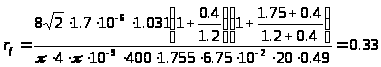 ,
,
По [4]:
 ,
,
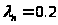 .
.
 .
.
2. Определяем эффективное число витков обмотки возбуждения:
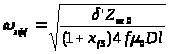 (5.32)
(5.32)
 витков.
витков.
4. Поскольку обмотка статора является концентрической и состоит из 5 секций [4], находим число витков в каждой из секций:
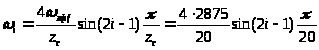 ,
i=1..5.
,
i=1..5.
После округления получаем количество витков в каждой секции:
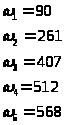
5. Определяем сечение провода обмотки возбуждения:
 (5.33)
(5.33)
 (5.34)
(5.34)
 мм2.
мм2.
 мм, округляем до 0,08 мм.
мм, округляем до 0,08 мм.
6. Определяем
эффективное число витков вторичной
обмотки [2], учитывая, что
 ,
где
,
где
 – коэффициент трансформации,
– коэффициент трансформации,
 :
:
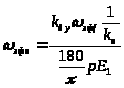 (5.35)
(5.35)
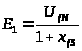 (5.36)
(5.36)
 В.
В.
 витков.
витков.
7. Обмотка ротора является концентрической и состоит из 3 секций [4], находим число витков в каждой из секций:
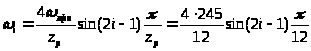 ,
i=1..3.
,
i=1..3.
После округления получаем количество витков в каждой секции:

8. Определяем сечение провода вторичной обмотки:
 (5.37)
(5.37)
 (5.38)
(5.38)
 мм2.
мм2.
 мм. Принимаем 0,15 мм.
мм. Принимаем 0,15 мм.
Используя полученные величины, вычерчиваем рабочие чертежи пластин статора и ротора.
6. КИДУ со скосом пазов
КИДУ со скошенными пазами можно представить как совокупность нескольких элементарных преобразователей с прямыми пазами, сдвинутых относительно друг друга по углу.
Для простоты будем считать, что скос паза произведен только на роторе. Пусть Е>э> = f(а) – функциональная зависимость э. д. с, воспроизводимая элементарным преобразователем. В общем случае Е>э>=f(a) – периодическая несинусоидальная функция, причем в силу своей симметрии относительно начала координат она содержит только нечетные гармоники. Если скос паза выполнен по закону у>ск> = у(х) (рисунок 6.1), то с учетом скоса функцию Е>э> = f(а) запишем в виде
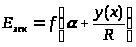 (6.1)
(6.1)
где R - радиус расточки.
Расположим начало координат посредине пакета. Тогда выходная э. д. с. преобразователя будет равна
 (6.2)
(6.2)
Если угол скоса паза выполнить по закону
 , (6.3)
, (6.3)
то выходная э. д. с. преобразователя будет изменяться по синусоидальному закону от угла поворота ротора. Действительно, представим периодическую функцию (6.1) в виде ряда Фурье, содержащего нечетные гармоники
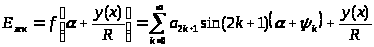 (6.4)
(6.4)
где k = 1; 2; 3...
Подставляя это выражение в (6.2), получим
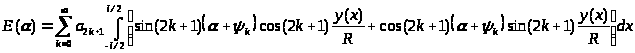 (6.5)
(6.5)
Используя приведенную выше формулу (6.3) для у(х) и выполняя интегрирование, получим:
 (6.6)
(6.6)
На практике выполнение скоса паза по закону (6.3) трудно осуществимо по технологическим соображениям; чаще всего при меняется равномерный скос пластин магнитопровода ротора (рисунок 6.2). При таком скосе:
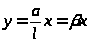 . (6.7)
. (6.7)
В этом случае выходная э. д. с. равна
 (6.8)
(6.8)

Рисунок 6.1
Магнитная система со скосом паза,
выполненным по закону


Рисунок 6.2 Магнитная система с равномерным скосом паза
Из этого выражения следует, что при равномерном скосе паза возможно уничтожение какой-либо одной гармоники и кратных ей. Условием уничтожения гармоник порядка (2k + 1) будет
 (6.9)
(6.9)
Поскольку наибольшей по амплитуде из высших гармоник является третья, то скос чаще всего выполняется для уничтожения третьей гармоники. В этом случае уравнение линии скоса приобретает вид
 (6.10)
(6.10)
В нашем случае примем величину угла скоса пазов 30 градусов.
Заключение
В данной
курсовой работе был спроектирован
кольцевой индукционный датчик угла,
представляющий собой поворотный
трансформатор, при этом была использована
соответствующая методика расчета.
Характеристики спроектированного КИДУ
удовлетворяют величинам, заданным в
техническом задании: крутизна датчика
k>ду>=6,00
в/град, напряжение возбуждения U>1>
= 36 В, номинальная частота f
= 400 Гц, наружный диаметр корпуса D>k
>=
32 мм, внутренний диаметр ДУ D>ac>
= 4 мм, длина корпуса ДУ l>k>
= 14 мм, толщина обмотки l>об>=12
мм,
количество витков концентрической
обмотки статора
 ,
диаметр провода обмотки статора 0,08,
количество витков концентрической
обмотки ротора
,
диаметр провода обмотки статора 0,08,
количество витков концентрической
обмотки ротора
 ,
диаметр проволоки обмотки ротора 0,15
мм. На основе рассчитанных геометрических
параметров были вычерчены пластины
магнитопроводов статора и ротора КИДУ.
,
диаметр проволоки обмотки ротора 0,15
мм. На основе рассчитанных геометрических
параметров были вычерчены пластины
магнитопроводов статора и ротора КИДУ.
Список использованных источников
Никитин Е.А. Гироскопические системы, ч.III. Элементы гироскопических приборов: учеб. пособие для вузов / Е. А. Никитин и др.; под ред. Д. С. Пельпора., – М.: «Высшая школа». 1979. –472 с.: ил.
Бабаева Н.Ф. Расчет и проектирование элементов гироскопических устройств: учеб. пособие для приборостроительных спец. вузов / Н. Ф. Бабаева и др. – Л.: «Машиностроение». 1967. –480 с.
Хрущев В.В. Электрические машины систем автоматики: учебник для вузов / В.В. Хрущев; – 2-изд., перераб. и доп. – Л.: Энергоатомиздат. Ленингр. отд-ние. 1985. –186 с.
Хрущев В.В. Электрические микромашины / В.В. Хрущев; – Л., «Энергия». 1969. –278 с. с ил.
Сломянский Г.А. Детали и узлы гироскопических приборов: атлас конструкций / Г.А. Сломянский, А.В. Агапов, Е.М. Радионов и др.; – М.: Машиностроение. 1975. –306 с.