Исследование частотных характеристик типовых динамических звеньев
Министерство образования и науки Украины
Донбасская Государственная Машиностроительная Академия
Кафедра АПП
Лабораторная работа
по дисциплине
Теория автоматического управления
Тема
Исследование частотных характеристик типовых динамических звеньев
Краматорск
Задание
Таблица 1
|
№ п/п |
Параметры динамических звеньев |
||||||
|
Безынерцион. |
Апериодич. 1-го порядка |
Апериодич. 2-го порядка |
Колебательное |
Реальные дифференцирующие и интегрирующие, звено запаздывания |
|||
|
K |
T, с |
T1, с |
T2, с |
T, с |
ξ |
T, с |
|
|
14 |
25-37 |
0.06 – 0.5 |
0.26 |
0.06 – 0.5 |
0.06 – 0.5 |
0.1-0.9 |
0.06 – 0.5 |
Исследование безынерционного звена
1.1 Исследование частотных характеристик безынерционного звена
Для исследования частотных характеристик безынерционного звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 1 для трех значений K:
.
ЛАЧХ звеньев представлены на рисунке 2, графики переходной функции – на рисунке 3.
Рисунок 1 – Структурная схема для исследования безынерционного звена
Рисунок 2 – ЛАЧХ безынерционных звеньев
Рисунок 3 – Переходные функции безынерционных звеньев
1.2 Реализация безынерционного звена
Реализуем безынерционное звено
с коэффициентом усиления
на операционных усилителях (рисунки 4
и 7). ЛАЧХ и ЛФЧХ инвертирующего и
неинвертирующего усилителей представлены
на рисунках 5 и 8, переходные функции –
на рисунках 6 и 9. Для сравнения частотных
характеристик идеальных и реальных
звеньев изобразим их ЛЧХ в совмещенных
координатах (рисунок 10).
Рисунок 4 –
Электрическая принципиальная схема
инвертирующего усилителя с коэффициентом
усиления
Рисунок 5 – ЛАЧХ и ЛФЧХ инвертирующего усилителя
а)
б)
Рисунок 6 – Переходные функции идеального безынерционного звена и инвертирующего усилителя
Рисунок 7 –
Электрическая принципиальная схема
неинвертирующего усилителя с коэффициентом
усиления
Рисунок 8 – ЛАЧХ и ЛФЧХ неинвертирующего усилителя
а)
б)
Рисунок 9 – Переходные функции идеального безынерционного звена и неинвертирующего усилителя
Рисунок 10 – ЛАЧХ и ЛФЧХ идеального безынерционного звена, инвертирующего усилителя и неинвертирующего усилителя
При рассмотрении частотных и временных характеристик безынерционных звеньев можно сделать следующие выводы:
при прохождении через безынерционный элемент амплитуда и фаза выходного сигнала не зависит от частоты входного сигнала
при увеличении (уменьшении) коэффициента усиления ЛАЧХ увеличивается (уменьшается) во столько же раз, а ЛФЧХ не меняется.
Исследование апериодического звена 1-го порядка
Исследование частотных характеристик апериодического звена 1-го порядка
Для исследования частотных
характеристик апериодического
звена 1-го порядка в прикладном пакете
Proteus\ISIS
составляем структурную схему,
представленную на рисунке 11, для трех
значений
:
.
Логарифмические частотные характеристики апериодических звеньев представлены на рисунке 12, графики переходной функции – на рисунке 13.
Рисунок 11 – Структурная схема для исследования апериодических звеньев 1-го порядка
Рисунок 12 – Логарифмические частотные характеристики апериодических звеньев 1-го порядка
Рисунок 13 – Переходные функции апериодических звеньев 1-го порядка
Реализация апериодического звена 1-го порядка
Реализуем апериодическое звено
1-го порядка с постоянной времени
на
-цепочке
и на
-цепочке
(рисунок 14). ЛАЧХ и ЛФЧХ
-цепочки
и на-цепочки
представлены на рисунке 15, а и 15, б. Для
сравнения частотных характеристик
идеальных и реальных апериодических
звеньев изобразим их ЛЧХ в совмещенных
координатах (рисунок 15, в).
а)б)
а)
-цепочка;
б)
-цепочка
Рисунок 14 –
Электрическая принципиальная схема
апериодических звеньев 1-го порядка с
постоянной времени
а) б)
в)
Рисунок 15 – ЛАЧХ и ЛФЧХ апериодических звеньев
а)
-цепочка;
б)
-цепочка;
в) совмещенные ЛЧХ идеального
апериодического звена,
-цепочка
и
-цепочка
При анализе частотных характеристик апериодических звеньев 1-го порядка можно сделать следующие выводы:
увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
чем меньше постоянная времени
Т, тем шире полоса пропускания (т.к.
~
).
при уменьшении постоянной времени уменьшается время переходного процесса и наоборот.
чем меньше постоянная времени, тем меньше время переходного процесса и шире полоса пропускания, следовательно, чем меньше время переходного процесса, тем шире полоса пропускания.
если на график ЛАЧХ заменить
ломаной кривой и из точки ''разлома''
опустить прямую на ось
,
то это и будет сопрягающая частота.
Постоянную времени можно определить,
зная сопрягающую частоту
:
.
Исследование частотных характеристик апериодического звена 2-го порядка
Для исследования частотных
характеристик апериодического
звена 2-го порядка в прикладном пакете
Proteus\ISIS
составляем структурную схему,
представленную на рисунке 16, при
неизменной первой постоянной времени
и для трех значений
:
.
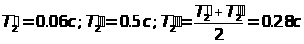Логарифмические частотные характеристики апериодических звеньев 2-го порядка представлены на рисунке 17, графики переходной функции – на рисунке 18.
Рисунок 16 – Структурная схема для исследования апериодических звеньев 2-го порядка
Рисунок 17 – Логарифмические частотные характеристики апериодических звеньев 2-го порядка
Рисунок 18 – Переходные функции апериодических звеньев 2-го порядка
Реализация апериодического звена 2-го порядка
Попробуем реализовать апериодическое
звено 2-го порядка с постоянными времени
и
на двух последовательно соединенных
-цепочках,
отдельно каждая из которых представляет
собой апериодическое звено 1-го порядка
(рисунок 19). ЛАЧХ и ЛФЧХ данного звена и
необходимого апериодического звена
2-го порядка представлены на рисунке
20, а, а их переходные функции – на рисунке
20, б.
Рисунок 19 –
Электрическая принципиальная схема
двух последовательно соединенных
апериодических звеньев 1-го порядка с
постоянными времени
и
а)б)
а) ЛАЧХ и ЛФЧХ; б) переходная функция
Рисунок 20 –
Характеристики последовательно
соединенных
-цепочек
Реализуем апериодическое звено
2-го порядка с постоянными времени
и
на двух последовательно соединенных
-цепочках,
разделенных промежуточным (разделяющим,
развязывающим) усилителем (повторителем)
(рисунок 21). ЛАЧХ и ЛФЧХ данного звена и
необходимого апериодического звена
2-го порядка представлены на рисунке
22, а, а их переходные функции – на рисунке
22, б.
Рисунок 21 –
Электрическая принципиальная схема
двух
-цепочек
с постоянными времени
и
,
разделенных операционным усилителем
а) б)
а) ЛАЧХ и ЛФЧХ;
б) переходная функция
Рисунок 22 –
Характеристики последовательно
соединенных
-цепочек
с разделительным усилителем
При анализе частотных характеристик апериодических звеньев 2-го порядка можно сделать следующие выводы:
увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
увеличение (уменьшение) постоянной времени звена приводит к увеличению (уменьшению) времени переходного процесса.
на полосу пропускания большее влияние оказывает большая постоянная времени
при увеличении постоянной времени звена время переходного процесса увеличивается, а полоса пропускания уменьшается, следовательно, при увеличении времени переходного процесса полоса пропускания уменьшается и наоборот.
Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка
Ввиду того, что апериодическое
звено 2-го порядка можно аппроксимировать
звеном 1-го порядка, если одна постоянная
времени намного превышает вторую (
в 10 раз), сравним характеристики звена
с постоянными времени
и
со звеном 1-го порядка, изображенным на
рисунке 23.
Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка
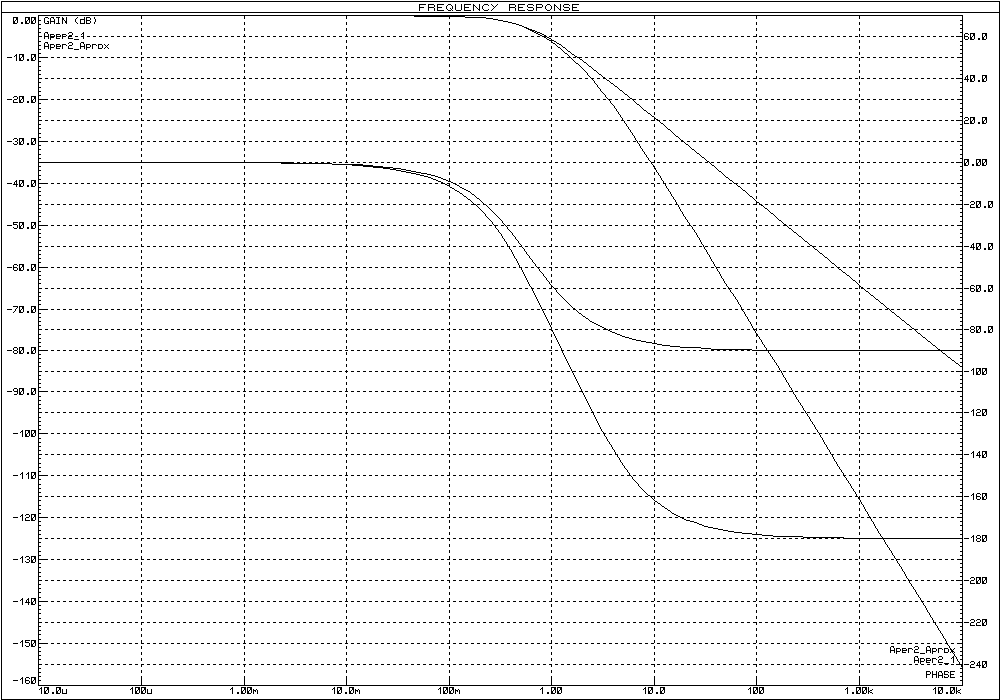
а) б)
а) ЛАЧХ и ЛФЧХ;б) переходные функции
Рисунок 24 – Характеристики апериодического звена 2-го порядка и инерционного звена
При анализе характеристик апериодических звеньев (рисунок 24) можно сделать следующие выводы:
апериодическое звено 2-го порядка можно аппроксимировать апериодическим звеном 1-го порядка, если первая постоянная времени намного меньше второй, т.к. в таком случае влияние первой экспоненты на форму выходного сигнала несущественно.
Исследование колебательного звена
При исследовании колебательного
звена необходимо пронаблюдать за
характером его частотных характеристик
при изменении постоянной
времени и декремента затухания в
пределах, указанных в индивидуальном
задании. Т.е. необходимо исследовать
частотные характеристики при постоянных
времени
и декременте затухания
.
Исследование частотных
характеристик колебательного звена
при изменении постоянной времени (
)
и неизменном декременте затухания (
)
Для исследования колебательного
звена при изменении постоянной времени
()
и неизменном декременте затухания в
прикладном пакете Proteus\ISIS
составляем структурную схему,
представленную на рисунке 25. Логарифмические
частотные характеристики колебательного
звена представлены на рисунке 26, графики
переходной функции – на рисунке 27.
Рисунок 25 –
Структурная схема для исследования
колебательных звеньев
при изменении постоянной времени ()
и неизменном декременте затухания ()
Рисунок 26 –
Логарифмические частотные характеристики
колебательных звеньев при изменении
постоянной времени ()
и неизменном декременте затухания ()
Рисунок 27 –
Переходные функции колебательных
звеньев при изменении
постоянной времени ()
и неизменном декременте затухания ()
Исследование частотных
характеристик колебательного звена
при изменении постоянной времени ()
и неизменном коэффициенте демпфирования
(
)
Для исследования колебательного
звена при изменении постоянной времени
()
и неизменном декременте затухания ()
в прикладном пакете Proteus\ISIS
составляем структурную схему,
представленную на рисунке 28. Логарифмические
частотные характеристики колебательного
звена представлены на рисунке 29, графики
переходной функции – на рисунке 30.
Рисунок 28 –
Структурная схема для исследования
колебательных звеньев
при изменении постоянной времени ()
и неизменном декременте затухания ()
Рисунок 29 –
Логарифмические частотные характеристики
колебательных звеньев при изменении
постоянной времени ()
и неизменном декременте затухания ()
Рисунок 30 –
Переходные функции колебательных
звеньев при изменении
постоянной времени ()
и неизменном декременте затухания ()
Исследование частотных
характеристик колебательного звена
при неизмененной постоянной времени
(
)
и изменении декремента затухания (
).
Для исследования колебательного
звена при неизмененной постоянной
времени ()
и изменении коэффициента демпфирования
()
в прикладном пакете Proteus\ISIS
составляем структурную схему,
представленную на рисунке 31. Логарифмические
частотные характеристики колебательного
звена представлены на рисунке 32, графики
переходной функции – на рисунке 33.
Рисунок 31 –
Структурная схема для исследования
колебательного звена при неизмененной
постоянной времени ()
и изменении декремента затухания ()
Рисунок 32 –
Логарифмические частотные характеристики
колебательных звеньев при изменении
постоянной времени (
)
и неизменном декременте затухания ()
Рисунок 33 –
Переходные функции колебательного
звена при неизмененной постоянной
времени ()
и изменении декремента затухания ()
Реализация колебательного звена
Реализуем колебательное звено
с постоянной времени
и коэффициентом демпфирования
на
-контуре
(рисунок 34). ЛАЧХ и ЛФЧХ данного звена и
необходимого колебательного звена
представлены на рисунке 35, а, а их
переходные функции – на рисунке 35, б.
Рисунок 34 –
Электрическая принципиальная схема
колебательного
-контура
а) б)
а) ЛАЧХ и ЛФЧХ;б) переходная функция
Рисунок 35 –
Характеристики колебательного звена
и
-контура
При анализе графиков частотных характеристик и переходных процессов (рисунок 35) колебательных звеньев можно сделать следующие выводы:
увеличение (уменьшение) постоянной времени звена при неизменном декременте затухания приводит к сдвигу частотных характеристик влево (вправо).
при неизменном коэффициенте демпфирования увеличение постоянной времени звена приводит к сужению полосы пропускания; колебательность переходного процесса не меняется.
при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) колебательности переходного процесса и к более плавной ЛФЧХ.
при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) перерегулирования, сужению (расширению) полосы пропускания и уменьшению (увеличению) колебательности.
Исследование дифференцирующих звеньев
Исследование частотных характеристик идеального дифференцирующего звена
Для исследования частотных характеристик идеального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 36. Логарифмические частотные характеристики идеального дифференцирующего звена представлены на рисунке 37, график переходной функции – на рисунке 38.
Рисунок 36 – Структурная схема для исследования идеального дифференцирующего звена
Рисунок 37 – Логарифмические частотные характеристики идеального дифференцирующего звена
Рисунок 38 – Переходная функция идеального дифференцирующего звена
Реализация идеального дифференцирующего звена
Реализуем идеальное дифференцирующее звено схемой, изображенной на рисунке 39. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 40 и 41, переходная функция – на рисунке 42.
Рисунок 39 – Электрическая принципиальная схема дифференцирующего звена
Рисунок 40 – ЛАЧХ и ЛФЧХ дифференцирующего звена
Рисунок 41 – ЛАЧХ и ЛФЧХ дифференцирующего звена с инвертором
а)
б)
Рисунок 42 – Переходная функция схемы реализации идеального дифференцирующего звена
Исследование частотных характеристик реального дифференцирующего звена
Для исследования частотных характеристик реального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 43. Логарифмические частотные характеристики реального дифференцирующего звена представлены на рисунке 44, переходные функции – на рисунке 45.
Рисунок 43 – Структурная схема для исследования реального дифференцирующего звена
Рисунок 44 – Логарифмические частотные характеристики реального дифференцирующего звена
Рисунок 45 – Переходные функции реального дифференцирующего звена
Реализация реального дифференцирующего звена
Реализуем реальное дифференцирующее звено с помощью схем, изображенных на рисунке 46. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 47, переходные функции – на рисунке 48.
а)б)
а)
-цепочка;б)
-цепочка
Рисунок 46 – Электрические принципиальные схемы реального дифференцирующего звена
Рисунок 47 – ЛАЧХ и ЛФЧХ схем реализации дифференцирующего звена
Рисунок 48 – Переходная функция схемы реального дифференцирующего звена
Исследование интегрирующих звеньев
Исследование частотных характеристик идеального интегрирующего звена
Для исследования частотных характеристик идеального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 49. Логарифмические частотные характеристики идеального интегрирующего звена представлены на рисунке 50, график переходной функции – на рисунке 51.
Рисунок 49 – Структурная схема для исследования идеального интегрирующего звена
Рисунок 50 – Логарифмические частотные характеристики идеального интегрирующего звена
Рисунок 51 – Переходная функция идеального интегрирующего звена
Реализация идеального интегрирующего звена
Реализуем идеальное интегрирующее звено схемой, изображенной на рисунке 52. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 53 и 54, переходная функция – на рисунке 55.
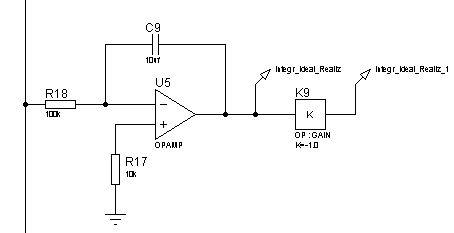
Рисунок 52 – Электрическая принципиальная схема интегрирующего звена
Рисунок 53 – ЛАЧХ и ЛФЧХ интегрирующего звена
Рисунок 54 – ЛАЧХ и ЛФЧХ интегрирующего звена с инвертором
Рисунок 55 – Переходная функция схемы реализации идеального интегрирующего звена
Исследование частотных характеристик реального интегрирующего звена
Для исследования частотных характеристик реального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 56. Логарифмические частотные характеристики реального интегрирующего звена представлены на рисунке 57, переходные функции – на рисунке 58.
Рисунок 56 – Структурная схема для исследования реального интегрирующего звена
Рисунок 57 – Логарифмические частотные характеристики реального интегрирующего звена
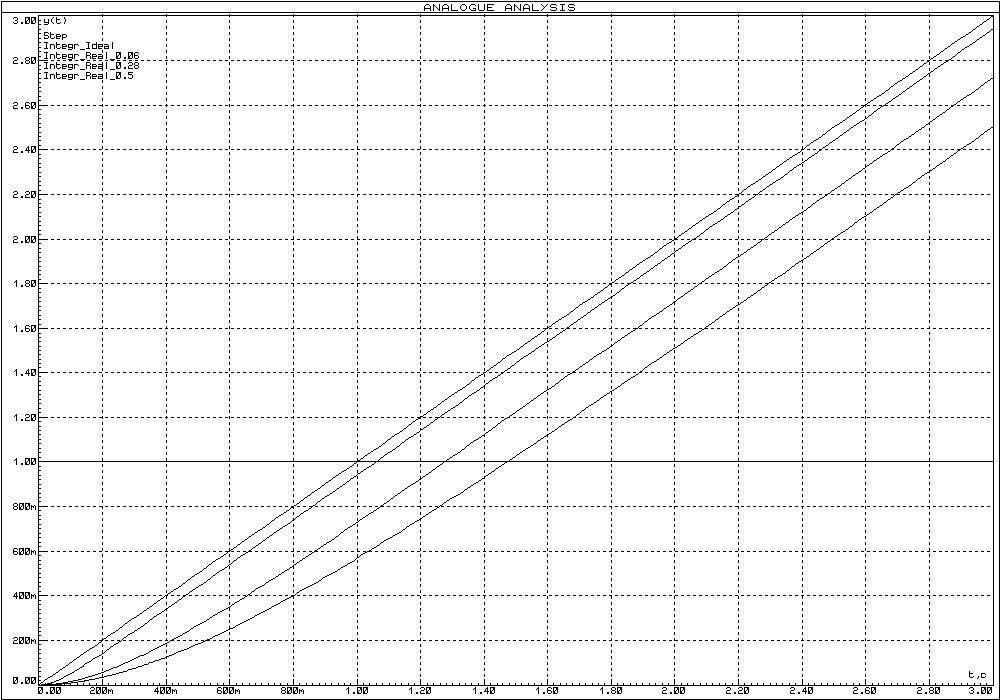
Рисунок 58 – Переходные функции реального интегрирующего звена
При анализе частотных и переходных характеристик реального интегрирующего звена и его реализации можно сделать следующие выводы:
Исследование изодромного звена
Изодромное звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, - идеального интегрирующего и безынерционного. Поэтому данное звено совмещает полезные качества обоих звеньев и часто используется в качестве регулирующего устройства ПИ-регулятора (пропорционально-интегрального регулятора).
Исследование частотных характеристик изодромного звена
Для исследования частотных характеристик изодромного звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 59. Логарифмические частотные характеристики изодромного звена представлены на рисунке 60.
Рисунок 59 – Структурная схема для исследования изодромного звена
Рисунок 60 – Логарифмические частотные характеристики изодромного звена
Реализация изодромного звена
Реализуем изодромное звено схемой, изображенной на рисунке 61. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 62 и 63, переходная функция – на рисунке 64.
Рисунок 61 – Электрическая принципиальная схема изодромного звена
Рисунок 62 – ЛАЧХ и ЛФЧХ изодромного звена
Рисунок 63 – ЛАЧХ и ЛФЧХ изодромного звена с инвертором
а) б)
а) без инвертора;
б) с инвертором
Рисунок 64 – Переходная функция изодромного звена
Исследование звена запаздывания
Для исследования частотных характеристик звена запаздывания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 65. Логарифмические частотные характеристики изодромного звена представлены на рисунке 66, переходные характеристики – на рисунке 67.
Рисунок 65 – Структурная схема для исследования звена запаздывания
Рисунок 66 – Логарифмические частотные характеристики звена запаздывания
Рисунок 67 – Переходные функции звена запаздывания