Электрические машины (работа 2)

КУРСОВАЯ РАБОТА

Электрические машины

Содержание

Введение

1. Техническое задание на курсовую работу

2. Расчёт геометрических размеров сердечника статора, ротора и расчет постоянных

3. Расчёт обмоток статора и ротора

4. Расчёт магнитной цепи

5. Активные и индуктивные сопротивления обмоток статора и ротора

6. Потери в стали, механические и добавочные потери

7. Расчет рабочих характеристик

8. Расчет пускового тока и момента

Список литературы

Введение

Электрические машины в основном объёме любого производства занимают первое место. Они являются самыми массовыми приёмниками электрической энергии и одним из основных источников механической и электрической энергий. Поэтому очень важная роль отведена электрическим машинам в экономике и производстве.

Сделать электрические машины менее энергоёмкими, более дешёвыми с лучшими электрическими и механическими свойствами. Это задача, решаемая постоянно при проектировании машин новых серий. Проектирование электрических машин процесс творческий требующий знания ряда предметов общетехнического цикла, новинок производства в области создания новых конструкционных, изоляционных материалов, требований спроса рынка, условий применения в электроприводе. В настоящее время практикуется создание не индивидуальных машин, а серий электрических машин, на базе которых выполняются различные модификации.

Целью расчета является определение мощности и технических характеристик асинхронного двигателя, рассчитанного на базе вышедшего из строя асинхронного двигателя.

1. Техническое задание для курсовой работы

Спроектировать трёхфазный асинхронный двигатель с короткозамкнутым ротором серии 4А климатического исполнения “У3”. Напряжение обмотки статора U=220/380 В.

Исходные данные для электромагнитного расчета асинхронного двигателя являются:

1. Номинальное фазное напряжение – U1н= 220 B.

2. Схема соединение концов обмотки статора –

3. Частота питающей сети – ƒ1= 50 Гц.

4. Синхронная частота вращения поля статора – n1= 3000об/мин.

5. Степень защиты.

6. Геометрические размеры сердечника.

6.1 Наружный диаметр сердечника статора – Da = 0,52м.

6.2 Внутренний диаметр сердечника статора – D = 0,335м.

6.3 Длина сердечника статора – l1= 0,05 + 0,3D.

6.4 Воздушный зазор – δ = 0,001м.

6.5 Размеры пазов статора (рис. 1.1) – b11 = 0,0081м.

b12 = 0,011м.

H21 = 0,04м.

bш1 = 0,0045м.

hш1 = 0,001м.

6.6 Размеры пазов ротора (рис. 1.2) – b21 = 0,006м.

b22 = 0,0033м.

h21 = 0,04м.

bш2 = 0,0015м.

hш2 = 0,001м.

7. Число пазов статора – Z1 = 72.

8. Число пазов ротора – Z2 =82.

9. Скос пазов ротора – bск = 0м.

10. Ширина короткозамыкающего кольца – aкл = 0,037м.

11. Высота короткозамыкающего кольца – bкл = 0,042м.

12. Высота оси вращения – h = 280мм.

2. Расчет геометрических размеров сердечников статора, ротора, расчет постоянных

Рис. 1 – Размеры пазов статора.

Расчетная длина сердечника статора. lδ = l1 = 0,05 + 0,3D = 0,05 + 0,3 · 0,335 = 0,151м

Размеры пазов статора. (см. рис. 1)

– высота паза hn1 = h11 + hш1 = 0,04 + 0,001 = 0,041м

– высота зубца hz1 = hn1 = 0,041м

– высота коронки hк1 = (b11 + bш1)/ 3,5 = (0,0081– 0,0045)/ 3,5 = 0,001м

– размер паза h12 = h11 – hк1 = 0,04 – 0,001 = 0,039м

Зубцовый шаг статора. t1 = π D/ Z1 = 3,14 · 0,335 / 72 = 0,0146м

Ширина зубца статора^

Средняя ширина зубца статора: bz1 = (b'z1 + b"z1)/2 = (0,0067 + 0,007)/2 = 0,0069м

Высота ярма статора. ha = [Da – (D + 2hn1)]/2 =[0,52 – (0,335 + 2 · 0 041)]/2 = 0,052м

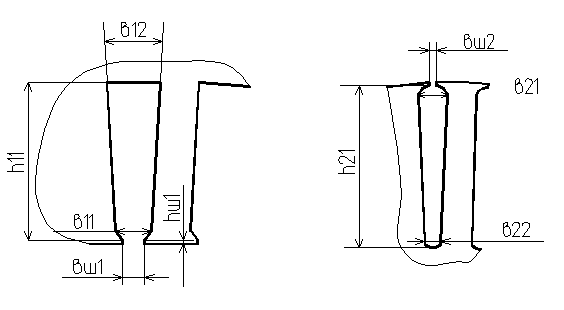
Рис. 2 – Размеры пазов ротора.

Длина сердечника ротора: l2 = l1 + 0,005 = 0,151 + 0,005 = 0,156м

Наружный диаметр сердечника ротора: D2 = D – 2δ = 0,335 – 2 · 0,001 = 0,333м

Внутренний диаметр сердечника ротора: DJ = 0,3D = 0,3 · 0,335 = 0,1005м

Размеры пазов ротора. (см. рис. 2)

– высота паза ротора: hn2 = h21 + hш2 = 0,04 + 0,001 = 0,041м

– высота зубца ротора: hz2 = hn2 = 0,041м

– размер паза: h22 = h21 – (b21 + b22)/ 2 = 0,04 – (0,006 + 0,0033)/ 2 = 0,01535м

Зубцовый шаг ротора: t2 = πD2/ Z2 = 3,14 · 0,333/ 82 = 0,0128м

Ширина зубца ротора:

Средняя ширина зубца ротора: bz2 = (b'z2 + b"z2)/ 2 = 0,0064 + 0,008/ 2 = 0,0072м

Высота ярма ротора: hJ = (D2 – DJ – 2hn2)/ 2 = (0,333 – 0,0999 – 2 · 0,041)/ 2 = 0,0756м, где DJ = 0,3D2 = 0,3 · 0,333 = 0,0999м

Относительная величина скоса пазов: b'ск = bск/ t2 = 0/ 0,0128 = 0

Площадь поперечного сечения паза ротора, сечения стержня к.з. обмотки ротора.

[3,14(0,0062 + 0,00332)/8 +

+ 0,01535(0,006 + 0,0033)/2] · 106 = 96мм2

Площадь поперечного сечения короткозамыкающего кольца обмотки ротора: qкл = aкл · bкл · 106 = 0,037 · 0,042 · 106 = 1554мм2

Синхронная угловая скорость вращения магнитного поля: Ω = π · n1/ 60 = 3,14 · 3000/ 60 = 157рад/c

Число пар полюсов машины: p = 2(60ƒ)/ n1 = 2(60 · 50)/ 3000 = 2

Полюсное деление: τ = πD/ 2p = 3,14 · 0,335/ 2 · 2 = 0,263м

Число пазов на полюс и фазу: q = Z1/ 2p · m1 = 72/ 2 · 2 · 3 = 6, где m1 = 3 – число фаз обмотки статора.

3. Расчет обмоток статора и ротора

Выбор типа обмотки статора:

Однослойные обмотки применяются в асинхронных машинах – малой мощности, двухслойные – в машинах средней и большой мощности – как более технологичные для таких мощностей и обеспечивающие оптимальное укорочение шага. Всвязи с этим в машинах с h > 132мм (где h – высота оси вращения) рекомендуется однослойная обмотка, при 280мм > 132мм – двухслойная.

Коэффициент укорочения шага: β = γ/τ , где γ – шаг обмотки

Для двухслойной обмотки β = 0,75 ÷ 0,83.

Отсюда шаг обмотки: γ = β · Z1/2p = 0,75 · 72/ 2 · 2 = 14

Обмоточный коэффициент. kоб = kγ1 · kp1 = 0,924 · 0,956 = 0,882, где kγ1 = sin(β90˚) – коэффициент укорочения, kγ1 = sin(β · 90˚) = sin(0,75 · 90˚) = 0,924, kp1 – коэффициент распределения, является функцией q – числа пазов на полюс и фазу и определяется по таблице 1, откуда kp1 = 0,956

Расчетная мощность асинхронного двигателя.

P' = 1,11D2 · lδ · Ω · kоб1 · А · Вδ = 1,11 · 0,3352 · 0,151 · 157 · 0,882 ·

· 38000 · 0,6 = 58540Вт

где А – линейная нагрузка, Вδ – магнитная индукция, определяется по графикам зависимостей линейной нагрузки и магнитной индукции от Da (рис. 3).

Номинальный ток обмотки статора. I1н = Р'/ 3E1 = 58540/ 3 · 213,4 = 91,44А, где Е1 = kE · U1н = 0,97 · 220 = 213,4

Сечение проводников фазы обмотки статора. qф = I1н/ J1 = 91,44/ 4 = 22,86 мм2, где J – плотность тока (5,5 ÷ 6,0), А/мм2

Выбор диаметра и сечения элементарного проводника.

Диаметр голого элементарного проводника d должен удовлетворять двум условиям:

d = (0,5 ÷ 1,0) · h / 100 = 0,64 · 280/ 100 = 1,79мм

где h высота оси вращения, h = 280мм, а d < 1,8мм => 1,79 < 1,8мм

Руководствуясь этими условиями, выбираем диаметр голого провода d по приложению Б, округляя его до ближайшего стандартного значения. По той же таблице находим сечение элементарного проводника qэл и диаметр изолированного провода dиз.

qэл = 2,54мм2; dиз = 1,895мм.

Значение диаметра изолированного провода должно удовлетворять условию: dиз + 1,5 bш1, 1,895 + 1,5 4,5мм.

Число параллельных элементарных проводников в фазе.

nф = qф/ qэл = 22,86/ 2,54 = 9

По таблице 2.2 выбираем число параллельных ветвей обмотки – а. а = 3

Число элементарных проводников в одном эффективном, т.е. число проводников в одной параллельной ветви обмотки. nэл = nф /а = 9/ 3 = 3, при этом должны выполняться условия: nэл < 4, а nэл ; 3 < 4, 3 3

Уточняем значение плотности потока: J1 = I1н/ qф = 91,44/ 22,86 = 4А/мм2, где qф = qэл · nэл · а = 2,54 · 3 · 3 = 22,86мм2

Расчет магнитного поля и индукции.

Основной магнитный поток и линейная нагрузка:

Ф = Вδ · D · lδ/ p = 0,6 · 0,335 · 0,151/ 2 = 0,015Вб

А = 6w1 · I1н/ πD = 6 · 72 · 91,44/ 3,14 · 0,335 = 38450А/м

Число витков в фазе (предварительное): w1 = E1/ (4,44 · kоб1 · ƒ1 · Ф) = 231,4/ 4,44 · 0,882 · 50 · 0,015 = 72

Число эффективных проводников в пазу: Un = 2w1 · a · m1/Z1 = 2 · 72 · 3 · 3/ 72 = 18.

Уточненное значение числа витков.

w1

Уточненное значение потока.

ФВб

Уточненное значение магнитной индукции в воздушном зазоре.

Вδ = Ф · р/ D · lδ = 0,015 · 2/ 0,335 · 0,151 = 0,6 Тл

Магнитная индукция в зубцах статора и ротора.

где kc = 0,97 коэффициент заполнения пакета сталью.

Магнитная индукция в ярмах статора и ротора:

Значения магнитных индукций в зубцах и ярмах должны удовлетворять условиям:

Bz1, Bz2 < 1,9 Тл;Ba, BJ < 1,6Тл

1,32; 1,04 < 1,9Тл; 0,99; 0,66 < 1,6Тл

Расчет коэффициента заполнения паза статора.

Размеры b11, b12 , h12 .

b'11 = b11 · 103 = 0,0081 · 103 = 8,1мм

b'12 = b12 · 103 = 0,011 · 103 = 11мм

h'12 = h12 · 103 = 0,039 · 103 = 39мм

Свободная площадь паза статора – площадь, занимаемая проводниками – для однослойной обмотки.

S'nc = ½(b'11 + b'12) · h'12 – Lu · ∆u + ∆b = ½(8,1 + 11) · 39 – 116,2 · 0,4 +

+ 0,2 = 302,73мм2,

где Lu – длина пазовой изоляции по периметру паза.

Lu = 2h'12 + b'11 + b'12 = 2(39 + 8,1 + 11) = 116,2мм

∆u = 0,4 – толщина пазовой изоляции;

∆b = 0,2 – (для h > 100) припуск на расшихтовку сердечника.

Свободная площадь паза статора для двухслойной обмотки.

S"nc = S'nc – 0,75 · ∆u(b'11 + b'12) = 302,73 – 0,75 · 0,4(8,1 + 11) = 297мм2

Коэффициент заполнения паза статора.

kз = (d2uз · Un · nэл)/ S"nc = (1,8952 · 18 · 3)/ 297 = 0,7,

где Snc = S"nc – для двухслойной обмотки.

Значения коэффициента заполнения должны находиться в пределах

kз = (0,7 ÷ 0,73)

Ток в стержне ротора.

I2 = 0,9(6 · w1 · kоб) · I1н/ Z2 = 0,9(6 · 72 · 0,882) · 91,44/ 82 = 382,4А

Плотность тока в стержне ротора.

J2 = I2/ qc = 382,4/ 96 = 3,98А

Плотность тока в стержне должна быть в пределах J2 = (2 ÷ 4)А/мм2

Ток кольца короткозамкнутой обмотки ротора.

Iкл = I2/ ∆ = 382,4/ 0,153 = 2499,35А,

где ∆ = 2sin(180˚ · p/Z2) = 2sin(180˚ · 2/ 82) = 0,153

Плотность тока в кольце.Jкл = Iкл / qкл = 2499,35/ 1554 = 1,61А/мм2

Плотность тока в кольце должна быть в пределах Jкл = (1 ÷ 4,5) А/мм2

4. Расчет магнитной цепи

Расчет магнитной цепи проводится для определения МДС и намагничивающего тока статора, необходимого для создания в двигателе требуемого магнитного потока. На рисунке 4 представлена расчетная часть магнитной цепи четырехполюсной машины, которая состоит из пяти последовательно соединенных участков: воздушного зазора, зубцовых слоев статора и ротора, спинки статора и ротора. МДС на магнитную цепь, на пару полюсов Fц определяется как сумма магнитных напряжений всех перечисленных участков магнитной цепи.

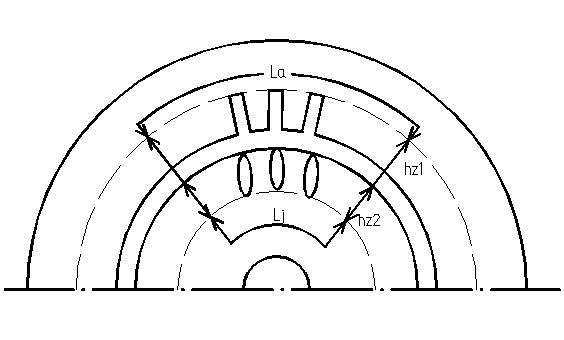
Рис. 4 – Магнитная цепь асинхронного двигателя.

Fц = Fδ + Fz1 + Fz2 + Fa + FJ

Магнитное напряжение воздушного зазора на пару полюсов.

Fδ = 1,6 · Bδ · δ · kδ · 106 = 1,6 · 0,6 · 0,001 · 1,31 · 106 = 1257,7А,

где kδ – коэффициент воздушного зазора, учитывающий зубчатость статора и ротора.

kδ = kδ1 · kδ2 = 1,22 · 1,07 = 1,31

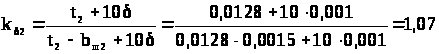
Магнитное напряжение зубцового слоя статора.

Fz1 = Hz1 · Lz1 = 584 · 0,082 = 47,89А,

где Hz1 – напряженность магнитного поля в зубцах статора, при трапецеидальных пазах определяется по приложению В для выбранной марки стали и для индукции рассчитанной в п. 3.2.7.

Hz1 = 584А/м

Lz1 = 2 · hz1 = 2 · 0,041 = 0,082м

Магнитное напряжение зубцового слоя ротора.

Fz2 = Hz2 · Lz2 = 360 · 0,082 = 29,52А,

где Hz2 – напряженность магнитного поля в зубцах ротора, определяется по приложению В для выбранной марки стали и для индукции рассчитанной в п. 3.2.7.

Hz2 = 360А/м

Lz2 = 2 · hz2 = 2 · 0,041 = 0,082м

Магнитное напряжение ярма статора.

Fa = Ha · La = 206 · 0,37 = 76,22А,

где Ha – определяется по приложению В для выбранной марки стали и для индукции рассчитанной в п. 3.2.8.

Ha = 206А/м

La = π(Da – ha)/ 2p = 3,14(0,52 – 0,052)/ 2 · 2 = 0,37м

Магнитное напряжение ярма ротора.

FJ = HJ · LJ = 113 · 0,14 = 15,82А,

где HJ – определяется по приложению В для выбранной марки столи и для индукции рассчитанной в п. 3.2.8.

HJ = 113А/м

LJ = π(D2 – 2hz2 – hJ)/ 2p = 3,14(0,333 – 2 · 0,041 – 0,0756)/ 2 · 2 = 0,14м

Суммарное магнитное напряжение магнитной цепи.

Fц = Fδ + Fz1 + Fz2 + Fa + FJ = 1257,7 + 47,89 + 29,52 + 76,22 + 15,82 =

= 1427,15А

Коэффициент насыщения магнитной цепи двигателя.

kµ = Fц / Fδ = 1427,15 / 1257,7 = 1,13

kµ = (1,1 ÷ 1,6)

Расчет намагничивающего тока

Намагничивающий ток.

Относительное значение намагничивающего тока.

Iµ* = Iµ/ I1н = 16,65/ 91,44 = 0,18

5. Активные и индуктивные сопротивления обмоток статора и ротора

Сопротивление обмоток статора.

Среднее значение зубцового деления статора.

tср1 = π(D + hz1)/ Z1 = 3,14(0,335 + 0,041)/ 72 = 0,016м

Средняя ширина катушки (секции) статора.

bср1 = tср1 · y = 0,016 · 14 = 0,224м,

где y – шаг обмотки.

Средняя длина лобовой части (секции) статора.

lл1 = (1,16 + 0,14p)bср1 = (1,16 + 0,14 · 2) · 0,224 = 0,323м

Средняя длина витка обмотки статора.

lср1 = 2(l1 + lл1) = 2(0,151 + 0,323) = 0,948м

Длина вылета лобовой части обмотки статора.

lb1 = (0,12 + 0,15p) · bср1 + 0,01 = (0,12 + 0,15 · 2) · 0,224 + 0,01 = 0,104м

Длина проводников фазы обмотки.

L1 = lср1 · w1 = 0,948 · 72 = 68,26м

Активное сопротивление обмотки статора, приведенное к рабочей температуре 115ºС (для класса изоляции F).

ρ115,

где ρ115 = 1/41 (Ом/мм2) – удельное сопротивление меди при 115˚.

То же в относительных единицах.

r1* = r1 · I1н/U1н = 0,11 · 91,44/ 220 = 0,05,

где I1н и U1н – номинальные значения фазного тока и напряжения.

Индуктивное сопротивление рассеяния обмотки статора зависит от проводимостей: пазового рассеяния, дифференциального рассеяния и рассеяния лобовых частей. Коэффициент магнитной проводимости пазового рассеяния при трапецеидальном пазе .

где kβ1, k'β1 – коэффициенты, учитывающие укорочение шага обмотки β, определяется по таблице 3.

Коэффициент проводимости дифференциального рассеяния статора.

λg1 = 0,9t1 · (q · kоб1)2 · kσ · kш1/δ · kδ = 0,9 · 0,0146 · (6 · 0,882)2 · 0,003

· 1,34/ 0,001 · 1,31 = 1,13

где kσ = ƒ(q) – коэффициент дифференциального рассеяния, определяется по таблице 4.

kш1 – коэффициент, учитывающий влияние открытия паза.

kш1 = (1 – 0,033) · b2ш1/t1 · δ = (1 – 0,033) · 0,00452/ 0,0146 · 0,001 = 1,34

Коэффициент проводимости рассеяния лобовых частей обмотки статора.

λл1 = 0,34(q/l1) · (lл1 – 0,064 · β · τ) = 0,34(6/0,151) · (0,323 – 0,64 · 0,75 ·

· 0,263) = 2,6

Коэффициент магнитной проводимости обмотки статора.

λ1 = λn1 + λg1 + λл1 = 1,74 + 1,13 + 2,6 = 5,47

Индуктивное сопротивление рассеяния фазы обмотки статора.

То же в относительных единицах.

x1* = x1 · I1н/U1н = 0,28 · 91,44/220 = 0,12

Индуктивное сопротивление взаимной индукции основного магнитного потока.

x12 = U1н/Iµ = 220/16.65 = 13,2Ом

Сопротивление обмотки ротора.

Активное сопротивление стержня.

rc = ρ115 · l2/qc =,

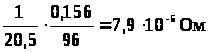где ρ115 = 1/20,5(Ом/мм2) удельное сопротивление литой алюминиевой обмотки ротора при 115˚. Сопротивление участка кольца между двумя соседними стержнями.

где Dкл.ср – средний диаметр кольца.

Dкл.ср = D2 – bкл = 0,333 – 0,042 = 0,291

Коэффициент приведения тока кольца к току стержня.

∆ = 2Sin (πp/Z2) = 2Sin (3,14 · 2/82) = 0,153

Сопротивление кольца, приведенное к стержню. rкл.пр = rкл /∆2 = 0,00000035/0,1532 = 1,5 · 10-5 Ом

Активное сопротивление обмотки ротора (стержня и двух колец).

r2 = rc + 2 · rкл.пр = 7,9 · 10-5 + 2 · 1,5 · 10-5 = 10,9 · 10-5 Ом

Активное сопротивление обмотки ротора, приведенное к обмотке статора.

То же в относительных единицах.

r'2* = r'2 · I1н/U1н = 0,064 · 91,44/220 = 0,027

Коэффициент магнитной проводимости пазового рассеяния ротора при овальном пазе.

Коэффициент проводимости дифференциального рассеяния ротора.

λg2 = t2/(12 · δ ·kδ) = 0,0128/(12 · 0,001 · 1,31) = 0,81

Коэффициент проводимости лобового рассеяния ротора.

Коэффициент проводимости рассеяния обмотки ротора.

Индуктивное сопротивление обмотки ротора.

x2 = 7,9 · ƒ1 · l1 · λ2 · 10-6 = 7,9 · 50 · 0,151 · 4,96 · 10-6 = 0,000296Ом

Индуктивное приведенное сопротивление обмотки ротора.

То же в относительных единицах.

x'2* = x'2 · I1н/U1н = 0,17 · 91,44/220 = 0,07

6. Потери в стали. Механические и добавочные потери

Потери в стали (магнитные потери) и механические не зависят от нагрузки, поэтому они называются постоянными потерями и могут быть определены до расчета рабочих характеристик. Расчетная масса стали зубцов статора при трапецеидальных пазах.

Gz1 = 7,8 · Z1 · bz1 · hz1 · l1 · kc· 103 = 7,8 · 72 · 0,0067 · 0,041 · 0,151 · 0,97 · 103 = 22,6кг

Магнитные потери в зубцах статора для стали 2013. Pz1 = 4,4 ·B2z1 · Gz1 = 4,4 · 1,322 · 22,6 = 173,26Вт

Масса стали ярма статора. Ga1 = 7,8π(Da – hz1) · ha · l1 ·kc · 103 = 7,8 · 3,14(0,52 – 0,041) · 0,052 · 0,151 · 0,97 · 103 = 89,5кг

Магнитные потери в ярме статора. Pa1 = 4,4 · B2a · Ga1 = 4,4 · 0,992 · 89,5 = 385,96Вт

Суммарные магнитные потери в сердечнике статора, включающие добавочные потери встали.

Механические потери.

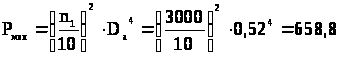Вт

Дополнительные потери при номинальной нагрузке определяются по эмпирической формуле.

Pдоп.н = 0,004 · P' = 0,04 · 58539,9 = 2341,6Вт

7. Расчет рабочих характеристик

Под рабочими характеристиками асинхронного двигателя понимаются зависимости:

P1, I1, I'2, cos φ', η, M, n = ƒ(P2),

Где Р1, Р2 – потребляемая и полезная мощности двигателя.

В основу рабочих характеристик положена система уравнений токов и напряжений, полученных из Г- образной схемы замещения асинхронного двигателя с вынесенными на выходные зажимы намагничивающим контуром. Рис. 5.

Рисунок 5 – Г- образная схема замещения и векторная диаграмма.

Коэффициент приведения параметров двигателя к Г- образной схеме замещения.

С1 = 1 + (x1/x12) = 1 + (0,28/13,2) = 1,021

Активное сопротивление обмотки статора, приведенное к Г- образной схеме замещения.

r'1 = C1 · r1 = 1,021 · 0.11 = 0,112Ом

Индуктивное сопротивление короткого замыкания, приведенное к Г- образной схеме замещения.

x'к = С1 · x1 + C21 · x'2 = 1,021 · 0,28 + 1,0212 · 0,17 = 0,463Ом

Активная составляющая тока холостого хода.

Ioa = (Pcm + 3 · I2µ · r1)/3 · U1н = (689 + 3 · 16,652 · 0,11)/3 · 220 = 1,18А

Расчет рабочих характеристик проводим для 5 значений скольжения в диапазоне:

S = 0,005 ÷ 1,25Sн,

где Sн – ориентировочно номинальное скольжение принимаем равным:

Sн = r'2* = 0,027

Все необходимые для расчета характеристик данные формулы сведены в таблицу 5.

Таблица 5

№ п/п	Расчетная формула	Ед. изм.	Скольжение
0,25Sн	0,50Sн	0,75Sн	1,0Sн	1,25Sн
1	C21 · r'2/S	Ом	9,88	4,94	3,29	2,47	1,98
2	R = r'1 + C21 ·r'2/S	Ом	26,48	13,33	8,89	6,67	5,34
3	x = x'к		0,463	0,463	0,463	0,463	0,463
4	Z = √R2 + x2	Ом	26,48	13,34	8,9	6,7	5,32
5	I"2 = U1н/Z	А	8,3	16,49	24,72	32,84	40,74
6	cosφ'2 = R/Z		1	0,99	0,99	0,99	0,98
7	sinφ'2 = x/Z		0,02	0,034	0,05	0,069	0,087
8	I1a = Ioa + I"2 · cosφ'2	А	9,48	17,5	25,65	33,69	41,11
9	I1p = Iop + I"2 · sinφ'2	А	16,82	17,21	17,89	18,91	20,19
10	I'2 = C1 · I"2	А	8,47	16,83	25,24	33,53	41,6
11	I1 = √I21a + I21p	А	26,3	34,71	43,54	52,6	61,3
12	P1 = 3 · I"22· r'2 · 10-3	кВт	9,27	11,55	16,87	22,23	27,13
13	Pэ1 = 3 · I21 · r1· 10-3	кВт	0,23	0,4	0,63	0,93	1,26
14	Pэ2 = 3 · I"22 · r'2 · 10-3	кВт	0,013	0,05	0,12	0,21	0,32
15	Pдоб = Pдоб.н(I1/I1н)2	кВт	0,58	1,01	1,59	2,32	3,15
16	∑P = Pcm + Pмех + Pэ1 + Pэ2 + Pдоб	кВт	8,092	8,729	9,609	10,729	11,999
17	P2 = P1 - ∑P	кВт	1,178	2,821	7,261	11,501	15,131
18	η = 1 - ∑P/P1		0,18	0,24	0,43	0,52	0,56
19	cosφ = I1a/I1		0,36	0,5	0,59	0,64	0,67
20	Pэм = P1 – Pэ1 – Pсm	кВт	8,351	10,46	15,55	20,61	25,18
21	ω1 = 2π · n1/60	Рад/с	314	314	314	314	314
22	M = Pэм · 103/ω1	Н.м	26,6	33,3	49,5	65,6	80,2
23	n = n1 ·(1 – S)	Об/мин	2980	2960	2940	2919	2899

После расчета рабочих характеристик производим их построение

По номинальному току определяются номинальные параметры двигателя:

Р2н = 7,2кВт

Р1н = 17,5кВт

I'2н = 51,2А

сosφн = 0,61

ηн = 0,40

Мн = 50Н·м

nн = 2800об/мин

Sн = 0,018

Максимальный момент в относительных единицах.

Мmax* =Mmax / Mн =[(Sн /Sm) + (Sm/Sн)]/2 = [(0,018/0,20) + (0,20/0,018)]/2 =5,6

8. Расчет пускового тока и момента

При пуске в роторе АД имеют место два физических явления, оказывающих большое влияние на активное и индуктивное сопротивления, а следовательно, на пусковой ток и момент:

1) Эффект вытеснения тока в верхнюю часть паза, за счет которого расчетная высота паза и индуктивное сопротивление уменьшается, активное сопротивление увеличивается;

2) Эффект насыщения коронок зубцов потоками рассеяния, обусловленными большими пусковыми токами, за счет этого явления магнитные проводимости и индуктивные сопротивления уменьшаются.

Расчет активных и индуктивных сопротивлений обмотки ротора с учетом эффекта вытеснения тока.

Приведенная высота стержня для литой алюминиевой обмотки ротора при температуре 115˚С (класс изоляции F).

ξ = 63,61 · h21 = 63,61 · 0,040 = 2,54м

где h21 – высота стержня в пазу. Расчетный коэффициент увеличения активного сопротивления стержня φ в функции ξ. φ = 1,4. Глубина проникновения тока – расчетная высота стержня.

hr = h21 /(1 + φ) = 0,040/(1 + 1,4) = 0,017

Относительное увеличение активного сопротивления стержня.

kr = qc/qr = 96/81,33 = 1,18

где qr – площадь сечения стержня, ограниченная высотой hr.

qc – площадь сечения всего стержня.

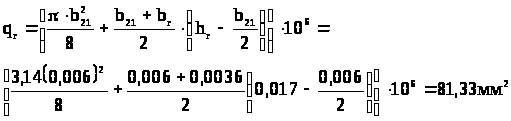
Коэффициент общего увеличения активного сопротивления фазы ротора за счет вытеснения тока.

Приведенное активное сопротивление ротора с учетом вытеснения тока.

Расчетный коэффициент уменьшения индуктивного сопротивления стержня φ' в функции ξ. φ' = 0,6. Расчетный коэффициент уменьшения индуктивного сопротивления фазы ротора за счет вытеснения тока.

kx = λn2ξ /λ2 = 4,14/4,96 = 0,83

где λ2ξ – коэффициент магнитной проводимости рассеяния ротора с учетом вытеснения тока.

λ2ξ = λn2ξ + λл2 + λg2 = 1,23 + 2,1 + 0,81 = 4,14

λ2ξ = λn2 · φ' = 2,05 · 0,6 = 1,23

Приведенное индуктивное сопротивление ротора с учетом вытеснения тока.

x'2ξ =kx · x'2 = 0,83 · 0,17 = 0,14Ом

Расчет индуктивного сопротивления обмотки ротора с учетом влияния насыщения магнитопровода полями рассеяния.

Ток ротора, рассчитанный по Г-образной схеме замещения, без учета насыщения при S = 1.

То же с учетом насыщения. I'2нас ≈ I1нас = I1 · kнас = 458,33 · 1,3 = 595,83А, где kнас – коэффициент насыщения, предварительно выбирается в пределах: kнас = 1,25 ÷ 1,4. Средняя МДС обмотки, отнесенная к одному пазу статора.

Фиктивная индукция потока рассеяния в воздушном зазоре.

Коэффициент γδ, учитывающий отношение потока рассеяния при учете насыщения к потоку рассеяния ненасыщенной машины, по рис.8.

γδ = 0,8

Коэффициент магнитной индукции проводимости пазового рассеяния обмотки статора с учетом насыщения.

С1 = (t1-bш1) ·(1- γδ) = (0,0146 – 0,0045) · (1 – 0,80) = 0,00202

Коэффициент магнитной проводимости дифференциального рассеяния обмотки статора с учетом насыщения. λg1нас = λg1 · γδ = 1,13 · 0,8 = 0,9

Окончательное индуктивное сопротивление фазы обмотки статора с учетом насыщения, Ом

x1нас = x1 · ∑λ1нас/λ1 = 0,28 · 5,16/5,47 = 0,26 Ом

∑λ1нас = λn1нас + λg1нас + λл1 = 1,66 + 0,9 + 2,6 = 5,16

Аналогично для ротора: Коэффициент магнитной проводимости пазового рассеяния с учетом насыщения.

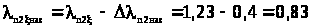
Δλn2нас = hш2/bш2 · С2/bш2 + С2 = 0,001/0,0015 · 0,00226/0,0015 + + 0,00226 = 0,4

С2 = (t2 – bш2) · (1- γδ) = (0,0128 – 0,0015) · (1- 0,80) = 0,00226

Коэффициент магнитной проводимости дифференциального рассеяния обмотки ротора с учетом насыщения.

λg2нас = λg2 · γδ = 0,81 · 0,8 = 0,65

Окончательно приведенное индуктивное сопротивление фазы обмотки ротора с учетом влияния вытеснения тока и насыщения.

x'2ξнас = x'2 · ∑λ2gнас/λ2 = 0,17 · 3,58/4,96 = 0,12Ом

∑λ2gнас = λn2нас + λg2нас + λл2 = 0,83 + 0,65 + 2,1 = 3,58

Коэффициент С1 в Г- образной схеме замещения.

С1nнас = 1 + (x1нас/x12n) = 1 + (0,26/14,92) = 1,02

x12n ≈ x12 · kμ = 13,2 · 1,13 = 14,92

Ток в обмотке ротора с учетом насыщения при S = 1.

аnнас = r1 + C1nнас · r'2ξ = 0,11 + 1,02 · 0,072 = 0,18

bnнас =x1нас + C1nнас · x'2ξнас = 0,26 + 1,02 · 0,12 = 0,38

Ток в обмотке статора при S = 1.

Пусковой ток в относительных единицах.

I1n* = I1n/I1н = 526,59/91,44 = 5,76

Кратность пускового момента.

, Sn = 1

Mn = Mn* · Mн = 2,15 · 50 = 107,5H.м

СПИСОК ЛИТЕРАТУРЫ

1.Костенко Г.Н., Пиотровский Л.М. Электрические машины.- Л.: 1972.

2.Брускин Д.Э., Зорохович А.Е., Хвостов В.С.- Электрические машины. М.: 1979. Ч I. Ч II.

3.Кацман М.М. Электрические машины.- М.: 1983.

4.Копылов И.П. Электрические машины. -Л.: 1972.

5.Проектирование электрических машин. /Под ред. И.П.Копылова М.: 1980.

6.Зимин В.И., Каплай М.Я., Палей А.М. Обмотки электрических машин.- М.: 1975

7.Чичетян В.И. Электрические машины. Сборник задач.- М. : Высшая школа 1988.