Устойчивость прямоугольных пластин судового корпуса

Курсовая работа

"Расчёт устойчивости прямоугольных пластин судового корпуса"

Исходные данные

№ п/п	Размер пластины (a), м	Размер пластины (b), м	Модуль упругости материала Е ·103МПа	Толщина пластины (h), м
19	1.90	1,30	210	0.020

Дифференциальное уравнение нейтрального равновесия прямоугольной пластины, сжатой в двух взаимно перпендикулярных направлениях (1), (2)

Начнем изучение устойчивости пластин со случая, когда на свободно опертую прямоугольную пластину действуют сжимающие напряжения в двух взаимно перпендикулярных направлениях (рис.1).

Рис.1

Пусть σ_>1> - абсолютная величина сжимающего напряжения, действующего в направлении оси ох; σ_>2>-абсолютная величина сжимающего напряжения, действующего в направлении оси оу; "а" и "b"-размеры пластины в плане; "h"-толщина пластины.

Тогда дифференциальное уравнение нейтрального равновесия рассматриваемой пластины будет:

(1)

(2)

Задание формы упругой поверхности свободно опертой пластины при потере устойчивости в виде двойного тригонометрического ряда (3)

Упругая поверхность свободно опертой пластины при потере устойчивости в самом общем виде может быть представлена тригонометрическим рядом:

(3)

Граничные условия на кромках рассматриваемой прямоугольной свободно опёртой по контуру пластины (4)

Каждый член ряда (3) удовлетворяет граничным условиям на контуре рассматриваемой пластины, т.е. условиям равенства нулю в точках на контуре величины прогиба пластины и изгибающих моментов:

(4)

Уравнение, устанавливающее сочетание нагрузок Т_>1> и Т_>2>, при котором свободно опёртая по контуру прямоугольная пластина может потерять устойчивость (8)

Подставляя формулу (3) в дифференциальное уравнение (1), Получим

или

(5)

Рассматриваемая пластина может потерять устойчивость при таком сочетании нагрузок Т_>1> и Т_>2>, при котором какая-либо из скобок, входящих в выражение (5), обратится в нуль.

При этом соответствующее А_>mn> может стать отличным от нуля и форма потери устойчивости пластины будет

(6)

Таким образом, эйлерово сочетание нагрузок Т_>1> и Т_>2> определится из условия:

Учитывая обозначения (2), получим

(7)

Или

(8)

Устойчивость прямоугольной свободно опёртой по контуру пластины, одинаково сжатой в обоих направлениях. (11)

Для дальнейшего исследования полезно выражение (7) переписать следующим образом:

(9)

При различных комбинациях чисел "m" и "n" мы имеем, на основании выражения (9) линейную зависимость между напряжениями σ_>1> и σ_>2>.

Будем откладывать на оси абсцисс некоторой системы координатных осей напряжение σ_>1>, а на оси ординат-напряжение σ_>2> (рис.2). Тогда любой точке плоскости будет соответствовать некоторая комбинация напряжений σ_>1> и σ_>2>

Рис.2

Рассматривая пластину с определенным отношением сторон а: b, можем, задаваясь различными "m" и "n", построить ряд прямых по уравнениям (9). Область тех напряжений, при которых пластина не теряет устойчивости, будет ограничена ближайшими к началу координат участками всех построенных прямых различных "m" и "n".

Легко убедиться, что для определения этих участков нужно построить лишь прямые, соответствующие различным "m" при n=1 и различным "n" при m=1.

Если σ_>1>=σ_>2>_>.,> т.е. пластина одинаково сжата в обоих направлениях, то на основании выражения (9) получим

σ_>1>=σ_{>2 (}>10)

Правая часть формулы (10) растет при увеличении чисел "m" и "n". Поэтому в таком случае для разыскания эйлеровых значений сжимающих напряжений следует в формуле (10) положить m = n =1. Тогда получим

(11)

где - цилиндрическая жесткость пластины.

Следовательно, одинаково сжатая в двух пластина теряет устойчивость с образованием одной полуволны независимо от величины отношения а: b.

Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, одинаково сжатой в обоих направлениях.

Устойчивость прямоугольной свободно опёртой по контуру пластины, сжатой в одном направлении вдоль длинной стороны пластины. (12)

Если пластина сжата лишь в одном направлении, то ее эйлерову нагрузку можно найти из общих зависимостей предыдущего параграфа, положив в них σ_>2>=0. На основании формулы (9) получим

(12)

Установление числа полуволн формы потери устойчивости прямоугольной свободно опёртой по контуру пластины, сжатой в одном направлении вдоль длинной стороны (15).

Число полуволн "m", образующихся вдоль направления сжатия при потере устойчивости пластины, будет зависеть от отношения а: b.

Действительно, каждому отношению а: b должно соответствовать определенное число "m", при подстановке которого в формулу скобка, входящая в ее правую часть, будет принимать наименьшее значение.

(13)

Это число "m" должно, очевидно, удовлетворять тому условию, при котором при подстановке в правую часть формулы вместо m величины (m+ 1) и (m - 1) значение скобки будет увеличиваться. Это условие запишется в виде:

(14)

Из выражения (15) можно получить:

(15)

Последние неравенства показывают, что на длине пластины образуется следующее число полуволн:

Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, сжатой вдоль короткой стороны опорного контура (16)

Для стальной пластины с параметрами Е=2,15*10⁶ кг/см²; μ=0,3, сжатой вдоль короткой стороны опорного контура, эйлерово напряжение определяется:

(16)

Для определения эйлерова напряжения пластины с параметрами Е=210·10³ МПа = 2,1·10⁶ кг/см² и μ=0,3 вдоль короткой стороны необходимо формулу (21) домножить на Е/Е_>ст>, тогда:

Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, сжатой вдоль длинной стороны опорного контура (17)

Для стальной пластины с параметрами Е=2,15*10⁶ кг/см²; μ=0,3, сжатой вдоль длинной стороны опорного контура, эйлерово напряжение определяется:

(17)

Для определения эйлерова напряжения пластины с параметрами Е=210·10³ МПа = 2,1·10⁶ кг/см² и μ=0,3 вдоль длинной стороны необходимо формулу (21) домножить на Е/Е_>ст>, тогда:

Устойчивость пластин, свободно опертых по двум кромкам. Решение в виде ординарного тригонометрического ряда. Расчётная схема (рис.3)

Рис.3

Решение для упругой поверхности пластины, у которой кромки х = const свободно оперты на жесткий контур (18)

Рассмотрим пластину, у которой кромки х = const свободно оперты на жесткий контур, и загруженную сжимающими усилиями в направлении оси ох. Решение для упругой поверхности такой пластины можно искать в виде ординарного тригонометрического ряда:

(18)

Дифференциальное уравнение нейтрального равновесия пластины (24). Дифференциальное уравнение, которому должны удовлетворять функции (20)

Дифференциальное уравнение нейтрального равновесия пластины:

(19)

где Т_>1>= - σ_>1>h

Функции должны удовлетворять дифференциальному уравнению:

(20)

Общий интеграл для функций (21)

На основании решения, полученного при рассмотрении изгиба пластин, свободно опертых по двум кромкам, формула общего интеграла для функций запишется в виде:

(21)

Где

(22)

Граничные условия для функции, для пластины, жестко заделанной по своим продольным кромкам, (25)

Рассматриваемое решение позволяет исследовать устойчивость пластин при различных условиях закрепления на кромках, параллельных сжимающей нагрузке.

Продольные кромки жестко заделаны (рис.4).

Рис.4

В этом случае граничные условия для упругой поверхности пластины w (х, у) будут:

(23)

Учитывая, что ожидаемая форма потери устойчивости будет симметрична относительно оси ох, можем в общем интеграле функции сохранить лишь четные члены, т.е. записать его в виде

(24)

и подчинить это выражение граничным условиям на кромке .

Учитывая выражения (18) и (23), получим следующие граничные условия для функции:

(25)

Система линейных однородных уравнений относительно постоянных A_>m> и С_>m> (26)

Подчиняя выражение (24) условиям (25), получим

(26)

Определение эйлеровых напряжений пластины, жестко заделанной по своим продольным кромкам (27)

Определение эйлеровых напряжений пластины, жестко заделанной по своим продольным кромкам, по формуле:

(27)

Где k выбирается из таблицы в зависимости от соотношения сторон пластины b: a

b: а	0,4	0,5	0,6	0,7	0,8	0,9	1,0
k	9,44	7,69	7,05	7,00	7,29	7,83	7,69

Примем коэффициент k=7,00 тогда

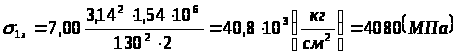
Устойчивость пластины, одна продольная кромка которой свободно оперта, другая совершенно свободна. Расчётная схема (рис.5)

Одна продольная кромка пластины свободно оперта, другая совершенно свободна

Рис.5

Определение эйлеровых напряжений пластины, одна продольная кромка которой свободно оперта, другая совершенно свободна (28)

Для стальной пластины с параметрами Е=2,15*10⁶ кг/см²; μ=0,3, сжатой вдоль длинной стороны опорного контура, при закреплении показанном на Рис.6, эйлерово напряжение определяется по формуле:

(28)

Для определения эйлерова напряжения пластины с параметрами Е=210·10³ МПа = 2,1·10⁶ кг/см² и μ=0,3 необходимо формулу (28) домножить на Е/Е_>ст>, тогда:

Устойчивость пластин при действии касательных напряжений. Расчётная схема (Рис.6)

Рассмотрим свободно опертую пластину, находящуюся в условиях чистого сдвига под действием касательных напряжений τ (Рис.6).

Сдвигающие усилия на единицу длины пластины будут

Рис.6

Вычисление эйлеровой нагрузки пластин при действии касательных напряжений (29)

(29)

Заключение

Анализ прямоугольных пластин позволяет сделать вывод об их устойчивости и как следствие прочности всей судовой конструкции. Полученные значения касательных и эйлеровых напряжений допустимы.

Список литературы

Основная литература

1. Ипатовцев Ю.Н., Короткин Я.И. Строительная механика и прочность корабля: Учебник. Л.: Cудостроение, 1991

2. Короткин Я.И., Ростовцев Д.М., Сиверс Н.Л. Прочность корабля: Учебник. Л.: Судостроение, 1974

3. Постнов В.А. и др. Строительная механика корабля и теория упругости: Учебник: в 2-х томах. Л.: Cудостроение, 1987

Дополнительная литература

1. Архангородский А.Г., Беленький Л.М. Аналитический метод проектирования корпуса корабля, Л.: Судпромгиз. 1961

2. Короткин Я.И., Локшин А.З., Сиверс Н.Л. Изгиб и устойчивость стержней и стержневых систем: Учебное пособие, М.Л. .: Машгиз, 1953

3. Короткин Я.И., Локшин А.З., Сиверс Н.Л. Изгиб и устойчивость пластин и круговых цилиндрических оболочек: Учебное пособие, Л.: Судпромгиз, 1955

4. Крыжевич Г.Б. Основы расчётов надёжности судовых конструкций: Учебное пособие, Санкт-Петербург.: СПбГМТУ, 1995

5. Локшин А.З., Рябов Л.И. Судовые кничные соединения, Л.: Cудостроение, 1973

6. Попов Ю.Н. и др. Прочность судов, плавающих во льдах, Л.: Cудостроение, 1967

7. Справочник по строительной механике корабля: в 3-х томах / Под ред. акад. Ю.А. Шиманского. Л.: Судпромгиз. 1960

8. Справочник по строительной механике корабля: в 3-х томах/Бойцов Г.В., Палий О.М., Постнов В.А., Чувиковский В.С. Л.: Cудостроение, 1982

9. Чибиряк И.М. Методические указания к выполнению курсовой работы по конструкции корпуса корабля. Владивосток, изд. ДВПИ им.В. В. Куйбышева, 1977.