Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Севастопольский национальный технический университет
Кафедра технической кибернетики
КУРСОВОЙ ПРОЕКТ
По дисциплине «Системы автоматики»
На тему: «Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений»
(альбом документов)
Выполнил: студент группы А-42д
Севастополь
2006
ОПИСЬ АЛЬБОМА
Отчет по курсовому проектированию на тему «Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений» содержит документы:
- Техническое задание, где обозначены цель проекта, технические требования, основные этапы работы и график их выполнения (на 2-х листах);
- Пояснительная записка (22 листа);
- Приложения (4 листа), включающие в себя таблицы экспериментальных данных и листинг m-файла.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Севастопольский национальный технический университет
Кафедра технической кибернетики
КУРСОВОЙ ПРОЕКТ
По дисциплине «Системы автоматики»
На тему: «Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений»
(техническое задание)
Выполнил: студент группы А-42д
Севастополь
2006
ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Цель проекта
Целью курсового проекта является разработка синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений.
Общие требования к выполнению курсового проекта
К установленному сроку студент должен предоставить к защите расчетно-пояснительную записку и графический материал проекта, выполненные аккуратно и в соответствии с требованиями следующих стандартов ЕСКД:
ГОСТ 2.105-95 ЕСКД. Общие требования к текстовым документам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Севастопольский национальный технический университет
Кафедра технической кибернетики
КУРСОВОЙ ПРОЕКТ
По дисциплине «Системы автоматики»
На тему: «Синтез закона управления и настройка промышленного регулятора для стабилизации температуры в условиях возмущений»
(пояснительная записка)
Выполнил: студент группы А-42д
Севастополь
2006
Оглавление
ВВЕДЕНИЕ8
1 ОПИСАНИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ ТЕМПЕРАТУРЫ ЭЛЕТРОПЕЧИ
2 ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ
2.1 Методы математического описания объектов управления
2.2 Экспериментальные данные
2.3 Нахождение коэффициента усиления
2.4 Построение математической модели звена первого порядка геометрическим методом
2.5 Построение модели звена второго порядка методом площадей
2.6 Построение математической модели звена второго порядка методом Ротача
2.7 Выбор наилучшей аппроксимирующей модели
3 СИНТЕЗ РЕГУЛЯТОРА
3.1 Синтез регулятора методом ЛАЧХ
3.2 Переходная характеристика замкнутой системы
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
ПРИЛОЖЕНИЕ А (ОБЯЗАТЕЛЬНОЕ)
ПРИЛОЖЕНИЕ Б (ОБЯЗАТЕЛЬНОЕ)
ПРИЛОЖЕНИЕ В (РЕКОМЕНДУЕМОЕ)
ВВЕДЕНИЕ
Современная теория автоматического управления содержит результаты, применимые для различных классов общих многомерных систем, включая системы, задаваемые:
линейными дифференциальными уравнениями с переменными коэффициентами;
нелинейными дифференциальными уравнениями;
дифференциально-разностными и другими уравнениями с последействием;
уравнениями с частными производными и интегральными уравнениями.
Современная теория управления включает так называемую теорию оптимального управления, с помощью которой можно разрабатывать оптимальные системы, то есть системы, при функционировании которых минимизируется или максимизируется некоторый выбранный заранее критерий качества.
Автоматическое регулирование широко применяется в электротермии, в электрических печах сопротивления, также применяется автоматическое управление работой различных механизмов печного аппарата.
В индукционных печах и устройствах автоматически регулируется напряжение источников питания и коэффициент мощности установки, длительность отдельных процессов нагрева и их тепловой режим. В дуговых и рудно-термических печах применяют автоматические регуляторы, стабилизирующие их режим и обеспечивающие поддержание их мощности на заданном уровне.
Некоторые из электротермических процессов вообще не могут быть осуществлены в промышленных масштабах без их автоматизации. В других случаях автоматизация снижает брак, улучшает качество изделий, повышает производительность труда, улучшает качество технологических показателей производства, высвобождение обслуживающего персонала и облегчает условия его труда.
В электрических печах сопротивления осуществляется нагрев различных материалов до заданной температуры.
Во многих случаях после нагрева следует период выдержки, необходимый для выравнивания температуры в нагреваемых изделиях или для прохождения в цепях процессов, требующих времени. В связи с этим, основная задача устройств автоматического регулирования температуры состоит в обеспечении нагрева изделий до заданной температуры и в поддержании на заданном уровне с точностью, соответствующей требованиям технического процесса. Эти требования могут изменяться в широких пределах.
Различные электронные печи получили широкое распространение. Их существенные особенности:
Возможность компенсации большого количества энергии в весьма малых объектах и получение высоких скоростей нагрева и любой необходимой температуры;
возможность обеспечения высокой равномерности нагрева изделий;
легкость регулирования подводимой мощности, а также, следовательно, температуры, легкость автоматизации регулирования температурного режима.
В данном курсовом проекте осуществляется исследование системы автоматического регулирования температуры на базе промышленного регулятора Р-111.
В процессе исследований необходимо получить математическую модель объекта управления в виде передаточной функции.
Осуществить выбор параметров настройки регулятора, при которых система удовлетворяет заданным требованиям по точности и качеству.
1 ОПИСАНИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ ТЕМПЕРАТУРЫ ЭЛЕТРОПЕЧИ ВРТ-3
Автоматическое регулирование температурного режима осуществляется системами управления с обратной связью, вырабатывающими управляющие воздействия в зависимости от величины знака отклонения регулируемой величины от заданного значения.
В качестве объекта исследования рассмотрим промышленную электрическую печь СУОП-015.20/12М-43 в системе автоматической стабилизации температуры, выполненной на базе высокочастотного регулятора температуры ВРТ-3.
Система автоматической стабилизации температуры электропечи выполнена на промышленных приборах государственной системы промышленных приборов и средств автоматизации (ГСП) аналоговой электрической ветви. Ее функциональная схема представлена на рис.1.1.

Рисунок 1.1 – Функциональная схема системы стабилизации температуры на основе высокочастотного регулятора температуры ВРТ-3
На рис. 1.1 приняты следующие обозначения:
– И-102 - измерительный блок;
– Р-111 - регулятор;
– У-252 - усилитель мощности;
– ЭП - электрическая печь (объект управления);
– ДТ - датчик температуры.
Сигнал с датчика температуры ДТ поступает на вход измерительного блока И102. В приборе И-102 формируется сигнал рассогласования, равный разности сигнала задатчика (задатчик входит в состав И-102) и сигнала температуры.
Усиленный сигнал ошибки поступает на вход регулирующего аналогового прибора Р-111, в котором могут быть сформированы П, ПИ, ПИД законы регулирования.
Реализация типовых законов регулирования осуществляется на базе операционного усилителя с использованием специально подключённых сопротивлений и емкостей на вход исполнительного устройства, которым является тиристорный усилитель мощности У-252.
Усиленный сигнал в виде напряжения подаётся в цепи нагрева электропечи.
В качестве возмущений используется два вида воздействий. Возмущения, вызванные изменением внутренних параметров электропечи, имитируются введением в активную зону печи металлических трубок из различных материалов (железо, алюминий, латунь) с различной теплоемкостью. Возмущение, вызванное внешней средой, создаётся вентилятором, т.е. принудительным воздушным охлаждением электропечи.
Система ВРТ-3 предназначена для прецизионного регулирования температуры и может применяться в электротехнической, электронной, теплоэнергетической и других отраслях промышленности.
Система ВРТ-3 состоит из трёх приборов:
– измерительного блока И-102;
– регулирующего устройства Р-111;
– усилителя мощности У-252.
Опишем основные блоки:
Измерительный блок И-102 представляет собой помехозащищенный усилитель с задатчиком. В блоке происходит компенсация ЭДС термопары и задатчика. В комплекте с термопарой и регулирующим устройством Р-111 блок применяется в системах высокоточного регулирования температуры.
В блоке И-102 сигнал термопары компенсируется сигналом от встроенного задатчика, и разница этих сигналов усиливается предварительным усилителем.
С выхода блока И-102 усиленный сигнал рассогласования поступает на вход устройства Р-111. Устройство формирует закон регулирования и преобразует входной сигнал в унифицированный сигнал постоянного тока 0-5 мА, который затем может быть использован в блоках питания (тиристорных, магнитных) или других устройствах управления нагревом.
Р-111 имеет индикаторы, по которым можно контролировать величину рассогласования и выходной ток, органы динамической настройки, а также переключатель управления, позволяющий перейти на ручное управление объектом и обеспечивающий "безударное" переключение.
Система ВРТ-2 в комплекте с тиристорным усилителем У-252 образует систему ВРТ-3.
Р-111 является аналоговым регулирующим прибором, осуществляющим пропорциональный (П), пропорционально-дифференциальный (ПД), пропорционально-интегральный (ПИ) или пропорционально-интегрально-дифференциальный (ПИД) законы регулирования.
Прибор работает в комплекте с измерительным блоком типа И-102, а так же может работать непосредственно с датчиками унифицированного сигнала 0-5мА или 0-20мА постоянного тока. В качестве исполнительного механизма для прибора Р-111 используются пропорциональные усилители мощности или электрические позиционеры.
Р-111 выпускается в 3-х модификациях, отличающихся величинами диапазонов времени интегрирования и времени дифференцирования.
Основные технические данные системы ВРТ-3
|
Выходной сигнал |
0-5 мА постоянного тока |
|
Сопротивление нагрузки |
0-3 кОм |
|
Минимальная цена деления задатчика |
1 мкВ |
|
Законы регулирования |
П, ПИ, ПИД |
|
Коэффициент пропорциональности Кп |
0,3-50 |
|
Время интегрирования в ПИ- и ПИД-законах регулирования, Ти |
2-75 с |
|
Отношение времени дифференцирования ко времени интегрирования в ПИД-законе регулирования, Тд/Ти |
0-0,9 |
|
Система ВРТ-3 обеспечивает помехозащищенность от продольной помехи величиной до 220 В 50 Гц и поперечной помехи величиной до 1 кВ 50 Гц |
|
|
Питание системы |
Промышленная сеть 220 В 50 Гц, не связанная с силовой сетью |
|
Габаритные размеры каждого блока: |
|
|
Ширина |
160 мм |
|
Высота |
80 мм |
|
Глубина |
535 мм |
|
Напряженность внешнего магнитного поля в месте установки ВРТ-3 не должна превышать: |
|
|
Для И-102 |
40 А/м |
|
Для Р-111 |
400 А/м |
2 ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ
2.1 Методы математического описания объектов управления
Для построения высокоэффективной системы управления необходимо иметь описание объекта управления в виде математической модели.
Для описания объектов управления, в которых отсутствует зависимость переменных состояния, управления от пространственных координат (линейные многомерные системы с сосредоточенными параметрами), используются системы линейных обыкновенных дифференциальных уравнений или соответствующие изображения по Лапласу. Рассмотрим многомерную линейную систему с m управлениями, l возмущениями и k входами. Модель линейной системы с сосредоточенными параметрами во временной области:

где х(t) – вектор состояния
системы,
 ;
;
u(t) – вектор управлений (входов),
 ;
;
у(t) – вектор выходов,
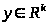 ;
;
f(t) – вектор возмущений,
 ;
;
А – матрица размерности n x n;
В – матрица размерности n x m;
D – матрица размерности n x l;
С – матрица размерности k x n.
Применяя преобразование Лапласа к системе, получим эквивалентную модель в комплексной области:
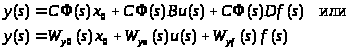
Частотное или временное представления выбираются из соображений удобства, так как в случае постоянных матриц A, B,C и D они эквивалентны.
Для построения подобных моделей можно использовать два пути: применять фундаментальные физические соотношения в виде законов сохранения вещества, энергии или восстанавливать параметры моделей по эмпирическим данным, причем второй путь более часто применяется на практике.
2.2 Экспериментальные данные
Для построения математической модели объекта управления использовался метод восстановления параметров модели по эмпирическим данным. Для этого с помощью лабораторной установки были получены экспериментальные данные для исследования объекта управления и построения его математической модели. Результаты снятия экспериментального переходного процесса приведены в Приложении Б. Полученные данные были аппроксимированы в среде научных исследований MatLab. В результате получился график переходного процесса, представленный на рисунке 2.1.
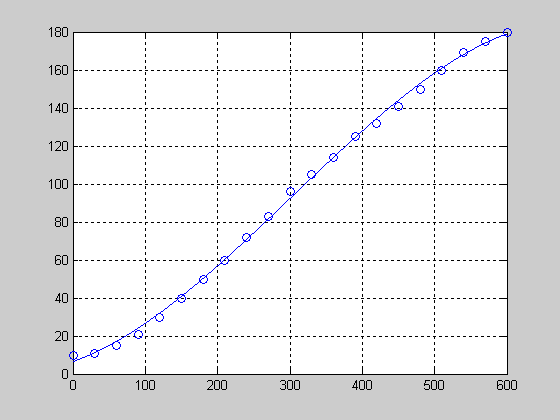
Рисунок 2.1 – Экспериментальный переходный процесс
На рисунке 2.1 по оси ординат отложена температура в °C, а по оси абсцисс – время в секундах. При этом на самом графике кружочками обозначены непосредственно экспериментальные точки, определенные в дискретные моменты времени.
Нормированный переходный процесс представлен на рисунке 2.2.

Рисунок 2.2 – Нормированный переходный процесс
Структура аппроксимирующего выражения для передаточной функции объекта может быть выбрана в общем случае в виде:
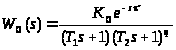
Коэффициент усиления объекта управления K>о> можно найти по графику переходного процесса. Постоянные времени передаточной функции могут быть найдены методом площадей, геометрическим и методом Ротача.
2.3 Нахождение коэффициента усиления
Коэффициент усиления может быть определен из следующего соотношения:

Отсюда получаем, что
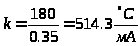 .
.
2.4 Построение математической модели звена первого порядка геометрическим методом
Звено первого порядка с запаздыванием имеет следующий вид:
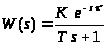
Для определения величины запаздывания и постоянной времени обратимся к графику переходного процесса (рисунок 2.1). Для нахождения постоянной времени необходимо провести прямую до пересечения с графиком процесса параллельно оси абсцисс на уровне 0.63kc (см. рисунок 2.3).

Рисунок 2.3 – Определение постоянной времени по переходному процессу
Постоянная времени T
= 360.53 (с).
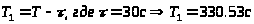 .
Построим переходный процесс для такого
звена и посмотрим насколько он совпадает
с экспериментальным.
.
Построим переходный процесс для такого
звена и посмотрим насколько он совпадает
с экспериментальным.
Схема модели в MatLab представлена на рисунке 2.4.
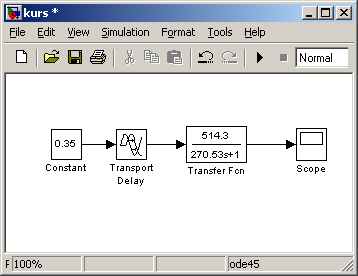
Рисунок 2.4 – Схема модели
Полученный переходный процесс представлен на рисунке 2.5.

Рисунок 2.5 – Переходный процесс,
полученный по передаточной функции
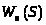
Таким образом, передаточная функция объекта в данном случае имеет следующий вид:
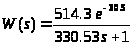
2.5 Построение модели звена второго порядка методом площадей
При q=1 и =0 получаем объект второго порядка. Рассчитаем постоянные времени T>1> и T>2> при помощи метода площадей:

Для определения параметров передаточной функции методом площадей необходимо построить графики функций:
1)
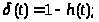
2)
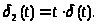
Тогда можно определить площади под графиками данных функций (S>1> и S>2> соответственно). Результаты вычислений представлены ниже.
S1 =
309.8824
S2 =
5.9162e+004
Графики данных функций приведены на рисунках 2.6 и 2.7 соответственно.
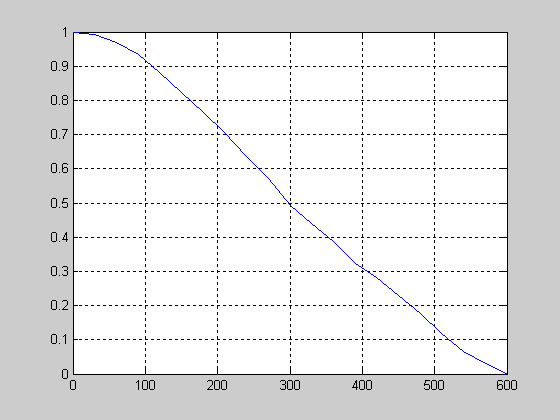
Рисунок 2.6 – График функции
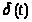
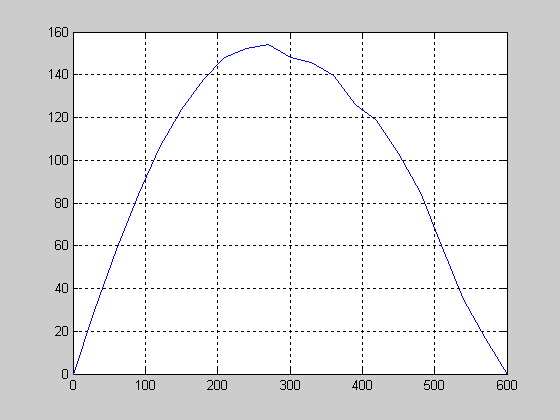
Рисунок 2.7 – График функции

Теперь необходимо проверить
соотношение
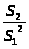 .
Если
.
Если
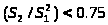 ,
то метод площадей применять нельзя,
необходимо использовать метод грубых
площадей. В нашем случае
,
то метод площадей применять нельзя,
необходимо использовать метод грубых
площадей. В нашем случае
 (полный листинг m-файла приведен в
приложении В). Значит, применим метод
грубых площадей.
(полный листинг m-файла приведен в
приложении В). Значит, применим метод
грубых площадей.
Для этого нужно найти точку перегиба графика переходного процесса. Точка перегиба имеет координаты: t = 90 c, , y(t>п>)=0.09.
Берем точку t правее точки перегиба (t>tп) воспользуемся формулой:
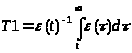 ,
где
,
где
In= ,
площадь кривой после точки перегиба
(пределы интегрирования: от 90(tп) до
600()),
причем,
,
площадь кривой после точки перегиба
(пределы интегрирования: от 90(tп) до
600()),
причем,
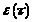 =k*(t),
где (t)=1-h(t),
следовательно:
=k*(t),
где (t)=1-h(t),
следовательно:

Таким образом, реализуя данный алгоритм, получаем следующие результаты:
T1 =
237.2624
T2 =
72.6200
Transfer function:
514.3
---------------------------
1.723e004 s^2 + 309.9 s + 1
График переходного процесса для такого звена представлен на рисунке 2.8
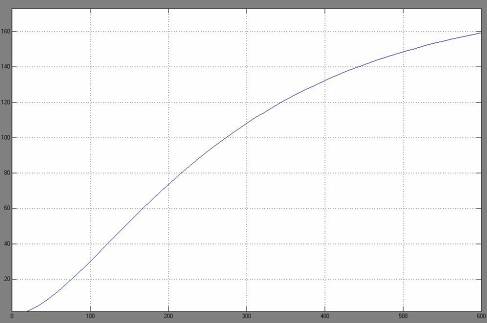
Рисунок 2.8 – График переходного процесса для звена второго порядка, рассчитанного с помощью метода площадей
2.6 Построение математической модели звена второго порядка методом Ротача
Проведем в точке перегиба касательную, для определения интервала времени Т>0>, заключенного между точками пересечения этой касательной оси абсцисс и линии установившегося значения h>∞> переходной характеристики:

Рисунок 2.9 – Нормированный переходный процесс
Таким образом, запишем величины, являющиеся входными данными:
T>0>=526 tп=90, y(tп)=0,09.
Введем обозначение:

Так как
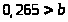 ,
то возможна аппроксимация инерционным
звеном второго порядка без запаздывания
(т.е. q=1, =0),
следовательно, получаем следующую
модель:
,
то возможна аппроксимация инерционным
звеном второго порядка без запаздывания
(т.е. q=1, =0),
следовательно, получаем следующую
модель:
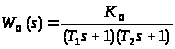
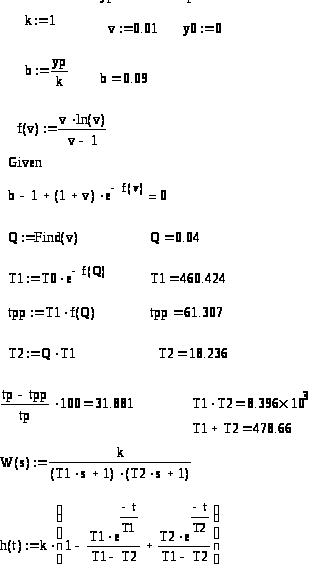
Таким образом, запишем модель звена второго порядка без запаздывания:
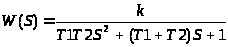 или
или
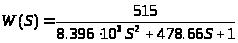
Теперь построим переходный процесс для данной передаточной функции.
w=tf([514.3],[8396 478.66 1]);
step(w, 600)
grid on
Результат представлен на рисунке 2.10.

Рисунок 2.10 – График переходного процесса для звена второго порядка, рассчитанного методом Ротача
2.7 Выбор наилучшей аппроксимирующей модели
Для выбора лучшей аппроксимирующей модели объекта управления среди найденных моделей сравним теоретические и экспериментальный переходные процессы. Для оценки качества полученных передаточных функций, описывающих объект управления, вычислим оценку χ2 по формуле:



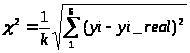
Проведенный расчет дает следующие результаты:
%Расчет погрешностей
k=514.3;
y_real=[24.44 60 93.33 125.5 154.44 180];
y1=[32 72 101 122 136 146];
y2=[31.1 73.3 106.67 131.11 148.89 160];
y3=[30 58.33 63.33 103.33 116.67 128.33];
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y1(i))^2;
end
x1=sqrt(tmp)/k
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y2(i))^2;
end
x2=sqrt(tmp)/k
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y3(i))^2;
end
x3=sqrt(tmp)/k
x1 =
0.0818
x2 =
0.0571
x3 =
0.1445
x>1> – соответствует оценке звена запаздывания; x>2> – соответствует апериодическому звену второго порядка, рассчитанному методом площадей; x>3> – соответствует апериодическому звену второго порядка, рассчитанному методом Ротача.
Так как наименьшая оценка χ2 получилась у апериодического звена второго порядка, рассчитанного интегральным методом, то это звено и возьмем в качестве модели нашей системы. Передаточная функция объекта управления имеет вид:

3 СИНТЕЗ РЕГУЛЯТОРА
3.1 Синтез регулятора методом ЛАЧХ
Для того чтобы система удовлетворяла
заданным требованиям по точности и
качеству (перерегулирование
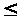 5 %, время регулирования t>P>
5 %, время регулирования t>P>
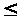 420 с, коэффициент статической ошибки С>0
>=> >0),
необходимо в систему, структурная схема
которой изображена на рисунке 3.1, ввести
регулятор.
420 с, коэффициент статической ошибки С>0
>=> >0),
необходимо в систему, структурная схема
которой изображена на рисунке 3.1, ввести
регулятор.

Рисунок 3.1 – Структурная схема замкнутой системы
Преобразуем структурную схему, представленную на рисунке 3.1, введем в систему регулятор как корректирующее звено последовательного типа:

Рисунок 3. 2 – Структурная схема замкнутой системы с регулятором
Найдем передаточную функцию неизменяемой части прямой цепи:

где W>ДТ>=k>Д >– передаточная функция датчика температуры Тд;
W>И>=k>И> – передаточная функция измерительного блока;
W>О> – передаточная функция объекта управления.
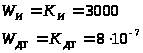
Передаточная функция прямой цепи (неизменяемой части системы):

Тогда коэффициент усиления неизменяемой части K:

Передаточная функция неизменяемой части прямой цепи будет иметь вид:

Передаточную функцию синтезируемого регулятора найдём методом логарифмических частотных характеристик. Для этого построим ЛАЧХ неизменяемой части прямой цепи исследуемой САУ:

Примем желаемую передаточную функцию в виде
 .
.
Желаемый коэффициент усиления определяется из соотношения:
 .
.
Kж=0,0186.
Передаточная функция регулятора:

Практически реализуемые регуляторы строятся с использованием следующих допущений и приближений: объект управления инерционен, и в цепях регулятора нет высокочастотных помех или они достаточно малы. Тогда высокочастотной частью регулятора можно пренебречь и считать, что T>3>=0. При этом желаемая ЛАЧХ рассчитывается из требования T>1>=T>2>, при желаемой ЛАЧХ в общем виде:
 .
.
Для определения параметров регулятора воспользуемся следующими соотношениями:
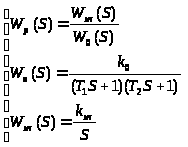
Тогда передаточная функция регулятора будет иметь следующий вид:
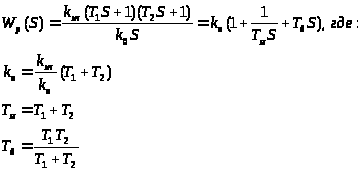
С учетом параметров объекта и звеном чистого запаздывания передаточная функция регулятора окончательно примет вид:
 .
.
Полученный регулятор является ПИ-регулятором с запаздыванием.
3.2 Переходная характеристика замкнутой системы
Модель построения переходной характеристики представим системе MatLab в виде передаточной функции.
Передаточная функция прямой цепи:
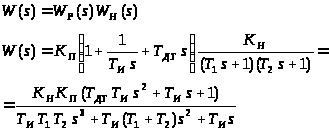
Получим передаточную функцию замкнутой системы:
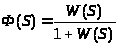

введем следующие обозначения:
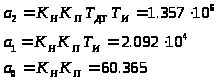
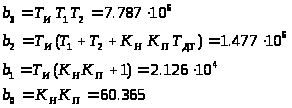
тогда передаточная функция замкнутой системы будет иметь следующий вид:

kp=4.67;
kn=1.23432;
Td=55.6;
Tu=309.8824;
T1=237.2624;
T2=72.62;
a1=kn*kp*Td*Tu
a1 =
9.9315e+004
a2=kn*kp*Tu
a2 =
1.7862e+003
b1=Tu*T1*T2
b1 =
5.3393e+006
b2=Tu*(T1+T2+kn*kp*Td)
b2 =
1.9534e+005
b3=Tu*(kn*kp+1)
b3 =
2.0961e+003
b4=kn*kp
b4 =
5.7643
a3=kn*kp
a3 =
5.7643
W=tf([a1 a2 a3],[b1 b2 b3 b4])
Transfer function:
9.932e004 s^2 + 1786 s + 5.764
----------------------------------------------
5.339e006 s^3 + 1.953e005 s^2 + 2096 s + 5.764
Переходный процесс для такой передаточной функции замкнутой системы представлен на рисунке 3.3.

Рисунок 3.3 – График переходного процесса замкнутой системы
Экспериментальные данные, полученные в ходе проверки спроектированного регулятора на стенде, представлены в приложении. График переходного процесса представлен на рисунке 3.4.
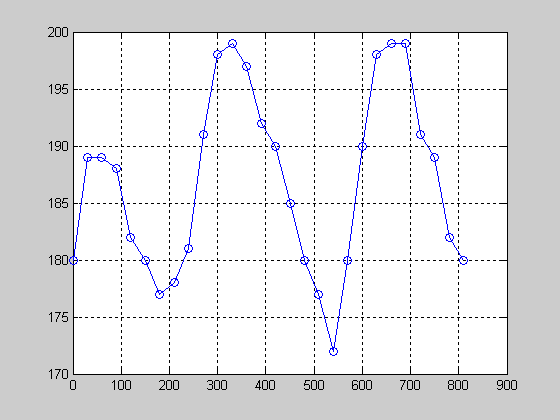
Рисунок 3.4 – График экспериментального переходного процесса замкнутой системы
Рабочая температура по варианту задания соответствует 180°C. Как видно из рисунка 3.4 все значения температуры лежат 10% коридоре, что является допустимым.
На рисунке 3.5 показан график поведения системы и установления температуры к заданному значению после действия на систему возмущения.
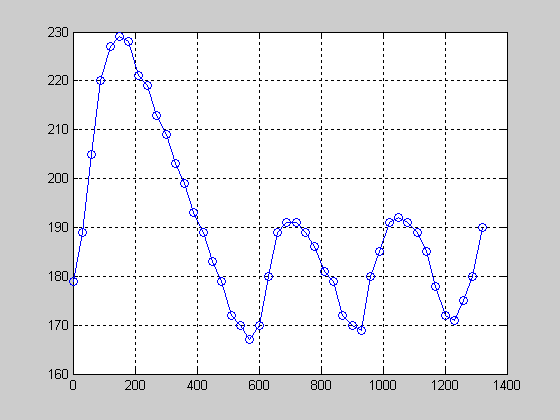
Рисунок 3.5 – График переходного процесса замкнутой системы при действии возмущающего воздействия
Из рисунка 3.5 видно, что система стабилизируется за 400 секунд, что соответствует требованиям технического задания.
ЗАКЛЮЧЕНИЕ
В ходе проектирования по экспериментальным данным была определена передаточная функция объекта. Передаточная функция определялась 3 различными способами. Причем одна передаточная функция была получена для апериодического звена первого порядка, два оставшихся метода позволяют определить параметры апериодического звена второго порядка. Именно такая передаточная функция наиболее точно описывает реальный объект.
По полученной передаточной функции был рассчитан ПИД-регулятор. Полученные параметры регулятора были, выставлены на стенде и проведены соответствующие экспериментальные исследования. Система оказалась устойчива, что подтверждает правильность расчета параметров регулятора. Соответствующие графики, иллюстрирующие поведение системы, приведены на рисунках 3.4 и 3.5.
Параметры синтезированного регулятора:
k>п> = 4.67
T>и> = 310
T>д> = 55.6
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М. "Наука",1975.
Ротач В.Я. Расчет динамики промышленных автоматических систем. М. "Энергия".1973.
ПРИЛОЖЕНИЕ А (ОБЯЗАТЕЛЬНОЕ)
Экспериментальные данные для получения передаточной функции объекта
|
t, с |
T, °C |
ε, В |
|
0 |
10 |
0.17 |
|
30 |
11 |
0.17 |
|
60 |
15 |
0.21 |
|
90 |
21 |
0.3 |
|
120 |
30 |
0.4 |
|
150 |
40 |
0.55 |
|
180 |
50 |
0.7 |
|
210 |
60 |
0.89 |
|
240 |
72 |
1.09 |
|
270 |
83 |
1.28 |
|
300 |
96 |
1.47 |
|
330 |
105 |
1.69 |
|
360 |
114 |
1.89 |
|
390 |
125 |
2.1 |
|
420 |
132 |
2.3 |
|
450 |
141 |
2.52 |
|
480 |
150 |
2.71 |
|
510 |
160 |
2.90 |
|
540 |
169 |
3.08 |
|
570 |
175 |
3.24 |
|
600 |
180 |
3.4 |
ПРИЛОЖЕНИЕ В (РЕКОМЕНДУЕМОЕ)
Листинг m-файла
clear; clc;
%Исходные данные: время t в секундах, температура T в градусах Цельсия и
%рассогласование E в вольтах:
t(1)=0;
for i=2:21
t(i)=t(i-1)+30;
end
T=[10 11 15 21 30 40 50 60 72 83 96 105 114 125 132 141 150 160 169 175 180];
E=[0.17 0.17 0.21 0.3 0.4 0.55 0.7 0.89 1.09 1.28 1.47 1.69 1.89 2.1 2.3 2.52 2.71 2.9 3.08 3.24 3.4];
%Построение экспериментальных точек
figure
plot(t, T, 'o');
grid on;
hold on;
%График экспериментального переходного процесса
%Регрессия 3-ого порядка
p3 = polyfit(t, T, 3);
ti = 0:0.01:600;
P3 = polyval(p3, ti);
plot(ti, P3);
%Нормирование исходных данных
Tfin = 180;
Tbegin = 10;
for i=1:21
Tnorm(i)=(T(i)-Tbegin)/(Tfin-Tbegin);
end;
%Нормированный график переходного процесса
figure
plot (t, Tnorm);
grid on;
%Построение звена второго порядка методом площадей
delta1 = 1 - Tnorm;
figure
plot(t, delta1);
grid on;
for i=1:21
delta2(i) = t(i) * delta1(i);
end
figure
plot(t, delta2);
grid on;
%Определение площадей
S1=trapz(t, delta1)
S2=trapz(t, delta2)
a1=S1;
if ((S2/(S1^2)) > 0.75)
a2=S1^2-S2
a1=S1
%Расчет постоянных времени
T1=a1/2+sqrt((a1^2)/4-a2)
T2=a1/2-sqrt((a1^2)/4-a2)
else
%Метод грубых площадей
%Найдем точку перегиба
t1=90:30:600;
delta_1=[0.9353
0.8824
0.8235
0.7647
0.7059
0.6353
0.5706
0.4941
0.4412
0.3882
0.3235
0.2824
0.2294
0.1765
0.1176
0.0647
0.0294
0];
k = 514.3;
delta_2=k*delta_1;
delta_2tn=0.9353*k;
In=trapz(t1,delta_2);
T1=In/delta_2tn
T2=a1-T1
T_1=T1*T2;
T_2=T1+T2;
%строим передаточную функцию и по ней переходный процесс для звена
%второго порядка
tf_reg=tf([k],[T_1 T_2 1])
figure
step(tf_reg, 600);
grid on;
end;