Расчет параметров гидропривода
Омский государственный технический университет
Кафедра «Авиа- и ракетостроения»
Курсовая работа
Выполнение расчетов по курсу «Гидропривод ЛА»
за II семестр 2005 учебного года
Омск 2005
Задача №1
Вентиляционная труба
диаметром
 имеет длину
имеет длину
 .
Определить давление
.
Определить давление
 ,
которое должен развивать вентилятор,
если расход воздуха, подаваемый по
трубе,
,
которое должен развивать вентилятор,
если расход воздуха, подаваемый по
трубе,
 .
Давление на выходе из трубы равно
атмосферному. Местных сопротивлений
по пути не имеется. Кинематическая
вязкость воздуха при
.
Давление на выходе из трубы равно
атмосферному. Местных сопротивлений
по пути не имеется. Кинематическая
вязкость воздуха при
 ,
плотность
,
плотность
 ,
шероховатость внутренней поверхности
трубы
,
шероховатость внутренней поверхности
трубы
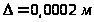 .
.
Исходные данные:
 .
.
Найти:
 .
.
Решение:
 -
давление на входе в вентиляционную
трубу.
-
давление на входе в вентиляционную
трубу.
 -
суммарные потери давления.
-
суммарные потери давления.
 – местных сопротивлений по пути
не имеется.
– местных сопротивлений по пути
не имеется.
 -
скорость течения.
-
скорость течения.
 -
потери давления на создание скорости.
-
потери давления на создание скорости.
 -
число Рейнольдса. При
-
число Рейнольдса. При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При
 ;
;
 – коэффициент трения.
– коэффициент трения.
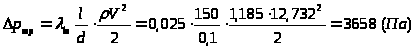 -
потери давления на трение.
-
потери давления на трение.
 .
.
Задача №2
Расход воды
 в горизонтальной трубе кольцевого
сечения, состоящей из двух концентрических
труб. Внутренняя труба имеет наружный
диаметр
в горизонтальной трубе кольцевого
сечения, состоящей из двух концентрических
труб. Внутренняя труба имеет наружный
диаметр
 ,
а наружная труба имеет внутренний
диаметр
,
а наружная труба имеет внутренний
диаметр
 .
Найти потери напора
.
Найти потери напора
 на трение на длине трубы
на трение на длине трубы
 .
Кинематическая вязкость воды при
.
Кинематическая вязкость воды при
 ,
шероховатость труб
,
шероховатость труб
 ,
плотность
,
плотность
 .
.
Исходные данные:
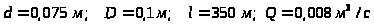 .
.
Найти:
 .
.
Решение:
 -
потери напора на трение.
-
потери напора на трение.
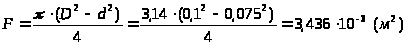 -
площадь проходного сечения.
-
площадь проходного сечения.
 .
.
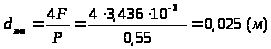 -
эквивалентный диаметр,
-
эквивалентный диаметр,
где
 -
смачиваемый периметр.
-
смачиваемый периметр.
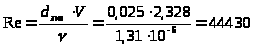 .
При
.
При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При
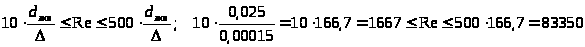 .
.
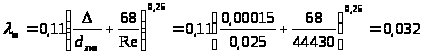 .
.
 -
потери давления на трение.
-
потери давления на трение.
 .
.
Задача №3
Определить потери
давления на трение в трубах круглого
 ,
квадратного
,
квадратного
 и треугольного
и треугольного
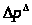 (равносторонний треугольник) сечения
при равных длине, площади «живого»
сечения труб и скоростях движения воды.
Длина труб
(равносторонний треугольник) сечения
при равных длине, площади «живого»
сечения труб и скоростях движения воды.
Длина труб
 ,
площадь «живого» сечения
,
площадь «живого» сечения
 ,
средняя скорость движения воды
,
средняя скорость движения воды
 .
кинематическая вязкость воды при
.
кинематическая вязкость воды при
 ,
плотность
,
плотность
 ,
шероховатость труб
,
шероховатость труб
 .
.
Исходные данные:
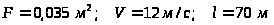 .
.
Найти:
 ,
,
 ,
,
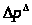 .
.
Решение:
Определим потери
давления на трение в трубах круглого
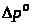 сечения.
сечения.
Площадь круглого
сечения
 .
.
 .
При
.
При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При

 .
.
 .
.
Определим потери
давления на трение в трубах квадратного
 сечения.
сечения.
Площадь квадратного
сечения
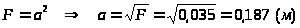 ,
,
где
 -
сторона квадрата.
-
сторона квадрата.
 .
.
где
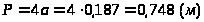 .
.
 .
При
.
При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При
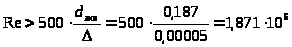
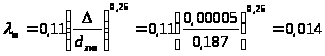
 .
.
Определим потери
давления на трение в трубах треугольного
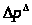 (равносторонний треугольник)
(равносторонний треугольник)
сечения.
Площадь треугольного
сечения
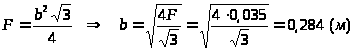 ,
,
где
 -
сторона треугольника.
-
сторона треугольника.
 .
.
где
 .
.
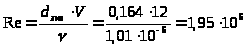 .
При
.
При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При


 .
.
Задача №4
Как изменится расход
мазута
 при подаче его по круглой трубе диаметром
при подаче его по круглой трубе диаметром
 ,
длиной
,
длиной
 ,
если потери давления в трубе составляют
,
если потери давления в трубе составляют
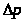 ,
а температура мазута составляет от
,
а температура мазута составляет от
 до
до
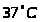 ?
Кинематическая вязкость мазута при
?
Кинематическая вязкость мазута при
 ,
при
,
при
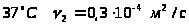 ,
плотность
,
плотность
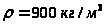 и изменяется незначительно, шероховатость
трубы
и изменяется незначительно, шероховатость
трубы
 .
.
Исходные данные:
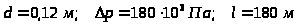 .
.
Найти:
 .
.
Решение:
При решении данной задачи не будем брать во внимание потери давления на создание скорости и считаем, что местных сопротивлений по пути не имеется:
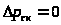 и
и
 .
.
Формула расхода
имеет вид:

1) Температура мазута
составляет
 .
.
Примем:
 .
.
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
2) Температура мазута
составляет
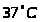 .
.
Примем:
 .
.
 .
При
.
При
 -
турбулентный режим течения.
-
турбулентный режим течения.
При
 ;
;
 .
.
 ;
;

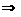
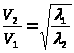 .
.
 -
при повышении температуры расход мазута
увеличился.
-
при повышении температуры расход мазута
увеличился.
Задача №5
Определить потери
давления
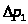 и
и в магистралях гидропередачи (рис. 1),
если расходы жидкости:
в магистралях гидропередачи (рис. 1),
если расходы жидкости:
 и
и
 ,
диаметры трубопроводов:
,
диаметры трубопроводов:
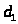 и
и
 ,
длины магистралей:
,
длины магистралей:
 и
и
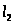 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
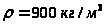 ,
кинематическая вязкость жидкости при
,
кинематическая вязкость жидкости при
 .
.

Исходные данные:
 .
.
Найти:
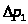 ;
;
 .
.
Решение:
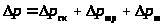 -
суммарные потери давления.
-
суммарные потери давления.
1) Определим
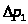 .
.
 -
скорость течения.
-
скорость течения.
 -
потери давления на создание скорости.
-
потери давления на создание скорости.
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
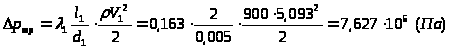 -
потери давления на трение.
-
потери давления на трение.
 ,
,
где
 -
для угла поворота, равного
-
для угла поворота, равного
 .
.
 .
.
2) Определим
 .
.
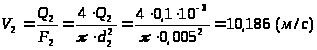 .
.
 -
потери давления на создание скорости.
-
потери давления на создание скорости.
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
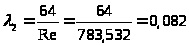 .
.
 -
потери давления на трение.
-
потери давления на трение.
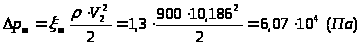 .
.
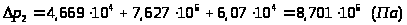 .
.
Задача №7
Определить потери
давления
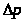 при внезапном расширении трубопровода
с
при внезапном расширении трубопровода
с
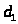 до
до
 ,
если скорость воды в подводящем
трубопроводе
,
если скорость воды в подводящем
трубопроводе
 ,
кинематическая вязкость при
,
кинематическая вязкость при
 ,
плотность
,
плотность
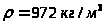 .
.
Исходные данные:
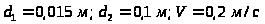 .
.
Найти:
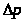 .
.
Решение:
 ,
,
где
 ;
;
 ;
;
 .
.
Подставляя данные
равенства в формулу для
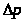 ,
получим:
,
получим:
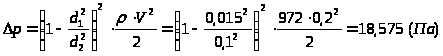 .
.
Задача №8
Для ограничения
расхода воды в водопроводной линии
установлена диафрагма. Избыточное
давление в трубе до и после диафрагмы
постоянны и равны соответственно
 и
и
 ,
диаметр трубы
,
диаметр трубы
 .
Определить необходимый диаметр отверстия
диафрагмы
.
Определить необходимый диаметр отверстия
диафрагмы
 с таким расчётом, чтобы расход в линии
был равен
с таким расчётом, чтобы расход в линии
был равен
 ,
если плотность воды при
,
если плотность воды при

 .
.
Исходные данные:
 .
.
Найти:
 .
.
Решение:
Формула расхода жидкости через диафрагму:
 ,
,
где
 -
коэффициент расхода:
-
коэффициент расхода:
 ;
;
 -
площадь проходного сечения:
-
площадь проходного сечения:
 ;
;
 -
перепад давлений.
-
перепад давлений.
Преобразовав, получим:

Задача №6
Определить расходы
воды в трубе прямоугольного поперечного
сечения
 с отношением сторон
с отношением сторон
 и в круглой трубе
и в круглой трубе
 при той же площади поперечного сечения
при той же площади поперечного сечения
 ,
если потери давления в этих трубопроводах
одинаковы и равны
,
если потери давления в этих трубопроводах
одинаковы и равны
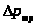 ,
а длина каждой трубы
,
а длина каждой трубы
 .
Кинематическая вязкость воды при
.
Кинематическая вязкость воды при
 ,
плотность
,
плотность
 .
.
Исходные данные:
 .
.
Найти:
 ,
,
 .
.
Решение:
Формула расхода
имеет вид:
 .
.
Определим стороны прямоугольной трубы:
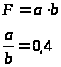
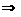
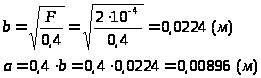
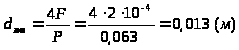 -
эквивалентный диаметр,
-
эквивалентный диаметр,
где
 .
.
Определим диаметр круглой трубы:
 .
.
Предположим, что режим течения ламинарный. Тогда
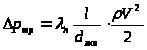 ,
где
,
где
 и
и
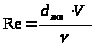 .
.
Откуда для прямоугольной трубы получаем:
 .
.
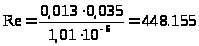 .
При
.
При
 -
ламинарный режим течения. Предположение
верно.
-
ламинарный режим течения. Предположение
верно.
 .
.
Для круглой трубы получаем:
 .
.
 .
При
.
При
 -
ламинарный режим течения. Предположение
верно.
-
ламинарный режим течения. Предположение
верно.
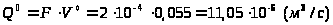 .
.
Задача №9
Определить теоретическую
 ,
полезную
,
полезную
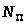 и приводную
и приводную
 мощности насоса и крутящий момент
мощности насоса и крутящий момент
 на его валу при расчётной подаче
на его валу при расчётной подаче
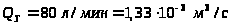 и числе оборотов
и числе оборотов
 ,
если давления на выходе насоса
,
если давления на выходе насоса
 и на входе
и на входе
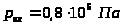 ;
объёмный КПД
;
объёмный КПД
 и механический КПД
и механический КПД
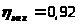 .
.
Решение:
 .
.
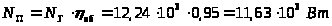 .
.
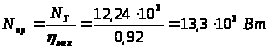 .
.
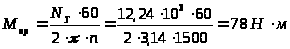 .
.
Задача №10
Определить эффективную
мощность
 и эффективный крутящий момент
и эффективный крутящий момент
 на валу гидромашины с указанными в
задаче №10 параметрами при работе её в
режиме гидромотора.
на валу гидромашины с указанными в
задаче №10 параметрами при работе её в
режиме гидромотора.
Решение:
 .
.

 .
.

Задача №11
Рассчитать усилие
 на
штоке гидроцилиндра и скорость
на
штоке гидроцилиндра и скорость
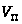 его перемещения при дроссельном
регулировании. Сечение регулирующего
дросселя
его перемещения при дроссельном
регулировании. Сечение регулирующего
дросселя
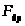 ;
давление в напорной магистрали
;
давление в напорной магистрали
 (объёмные
и механические потери и давление в
сливной магистрали не учитывать); рабочая
площадь поршня
(объёмные
и механические потери и давление в
сливной магистрали не учитывать); рабочая
площадь поршня
 ;
коэффициент расхода дросселя
;
коэффициент расхода дросселя
 ;
плотность жидкости
;
плотность жидкости
 .
.
Исходные данные:
 .
.
Найти:
 ,
,
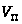 .
.
Решение:
 Полагаем, что
давление слива мало:
Полагаем, что
давление слива мало: .
.


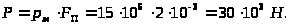
Задача №12
Рассчитать мощность
 ,
подводимую к гидроцилиндру потоком
жидкости с параметрами: нагрузка на
штоке
,
подводимую к гидроцилиндру потоком
жидкости с параметрами: нагрузка на
штоке
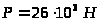 ,
скорость поршня
,
скорость поршня
 ,
рабочая площадь поршня
,
рабочая площадь поршня
 ,
сила трения в подвижных сочленениях
,
сила трения в подвижных сочленениях
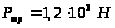 ,
коэффициент перетечек через уплотнение
поршня
,
коэффициент перетечек через уплотнение
поршня
 .
.
Решение:
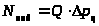 ;
;
 ;
;
Запишем условие равновесия поршня:
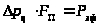 .
.
Отсюда
 ;
;
 ;
;
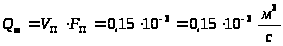 ;
;
 ;
;
 .
.
Задача №22
Определить давление
 на входе в силовой цилиндр. Нагрузка на
штоке
на входе в силовой цилиндр. Нагрузка на
штоке
 ,
скорость поршня
,
скорость поршня
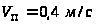 ,
диаметры поршня
,
диаметры поршня
 ,
штока
,
штока
 ,
трубопровода
,
трубопровода
 ,
длина трубопровода
,
длина трубопровода
 .
Плотность жидкости
.
Плотность жидкости
 ,
вязкость
,
вязкость
 .
.
Решение:
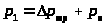 -
давление на выходе силового цилиндра.
-
давление на выходе силового цилиндра.
 -атмосферное
давление.
-атмосферное
давление.
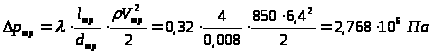 ,
,
где
 ;
;
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
Отсюда
 .
.
Запишем условие равновесия поршня:
 .
.
Отсюда
 .
.
Задача №23
Определить нагрузку
на штоке
 и скорость поршня
и скорость поршня
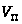 силового гидроцилиндра при перемещении
его вверх, если диаметры поршня
силового гидроцилиндра при перемещении
его вверх, если диаметры поршня
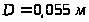 ,
штока
,
штока
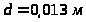 ,
трубопровода
,
трубопровода
 ,
длина трубопровода
,
длина трубопровода
 .
Давление на входе в гидроцилиндр
.
Давление на входе в гидроцилиндр
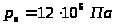 ,
производительность насоса
,
производительность насоса
 .
Плотность рабочей жидкости
.
Плотность рабочей жидкости
 ,
вязкость
,
вязкость
 .
.
Решение:
 .
.
 .
.
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
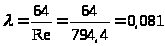 .
.
 .
.
 .
.
Запишем условие равновесия поршня:
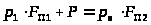 .
.
Отсюда

Задача №24
Определить давление,
создаваемое насосом
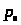 ,
и скорость поршня
,
и скорость поршня
 ,
если длина трубопроводов до и после
гидроцилиндра равна
,
если длина трубопроводов до и после
гидроцилиндра равна
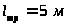 ,
их диаметры
,
их диаметры
 ,
диаметры поршня
,
диаметры поршня
 ,
штока
,
штока
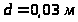 ,
нагрузка на штоке
,
нагрузка на штоке
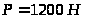 ,
подача насоса
,
подача насоса
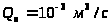 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
вязкость
,
вязкость
 .
.
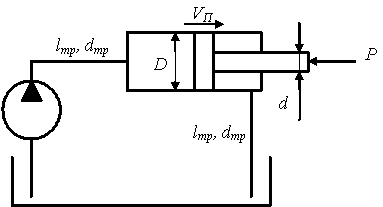
Решение:
 ;
;
Давление в гидроцилиндре:
 .
.
Уравнение расходов:
 .
.
Потери давления в трубопроводах:
 ;
;
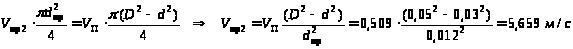
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
 .
.
 .
.
 .
.
 .
.
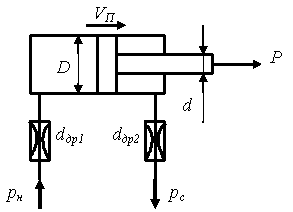
Задача №25
Определить скорость
поршня
 и
минимально допустимый диаметр
и
минимально допустимый диаметр
 дроссельной шайбы в напорной линии
гидропривода, обеспечивающий перемещение
поршня гидроцилиндра без кавитации.
Растягивающая нагрузка на штоке
дроссельной шайбы в напорной линии
гидропривода, обеспечивающий перемещение
поршня гидроцилиндра без кавитации.
Растягивающая нагрузка на штоке
 ,
давление насоса
,
давление насоса
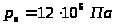 ,
слива
,
слива
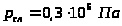 ,
насыщенных паров жидкости
,
насыщенных паров жидкости
 ,
диаметры дроссельной шайбы на сливе
,
диаметры дроссельной шайбы на сливе
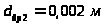 ,
поршня
,
поршня
 ,
штока
,
штока
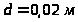 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
коэффициент расхода дроссельных шайб
,
коэффициент расхода дроссельных шайб
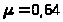 .
.
Решение:
Условие работы без кавитации:
 ;
;
 ;
;
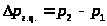 ;
;
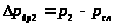 ;
;
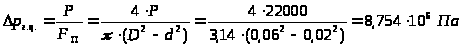 .
.
 .
.
Расход через второй дроссель равен:
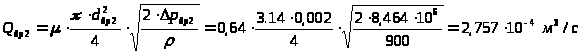 .
.
 .
.
 .
.
 .
.
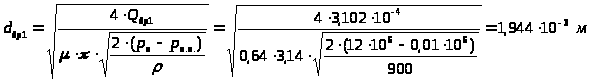 .
.
Задача №26
Пренебрегая
гидравлическими потерями в трубопроводах,
определить давление
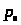 за насосом и скорость перемещения поршня
за насосом и скорость перемещения поршня
 .
Нагрузка на штоке
.
Нагрузка на штоке
 ,
диаметр поршня
,
диаметр поршня
 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
коэффициент расхода дроссельной шайбы
,
коэффициент расхода дроссельной шайбы
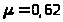 ,
площадь проходного сечения дросселя
,
площадь проходного сечения дросселя
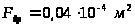 ,
подача насоса
,
подача насоса
 .
.

Решение:
Уравнение давлений:
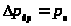 .
.
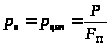 .
.
 .
.
Уравнение расходов:
 .
.
 .
.
 .
.
Скорость поршня:
 .
.
 .
.
Задача №27
Определить давление
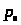 за насосом и диаметр дросселя
за насосом и диаметр дросселя
 для перемещения поршня со скоростью
для перемещения поршня со скоростью
 .
Нагрузка на штоке
.
Нагрузка на штоке
 ,
диаметры поршня
,
диаметры поршня
 ,
штока
,
штока
 ,
трубопроводов
,
трубопроводов
 ,
длины трубопроводов до и после
гидроцилиндра
,
длины трубопроводов до и после
гидроцилиндра
 и
и
 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
вязкость
,
вязкость
 ,
коэффициент расхода дроссельной шайбы
,
коэффициент расхода дроссельной шайбы
 ,
подача насоса
,
подача насоса
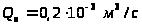 .
.

Решение:
 ;
;
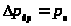 ;
;
Уравнение расходов:
 .
.
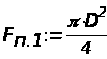

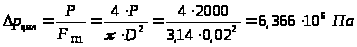 .
.
Из условий равенства расходов найдём:
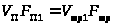 и
и
 ;
;
 ;
;

 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
 .
.
 .
.
 .
.
Находим давление насоса:
 .
.
 .
.
 .
.
 .
.
 .
.
Задача №28
Определить давление
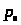 на входе в гидроцилиндр для перемещения
поршня вправо со скоростью
на входе в гидроцилиндр для перемещения
поршня вправо со скоростью
 .
Нагрузка на штоке
.
Нагрузка на штоке
 ,
диаметры поршня
,
диаметры поршня
 ,
штока
,
штока
 ,
дросселя
,
дросселя
 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
коэффициент местного сопротивления
дроссельной шайбы
,
коэффициент местного сопротивления
дроссельной шайбы
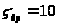 .
Другими местными сопротивлениями и
потерей давления на трение по длине
трубопроводов пренебречь.
.
Другими местными сопротивлениями и
потерей давления на трение по длине
трубопроводов пренебречь.

Решение:
Уравнение давлений:

 ;
;
 ;
;
Из условия равенства расходов имеем:
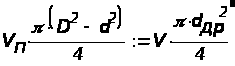
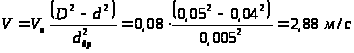 ;
;
Тогда:
 ;
;
Давление, создаваемое насосом:
 .
.
Задача №29
Определить коэффициент
местного сопротивления дроссельной
шайбы
 ,
пренебрегая другими местными
сопротивлениями, для перемещения поршня
вправо со скоростью
,
пренебрегая другими местными
сопротивлениями, для перемещения поршня
вправо со скоростью
 .
Нагрузка на штоке
.
Нагрузка на штоке
 ,
диаметры поршня
,
диаметры поршня
 ,
штока
,
штока
 ,
дросселя
,
дросселя
 ,
трубопроводов
,
трубопроводов
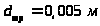 ,
длины трубопроводов до и после
гидроцилиндра
,
длины трубопроводов до и после
гидроцилиндра
 и
и
 ,
плотность рабочей жидкости
,
плотность рабочей жидкости
 ,
вязкость
,
вязкость
 ,
давление на входе в гидроцилиндр
,
давление на входе в гидроцилиндр
 .
.

Решение:
Уравнения давлений:
 ;
;
 .
.
 .
.
Из условий равенства расходов найдём:
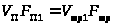 и
и
 ;
;
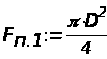

 ;
;
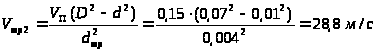 .
.
 .
При
.
При
 -
ламинарный режим течения.
-
ламинарный режим течения.
 .
.
 .
.
 .
.
 .
.
 .
.
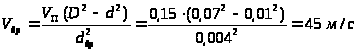 .
.
 .
.