Разработка электромеханического привода главного движения станка 1П756ДМ

Содержание

Введение

Техническое задание

1. Электропривод СТАНКА 1П756ДФ3

1.1 Кинематический анализ и выбор двигателя

1.1.1 Кинематический анализ

1.1.2 Выбор двигателя

1.2 Получение математической модели механики привода

1.2.1 Построение расчётной схемы привода

1.2.2 Расчёт моментов инерции деталей привода

1.2.3 Расчёт податливостей деталей привода

1.2.4Моделирование привода в пакете DYNAR

Техническое задание

2. РАЗРАБОТКА ПНЕВМАТИЧЕСКОГО ПРИВОДА ПЕРЕКЛЮЧЕНИЯ СКОРОСТЕЙ ШПИНДЕЛЯ СТАНКА 1П756ДФ3

2.1 Краткое описание пневмопривода и его работы

2. 2 Определение площади условного сечения регулирующей аппаратуры

2.3 Математическая модель механики привода

2.4 Математическая модель состояния газа в полости пневмоцилиндра

2.5 Разработка математической модели аэромеханики пневмопривода

2.6 Разработка схемы модели пневмопривода в приложении Simulink

2.7 Результаты моделирования и идентификация математической модели пневмопривода для САУ

Заключение

Список литературы

Введение

Автоматизированный электропривод играет в станкостроении и робототехнике исключительно важную роль. Его значение не ограничивается только преобразованием электрической энергии в механическую, хотя это одна из основных функций, выполняемых электроприводом в производственных машинах. Электропривод – это основной конструктивный элемент металлорежущего станка или робота.

Электропривод влияет на конструкцию станка и промышленного робота (ПР). Это влияние может проявляться непосредственно, поскольку конструкция любого узла станка зависит от конструкции и типа электродвигателя. Особое значение электропривод приобрёл на современном этапе развития машиностроения как основное звено автоматизации.

Техническое задание

В курсовой работе необходимо получить математическую модель механики привода в пакете SIMULINK, построить график АЧХ динамической податливости по углу в пакете DYNAR.

Исходные данные:

- обороты шпинделя n=1000 об/мин;

- момент инерции детали Jдет=0,025 кг*м²;

- диаметр детали Dдет=80 мм;

- сила резанья Pz=1500 Н;

- коэффициент перегрузки Kn=2,6;

- время разгона tраз=2,0 c;

1 ЭЛЕКТРОПРИВОД СТАНКА 1П756ДФ3

1.1 Кинематический анализ и выбор двигателя

1.1.1 Кинематический анализ и описание станка

На лицевой стороне консольной части станины станка крепится кронштейн, на котором установлена шпиндельная коробка. Привод монтируется на поворотной плите, которая болтами крепится к основанию станка. На кронштейне шарнирно установлен редуктор механизма привода главного движения, связанный с электродвигателем поликлиновой ременной передачей со шкивом. Вращение от выходного вала редуктора передается шпиндельной коробке через ременную передачу с двумя поликлиновыми ремнями. Натяжение ременной передачи осуществляется качанием корпуса редуктора на оси кронштейна с помощью гидроцилиндра.

Гидроцилиндр натяжения ремней подключен к гидросистеме по дифференциальной схеме: полости его соединены с полостями гидроцилиндра управления редуктором главного движения. Таким образом, усилие натяжения ремней – переменное и зависит от переключения диапазона частот вращения шпинделя. В первом диапазоне (до 630 или 800об/мин) оно равно 10 кН, а во втором диапазоне (до 2500 или 3150об/мин) – 4 кН. При включении гидросистемы пружина, встроенная в гидроцилиндр, создает предварительное усилие натяжения ремней, равное 1 кН.

Переключение диапазонов частот вращения шпинделя осуществляется гидроцилиндром. Шток гидроцилиндра связан с вилкой, перемещающей зубчатый блок и дополнительный венец с внутренними зубьями, который зацепляется с валом шестерней. Промежуточные зубчатые колеса и вместе с блоком обеспечивают дополнительную редукцию для получения 1-го диапазона частот вращения. Контроль переключения зубчатых передач редуктора осуществляют конечные выключатели.

Шпиндельная коробка станка выполнена в виде жесткого литого корпуса, в расточке которого смонтирован шпиндель на двух подшипниковых опорах и с предварительным натягом. В задней части шпинделя на шпонке установлен ведомый шкив поликлиновой ременной передачи. К торцу крепится шкив зубчато-ременной передачи привода датчика резьбонарезания, а также гидромеханизм привода зажимного патрона.

Базирование шпиндельной коробки на кронштейне , а кронштейна – на станине обеспечивает возможность регулирования положения оси шпинделя в горизонтальной и вертикальной плоскостях.

Определяем передаточное отношение между валом двигателя и валом передаточного механизма. Для этого по заданной скорости определяем передаточное отношение двигателя и добиваемся его реализации путем изменения числа зубьев в приводе, сохраняя при этом общее число зубьев в сумме.

На рисунке 1 приведена принципиальная кинематическая схема привода главного движения станка с учетом индивидуального задания, согласно которому общее передаточное отношение

.

Рисунок 1 – Кинематическая схема привода

1.1.2 Выбор двигателя

Для выбора двигателя воспользуемся следующим дифференциальным уравнением:

, (1.1)

где - суммарный момент инерции, приведённый к валу двигателя, ;

- номинальный момент двигателя, ;

- момент сил трения, .

Все вращающиеся части привода имеют момент инерции, который должен быть приведён к валу двигателя:

, (1.2)

тогда суммарный момент инерции:

(1.3)

Момент сил трения считается через КПД всего механизма:

, (1.4)

где - момент механики двигателя, ;

- КПД всего механизма, которое находят:

, (1.5)

где - КПД i – элемента механизма.

В механике участвуют следующие элементы:

- КПД зубчатой открытой передачи, ;

- КПД зубчатой закрытой передачи, ;

- КПД ремённой передачи, ;

- КПД пары подшипников, .

Рассчитаем КПД нашего механизма:

.

Решим наше дифференциальное уравнение:

, (1.6)

где - угловая скорость, рад/с, которую находим:

; (1.7)

- время разгона, с.

Определение приведённого момента сил трения

Обычно момент сил трения приводят к валу исполнительного двигателя. Он существенно зависит от нагрузки привода и незначительно от скорости:

, (1.8)

где - момент механики приведённый к валу двигателя, Н*м, который определяется из уравнения:

, (1.9)

где - функция, которая при нулевом смещении зависит только от z1, обычно ;

m – модуль зубчатого колеса, мм;

b – ширина зуба, мм;

z1 – число зубьев.

Найдём момент механики , Н*мм:

. (1.10)

Приведём момент механики к валу двигателя:

.

Рассчитаем номинальный момент двигателя из формулы (6):

. (1.11)

Окончательный выбор двигателя

Выберем наш двигатель из каталога по номинальному двигательному моменту с запасом и выпишем его технические данные.

Технические данные на двигатель фирмы Siemens 1GL5108-OWY40-6HU1

- номинальный момент Mн=28,301 Н*м;

- номинальная мощность Pн=4,5 кВт;

- номинальная скорость nн=1450, об/мин;

- КПД двигателя ;

- сопротивление якоря Rя=3,47, Ом;

- индуктивность якоря Lя=14,2 мГн;

- момент инерции двигателя J=0,021 кг*м².

1.2 Получение математической модели механики привода

1.2.1 Построение расчётной схемы привода

Для дальнейшего моделирования рассматриваемого привода необходимо произвести построение расчетной схемы его механической части для каждого вала.

Первый вал – вал ротора двигателя. Построение схемы начинается со статора двигателя, рассматриваемого как абсолютно жесткую, неподвижно закрепленную систему. Через податливость магнитного поля ротор двигателя с моментом инерции соединен со статором. Ротор через податливость призматической шпонки передает вращение шкиву с моментом инерции . Передача вращения на входной вал редуктора осуществляется ремнем с податливостью . Расчетная схема вала ротора двигателя приведена на рисунке 2.

Рисунок 2 – Расчетная схема вала ротора двигателя

Второй вал – входной вал коробки скоростей. Вращение на него передается ременной передачей с вала ротора электродвигателя. Первым элементом схемы является шкив с моментом инерции . Он через шпонку с податливостью соединен с участком вала с моментом инерции . Сечение на валу проводим посередине между насаженными шкивом и шестерней , податливость этого участка - . От участка вала через податливость шлица движение передается шестерне с моментом инерции , от которой движение переходит на третий вал привода (второй вал редуктора) через податливость зубчатой передачи . Расчетная схема входного вала коробки скоростей приведена на рисунке 3.

Рисунок 3 – Расчетная схема входного вала коробки скоростей

Третий вал – второй вал коробки скоростей привода. Движение к нему приходит с входного вала через зубчатую передачу . Блок через податливость шлица соединен с участком вала с моментом инерции . Сечение на валу проводим посередине между насаженными шкивом и шестерней , податливость этого участка - . Вал 3 с моментом инерции , через податливость шпоночного соединения сопряжен со шкивом, момент инерции которого . Передача вращения осуществляется ремнем с податливостью . Расчетная схема третьего вала привода приведена на рисунке 4.

Рисунок 4 – Расчетная схема третьего вала привода

Четвертый вал. Движение ему передается с третьего вала через ременную передачу . Первым элементом схемы является шкив с моментом инерции . Он через шпонку с податливостью соединен с участком вала с моментом инерции . Вал 4 с моментом инерции , через податливость сопряжен со деталью, момент инерции которой . Расчетная схема четвертого вала привода приведена на рисунке 5.

Рисунок 5 - Расчетная схема четвертого вала привода

Соединив вместе расчетные схемы всех валов привода, получим единую схему, приведенную на первом листе графической части работы. Число узловых точек расчетной схемы меньше двадцати, что позволяет, не упрощая схемы, воспользоваться программой DYNAR.

1.2.2 Расчёт моментов инерции деталей привода

Детали привода (валы, шестерни, зубчатые колёса) имеют цилиндрическую форму с некоторым количеством уступов. Для вычисления момента инерции i – детали , кг*м², используют формулу:

, (1.12)

где - плотность стали, 7800 кг/м³;

- длина i – детали, м;

- наружный и внутренний диаметры i – детали, м.

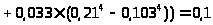
Найдём передаточные отношения, на валах приведённые к валу двигателя:

;

;

;

.

Найдём суммарный момент инерции..

.

1.2.3 Расчёт податливостей деталей привода

Крутильная податливость участка вала определяется по формуле:

, (1.13)

где G – модуль упругости второго рода, , Па;

D – наружный диаметр вала, м;

e – эквивалентная длина вала, м,

, (1.14)

где - расстояние между ступицами, м;

- ширина ступиц, м.

Коэффициент Kc для гладкого сплошного вала равен 1. Для полого Kc рассчитывается:

, (1.15)

где d – внутренний диаметр вала, м.

.

Крутильная податливость шлицевых и шпоночных соединений определяется по формуле:

, (1.16)

где e – длина соединения, м;

h – активная высота шпонки или шлица, м;

z – число шпонок или шлицов;

d – диаметр соединения, м.

Коэффициент - для шлицевого соединения равен рад/(Н*м), для шпоночного соединения равен рад/(Н*м).

.

Податливость зубчатой передачи определяется:

, (1.17)

где - крутильная податливость, учитывающая деформацию зубьев, определяется по формуле:

, (1.18)

где b – ширина венца зубчатого колеса, м;

R – радиус начальной окружности зубчатого колеса, расположенного на валу, к которому приводится податливость передачи, м;

- угол зацепления;

Kз – постоянный коэффициент, равный для прямозубых колёс , для косозубых м²/Н.

Податливость ремённой передачи определяется:

, (1.19)

где R – радиус ведущего шкива, м;

Eэф – эффективная длина ветви ремня, м;

F – площадь поперечного сечения ремня, м²;

E – модуль упругости ремня, , Па;

n – число ремней в передачи;

a – коэффициент, учитывающий влияние предварительного натяжения ремня;

, (1.20)

где e – межосевое расстояние передачи, м;

R1, R2 – радиусы шкивов, м.

.

Упростим нашу расчетную схему, запишем новые податливости и моменты инерции привода:

; ;

; ;

; ;

; ;

; ;

. .

При моделировании привода принять коэффициент рассеивания энергии :

- для стали ;

- для резины .

1.2.4 Моделирование привода в пакете DYNAR

Расчётная схема привода моделируется на ЭВМ в интерактивном режиме с помощью пакета прикладных программ DYNAR.

Ввод данных производится при помощи следующих таблиц:

Таблица 1 – Общие сведения

Количество узловых точек

6

Количество упругих элементов

6

Количество валов

4

Таблица 2 – Топология и параметры РС

№

Элем.

Узловые точки

№

Вала

Податл. элем.

[рад/Н*м]*1000

Относ. коэф.

рас. энергии

от

до

1

0

1

1

1,02000

0,20

2

1

2

2

0,40000

0,60

3

2

3

2

0,02400

0,20

4

3

4

3

0,00004

0,20

5

4

5

3

0,02200

0,20

6

5

6

4

0,23000

0,60

Таблица 3 – Инерционные характеристики

№ Узла

Момент инерции массы [кг*м²]

№ Вала

1

0,2770

1

2

0,1480

2

3

0,0009

2

4

0,0244

3

5

0,0335

3

6

0,6500

4

Таблица 4 – Передаточные отношения

№ Вала

D Ведущ. [мм]

D Ведом. [мм]

1

1,00

1,00

2

180,00

226,00

3

93,00

135,00

4

187,00

236,00

Результаты расчёта в пакете DYNAR:

1) Модальные параметры собственной частоты, коэффициенты и формы колебаний по углу

Таблица 5 - Модальные параметры собственной частоты

Динамическая податливость по углу

Таблица 6 – Таблица динамических податливостей по углу

Рисунок 6 – Амплитудно-частотная характеристика (АЧХ) динамической податливости по углу

Динамическая податливость по моменту

Таблица 7 - Таблица динамических податливостей по моменту

Рисунок 7 – Амплитудно-частотная характеристика (АЧХ) динамической податливости по моменту

Составим математическую модель механики привода в общем виде:

Рисунок 8 – Структурная схема механики привода в общем виде

где - собственная частота, Гц;

- коэффициент демпфирования;

- модальная податливость, которая находиться: при , где - амплитуда, Дб,

.

Составим математическую модель механики привода в SIMULINK:

Рисунок 9 - Математическая модель механики привода в SIMULINK

  1. РАЗРАБОТКА ПНЕВМАТИЧЕСКОГО ПРИВОДА ПЕРЕКЛЮЧЕНИЯ СКОРОСТЕЙ ШПИНДЕЛЯ СТАНКА 1740РФ3

2.1 Краткое описание пневмопривода и его работы

Пневматическая система станка содержит: узел подготовки воздуха; пневмопанели (основную и вспомогательные для устройств смены инструментального барабана и зажима патрона); пневмогидроразводку (воздушные трубопроводы, шланги для подачи СОЖ в рабочую зону, трубопроводы для дозированной смазки направляющих и ходовых винтов суппорта).

Воздух, очищенный фильтрами, поступает к распределителю, от которого направляется к револьверной головке, инструментальному барабану и маслораспределителю. От маслораспределителя через клапан наполнения воздух поступает к основной и дополнительным панелям. Клапан наполнения служит для плавного увеличения давления в пневмосистеме и состоит из ходового клапана, дросселя с обратным клапаном, ходового клапана с глушителем и реле давления. При срабатывании ходового клапана с глушителем пневмосистема станка соединяется с узлом подготовки воздуха через дроссель.

При достижении необходимого давления срабатывают реле давления и ходовой клапан, соединяющий напрямую пневмосистему с узлом подготовки воздуха. Время наполнения регулируется дросселем. От клапана наполнения воздух поступает к распределительной колодке, откуда по трубопроводам направляется к пневмопанелям.

Пневмопанели станка включают в себя ходовые клапаны для управления исполнительными пневмоцилиндрами или соплами для обдувки воздухом базовых поверхностей. Расход воздуха регулируется дросселями, установленными параллельно с ходовыми клапанами, клапаны могут оснащаться глушителями. Наличие давления в выходных магистралях клапанов контролирует реле давления.

2.2 Определение площади условного сечения регулирующей аппаратуры

В качестве управляющей аппаратуры для пневмоцилиндра принимаем пневмораспределитель. Принципиальная схема системы изображена на рисунке17, на котором обозначены: 1 – компрессор, питающий систему, 2 – пневмоцилиндер, 3 – пневмораспределитель. При расчете системы принимается движение из крайнего левого положения в крайнее правое. Для выбора управляющей аппаратуры необходимо рассчитать площади условного прохода преобразовательного устройства. Для этого воспользуемся уравнением гидродинамики движения воздуха по трубопроводам:

, (2.1)

В формуле 2.1обозначены:

Q – требуемый объемный расход воздуха в нормальных м3/с;

S>др> – условная площадь дросселя, м3;

μ – кинематическая вязкость воздуха, 0,73;

ρ – плотность воздуха, 1,29 кг/м3;

р>1>, р>2> – входное и выходное давление для полости, Па.

Входное давление р>1> для левой полости является абсолютным давлением питания системы:

р>1=> р>пит>=0,4МПа.

Примем установившееся значение скорости движения поршня V>x> равным 0,3 м/с. Значение давления в полости р>2> при этом будет 0,35 МПа.

Требуемые расход также можно найти по формуле:

, (2.2)

где S>ц> – площадь цилиндра, м3;

Р>атм> – атмосферное давление, 0,1 МПа.

Площадь цилиндра S>ц> определяется по формуле:

. (2.3)

Из формул 2.2 и 2.3 получим выражение для расчета условной площади дросселя S>др>:

, (2.4)

.

Рисунок 10 – Принципиальная схема управления пневмоцилиндром

2.3 Разработка математической модели механики пневмопривода

Математической моделью механики пневмопривода является дифференциальное уравнение, составленное по принципу Даламбера:

, (2.5)

где m - масса подвижной части, 50 кг;

К>ж.тр.> – коэффициент жидкостного трения поршня о цилиндр, (Н·м)/(м·с-1);

S>п> – площадь поршня, 0,015м2;

Р>1>, Р>2> – давление в левой и правой полостях соответственно, МПа;

F>с.тр.> – сила сухого трения в уплотнениях пневмоцилиндра, Н;

F>тех.> – технологическая сила – сила трения подвижной части привода о стальную поверхность, Н.

Коэффициент жидкостного трения поршня о цилиндр К>ж.тр> определяется по формуле:

, (2.6)

где .

.

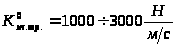Сила сухого трения в уплотнениях пневмоцилиндра F>с.тр> определяется по формуле:

, (2.7)

где d>шт> – диаметр штока, м;

.

Диаметр штока принимаем равным 20% от диаметра поршня:

.

По формуле 2.7 получаем:

.

Сила трения подвижной части привода о стальную поверхность F>тех. >находим из выражения:

, (2.8)

где k – кэффициент трения стали о стальную поверхность, 0,1;

m - масса подвижной части, 50 кг.

Находим F>тех.>:

.

Пусть , тогда уравнение 2.5 примет вид:

. (2.9)

Преобразовав по Лапласу выражение 2.9 имеем:

.

Получаем передаточную функцию механики привода W(s):

. (2.10)

Структурная схема S-модели механики пневмопривода изображена на рисунке 11.

Рисунок11 – S-модель механики пневмопривода

2.4 Разработка математической модели состояния воздуха в полостях пневмоцилиндра

Математическая модель состояния воздуха описывается адиабатой:

. (2.11)

где р – давление в полости, МПа;

V – объем полости, м3.

Принимаем произведение пропорциональным массе воздуха в полости:

. (2.12)

Для определения пропорциональности k берем 1м3 воздуха при атмосферном давлении. Тогда выражение 2.12 примет вид:

.

Следовательно:

.

Для разработки математической модели необходимо рассмотреть состояние воздуха в левой и правой полости.

Левая полость

Правая полость

,

где V>01> – начальный объем полости,

1,6956·10-4м3.

,

где V>02> – начальный объем полости,

24,6898·10-4м3.

С учетом уравнения массового расхода

,

масса воздуха определяется по формуле: .

.

.

На рисунках 12, 13 приведены S-модели состояния воздуха в левой и правой области соответственно.

Рисунок 12 – S-модель состояния воздуха в левой полости пневмопривода

Рисунок 13 – S-модель состояния воздуха в правой полости пневмопривода

2.5 Разработка математической модели аэромеханики пневмопривода

Математическая модель аэромеханики пневмопривода выражается уравнениями гидродинамики для двух полостей. Выражение 2.13 определяет массовый расход Q>m>>1> воздуха в левой полости, выражение 2.14 – массовый расход Q>m>>2> в правой полости.

. (2.13)

. (2.14)

Из выражений 2.13, 2.14 видно, что входной величиной для моделей аэромеханики воздуха в полостях пневмоцилиндра является давление в соответствующих областях, а выходной – массовый расход в соответствующих областях.

На рисунках 14, 15 приведены S-модели аэромеханики соответственно для левой и правой полости.

Рисунок 14 – S-модель аэромеханики в левой полости пневмопривода

Рисунок 15– S-модель аэромеханики в правой полости пневмопривода

2.6 Разработка схемы модели пневмопривода в приложении Simulink

Рассчитанные в пунктах 2.3, 2.4 и 2.5 данной работы модели для получения общей математической модели пневмопривода следует собрать в одну систему. При разработке модели всего привода пользуемся приложением Simulink пакета программ MATLAB.

На рисунке 23 приведена общая схема S-модели пневмопривода.

Рисунок 16 - Общая схема S-модели пневмопривода

2.7 Результаты моделирования и идентификация математической модели пневмопривода для САУ

Результаты моделирования представим в виде графиков.

На рисунке 17 приведен график зависимости перемещения поршня цилиндра от времени до достижения им крайнего правого положения (x=h=200мм).

На рисунке 18 показано изменение скорости поршня пневмоцилиндра за время движения к крайнему правому положению.

На рисунках 19, 20 отображена зависимость изменения величины давления воздуха соответственно в левой и правой полостях пневмоцилиндра.

На рисунках 21, 22 представлены графики расхода воздуха в левой и правой полостях цилиндра соответственно.

Рисунок 17 - График зависимости перемещения поршня от времени

Рисунок 18 - Изменение скорости поршня пневмоцилиндра

Рисунок 19- Зависимость изменения величины давления в левой полости

Рисунок20 - Зависимость изменения величины давления в правой полости

Рисунок 21 - График расхода воздуха в левой полости

Рисунок22 - График расхода воздуха в правой полости

Идентификацию пневмоцилиндра как объекта регулирования проводим по графику перемещения поршня.

Передаточную функцию цилиндра принимаем:

, (2.15)

Подбираем параметры К>об> и Т>об> так, чтобы полученная функция наиболее точно совпадала с графиком перемещения поршня, полученным при разработке математической модели пневмоцилиндра. Воспользуемся возможностью приложения Simulink создания подсистем для уменьшения визуального представления математической модели цилиндра. На рисунке 23 представлена S-модель идентификации математической модели пневмопривода для САУ.

Рисунок 23 - S-модель идентификации ММ пневмопривода

Окончательно передаточная функция цилиндра принимает вид:

.

На рисунке 24 показаны два графика математических моделей, рассчитанной и принятой в результате идентификации.

На рисунке 25 приведен график невязки двух рассматриваемых моделей. Из него следует, что полученная в результате идентификации модель может быть принята как передаточная функция объекта, так как разница между принятой и рассчитанной моделями не превышает 5% от максимального значение перемещения поршня x .

Рисунок 24 – Графики рассчитанной и принятой математических моделей

Рисунок 25 - график невязки двух рассматриваемых моделей

Для осуществления автоматического управления рассматриваемым пневмоприводом необходимо определить параметры датчиков, которые будут использованы в системе.

Для САУ пневмопривода требуются два датчика: перемещения и скорости, с коэффициентами усиления сигнала К>x> и К>x`> соответственно. Для их определения примем все управляющие аналоговые сигналы равными в диапазоне от –1 до +1В.

Коэффициент усиления датчика перемещения К>x> определим по формуле:

, (2.16)

.

, (2.17)

.

Заключение

В результате выполнения данной работы была проведена разработка электромеханического привода главного движения станка 1П756ДМ и пневматического привода переключения скоростей шпинделя станка 1740РФ3, были получены математические модели вышеперечисленных систем как объектов управления САУ, рассчитаны параметры датчиков, необходимых для осуществления автоматизированного управления.

Список использованных источников

  1. Металлорежущие станки /Под ред.В.Э.Пуша. --М.: Машинострое-ние, 1985.-468с.

  2. Коловский М.З. Динамика машин .- Л.: Машиностроение, 1989.- 288с.

  3. Решетов Д.Н., Портман В.Т. Точность металлорежущих станков.-М.: Машиностроение, 1986.-386с.

  4. Ривин Е.И. Динамика приводов станков. - М.: Машиностроение, 1966.- 203 с.

  5. Программа дисциплины и методические указания к выполнению курсовой работы по дисциплине "Технические средства автоматизации" для студентов специальности 2102 - Автоматизация технологических процессов и производств для студентов очной и заочной формы обучения/Кубан. гос. технол. ун-т. Сост.: Ю.Е. Кичкарь, Краснодар, 2005. - 47 с.