Проектирование траектории перемещения роботов

Федеральное агентство по образованию

Пермский Государственный Технический Университет

Реферат:

«ПРОЕКТИРОВАНИЕ ТРАЕКТОРИЙ ПЕРЕМЕЩЕНИЯ РОБОТОВ»

ВВЕДЕНИЕ

Мы изучили, каким образом можно описать задачу робототехнического манипулирования при помощи однородных преобразований; теперь нужно рассмотреть методы проектирования траекторий перемещения робота.

Рис. 4.7.1. Робот, размещающий МОП-пластины. (С разрешения PRI.)

Нужно описать желаемые движения манипуляционных роботов либо в пространстве обобщенных координат, либо в трехмерном рабочем пространстве, либо в координатах схвата в зависимости от того, интересуют ли нас зависимости от времени положения, ориентации, линейной скорости, угловой скорости, линейного ускорения и углового ускорения (рис. 4.7.1).

С точки зрения интересов человека-оператора робототехническая система должна быть способна позаботиться о деталях траектории движения, как только введены преобразования, описывающие задачу. Например, оператор может просто ввести желаемое кинематическое положение схвата робота для манипулирования объектом и предоставить системе управления роботом планировать форму траектории перемещения и такие детали, как профили изменения скорости и ускорения. Это определенным образом связано с так называемым программированием на уровне задачи, которое будет рассмотрено и гл. 9. Мы же обратимся к вопросу о том, каким образом траектории перемещения роботов интерпретируются управляющей ЭВМ и каким образом управляющая ЭВМ в действительности строит такие траектории и выдает команды роботу на выполнение желаемых задач. Цифровой природой управляющей ЭВМ обусловлено то, что генерация траекторий осуществляется дискретным образом. Так, генерация каждой дискретной точки на траектории движения происходит за так называемое время просчета траектории. Точки могут генерироваться с частотой 10—300 Гц в зависимости от того, какая частота вычисления точек траектории может быть достигнута на управляющей ЭВМ. Задача состоит в том, чтобы переместить схват робота из начального кинематического положения Н(0) в заданное кинематическое положение H(t) за время t. Естественным представляется описать движение гораздо более детально, чем определить лишь начальную и конечную точки, с тем чтобы избежать столкновений с предметами, находящимися в рабочей области. Таким образом, определяются промежуточные точки, в которых должно быть найдено кинематическое положение схвата робота. Для более подробно описанных траекторий должны быть определены значения обобщенной скорости и обобщенного ускорения. Очевидно, чтобы получить изменяющееся во времени кинематическое положение схвата робота Н(t), необходимо прибегнуть к множеству изменяющихся во времени углов в сочленениях, или, иначе, к зависящему от времени вектору углов в сочленениях Q(t), такому, что

(4.7.1)

где (t) - не что иное, как зависящее от времени решение об- ратной задачи кинематики с начальным Н(0) и конечным Н(t) кинематическими положениями схвата робота.

Далее мы опишем множество способов, применяемых для планирования и генерации желаемых векторов углов в сочленениях манипулятора.

КУБИЧЕСКИЕ ЗАКОНЫ ИЗМЕНЕНИЯ УГЛОВ В СОЧЛЕНЕНИЯХ

Простейший и наиболее часто используемый способ определения закона изменения угла в сочленении >i>(t) - это определение начального и конечного значений >i>(t) и >i>(t), которые обычно принимают следующие значения:

>i>(0) = >i0 >(4.7.2)

>i>(t>f>) = >if> (4.7.3)

>i>(0) = 0 (4.7.4)

>i>(t>f>) = 0 (4.7.5)

где t>f> — конечный момент времени, а к схвату робота предъявляется требование, чтобы он находился в состоянии покоя в начальный момент времени t=0 и достигал состояния покоя в момент времени t = t.

Условиям (4.7.2) — (4.7.5) могут удовлетворить многочлены третьей степени от времени, т. е.

>i>(t)= >i0> + a>1i>t + a>2i>t2 + a>3i>t3, (4.7.6)

такие, что

>if> = >i0> + a>1i>t>f> + a>2i>t2>f> + a>3i>t3>f>, (4.7.7) 0 = a>1i>, (4.7.8)

0 = 2a>2i>t>f> + 3a>3i>t>f>, (4.7.9)

откуда a>2i> и a>3i> получаются равными

a>2i> = 3(if - >i0 >) t -2>f>, (4.7.10)

a>3>>i> = 2(if - >i>>0 >) t -3>f>. (4.7.11)

Если начальная и конечная скорости не равны нулю, как в ситуации с роботом, отслеживающим движение конвейера, коэффициенты полинома получаются из условий выполнения следующих ограничений:

>i>(0) = >i>>0> , (4.7.12)

>i>(t>f>) =>if>. (4.7.13)

После этого легко определить коэффициенты в формуле (4.7.6):

a>ix> = >i0> , (4.7.14)

a>2i> = 3(if - >i0 >) t -2>f> - >i0> t>f> -1 - >if> t>f> -1 (4.7.15)

a>3i> = 2(if - >i0 >) t -3>f> + (>i0> + >if>), (4.7.16)

Заметим, что соотношения (4.7.14) — (4.7.16) носят достаточно общий характер, чтобы быть применимыми к любой промежуточной точке между начальной и конечной точками траектории. Однако вследствие требования непрерывности положения, скорости и ускорения решение уравнений относительно коэффициентов становится более сложным.

Пример 4.7.1

Найдите коэффициенты для двух кубических законов изменения углов в сочленениях, приняв равными продолжительности прохождения по обоим участкам траектории. Решение. Заметим, что в этом случае для первого и второго участков траектории движения

>1>(t)= a>10> + a>11>t + a>12>t2 + a>13>t3, (4.7.17)

>2>(t)= a>20> + a>21>t + a>22>t2 + a>23>t3. (4.7.18)

Ограничения имеют вид

>1>(0) = >10>, >2>(0)=>1>(t>f>>1>); (4.7.19) >1>(t)=>10>, >2>(0)=>1>(t>f>>1>); (4.7.20)

>2>(t>f>>2>)=>2>>f>, >2>(t>f>>2>)=>2>>f>; (4.7.21)

>1>(0) = >10>, >2>(0)= >1>(t>f>>1>); (4.7.22)

Из приведенных восьми формул могут быть найдены восемь коэффициентов a>10>, a>11>, a>12>, a>13>, a>20>, a>21>, a>22>, и a>23> (см.домашнее задание 6)

Рис. 4.7.5. Сложное движение манипулятора.

ОБЩИЕ АСПЕКТЫ ПЛАНИРОВАНИЯ ТРАЕКТОРИЙ

Вообще говоря, при планировании траектории робота нужно учитывать следующие обстоятельства.

1. Когда схват поднимает предмет, его движение должно быть направлено от опорной поверхности, чтобы избежать столкновения с ней.

2. Конечная точка подъема предмета должна лежать на нормали к поверхности, а начало системы координат схвата должно пройти через эту точку. Таким образом, будет обеспечено допустимое движение схвата. Контроль за скоростью, с которой должен подниматься предмет, может осуществляться путем слежения за временем, требуемым для перехода в эту точку.

3. Расстояние от конечной точки подъема до опорной поверхности рекомендуется выбирать равным не меньше 25 % длины последнего звена робота (0.25d>6> + длина инструмента) (рис. 4.8.1).

4. Требования 1 - 3 относятся и к начальной точке спуска, т. е. схват должен перемещаться в направлении, перпендикулярном поверхности, и замедляться при подходе к опорной поверхности.

5. Из приведенных выше соображений следует, что на каждой траектории робота имеются четыре типа точек - начальная точка, конечная точка подъема, начальная точка спуска, конечная точка (рис. 4.8.2).

Таким образом, на процесс планирования траектории можно наложить следующие ограничения.

1. Начальное положение фиксировано.

2. Начальная скорость обычно равна нулю.

3. Начальное ускорение обычно равно нулю.

4. Конечное положение фиксировано.

5. Конечная скорость обычно равна нулю.

6. Конечное ускорение обычно равно нулю.

7. Конечная точка подъема должна находиться от опорной поверхности на расстоянии 0.25 d>6> + длина инструмента.

8. Начальная точка спуска должна находиться от опорной поверхности на расстоянии 0.25 d>6> + длина инструмента.

Рис. 4.8.1. Рекомендуемая конечная точка подъема.

Рис. 4.8.2. Типичная траектория движения i-го сочленения.

К перечисленным выше ограничениям можно также добавить, ограничения на скорость и ускорение в промежуточных положениях, т. е. в точках подъема и спуска. Однако, опустив эти ограничения, мы будем иметь восемь ограничений, которые можно было бы удовлетворить полиномом с неизвестными коэффициентами не менее чем седьмой степени. Так, для любого угла в сочленении >i>> >можно записать

>i>(t) =a>ni> tn, (4.8.1)

где a>ni> - элементы матрицы размера 8 x i.

Так как это выражение - полином седьмой степени, возможно, он будет иметь значительное число экстремумов (максимумов и минимумов), что было бы нежелательно для траекторий перемещения роботов. Кроме того, вычисление всех неизвестных коэффициентов может занять много времени (если i = 6,имеем 48 коэффициентов).

Ограничения, относящиеся к траекториям сочленений

Описание ограничения

Уравнения ограничения

1

2

3

4

5

6

7

8

9

10

11

12

13

14

Начальное положение схвата

Начальная скорость робота

Начальное ускорение робота

Конечное положение робота при захвате

Непрерывность по положению в момент t>1>

Непрерывность по скорости в момент t>1>

Непрерывность по ускорению в момент t>1>

Начальное положение робота при установке

Непрерывность по положению в момент t>2>

Непрерывность по скорости в момент t>2>

Непрерывность по ускорению в момент t>2>

Конечное положение робота

Конечная скорость робота

Конечное ускорение робота

>i>(t>0>) = *>i0>

>i>(t>0>) = *>i0>

>i>(t>0>) = *>i0>

>i>(t>1>) = *>i1>

>i>(t>1>-) = >i>(t>1>+)

>i>(t>1>-) = >i>(t>1>+)

>i>(t>1>-) = >i>(t>1>+)

>i>(t>2>) = *>i2>

>i>(t>2>-) = >i>(t>2>+)

>i>(t>2>-) = >i>(t>2>+)

>i>(t>2>-) = >i>(t>2>+)

>i>(t>3>) = *>i3>

>i>(t>3>) = *>i3>

>i>(t>3>) = *>i3>

Рис. 4.8.3. Применение робота в лазерной резке.

Нужно также найти экстремальные значения на траектории перемещения робота с тем, чтобы убедиться, что эти экстремумы не выходят за рабочую поверхность. Таким образом, желательно прибегнуть к полиномам низких степеней путем деления траектории на участки, для которых вычисления выполняются сравнительно легко. Преимуществом таких полиномов низких степеней является то, что для них легче вычислить неизвестные коэффициенты и найти корни их производных при вычислении экстремумов.

Все такие разделенные на участки траектории должны быть непрерывны по положению, скорости и ускорению для достижения плавности движений робота. Для того чтобы это выполнялось, значения перечисленных параметров должны совладать на пересечениях участков.

Приняв во внимание все подобные ограничения, приходим, в конце концов к 14 ограничениям для вычисления неизвестных коэффициентов в точках пересечения трех участков траектории, т. е. траектории типа 4—3—4 и 3—5—3. Три участка начальный, промежуточный и конечный. В табл. 4.8.1 указаны 14 ограничений, относящихся к траекториям, разделенным на участки (рис. 4.8.3).

Чтобы полностью определить три полинома низкой степени при наложении приведенных выше 14 ограничений, сумма показателей степеней переменной t должна быть 14—3, потому что для этих трех различных полиномов имеются три свободных константы. Другими словами, должно быть 14 неизвестных, являющихся коэффициентами полиномов. Три из них являются свободными, так как оyи не умножаются на t. Таким образом, из-за того что полином m-й степени от t должен иметь m+1 коэффициентов, сумма степеней этих полиномов, относящихся к трем участкам, должна быть равна, по меньшей мере 11. Существует множество способов удовлетворить этому условию, в частности 4+3+4, 3+5+3 или 5+2+4. Рассмотрим подробнее некоторые из этих траекторий.

ТРАЕКТОРИЯ ТИПА 4 — 3 — 4

Для трех участков траектории перемещения, а именно: подъем, промежуточный участок и спуск, существуют полиномы четвертой, третьей и четвертой степеней, которые могут до- вольно хорошо аппроксимировать их. Для поиска решения на каждом из участков удобно ввести безразмерную переменную времени τ, такую, что

τ = и τ>m> = t>m>> >- t>m>>-1>

где индексы m и m-1 относятся к m-му и (m—1)-му участкам траектории движения робота. Таким образом, при движении по m-му участку траектории безразмерное время τ изменяется от 0 до 1, тогда как реальное время меняется от t>m>>-1> до t>m>. Введение соотношений (4.8.2) значительно упростит выкладки.

Участок 1: Полином четвертой степени. Пусть ρ>mi>(τ) является полиномиальным представлением m-го участка траектории движения для i-го сочленения. Тогда

ρ>1>>i>(τ) = 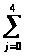C>1>>j> τj = C>10> + C>11> τ + C>12> τ2 + C>13> τ3 + C>14> τ4, (4.8.3)

τ>1>>1>>i>(τ) = 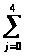jC>1>>j> τj-1 = C>11> + 2C>12> τ + 3C>13> τ2 +4 C>14> τ3 , (4.8.4)

τ2>1>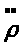>1>>i>(τ) = 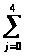j(j-1)C>1>>j> τj-2 = 2C>12> + 6C>13> τ +12 C>14> τ2. (4.8.5)

Заметим, что эти полиномы должны удовлетворять ограничениям, приведенным в табл. 4.8.1. Таким образом,

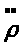ρ>1>>i>(0) = *>i>>0>, >i>(0) = *>i>>0>, >i>(0) = *>i>>0>. (4.8.6)

Налагая приведенные ограничения на (4.8.3), (4.8.4) и (4.8.5), получим

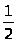
ρ>1i>(τ) = C>14> τ4+ C>13> τ3 +*>i0>τ2>1> τ2 + *>i0 >τ>1> τ + *>i0>. (4.8.7)

Пример 4.8.1

Определить закон движения схвата при подъеме.

Решение. Искомая зависимость относится к углу 9е и, следовательно, нужно положить i = 6 в (4.8.7). Таким образом,

ρ>1>>i>(τ) = C>14> τ4+ C>13> τ3 +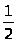*>i>>0>τ2>1> τ2 + *>i>>0 >τ>1> τ + *>i>>0> . (4.8.8)

Заметим, что в (4.8.7) имеются две неизвестные величины, которые нужно найти, — C>14> и C>13> ; они определяются из условий непрерывности:

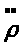>1i>(1) = >2i>(0), >1i>(1) = >2i>(0), >1i>(1) = 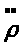>2i>(0). (4.8.9)

Итак, нужно сначала вычислить >2i>(τ).

Участок 2: Полином третьей степени. Используя подход, примененный для участка 1, получаем

>2i>(τ) = C>2j> τj = C>20> + C>21> τ + C>22> τ2 + C>23> τ3, (4.8.10)

τ>2>>2i>(τ) = jC>2j> τj-1 = C>21> + 2C>22> τ + 3C>23> τ2, (4.8.11)

τ2>2>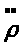>2i>(τ) = j(j-1)C>2j> τj-2 = 2C>22> + 6C>23> τ. (4.8.12)

Эти величины должны удовлетворять следующим условиям:

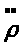>2>>i>(0) = *>i>>1>, >2>>i>(0) = *>i>>1>, >2>>i>(0) = *>i>>1>. (4.8. 13)

Соотношения (4.8.2) и (4.8.9) определяют некоторые из неизвестных коэффициентов. Имеем

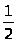
C>20> = *>i>>0>, C>21> = *>i>>1 >τ>2>, C>22> =*>i>>1>τ2>2> , (4.8.14)

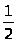
C>14> + C>13> =*>i1> - (*>i0> + *>i0 >τ>1> + *>i0>τ2>1>), (4.8.15)

4τ>1>-1C>14> + 3τ-1C>13> + τ>2>-1C>21> = - (*>i0> + τ >1>*>i0>), (4.8.16)

6τ>1>-2C>13> + 12τ-2C>14> - 2τ>2>-2C>22> = - *>i>>0>. (4.8.17)

В конце второго участка мы, однако, должны обеспечить выполнение условий непрерывности, т. е.

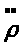>2>>i>(1) = >3>>i>(0), >1>>i>(1) = >3>>i>(0), >2>>i>(1) = 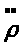>3>>i>(0). (4.8.18)

Таким образом, чтобы вычислить дополнительные коэффициенты, нужно найти полином для третьего участка.

Участок 3: Полином четвертой степени. По аналогии с подходами, использованными для участков 1 и 2, имеем

>3i>(τ) = 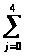C>3j> τj = C>30> + C>31> τ + C>32> τ2 + C>33> τ3 + C>34> τ4, (4.8.10)

τ>3>>3i>(τ) = 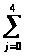jC>3j> τj-1 = C>31> + 2C>32> τ + 3C>33> τ2 + 4C>34> τ3, (4.8.11)

τ2>3>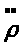>3i>(τ) = 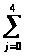j(j-1)C>3j> τj-2 = 2C>32> + 6C>33> τ + 12C>34>τ2. (4.8.12)

Начальные условия имеют вид

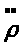>3>>i>(0) = *>i>>2>, >3>>i>(0) = *>i>>2>, >3>>i>(0) = *>i>>2>, (4.8.22)

которые в сочетании с формулами (4.8.8) - (4.8.10) дают

C>30> = *>i>>1>, C>31> = *>i>>1> τ>3>, C>32> = *>i>>1> τ2>3>.

Соотношения непрерывности (4. 8.18) дают теперь

C>20> + C>21> + C>22> = *>i>>2> - *>i>>1>, (4.8.24)

τ>2>-1C>21> + 2τ>2>-1C>22> + 3τ>2>-1C>23> - τ>3>-1C>31> = 0, (4.8.25) 2τ>2>-2C>22> + 6τ>2>-2C>23> - 2τ>3>-2C>32> = 0, (4.8.26)

Наконец, на конце участка должны выполняться ограничения:

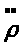>3>>i>(1) = *>if>, >3>>i>(1) = *>if>, >3>>i>(1) = *>if>, (4.8.27)

Используя соотношения (4.8.27) и (4. 8.19) — (4.8.21), получаем

C>31> + C>32> + C>33> + C>34> = *>if> - *>i2>, (4.8.28)

C>31> + 2C>32> + 2C>33> + 4C>34> =*>if>τ>3>, (4.8.29) 2C>32> + 6C>33> + 12C>34> = *>if>τ2>3,> (4.8.31)

Отметим, что, так как в общем случае *>i>>1> , *>i>>1> , *>i>>2> и *>i>>2> неизвестны, мы определили в явном виде только пять из 14 неизвестных коэффициентов, которыми являются C>10>, C>11>, C>12>, C>13>, C>14>, C>20>, C>21>, C>22>, C>23>, C>30>, C>31>, C>33> и C>34>. Известные коэффициенты – это

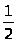
(C>10>, C>11>, C>12>, C>20>, C>30>) ≡ (*>i>>0>, *>i>>0 >τ>1>, *>i>>0>τ2>1>,*>i>>1>,*>i>>2>).(4.8.31)

Остальные девять уравнений (4.8.15) - (4.8,17), (4.8.24) - (4.8.26) и (4.8.28) — (4.8.30) могут быть представлены в матричной форме, а именно

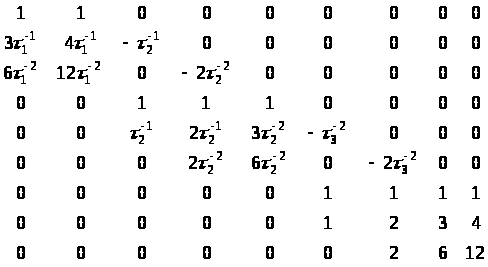Х =

= (4.8.32)

Представляя для простоты уравнение (4.8.32) в компактной форме, получаем

ВС = δ, (4.8.33)

где В — 9Х9-матрица коэффициентов С, а δ — некоторый век- торный массив, относящийся к изменениям углов в сочленениях и их производных по времени, как показано в (4.8.32). Полное решение для С (остальные девять коэффициентов, которые нужно найти) имеет вид

С = В-1 δ (4.8.33)

Пример 4.8.2

Найти полные решения в явной форме для трех полиномов >1>(τ), >2>(τ) и >3>(τ)

Решение. Можно показать, что выражения для коэффициентов C>13>, C>14>, C>21>, C>22>, C>23>, C>31>, C>33> и C>34> имеют вид (см. положение А)

C>13> = (τ>2>-1τ>3> + 2τ>1>-1 τ>3 >+ 2 + 3τ>1>-1 τ>2>)-1 × {2 δ>1>*(4 + 2 τ>2>-1τ>3> + 2τ>1>-1 τ>3 >+ 3τ>1>-1 τ>2>) – δ>2>* τ>2>-1 τ>1>(3 + τ>2>-1τ>3>) + 2δ>1>

ТРАЕКТОРИЯ ТИПА 3 — 5 — 3

Используя ту же процедуру, что и при выводе соотношений (4.8.41) — (4.8.47), легко показать, что для трех участков траектории можно получить следующие выражения, описывающие движение сочленений:

- для первого участка,

-

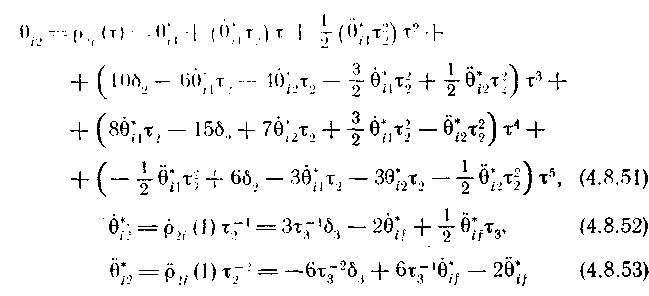для второго участка и

ДОПУСТИМЫЕ ТРАЕКТОРИИ ДВИЖЕНИЯ

На траектории типа 4 — 3 — 4 и 3 — 5 — 3, которые были представлены в предыдущих двух разделах в виде полиномов ρ>1>>i>, ρ>2>>i> и ρ>3>>i>, в действительности налагаются геометрические или какие-либо другие ограничения, например недопустимость прохождения через любые недостижимые точки в пространстве обобщенных координат. Если робот, перемещающийся по траектории, сталкивается с препятствием, он может остановиться, начать потреблять значительный ток, который может сжечь плавкие предохранители, транзисторы и другие электронные компоненты. Длительное пребывание в заторможенном состоянии может закончиться серьезным повреждением в двигателях, их приводных электрических цепях и устройстве управления. Нет необходимости говорить о том, что это также может серьезно повредить или деформировать звенья робота.

Рассмотрим траекторию типа 4—3—4 и проверим ее на недопустимые точки. Все, что надо сделать, — это найти экстремум для каждого полинома и удостовериться, что этот экстремум не выходит за допустимую рабочую область. Итак, нужно проверить значения

ρ>im>В>1>), ρ>im>В>2>), ρ>im>В>k>)

где В>k>, k = 1, 2, …, n, - это n действительных корней производной ρ>im>> >по времени τ. Так как для траектории типа 4—3—4 наивысшая степень полинома — это четвертая степень, то отсюда следует, что имеется максимально три локальных экстремума. Здесь мы имеем дело с уравнением вида

τ 3 + α>1> τ2 + α>2> τ + α>3> = 0, (4.9.1)

для которого надо найти корни. Если экстремум полинома ρ>i>>1> или ρ>i>>3> лежит вне границы допустимой области, простейшим решением будет сместить конечную точку подъема и начальную точку спуска, пока соответствующий участок целиком не будет лежать внутри рабочего пространства. Участком, доставляющим наибольшие трудности и приводящим к выходу за границы рабочего пространства, является участок ρ>i>>2>. В этом случае мы должны разбить промежуточный участок траектории на два или более участков, введя дополнительные допустимые точки. Например, вычислив ρ>i>>1> — ρ>i>>2 >— ρ>i>>3>, мы вычислим затем траекторию , ρ′>i>>2 >— ρ″>i>>2 >— ρ>i>>3>, используя условия yа конце участка ρ>i>>1>.