Проектирование деталей машин (работа 1)

1. ЭНЕРГЕТИЧЕСКИЙ И КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДА

1.1. Исходные данные

Для приводов ленточных конвейеров:

F_>t> – окружная сила на барабане, кН, F_>t>=2.50 кН;

V – скорость движения ленты, м/с, V=0,6 м/с;

D_>б> – диаметр барабана, м, D_>б>=0.25 м.

1.2 Выбор электродвигателя

1.2.1 Определение потребляемой мощности привода

Потребляемую мощность привода (мощность на выходе) для ленточного конвейера определяют по формуле

где Р_>вых.> – потребляемая мощность привода, кВт.

1.2.2 Определение потребной мощности электродвигателя

где - общий КПД привода, определяемый как произведение КПД отдельных передач и муфт

Значения КПД передач и муфт приведены в таблице.

1.2.3 Определение предполагаемой частоты вращения вала электродвигателя

Каждому значению номинальной мощности соответствует не один, а несколько типов электродвигателя с различными синхронными частотами вращения: 3000,1500,750 мин^-1. С увеличением быстроходности электродвигателя снижается его масса и стоимость. Однако с увеличением частоты вращения вала электродвигателя растет передаточное отношение привода. А так как передаточные числа отдельных передач имеют оптимальные значения, то реализовать большое передаточное отношение не всегда возможно. Поэтому, задаваясь рекомендуемыми значениями передаточных чисел, необходимо определить предполагаемую частоту вращения и по ней выбрать подходящий электродвигатель

где - рекомендуемые значения передаточных чисел передач привода;

- частота вращения приводного вала, мин^-1;

- предполагаемая частота вращение вала электродвигателя, мин^-1.

Частота вращения приводного вала для ленточного конвейера определяется по следующей зависимости:

; ;

По найденным значениям мощности и частоты вращения вала выбирают электродвигатель. При выборе электродвигателя допускается его перегрузка до 5-8% при постоянной нагрузке и до 10-12% - при переменной нагрузке.

По найденным значениям выбираем электродвигатель АИР112МА8/709 ТУ 16-525.564-84 с параметрами:

мощность – 2,2 кВт, частота – 709 .

1.3 Определение общего передаточного отношения привода и разбивки его по ступеням

После выбора электродвигателя определяют общее передаточное отношение привода

где - номинальная частота вращения вала выбранного электродвигателя (частота, соответствующая его паспортной мощности ), .

Если в схеме привода отсутствует ременная или цепная передачи, то передаточное отношение редуктора . Далее производят распределение передаточного отношения редуктора между его ступенями. От того, как распределено передаточное отношение, зависит масса и габариты редуктора. Лучшие показатели имеют редукторы, у которых диаметры колес всех ступеней близки между собой, что благоприятно и с точки зрения смазки.

Так как быстроходная ступень менее нагружена, чем тихоходная, то передаточное число этой ступени рекомендуется брать больше, чем тихоходной.

Полученные передаточные числа отдельных ступеней редуктора необходимо согласовать со стандартными значениями. Номинальные передаточные числа зубчатых передач стандартизованы по СТ СЭВ 229-75.

Передаточное число тихоходной передачи:

; ;.

Передаточное число быстроходной передачи:

; .

Выбираем стандартные передаточные числа:

быстроходной – 2,8;

тихоходная – 5,6.

1.4 Определение мощности на валах, частоты вращения валов и крутящих моментов на валах

Мощности на валах определяют через мощность электродвигателя

где - мощность на первом валу, кВт;

- КПД муфты.

где - мощности на предыдущем и последующем валах, кВт;

- КПД зубчатой передачи.

; ;

; .

Частоты вращения валов могут быть определены через частоту вращения вала электродвигателя. Если вал редуктора непосредственно соединяется с валом электродвигателя, то:

;

где - частота вращения соответственно и валов, ;

- передаточное число ступени редуктора.

;

Крутящие моменты на валах определяют по формуле

;

где - крутящий момент на валу, ;

- мощность на валу, кВт;

- частота вращения вала, .

;

Результаты произведенных расчетов заносим в таблицу.

Валы	Мощности на валах, кВт	Частоты вращения валов,	Крутящие моменты на валах,	Передаточные числа передач
1	2,156	709	29	u_>р>=15,47
2	2	253	78	2,8
3	1,92	45	405	5,6

2. РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ

2.1 Выбор материала и термической обработки колес

В зависимости от требований к габаритам передачи и условий эксплуатации применяем материал изготовления зубчатых колес сталь марки 40Х и термическую обработку колеса – улучшение с твердостью 235 – 262 НВ, а шестерни – улучшение с твердостью 269 – 302 НВ.

2.2 Определение допускаемых напряжений

2.2.1 Определение срока службы передачи - , ч

2.2.2 Определение допускаемых напряжений на контактную прочность

Допускаемые контактные напряжения , МПа, определяем для шестерни и колеса отдельно, при этом

где - базовое допускаемое напряжение, МПа;

- коэффициент долговечности.

Базовые допускаемые напряжения для зубчатых колес, работающих при постоянном режиме в зоне горизонтального участка кривой усталости, определяются по формуле

где - длительный предел контактной выносливости, определяемый в зависимости от термообработки и группы материалов, МПа;

- коэффициент, учитывающий шероховатость сопряженных поверхностей, ;

- коэффициент, учитывающий влияние скорости, ;

- коэффициент запаса прочности, .

Базовое допускаемое напряжение шестерен

, МПа,

колес –

, МПа.

Коэффициент долговечности определяется по формуле

где - базовое число циклов нагружения;

- эквивалентное число циклов нагружения;

- показатель степени кривой усталости поверхностных слоев зубьев, .

Базовое число циклов нагружения принимается равным

Если получилось больше , то принимают равным .

Базовое число циклов нагружения шестерен - , колес - .

Эквивалентное число нагружения определяется по зависимости

где - коэффициенты с графика нагрузки.

В случае получения .

Эквивалентное число нагружения шестерен косозубой передачи

Эквивалентное число нагружения колес косозубой передачи

Эквивалентное число нагружения колес косозубой передачи и шестерен прямозубой передачи равно .

Эквивалентное число нагружения колес прямозубой передачи

Коэффициент долговечности шестерен косозубой передачи равен .

Коэффициент долговечности колес косозубой передачи равен

Коэффициент долговечности шестерен прямозубой передачи равен . Коэффициент долговечности колес прямозубой передачи равен

Допускаемые контактные напряжения шестерен косозубой передачи равны

Допускаемые контактные напряжения колес косозубой передачи равны

Допускаемые контактные напряжения шестерен прямозубой передачи равны

Допускаемые контактные напряжения колес прямозубой передачи равны

За расчетное допускаемое напряжение для косозубой передачи принимаем наименьшее из двух допускаемых напряжений для материала шестерни или колеса .

Принимаем допускаемое напряжение для косозубой передачи , для прямозубой передачи .

2.2.3 Определение допускаемых напряжений при расчете зубьев на изгиб

Допускаемые напряжения на изгиб , МПа, определяют для шестерни и колеса отдельно, при этом

где - базовые допускаемые напряжения изгиба при нереверсивной нагрузке, МПа;

- коэффициент, вводимый при двухстороннем приложении нагрузки: - односторонняя нагрузка;

- коэффициент долговечности.

Базовые допускаемые напряжения на изгиб для зубчатых колес, работающих в зоне горизонтальной ветви кривой усталости при нереверсивной нагрузке, определяются по формуле

где - предел выносливости, определяемый на зубьях при отнулевом цикле, МПа;

- коэффициент, учитывающий шероховатость переходной поверхности; при зубофрезеровании и шлифовании с ;

- коэффициент размеров (при проектном расчете можно принимать );

- коэффициент, учитывающий чувствительность материала к концентрации напряжений (при проектном расчете );

- коэффициент запаса прочности, .

Базовые допускаемые напряжения на изгиб шестерен

Базовые допускаемые напряжения на изгиб колес

Коэффициент долговечности определяют как

где - базовое число циклов нагружения, ;

- эквивалентное число циклов нагружения;

- показатель степени кривой выносливости: - улучшение, нормализация, азотирование.

Эквивалентное число циклов нагружения определяется по выражению

При 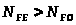коэффициент долговечности .

Эквивалентное число циклов нагружения шестерен косозубой передачи

Эквивалентное число циклов нагружения колес косозубой передачи

Эквивалентное число циклов нагружения шестерен прямозубой передачи

Эквивалентное число циклов нагружения колес прямозубой передачи

Коэффициент долговечности шестерен косозубой передачи .

Коэффициент долговечности колес косозубой передачи .

Коэффициент долговечности шестерен прямозубой передачи .

Коэффициент долговечности колес прямозубой передачи

Базовые допускаемые напряжения на изгиб шестерен косозубой передачи

Базовые допускаемые напряжения на изгиб колес косозубой передачи

Базовые допускаемые напряжения на изгиб шестерен прямозубой передачи

Базовые допускаемые напряжения на изгиб колес прямозубой передачи

2.3 Расчет закрытых зубчатых цилиндрических передач

2.3.1 Определение межосевого расстояния

где - межосевое расстояние, мм; - вспомогательный коэффициент, для прямозубых колес , для косозубых колес ;

- коэффициент нагрузки;

- коэффициент ширины, .

Коэффициент нагрузки определяется как произведение трех коэффициентов

где - коэффициент распределения нагрузки между зубьями: для прямозубых колес , для косозубых колес в проектных расчетах принимают среднее значение ;

- коэффициент концентрации нагрузки, ;

- коэффициент динамичности нагрузки, - для прирабатывающихся колес.

Коэффициент нагрузки косозубой передачи

Коэффициент нагрузки прямозубой передачи

Определение межосевого расстояния косозубой передачи

(из стандартного ряда).

Определение межосевого расстояния прямозубой передачи

(из стандартного ряда).

2.3.2 Определение модуля передачи

Для зубчатых колес при твердости зубьев модуль назначают

Определяем модуль для прямозубой передачи

(из стандартного ряда).

2.3.3 Определение суммарного числа зубьев для косозубой передачи

где - угол наклона зубьев, обычно назначают угол .

Полученное значение округляют в ближайшую сторону до целого числа и уточняют угол.

Уточняем угол

Определение суммарного числа зубьев для прямозубой передачи

, .

2.3.4 Определение числа зубьев шестерни

Если число зубьев шестерни получится меньше минимального допустимого из условия неподрезания, т.е.

где - для прямозубых передач;

- для косозубых передач,

то необходимо проектировать равносмещенную передачу.

Определение числа зубьев шестерни косозубой передачи

(округляем до ближайшего целого).

Сравниваем число зубьев шестерни косозубой передачи с минимальным допустимым из условия неподрезания

Определение числа зубьев шестерни прямозубой передачи

Сравниваем число зубьев шестерни прямозубой передачи с минимальным допустимым из условия неподрезания

2.3.5 Определение числа зубьев колеса

Определение числа зубьев колеса косозубой передачи

Определение числа зубьев колеса прямозубой передачи

2.3.6 Определение геометрических размеров колес и размеров заготовок

Определяем геометрические размеры у косозубой передачи:

- делительные диаметры

шестерни , ,

колеса , ,

- начальные диаметры

шестерни ,

колеса ,

- диаметры вершин зубьев

шестерни , ,

колеса , ,

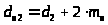- диаметры впадин зубьев

шестерни , ,

колеса , ,

- ширина колеса , ,

- ширина шестерни , .

Определяем геометрические размеры у прямозубой передачи:

- делительные диаметры

шестерни , ,

колеса , ,

- начальные диаметры

шестерни ,

колеса ,

- диаметры вершин зубьев

шестерни , ,

колеса , ,

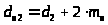- диаметры впадин зубьев

шестерни , ,

колеса , ,

- ширина колеса , ,

- ширина шестерни , .

Чтобы получить при заданной термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры заготовок колес не превышали предельно допустимых значений:

Значения вычисляют по формулам:

для цилиндрической шестерни косозубой передачи

, ;

для колеса с выточками

, ;

, .

Проверяем с предельными , , , - условие выполняется.

2.3.7 Определение усилий в зацеплении

Окружное усилие

где - окружное усилие, кН;

- крутящий момент на зубчатом колесе, ;

- делительный диаметр колеса, мм.

Окружное усилие косозубого колеса

Окружное усилие прямозубой передачи

Радиальное усилие для прямозубой передачи

где - угол зацепления, для стандартной и равносмещенной передачи.

Радиальное усилие для косозубой передачи определяют по формуле

, .

Осевое усилие для косозубой передачи

, .

2.3.8 Проверка зубьев колес по напряжениям изгиба

Для этого производят оценку изгибной прочности, т.е. находят отношения

и .

Коэффициенты форм зубьев и для прямозубых колес определяют по фактическому числу зубьев и , а для косозубых колес по эквивалентному числу зубьев шестерни и колеса

Для косозубой передачи

и ,

, .

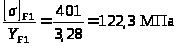Проверочный расчет на изгиб ведется по тому из колес, для которого это отношение меньше. У первого колеса отношение меньше.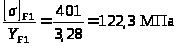

Проверочный расчет на изгиб косозубых передач производится по формуле

где - коэффициент распределения нагрузки между зубьями, ;

- коэффициент угла наклона зубьев:

Проверяем с допустимым изгибом , , передача по изгибу подходит.

Для прямозубой передачи

и ,

, .

Проверочный расчет на изгиб ведется по тому из колес, для которого это отношение меньше. У первого колеса отношение меньше

Проверочный расчет на изгиб прямозубых передач производится по формуле

где 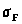- рабочее напряжение изгиба, МПа;

- коэффициент концентрации нагрузки;

- коэффициент динамичности нагрузки.

При постоянной нагрузке, твердости и скорости коэффициент .

Для определения коэффициента динамичности нагрузки предварительно необходимо определить окружную скорость колеса

где - скорость колеса, м/с;

- делительный диаметр, мм;

- частота вращения колеса, мин^-1.

По скорости назначают степень точности передачи и коэффициент динамичности . Наибольшее распространение имеют 6, 7 и 8-я степень точности.

Проверяем с допустимым изгибом , , передача по изгибу подходит.

2.3.9 Проверка зубьев колес на контактную прочность

где - контактные напряжения, МПа;

- вспомогательный коэффициент, - для прямозубых передач, - для косозубых передач;

- коэффициент распределения нагрузки между зубьями, для прямозубых передач ;

- коэффициент концентрации нагрузки, определяемый в зависимости от коэффициента ширины ;

- коэффициент динамичности нагрузки;

- окружное усилие, Н;

- делительный диаметр шестерни, мм;

- ширина колеса, мм.

При проверке зубьев на контактную прочность допускается перенапряжение до 5%.

Проверка косозубых колес

Сравниваем с допускаемой контактной прочностью , , передача по прочности проходит.

Проверка прямозубых колес

Сравниваем с допускаемой контактной прочностью , , передача по прочности проходит.

3. РАСЧЕТ ВАЛОВ

3.1 Материалы и термообработка валов

Основными материалами для валов и осей служат углеродистые и легированные стали, благодаря высоким механическим характеристикам, способности к упрочнению и легкости получения цилиндрических заготовок прокаткой.

Для изготовления средненапряженных, среднескоростных валов применяем сталь 40Х, подвергаемых улучшению.

3.2 Проектный расчет валов

В начале расчета известен только крутящий момент Т , изгибающие моменты М_>И> не известны, так как неизвестна конструкция вала и его длина. Поэтому проектный расчет вала ведется условно на чистоте кручения по заниженным допускаемым напряжениям.

Диаметры различных участков валов редуктора определяют по формулам:

для быстроходного вала

где t – высота буртика, , r – координата фаски подшипника, , - размер фаски колеса,;

для промежуточного вала

при , ;

для тихоходного вала

при , , .

3.3 Проверочный расчет валов

3.3.1 Быстроходный вал

Определяем реакции в подшипниках , , .

В плоскости xoz:

: ,

моменты и возникают при переносе сил и , соответственно, в центр шестерен:

, ,

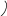
В плоскости yoz:

: ,

Находим изгибающий момент M_>z>:

1) сечение 1-1

при ,

2) сечение 2-2

при ,

Находим изгибающий момент M_>y>:

1) сечение 1-1

при , ,

при ,

2) сечение 2-2

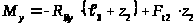
при ,

Находим сжимающую силу:

Опасные сечения в центре шестеренок.

Вал подходит если выполняется условие:

где - эквивалентное напряжения;

- коэффициент запаса ();

- эффективный коэффициент концентрации нормальных напряжений ();

- коэффициент влияния абсолютных размеров поперечного сечения ();

где - номинальное напряжение изгиба, МПа

;

- напряжение кручения, МПа

Из этого условия устанавливаем, что вал подходит.

3.3.2 Промежуточный вал

Определяем реакции в подшипниках

, , , .

В плоскости xoz:

: ,

моменты и возникают при переносе сил и , соответственно, в центр шестерен:

, ,

В плоскости yoz:

: ,

Находим изгибающий момент M_>z>:

1) сечение 1-1

при , ,

при ,

2) сечение 2-2

при ,

3) сечение 3-3

при

Находим изгибающий момент M_>y>:

1) сечение 1-1

при , ,

при ,

2) сечение 2-2

при ,

3) сечение 3-3

при ,

Находим сжимающую силу:

Опасное сечение в центре шестеренки.

Вал подходит если выполняется условие:

где - эквивалентное напряжения;

- коэффициент запаса ();

- эффективный коэффициент концентрации нормальных напряжений ();

- коэффициент влияния абсолютных размеров поперечного сечения ();

где - номинальное напряжение изгиба, МПа

;

- напряжение кручения, МПа

Из этого условия устанавливаем, что вал подходит.

3.3.3 Тихоходный вал

Определяем реакции в подшипниках .

В плоскости xoz:

: ,

, .

В плоскости yoz:

: ,

Находим изгибающий момент M_>z>:

Находим изгибающий момент M_>y>:

Опасное сечение в центре колеса.

Вал подходит если выполняется условие:

где - эквивалентное напряжения;

- коэффициент запаса ();

- эффективный коэффициент концентрации нормальных напряжений ();

- коэффициент влияния абсолютных размеров поперечного сечения ();

где - номинальное напряжение изгиба, МПа

- напряжение кручения, МПа

Из этого условия устанавливаем, что вал подходит.

4. ВЫБОР И РАСЧЕТ ПОДШИПНИКОВ КАЧЕНИЯ

4.1 Выбор типа подшипников

Для опор цилиндрических прямозубых и косозубых колес редукторов и коробок передач применяют чаще всего шариковые радиальные подшипники:

1) для тихоходного и быстроходного валов - шариковые радиальные;

2) для промежуточного вала – роликовые радиальные;

3) первоначально – легкая серия;

4) класс точности «0», т.к. он дешевле.

4.2 Расчет подшипников качения

Основными критериями работоспособности подшипников качения является долговечность по усталостному выкрашиванию и статическая грузоподъемность по пластическим деформациям.

Расчет подшипников на долговечность производят по формуле:

где - расчетная долговечность подшипника, ч;

- частота вращения вала, мин^-1;

- динамическая грузоподъемность подшипника, кН;

- эквивалентная нагрузка, кН;

- показатель степени, равный в соответствии с результатами экспериментов для шарикоподшипников , для роликоподшипников ;

- коэффициент, учитывающий надежность работы подшипника;

- коэффициент, учитывающий качество метала подшипника и условия эксплуатации;

- требуемая долговечность подшипника (для редуктора она равна сроку службы передачи ),ч.

Эквивалентную радиальную нагрузку для радиальных шарикоподшипников и радиально -упорных шарико – и роликоподшипников определяют по формуле:

Эквивалентная нагрузка для подшипников с короткими цилиндрическими роликами:

где - радиальная нагрузка (суммарная реакция в опоре), кН;

- осевая нагрузка, кН;

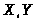- коэффициенты радиальной и осевой нагрузок;

- коэффициент вращения, равный 1 при вращении внутреннего кольца относительно направления нагрузки и 1,2 при вращении наружного;

- коэффициент безопасности, для редукторов и коробок передач ;

- температурный коэффициент, вводимый при >100⁰С.

Расчетная зависимость эквивалентной нагрузки Р от радиальной и осевой учитывает изменение углов контакта и числа шариков, принимающих участие в восприятии нагрузки. Поэтому коэффициенты и зависят от отношения составляющих и их уровня, который задается отношением .

4.2.1 Расчет подшипников качения тихоходного вала

Определяем суммарные реакции для каждой опоры.

В опоре А–.

В опоре В – .

Определяем коэффициент вращения, коэффициент безопасности и температурный коэффициент:

, , .

По отношению составляющих и находим и (,,):

, , .

Определяем эквивалентную радиальную нагрузку:

Определяем долговечность подшипника и сравниваем с нужной:

Из условия видно, что подшипник подходит.

4.2.2 Расчет подшипников качения промежуточного вала

Определяем суммарные реакции для каждой опоры.

В опоре С–.

В опоре D –.

Определяем коэффициент вращения, коэффициент безопасности и температурный коэффициент:

, , .

Определяем эквивалентную радиальную нагрузку:

Определяем долговечность подшипника и сравниваем с нужной:

Из условия видно, что подшипник подходит.

4.2.3 Расчет подшипников качения тихоходного вала

Определяем суммарные реакции для каждой опоры.

В опоре E–.

В опоре F –.

Определяем коэффициент вращения, коэффициент безопасности и температурный коэффициент:

, , .

По отношению составляющих и находим и .

Определяем эквивалентную радиальную нагрузку:

Определяем долговечность подшипника и сравниваем с нужной:

Из условия видно, что подшипник подходит.

5. РАСЧЕТ ШПОНОЧНЫХ СОЕДИНЕНИЙ

5.1 Расчёт шпонки быстроходного вала

Материал: Сталь 45, т.о. нормализация, .

Шпонка призматическая, размеры: глубина паза вала ;глубина паза ступицы ; .

Шпонка ГОСТ 23360 – 78.

Проверяю шпонку на смятие

где – крутящий момент на валу, ;

– диаметр вала, ;

– расчётная длина шпонка, .

; ; .

Условие выполняетсяшпонка подходит.

5.2 Расчёт шпонки промежуточного вала

Материал: Сталь 45, т.о. нормализация, .

Шпонка призматическая, размеры: ;; .

Шпонка ГОСТ 23360 – 78.

Проверяю шпонку на смятие

,; ; .

Условие выполняетсяшпонка подходит.

5.3 Расчёт шпонки тихоходного вала

1) Шпонка под колесом. Материал: Сталь 45, т.о. нормализация, .

Шпонка призматическая, размеры: ;; .

Шпонка ГОСТ 23360 – 78.

Проверяю шпонку на смятие

,; ; .

Условие выполняетсяшпонка подходит.

2) Шпонка на выходном конце вала.

Материал: Сталь 45, т.о. нормализация, .

Шпонка призматическая, размеры: ;; .

Шпонка ГОСТ 23360 – 78.

Проверяю шпонку на смятие

,; ; .

Условие выполняетсяшпонка подходит.

6. ПОДБОР МУФТ

Муфту подбирают по расчетному моменту и диаметру вала

где Т_>н> – наиболее длительно действующий момент, Н·м;

к – коэффициент динамичности, к =1,5;

Т_>табл> – табличное значение передаваемого момента.

Для соединения вала электродвигателя с валом редуктора используем муфту со звездочкой. За счет использования в конструкции упругих элементов данные муфты обладают способностью амортизировать толчки и удары, демпфировать отдельные элементы привода.

Т_>р>=29 ·1,5=43,5 Н·м

Принимаем муфту упругую со звездочкой 125-32-1-28-2-У3 ГОСТ 14084-76 d_>э>=32мм ; d_>вала>=28мм ; Т_>н>=125Н·м

Для соединения выходного вала редуктора с валом барабана конвейера использую зубчатую муфту.

Достоинства: компенсирует эксцентриситет и перекос валов, продольное смещение валов, передает большие крутящие моменты

Т_>р>=405 ·1,5=607,5 Н·м

Принимаю муфту зубчатую МЗ-40 ГОСТ 5066-83 d_>м>=40мм; Т_>м>=710Н·м.

7. ВЫБОР И ОБОСНОВАНИЕ СПОСОБА СМАЗКИ ПЕРЕДАЧ И ПОДШИПНИКОВ

Для смазки зубчатых колес и подшипников применяю картерную смазку масляным туманом.

Определяем необходимый объем масла

V=b·h·l,

где b – ширина масляной ванны, дм;

h – уровень масла, дм;

l – длина масляной ванны, дм.

V=1,86·1,52·4,94=14 дм³=14л

Окружная скорость колеса

Выбираем масло И-Г-C-68

Смазка подшипников.

Окружная скорость колеса на выходном валу выше 1м/с, значит, подшипники будут смазываться покрывающими внутренние поверхности стенок корпуса. Для смазывания подшипников быстроходного вала в плоскости разъема делаю канавки, в крышке корпуса – скосы.

Литература

1.Черемисинов В.И. Курсовое проектирование деталей машин. – 3-е изд., перераб. и доп. – Киров: РИО ВГСХА, 2002. – 163 с.: ил.

2. Дунаев П.Ф., Леликов О.Н. Конструирование узлов и деталей машин. – 5-е изд., перераб. и доп. – М.: Высш. шк., 1998. – 447с., ил.