Проектирование главного редуктора вертолета
Министерство образования Российской Федерации
Самарский Государственный Аэрокосмический Университет
имени академика С.П. Королёва
Кафедра основ конструирования машин
РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовому проекту по проектированию главного редуктора вертолета
Студент: Кондратенко Е.А. гр.1310
Руководитель проекта: Силаев Б.М.
Самара 2008
Техническое задание

Кинематическая схема редуктора
Исходные данные:
Сила тяги на несущем винте 8,8 кН;
Несущая сила на винте 0,4 кН;
Частота вращения выходного вала 210 об/мин;
Мощность на выходном валу 120 кВт;
Частота вращения входного вала 1600 об/мин;
Расчетная долговечность 1300 ч;
Расстояние от плоскости подвески до несущего винта 650 мм;
Привод работает спокойно без толчков и вибраций. Режим нагружения нулевой.
Реферат
Пояснительная записка к курсовому проекту по проектированию зубчатых передач.
Стр.40, рис.1, приложения, исп. источники 3.
Коническая передача, цилиндрическая передача, крутящий момент, контактное напряжение, напряжение изгиба, коэффициент запаса, передаточное число, межосевое расстояние, вал, гайка, подшипник.
Разработана конструкция редуктора для передачи и усиления крутящего момента с вала двигателя на винт. Обоснована целесообразность использования цилиндрических колёс.
Содержание
Введение
1. Описание редуктора и принципа его работы
2. Кинематический и энергетический расчет редуктора
2.1 Разбивка общего передаточного отношения
2.2 Определение частот вращения валов
2.3 Выбор КПД и определение мощностей на валах
2.4 Определение крутящих моментов на валах
3. Расчет цилиндрической передачи
3.1 Определение допускаемых контактных напряжений
3.2 Определение допускаемых напряжении изгиба
3.3 Определение основных габаритов передачи для второй ступени
3.4 Проверка передачи по контактной прочности
3.5 Проверка прочности при изгибе для второй ступени
3.6 Расчет геометрических параметров зубчатой передачи
4. Проверка на статическую прочность при перегрузке
5. Предварительное определение диаметров валов
6. Предварительный подбор подшипников
7. Определение усилий в зацеплениях
7.1. Определение усилий в зацеплениях на первой передаче
7.2. Определение усилий в зацеплениях на второй передаче
7.3 Определение реакций в опорах валов
7.3.1 Проверочный расчет валов на выносливость
7.4. Расчёт долговечности подшипников качения
8. Расчет шлицевых соединений
9. Система смазки
Заключение
Список использованных источников
Введение
Производственные процессы в большинстве отраслей народного хозяйства выполняют машины, и дальнейший рост материального благосостояния тесно связан с развитием машиностроения.
К важнейшим требованиям, предъявляемым к проектируемой машине, относятся экономичность в изготовлении и эксплуатации, удобство и безотказность обслуживания, надёжность и долговечность.
Для обеспечения этих требований детали должны удовлетворять ряду критериев, важнейшие среди которых - прочность, надёжность, износостойкость, жёсткость, виброустойчивость, теплостойкость, технологичность.
Зубчатые передачи в современной промышленности имеют важные значения. Благодаря высокому КПД они широко применяются в технике В данной работе произведен расчет, необходимый для того, чтобы спроектировать редуктор вертолёта.
Курсовой проект по деталям машин является первой конструкторской работой студента и поэтому её значение весьма существенно. Изучение основ конструирования (проектирования) начинают с конструирования простейших узлов машин - приводов, редукторов. Опыт и знания, приобретенные студентом при конструировании этих узлов машин, являются основой для его дальнейшей конструкторской работы, а также для выполнения курсовых проектов по специальным дисциплинам и дипломного проекта.
1. Описание редуктора и принципа его работы
В данной работе рассматривается главный редуктор вертолета. Входная коническая ступень. Вторая ступень - цилиндрическая. Редуктор предназначен для понижения оборотов и повышения крутящего момента на валах.
2. Кинематический и энергетический расчет редуктора
2.1 Разбивка общего передаточного отношения
Общее передаточное число определяем по формуле

частота вращения входного вала;
 - частота вращения
- частота вращения
 несущего винта.
несущего винта.
Для двухступенчатого редуктора

где U>1> - передаточное число первой ступени, U>2> - передаточное число второй ступени.
В двухступенчатом
цилиндрическом редукторе для рациональной
разбивки передаточных чисел рекомендуется
эмпирическая зависимость .

Передаточное число второй ступени

2.2 Определение частот вращения валов
Частоты вращения входного и выходного валов заданы
 мин
мин
 мин
мин
Определяем частоту вращения промежуточного вала исходя из передаточного отношения

Для выбранного
передаточного отношения


2.3 Выбор КПД и определение мощностей на валах
Принимаем КПД
для цилиндрической передачи передачи
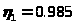 ,
для конической передачи
,
для конической передачи
 .
Мощность на валах определяется по
формуле:
.
Мощность на валах определяется по
формуле:

где
 - мощность на валу,
- мощность на валу,
 - мощность на предыдущем валу, кВт,
- мощность на предыдущем валу, кВт,
 - КПД ступени.
- КПД ступени.
Для выходного
вала задана мощность Р =130
кВт.
=130
кВт.
Исходя из этого условия, определяем мощности на остальных валах:


2.4 Определение крутящих моментов на валах
Определение крутящих моментов на всех валах редуктора производится по формуле:

где Т - крутящий момент, Нмм,
Р - мощность, кВт,
n - обороты вала, мин-1,После подстановки получим:
 Нмм
Нмм
 Нмм
Нмм
 Нмм
Нмм
3. Расчет цилиндрической передачи
3.1 Определение допускаемых контактных напряжений
Допускаемое контактное напряжение определяем по формуле

 ,
,
где
 -
базовый предел контактной выносливости,
МПа,
-
базовый предел контактной выносливости,
МПа,
коэффициент безопасности по контактным напряжениям,
 -
коэффициент долговечности.
-
коэффициент долговечности.
Коэффициент долговечности определяется по формуле:

где N>H>>0> - базовое число циклов напряжений,
N>HE> - расчетное число циклов нагружений.
Расчетное число циклов для постоянного режима работы находим по формуле:

где n - частота вращения, об/мин,
t>h> - долговечность, ч,
С - число нагружений зуба за один оборот зубчатого колеса.
Принимаем для цилиндрической передачи С=1.
Зубчатые колеса изготовляются из стали 12ХН4А с термообработкой зубьев цементацией на глубин (1,0. .1,2) мм. При этом твердость поверхности составит 58. .63 HRC. Принимаем HRC=59.
Предел контактной выносливости поверхности зуба по /2/
 МПа.
МПа.
 Коэффициент
безопасности S н = 1,2.
Коэффициент
безопасности S н = 1,2.
Базовое число циклов нагружений при HRC 56 принимаем
Рассчитаем число циклов для первой и второй ступени
Расчетное число циклов для шестерни

Расчетное число циклов для колеса

Коэффициент долговечности для шестерни
 .
.
Коэффициент долговечности для колеса
 .
.
Допускаемые контактные напряжения для шестерни
 МПа.
МПа.
Допускаемые контактные напряжения для колеса
 МПа.
МПа.
В качестве
допускаемых контактных напряжений для
передачи принимаем наименьшее значение
 1206,877МПа.
1206,877МПа.
3.2 Определение допускаемых напряжении изгиба
Допускаемое напряжение изгиба определяем по формуле
 ,
,
где
 - базовый предел выносливости по изгибу,
МПа,
- базовый предел выносливости по изгибу,
МПа,
 - коэффициент безопасности по напряжениям
изгиба,
- коэффициент безопасности по напряжениям
изгиба,
 - коэффициент долговечности,
- коэффициент долговечности,
 - коэффициент, учитывающий условия
нагружения.
- коэффициент, учитывающий условия
нагружения.
Для одностороннего
нагружения зуба принимаем
Коэффициент долговечности определяем по формуле

где
 - базовое число циклов нагружений,
- базовое число циклов нагружений,
 - расчетное число циклов нагружений.
- расчетное число циклов нагружений.
Расчетное число циклов для постоянного режима работы находим по формуле

Базовый предел
выносливости по изгибу принимаем
 = 800 МПа.
= 800 МПа.
Коэффициент
безопасности
 .
.
Базовое число
циклов нагружений будет
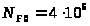 .
.
Расчетное число циклов нагружений для шестерни
Расчетное число циклов нагружений для колеса

Коэффициент долговечности для шестерни

Коэффициент долговечности для шестерни

Принимаем значения этих коэффициентов равными единице.
Допускаемое напряжение для шестерни и колеса
 МПа,
МПа,
 МПа.
МПа.
3.3 Определение основных габаритов передачи для второй ступени
Определяем межосевое расстояние

где
 -
коэффициент ширины венца относительно
межцентрового расстояния.
-
коэффициент ширины венца относительно
межцентрового расстояния.
Принимаем K=1,3, >ba> = 0,3. Округляем до а>w>=227,69 мм.
Определяем рабочую ширину венца. >ba> = 0,3. т.к. шестерня расположена не симметрично относительно опор, а твердость поверхности зубьев НВ>350.

Определяем модуль
 мм.
мм.
Округляем модуль до ближайшего значения по ГОСТу: принимаем m= 6 мм.
Определяем число зубьев для шестерни
Округляем значение до ближайшего целого числа. Принимаем z>1> = 19.

Определяем диаметр делительной окружности шестерни
 6
19=114 мм.
6
19=114 мм.
Определяем число зубьев для колеса
 .
.
Принимаем z>2> =58
Фактическое передаточное число
 .
.
Погрешность
 .
.
3.4 Проверка передачи по контактной прочности
Определяем окружную скорость шестерни
 м/c.
м/c.
Принимаем K>v>=1,2.
Определяем коэффициент ширины зубчатого венца относительного делительного диаметра шестерни

Принимаем K>>=1,1.
 .
.
 МПа.
МПа.
 =
= .
.
Контактное напряжение в зубьях находится в допустимых пределах.
3.5 Проверка прочности при изгибе для второй ступени
Напряжение изгиба шестерни
 ,
,
где Y>F>>3>=3,875, b>w>>3>=b>w>+1=69+1=70 мм.
Напряжение изгиба зубчатого колеса
 ,
,
где Y>F>>4>=3,61, b>w>>4>=b>w>=70 мм.
Приведенные расчеты показывают, что напряжение изгиба меньше допустимых значений.
3.6 Расчет геометрических параметров зубчатой передачи
Определяем межосевое расстояние. Делительное межосевое расстояние вычисляется по формуле
 мм.
мм.
Тогда межосевое расстояние
> >,
>,
где
 ;
;
 ;
;
 .
.
Исходя из
условий, получаем, что
 =231
мм.
=231
мм.
Определяем угол зацепления

Тогда >w>=20.
Делительные диаметры
 мм,
мм,
 мм.
мм.
Основные
диаметры
 мм.
мм.
 мм.
мм.
Шаг делительный
 мм.
мм.
Шаг основной
 мм.
мм.
Диаметры начальных окружностей

 мм.
мм.
 мм.
мм.
Диаметры впадин
 114-2
(1+0.25) 6=99 мм,
114-2
(1+0.25) 6=99 мм,
 348-2
(1+0.25) 6=333 мм,
348-2
(1+0.25) 6=333 мм,
где
 ,
,
 .
.
Диаметры вершин
 462-333-260.25=126
мм,
462-333-260.25=126
мм,
 462-99-260.25=360мм.
462-99-260.25=360мм.
Делительная толщина зубьев
 мм,
мм,
 мм.
мм.
Основная толщина зуба
 мм,
мм,
 мм.
мм.
Толщина зубьев по окружности вершин

 ,
,

 ,
,
 мм,
мм,
 мм.
мм.
Толщина зуба по начальной окружности
 мм,
мм,
 мм.
мм.
Определяем радиус кривизны
 мм
мм
 мм
мм
Коэффициент перекрытия
 .
.
Находим
 мм
мм
 мм
мм
Находим скорости скольжения
 ,
м/с
,
м/с
 ,
м/с
,
м/с
 ,
м/с
,
м/с
 .
м/с
.
м/с
Длина общей нормали
 мм,
мм,
где

 мм,
мм,
где

4. Проверка на статическую прочность при перегрузке
Для второй ступени
 Hмм,
Hмм,
 МПа,
МПа,
 МПа,
МПа,
 .
.
Найдем максимальное напряжения изгиба при перегрузке
 МПа,
МПа,
 МПа.
МПа.
Для стали 12ХН4А с >в>=1200 МПа
 МПа.
МПа.
 .
.
5. Предварительное определение диаметров валов
Для полного расчета вала на прочность необходимо знать изгибающие и крутящие моменты, действующие на вал. В данный момент расчета неизвестны изгибающие моменты. Для приближенного расчёта валов считаем, что они нагружены только крутящими моментами. При этом допускаемые напряжения кручения принимаем заниженными.
Исходя из условия прочности вала только на кручение
 ,
,
где T - крутящий момент на валу,
W>> - момент сопротивления.
Для полого вала
 ,
,
где d>o > d - коэффициент пустотелости.
Получаем

Примем 0,8, = 65 Мпа для входного вала
Примем 0,75, = 75 Мпа для промежуточного вала
Примем 0,75, = 75 Мпа для выходного вала
Тогда:
 ;
;
 мм
мм
 .
.
Принимаем диаметры валов из условий установки подшипников качения: d> 1> = 45 мм, d> 2> = 60 мм, d> 3> = 85 мм.
6. Предварительный подбор подшипников
Опоры входного вала-шестерни нагружены осевой и радиальной силой. Устанавливаем подшипники шариковый радиально-упорный с разрезным внутреннем кольцом №176311 и роликовый радиальный №2111.
Для промежуточного вала устанавливаем подшипники конические радиально-упорные подшипники №7212.
Опоры третьего вала воспринимают большие радиальные и осевые нагрузки от несущего винта и зубчатого колеса, поэтому устанавливаем конические роликовые подшипники. По посадочному месту (d = 85 мм) предварительно принимаем роликовые конические подшипники №7217.
Табл.1
|
Усл. обозначение |
C |
C>0> |
|
176311 |
65000 |
52600 |
|
2111 |
32000 |
24200 |
|
7212 |
72200 |
58400 |
|
7212 |
72200 |
58400 |
|
7217 |
109000 |
91000 |
|
7217 |
109000 |
91000 |
7. Определение усилий в зацеплениях
7.1. Определение усилий в зацеплениях на первой передаче
Окружная сила F>t1> = 2 ∙ T>1/>d>1>, где T>1> - максимальный момент на шестерне, Н ∙ м;
F>t>=2∙0,941∙106 /120=15,69 кН.
Радиальная сила Fr>1>=Ft ∙ tg () ∙соsδ>1>, для стандартного угла = 20 tg () = 0,36397, cos δ>1=>0,9257.
Fr>1>=15,69∙0,36397∙0,9257=5,286 кН.
Fа>1>=Ft>1> ∙ tg () ∙sinδ>1>
Fа>1>=15.69∙0.36397∙0.3782=2,159 кН
7.2. Определение усилий в зацеплениях на второй передаче
Окружная сила F>t3> = 2 T>2/>d>3>, где T>3> - максимальный момент на шестерне, Н ∙ м;
F>t3>=2∙2,269∙106/114= 39,8 кН.
Радиальная сила Fr>3>=Ft>3> tg () (для стандартного угла = 20 tg () = 0,364.
Fr>3>=39,8∙0,364=14,49 кН.
7.3 Определение реакций в опорах валов
Упрощенно представим вал в виде балки нагруженной осевыми, окружными и радиальными силами, действующими в зацеплениях. Расчёт ведётся исходя из уравнений равновесия балки. Реакции опор определяем из уравнений статического равновесия: сумма моментов внешних сил относительно рассматриваемой опоры и момента реакции в другой опоре равна нулю. Входной вал: находим реакции опор. Схема нагружения в вертикальной плоскости.
∑М>Ав>=0,R>Вв>∙0,064+0,130-F>r>∙0.019=0,R>Вв>= 0,456 кН,
∑М>Вв>=0,R>Ав>∙0,064+0,130-F>r>∙ (0,064-0,019) =0,R>Ав>= 5,742 кН.
Схема нагружения в горизонтальной плоскости.
∑М>Аг>=0,R>Вг>∙0,064-F>t>∙0,019=0,R>Вг>= 4,658 кН,
∑М>Вг>=0,R>Аг>∙0,064 - F>t>∙ (0,064-0,019) =0,R>Аг>=11,031 кН.
Осевая реакция А=F>a>>.>. Определяем изгибающие моменты.
М'>В1>= R>Ав>∙0,019=0,109 кН∙м, М''>В1>= - R>Вв>∙ (0,064-0,019) =0,021 кН∙м,
М>Г1>= R>Аг>∙0,019=0,210 кН∙м.
Определяем суммарные реакции опор.
R>A>= кН,
кН,
R>В>= кН.
кН.
Определяем суммарный момент.
М '>сум>=
 кН∙м,
кН∙м,
М ''>сум>=
 кН∙м.
кН∙м.
Находим приведенные моменты.
М '>прив>=
 кН∙м,
кН∙м,
М ''>прив>=
 кН∙м.
кН∙м.
Находим амплитуду приведенного момента
М '>пра>=
 кН∙м
кН∙м
М ''>пра>=
 кН∙м
кН∙м
Промежуточный вал:
Находим реакции опор.
Схема нагружения в вертикальной плоскости.
∑М>Ав>=0,R>Вв>∙0,273-0,764-F>r>>2>∙0,168+ F>r>>3>∙0,086=0,R>Вв>= 0,437 кН,
∑М>Вв>=0,R>Ав>∙0,273-0,764-F>r>>3>0,187+ F>r>>2>∙0,105=0,R>Ав>= 11,89 кН.
Схема нагружения в горизонтальной плоскости.
∑М>Аг>=0,R>Вг>∙0,273-F>t>>2>∙0,168+ F>t>>3>∙0,187=0,R>Вг>= 2,88 кН,
∑М>Вг>=0,R>Аг>∙0,273+F>t>>2>∙0,105 - F>t>>3>∙0,187=0,R>Аг>=21,23 кН.
Определяем суммарные реакции опор.
R>A>= кН,
кН,
R>В>= кН.
кН.
Осевая реакция
Определяем осевые составляющие от радиальных нагрузок в опорах.
 ,
где е=tga=0.35
,
где е=tga=0.35
 кН,
кН,
 кН.
кН.
F>a>>2>=5,286 кН
S>A>>S>B>
S>B> - S>A>=6,222 кН,
R>aA>= S>A>=7,068 кН,
R>a>>В>= S>A> - F>a>>2>=1,782 кН,
Определяем изгибающие моменты.
М'>В1>= R>Ав>∙0,086=1,02 кН∙м,
М>Г1>= R>Аг>∙0,086=1,83 кН∙м,
М''>В2>= - R>Вв> (0,086+0,082) - F>r>>3>∙0,082=0,81 кН∙м,
М'>В2>= - R>Вв>∙0,105=0,05 кН∙м,
М>Г2>= - R>Вг>∙0,105=0,3 кН∙м.
Определяем суммарный момент.
М'>сум1>=
 кН∙м,
кН∙м,
М ''>сум2>=
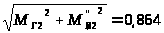 кН∙м.
кН∙м.
М''>сум2>=
 кН∙м.
кН∙м.
Находим приведенные моменты.
М'>прив1>=
 кН∙м,
кН∙м,
М''>прив2>=
 кН∙м.
кН∙м.
М ''>прив2>=
 кН∙м.
кН∙м.
Находим амплитуду приведенного момента
М '>пра>=
 кН∙м
кН∙м
М''>пра>=
 кН∙м
кН∙м
М ''>пра>=
 кН∙м
кН∙м
Выходной вал:
Находим реакции опор.
Схема нагружения в вертикальной плоскости.
∑М>Ав>=0,R>Вв>∙0,282+F>н>∙ (0,282+0,597) - F>r>>4>∙0,095=0,R>Вв>= 3,63 кН,
∑М>Вв>=0,R>Ав>∙0,282+ F>н>∙0,597-F>r>>4>∙ (0,282-0,095) =0,R>Ав>= 10,46 кН.
Схема нагружения в горизонтальной плоскости.
∑М>Аг>=0,R>Вг>∙0,282-F>t>>4>∙0,095=0,R>Вг>= 13,41 кН,
∑М>Вг>=0,R>Аг>∙0,282 - F>t>>4>∙ (0,282-0,095) =0,R>Аг>=26,39 кН.
Определяем суммарные реакции опор.
R>A>= кН,
кН,
R>В>= кН.
кН.
Осевая реакция.
Определяем осевые составляющие от радиальных нагрузок в опорах,
 ,
где е=tga=0,43
,
где е=tga=0,43
 кН,
кН,
 кН.
кН.
F>т>=8,8 кН
S>A>>S>B>
S>B> - S>A>=4,501 кН,
R>aA>= S>В>+ F>т> =13,113 кН,
R>a>>В>= S>В> =4,312 кН,
Определяем изгибающие моменты.
М'>В1>= R>Ав>∙0,095=0,994 кН∙м,
М>В2>= F>н> ∙0,597=0,24 кН∙м,
М>Г1>= R>Аг>∙0,095=2,6 кН∙м.
Определяем суммарный момент.
М '>сум>=
 кН∙м,
кН∙м,
М ''>сум>=
 кН∙м.
кН∙м.
Находим приведенные моменты.
М '>прив>=
 кН∙м,
кН∙м,
М ''>прив>=
 кН∙м.
кН∙м.
Находим амплитуду приведенного момента
М '>пра>=
 кН∙м
кН∙м
М ''>пра>=
 кН∙м
кН∙м
Входной вал:
Проверяем опасное сечение концентратор напряжения шестерня.
К>σ>=2,5, где К>σ - >эффективный коэффициент концентрации напряжений.
Определяем допускаемое напряжение при расчете на статическую прочность
[σ] >Ι>= ,
где S>T>=2,
,
где S>T>=2,

[σ] >Ι>= МПа.
МПа.
При проектировочном расчете запас усталостной прочности принимаем равным S=2
Допускаемое напряжение при расчете на усталостную прочность
[σ] >Ι Ι Ι>= МПа,
МПа,
Определяем диаметр вала из расчета на статическую прочность
 м.
м.
Определяем диаметр вала из расчета на усталостную прочность
 м
м
Промежуточный вал:
Проверяем опасное сечение концентратор напряжения шлицы К>σ>=2,5.
[σ] >Ι Ι Ι>= МПа
МПа
Проверяем опасное сечение концентратор напряжения напряженная посадка ступицы на вал К>σ>=4,5
[σ] >Ι Ι Ι>= МПа
МПа
Проверяем опасное сечение концентратор напряжения шестерня К>σ>=2,5.
[σ] >Ι Ι Ι>= МПа
МПа
Определяем диаметр вала из расчета на статическую прочность по шлицам
 м.
м.
Определяем диаметр вала из расчета на статическую прочность по шестерне
 м.
м.
Определяем диаметр вала из расчета на усталостную прочность по шлицам
 м
м
Определяем диаметр вала из расчета на усталостную прочность по напряженной посадки ступицы на вал
 м
м
Определяем диаметр вала из расчета на усталостную прочность по шестерне
 м
м
Выходной вал:
Проверяем опасное сечение концентратор напряжения шлицы К>σ>=2,5.
[σ] >Ι Ι Ι>= МПа
МПа
Проверяем опасное сечение концентратор напряжения напряженная посадка ступицы на вал К>σ>=4,5
[σ] >Ι Ι Ι>= МПа
МПа
Проверяем опасное сечение концентратор напряжения напряженная посадка кольца подшипника на вал К>σ>=4,5
[σ] >Ι Ι Ι>= МПа
МПа
Определяем диаметр вала из расчета на статическую прочность по шлицам
 м.
м.
Определяем диаметр вала из расчета на статическую прочность по кольцу подшипника
 м.
м.
Определяем диаметр вала из расчета на усталостную прочность по шлицам
 м
м
Определяем диаметр вала из расчета на усталостную прочность по напряженной посадки ступицы на вал
 м
м
Определяем диаметр вала из расчета на усталостную прочность по кольцу подшипника
 м
м
7.3.1 Проверочный расчет валов на выносливость
Входной вал:
Проверяем запас прочности по приделу выносливости в сечение где концентратор напряжения является шестерня
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=1,735 по кручению К>τ>=1,59
Значение масштабных факторов по изгибу ε>σ>=0,62 по кручению ε>τ>=0,74, d=120 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8.
Значение коэффициента учитывающего влияние асимметрии цикла при кручении принимаем ψ>τ>=0,15
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
 м3
м3
Так как действующая нагрузка неподвижна относительно корпуса, дисбалансная нагрузка отсутствует, а осевую нагрузку в следствии малости не принимаем в расчет, средние напряжение цикла можно принять равным нулю, т.е. σ>ср>=0. Определяем запас усталостной прочности по шестерне.
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратор напряжений является галтель R=2 мм d>1>=55 мм, d>2=>61мм.
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=1,735 по кручению К>τ>=2,21
Значение масштабных факторов по изгибу ε>σ>=0,7 по кручению ε>τ>=0,76, d=55 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе
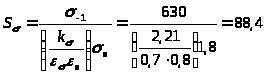
Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Определяем в этом сечение запас статической прочности по пределу текучести: минимальное напряжение изгиба
 МПа,
МПа,
максимальное напряжение кручения
 МПа
МПа
Коэффициенты запаса прочности составляют:



Что значительно выше допустимых
Промежуточный вал:
Проверяем сечение где концентратором напряжений является шлицы
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=1,75 по кручению К>τ>=1,6
Значение масштабных факторов по изгибу ε>σ>=0,67 по кручению ε>τ>=0,74, d=65 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8.
Значение коэффициента учитывающего влияние асимметрии цикла при кручении принимаем ψ>τ>=0,15
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратором напряжений является напрессованное зубчатое колесо
Значение эффективных коэффициентов концентрации принимаем по изгибу к>σ>/ε>σ>=3,98 по кручению к>τ>/ε>τ>=2,83
Значение коэффициента чистоты поверхности ε>n>=0,8
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратором напряжений является шестерня
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=1,75 по кручению К>τ>=1,6
Значение масштабных факторов по изгибу ε>σ>=0,64 по кручению ε>τ>=0,72, d=100 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8.
Значение коэффициента учитывающего влияние асимметрии цикла при кручении принимаем ψ>τ>=0,15
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратор напряжений является галтель R=1,5 мм d>1>=65 мм, d>2=>114мм.
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=3 по кручению К>τ>=2,5
Значение масштабных факторов по изгибу ε>σ>=0,67 по кручению ε>τ>=0,74, d=65 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Что меньше допускаемого. Применяем в качестве упрочняющей технологии дробеструйную обработку, что повысит придел выносливости на 70%. S=1,7∙S=2.85
Определяем в этом сечение запас статической прочности по пределу текучести: минимальное напряжение изгиба
 МПа,
МПа,
максимальное напряжение кручения
 МПа
МПа
Коэффициенты запаса прочности составляют:



Что является выше допустимого
Выходной вал:
Проверяем сечение где концентратором напряжений является шлицы
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=1,75 по кручению К>τ>=1,6
Значение масштабных факторов по изгибу ε>σ>=0,64 по кручению ε>τ>=0,72, d=86 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8.
Значение коэффициента учитывающего влияние асимметрии цикла при кручении принимаем ψ>τ>=0,15
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
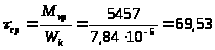 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратором напряжений является напрессованное зубчатое колесо. Значение эффективных коэффициентов концентрации принимаем по изгибу к>σ>/ε>σ>=3,98 по кручению к>τ>/ε>τ>=2,83
Значение коэффициента чистоты поверхности ε>n>=0,8
 м3,
м3,
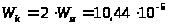 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
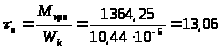 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратором напряжений является напрессованное кольцо подшипника
Значение эффективных коэффициентов концентрации принимаем по изгибу к>σ>/ε>σ>=4,1 по кручению к>τ>/ε>τ>=3
Значение коэффициента чистоты поверхности ε>n>=1
 м3
м3
 м3
м3
Амплитуда изгибных напряжений
 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Проверяем сечение где концентратор напряжений является галтель R=2 мм d>1>=92 мм, d>2=>100мм.
Значение эффективных коэффициентов концентрации принимаем по изгибу К>σ>=2,66 по кручению К>τ>=2,4
Значение масштабных факторов по изгибу ε>σ>=0,64 по кручению ε>τ>=0,72, d=92 мм.
Значение коэффициента чистоты поверхности ε>n>=0,8
Определяем моменты сопротивления изгибу и кручению.
 м3
м3
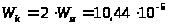 м3
м3
Амплитуда изгибных напряжений
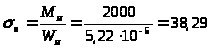 МПа;
МПа;
Номинальное (средние) напряжение кручения
 МПа;
МПа;
амплитуда напряжений кручения
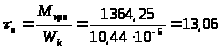 МПа
МПа
Определяем коэффициент запаса прочности при изгибе

Определяем коэффициент запаса при кручение

Запас прочности по усталости в данном сечение

Определяем в этом сечение запас статической прочности по пределу текучести: минимальное напряжение изгиба
 МПа,
МПа,
максимальное напряжение кручения
 МПа
МПа
Коэффициенты запаса прочности составляют:



Что является выше допустимого
Все опасные сечения были проверены на выносливость.
7.4. Расчёт долговечности подшипников качения
Для всех подшипников принимаем:
Кинетический коэффициент V=1, т.к в каждом случае вращается внутреннее кольцо, а наружное неподвижно относительно приложенной нагрузки;
Коэффициент безопасности K>> = 1,2;
Температурный коэффициент K>t> = 1.
Расчет долговечности подшипников входного вала
Выбраны подшипники - 176311 и 2111
Опора 176311 шарикоподшипник радиально - упорный, его динамическая грузоподъемность равна С=65000 Н, статическая С>0>=52600 Н
Динамическая приведенная нагрузка равна:
 ,
,
 ,
,
 Н
Н
Долговечность подшипника равна:
 млн. обр.
млн. обр.
 ч< t>h>=1600
ч
ч< t>h>=1600
ч
Чтобы повысить ресурс подшипника применяем более качественную подшипниковую сталь электрошлакового переплава, которая повысит грузоподъёмность подшипника на 20%.
 млн. обр,
млн. обр,
 ч. > t>h>=1600
ч.
ч. > t>h>=1600
ч.
Значит устанавливаем окончательно подшипник 176311.
Опора 2111 роликоподшипник радиальный, его динамическая грузоподъемность равна С=32000 Н, статическая С>0>=24020 Н
Динамическая приведенная нагрузка равна:
 Н
Н
Долговечность подшипника равна:
 млн. обр.
млн. обр.
 ч> t>h>=1600
ч
ч> t>h>=1600
ч
Расчет долговечности подшипников промежуточного вала
Выбраны подшипники - 7212 и 7212
Опора 7212 конический роликоподшипник радиально - упорный, его динамическая грузоподъемность равна С=72200 Н, статическая С>0>=58400 Н.
Динамическая приведенная нагрузка равна:
 ,
,
 ,
,
 Н
Н
Долговечность подшипника равна:
 млн. обр.
млн. обр.
 ч< t>h>=1600
ч
ч< t>h>=1600
ч
Чтобы повысить ресурс подшипника применяем: более качественную подшипниковую сталь двойного (электрошлакового + вакуумно - дугового) переплава, которая повысит грузоподъёмность подшипника на 50%.
 млн. обр,
млн. обр,
 ч. > t>h>=1600
ч.
ч. > t>h>=1600
ч.
Значит устанавливаем окончательно подшипник 7212 из стали двойного (электрошлакового + вакуумно-дугового) переплава.
Опора 7212 конический роликоподшипник радиальный, его динамическая грузоподъемность равна С=72200 Н, статическая С>0>=58400 Н
Динамическая приведенная нагрузка равна:
 Н
Н
Долговечность подшипника равна:
 млн. обр.
млн. обр.
 ч> t>h>=1600
ч
ч> t>h>=1600
ч
В целях унификации окончательно устанавливаем подшипник 7212
Расчет долговечности подшипников выходного вала
Выбраны подшипники - 7217 и 7217
Опора 7217 конический роликоподшипник радиально - упорный, его динамическая грузоподъемность равна С=109000 Н, статическая С>0>=91400 Н.
Динамическая приведенная нагрузка равна:
 ,
,
 ,
,
 Н
Н
Долговечность подшипника равна:
 млн. обр.
млн. обр.
 ч> t>h>=1600
ч
ч> t>h>=1600
ч
Значит устанавливаем окончательно подшипник 7217.
Опора 7217 конический роликоподшипник радиальный, его динамическая грузоподъемность равна С=109000 Н, статическая С>0>=91400 Н
Динамическая приведенная нагрузка равна:
 Н
Н
Долговечность подшипника равна:
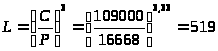 млн. обр.
млн. обр.
 ч> t>h>=1600
ч
ч> t>h>=1600
ч
В целях унификации окончательно устанавливаем подшипник 7212
8. Расчет шлицевых соединений
Шлицевые соединения рассчитываются на напряжения смятия:
 ,
,
Где R - средний радиус шлицев; f - коэффициент высоты профиля; i =0,8 для шлицев воспринимающих нагрузку; L - длина шлицев.
Допускаемое напряжение смятия [σ>см>] =100 МПа.
Входной вал:
Модуль m=2 мм; число зубьев Z=22; L=45 мм.
 .
.
Промежуточный вал:
Модуль m=2 мм; число зубьев Z=32; L=65 мм
 .
.
Выходной вал:
Модуль m=3 мм; число зубьев Z=29; L=68 мм

Модуль m=3 мм; число зубьев Z=22; L=70 мм

9. Система смазки
Для смазывания зубчатых передач, подшипников качения, шлицевых соединений применяем циркуляционную систему смазки. Масло из поддона редуктора поступает по системе каналов к точкам смазывания ответственных узлов подшипников и зубчатых колес охлаждая и защищая от разрушения, горячие масло сливается обратно в поддон где охлаждается до нужной температуры после чего процесс повторяется. В качестве смазочного материала выбираем минеральное масло МН-7,5У ГОСТ 17748-72 которое наилучшим образом подходит под наши требования.
В качестве уплотнительных устройств применяем манжетные уплотнения из-за их надежности.
Заключение
В данной работе произведён расчёт конической и цилиндрической зубчатых передач редуктора вертолёта. Выбран материал для зубчатых колёс и определены допускаемые напряжения. Определены геометрические параметры зубчатых передач. Выполнены кинематический и энергетический расчёты редуктора. Проведена проверка прочности зубчатых передач по контактным и изгибным напряжениям. Выполнена проверка на статическую прочность при перегрузке. Проведен подбор и расчет подшипников на долговечность, проектировочный и проверочные расчеты валов, расчет шлицевых соединений, резьбовых, продумана система смазки, уплотнения.
Список использованных источников
1. “Оси, валы и опоры качения" А.М. Циприн, М.И. Курушин, Е.П. Жильников. Куйбышев, КуАИ, 1976.
2. ”Подшипники качения" Справочник-каталог. Под. ред.В.Н. Нарышкина и Р.В. Коросташевского.М., Машиностроение, 1984.
3. ”Конструирование узлов и деталей машин" П.Ф. Дунаев, О.П. Леликов. М., Выс. шк., 1985
4. ”Курсовое проектирование деталей машин" В.Н. Кудрявцев и др., Л., Машиностроение, 1984.
5. ”Расчёт на прочность цилиндрической зубчатой передачи с использованием ЭВМ “ Электроника ДЗ-28 ".
6. ”Курсовое проектирование по деталям машин для авиационных специальностей".
7. “Расчет соединения вал-ступица ", Метод. указания.