Однозонный тиристорный электропривод постоянного тока

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

И ПОСЛЕВУЗОВСКОГО ОБРАЗОВАНИЯ

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Электропривод и автоматизация промышленных установок

Заведующий кафедрой

Хватов С.В.

(подпись) (фамилия. и. о.)

(дата)

Однозонный тиристорный электропривод постоянного тока

с обратной связью по ЭДС и стабилизацией тока возбуждения двигателя

(наименование темы проекта или работы)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту

(вид документа)

вариант 2.7

(номер варианта)

РУКОВОДИТЕЛЬ

Соколов В.В.

(подпись) (фамилия. и. о.)

(дата)

СТУДЕНТ

Кирасиров Д.В.

(подпись) (фамилия. и. о.)

04-ЭПА

(дата) (группа или шифр)

Проект защищен (дата)

Протокол №

С оценкой

Нижний Новгород 2008 г.

СОДЕРЖАНИЕ

Исходные данные

Введение

1. Выбор основного оборудования

2. Функциональная схема электропривода

3. Расчёт параметров силовой цепи электропривода

4. Расчёт запаса по напряжению

5. Расчёт параметров регулятора тока якоря и ЭДС

6. Расчёт параметров регулятора тока возбуждения

7. Расчёт скоростных характеристик и их статизма в разомкнутой и замкнутой системе электропривода

8. Расчёт величины динамического падения скорости двигателя при набросе момента нагрузки

9. Оценка влияния внутренней обратной связи по ЭДС на процессы, протекающие в контуре тока

10. Исследование динамических процессов в контуре тока якоря и ЭДС на цифровой модели

Перечень элементов

ИСХОДНЫЕ ДАННЫЕ

Тип двигателя: П132-4К;

Номинальная мощность: Р>н>> >= 75 кВт;

Номинальное напряжение: U>н> = 220 В;

Номинальный ток: I>н> = 385 А;

Номинальная частота вращения: n>н> = 300 об/мин;

Момент инерции: J>м> = 100 кгм2;

Передаточное отношение редуктора: К>р> = 5;

Тип ЭП: реверсивный.

Данные электродвигателя

Номинальная мощность: Р>н>> >= 75 кВт;

Номинальное напряжение: U>н> = 220 В;

Номинальный ток: I>н> = 385 А;

Номинальная частота вращения: n>н> = 300 об/мин;

Максимальная частота вращения: n>МАКС>=1500 об/мин;

Максимальный ток: I>max>> >= 2,5I>н>;

Маховой момент: GD2 = 73 кгм2;

Число полюсов: 2р = 4;

Число витков обмотки якоря: w>я> = 135;

Сопротивление обмотки якоря при 20С: R>я> = 0,025 Ом;

Число параллельных ветвей обмотки якоря: 2а = 2;

Сопротивление добавочных полюсов при 20С: R>дп> = 0,004 Ом;

Число витков на полюс: w>в> = 639;

Сопротивление обмотки главных полюсов: R>ов> = 12 Ом;

ВВЕДЕНИЕ

Целью данного курсовой работы является разработка однозонного реверсивного тиристорного электропривода постоянного тока с обратной связью по ЭДС и стабилизацией тока возбуждения двигателя.

Данный электропривод постоянного тока разрабатывается на основе комплектного тиристорного электропривода ЭПУ.

Применение тиристорного электропривода позволяет оптимизировать его работу на отработку необходимых технологических операций. В данной курсовой работе необходимо стабилизировать скорость вращения электродвигателя при помощи обратной связи по ЭДС и стабилизации тока возбуждения двигателя. Это осуществляется путём нахождения требуемых регуляторов и расчёта их параметров.

1 ВЫБОР ОСНОВНОГО ОБОРУДОВАНИЯ

Тиристорный преобразователь:

ЭПУ 1М 46 27 Е УХЛ4

Модификация по выпрямленному напряжению блока управления (115 В)

Напряжение питающей сети (380 В, 50 Гц)

Функциональная характеристика (однозонный, главного движения с обратной связью по ЭДС )

Климатическое исполнение

Категория размещения

Силовой согласующий трансформатор:

Тип: ТСЗП-200/0,7;

Напряжение сетевой обмотки: U>1> = 0,38 кВ;

Фазное напряжение вентильной обмотки: U>2ф> = 117 В;

Напряжение короткого замыкания: U>к> = 5,2 %;

Потери короткого замыкания: Р>кз> = 2960 Вт;

Номинальный выпрямленный ток I>d>>н >= 500 А.

Сглаживающий дроссель:

Тип: ФРОС-125/0,5;

Индуктивность: L>сд> = 0,75 мГн;

Потери в меди при номинальном выпрямленном токе: Р>сд> = 960 Вт.

Шунт:

Шунт в цепи якоря выбираем из условия, чтобы его номинальный ток был не меньше номинального тока двигателя. Номинальный ток двигателя I>н> = 385 А, т. о. выбираю шунт типа 75 ШСМ на номинальный ток I>шня> = 500 А и номинальное напряжение U>шн> = 75 мВ.

Задатчик регулируемой величины:

В качестве задатчика скорости выбираем потенциометр типа ППБ – 15 –1000 Ом. Т.к U>п> = 15 В, а U>з(max)> = 10 В, последовательно необходимо включить добавочный резистор, R>доб> = 500 Ом, на котором будет погашено излишне напряжение.

В состав электропривода входит:

- блок управления,

- электродвигатель,

- трансформатор,

- сглаживающий реактор,

- источник питания обмотки возбуждения,

- блок ввода (для подключения возбудителя к сети).

Электропривод выполнен с принудительным охлаждением, защита преобразователя производится автоматическими выключателями.

Обмотка возбуждения подключается к двум фазам вторичной силовой обмотки трансформатора. Тиристорный преобразователь возбудителя ТПВ выполнен по однофазной мостовой схеме.

Управление тиристорами ТПЯ производится от трехканальной СИФУ, содержащей формирователи импульсов ФИ1—ФИЗ. Ввод управляющего сигна­ла в СИФУ, регулирование углов и их ограничение осуществляется с помощью переменных резисторов в управляющем органе (УО) СИФУ. Переключение импульсов управления в преобразователе ТПЯ производится блоком логи­ческого устройства ЛУ, которое работает в функции сигнала заданного направления тока и выходного сигнала датчика проводимости вентилей ДП.

Токоограничение обеспечивается за счет ограничения выходного напряжения регулятора ЭДС. При этом исключение бросков тока осуществляется за счет ограничения выходного напряжения регулятора тока.

2 ФУНКЦИОНАЛЬНАЯ СХЕМА ЭЛЕКТРОПРИВОДА

Данная система с регулированием скорости и стабилизацией тока возбуждения построена по принципу подчиненного регулирования и имеет два контура регулирования: внутренний контур тока якоря и внешний контур ЭДС, а также независимый контур тока возбуждения.

Во внутренний контур тока якоря входят: регулятор тока якоря, вентильный преобразователь якоря двигателя ВПЯ, якорная цепь двигателя и датчик тока якоря.

Внешний контур ЭДС состоит из регулятора ЭДС, замкнутого контура тока якоря, механической цепи двигателя и датчика напряжения.

В данной системе существует два способа ограничения тока якоря двигателя: путем ограничения выходного сигнала регулятора ЭДС, который является задающим сигналом на ток, и за счет “токовой стенки”, реализованной в ЭПУ.

Рассматривая работу системы при набросе момента нагрузки.

Предполагаем, что двигатель пускался на холостом ходу и к моменту наброса нагрузки вышел на заданную скорость. На входе регуляторов тока и ЭДС нули. После появления момента нагрузки по якорю начинает протекать статический ток, а скорость двигателя начинает уменьшаться. В результате на входе регулятора ЭДС возникает сигнал рассогласования положительного знака, а на вход регулятора тока подается отрицательный сигнал обратной связи по току. По мере уменьшения скорости растет рассогласование на входе регулятора ЭДС и пропорционально растет выходной сигнал регулятора, который компенсирует сигнал отрицательной обратной связи по току. В некоторый момент времени скорость уменьшается до той величины, при которой сигнал на входе регулятора тока становиться равным нулю. Это момент окончания переходного процесса. Система входит в установившийся режим с некоторой ошибкой по скорости.



Рисунок 2.1 – Функциональная схема электропривода

3 РАСЧЕТ ПАРАМЕТРОВ СИЛОВОЙ ЦЕПИ ЭЛЕКТРОПРИВОДА

Падение напряжения на щеточном контакте принимаем равным

U>щ>=2 В.

Номинальная угловая скорость

рад/с. (3.1)

Сопротивление якорной цепи электродвигателя

Ом. (3.2)

где β>т> – коэффициент, учитывающий изменение сопротивления обмоток при нагреве на 60С, β>т> = 1.24.

Номинальная ЭДС электродвигателя

В. (3.3)

Конструктивный коэффициент электродвигателя

, (3.4)

где – число витков обмотки якоря, = 135 витка;

2а – число параллельных ветвей, 2а = 2;

2р – число полюсов, 2р = 4.

Коэффициент ЭДС и момента электродвигателя

вс/рад. (3.5)

Номинальный поток

Вб. (3.6)

Сопротивление обмотки возбуждения при температуре 80 С

Ом . (3.7)

Номинальный ток возбуждения

А . (3.8)

Коэффициент наклона кривой намагничивания при Ф = Ф>н>

Вб/А , (3.9)

где определяется по кривой намагничивания [1].

Индуктивность обмотки возбуждения

Гн. (3.10)

Электромагнитная постоянная времени цепи возбуждения

с. (3.11)

Постоянная времени контура вихревых токов

с . (3.12)

Индуктивность якоря двигателя

Гн , (3.13)

где = 0.1 – для компенсированных машин.

Электромагнитная постоянная времени якоря электродвигателя

с. (3.14)

Момент инерции двигателя

кгм2 . (3.15)

Момент инерции механизма, приведенный к валу электродвигателя

кгм2.> >(3.16)

Момент инерции привода

кгм2. (3.17)

Номинальный момент электродвигателя

Нм. (3.18)

Максимальное ускорение электродвигателя при пуске от задатчика интенсивности

рад/с2 >,> (3.19)

при М>дин> = М>н>.

Приведенное к цепи выпрямленного тока сопротивление трансформатора

Ом. (3.20)

Максимальная выпрямленная эдс преобразователя цепи якоря

В. (3.21)

где k>сх1> = 2.34 – коэффициент трехфазной мостовой схемы выпрямления.

Индуктивное сопротивление трансформатора, приведенное к цепи вторичной обмотки

Ом. (3.22)

где k>сх2> = 0,815 – для трехфазной мостовой схемы выпрямления.

Эквивалентное сопротивление трансформатора, учитывающее снижение выпрямленного напряжения при коммутации вентиля

Ом. (3.23)

Сопротивление сглаживающего дросселя

Ом. (3.24)

Сопротивление шин и кабелей

Ом. (3.25)

Сопротивление цепи ТП – якорь двигателя

. 3.26)

Индуктивность рассеяния трансформатора

Гн. (3.27)

Индуктивность цепи ТП – электродвигатель

Гн. (3.28)

Максимальное значение коэффициента усиления ТП в цепи якоря с СИФУ, выполненной по вертикальному принципу управления с пилообразным напряжением сравнения

. (3.29)

где U>оп> – амплитуда опорного напряжения в СИФУ, U>оп> = 10 В.

Электромагнитная постоянная времени цепи ТП – электродвигатель

с . (3.30)

Электромеханическая постоянная времени

с. (3.31)

Передаточный коэффициент шунта в цепи якоря

Ом. (3.32)

Коэффициент усилителя датчика тока якоря

. (3.33)

Коэффициент передачи усилителя датчика тока якоря

, (3.34)

где U>ДТ>>max> – максимально допустимое значение напряжения на выходе датчика тока, U>ДТ>>max> = 10 В.

Шунт в цепи возбуждения выбираю по номинальному току возбуждения электродвигателя. Выбираем шунт на ток I>ншв> = 15 А.

Передаточный коэффициент шунта в цепи возбуждения

. (3.35)

Коэффициент усилителя датчика тока в цепи возбуждения

Напряжение датчика тока возбуждения принимаю 4,5 В, тогда

, Ом. (3.36)

Коэффициент передачи усилителя датчика тока якоря

. (3.37)

Не скомпенсированные постоянные времени контуров тока якоря и тока возбуждения примем Т>> = 0.005 с; Т>>>в> = 0.04 с.

4 РАСЧЕТ ЗАПАСА ПО НАПРЯЖЕНИЮ

Определяем необходимый запас по напряжению

, (4.1)

где , (4.2)

где E>дн> – номинальная ЭДС двигателя.

E>дн> = 204 В,

ΔE>дзап> = max {ΔE>d>>стат>; ΔE>d>>дин>} (4.3)

ΔE>d>>стат> = I>max>∙R>э> =2.5∙385·0.069 = 66.6 В. (4.4)

В. (4.5)

.

Определяю фактический коэффициент запаса

. (4.6)

Предельная величина ЭДС, до которой будет осуществляться настройка контура на модульный оптимум

E>dпред> = E>doя> – E>dзап> = 273.1 – 124.9 = 144.1 В. (4.7)

Предельная ЭДС двигателя при снижении напряжении питающей сети на 10%

E>dпред> = E>doя> – E>dзап> = 0.9∙273.1 – 124.9 = 117.2 В. (4.7)

. (4.8)

По полученному значению следует, что настройка на модульный оптимум будет выполняться в достаточно большом диапазоне скоростей.

5 РАСЧЕТ ПАРАМЕТРОВ РЕГУЛЯТОРОВ ТОКА ЯКОРЯ И ЭДС

Оптимизацию системы, построенной по принципу подчинённого регулирования, начинаем с внутреннего контура тока якоря.

5.1 Контур тока якоря

5.1.1 Оптимизация контура тока якоря

РТ – регулятор тока;

ТП – тиристорный преобразователь якоря двигателя;

ЯЦ – якорная цепь двигателя;

ДТ – датчик тока.

Рисунок 5.1 – Структурная схема контура тока якоря

Оптимизацию проводим при допущениях:

1) датчик тока считаем без инерционным

(5.1.1.1)

2) все малые инерционности, которые имеет контур, включены на входе ТП:

. (5.1.1.2)

3) ЭД заторможен (Е = 0) или (Е  0), а значит отсутствует ОС по ЭДС.

Оптимизируем контур тока на модульный оптимум

, (5.1.1.3)

тогда

, (5.1.1.4)

где (5.1.1.5)

Получили пропорционально-интегральный регулятор (ПИ - регулятор) тока.

Передаточная функция замкнутого контура тока имеет вид

. (5.1.1.6)

Т. к. величина Т>> мала, то слагаемым можно пренебречь, тогда считаем , получаем

(5.1.1.7)

где Т>т> = 2∙Т>µ> – эквивалентная постоянная времени настроенного на модульный оптимум контура тока.

Структурная схема замкнутого контура тока имеет вид:

U>зт>

I>d>


Рисунок 5.2 – Структурная схема замкнутого контура тока

5.1.2 Расчёт параметров регулятора тока якоря

Рисунок 5.3 – Регулятор тока якоря

Коэффициент регулятора тока

. (5.1.2.1)

Задаемся величиной ёмкости конденсатора в цепи обратной связи операционного усилителя регулятора тока Ф

Сопротивление резистора в цепи обратной связи операционного усилителя регулятора тока


Ом . (5.1.2.2)

Сопротивление в цепи датчика тока

Ом. (5.1.2.3)

Чтобы в установившемся режиме сигнал РТ не изменялся, нужно, чтобы входной ток не поступал в канал ОС. , считаем

Ом. (5.1.2.4)

Коэффициент усилителя датчика тока якоря определён в разделе 3.

Принимаем R>1> = 5 кОм, тогда

R>2> = R>1>∙k>удтя> = 5∙66.6=333 кОм. (5.1.2.5)

5.2 Контур ЭДС

5.2.1 Оптимизация контура ЭДС

РЭ – регулятор ЭДС;

ЗКТ – замкнутый контур тока;

ЭМ – электромеханическая часть двигателя;

ДЭ – датчик ЭДС.

Т>яц> – постоянная времени якорной цепи двигателя, с которой снимается сигнал обратной связи по ЭДС.

Рисунок 5.4 – Структурная схема контура ЭДС

Допущение:

Ic = 0 (Х.Х.)

В контуре есть два звена с малыми постоянными времени, которые включены последовательно и поэтому могут быть преобразованы к одному звену с малой постоянной времени, равной их сумме

(5.2.1.1)

где Т>>>э> – малая постоянная времени контура ЭДС, c.

Т>>>э> = Т>т> + Т>яц> (5.2.1.2)

Передаточная функция разомкнутого контура ЭДС, настроенного на модульный оптимум

, (5.2.1.3)

откуда

. (5.2.1.4)

Получил пропорциональный регулятор (П-регулятор) ЭДС.

С таким регулятором система будет астатичной по заданию (при отсутствии возмущающего воздействия) и статичной по возмущению.

Передаточная функция замкнутого контура ЭДС

. (5.2.1.5)

Таким образом, в замкнутой передаточной функции контура ЭДС присутствует форсирующее звено.

Из-за наличия инерционности в датчике ЭДС переходный процесс будет идти с большим перерегулированием. Для уменьшения перерегулирования на вход системы включаю фильтр с постоянной времени, равной инерционности датчика.

Передаточная функция фильтра .

(5.2.1.6)

Структурная схема замкнутого контура ЭДС имеет вид:

ЗЭК+Ф


ЭМ2



U>зэ>



Рисунок 5.6 – Структурная схема замкнутого контура ЭДС

5.2.2 Расчет параметров регулятора ЭДС с применением датчика напряжения

Рисунок 5.7 – Регулятор ЭДС

Коэффициент датчика напряжения

. (5.2.2.1)

Коэффициент передачи регулятора ЭДС

. (5.2.2.2)

Задаемся ёмкостью в цепи датчика напряжения С>дн> = 1 мкФ.

Сопротивление в цепи датчика напряжения:

если RI>дн> = RII>дн> = 0,5∙R>дн>, то .

Ом. (5.2.2.3)

(5.2.2.4)

Сопротивление в цепи обратной связи операционного усилителя регулятора напряжения:

R>оэ> = k>рэ>R>дн> = 0.547= 129.3 кОм. (5.2.2.5)

Сопротивление в цепи задания ЭДС находим из условий установившегося режима:

, I>зэ> = I>дн>, т.е. U>зэ>max = U>дн>max = 10 В, следовательно

R>зэ> = R>дн> =129.3 кОм. (5.2.2.6)

Ёмкость фильтра в цепи определяем из условия

если RI>зэ> = RII>зэ> = 0,5∙R>зэ>, то .

При R>зэ >= R>дн> С>ф> = С>дн> = 1 мкФ.

Сопротивление резистора токовой компенсации находим из условий режима стопорения двигателя: Е>д> = 0 , U>дэ> = 0.

.

U>дт> = Ik>дт>, U>дн> = U>д>k>дн> = I R>a>k>дн>,

кОм. (5.2.2.7)

Сопротивления резисторов делителя. Считая k>пр> = 1 и принимая R>3> = 1 кОм, выражаю R>4>

кОм. (5.2.2.8)

Ограничение выходного сигнала регулятора ЭДС осуществляется двумя встречно включенными стабилитронами VD1 и VD2 . Поскольку выходной сигнал регулятора ЭДС является сигналом задания на ток, то его ограничение приводит к ограничению тока двигателя на уровне максимально допустимого.

Падение напряжения на стабилитронах принимаем ΔU>ст> = 1 В, максимально допустимое напряжение задания на ток U>зт>max = 10 В.

Тогда напряжение на стабилитронах будет равным

U>VD>>1> = U>VD>>2> = U>зт>max – ΔU>ст> = 10 – 1 = 9 В. (5.2.2.9)

6 РАСЧЁТ ПАРАМЕТРОВ РЕГУЛЯТОРА ТОКА ВОЗБУЖДЕНИЯ

6.1 Оптимизация контура тока возбуждения

Так как привод однозонный, то оптимизацию контура тока возбуждения проводим для точки Ф>н>.

РТВ – регулятор тока возбуждения;

ТПВ – тиристорный преобразователь обмотки возбуждения;

ОВ – электрическая цепь обмотки возбуждения;

МЦ – магнитная цепь обмотки возбуждения;

ДТВ – датчик тока возбуждения.

Рисунок 6.1 – Структурная схема контура тока возбуждения

Проводим оптимизацию контура тока на модульный оптимум. Для разомкнутой системы:

. (6.1.1)

Передаточная функция регулятора тока возбуждения

, (6.1.2)

где k>ртв> – коэффициент регулятора тока.

Получаем пропорционально-интегральный регулятор (ПИ-регулятор) контура тока возбуждения.

6.2 Расчёт параметров регулятора тока возбуждения

Рисунок 6.2 – Принципиальная схема стабилизации тока возбуждения

Коэффициент тиристорного преобразователя цепи возбуждения

, (6.2.1)

где E>d>>0В> – максимальная выпрямленная ЭДС преобразователя цепи возбуждения;

α – номинальный угол управления преобразователя.

В. (6.2.2)

. (6.2.3)

. (6.2.4)

. (6.2.5)

Определяем коэффициент регулятора тока возбуждения

, (6.2.6)

где T>В∑> - электромагнитная постоянная времени.

T>В∑> = T>в> + T>вт> = 0.624 + 0.062= 0.686. (6.2.7)

Задаюсь величиной емкости конденсатора в цепи датчика тока возбуждения

C>дтв> = 5 мкФ.

Определяю сопротивление датчика тока возбуждения

кОм. (6.2.8)

Определяем сопротивление обратной связи регулятора тока возбуждения

R>отв> = k>ртв>∙R>дтв> = ∙= 321.2 кОм. (6.2.9)

Сопротивление резистора в цепи задатчика тока возбуждения

кОм. (6.2.10)

Задаемся сопротивлением R>5> = 5 кОм.

Находим сопротивление R>6>

кОм. (6.2.11)

7 РАСЧЁТ СКОРОСТНЫХ ХАРАКТЕРИСТИК И ИХ СТАТИЗМА В РАЗОМКНУТОЙ И ЗАМКНУТОЙ СИСТЕМЕ ЭЛЕКТРОПРИВОДА

Механические характеристики двигателя постоянного тока линейны, поэтому их построение произвожу по двум точкам, соответствующим режимам холостого хода и номинальной нагрузки.

Выражение для расчета механических характеристик имеет вид

Ω = Ω>0> – Δ Ω, (7.1)

где Ω>0> –– угловая скорость идеального холостого хода.

рад/с. (7.2)

Падение скорости при номинальной нагрузке на естественной характеристике

рад/с. (7.3)

Падение скорости при номинальной нагрузке в разомкнутой системе

рад/с. (7.4)

Падение скорости при номинальной нагрузке в замкнутой системе

рад/с. (7.5)

Рисунок 7.1 – Скоростные характеристики электропривода

Статизм естественной характеристики

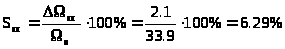. (7.6)

Статизм характеристики разомкнутой системы

. (7.7)

Статизм характеристики замкнутой системы

. (7.8)

Напряжение задания на скорость холостого хода >о>

U>ЗС1> = >о>k>дн>C>e>Ф>н> = 33.90.04585.940.076 = 10 В. (7.9)

Напряжение задания на скорость холостого хода  = 0,7∙>о> на искусственной механической характеристике при пониженном напряжении

U>ЗС2> = 0,7>о>k>дн>C>e>Ф>н> = 0.733.90.04585.940.076 = 7 В. (7.10)

Из полученных графиков механических характеристик можно сказать, что естественная характеристика самая жесткая, характеристика разомкнутой системы более мягкая, чем естественная, а характеристика замкнутой системы – самая мягкая.

Большая мягкость механической характеристики – недостаток замкнутой системы, но в то же время система настроена на модульный оптимум и переходные процессы будут идти с малым (4,3 %) перерегулированием и достаточно высоким (8,4Т>>) быстродействием.

При наличие датчика ЭДС, имея соответственную обвязку этого датчика, можно в определенном частотном диапазоне скомпенсировать инерционность датчика, что позволит повысить жесткость механической характеристики.

8 РАСЧЁТ ВЕЛИЧИНЫ ДИНАМИЧЕСКОГО ПАДЕНИЯ СКОРОСТИ ДВИГАТЕЛЯ ПРИ НАБРОСЕ МОМЕНТА НАГРУЗКИ

Рисунок 8.1 – Структурная схема контура тока якоря по возмущению

Находим передаточную функцию замкнутого контура ЭДС по возмущению

. (8.1)

Установившейся режим:

. (8.2)

Структурная схема замкнутого контура ЭДС имеет вид:

Ic

Ω



Рисунок 8.2 – Структурная схема замкнутого контура ЭДС

Падение скорости в разомкнутой системе по Лапласу имеет вид

. (8.3)

Следовательно, падение скорости в замкнутой системе в операторной форме запишется

. (8.4)

Воспользуемся программой Maht Cad для перехода от изображения к оригиналу, падение скорости в замкнутой системе запишется

. (8.5)

На рисунке представлена кривая изменения падения скорости  в функции времени t, получаемая пересчетом кривой изменения относительного падения скорости  = />Iн>зс в функции относительного времени  = t/T>>>э>. Параметры переходного процесса соответствуют настройке на модульный оптимум.

Рисунок 8.3 – Кривая изменение скорости при набросе момента

Переходный процесс идет с перерегулированием 4,3% и быстродействием 8,4Т>>.

9 ОЦЕНКА ВЛИЯНИЯ ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗИ ПО ЭДС

НА ПРОЦЕССЫ, ПРОТЕКАЮЩИЕ В КОНТУРЕ ТОКА

Рисунок 9.1 – Структурная схема контура регулирования тока якоря с учетом действия внутренней обратной связи по ЭДС.

При исследовании считаем, что нагрузки на валу нет, т.е. I>c> = 0.

Передаточная функция звена якорной цепи с учетом влияния внутренней обратной связи по ЭДС

. (9.1)

Передаточная функция звена якорной цепи в данном случае обладает дифференцирующими свойствами, следовательно, компенсирует интегральные свойства регулятора.

Определяю передаточную функцию разомкнутого контура тока с учетом действия внутренней обратной связи по ЭДС и регулятором, рассчитанным на режим заторможенного двигателя


(9.1) (9.2)

Передаточная функцию замкнутого контура тока с учетом действия внутренней обратной связи по ЭДС:

(9.3)

В установившемся режиме:

. (9.4)

В контуре тока без учета действия внутренней обратной связи по ЭДС

Структурная схема.

Рисунок 9.2 – Структурная схема

, (9.5)

где (9.6)

. (9.7)

Контур тока, который с ПИ-регулятором был астатическим при заторможенном роторе, становится статическим в переходном режиме (Е  0). Ошибка регулирования тем больше, чем меньше постоянная времени Т>м>. Другое следствие влияния ОС по ЭДС это увеличенное перерегулирование. По отношению к новому установившемуся уровню тока перерегулирование увеличивается, но по абсолютной величине остается тем же.

Если ЭП имеет большую Т>м>, то за время выхода тока на заданный уровень ЭДС электродвигателя практически не меняется и ее влияние на ток минимально.

В ЭП с высокомоментными ЭД, где Т>м> мала, влияние внутренней ОС по ЭДС существенно, что иногда приходится учитывать изменением передаточной функции регулятора.

Для компенсации действия внутренней обратной связи по ЭДС иногда применяют более сложный регулятор, например, (ПИ)2 – типа.

10 ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В КОНТУРЕ ТОКА ЯКОРЯ И ЭДС НА ЦИФРОВОЙ МОДЕЛИ

10.1 Контур тока

Динамический ток I>дин> = 0.5∙I>н> = 0.5∙385 = 192.5 А.

Статический ток I>с> = 0.6 ∙I>н> = 0.6∙385 = 231 А.

Из пункта 7:

– напряжение задания на скорость холостого хода >о>U>ЗС1> = 10 В.

– напряжение задания на скорость холостого хода  = 0,7∙>о >U>ЗС2> = 7 В.

Рисунок 10.1 – Исследование настройки контура тока

На рисунке 10.1 представлены 9 графиков переходных процессов. Графики расположены слева направо по возрастанию постоянной времени регулятора , и сверху вниз по уменьшению коэффициента передачи регулятора k>Р>. На центральном графике - переходный процесс при настройке системы на модульный оптимум. Как видно из графиков, при увеличении постоянной времени регулятора уменьшается колебательность переходного процесса, а при уменьшении коэффициента передачи регулятора уменьшается перерегулирование. Оптимальный переходный процесс наблюдается в системе, настроенной на модульный оптимум. Его параметры: длительность процесса 8,4Т>µ>, перерегулирование 4,3%.

Рисунок 10.2 – Исследование контура тока

На рисунке 10.2 представлены переходные процессы в контуре тока. Как видно из графика, процессы носят апериодический характер, ток выходит на максимальный уровень в соответствии с сигналом задания с перерегулированием приблизительно 4%, причем при реверсе абсолютная величина перерегулирования больше в 2 раза, чем при пуске, поскольку больше фактическое задание на ток: при пуске фактическое задание с 0 на I>ст>, а при реверсе с I>ст> на –I>ст,> т. е. 2 I>ст> – в 2 раза больше.

10.2 Контур ЭДС

Рисунок 10.3 – Осциллограммы переходных процессов в контуре ЭДС

На рисунке 10.3 приведены кривые тока и скорости двигателя.

При разгоне на холостом ходу, без задатчика интенсивности, по якорю двигателя протекает динамический ток достаточно большой величины, идет разгон двигателя. После выхода двигателя на установившуюся скорость, ток в якоре спадает практически до нуля, т.к. разгон окончен и динамический ток равен нулю, а момент нагрузки еще не наброшен и, следовательно, статический ток равен нулю. При набросе момента нагрузки по якорю двигателя начинает протекать статический ток, а скорость двигателя уменьшается на некоторую величину ΔΩ, соответствующую падению скорости при данной нагрузке, что показывает, что система статическая по возмущению. Во время реверса ток в двигателе увеличивается за счет броска динамического тока и одновременно меняет свое направление. Когда переходный процесс реверса заканчивается, ток в двигателе спадает до статического значения, а при снятии нагрузки – уменьшается до нуля.

В последнем случае скорость двигателя увеличивается на величину падения скорости при набросе нагрузки ΔΩ. Далее идет процесс торможения на холостом ходу, при этом скорость двигателя уменьшается до нуля, а в якоре двигателя возникает динамический ток, обеспечивающий переходный процесс торможения.

П-регулятор ЭДС с применением задатчика интенсивности.

Рисунок 4 – Осциллограммы переходных процессов в контуре ЭДС с задатчиком интенсивности

В системе с задатчиком интенсивности кривые переходного процесса качественного имеют тот же вид, но более растянуты во времени, поскольку задатчик интенсивности ограничивает на заданном уровне динамический ток, обуславливающий ускорение.

ЛИТЕРАТУРА

1 Методические указания к курсовому проекту по дисциплине Системы управления электроприводами. / ГПИ. 1983г.

2 Справочник по электрическим машинам/ Под общ. ред. И.П. Копылова и Б.К. Клокова.- М.: Энергоатомиздат. 1988г.

3 Стандарт предприятия. Общие требования к оформлению пояснительных записок и чертежей. СТП-1-У-НГТУ-98. / НГТУ, Нижний Новгород, 1998 г.