Дюкер
Дюкер
Определение диаметра труб дюкера. Построение напорной и пьезометрической линии. Нахождение разности уровней воды в подводящем и отводящем участках канала
Курсовая работа Еронько Ирины 3016/I группы
МВ и ССО РФ
Санкт-Петербургский Государственный технический университет
Гидротехнический факультет, кафедра гидравлики
САНКТ-ПЕТЕРБУРГ
1996
Cодержание
1. Определение диаметра труб дюкера ( для случая , когда работает только одна труба дюкера)
2. Построение напорной и пьезометрической линии ( для случая , когда работает только одна труба дюкера )
3. Нахождение разности уровней воды в подводящем и отводящем участках канала ( для случая , когда работают обе трубы дюкера )
Литература
1. Определение диаметра труб дюкера ( для случая , когда работает только одна труба дюкера ) .
Свяжем уравнением Бернулли сечения 1-1 и 2-2 нашей системы . В общем виде оно выглядит следующим образом :
, ( 1.1 )
где
,
-
превышения над плоскостью сравнения
0-0 сечения 1-1 и 2-2 соответственно , м ;
,
- гидродинамические давления в сечениях
1-1 и 2-2 соответственно , Па ;
- удельный вес жидкости , Н/м3 ;
,
- коэффициенты ( коррективы ) кинетической
энергии ( коэффициенты Буссинеска ) для
сечения 1-1 и 2-2 соответственно ;
,
- средние скорости в сечениях 1-1 и 2-2
соответственно , м/с ;
-
ускорение свободного падения , м/с2 ;
- полная потеря напора , м .
В нашем случае
отдельные члены , входящие в это уравнение
имеют следующие значения :
;
;
;
,
где
-
наибольшая допустимая разность уровней
воды в подводящем и отводящем участках
канала , м .
Подставляя наши данные в уравнение ( 1.1 ) , получаем :
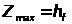( 1.2 )
Полная потеря напора
может быть выражена иначе :
, ( 1.3 )
где
- полный коэффициент сопротивления
трубы;
- скорость в трубе, м/с .
Подставим в выражение ( 1.2 ) выражение ( 1.3 ) , имеем :
( 1.4 )
и , следовательно ,
, ( 1.5 )
откуда
, ( 1.6 )
где
-
расход жидкости в трубе , м3/с ;
- коэффициент расхода ;
- площадь поперечного сечения трубы ,
м2 .
Полный коэффициент сопротивления трубы равен :
,
( 1.7 )
где
- сумма местных коэффициентов сопротивления;
- коэффициент сопротивления по длине .
В нашем случае имеют место следующие местные коэффициенты сопротивления :
, ( 1.8 )
где
- коэффициент сопротивления входной
решетки ;
- коэффициент сопротивления при резком
повороте ;
- коэффициент сопротивления выхода .
Коэффициент сопротивления по длине равен :
, ( 1.9 )
где
- коэффициент гидравлического трения
;
-
длина трубы , м ;
- диаметр поперечного сечения трубы , м
.
Подставляем формулы ( 1.8 ) и ( 1.9 ) в выражение ( 1.7 ) , имеем :
( 1.10 )
Найдем значения местных коэффициентов сопротивления :
а) коэффициент сопротивления входной решетки ищем по формуле Киршмера :
, ( 1.11 )
где
- средняя скорость перед решеткой , м/с
;
- потеря напора решетки , м ;
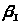- коэффициент, принимаемый по таблице
4-22 /1, с.202/ , в зависимости от формы
поперечного сечения стержней решетки
( принимаем тип стержней - №1 , соответствующее
ему значение
=
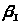2.34 ) ;
,
- толщина стержней и ширина просвета
между ними соответственно ( принимаем
=1
) ;
- угол наклона стержней решетки к
горизонту ( принимаем
= 90
) .
По формуле ( 1.11 ) получаем :
;
б) коэффициент сопротивления при резком повороте ищется по формуле :
, ( 1.12 )
где
и
- эмпирические коэффициенты , принимаемые
по таблице 4-6 и 4-7 /1, с.196/ , в зависимости
от угла поворота трубы ( для заданного
в задании угла поворота трубы
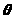= 45
,=
1.87 и
=
0.17 ) .
По формуле ( 1.12 ) получаем :
;
в) коэффициент сопротивления выхода принимаем равным 1 :
.
Диаметрпоперечного
сечения трубы находится графическим
способом , поскольку от величинызависят
: площадь живого сечения
; коэффициент гидравлического трения
,
ReD )
( где
- относительная шероховатость
и число Рейнольдса ReD =v
(
- кинематический коэффициент вязкости
, м2/с )) , а также некоторые коэффициенты
местных сопротивлений . График зависимости
диаметра
поперечного сечения трубы от известного
произведения строится по результатам
вычислений , выполненных в таблице 1.1 .
Таблица 1.1 “ Параметры трубопровода “
|
D ,м |
,м2 |
v ,м/с |
ReD |
|
|
l |
j |
T |
T ,м2 |
|
0.3 |
0.071 |
39.43 |
9.06 .106 |
0.0100 |
0.0435 |
6.96 |
4.61 |
0.294 |
0.021 |
|
0.6 |
0.283 |
9.89 |
4.54 .106 |
0.0050 |
0.0300 |
2.40 |
4.61 |
0.378 |
0.107 |
|
0.9 |
0.636 |
4.40 |
3.03 .106 |
0.0033 |
0.0265 |
1.41 |
4.61 |
0.408 |
0.260 |
|
1.2 |
1.131 |
2.48 |
2.28 .106 |
0.0025 |
0.0250 |
1.00 |
4.61 |
0.422 |
0.477 |
|
1.5 |
1.767 |
1.58 |
1.81 .106 |
0.0020 |
0.0235 |
0.75 |
4.61 |
0.432 |
0.763 |
Пример расчета одной
строки таблицы ( для
м
):
а) площадь поперечного сечения трубы ищется по формуле :
=
м2
; ( 1.13 )
б) средняя скорость жидкости рассчитывается по формуле :
, ( 1.14 )
где Q - расчетный расход дюкера ( из задания Q = 2.8 м3/ с ) ;
в) число Рейнольдса считается по формуле :
ReD=
,
( 1.15 )
где
- кинематический коэффициент вязкости
, принимаемый по таблице 4-1 /1, с.138/ в
зависимости от температуры жидкости ,
м2/с ( принимаем температуру воды t=10C
, соответствующее этой температуре
значение
)
;
г) относительную шероховатость считаем по формуле :
, ( 1.16 )
где
-
шероховатость трубы , принимаемая по
таблице 4-2 /1, с.166/ в зависимости от
качества трубы , м ( принимаем качество
трубы “ грубое ” , соответствующее
значение
).
д) коэффициент
гидравлического трения принимаем по
графику Кольбрука ( рис. 4-25 /1, с.163/ ) в
зависимости от числа Рейнольдса и
относительной шероховатости . Числу
Рейнольдса ReD= =
и
относительной шероховатости
соответствует коэффициент гидравлического
трения
;
е) коэффициент потери напора по длине ищется по формуле ( 1.9 ) :
;
ж) cумму местных коэффициентов потери напора ищется по формуле ( 1.8 ) , применяя значения , найденные выше :
;
з) коэффициент расхода ищем по формуле :
, ( 1.17 )
где полный коэффициент
расхода
ищется по формуле ( 1.7 ) :
;
и) произведение коэффициента расхода и площади поперечного сечения находим :
=
м2
;
По данным таблицы 1.1 строим график зависимости произведения коэффициента расхода и пло-щади поперечного сечения от величины диаметра поперечного сечения ( рис.1.1 ) .
По данным в задании величинам расхода жидкости и допустимой разности уровней можем найти необходимое значение произведения коэффициента расхода и площади поперечного сечения :
()необх=
=
( 1.18 )
По графику ,
изображенному на рисунке 1.1 , необходимому
значению произведения коэффициента
расхода и площади поперечного сечения
соответствует значение диаметра
поперечного сечения трубы
.
2. Построение напорной и пьезометрической линии ( для случая , когда работает только одна труба дюкера ) .
Прежде чем строить
напорную и пьезометрическую линии
следует отметить , что найденное в
результате расчета в п.1 значение диаметра
трубы следует округлить до ближайшего
большего сортаментного значения (
поскольку трубы выпускаются промышленностью
только сортаментных диаметров ) . По
таблице 6-2 /1, с.260/ принимаем ближайшее
большее сортаментное значение -
.
Так как мы приняли значение диаметра по сортаменту ( больший , чем требовалось по расчету ) , мы соответственно увеличиваем пропускную способность трубы . Это означает , что эта труба будет пропускать заданный расход , но при разности уровней , меньшей , чем заданная . Поэтому нужно рассчитать действительную разность уровней воды Zдейств по формуле :
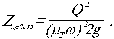( 2.1 )
для нахождения
площади поперечного сечения и коэффициента
расхода производим расчеты , аналогичные
выполненным в таблице 1.1 , для диаметра
поперечного сечения
м
:
а) площадь поперечного сечения трубы ищется по формуле ( 1.13 ) :
=
м2
;
б) средняя скорость жидкости рассчитывается по формуле ( 1.14 ) :
в) число Рейнольдса считается по формуле ( 1.15 ) :
ReD =
;
г) относительную шероховатость считаем по формуле ( 1.16 ) :
;
д) коэффициент
гидравлического трения принимаем по
графику Кольбрука ( рис. 4-25 /1, с.163/ ) в
зависимости от числа Рейнольдса и
относительной шероховатости . Числу
Рейнольдса ReD= =
и
относительной шероховатости
соответствует коэффициент гидравлического
трения
;
е) коэффициент потери напора по длине ищется по формуле ( 1.9 ) :
;
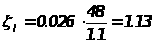ж) cумма местных коэффициентов потери напора была найдена в п.1 по формуле ( 1.8 )
;
з) полный коэффициент
расхода
ищется по формуле ( 1.7 ) :
;
и) коэффициент расхода ищем по формуле ( 1.17 ) :
.
Указанная выше величина будет равна :
Zдейств=
Для построения пьезометрической и напорной линий вычисляем все потери напора .
Потери напора по длине вычисляются по формуле :
, ( 2.2 )
где lj - длина j-ого участка трубопровода , м .
Из задания :
Потери напора по длине на выше указанных участках будут равны :
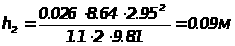
Потеря напора на резкий поворот вычисляется по формуле :
( 2.3 )
Потеря напора на вход рассчитывается по формуле :
( 2.4 )
Потеря напора на выход рассчитывается по формуле :
( 2.5 )
Найденные величины потерь напора откладываются в масштабе и строится напорная линия Е-Е , которая начинается на уровне воды в питающем баке ( сечение 1-1 ) и заканчивается на уровне воды в нижнем бьефе ( сечение 2-2 ) . Пьезометрическая линия P-P всюду отстоит от напорной на величину скоростного напора ( рис. 2.1 ).
Величина скоростного напора ищется по формуле :
( 2.6 )
3. Нахождение разности уровней воды в подводящем и отводящем участках канала ( для случая , когда работают обе трубы дюкера ) .
Разность уровней воды в подводящем и отводящем участках канала находим по формуле ( 2.1 ) , учитывая , что в этом случае площадью поперечного сечения будет две площади поперечного сечения трубы :
Z =
Список литературы
1. Чугаев Р.Р. Гидравлика ( техническая механика жидкости ) . - Л.: Энергоиздат , 1982. - 672 с.
2. Кожевникова Е.Н. , Орлов В.Т. Методические указания по выполнению курсовых и расчетно-грвфических работ по курсу гидравлики . - Л. : Издание ЛПИ им. М.И. Калинина , 1985. - 48 с.