О происхождении “высокотемпературных” осцилляций кинетических коэффициентов в висмуте и полуметаллических сплавах на его основе

Ю. А. Богод

Рассмотрен квантовый кинетический эффект, наблюдаемый вплоть до температур, близких к температуре кипения жидкого азота («высокотемпературные осцилляции»). Обсуждаются альтернативные модели, объясняющие происхождение эффекта.

“Высокотемпературные” осцилляции (ВТО) вначале наблюдались при изучении магнетосопротивления висмута и его сплавов[1-8], а затем при измерении термоэдс висмута [9,14] (в итоговом списке публикаций, касающемся ВТО, статьи следуют в хронологическом порядке). Подобно осцилляциям Шубникова-де Гааза (D. Shoenberg, F.A.S. Magnetic Oscillations in Metals. Cambridg University Press (1984)) и магнетофононному резонансу (Р.В. Парфеньев, Г.И. Харус, И.М. Цидильковский, С.С. Шалыт, УФН 112, 3 (1974); Р.В.Поморцев, А.И. Пономарев, Г.И.Харус, И.М. Цидильковский, ЖЭТФ 54, 1347 (1968)), ВТО обусловлены квантованием уровней энергии в магнитном поле, однако данный тип осцилляций принципиально отличается от названных эффектов. От осцилляций Шубникова-де Гааза ВТО отличаются величиной периода (период ВТО в обратном магнитном поле существенно меньше) и температурной зависимостью амплитуды: ВТО наблюдаются как при Т<< , так и в области температур Т , где амплитуда эффекта Шубникова-де Гааза экспоненциально мала – отсюда и название “высокотемпературные” осцилляции (Т – температура, - циклотронная частота, - постоянная Больцмана). Попытка отождествления ВТО с магнетофононным резонансом приводит к граничной энергии оптических фононов, в несколько раз большей своего действительного значения.

В ходе исследований было, в частности, экспериментально изучено влияние на свойства ВТО температуры [5,7], ультраквантовых магнитных полей [4, 17-19, 21], всесторонних и анизотропных деформаций [13, 16], легирования висмута примесями Sb, Te, Sn [7, 8]. Установлено, что период ВТО связан с циклотронной массой носителей заряда и не зависит от энергии ферми [5, 7, 8].

Существуют две альтернативные модели, в которых сделана попытка описать свойства ВТО. Согласно первой из них [10,11] причиной возникновения ВТО являются электрон – дырочные переходы у границ энергетических зон. Возможность таких переходов связана с тем обстоятельством, что в висмуте даже при низких (гелиевых) температурах относительное число занятых состояний носителей заряда над ферми – уровнем, задаваемое выражением

|, (1)

достигает 10-2-10-3 (Уширение энергетических уровней обусловлено релаксационными процессами). Уширение уровней в висмуте, соответствующее электрон – примесным, электрон – электронным и электрон – фононным частотам столкновений в гелиевой области температур, составляет (В.С. Винник, И.Я. Коренблит, Е.А. Охрем, А.Г. Самойлович, ЖЭТФ 80, 2031 (1981); R. Hartman, Phys.Rev. 181, 1070 (1969); M.P. Vecchi, J.R. Pereira, M.S. Dresselhaus, Phys.Rev. B14, 298 (1976); В.С. Эдельман, УФН 123, 257 (1977)). Расстояние от края зоны до ферми-уровня . ( Здесь энергия ферми электронов (дырок) в висмуте, импульс носителей заряда, энергия края зоны в и - точках зоны Бриллюэна). Таким образом значение оказывается по порядку величины совпадающим с относительной амплитудой ВТО. Следуя (1), для абсолютной амплитуды ВТО образца размерами 1х1х10 мм получаем: висмут-~ 10-2ом (в соответствии с экспериментом); сурьма-~ 10-6 ом; типичный металл-~ 10-12 ом. Параметр квазиклассичности может уменьшить значение абсолютной амплитуды ВТО в типичном металле еще на 2-3 порядка.

В соответствии с [10,11], при квазиупругом междолинном рассеянии носителей заряда период ВТО в стандартной модели дается соотношением

(2)

где - энергия перекрытия электронной и дырочной зон, 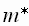- циклотронная масса. При неупругом междолинном рассеянии на акустических фононах с энергией возникает наложение мод с периодами [15]

(3)

С помощью соотношений (2), (3) для висмута получены усредненные значения энергии перекрытия зон мэв и энергии “межзонных” акустических фононов мэв. Первое из этих значений соответствует мэв, что согласуется с наиболее достоверной величиной ферми – энергии электронов, приведенной в цитированном выше обзоре В.С. Эдельмана. Энергия “межзонных” акустических фононов соответствует данным A.A. Lopez, Phys.Rev. 175, 823 (1968). Установлено, что в диапазоне температур 10-70K энергия перекрытия увеличивается примерно на 30% [2,5,7], и это связывается с температурной зависимостью анизотропии решетки.

Оказывается, что ВТО обнаруживают эффект, близкий к удвоению частоты, которое наблюдается в широком интервале направлений магнитного поля H [3]. При этом вторая гармоника по амплитуде соизмерима с первой. Поскольку угловая зависимость периода второй гармоники определяется анизотропией циклотронной массы дырок, ее происхождение связывается с электрон – дырочными переходами вблизи горизонтали, определяемой вершиной валентной зоны в точке зоны Бриллюэна. Структура выражения для соответствующего периода при квазиупругих межзонных переходах совпадает с формулой (2), в которую вместо энергии перекрытия входит сумма . Полученное значение энергетической щели мэв [17] соответствует результатам IR- исследований, и близко к приведенному в обзоре В.С. Эдельмана (см. ссылку выше).

Известно, что циклотронная масса дырок в висмуте не зависит от энергии. Поэтому, комбинируя данные, полученные при измерениях эффекта Шубникова – де Гааза и ВТО, можно получить информацию о ферми – энергии электронов и энергетической щели в точке для полуметаллических сплавов на основе висмута.

В работе [12] предложена альтернативная модель ВТО, согласно которой осцилляции возникают в результате электронно-дырочных переходов между экстремумами подзон Ландау вблизи уровня ферми. При этом циклотронные массы электронов и дырок должны быть кратны. Здесь, как и в [10,11], при некоторых предположениях (см. ниже) период ВТО определяется величиной перекрытия энергетических зон. Казалось бы, экспериментальные результаты полнее описываются в рамках моделей [10,11]. Это прежде всего относится к совместному наблюдению электронных и дырочных периодов ВТО [7,14], реализации ВТО в ультраквантовом пределе [4,18], слабой зависимости относительной амплитуды осцилляций от направления магнитного поля (по этому поводу проводились специальные контрольные измерения). Однако появление теоретических работ, рассматривающих слабозатухающие по температуре осцилляции кинетических коэффициентов в слоистых структурах и тонких пленках (M.V. Kartsovnik et al, Phys. Rev. Lett. 89, 126802 (2002); О.В. Кириченко, И.В. Козлов, ФНТ 28, 509 (2002); И.В. Козлов, ФНТ 29, 1341 (2003)), вновь стимулировало интерпретацию экспериментальных результатов с позиций [12].

В работе [20] была сделана попытка рассчитать и сравнить с измерениями зависимость периода ВТО висмута от направления магнитного поля в трех главных кристаллографических плоскостях (угловые зависимости). В духе модели [12] период ВТО [20]

(4)

связывался с комбинационным сечением

, (5)

равным сумме экстремальных сечений ферми-поверхностей электронов и дырок с целочисленными коэффициентами, относящимися как циклотронные массы дырок и электронов. На первый взгляд создается впечатление об удовлетворительном согласии эксперимента и расчета. Два близких семейства точек на расчетных угловых зависимостях, по мысли автора [20], описывают экспериментально наблюдаемые биения ВТО, а вместо дырочных и электронных осцилляций рассматриваются единые колебания интерференционной природы.

Однако рассмотрение результатов эксперимента в наглядном масштабе [5,7] сразу же демонстрирует издержки подхода [20] – измеренная в бинарной плоскости с весьма малым шагом (1-2 градуса) угловая зависимость периода ВТО совпадает ( с учетом биений) с угловой зависимостью обратных циклотронных масс, в соответствии с [10,11]. Плодотворность идеи о биениях, как следствии электрон – дырочных переходов при испускании и поглощении междолинных акустических фононов [15], демонстрируется определением по экспериментальным данным ВТО характерной фононной энергии, согласующейся с известными из специальных опытов результатами (см. выше), а также аналитическим описанием возрастающего участка температурной зависимости амплитуды ВТО (4-12К) в чистых образцах висмута (данный участок связан с экспоненциальным ростом числа междолинных акустических фононов [15]).

Известно, что введение в висмут примерно одного атомного процента сурьмы приводит (вблизи 4К) к превышению на три порядка частоты междолинных квазиупругих столкновений над частотой междолинных столкновений при рассеянии носителей тока на акустических фононах (ссылки и текст в [15]). Соответственно исчезает нарастание амплитуды ВТО в диапазоне 4-12К, сменяясь затуханием по экспоненциальному закону ( с показателем экспоненты -0.12Т [15]), присущему как висмуту (выше 12К), так и всем исследованным сплавам висмут - сурьма разного состава [7]. Кроме того, при температурах от 4К до 15К ВТО остаются монохроматическими, а биения появляются лишь при дальнейшем увеличении температуры, когда частота междолинных столкновений на акустических фононах сравнивается с частотой междолинных квазиупругих столкновений [15].

По мере легирования висмута сурьмой на угловой зависимости растет относительное число периодов ВТО, связываемых с электронами.

При содержании сурьмы 2.6 ат. процента наблюдаемая в бинарной плоскости угловая зависимость периодов ВТО в целом совпадает с угловой зависимостью обратных циклотронных масс электронов [7].

В соответствии с установленной в чистом висмуте с помощью прецизионных измерений разницей (примерно в 7%) циклотронных масс электронов и дырок (дырочная масса больше) при направлении магнитного поля вдоль тригональной оси (В.С. Эдельман, УФН 123, 257 (1977)), периоды ВТО для данного направления магнитного поля (биссекторная плоскость [14]), идентифицированные как дырочные и электронные, отличаются на 7-9%.

Перечисленная совокупность данных подтверждает связь периода ВТО с циклотронной массой носителей заряда [10], а не с комбинационным сечением [12, 20]. Здесь же уместно отметить формальное сходство моделей [10, 11] и [12, 20]: при равных циклотронных массах электронов и дырок – приближенное равенство реализуется вблизи ориентации Н вдоль тригональной оси – выражение (4) для периода ВТО в квадратичной модели спектра точно совпадает с формулой (2). По этой причине одинаково успешное описание в рамках цитируемых альтернативных моделей [10, 11, 12, 20] влияния внешних воздействий (температуры, деформаций, легирования) на период ВТО не может служить решающим аргументом в пользу какой-либо из рассматриваемых моделей.

Согласно модели [12], ВТО должны исчезать в ультраквантовом пределе по магнитному полю одновременно с осцилляциями Шубникова –де Гааза. Исследования в сильных магнитных полях проводились в работах [4, 17 – 19, 21], и характерные данные сводятся к следующему. Когда поле параллельно бинарной оси , при 15 кэ легкие электроны переходят в ультраквантовый предел (две долины, спиновое расщепление на 10% больше орбитального); при 111 кэ наблюдается последний экстремум ВТО; при 120 кэ дно тяжелых электронов пересекает уровень Ферми [19, 21] (ультраквантовый предел). С другой стороны, при 120 кэ выше уровня Ферми остается несколько (2 - 3 по грубым оценкам с учетом движения ферми - уровня ) дырочных подзон Ландау, т.е. для дырок ультраквантовый предел еще не реализуется. Полученный результат противоречит данным [4, 18], согласно которым в магнитном поле, параллельном биссекторной оси , после перехода всех электронных долин в ультраквантовый предел (12 кэ для самых легких электронов, 25 кэ для более тяжелых, спиновое расщепление на 10% больше орбитального, см. обзор В.С. Эдельмана) ВТО продолжают наблюдаться (эксперименты в цитируемых работах велись до 60 кэ, когда по оценкам выше ферми – уровня остается 5-6 дырочных подзон Ландау). В этой связи отметим, что отсутствие в работе [21], где измерения проводились в полях до 330 кэ, экспериментальных данных в геометрии , так же, как и отсутствие соответствующих комментариев, несколько настораживает.

Далее, когда поле параллельно тригональной оси , ВТО исчезают одновременно с последней дырочной осцилляцией Шубникова-де Гааза вблизи 100 кэ [21] (спиновое расщепление дырок вдвое больше орбитального). При этом, наряду с дном электронной зоны, ниже ферми-уровня остается нулевая подзона Ландау с положительно ориентированными спинами электронов ( спиновое расщепление электронов вдвое меньше орбитального), пересекающая ферми-уровень в существенно больших магнитных полях [22].

Таким образом, в идеологии [12] трудно обобщить наблюдаемые особенности исчезновения ВТО в сильных магнитных полях. Между тем экспериментальные результаты просто понять в рамках модели [10, 11] на основе особенностей зонной структуры висмута. При этом следует учесть, что в магнитном поле, направленном вдоль главных осей, ВТО определяются циклотронными массами дырок (эксперимент).

Выше упоминалось, что в магнитном поле, параллельном бинарной оси, реализуются легкие и тяжелые электроны (при этом, как уже было сказано, величины спинового расщепления соответствующих уровней Ландау также существенно различны). Дно зоны тяжелых электронов с ростом магнитного поля достаточно быстро смещается вверх по энергии, а дно каждой зоны легких электронов быстро смещается вниз по энергии. Соответственно, заселенность дырочных состояний на уровне дна зоны тяжелых электронов растет в меру уменьшения разности ферми –энергии и энергии дна зоны [11]. Ясно, что в такой ситуации в достаточно сильном магнитном поле определяющий вклад в амплитуду ВТО будут вносить дырочные переходы в зону тяжелых электронов. При пересечении дна этой зоны и ферми-уровня амплитуда ВТО должна резко уменьшиться по крайней мере на порядок, будучи связанной лишь с дырочными переходами в зоны легких электронов, нулевые уровни энергии которых удалены от ферми-уровня на расстояние примерно 10 мэв. Возможно, регистрация этих остаточных осцилляций в реализуемых экспериментальных условиях [19, 21] затруднительна. В магнитном поле, параллельном тригональной оси, выше 100 кэ дырочные состояния оказываются сосредоточенными вблизи нулевого экстремума, выше исходного потолка валентной зоны на величину порядка дырочной энергии ферми. При этом число дырочных состояний на уровне дна электронной зоны существенно уменьшится, что равносильно резкому (примерно на два порядка) уменьшению числа приграничных межзонных переходов, т.е. амплитуды дырочных ВТО. Последний перед скачком амплитуды экстремум ВТО должен реализоваться чуть ниже 100 кэ, что соответстствует эксперименту [21]. Более подробное описание данного сценария исчезновения ВТО содержится в работе [22].

Согласно [12], при точном целочисленном отношении циклотронных масс дырок и электронов амплитуда ВТО с повышением температуры не затухает. Однако дингловское уширение уровней Ландау делает возможной реализацию ВТО в случае электронов и дырок с несколько отличающимися циклотронными массами, и это обстоятельство должно приводить к заметному температурному затуханию осцилляций. Поскольку разность масс чувствительна к ориентации магнитного поля, интенсивность затухания должна существенно меняться при вращении магнитного поля в главных кристаллографических плоскостях. Естественно, интенсивность затухания должна также зависеть и от частоты столкновений, определяющей величину дингловского уширения, т.е. допустимую разность масс. Однако, согласно всей совокупности экспериментальных данных, закон температурного затухания амплитуды ВТО в висмуте и сплавах висмут-сурьма одинаков и не зависит ни от ориентации магнитнитного поля, ни от концентрации примесей сурьмы ( в полуметаллической области; максимальная концентрация примеси в эксперименте 3.4 ат.% Sb – Ю.А. Богод, докторская диссертация, 1984 г.), меняющих частоту столкновений носителей заряда в сплавах относительно чистого висмута примерно на два порядка. Введение в сплавы висмута с сурьмой примесей теллура или олова кардинально – в 2.4 –4 раза уменьшает показатель экспоненты в законе затухания [9]. Этот результат может стать ключевым при поиске причин возникновения осцилляций. Так, можно полагать, что взаимодействие с примесными уровнями Te, Sn уширяет дно зоны проводимости, уменьшая тем самым амплитуду ВТО и влияние температуры, в духе [10, 11]. Если это верно, то одинаковое затухание амплитуды ВТО в висмуте и сплавах висмут – сурьма можно связать с температурным размытием идентичных зонных экстремумов. Данные предположения нуждаются в экспериментальной проверке.

Итак, в настоящее время, по-видимому, рано ставить точку при обсуждении природы ВТО: с одной стороны, представленные выше данные трудно адекватно объяснить в рамках теории [12], с другой – существуют проблемы при сопоставлении результатов с выводами [10, 11].

Список литературы

Ю.А. Богод, Вит.Б. Красовицкий, “О наблюдении при водородных температурах нового периода осцилляций магнетосопротивления висмута”, Препринт, Физико- технический институт низких температур АН УССР, Харьков (1973)

Ю.А. Богод, Вит.Б. Красовицкий, В.Г. Герасимечко, ЖЭТФ 66, 1362 (1974)

Ю.А. Богод, В.Г. Герасимечко, Вит.Б. Красовицкий, ФНТ 1, 1472 (1975)

Ю.А. Богод, Вит.Б. Красовицкий, Письма в ЖЭТФ 24, 585 (1976)

Ю.А. Богод, Вит.Б. Красовицкий, С.А. Миронов, ЖЭТФ 78, 1099 (1980)

Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 7, 1530 (1981)

Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 9, 832 (1983)

Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 12, 435 (1986)

Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 12, 610 (1986)

Ю.А. Богод, ФНТ 12,1004 (1986)

Ю.А. Богод, Л.Ю. Горелик, А.А. Слуцкин, ФНТ 13, 626 (1987)

В.М. Поляновский, Письма в ЖЭТФ 46, 108 (1987)

А.Г. Бударин, В.А. Вентцель, А.В. Руднев, Ю.А. Богод, Вит.Б. Красовицкий, ФНТ 14, 875 (1988)

Ю.А. Богод, Вит.Б. Красовицкий, В.Я. Левантовский, Е.Т. Лемешевская, ФНТ 14, 1251 (1988)

Ю.А. Богод, Вит.Б. Красовицкий, ФНТ 16, 900 (1990)

Вит.Б. Красовицкий, В.В. Хоткевич, ФНТ 17, 710 (1991)

Yu.A. Bogod, A. Libinson, Solid St. Communs. 96, 609 (1995)

Yu.A. Bogod, A. Libinson, Phys.Stat.Sol.(b) 197, 137 (1996)

Вит.Б. Красовицкий, В.В. Хоткевич, А.Г.М. Янсен, П. Видер, ФНТ 25, 903, (1999)

Ю.Ф. Комник, ФНТ 29, 1231 (2003)

Vit. B. Krasovitsky, Phys.Rev. B68, 075110 (2003)

Ю.А. Богод. К вопросу о “высокотемпературных” осцилляциях магнетосопротивления висмута в ультраквантовом пределе - http://www.laboratory.ru

Для подготовки данной работы были использованы материалы с сайта http://www.sciteclibrary.ru