Использование компьютерных технологий в изучении наглядной геометрии
Введение
Преподавание геометрии не может обойтись без наглядности. В тесной связи с наглядностью обучения находится и его практичность. Ведь именно из жизни мы черпаем конкретный материал для формирования наглядных геометрических представлений, делая обучение согласованным с жизнью ребенка, его опытом. Процесс обучения упрощается при разумном использовании принципа наглядности. Обучение не должно быть перенасыщено иллюстрациями, схемами, таблицами и другими формами наглядности, но в некоторых труднодоступных вопросах применение наглядности необходимо. И именно использование средств мультимедиа позволяет учителю разнообразить урок новыми видами деятельности, насытить его наглядной информацией, повысить мотивацию учащихся, интерес к предмету.
В процессе изучения геометрии, как известно, у учащихся развивается пространственное мышление как разновидность образного, формируются абстрактные образы, в которых фиксируются формы, величина, взаимное положение объектов, расположение фигур на плоскости и в пространстве относительно заданной точки отсчёта.
Геометрия как учебный предмет способствует развитию таких психических функций человека как мышление, ощущение и интуиция. Только при взаимно дополняющем развитии этих функций, обеспечиваемом межполушарными взаимодействиями головного мозга, из человека получается гармонично развитая личность.
Все эти замечательные характеристики геометрии делают её незаменимым элементом общей культуры, в равной степени нужным художнику и математику, инженеру и физику, биологу и экономисту.
Анализ методической литературы свидетельствует о том, что геометрия в современной общеобразовательной школе становится непреодолимым барьером для многих учащихся. Причину этого многие ученые видят в преобладании в традиционном обучении аналитических методов, наличии непосильных для понимания учеников скрупулезных доказательств очевидных фактов, тогда как логическое мышление школьников, особенно к началу изучения геометрии, развито недостаточно, а образное мышление не окончательно упорядочено. Поэтому целесообразно и психологически обоснованно, особенно на первых этапах изучения геометрии, опираться на наглядно-действенное мышление как первую и основную ступень в развитии мышления, опору для формирования образов и понятий и включить в процесс обучения геометрии практическую, конструктивную деятельность.
Всё это создаёт проблему необходимости разработки методов обучения геометрии, сочетающих наглядность, конструктивную практическую деятельность, словесно-логический анализ.
Таким образом, метод геометрических преобразований, как реализация конструктивного подхода к преподаванию систематического курса геометрии, открывает путь к развитию пространственного мышления.
Метод геометрических преобразований является одной из фундаментальных идей, последовательно применяемых в систематическом курсе геометрии, что обусловлено следующими положениями:
- практические операции играют важную роль в мышлении (согласно Ж Пиаже, все мыслительные операции образуют структуру группы, подобную группе преобразований в геометрии);
- с понятием преобразований связан «групповой подход» в геометрии, в соответствии с которым геометрия изучает свойства фигур, являющихся инвариантами фундаментальной группы преобразований;
- геометрические преобразования являются ни чем иным, как обобщением понятия о функции, их изучение открывает возможность «обозреть с одной точки зрения, как отдельные части геометрии, так и их взаимные связи» (Ф. Клейн), подчинить единой идее – идее функциональной зависимости – всю школьную математику;
- большая общность геометрических преобразований позволяет значительно упростить доказательство многих теорем;
- изучение геометрических преобразований способствует формированию пространственного мышления, использование их вооружает учащихся способами (методами) решения задач на построение, которые, в свою очередь, являются одним из эффективных средств развития геометрического мышления школьников;
- геометрические преобразования отражают общие закономерности взаимосвязи явлений природы, изучение их позволяет наиболее полно раскрыть практическую значимость, показать область применения геометрических знаний;
- геометрические преобразования используются не только в курсе геометрии, но и в школьных курсах алгебры (построение графиков функций), физики (механика, оптика), химии (кристаллические тела), черчения (построение изображений в различных проекциях) и др., то есть позволяет укрепить межпредметные связи геометрии с другими дисциплинами.
Анализ основных учебников, учебных пособий по рассматриваемой проблеме показывает, что в преподавании геометрии до сих пор недостаточно внимания уделяется геометрическим преобразованиям, в то время как развитие геометрической науки давно показало, что теория геометрических преобразований является одной из фундаментальных областей геометрии.
Авторы рассматривают вопросы построения теории геометрических преобразований, взаимосвязи между видами преобразований, методику их изложения. Но многие аспекты данной проблемы недостаточно разработаны. По-разному решается вопрос о роли геометрических преобразований в логическом построении геометрии, о том, в каком объеме должны изучаться преобразования в школьном курсе.
Таким образом, в настоящее время в процессе преподавания систематического курса геометрии:
- не всегда удается осветить вопросы прикладной направленности геометрических преобразований;
- не в полной мере используются возможности геометрических преобразований для установления межпредметных связей геометрии с другими дисциплинами;
- не учитываются профессиональные намерения, интересы, склонности учащихся;
- недостаточно осуществляется дифференцированный подход к изложению теоретического материала и подбору упражнений.
Методическая подготовка к преподаванию школьного курса геометрии традиционно сводится к подготовке учителя в рамках методики преподавания математики, она опирается на учебно-методический комплекс, который недостаточно ориентирован на подготовку учителя к работе в условиях многообразия подходов к построению курса геометрии, уровневой и профильной дифференциации в современной школе. Кроме того, методическая подготовка направлена в основном на усвоение будущим учителем методических и геометрических знаний и умений, но не на целенаправленное развитие его мыслительной деятельности при решении геометрических задач.
Средства мультимедиа способствуют более глубокому и осознанному усвоению изучаемого материала, так как ученик, освоив основные понятия на уроке, сможет без труда вернуться к просмотренному материалу для закрепления или повторения его во внеучебное время.
Все сказанное определяет актуальность проблемы нашей дипломной работы, которая состоит:
· в необходимости усиления роли геометрических преобразований в школьном курсе геометрии;
· в поиске путей усовершенствования методики изучения и применения геометрических преобразований путем разработки интерактивного дидактического пособия по теме раздела.
Как уже говорилось, прерогатива геометрии как учебного предмета общекультурного уровня – развитие абстрактного, логического, пространственного мышления, связь с реальностью – включает ее в число обязательных предметов. Однако, учитывая ее объективную сложность, гуманизация образования требует, чтобы дифференциация обучения математике, в частности геометрии, учитывала потребности всех школьников не только сильных, но и тех, кому это предмет дается с трудом, чьи интересы лежат в других областях.
Цель данной дипломной работы – на основе анализа психолого-педагогической, методической и учебной литературы разработать дидактическое пособие «Движения на уроках геометрии» для учащихся 8-9 классов, содержащее динамические иллюстрации, изучение которых позволит учащимся получить более глубокое представление о понятии движения и его видов.
Для достижения указанной цели необходимо было решить следующие задачи:
1. Изучить психолого-педагогические основы использования компьютерных изображений как средства наглядности в обучении школьников, в частности, установить роль и виды компьютерной наглядности в обучении, требования, предъявляемые к компьютерным средствам обучения;
2. Проанализировать содержание учебников, дидактических материалов, рабочих тетрадей различных авторов по геометрии по теме «Движение»;
3. Разработать мультимедийное дидактическое пособие по теме «Движения на уроках геометрии»;
4. Разработать методические рекомендации по использованию мультимедийного дидактического пособия.
5. Экспериментально проверить эффективность использования мультимедийного дидактического пособия «Движение на уроках геометрии»
Для решения поставленных в работе задач использовались следующие методы:
· анализ психолого-педагогической, научно-методической литературы по теме;
· анализ действующих школьных учебников и учебных пособий по геометрии;
· изучение опыта работы учителей;
· педагогическое наблюдение;
· беседы с учащимися и учителями;
· опытная проверка.
В соответствии с поставленными задачами разработана структура работы. Она состоит из двух глав, введения, заключения, библиографии и приложения.
Первая глава посвящена рассмотрению вопросов истории внедрения раздела о движениях в школьный курс геометрии, роли движений в геометрии как науке, возможностей программы Flash, предоставляющей среду разработки мультимедийных пособий; изучению психолого-педагогических основ использования компьютерных изображений в процессе обучения; анализу современных учебников по геометрии по теме «Движение». Рассматривается целесообразность использования компьютерной наглядности; выделяются возможности использования современных компьютерных средств в процессе обучения, определяются требования, предъявляемые к ним.
Во второй главе описывается мультимедийное пособие по теме «Движение», задача которого состоит в визуализации учебного материала, связанного с изучением понятия движения и его видов, а также методические рекомендации по применению дидактического пособия.
К работе прилагается компакт-диск, содержащий мультимедийное пособие по теме «Движения на уроках геометрии».
Глава I. Психолого-педагогические основы изучения движений в школьном курсе геометрии 7-9 классов
§1. Роль и место движений в геометрии
Идея геометрических преобразований как основы геометрии установлена еще немецким математиком Феликсом Клейном на базе теории групп в «Эрлангенской программе» 1872 года. Этот документ свидетельствует о том, что понятие геометрического преобразования играет в геометрии основополагающую роль и может быть положено в основу самого определения геометрии как науки. Понятие преобразования тесно связано с фундаментальными понятиями функции и группы. Поэтому одной из основных идей реформы математического образования 1967 года была идея внедрения в школьный курс математики геометрических преобразований. Она диктуется и методическими соображениями: доказательство многих геометрических теорем, связанных с геометрическими преобразованиями, доступнее учащимся, чем дедуктивные выводы из аксиом. Многие задачи на построение и доказательство решаются более естественно и просто, исходя из идеи геометрических преобразований.
«Многие из существующих курсов планиметрии неудачны, прежде всего, потому, что отсутствуют понятные учителям и ученикам, цементирующие курс математические идеи. Ученики знакомятся с наборами теорем, а не их системам. Одна из таких «цементирующих идей» – геометрические преобразования».
В программе по геометрии сформулированы цели и задачи обучения этому предмету в средней школе, в соответствии с которыми основными из них являются:
1) систематическое изучение основных фактов геометрии, методов их получения и возможностей их применения;
2) развитие умений и навыков учащихся, обеспечивающих применение полученных знаний для изучения смежных дисциплин и в сфере производства;
3) развитие пространственного воображения и логического мышления учащихся.
Особая роль в решении этих задач отводится последовательному применению в школьном курсе геометрии наряду с другими традиционными методами идеи геометрических преобразований и формированию понятия геометрического преобразования.
Понятия являются одной из главных составляющих содержания любого предмета, в том числе и геометрии. Начиная изучать геометрию, учащиеся сразу же встречаются с понятием точки, линии, угла, а далее — с целой системой понятий, связанных с видами геометрических объектов (линий, углов, треугольников и др.). Задача обучения в общеобразовательной школе обеспечить полноценное усвоение вводимых понятий.
Понятие преобразования является одним из фундаментальных понятий в геометрии. Это обусловлено, во-первых, ведущей ролью практических операций в мышлении (согласно Ж. Пиаже, все мыслительные операции образуют структуру группы, подобную группе преобразований в геометрии). Во-вторых, с понятием преобразования связан «групповой подход» к геометрии, в соответствии с которым геометрия — это наука, занимающаяся изучением свойств фигур, являющихся инвариантами фундаментальной группы преобразований.
Логика в любом понятии различает объем и содержание. Под объемом понимают тот класс объектов, которые относятся к этому понятию, объединяются им. Так, в объем понятия «преобразование» входят преобразования всех известных групп независимо от их конкретных характеристик: движения, подобия, аффинные, проективные, топологические, гиперболические, эллиптические преобразования. Под содержанием понятий понимается та система существенных свойств, по которой происходит объединение данных объектов в единый класс. Содержание понятия «преобразование» составляют свойства: отображение пространства на себя (при котором каждая точка пространства переходит в некоторую точку этого же пространства); взаимнооднозначное (биективное) отображение.
В совокупности свойства, по которым объекты объединяются в один класс, называется необходимыми и достаточными признаками. Важно отметить, что отношение между этими признаками в разных понятиях разное. Различают понятия с конъюнктивной и дизъюнктивной связью признаков. В понятиях с конъюнктивной связью эти признаки дополняют друг друга, образуя вместе то содержание, по которому и объединяются объекты в единый класс. Так, у объектов, относящихся к понятию «преобразование плоскости», обязательно должны быть два выше указанных признака (отображение плоскости на себя и биективность отображения), по отдельности ни один из них не позволяет опознать объекты этого класса. Как уже говорилось, в логике понятия с такой связью называются конъюнктивными: признаки связаны союзом «и» (в случае преобразования отображение должно быть и взаимнооднозначным и отображением плоскости на себя).
Итак, под преобразованием в
геометрии понимают, например, в случае
плоскости отображение всей плоскости
на себя, при котором каждая точка X
отображается в единственную точку
 ,
а каждой точке
,
а каждой точке
 соответствует единственная точка У.
соответствует единственная точка У.
Понятие не может быть передано учащимся в готовом виде, они должны получить его сами, взаимодействуя с относящимися к нему известными понятиями. Определение задает как бы точку зрения — ориентировочную основу — для оценки понятий, с которыми взаимодействует обучаемый. Так, получая определение понятия преобразования, ученик может анализировать различные преобразования с точки зрения наличия или отсутствия в них тех признаков, которые содержатся в определении. При этом, например, он может использовать аналогию между понятием движения в геометрии и равномерного прямолинейного движения предметов (твердых тел) в механике. Такая реальная работа по оценке различных предметов с точки зрения, заданной определением, и создает постепенно в голове учащихся идеальное понятие как обобщенный и абстрактный образ.
Обязательная программа не предусматривает широкого изучения различных свойств геометрических преобразований. Вопрос использования преобразований при решении геометрических задач предлагается вынести, как вариативный компонент, на факультативные занятия и внеклассную работу.
Геометрические преобразования являются обобщением понятия о функции, и поэтому позволяют «обозреть с одной точки зрения, как отдельные части геометрии, так и их взаимные связи» (Ф. Клейн) – это значит, что изучение геометрических преобразований открывает возможность подчинить единой идее – идее функциональной зависимости – всю школьную математику. Большая общность геометрических преобразований позволяет значительно упростить доказательство многих теорем. Также изучение преобразований вооружает учащихся способами (методами) решения задач на построение, которые являются одним из средств развития геометрического мышления учащихся.
Ф. Клейн (1849-1925) знаменит своей общей концепцией геометрии, в основу которой положил учение об «автоморфизмах» соответствующей геометрической теории. Хотя точка зрения Ф. Клейна не исчерпывает всего богатства современной геометрии, – в ее рамки не укладывается ряд современных геометрических теорий, – теоретико-групповой подход к построению геометрии охватывает практически все геометрические теории, изучаемые в высшей школе. Однако групповая точка зрения не была реализована в практике массового школьного обучения.
Приобщая школьников к основным идеям геометрии, можно доступно изложить им основные положения группового подхода, которые составляют вводную часть знаменитой лекции Ф. Клейна «Эрлангенская программа» (1872), примерно так.
«Что такое геометрия? Наука о геометрических свойствах фигур. Какие же свойства следует называть геометрическими? Те, что не зависят от положения, занимаемого фигурой в пространстве, от ее абсолютных размеров и, наконец, от ориентации (под этим понимают то свойство расположения, которое является источником различия между данной фигурой и ее зеркальным изображением). Отсюда вытекает, что геометрические свойства фигуры не изменяются от параллельных переносов и поворотов, от преобразований подобия, от зеркального отражения и от всех преобразований, которые могут быть составлены из перечисленных. Отметим, что все они в совокупности образуют группу. Можно сказать, геометрические свойства – это те, которые не изменяются в результате любого преобразования из группы перечисленных выше.
Будем говорить теперь о произвольной группе преобразований. Как обобщение геометрии тогда получится следующая задача. Дано пространство и в нем группа преобразований. Нужно исследовать те свойства фигур, которые не изменяются при преобразованиях этой группы. Иными словами, требуется развить теорию инвариантов этой группы. Это — общая задача, включающая в себя не только обыкновенную геометрию, но и новейшие геометрические теории. Так говорил Клейн. С тех пор каждую геометрию, порождаемую некоторой группой преобразований, называют клейновской геометрией.
Так, например, школьная евклидова геометрия порождена группой преобразований подобия, как отметил сам Клейн. Как одну из других клейновских геометрий было бы любопытно изложить неевклидову геометрию Лобачевского или Римана».
Итак, понятие преобразования как основной операции, охватывающей не только математические, но и другие, более широкие отношения, является важным основанием для развития геометрического мышления учащихся.
С понятием преобразования связывают различные представления у школьников. Одни из них опираются на представление перемещения некоторого материального «твердого» тела. Такую точку зрения принято называть механической или динамической, связанной с представлениями о силе, вызывающей движение (перемещение). Другая точка зрения, кинематическая, опирается на более отвлеченное представление о движении, не связанное с представлениями о силе, вызывающей это движение. На него опираются в школьном курсе геометрии при доказательстве признаков равенства треугольников наложением, при установлении равенства отрезков и углов и т.п. Наконец, принятая сейчас в школьном обучении точка зрения на преобразование опирается на теоретико-множественный подход к геометрии, несмотря на то, что ввиду методологической сложности он отсутствует в современных школьных учебниках.
Понятие геометрического преобразования неразрывно связано с развитием функционального мышления учащихся. Геометрическое преобразование трактуется с теоретико-множественной точки зрения как отображение (функция). Как известно, понятие функции — одно из фундаментальных математических понятий, непосредственно связанных с реальной действительностью. В нем ярко воплощены изменчивость и динамичность реального мира, взаимная обусловленность реальных объектов и явлений. Именно в понятии функции в определенной степени отображается бесконечное многообразие явлений реального мира.
В настоящее время существует несколько вариантов определения понятия функции. При одном из них под числовой функцией понимается отображение одного числового множества в другое, что адекватно сочетается с определением геометрического преобразования как точечного отображения плоскости (пространства) на себя.
Ф. Клейн считал понятие функции центральным понятием всей математики. По его мнению, оно должно играть руководящую роль в курсе средней школы, должно быть выяснено учащимися очень рано и пронизывать все преподавание алгебры и геометрии. С точки зрения Ф. Клейна, всякое научное знание не может быть усвоено школьниками без обращения к наглядности. Поэтому введение понятия функции с помощью геометрических образов, в геометрической форме, в частности с помощью элементарных геометрических преобразований, является наиболее целесообразной в школьном обучении.
Условия для введения понятий функции, геометрического преобразования создает теоретико-множественная концепция как основа школьного курса. В этой связи очень коротко остановимся на проблеме использования теории множеств в методике школьного обучения геометрии.
А.Н. Колмогоров и др. в своем учебнике включил теорию множеств в обучение геометрии, что в целом не сумела преодолеть общеобразовательная школа. В последующих учебниках геометрии (А.В. Погорелов, Л.С. Атанасян и др.) методология была достаточно умеренной, был сделан шаг назад, в частности, отказ от теоретико-множественного подхода. Это связано с определенными достоинствами и недостатками методологического подхода и методических принципов построения школьного курса геометрии и, в частности, методики введения понятия геометрических преобразований. Но в преподавании геометрии до сих пор не уделяется должного внимания геометрическим преобразованиям, в то время как развитие геометрической науки давно показало, что преобразования являются одной из фундаментальных областей научной геометрии, тесно связанной с курсом алгебры.
§2. Из истории возникновения раздела о движениях в школьном курсе геометрии
Геометрия – одна из наиболее древних математических наук, первые упоминания о которой можно найти в египетских папирусах (III тыс. до н.э.) и вавилонских клинописях.
Одним из важнейших обогащений геометрии стало создание теории геометрических преобразований и, в частности, движений (перемещений).
Движение и, в частности, наложение, было основным методом доказательства у Фалеса, а также играет существенную роль в «Началах» Евклида. Определение равенства фигур у Евклида основано на совмещении фигур. Евклид постоянно производит перенос отрезков с помощью циркуля, да и само описание прямых линий и окружностей производится с помощью движений. Например, Евклид определяет сферу как результат вращения полуокружности вокруг диаметра. Однако во всех случаях, когда Евклид может обойтись без движений, он так и поступает. Евклид не определяет движение и его виды.
Стремясь уточнить изложение геометрии у Евклида, Д. Гильберт в «Основаниях геометрии» (1899) отказался от самого понятия движения. Вместе с тем, существует вариант аксиоматики геометрии, предложенный Ф. Шуром, в которой гильбертовские аксиомы конгруэнтности заменены аксиомами движения.
Идея геометрических преобразований как основы геометрии выросла на базе теории групп. Впервые теорию групп применил к геометрии немецкий математик Ф. Клейн. В своей «Эрлангенской программе» (1872) он высказал идею построения геометрии на основе геометрических преобразований и определил геометрию как предмет, изучающий инварианты некоторой группы преобразований.
После публикации «Эрлангенской программы» Ф. Клейна реформисты постарались использовать идею геометрических преобразований при построении школьного курса геометрии. В учебниках геометрии идея движения находит свое отражение уже в XIX веке.
В Германии в 1882-1883 годах выходит «Учебник элементарной геометрии» Генрицы и Трейтлейна, в основу которого положена идея геометрического преобразования.
Наиболее полно геометрические преобразования представлены в учебнике А.Н. Глаголева «Элементарная геометрия» (1895). Автор вводит аксиому движения и при доказательстве ряда теорем пользуется наложением фигур. Наряду с симметрией в учебнике рассматривается параллельный перенос и вращение вокруг точки.
Использование геометрических преобразований при решении задач на построение находит широкое отражение в учебной литературе второй половины XIX века в книгах Ю. Петерсена «Методы и теории для решения геометрических задач на построение» (1866), И.И. Александрова «Методы решения геометрических задач на построение» (1883). Авторы дают характеристику каждому методу и иллюстрируют его на примере решения задач. В «Элементарной геометрии» Ж. Адамара (1898-1901) рассматриваются такие виды геометрических преобразований, как симметрия, поступательное перемещение, гомотетия и подобие, вращение, теория полюсов и другое. Однако геометрические преобразования не связываются с основным материалом курса.
Таким образом, геометрические преобразования присутствуют во многих учебниках XIX века, хотя применение они находят при незначительном числе доказательств и решении отдельных видов задач.
В начале XX века возрастает интерес к геометрическим преобразованиям и в русской школе. В учебнике «Элементарной геометрии» (1909) К.Н. Рашевский рассматривает такие виды геометрических преобразований, как симметрия относительно точки и прямой, параллельное перенесение, вращение около точки, гомотетия. Идея геометрических преобразований не охватывает весь курс геометрии. В «Геометрии пространства» Б.А. Марковича (1910) показывается применение движения при доказательстве теорем и построении курсов планиметрии и стереометрии. В 1911 году выходит работа Н.А. Извольского «Первые шаги курса геометрии», в которой автор при изучении материала пользуется наложением, вращением вокруг точки.
В 1911-1914 годах на I и II Всероссийских съездах преподавателей математики России в числе других вопросов был поставлен вопрос о внедрении в школьный курс геометрических преобразований. С докладом «Об упрощении построения курса геометрии и расширении ее содержания» выступил А.В. Годнев, где высказался за введение в курс геометрии движений. Аналогичную точку зрения осветил в докладе «Идея движения в современной геометрии и область ее применимости в курсе средней школы» А.Р. Кулишер.
Учебник А.П. Киселева «Элементарная геометрия для средних учебных заведений» (1923), который являлся долгое время основным учебником для средней школы, очень сдержан в применении геометрических преобразований. В нем присутствовали указания на применение параллельного переноса, вращения или симметрии относительно прямой к решению задач на построение. С 1938 года учебник А.П. Киселева выходит под редакцией Н.А. Глаголева, который выдвинул на первый план основные геометрические идеи о движении, о симметрии, о подобии, как геометрическом преобразовании.
В первом издании «Элементарной геометрии» (1944) Н.А. Глаголева усиливается роль геометрических преобразований. Наиболее полно рассматриваются гомотетия и симметрия, которые используются автором для доказательства соответственно признаков подобия треугольников и признаков равенства треугольников, что явилось значительным продвижением в реализации этой идеи в школьном преподавании геометрии.
Учебник «Геометрия» для 6-9 классов Н.Н. Никитина и А.И. Фетисова (1956) содержит материал о геометрических преобразованиях. Авторы рассматривают осевую и центральную симметрии, гомотетию и подобие.
К началу 60-х годов была объявлена реформа школьного образования. Основными среди целей геометрического образования были названы систематичность и научность. Академик А.Н. Колмогоров, возглавивший реформу, предпринял радикальную перестройку курса геометрии: он создал новую аксиоматику, которая готовила учащихся к лучшему пониманию геометрических положений. В учебном пособии под редакцией А.Н. Колмогорова преобразования занимали центральное место, именно они служили основой доказательства многих теорем, их обоснованию была посвящена специальная аксиома подвижности.
В 1963-1964 учебном году в программу по геометрии 9 класса была включена тема «Геометрические преобразования». Целью изучения этой темы явилось ознакомление учащихся с идеей и методом геометрических преобразований. Учебным пособием являлся учебник «Геометрия» В.Г. Болтянского и И.М. Яглома, где авторы рассматривают осевую и центральную симметрии, поворот, параллельный перенос, гомотетию. Раздел «Осевая симметрия» начинается с рассмотрения конкретных симметричных фигур. Далее дается определение точек, симметричных относительно прямой. При изложении теории центральной симметрии, параллельного переноса и поворота значительное место уделяется наглядности. Большое внимание в учебном пособии уделяется учению о гомотетии, которая рассматривается как с положительным, так и с отрицательным коэффициентом. После рассмотрения отдельных видов преобразований авторы знакомят читателя с понятием геометрического преобразования. В итоге дается определение движения и раскрывается его роль в курсе геометрии. В учебнике содержатся примеры на формирование у учащихся приемов метода геометрических преобразований.
В соответствии с действующей в настоящее время программой для средней общеобразовательной школы, геометрические преобразования плоскости включены в качестве обязательного материала в курс планиметрии 8-9 классов. Геометрические преобразования представляют собой некоторую часть (главу или отдельные параграфы) учебника геометрии.
§3. Содержание раздела «Движение» и требования к математической подготовке учащихся
Теоретические основы содержания общего среднего образования разработаны Г.В. Дорофеевым, И.Я. Лернером, М.Н. Скаткиным и др. В частности, разработаны принципы и критерии отбора содержания школьного математического образования. В педагогике «принципы... указывают общее направление деятельности по формированию содержания образования..., критерии же реализуют процедуру конструирования, отбор учебного материала, его последовательность [24]. Н.В. Метельский сформулировал два требования, предъявляемые к научной информации, которая отбирается для включения в школьный курс — информация должна обладать общеобразовательной ценностью и быть доступной учащимся. Оценку общеобразовательного значения материала автор предлагает производить с учетом его потенциальных возможностей: «1) формировать мировоззрение; 2) развивать мышление, творческие силы и способности; 3) вооружать жизненно - прикладными знаниями и умениями; 4) готовить к самообразованию; 5) расширять научный кругозор» [21]. Системы принципов и критериев отбора содержания обучения математике, по мнению В.А. Оганесяна, должны базироваться на принципах дидактики, которые автор объединил в четыре следующие группы:
1. Принцип воспитывающего и развивающего обучения;
2. Принцип научности и доступности обучения;
3. Принцип систематичности и последовательности обучения;
4. Принцип связи обучения с жизнью и его политехнической направленности.
В своей работе Г.В. Дорофеев подразделяет принципы отбора содержания на внешние, социально обусловленные, и внутренние, обусловленные психолого-педагогическими и методическими требованиями. К внешним относятся два принципа: информационной емкости и социальной эффективности, в соответствии с которыми обучение математике должно обеспечивать приобретение всеми учащимися объема знаний, достаточного для реализации цели математического образования и формирование кадрового потенциала общества во всех сферах деятельности, требующих математических знаний и интеллектуальной культуры. К внутренним автор относит принципы интеллектуальной емкости, дифференцированной реализуемости, познавательной емкости и др.
Г.В. Дорофеевым разработан также механизм отбора содержания, основанного на разделении знаний на целевые (непосредственно отражающие цели обучения математике) и вспомогательные, которые не являются необходимыми в плане достижения целей математического образования, но без предварительного изучения которых, не могут быть освоены знания
Результаты исследований А.К. Марковой, И.М. Смирновой, Г.И. Щукиной и др. содержат в себе особенности содержания учебного материала, влияющие на формирование познавательного интереса. Содержание в том случае стимулирует развитие познавательного интереса учащегося, если оно является занимательным, постоянно обновляется, включает исторические сведения, показывает современные достижения науки, имеет личностную значимость для учащегося. Именно эти особенности содержания оказывают положительное влияние и на формирование профессиональных интересов школьников.
Перечисленные особенности в полной мере можно отнести и к геометрическому материалу. Чисто геометрическое содержание материала не может оказать влияния на формирование интереса к другим учебным дисциплинам. Поэтому, чтобы в процессе изучения геометрических преобразований было возможно выявлять, учитывать и развивать познавательные интересы к различным предметным областям, содержание темы целесообразно дополнить сведениями межпредметного и практического характера.
Например, развитию математических способностей учащихся способствуют такие особенности содержания учебного материала как: абстрактность, обобщенность, логичность, формализованность, наличие взаимно обратных утверждений. Для развития способностей естественнонаучного мышления имеет значение исследовательский характер заданий, обобщенность изложения, привлечение наглядности. Развитию гуманитарных способностей отвечает содержание, излагаемое естественным языком и наполненное образами, личностными отношениями, эстетическими образами.
Рассмотрим дидактические особенности темы «Геометрические преобразования плоскости и пространства», которые включают в себя:
1. Наличие внутрипредметных связей.
Данная тема может быть использована при изучении других тем школьного курса геометрии. Например, при доказательстве пропорциональности отрезков, равенства фигур, при решении задач на построение, при изучении площадей фигур и т.д.
2. Наличие межпредметных связей.
Основные знания и умения, приобретенные при изучении данной темы, могут быть использованы при изучении других учебных предметов в школе. Например, понятие движения и его видов могут быть использованы в физике (механическое движение, симметрия законов природы и др.), в курсе алгебры (преобразование графиков функций); химии (кристаллы), изобразительном искусстве, черчении и т.д.
3. Прикладная направленность материала темы «Движение».
Знания и умения, полученные школьниками в результате изучения данной темы, могут быть использованы ими в определенных жизненных ситуациях. Например, нахождение расстояния до недоступной точки, нахождение высоты предмета, выполнение орнаментов и т.п.
4. Общекультурный характер темы «Движение».
Эта особенность естественным образом вытекает из той роли, которую играет данная тема в математике как науке и, в частности, в школьном предмете. Например, независимо от интересов учащихся и их ориентации на будущую профессиональную деятельность, изучение данной темы необходимо всем, так как она имеет большой спектр приложений.
5. Развивающий потенциал темы «Движение».
Данная тема позволяет развить логическое мышление, воображение, интуицию и т.д. Изучение геометрических преобразований способствует формированию и развитию мировоззрения учащихся. Геометрические преобразования позволяют показать учащимся фигуры в движении, способствуют представлению о различных фигурах не как о чем-то неподвижном, а как об изменяющемся и преобразующемся одно в другое.
6. Применение как эмпирических, так и логических методов обучения при обучении по теме «Движение».
При изучении данной темы возможно использование таких методов обучения как эксперимент, наблюдение, опыт и, в то же время, есть возможность применить анализ, синтез, аналогию, абстрагирование и т.п. Например, лабораторные работы позволяют ученикам экспериментальным путем установить основные свойства геометрических преобразований. В то же время, анализируя свойства одного из геометрических преобразований, можно установить аналогичные свойства другого (например, осевая и центральная симметрии).
7. Обучение по теме «Движение» может осуществляться двумя способами: конкретно-индуктивным (с опорой на наглядность) и абстрактно-дедуктивным.
8. Тема допускает различные уровни обучения: базовый, повышенный и углубленный.
В 8-9 классах учащиеся обучаются в одном классе, поэтому для того, чтобы учесть индивидуальные возможности и запросы каждого школьника, необходимо в уровневую дифференциацию ввести элементы профилирования. В результате этого в классе выделятся относительно устойчивые группы учащихся с гуманитарными наклонностями, прикладными, естественнонаучными.
При отборе содержания темы «Движение» для групп и классов различного направления (гуманитарное, естественнонаучное (физическое) и математическое) целесообразно использовать следующие критерии отбора содержания материала, при выборе которых мы исходили из того, что одной из центральных задач преподавания геометрии в школе является профильная ориентация учащихся в соответствии с их интересами и способностями, а также связь обучения с жизнью.
Выделим пять наиболее общих критериев, которые способствуют решению данной задачи.
1) Критерий дидактической значимости заключается в том, что знания должны быть предметом изучения и одновременно средством для последующего изучения геометрии и математики в целом. Значимость знаний определяется с учетом степени их применяемости к решению задач, доказательству теорем, обоснованию закономерностей и т.д.
2) Критерий применения устанавливает, что знания должны иметь большую прикладную направленность.
3) Критерий активности предполагает, что знания должны активно работать на протяжении длительного времени (времени изучения темы, раздела, курса) и быть необходимыми для продолжения образования.
4) Критерий соответствия задачам и целям обучения в классе данного профиля.
Изучение геометрических преобразований способствует развитию познавательного интереса учащихся, формированию их творческой активности, а также усилению прикладной направленности выбранного профиля обучения. Метод геометрических преобразований дает возможность учащимся применять графические (конструктивные) способы решения задач, требующие развитого пространственного воображения.
5) Мировоззренческий критерий.
Изучение геометрических преобразований способствует развитию мировоззрения учащихся и дает возможность:
- повысить уровень математической культуры школьников;
- пополнить свои знания самостоятельно;
- проявить свои склонности и интересы.
Таким образом, изучение темы «Геометрические преобразования»:
- необходимо для изучения последующего курса математики и это должно учитываться при определении логического курса математики и отборе содержания;
- обеспечивает изучение других предметов. Данную особенность необходимо учесть при отборе содержания и построении логической структуры курса;
- способствует достижению одной из главных целей курса математики развитие мышления школьников;
- обеспечивает учащихся некоторыми умениями и методами, необходимыми им в повседневной жизни.
Руководствуясь выделенными критериями отбора содержания материала, рассмотрим общие умения, которыми должны овладеть учащиеся 8-9 классов при изучении геометрических преобразований:
1. Строить образы фигур при осевой и центральной симметрии, параллельном переносе, повороте и гомотетии.
2. Задавать ось симметрии, центр поворота, определять угол поворота, направление параллельного переноса, его расстояние.
3. Видеть ситуации, в которых могут быть использованы определенные виды преобразований.
4. Переводить условия задачи на язык геометрических преобразований, а затем применять свойства конкретного преобразования к решению данной задачи, и тем самым решать задачи по геометрии и другим смежным дисциплинам методом геометрических преобразований.
Данные умения конкретизируются для каждой группы учащихся класса.
Изучение темы «Движение» целесообразно проводить в два этапа. На первом этапе в 8-9 классах рассматриваются геометрические преобразования на плоскости, а на втором этапе в 10-11 классах изучаются геометрические преобразования в пространстве. Данное распределение соответствует традиционному расположению материала по программе общеобразовательной школы. Тогда эффективность изучения темы будет зависеть от того, каким образом она будет реализована внутри каждого этапа. Для того, чтобы добиться значительного повышения эффективности изучения данной темы различными группами учащихся, необходимо учесть при ее построении их индивидуальные возможности, опираясь на основные дидактические принципы, на выделенные дидактические особенности темы.
Достижению этих целей будет способствовать использование возможностей профильной дифференциации предпрофильной подготовки при изучении темы «Движение».
Необходимо добавить, что содержание темы в 8-9 классах имеет значительную базовую часть, необходимую для изучения всеми учащимися, независимо от их интересов и стремлений. В то же время отметим, что, в основном, к этому возрасту математические способности учащихся уже проявились. Поэтому в данный период возникает острая необходимость учета индивидуальных особенностей учащихся, так как часть школьников по окончании 9 класса уже имеет твердые профессиональные намерения. Все перечисленные факты приводят к выводу о том, что в 8-9 классах целесообразно при построении курса «Геометрические преобразования плоскости» реализовать уровневую дифференциацию с элементами профильной, которые заключаются в отборе теоретического материала и в подборе системы задач для каждой группы учащихся класса в соответствии с их интересами и возможностями.
В 8-9 классах в содержании темы «Движение» выделяются три уровня обучения: базовый, повышенный и творческий.
Базовый уровень содержит основное ядро темы, которое должно быть изучено всеми учащимися класса. Причем нужно заметить, что данная часть должна содержать все три составляющие: гуманитарную, прикладную и естественнонаучную. На данном уровне целесообразно использовать фронтальные формы работы учебной деятельности учащихся.
Повышенный уровень характеризуется включением на этапе закрепления темы задач определенного практического характера, которые иллюстрируют приложения геометрических преобразований. На этом уровне уже нужно рекомендовать учитывать индивидуальные особенности учащихся, их интересы. В содержании этого уровня целесообразно выделить три составляющие и таким образом организовать работу на уроке, чтобы школьники, имеющие гуманитарные способности, больше работали с учебным материалом гуманитарного содержания и, наоборот, учащиеся с математическими способностями больше имели дело с материалами естественнонаучного содержания. Среди учащихся класса следует отобрать таких, которым больше подходит прикладная составляющая. При организации такой работы лучше использовать групповые и индивидуальные формы учебной деятельности. Таким образом, при обучении наблюдаются уже элементы профильной дифференциации.
Еще одно ее проявление возможно на третьем уровне обучения — творческом. Данный уровень может проявляться в двух видах: через факультативы и курс углубленного изучения математики. Факультативные занятия или курсы по выбору могут проводиться в двух направлениях:
1. В содержании факультатива преобладает естественнонаучная составляющая, т.е. рассматриваются вопросы, позволяющие углубить изучение теоретических вопросов данной темы. Занятия целесообразно рекомендовать тем школьникам, которые затем продолжат обучение в классах математического профиля.
2. В содержании факультатива преобладают вопросы прикладного характера, практические задачи. Данные занятия рекомендуется посещать учащимся, которые либо продолжат обучение в колледжах или будут обучаться в классах технического профиля.
Изучение темы «Движение» в классах с углубленным изучением математики предусмотрено государственной программой для этих классов. Оно может проводиться в два этапа, отвечающие возрастным возможностям и потребностям школьников и соответственно различающиеся по целям. Первый этап относится к основной школе, второй - к старшей школе.
Первый этап (8-9 классы) углубленного изучения математики является в значительной мере ориентационным. На этом этапе ученику следует помочь осознать степень своего интереса к предмету и оценить возможности овладения им с тем, чтобы по окончании основной школы он смог сделать сознательный выбор в пользу дальнейшего изучения математики – углубленного либо обычного.
В основу уровневой дифференциации с элементами профилирования закладывается принцип, согласно которому большую часть учебного времени три группы учащихся работают вместе. Так как работа идет в одном классе, то у учащихся есть возможность перейти из одной группы обучения в другую, если интересы приобрели другую профессиональную окраску. Данный подход способствует осознанному выбору профиля обучения в старших классах и наиболее эффективному обучению в нем.
§4. Анализ современных учебников, рабочих тетрадей и дидактических материалов по геометрии
Метод геометрических преобразований – метод обоснования некоторых отношений между объектами евклидовой геометрии, например, равенство, параллельность, подобие и др. Для доказательства теорем и решения задач (в частности, задач на построение) метод геометрических преобразований (как частный случай математического моделирования) выглядит следующим образом:
Выбрать геометрическое преобразование, которое позволит обосновать наличие указанного отношения между объектами евклидовой геометрии;
Выполнить выбранное преобразование так, чтобы один объект (или его часть) переходил в другой (новый, вспомогательный) объект, более удобный для исследования (или построения);
Исследовать полученный новый (вспомогательный) объект и его свойства;
Обосновать наличие указанного отношения между объектами с помощью свойств выбранного преобразования.
Частные случаи метода геометрических преобразований – методы осевой и центральной симметрии, поворота, параллельного переноса часто используют для обоснования равенства фигур, параллельности и перпендикулярности, отыскания кратчайшего расстояния.
У авторов школьных учебников по геометрии геометрические преобразования занимают разное место по объему и уровню строгости изложения.
В учебнике А.В. Погорелова «Геометрия 7-11» для общеобразовательных учреждений преобразованиям отведен один параграф «§9. Движение». Эта тема изучается в 8 классе. Основная цель изучения темы познакомить учащихся с примерами преобразований геометрических фигур. Поскольку в дальнейшем движения не применяются в качестве аппарата для решения задач и изложения теории, изучение материала рекомендуют дать в ознакомительном порядке, то есть не требуется от учащихся воспроизведение доказательств теорем, умения в овладении методом геометрических преобразований и применения его при решении задач. Основные виды движений – симметрия относительно прямой и точки, поворот, параллельный перенос – учащиеся должны усвоить при решении следующих задач:
1. Даны точки A и B. Постройте точку B’, симметричную точке B относительно точки A.
2. При симметрии относительно некоторой точки точка X переходит в точку X’. Постройте точку, в которую при этой симметрии переходит точка Y.
3. Даны точки A, B, C. Постройте точку C’, симметричную точке С относительно прямой AB.
4. Чему равны координаты точки, симметричной точке (-3; 4) относительно: 1) оси x; 2) оси y; 3) начала координат?
5. 1) Постройте точку А1, в которую переходит точка А при повороте около точки О на угол 60° по часовой стрелке.
2) Постройте фигуру, в которую переходит отрезок АВ при повороте около точки О на угол 60° по часовой стрелке.
6. Постройте фигуру, в которую переходит треугольник АВС при повороте его около вершины С на угол 60°.
7. Даны точки А, В, С. Постройте точку С’, в которую переходит точка С при параллельном переносе, переводящем точку А в В.
8. Параллельный перенос задается формулами х’ = х + 1, у’ = у - 1. В какие точки при этом параллельном переносе переходят точки (0; 0), (1; 0), (0; 2)?
9. Найдите величины a и b в формулах параллельного переноса х’ = х + а, у’ = у + b, если известно, что:
1) точка (1; 2) переходит в точку (3; 4); 2) точка (2; -3) – в точку (-1; 5); 3) точка (-1; -3) – в точку (0; -2).
В отличие от симметрии и поворота определение параллельного переноса дается с помощью формул, указывающих связь между координатами точки и ее образа при данном параллельном переносе. Такое определение выглядит формальным, а не конструктивным, как у предыдущих видов движения, однако, если проиллюстрировать на рисунке эти формулы, то можно заметить, что они тоже дают способ построения точки, в которую переходит данная точка при параллельном переносе: она смещается на а вдоль оси абсцисс и на b вдоль оси ординат. Это преобразование дает еще один пример движений, причем все свойства движений для параллельного переноса являются, видимо, самыми очевидными для учащихся.
В результате изучения материала учащиеся должны:
знать определение движения, его свойства; определения точек и фигур, симметричных относительно данной точки, симметричных относительно прямой; определение поворота, формулы, задающие параллельный перенос и геометрические свойства параллельного переноса;
уметь применять свойства движений для распознавания фигур, в которые переходят данные фигуры при движении, строить точки и простейшие фигуры, симметричные данным относительно данной точки и данной прямой, приводить примеры фигур, имеющих центр симметрии или ось симметрии, применять свойства движения в решении задач на симметрию фигур; строить образы простейших фигур при повороте и параллельном переносе; выявлять сонаправленные и противоположно направленные лучи в рассматриваемых конфигурациях.
Планирование изучения материала:
|
Номер пункта. |
Содержание материала. |
Количество часов. |
|
8 класс. § 9. Движение. |
12 ч. |
|
|
82, 83 84, 85 86 87, 88 89, 90 |
Преобразование фигур. Свойства движения. Симметрия относительно точки. Симметрия относительно прямой. Контрольная работа. Поворот. Параллельный перенос и его свойства. Существование и единственность параллельного переноса. Сонаправленность полупрямых. Равенство фигур. |
2 ч. 3 ч. 1 ч. 1 ч. 3 ч. 2 ч. |
В §9 понятие «преобразование» вводится на наглядно-интуитивном уровне: «Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной». Соответственно, движение понимается как преобразование одной фигуры в другую, если оно сохраняет расстояние между точками. Важно подчеркнуть, что в учебнике А.В. Погорелова рассматриваются преобразования не всей плоскости, а только фигур. В этом случае неизвестно что происходит с остальными точками плоскости, в отличие от преобразования плоскости, где для каждой точки плоскости можно указать ее образ и прообраз. Возможно, рассмотрение преобразований фигур, а не плоскости связано с толкованием понятия движения с механической точки зрения.
Еще одна особенность учебника А.В. Погорелова состоит в том, что определение преобразований и способ построения фигур при преобразованиях как бы слиты воедино. Определения обладают высокой степенью наглядности, чем позволяют воображению легко конструировать необходимые образы.
Далее рассматриваются теоретические основы свойств движений, симметрии относительно точки и прямой. Все вводимые понятия и доказательства теорем достаточно полно проиллюстрированы, но не приводится разбор конкретных задач, чего нельзя сказать о рассмотрении вопроса о повороте плоскости около данной точки. После рассмотрения теоретических сведений представлена решенная задача на построение точки (фигуры), в которую переходит точка (отрезок) при повороте около точки О на угол 60° по часовой стрелке. Некоторое внимание уделено вопросу использования метода координат в изучении свойств преобразований, например параллельного переноса.
Заметим также, что при изучении движений такое важное понятие, как композиция движений, в учебнике А.В. Погорелова специально не определяется.
В дидактических материалах В.А. Гусева и А.И. Медяника к учебнику А.В. Погорелова «Геометрия, 7-9» представлены четыре самостоятельные работы, контрольная работа в нескольких вариантах разного уровня сложности и дифференцированные задания как продолжение и развитие самостоятельных работ, где более четко учтены индивидуальные особенности учащихся. В то же время эти задания предполагают более высокий уровень развития учащихся, так как направлены на развитие у них логического мышления. В вариантах самостоятельных и контрольной работ основной акцент делают на такие обязательные результаты обучения школьников, как:
а) представления о движении и о связи его с понятием равенства фигур;
б) построение фигур, симметричных данным, при осевой и центральной симметриях.
В.Н. Литвиненко и А.Э. Попович разработали рабочую тетрадь для 8 класса к учебнику А.В. Погорелова «Геометрия 7-11», которая является методическим пособием для занятий классов общеобразовательной школы. Она предназначена помочь организовать работу учащихся в классе и дома. К каждому из пунктов «§9. Движение» учебника приведены задачи с готовыми чертежами, которые нужно дополнить построениями и записать полученный ответ или произведенные действия. И если в дидактических материалах, рассмотренных выше, авторами представлены задачи, направленные на расширение задачного материала учебника, то рабочая тетрадь содержит задачи на закрепление базовых понятий темы.
Учебник Л.С. Атанасяна и др. «Геометрия 7-9» выгодно отличается от других. Преимущество состоит в том, что учащиеся по данному учебнику самостоятельно могут освоить понятие движения и его видов.
Планирование изучения материала:
|
Номер параграфа. |
Содержание материала. |
Количество часов. |
|
8 класс. Глава V. Четырехугольники. |
3 ч. |
|
|
3 |
Прямоугольник, ромб, квадрат. [Осевая и центральная симметрии.] Контрольная работа. |
3 ч. 1 ч. |
|
9 класс. Глава XIII. Движения. |
8 ч. |
|
|
1 2 |
Понятие движения. Параллельный перенос и поворот. Решение задач. Контрольная работа. |
3 ч. 3 ч. 1 ч. 1 ч. |
Знакомство с осевой и центральной симметрией начинается в 8 классе. Эти преобразования рассматриваются не как преобразования плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости происходит в 9 классе в главе «Движения», где движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. Здесь же рассматриваются основные виды движений: осевая и центральная симметрии, параллельный перенос и поворот. На примерах показывается применение движений при решении геометрических задач разной степени сложности. Кроме того, исследуется важный вопрос о связи понятий наложения и движения. Понятие наложения, на основе которого определялось равенство фигур, относится в данном курсе геометрии к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Этот пункт «Наложения и движения» обозначен звездочкой, что говорит о необязательности его изучения. Задачный материал темы нацелен на выработку навыков построения образов точек, отрезков, треугольников при симметриях, параллельном переносе и повороте.
1. Даны две прямые a и b. Постройте прямую, на которую отображается прямая b при осевой симметрии с осью a.
2. Даны прямая a и четырехугольник ABCD. Постройте фигуру F, на которую отображается данный четырехугольник при осевой симметрии с осью a. Что представляет собой фигура F?
3. Даны точка O и прямая b. Постройте прямую, на которую отображается прямая b при центральной симметрии с центром O.
4. Даны точка O и треугольник ABC. Постройте фигуру F, на которую отображается треугольник ABC при центральной симметрии с центром O. Что представляет собой фигура F?
5. Даны треугольник, трапеция и
окружность. Постройте фигуры, которые
получаются из этих фигур параллельным
переносом на данный вектор
 .
.
6. Посторойте отрезок A1B1, который получается из данного отрезка AB поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на 75° против часовой стрелки; в) на 180°.
Учебное пособие для учащихся школ и классов с углубленным изучением математики «Геометрия, дополнительные главы к школьному учебнику 9 класса» Л.С. Атанасяна и др. является дополнением к основному учебнику «Геометрия, 7-9». Геометрическим преобразованиям посвящена одна из глав данного пособия, в которой движение дополняется и другими преобразованиями: центральным подобием, инверсией. Решается ряд интересных задач. Этот материал может заинтересовать учащихся в предпрофильной подготовке. Он расширяет их представления о движениях и подобиях, демонстрирует возможность применения метода геометрических преобразований при доказательстве теорем и решении задач.
Б.Г. Зив разработал дидактические материалы, содержащие самостоятельные и контрольные работы, математические диктанты и проверочные работы, рекомендованные преимущественно к учебнику Л.С. Атанасяна, Б.Ф. Бутузова и др. «Геометрия, 7-9», но могут быть использованы по утверждению автора и при работе по другим учебникам. В первом и втором вариантах самостоятельных работ предлагаются задачи, для успешного решения которых учащиеся должны применить знания на уровне минимальных программных требований. Третий и четвертый варианты состоят из задач среднего уровня сложности. Решение этих задач предусматривает умение распознавать понятия в стандартных ситуациях, применять знания в стандартных условиях или при небольших отклонениях от них. Задачи третьего и четвертого вариантов по сложности примерно соответствуют большинству основных задач учебника. Пятый и шестой варианты предназначены для наиболее подготовленных учащихся. При решении задач этих вариантов требуется уметь применять знания в усложненных ситуациях. По сложности эти задачи примерно соответствуют наиболее трудным из основных и дополнительных задач учебника.
Седьмой и восьмой варианты состоят из задач, при решении которых требуется творческое применение знаний. Здесь приходится анализировать сложные геометрические ситуации, самостоятельно открывать новые факты, устанавливать отношения между ними. Задачи из седьмого и восьмого вариантов рекомендовано давать учащимся после выполнения ими основной работы наравне со всеми учащимися класса в оставшееся время или использованы в качестве необязательного задания для домашней работы, а также на факультативных занятиях или занятиях математического кружка.
Математические диктанты предназначаются для систематизации теоретических знаний учащихся и могут предшествовать контрольной работе. Диктант представляет собой набор из 10 небольших задач по прямому применению полученных знаний о движениях из учебника.
В учебнике А.Д. Александрова и др. «Геометрия, 9» с углубленным изучением математики преобразования фигур рассматриваются в главе «Преобразования».
Планирование изучения материала:
-
Номер параграфа.
Содержание материала.
Количество часов.
9 класс. Глава 2. Преобразования.
18 ч.
6
7
8
Движения.
Симметрия фигур.
Подобие.
Контрольная работа.
7 ч.
3 ч.
7 ч.
1 ч.
Основной целью изучения данной главы является проникновение учащихся в сферу идей современной математики, в немалой степени являющейся математикой преобразований или же математикой, изучающей аксиоматически построенные теории. Материал, предложенный в учебнике, может быть освоен на уровне применения введенных понятий и теорем только в подготовленном классе.
Глава «Преобразования» изучается в 9 классе и завершает собой изучение планиметрии. При решении задач, предложенных авторами, наряду с материалом главы используются также практически все методы, теоремы и факты, которые были изучены ранее, для осуществления итогового повторения.
Определяются движения, заданные на всей плоскости и доказываются их свойства. На основе движений определяется равенство фигур. Изучаются виды движений: параллельный перенос, осевая симметрия, поворот и центральная симметрия. Проводится классификация движений, рассматривается композиция движений. Изложены теоремы о задании движений, замечание о распространении движения, теорема Шаля, неподвижные точки движений, два рода движений, ориентация. Большое внимание уделяется симметриям фигур. Учебник содержит различные задачи на геометрические преобразования, которые автор делит на разделы: разбираемся в решении (приведены решенные задачи), дополняем теорию, рисуем, планируем, находим величину, выводим уравнение, доказываем, исследуем, строим, применяем геометрию, занимательная геометрия, участвуем в олимпиаде. Например,
1. а) Докажите, что в результате переноса прямая переходит в прямую, ей параллельную, или в себя;
б) Даны две параллельные прямые. Каким переносом одна из них может быть получена другой?
в) Даны два равных и параллельных отрезка. каким переносом один из них может быть получен из другого?
г) Докажите, что в результате переноса вектор переходит в равный вектор.
Нарисуйте образ куба ABCDA1B1C1D1 в результате переноса на вектор
а)
 ;
б)
;
б)
 ;
в)
;
в)

а) В системе координат даны две точки A(2;1) и B(3;3). Как найти точку К на оси x, такую, что ломаная AKB кратчайшая? Как вычислить координаты точки К и длину этой ломаной?
б) Решите задачу «а» для точки L на оси y.
Учебник И.Ф. Шарыгина «Геометрия, 7-9» реализует авторскую концепцию построения школьного курса геометрии. Глава «Преобразования плоскости» изучается в 9 классе и завершает теоретическую часть курса планиметрии.
Планирование изучения материала:
-
Номер параграфа.
Содержание материала.
Количество часов.
9 класс. 12. Преобразования плоскости.
8 ч.
12.1
12.2
12.3
Движение плоскости.
Виды движений плоскости.
Гомотетия.
Систематизация и обобщение знаний.
Контрольная работа.
Резерв.
1 ч.
2 ч.
1 ч.
2 ч.
1 ч.
1 ч.
В отличие от геометрических курсов, в которых понятие движения положено в их основу, в данном учебнике такие виды движения, как симметрия относительно точки и относительно прямой, служат для доказательства теорем, а такие виды движения, как поворот и параллельный перенос являются объектом изучения.
В первом пункте вводится понятие движения: движением называется такое преобразование плоскости, которое не меняет расстояние между парами точек, т.е. если точки А и В в результате движения переходят в точки А’ и В’, то АВ = А’В’. Далее теорема 12.1. (основное свойство движений): результатом двух последовательных движений плоскости является движение плоскости – приводится доказательство теоремы, а затем рассматривают две основные теоремы о движении плоскости также с доказательствами. Теорема 12.2 (основной способ задания движения): любое движение плоскости полностью задается движением трех точек плоскости, не лежащих на одной прямой. И теорема 12.3 (о возможности представления любого движения через осевые симметрии): любое движение плоскости может быть получено с помощью не более чем трех осевых симметрий.
В следующем пункте рассматривают виды движений плоскости. Теорема 12.4. (о представлении параллельного переноса в виде двух симметрии): в результате двух последовательных осевых симметрии с параллельными осями любая точка А плоскости переходит в такую точку А’, что вектор АА’ постоянен для всех точек плоскости.
Такое преобразование называется параллельным переносом. Сам вектор АА’ называется вектором параллельного переноса.
И затем теорема 12.5 (о представлении
поворота в виде двух симметрий): пусть
две прямые
 и
и
 на плоскости пересекаются в точке О и
образуют между собой угол α (α ≤ 90). В
результате двух последовательных
симметрии относительно прямых
на плоскости пересекаются в точке О и
образуют между собой угол α (α ≤ 90). В
результате двух последовательных
симметрии относительно прямых
 и
и
 мы получим поворот на угол 2α вокруг
точки О. При этом направление поворота
то же, что и у поворота на угол α,
переводящего прямую
мы получим поворот на угол 2α вокруг
точки О. При этом направление поворота
то же, что и у поворота на угол α,
переводящего прямую
 в прямую
в прямую
 с доказательством.
с доказательством.
Здесь же рассматриваются такие темы как «Три осевые симметрии» и «Скользящая симметрия», отмеченные звездочкой, т.е. предназначены для углубленной подготовки. Задачный материал дифференцирован по уровню сложности.
К учебнику прилагается рабочая тетрадь В.Б. Алексеева, В.Я. Галкина и др., в которую включена тема «Преобразования плоскости». В тетради разобраны многие задачи, имеющиеся в учебнике, а также представлены другие задачи. Работа с тетрадью рекомендована строго после изучения материалов учебника. Задачи, содержащиеся в тетради, предполагают разную степень участия ученика в процессе решения. Решения некоторых задач приведены полностью, их надо внимательно прочитать и осознать, для того, чтобы следующие задачи решить по аналогии или с использованием похожих соображений. В решении большинства задач имеются пропуски, которые нужно заполнить: привести ссылку на формулы или теоремы, несложные вычисления. При этом оставленные отдельно слова и фразы помогут понять логику решения. Задания по теме «Преобразования плоскости» выделены в два занятия. В каждом занятии представлены задачи от простых, закрепляющих основные геометрические понятия и факты, до достаточно сложных, что помогает организовать работу учеников, как по базовой программе, так и по программе углубленного изучения движений.
Изучение геометрических преобразований в учебнике В.Г. Болтянского, Г.Д. Глейзера «Геометрия 7-9» начинается с центральной симметрии. Параграф 10 «Равенство фигур» имеет принципиальное значение для всего последующего курса. Здесь учащиеся впервые приобщаются к методу геометрических преобразований. Сравнение геометрических преобразований с функциями способствует как более легкому усвоению самого понятия геометрического преобразования, так и представлению о единообразии математики, о единстве алгебры и геометрии.
Заметим, что понятие функции, преобразования, или, как ещё говорят, отображения одного множества в другое, играет важнейшую роль не только в алгебре и геометрии, но и во всей современной математике, а также её приложениях.
Преобразования, при которых сохраняются расстояния, называются в геометрии движениями из общих свойств движений в этом параграфе рассматривается лишь предложение о том, что при движении пересечение фигур переходит в пересечение их образов (и то же для объединения). Это предложение представляет собой теорему, т. е. оно может быть доказано. Доказательство носит теоретико-множественный характер, незнакомый мышлению учащихся, и потому это доказательство не приводится. Смысл этого предложения будет ясен учащимся из рассмотрения рисунка в учебном пособии.
Далее вводится определение: две фигуры называются равными, если существует движение, отображающее одну из них на другую. Затем пишется: так как при движении длины сохраняются, то равные отрезки имеют равную длину. Справедливо и обратное утверждение: если два отрезка имеют равную длину, то они равны, т. е. существует движение, отображающее один из них на другой.
В параграфе 11 «Поворот и центральная симметрия» вводится один из видов движений – поворот. Приводятся рисунки для наглядного представления о повороте. Затем рассматриваются задачи (с решением). После решения первой задачи упоминаются «характерные точки» фигуры. В случае отрезка такими характерными точками являются его концы. Для ломанной (или многоугольника) характерными точками являются вершины. А чтобы найти образ окружности, надо построить образ её центра и провести окружность того же радиуса. Полуплоскость можно задать тремя точками: надо задать граничную прямую в этой полуплоскости (для этого нужно указать две точки) и задать ещё одну точку этой полуплоскости (не лежащую на прямой).
В следующей главе рассказывают
об осевой симметрии. При изложении
материала о движениях, определение
движения даётся лишь описательное, и
доказательство того, что рассматриваемое
преобразование является движением, то
есть сохраняет расстояния, не приводится.
О параллельном переносе такого сказать
нельзя: если при параллельном переносе
на вектор
 имеем
имеем
 ,
то
,
то
 -
параллелограмм, и поэтому
-
параллелограмм, и поэтому
 =
АВ. Иначе говоря, параллельный перенос
сохраняет расстояния, то есть является
движением. Что же касается поворота и
осевой симметрии, то они вводятся лишь
описательно. В частности, поворот может
быть определён как такое движение
плоскости, при котором только одна точка
остаётся неподвижной, то есть переходит
в себя. Приводится наглядная модель
поворота, которая заменяет учащимся
доказательство существования такого
движения.
=
АВ. Иначе говоря, параллельный перенос
сохраняет расстояния, то есть является
движением. Что же касается поворота и
осевой симметрии, то они вводятся лишь
описательно. В частности, поворот может
быть определён как такое движение
плоскости, при котором только одна точка
остаётся неподвижной, то есть переходит
в себя. Приводится наглядная модель
поворота, которая заменяет учащимся
доказательство существования такого
движения.
То же относится и к осевой
симметрии. Она может быть определена
как такое движение плоскости, при котором
все точки некоторой прямой L остаются
неподвижными, а любая точка A
не принадлежащая L переходит в точку
 ,
лежащую по другую сторону прямой L. Также
приводится наглядная модель осевой
симметрии, а вопрос о существовании
подобного движения не рассматривается.
Упрощённую модель можно получить
перегибанием чертежа по прямой L (в этом
случае рассматривается симметрия не
всей плоскости, а полуплоскости).
,
лежащую по другую сторону прямой L. Также
приводится наглядная модель осевой
симметрии, а вопрос о существовании
подобного движения не рассматривается.
Упрощённую модель можно получить
перегибанием чертежа по прямой L (в этом
случае рассматривается симметрия не
всей плоскости, а полуплоскости).
Как и при рассмотрении движений в предыдущих параграфах, проводится идея о том, что для построения образа фигуры надо выделить в ней характерные точки и построить их образы.
Материал следующего параграфа «Ось симметрии двух точек» традиционный. Материал о четырёхугольниках специального вида (прямоугольник, ромб, квадрат), традиционно выделяемый в отдельный параграф, здесь рассредоточен по разным параграфам учебного пособия. В частности, в этом параграфе рассматривается ромб. Вводится теорема: пусть L - ось симметрии точек А и В. Тогда: если точка М принадлежит прямой L, то AM = ВМ; если точка М не принадлежит прямой L, то AM не равно ВМ. Эту теорему можно формулировать и другими способами:
а) точка М, в том и только в том, случаи принадлежит оси симметрии точек А и В, если AM = ВМ;
б) ось симметрии точек А и В есть множество всех точек, равноудалённых от А и В.
Из рассмотренного решения первой задачи становится понятным, почему ось симметрии двух точек А и В часто называют средним перпендикуляром отрезка АВ.
§18. Свойства равнобедренного треугольника. Новым является в этом параграфе то, что акцент сделан на симметричность равнобедренного треугольника. Это систематизирует факты и упрощает доказательства. В этой главе есть ещё параграф 19. Расстояние от точки до прямой.
Содержание параграфа 36* «Композиция геометрических преобразований» нетрадиционно: прежде этот материал в школе не рассматривался. Операция композиции движений в каком-то смысле аналогична «умножению» движений (иногда вместо термина композиция преобразований говорят об их «произведении»). Однако неожиданным для учащихся является то, что композиция движений является, вообще говоря, некоммутативной операцией. Это поясняется примером. В некоторых случаях композиция движений обладает свойством коммутативности.
Далее в параграфе рассматривается
три задачи. Они дают образцы нахождения
композиции различных движений: в 1-й и
во 2-й задачах рассматриваются два
возможных случая нахождения композиции
осевых симметрии, а в задаче 3 речь идет
о композиции поворота и параллельного
переноса. В рассмотренных задачах
композиция симметрии, поворотов и
переносов снова была движением одного
из этих видов. Однако так будет не всегда:
композиция P*S, где S - симметрия относительно
прямой n, а Р - параллельный перенос на
вектор
 =0,
параллельной этой прямой, не является
ни поворотом, ни параллельным переносом,
ни осевой симметрией. Эта композиция
P*S называется скользящей симметрией и
является движением, меняющим ориентацию.
=0,
параллельной этой прямой, не является
ни поворотом, ни параллельным переносом,
ни осевой симметрией. Эта композиция
P*S называется скользящей симметрией и
является движением, меняющим ориентацию.
Далее вводится теорема: всякое сохраняющее ориентацию движение плоскости представляет собой либо поворот (в частности, центральную симметрию), либо параллельный перенос. Всякое меняющее ориентацию движение плоскости является осевой или скользящей симметрией.
В этом параграфе рассматривается лишь случай композиции движений. Можно также рассматривать композиции и других геометрических преобразований. В следующем параграфе рассматривается композиция гомотетии и движения.
И еще хотелось бы рассказать об учебнике Г.В. Дорофеева, И.Ф. Шарыгина «Математика 6». В нем существенно пересмотрено изучение геометрии. Геометрический материал в этом курсе охарактеризован как наглядно-деятельностная геометрия. Обучение организуется как процесс, направленный на развитие пространственных представлений, расширение геометрического кругозора.
Введению центральных понятий курса предшествует этап практической деятельности по средствам рабочей тетради, в ходе которого знания формируются на наглядно-интуитивном уровне. Симметрия изучается в середине года после изучения темы прямые и окружности. В главе рассматриваются осевая, центральная и зеркальная симметрии. В отдельный пункт выделен вопрос о применении симметрии к решению некоторых геометрических задач, где рассматривается традиционная для занимательной математики задача о пауке и мухе. Этот пункт советуют рассматривать только с сильными учащимися.
Изучение осевой и центральной симметрии строится по одной и той же схеме: в ходе физического действия вводится понятие точек, симметричных относительно прямой (центра); анализируются особенности их расположения относительно оси (центра) симметрии и на основе этого формулируется способ построения симметричных точек; рассматриваются фигуры, симметричные относительно прямой (точки), и фиксируется факт их равенства, вводится понятие оси (центра) симметрии фигуры; устанавливается наличие у известных фигур осей (центра) симметрии.
Изучение видов симметрий и ее свойств опирается на фактические действия и физический эксперимент. Для осевой симметрии – это перегибание по оси симметрии, для центральной – поворот на 180º, для зеркальной – опыт с зеркалом.
Таким образом, в учебных и методических пособиях по геометрии изложение отдельных видов геометрических преобразований занимает значительное место, но при этом:
- изложение теории не всегда раскрывает сущность геометрических преобразований;
- метод геометрических преобразований не рассматривается как один из наиболее эффективных методов решения задач;
- недостаточно освещены вопросы прикладной направленности геометрических преобразований;
- не устанавливаются межпредметные связи геометрии с другими дисциплинами курса посредством геометрических преобразований.
Как показывает анализ учебников и учебных пособий по проблеме изучения геометрических преобразований в средней школе, эти знания и умения представлены не как система, а как ряд частных явлений и их изучение растянуто на несколько лет. При этом каждое преобразование дается обособленно, вне связи с другими, несмотря на то, что эта связь существует. Свойства, которыми обладают преобразования, рассматриваются отдельно для каждого конкретного вида, в то же время многие свойства, например, преобразований группы движений, аналогичны.
Для каждого преобразования дается частный прием его совершения. Причем главным в действиях учащихся является исполнительная часть: ученики механически производят построения, не имея полной ориентировочной основы.
Нерациональный способ изложения теории геометрических преобразований приводит к трудностям, с которыми сталкиваются учителя при преподавании, а ученики - при усвоении этого раздела курса. По нашему мнению, при изучении геометрических преобразований следует стремиться к тому, чтобы учащиеся с самого начала усвоили те общие элементы, те основные единицы, которые характерны для всех изучаемых в школьном курсе геометрических преобразований, а затем – метод работы с этими единицами, позволяющий получать все виды данных преобразований. Таким образом, учащиеся должны усвоить обобщенное умение по выполнению данных преобразований.
Элементарные геометрические преобразования играют ведущую роль в обучении решению задач на построение. Трудно переоценить роль задач на построение в формировании математического мышления школьников.
С древних времен геометрические построения способствовали развитию не только самой геометрии, но и других разделов математики. Задачи на построение циркулем и линейкой и сегодня считаются математически весьма интересными, и вот уже более 100 лет это традиционный материал школьного курса геометрии.
Они по своей постановке и методам решения объективно призваны развивать способность отчетливо представлять себе ту или иную геометрическую фигуру и, более того, уметь мысленно оперировать элементами этой фигуры. Задачи на построение могут способствовать пониманию учащимися происхождения различных геометрических фигур, возможности их преобразования с помощью элементарных геометрических преобразований. Все это является важной предпосылкой становления пространственного мышления школьников, исследовательских и творческих умений, геометрической интуиции.
Таким образом, геометрические преобразования представляют одну из содержательных линий школьного курса геометрии. Их изучение позволяет наиболее полно раскрыть практическую значимость, показать область применения геометрических знаний. В то же время изучение геометрических преобразований обеспечивает развитие пространственного, логического, абстрактного мышления, математической интуиции учащихся именно в том возрасте, когда они имеют наиболее ярко выраженные способности к восприятию пространственных форм окружающего мира.
Перемены в жизни общества трансформируют взгляды на роль и место изучения геометрических преобразований в условиях дифференцированного обучения, на содержание программ и систему работы с учащимися профильных классов и классов, непосредственно предшествующих профильным, то есть предпрофильным.
При рассмотрении целей обучения теме «Геометрические преобразования» в 8-9 классах необходимо учитывать общие цели обучения математике, цели обучения геометрии, запросы общества, личностные потребности и возможности учащихся.
Цели обучения математике на современном уровне ее развития определены в работе Г.И. Саранцева:
1. Образовательные цели: овладение системой математических знаний, умений, навыков, дающих представление о предмете математики, ее языке, символике, методе познания, математическом моделировании, алгоритме, периодах развития математики, специальных математических приемах.
2. Воспитательные цели: формирование мировоззрения учащихся, логической и эвристической составляющих мышления, воспитание нравственности, культуры общения, самостоятельности, активности, эстетического воспитания школьников.
3. Практические цели: формирование умений строить математические модели простейших реальных явлений, исследовать явления по заданным моделям, конструировать приложение моделей; приобщение к опыту творческой деятельности и формирование умений применять его, ознакомление с ролью математики в научно-техническом прогрессе, современной науке и производстве.
Геометрические преобразования могут эффективно «работать» на достижение указанных целей.
По мнению В.А. Гусева, при обучении математике необходимо учитывать: 1) выполнение требования получения всеми учащимися основ математических знаний, умений, навыков, которые являются базовой составляющей развивающейся личности каждого школьника; 2) формирование основных стержневых качеств личности, в формировании которых обучение математике играет существенную роль (умственное воспитание, составляющие творческого потенциала, мировоззрение, нравственное и трудовое воспитание); 3) специальные задачи, характерные только для математического образования (устная и письменная математическая речь, использование математических приборов, построение моделей реальных ситуаций, развитие пространственного мышления, математической интуиции и воображения). Геометрические преобразования естественным образом вписываются в достижение этих целей.
Курс геометрии, по мнению Г.Д. Глейзера, должен быть сконструирован таким образом, чтобы он развивал у учащихся следующие качества интеллекта: геометрическую интуицию, пространственное и логическое мышление, способность к конструктивно-геометрической деятельности и владение символическим языком (хотя бы в минимальном объеме). Цели обучения геометрии автор представляет в виде синтеза прикладных, научных (собственно геометрических) и общекультурных целей.
Кроме общих целей обучения математике в программах есть уточнение, которое предусматривает формирование у учащихся устойчивого интереса к выбранному предмету, выявление и развитие их способностей, ориентацию на профессии, существенным образом связанные с выбранной деятельностью, подготовку к обучению в вузе.
Специфика процесса обучения геометрии должна состоять в ориентации учащихся на правильный выбор направления обучения в старших классах и способности (готовности) к обучению в классе определенного профиля.
Геометрические преобразования, таким образом, обладая мощным потенциалом обучения, развития и воспитания учащихся, очень слабо его реализуют на современном этапе.
§5. Основные затруднения учащихся по освоению материала по теме «Движение» и их причины, связанные с особенностями когнитивных процессов подростков
Геометрия является одной из самых сложных учебных дисциплин и вызывает у школьников определенные трудности. Ориентация на личность ученика требует, чтобы дифференциация обучения математике, в частности геометрии, учитывала потребности всех школьников – не только сильных, но и тех, кому этот предмет дается с трудом или чьи интересы лежат в других областях. Прерогатива и особенность математики – развитие абстрактного и логического мышления, т.е. качеств личности, необходимых для освоения новых областей знаний, облегчения адаптации к постоянно меняющимся условиям жизни.
Для практической реализации идеи дифференциации в обучении геометрии требуется перестройка всей методической системы. Необходимо создать разноуровневые и профильные программы и учебники, разнообразное научно-методическое обеспечение, направленное на организацию дифференциации обучения на уроках.
Основной отличительной чертой учебного процесса в 8-9 классах является то, что именно в этот период происходит подготовка учащихся к выбору профиля обучения в старших классах. Учитывая то, что в данных классах обучение происходит в рамках уровневой дифференциации, то добавление к имеющейся дифференциации элементов профилирования позволит сориентировать учащихся на выбор профиля обучения в старших классах в соответствии с возможностями и способностями школьников. Необходимо отметить, что часть учащихся заканчивает свое образование курсом основной школы и, следовательно, выделенный нами вид дифференциации поможет им при выборе дальнейшего направления обучения или профессиональной деятельности. При такой дифференциации обучения учитываются индивидуальные различия учащихся. Отнесение ученика к группе определенного уровня при обучении в 8-9 классе основывается на его общем интересе к предмету математики, учитывающем приоритетные склонности личности.
Основываясь на выделенных общих целях обучения геометрии, уточним цели обучения геометрическим преобразованиям для учащихся 8-9 классов. Наше уточнение, в первую очередь, обосновывается познавательными интересами учащихся.
При уровневой дифференциации обучения учитываются индивидуальные различия учащихся в обученности и общих умственных способностях. При разделении на группы учащихся 8-9 классов целесообразно использовать предметные познавательные интересы и специальные способности. Школьников, входящих в одну группу, могут объединять общие интересы к некоторой предметной области. Целесообразно выделять то количество групп учащихся в классе, чтобы по своему качеству они соответствовали профилям обучения в данной школе. Например, математическое направление, гуманитарное и естественнонаучное направления.
Для того чтобы разработать эффективную методику изучения геометрических преобразований, необходимо учитывать особенности развития учащихся в этом возрасте.
От 13 до 16 лет – подростковый возраст. Это период между детством и зрелостью. У подростка стремительно меняется физиология, проявляются неловкость в движениях, эмоциональная неуравновешенность, повышенная рефлексия.
В подростковом возрасте, подчеркивал Л.С. Выгодский [7], имеет место период разрушения и отмирания старых интересов, и период созревания новой биологической основы, на которой впоследствии развиваются новые интересы. Как правило, подростки не удовлетворены собой, семьей, собственной внешностью. Они недовольны школой, учебниками, учителями, оценками, взрослыми, так как «они нас не понимают», не доверяют родителям, не признают их мнения. Даже в тех семьях, где ребенок принимает мнение родителей, для него это период внутренних переживаний. Подросток открывает себя, познает себя в общении с окружающим.
В этот период открытий наступают и разочарования. Подросток старается доказать окружающим, что он личность и, что он или она достойны быть в коллективе; у ребят существуют определенные особенности в общении, сокращается круг вопросов к учителю и родителям – большинство ребят ориентированы на общение на улице.
Обратим внимание на развитие мышления в подростковом возрасте. Главное в развитии мышления – овладение подростком процессом образованием понятий, которые ведет к высшей форме интеллектуальной деятельности, новым способам поведения.
Существенные изменения происходят в этом возрасте и в развитии воображения. Под влиянием абстрактного мышления воображение «уходит в сферу фантазии». Говоря о фантазии подростка, отметим, что «она обращается у него в интимную сферу, которая скрывается обычно от людей, которая становится исключительно субъективной формой мышления, мышления исключительно для себя»[23].
Учителю очень важно в этот момент «не потерять» ученика-подростка, для этого необходимо применять разные формы и методы обучения, интересные ученику.
Индивидуальные различия отмечаются и в уровнях развития пространственного мышления.
В психологической литературе накоплен большой материал, свидетельствующий о стойких индивидуальных различиях в пространственном мышлении. Некоторые авторы полагают, что пространственное мышление формируется в процессе обучения и под влиянием его специальной организации индивидуальные различия нивелируются. Другие исследователи отстаивают ту точку зрения, что, хотя в процессе обучения и удается развивать пространственное мышление, пути его развития очень разные, а индивидуальные трудности в формировании пространственных образов и оперировании ими сохраняются у школьников.
Особенно ярко индивидуальные различия проявляются при создании пространственных образов на геометрической основе и оперировании ими. Это сказывается главным образом в умении изменять произвольно системы отсчета, в овладении способами мысленного преобразования наглядного геометрического материала, своеобразными способами его понятийной обработки, в избирательной направленности на оперирование отдельными элементами в структуре пространственного образа (его формой, величиной), пространственными отношениями, в легкости оперирования образами разной степени наглядности и т. п.
Все это свидетельствует о том, что пространственное мышление – это сложная динамическая система, обеспечивающая слаженной работой функциональных и операциональных механизмов, в основе которых лежат не только социальные, но и биологические (анатомо-физиологические) факторы.
Необходимость ориентации на индивидуальное своеобразие ученика при обучении начала осознаваться довольно давно. Признание за ребенком «права быть самим собой» - стало величайшим завоеванием современной педагогики. Один из вопросов индивидуализации: какие качества учащихся нужно учитывать в первую очередь?
Главное качество, которое выделяется практически всеми исследователями – уровень умственного развития учащегося. Это сложное понятие объединяет, по крайней мере, два: «обучаемость» - в качестве предпосылки к учению, «обученность» - в виде приобретенных знаний. К примеру, близко понятие «общих умственных способностей».
В действительности, данная характеристика, обуславливающая во многом результат учения, имеет большой размах индивидуальных различий у школьников одного и того же возраста.
Развивающее обучение должно быть приспособлено к уровню развития каждого школьника. Из этого вытекает два вывода: о настоятельной необходимости индивидуального подхода при обучении и экспериментального измерения описанных качеств.
Таким образом, конкретная реализация индивидуального подхода в обучении со всей остротой ставит проблемы научной диагностики индивидуальных различий учеников.
Как же более рационально использовать индивидуальные возможности памяти для полноценного усвоения школьных знаний?
Опираясь на сильные стороны учеников – стараясь развить в первую очередь то, что уже заложено в человеке, а также, исправляя, более эффективно и научно обоснованно осуществлять сам индивидуальный подход при их обучении.
При длительном наблюдении за школьниками, психологом И.С. Якиманской были выделены устойчивые группы по отношению к их склонности к различным предметам. Дети условно названы: «геометрами», «физиками», «географами», «алгебраистами», «литераторами» и «языковедами». Для школьников, относящихся к разным группам, существуют оптимальные пути формирования понятий и представлений при изучении предметов.
Современное массовое обучение не только мало учитывает особенности когнитивных процессов этих учащихся, связанные с непосредственным эмоциональном отношением к материалу. Но еще в меньшей мере реализуется своеобразие их мотивационной сферы и характера. И это не только не способствует развитию их ярко выраженной природной любознательности в зрелые познавательные потребности, но и приводит к их угасанию.
В этой связи разработка принципов выявления индивидуальных различий может помочь учителю разобраться в природе индивидуальности школьников, понять, какие условия необходимы для формирования именно тех видов способностей, к которым ребенок имеет природные склонности, раскрыть возможности для целенаправленного педагогического воздействия при определении наиболее оптимального для каждого ученика пути усвоения знаний.
Анализ основных учебников, учебных пособий, программ по данной проблеме показывает, что при традиционном подходе сначала вводятся конкретные геометрические преобразования как поточечные отображения. На заключительной стадии в ознакомительном порядке рассматриваются некоторые практические приложения и наглядные иллюстрации изученного материала, в частности (если речь идет о теме «Движения плоскости»), симметрии фигур.
При таком подходе геометрические преобразования вводятся и воспринимаются как абстрактный математический аппарат. Однако особенности данного учебного материала позволяют рассматривать геометрические преобразования не только в качестве формального теоретического аппарата, но и в качестве отражения явлений, наблюдаемых в окружающем мире. Тема «Геометрические преобразования» (в частности, «Движения плоскости») предоставляет богатый материал для использования ресурсов не только логического, но и образного мышления учащихся.
Проанализируем проявление особенностей образного мышления учащихся в процессе изучения геометрических преобразований.
К началу изучения геометрических отображений в школе учащиеся уже имеют стихийно складывающийся опыт преобразования реальных объектов. В своей игровой, конструктивно-технической, художественно-графической деятельности они задолго до систематического обучения геометрии симметрично отражают, параллельно переносят, поворачивают, строят проекции и т.д. Однако изучение геометрических преобразований в систематическом курсе геометрии во многом противоречит уже сложившемуся опыту учащихся. Например, в работе И.С. Якиманской по этому поводу сказано следующее: "Анализ особенностей усвоения геометрии показывает, что содержание основных геометрических преобразований, заданных геометрией как учебной дисциплиной, нередко не совпадает с содержанием тех мыслительных операций, которые выполняются школьниками на основе этого материала. … Неучет этого приводит к тому, что понятия о геометрических преобразованиях, способы их осуществления формируются у школьников с трудом. Ученики заучивают правила выполнения этих преобразований, но не могут ими самостоятельно пользоваться в условиях, не заданных обучением».
Выделим некоторые причины затруднений, возникающих при изучении темы "Геометрические преобразования плоскости" без учета особенностей образного мышления учащихся:
1) Последовательность изложения материала не соответствует этапам функционирования образного мышления.
Обучение традиционно строится с опорой в основном на третий этап образного мышления (этап оперирования образами), тогда как первым двум (созданию первичных и вторичных обобщенных образов) внимание не уделяется.
Иными словами, сразу после введения новых понятий традиционно начинается работа по формированию навыков осуществления конкретных преобразований фигур. В результате ресурсы образного мышления учащихся оказываются незадействованными, так как у них не формируются действенные образы, соответствующие изученным понятиям. Точнее, под влиянием слов учителя, используемых чертежей в сознании многих учащихся стихийно создаются некоторые образы, однако, так как этот процесс не управляется преподавателем, сформировавшиеся образы могут оказаться неадекватными соответствующим понятиям.
Также в методике изучения геометрических преобразований в основной школе в недостаточной степени представлены задания, требующие работы на четвертом этапе образного мышления (творческого создания новых образов).
2) Изучение начинается с наиболее сложного материала с точки зрения его абстрактности.
В большинстве учебников и учебных пособий изложение темы «Движение» начинается с введения формального определения конкретного преобразования или даже общих понятий отображения плоскости на себя и движения. Эти понятия имеют достаточно высокую степень абстрактности. По этой причине их усвоение вызывает определенные трудности у учащихся (учитель также может испытывать затруднения, создавая учебную ситуацию, мотивирующую необходимость изучения нового материала).
Симметрии фигур изучаются в последнюю очередь (причем чаще всего в ознакомительном плане), несмотря на то, что это наиболее наглядный, образный материал, позволяющий подключить практический опыт учащихся, сделать усваиваемые понятия личностно значимыми для них, создать мотивацию изучения данной темы, сформировать представление о геометрических преобразованиях не только как о формальном аппарате, но и как о способе отражения явлений реальной действительности.
3) У учащихся закрепляется наименее оптимальный способ оперирования геометрическими образами.
В работе И.Я. Каплуновича выделяется четыре способа оперирования пространственными образами: отображение фигуры по отдельным элементам; отображение одного элемента, а затем последовательное достраивание фигуры; отображение одного элемента, а затем мгновенное получение отображения всей фигуры; оперирование сразу всем образом фигуры. При этом отмечается, что первый способ оперирования является нерациональным.
Однако все определения конкретных преобразований вводятся на основе отображения отдельных точек. Это означает, что логика изложения данного материала закрепляет у учащихся именно «поэлементный», «поточечный» способ оперирования образами — наименее эффективный. По мнению И.Я. Каплуновича, «такой подход вполне оправдан с математической точки зрения, но абсолютно не эффективен для формирования пространственного мышления. Он затрудняет осуществление пространственных преобразований».
Не формируются навыки мысленного выполнения преобразований фигур.
При изучении темы «Геометрические преобразования» подавляющее большинство традиционно используемых заданий предполагает непосредственное выполнение некоторых построений в последовательности, строго заданной условиями задачи. «Решение геометрических задач методом «в воображении», то есть без графических опор в школе почти не используется: параллельный перенос осуществляется линейкой на листе бумаги, осевая симметрия - ... при помощи угольника и линейки и т.п. На начальных этапах изучения геометрических преобразований такие приемы работы учащихся, безусловно, необходимы и эффективны, т.к. способствуют правильному адекватному усвоению материала. Однако ограничивать учеников на протяжении изучения всего курса планиметрии только эффективными построениями нельзя». [12]
Действительно, динамичность формируемых у учащихся геометрических представлений – одно из важных условий успешности процесса обучения. В свою очередь, динамичность этих представлений в большой степени определяется умением мысленно оперировать образами. Однако вышесказанное позволяет сделать вывод, что при традиционной методике изучения геометрических преобразований в основной школе формированию этого умения не уделяется специальное внимание.
5) Не формируется система мыслительных операций над геометрическими образами.
Каждое геометрическое преобразование обычно вводится обособленно, связи между ними не устанавливаются, не указываются возможности их взаимопорождения (исключение составляет учебник И.Ф. Шарыгина).
В результате у учащихся не создаются представления о системе геометрических преобразований плоскости. Тогда как известно, что полноценное усвоение понятий невозможно без включения их в разнообразные связи друг с другом. По мнению Л.С. Выготского, «... самая природа каждого отдельного понятия предполагает уже наличие определенной системы понятий, вне которой оно не может существовать».
6) Не уделяется специального внимания формированию функционального геометрического мышления учащихся.
По мнению Я.М. Жовнира, «...одна из отличительных черт современной геометрии от древнегреческой – та, что в ней все фигуры считаются неизменными и «твердыми», тогда как в новой – подвижными, до некоторой степени изменяющимися (находящимися в состоянии постоянного перехода из одной формы в другую). Наша задача — ввести учащихся в современную науку, для этого они должны быть вовремя приучены к тому, чтобы понимать фигуры в постоянном изменении, при этом все время наблюдая взаимозависимость их частей (формировать функциональное мышление в геометрии)».
Между тем, внимание учащихся при выполнении отображений фигур сконцентрировано не на процессе преобразования, а только на его окончательном результате. Например, отображая фигуру с помощью осевой симметрии, они не представляют себе преобразования всей плоскости: не выполняют мысленно «перегибания» чертежа или поворота на 180° вокруг оси симметрии. По данным И.С. Якиманской, «...если надо было построить фигуру, симметричную данной, то, даже перегибая лист, испытуемые совершенно не интересовались самим процессом осуществления поворота. Все их внимание было направлено на установление «следа» исходной фигуры в новой части плоскости, на взаимное расположение исходной и полученной фигур».
В результате геометрические представления учащихся остаются статичными, их затрудняет мысленное выполнение непрерывных преобразований фигур (а такое умение часто оказывается полезным на этапе поиска решения различных геометрических задач).
7) Система заданий в теме «Геометрические преобразования» зачастую не соответствует принципу последовательного усложнения типа оперирования образами.
Обычно система заданий упорядочивается с точки зрения только содержательной трудности входящих в нее задач, которая определяется набором используемых при их решении математических понятий и фактов. Однако нередко бывает, что задача, объективно не очень сложная, требует в процессе своего решения оперирования образами на уровне третьего типа (длительное и неоднократное изменение пространственного положения и структуры образа). Иными словами, «образная сложность» такой задачи оказывается значительно выше, чем математическая.
Исследователи приводят данные, свидетельствующие о том, что последовательное нарастание «образной сложности» предлагаемых учащимся задач – один из факторов» подразумевается тип оперирования образами, который осуществляется при решении данной задачи (I тип – изменение пространственного положения, II тип – изменение структуры, III тип – длительное и неоднократное выполнение преобразований первых двух типов).
Иными словами, построение системы используемых заданий требует специального анализа последовательности их предъявления не только в контексте их математического содержания, но и с точки зрения некоторых характеристик образного мышления учащихся.
8) Доля образного материала, предлагаемого учащимся в процессе изучения темы «Геометрические преобразования», крайне мала.
Как уже отмечалось ранее, привлечение образов в процессе формирования понятий - одно из важных условий преодоления формализма в обучении: образы являются средством «наполнения получаемых знаний содержанием», «в образе происходит тот необходимый «сплав интеллекта и аффекта» (Выготский Л.С.), вне которого знания не могут стать личностно значимыми, то есть субъектно присвоенными».
Однако часто геометрические преобразования в основной школе рассматриваются только в качестве формального аппарата. Такой подход согласуется с логикой математики как области научного знания, однако не является достаточным для математики как учебного предмета. Учитывая вышесказанное, представляется целесообразным формировать представления о геометрических преобразованиях не только как об обобщении понятия функции, но и как о способе отражения явлений окружающего мира. Этот подход требует опоры на образный, наглядный материал, формирования образных моделей, соответствующих изучаемым понятиям, активного привлечения ресурсов образного мышления учащихся.
9) В недостаточной степени раскрываются возможности практического применения изучаемого теоретического материала.
Использование геометрических преобразований в практических ситуациях в основном демонстрируется на примерах решения особых типов задач (например, на нахождение кратчайшего пути). Практически не рассматриваются возможности использования геометрических преобразований для доказательства теорем, проведения дополнительных построений при решении задач, иллюстрации и обоснования фактов проявления симметрии в природе и быту и т.п.
Перечисленные причины затруднений при усвоении геометрических преобразований в основной школе свидетельствуют о необходимости пересмотра некоторых методических позиций при изложении данного материала.
§6. Использование компьютерных средств обучения в образовании
На ранних стадиях развития человечества, когда обучение было непосредственно связано с трудовой деятельностью взрослого, дети не испытывали значительных затруднений, чтобы представить и понять то, чему их учили. С появлением письменности и книг обучение стало более сложным и трудным. Возникает противоречие между личным опытом ребенка и общественным опытом, отражаемым в книгах.
Принцип наглядности являлся предметом обсуждения многих великих педагогов. Первым о нем заговорил чешский педагог Я.А. Коменский. Он говорил о том, что необходимо изучать сами вещи, а не свидетельства о них. В основе чувственного метода Коменского лежит необходимость более глубокой опоры на чувственное познание в процессе обучения. Наглядность в понимании Коменского – решающий фактор усвоения учебного материала. Песталоцци видит в наглядности единственную основу всякого развития. Чувственное познание сводится к наглядности обучения. Наглядность превращается в самоцель. Ж.Ж. Руссо вынес обучение непосредственно в природу. Поэтому наглядность обучения не приобретает самостоятельного и существенного значения. Ребенок находится в природе и непосредственно видит то, что должен узнать и изучить. К.Д. Ушинский дал глубокое психологическое обоснование наглядности начального обучения. Наглядные пособия являются средством для активизации мыслительной деятельности и формирования чувственного образа. Именно чувственный образ, сформированный на основе наглядного пособия, является главным в обучении, а не само наглядное пособие. Л.В. Занков рассматривал взаимодействие слова и наглядности в обучении. Психологи выделяют наглядный материал как внешнюю опору внутренних действий, совершаемых ребенком под руководством учителя в процессе овладения знаниями. Наглядность – показатель простоты и понятности для данного человека того психического образа, который он создает в процессе восприятия, памяти, мышления и воображения.
Много внимания уделяли восприятию ребенком предметов и явлений окружающего мира советские психологи середины XX век. В результате большинство из них пришли к выводу, что "наглядность не изолирует восприятие и представление от целостной аналитико-синтетической умственной деятельности".
Принцип наглядности обучения обусловлен рядом факторов [18]:
1. наглядность обучения является средством познания учащимися окружающего мира, и поэтому процесс этот происходит более успешно, если основан на непосредственном наблюдении и изучении предметов, явлений или событий;
2. познавательный процесс требует включения в овладение знаниями различных органов восприятия; согласно К.Д. Ушинскому, знания будут тем прочнее и полнее, чем большим количеством различных органов чувств они воспринимают;
3. наглядность обучения основана на особенностях мышления детей, которое развивается от конкретного к абстрактному; на ранних этапах ребёнок мыслит больше образами, чем понятиями; с другой стороны, понятия и абстрактные положения осмысливаются учащимися легче, если они подкрепляются конкретными фактами, примерами.
4. наглядность повышает интерес учащихся к знаниям и делает процесс обучения более лёгким; согласно К.Д. Ушинского: «Учите ребёнка каким-нибудь пяти неизвестным ему словам, и он будет долго и напрасно мучиться над ними; но свяжите с картинками двадцать таких слов и ребёнок усвоит их на лету…».
Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Он означает, что в обучении необходимо, следуя логике процесса усвоения знаний, на каждом этапе обучения найти его исходное начало в фактах и наблюдениях единичного или в аксиомах, научных понятиях и теориях. После чего определить закономерный переход от восприятия единичного, конкретного предмета к общему, абстрактному или, наоборот, от общего, абстрактного к единичному, конкретному.
Однако характер и степень использования наглядности различны на разных этапах обучения. Излишнее увлечение наглядностью в обучении может привести к нежелательным результатам. Конкретная наглядность (например, рассмотрение моделей геометрических тел) должна постепенно уступать место абстрактной наглядности (рассмотрению плоских чертежей).
Таким образом, понятия и абстрактные положения доходят до сознания учащихся легче, когда они подкрепляются конкретными фактами, примерами и образами; для раскрытия их необходимо использовать различные виды наглядности.
По характеру представления окружающей действительности выделяют такие виды наглядности, как:
– естественная наглядность предполагает ознакомление учащихся с реальными объектами в классе и за пределами школы;
– картинная и картинно-динамическая наглядность имеют целью дать отображение реального мира (фотографии, рисунки, диафильмы);
– объемная наглядность в системе учебных пособий представлена макетами, моделями, муляжами, геометрическими телами и фигурами и т.п.;
– символическая и графическая наглядность способствуют развитию абстрактного мышления, так как пособия этого типа отображают реальную действительность в условно-обобщенном символическом виде (схемы, чертежи, диаграммы, графики и т.п.);
– внутренняя, или опосредованная, наглядность представляет оперирование уже имеющимися представлениями для формирования новых представлений (получение представления о новом через сравнение с уже известным).
С возрастом учащихся предметная наглядность должна все более уступать место символической. Наглядность – сильнодействующее средство, которое при невнимательном и неумелом использовании может увести учащихся от решения главной задачи, подменить цель ярким средством. Чрезмерное количество наглядных пособий рассеивает внимание учащихся и мешает воспринимать главное, может вызвать замедленное развитие абстрактно-логического мышления.
Наглядность в обучении математике – это совокупность материальных, материализованных, идеальных действий, совершаемых как обучающим, так и обучаемым в ходе реализации дидактической цели наглядного обучения.
Выделяют следующие виды наглядности в обучении математике:
1. Оперативная наглядность – процесс формирования модели в учебной деятельности, базирующийся на опорных внешних действиях. К оперативной наглядности относится демонстрационная наглядность и технические средства обучения. Применение оперативной наглядности расширяет число каналов передачи и получения информации, ускоряя и углубляя восприятие изучаемого материала. В то же время применение оперативной наглядности может служить мотивацией творческой деятельности учащихся, позволяет увидеть процессы в динамике, способствует установлению межпредметных связей, расширяет область практического применения изучаемых вопросов.
2. Формализованная наглядность – процесс формирования модели в учебной деятельности, базирующийся на структурных внешних действиях, процесс формирования «внешней» структуры, структуры обозначения, выделения и размещения текста на доске или в учебном пособии. К этому виду наглядности относится форматирование текста, выделение формул, использование цвета. Это вид наглядности способствует лучшему восприятию, осмыслению и запоминанию материала.
3. Структурная наглядность – процесс формирования модели учебной деятельности, базирующийся на структурных внешних действиях, процесс формирования "внутренней" структуры. К этому виду наглядности относится выделение основного материала, построение модели с опорой на устойчивые ассоциации, характеризующиеся полнотой изложения основных понятий, методов, теорем, доведение изучаемого материала до узнаваемости объекта восприятия, построение системы непрерывного хранения информации (составление контролирующих программ для компьютера). Структурная наглядность активизирует мыслительную деятельность в процессе восприятия, учит логически мыслить, выделять существенное.
4. Фоновая наглядность – процесс моделирования специфических особенностей данного организованного набора знаний, носящий мотивированный сквозной характер, обеспечивающий лучшее восприятие и усвоение. Фоновая наглядность характеризуется длительностью, неодномоментностью, «ненавязчивостью» побочно применяемых действий. Примером применения наглядности этого вида могут служить приемы создания фона настроения, создания пониженного фона интенсивности вокруг опорной информации, привлечение исторического материала, применение мнемонических эффектов. Целевая установка, мотивация, внешнее ненавязчивое побуждение учителя к внутренним действиям ученика, адекватным поставленным целям – составляющие компоненты фоновой наглядности. Особое значение этот вид наглядности приобретает в условиях профильной дифференциации. Фоновая наглядность – это тот фактор, который позволяет проводить воспитательную работу в процессе обучения.
5. Дистрибутивная наглядность характеризуется структурными внешними действиями при изучении сформированной модели в процессе учебной деятельности. К этому виду наглядности относится структура размещения материала, выделение базовых определений, порций материала, классификацию методов доказательств. Этот вид наглядности широко используют авторы учебников и учебных пособий. Использование этого вида наглядности позволяет расставить акценты на изучаемом материале, делает его более доступным для восприятия и усвоения, учит логически мыслить, анализировать, выделять главное и устанавливать связи между изучаемыми понятиями, уметь ориентироваться в большом объеме информации, воспитывает критическое отношение, учит быть собранным.
6. Наглядность преемственности характеризуется опорностью ассоциативных связей внутри раздела, предмета и межпредметных. Сюда относится структура взаимосвязей, методы изложения, пропедевтика, опорные мотивационные исторические задачи, циклы задач исследовательского характера. Применение этого вида наглядности зависит от того, насколько глубоко учитель владеет материалом, от творческого использования им методов изложения материала, от его эрудиции, общей культуры, заинтересованности в результатах своего труда.
Различные виды наглядности выполняют различные функции. Одни содействуют оживлению представлений (картины, предметы жизни), другие являются опорой для отвлеченного мышления.
С целью реализации принципа наглядности многие учителя используют различные наглядные пособия на своих уроках. К наглядным пособиям относятся:
- реальные предметы и явления в их натуральном виде;
- модели объектов и процессов;
- муляжи (от фр. – формовать, отливать в форму);
- иллюстративные пособия: картины, рисунки, фотографии;
- графические пособия: диаграммы, графики, схемы, таблицы;
- различные технические средства обучения – устройства, помогающие учителю обеспечивать учащихся учебной информацией, управлять процессами запоминания, применения и понимания знаний, контролировать результаты обучения: учебные кинофильмы, средства программированного обучения, компьютерные программные средства.
Наглядность применяется и как средство познания нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего запоминания материала. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала учителем, при закреплении знаний, формировании умений и навыков, при выполнении домашних заданий, при контроле усвоения учебного материала.
Применение наглядных пособий в обучении подчинено ряду правил:
- ориентировать учащихся на всестороннее восприятие предмета с помощью разных органов чувств;
- обращать внимание учащихся на самые важные, существенные признаки предмета;
- показать предмет (по возможности) в его развитии; предоставить учащимся возможность проявлять максимум активности и самостоятельности при рассмотрении наглядных пособий;
- использовать средств наглядности ровно столько, сколько это нужно, не допускать перегрузки обучения наглядными пособиями, не превращать наглядность в самоцель.
Следовательно, умелое применение средств наглядности в обучении всецело находится в руках учителя. Учитель в каждом отдельном случае должен самостоятельно решать, когда и в какой мере надо применять наглядность в процессе обучения, ибо от этого в определенной степени зависит качество знаний учащихся.
Принцип наглядности, по выражению Я. А. Коменского, является «золотым правилом дидактики». Он требует сочетания наглядности и мысленных действий, наглядности и слова. Вредным является как недостаточное, так и избыточное применение средств наглядности. Их недостаток приводит к формальным знаниям, а избыток может затормозить развитие логического мышления, пространственного представления и воображения.
Роль наглядности в обучении очень велика. Изображение – это основа мышления. Изображение важнее слова – оно быстрее вспоминается. Для того чтобы его узнать не требуется никаких «дополнительных» условий, так как в процессе мышления человек чаще всего создаёт те или иные образы. В то же время слово нуждается в расшифровке. Понятийное мышление требует знания системы для расшифровки кодов. Слово осознаётся, как часть общей словесной конструкции, связанное с другими словами (понятиями) как элемент целого. Образное мышление нелинейно: каждое изображение завершено, представляет собой самостоятельный, независимый фрагмент.
Поэтому, процесс обучения невозможен без обращения к наглядности. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала учителем, при закреплении знаний, формировании умений и навыков, при выполнении домашних заданий, при контроле усвоения учебного материала.
Следует отметить, что в условиях технического прогресса и доступности компьютерных средств бесспорное преимущество занимает компьютерная графика и мультимедийные пособия в реализации принципа наглядности.
§7. История внедрения компьютерных технологий в обучение. Использование технологии Flash при разработке учебных пособий
Одной из актуальных задач в современных условиях является внедрение информационных технологий на всех уровнях образовательной системы и информационное наполнение компьютерных сетей системы образования. В истории информатизации образования выделяют четыре этапа.
Период с начала 50-х и до начала 70-х годов принято считать первым этапом на пути внедрения компьютерных обучающих средств в процесс образования. Компьютеризация в этот период не повысила эффективность обучения, поскольку не изменилась традиционная система организации обучения и отсутствовала возможность персонального доступа обучаемого к компьютеру. Компьютерные программы использовались лишь в качестве тренажеров и контролирующих средств.
Второй этап относится к 70-80 годам и связан с внедрением персональных компьютеров в образовательные системы. Помимо контролирующих программ появляются программы информационного характера, что способствует развитию новых форм обучения.
Третий этап датируется 80-90 годами и характеризуется расширением парка персональных компьютеров. Возрастают возможности индивидуализации и активности обучения. Именно третий этап дает начало инновационному обучению с помощью компьютеров, превосходящему традиционные образовательные технологии. На этом этапе компьютеризация обучения используется в качестве поддержки самостоятельной работы студентов в условиях сокращения количества часов по практически всем дисциплинам учебного плана и как средство для дистанционного обучения.
Начиная с 2000 года можно выделить четвертый этап в развитии информатизации образования. Этот этап связан с активным развитием сетевых технологий доступа к образовательным ресурсам и объединением информационных, обучающих и контролирующих программ в виртуальные курсы, обеспечивающие открытость образовательных процессов.
Выше говорилось о необходимости обращения к визуальному мышлению в процессе обучения. Среди важнейших проблем, составляющих сердцевину научного поиска в рамках концепции визуального мышления - восприятие и интерпретация изображений. Изначально, на заре истории, изображение, созданное человеком, было прежде всего неподвижным объектом. А ведь организм, обслуживаемый зрением, естественно, больше интересуют изменения, а не неподвижность. Злободневным симптомом состояния современной культуры является явное предпочтение, оказываемое ныне потоку динамических изображений по сравнению с изображениями статическими - это уже не количественная, статистическая, а качественная характеристика культуры.
Перспективы использования компьютерной графики в преподавании математики связаны, прежде всего, с эффективной реализацией общедидактического принципа наглядности в обучении. Его воплощение в обучении различным предметам, наряду с другими принципами дидактики, является одним из ведущих факторов обучения и развития.
Опыт широкого использования компьютерной графики в обучении математике позволяет выделить, по крайней мере, два направления повышения роли наглядности в формировании многих математических понятий. Первое – это непосредственное использование компьютера как специального средства, реализующего принцип наглядности. Второе – опосредованное формирование математических понятий в процессе обучения информатике, через призму ее собственных понятий и приемов работы с компьютером. В последнем случае необходимо еще специально акцентировать внимание на межпредметных связях курсов информатики и математики.
Как правило, учителя с опаской и осторожностью относятся к активному вмешательству компьютерной техники в привычный ход урока. Преподавателям свойственно противиться всему новому, «разрушающему» выстроенную годами методику изложения материала. С одной стороны, такой консерватизм вполне понятен и даже в некоторой степени полезен для людей этой профессии, но с другой – нет предела совершенству, и не разумно противиться процессу, направленному на развитие качеств ума учащихся, увеличение набора форм работ и облегчения нелегкого учительского труда.
Несмотря на то, что никто из специалистов не утверждает, что компьютер может полностью заменить учителя, время от времени в печати появляются материалы, авторы которых доказывают, что преподаватель незаменим. При этом в пылу полемики, утверждает кандидат психологических наук Е.И. Машбиц, они зачастую оперируют больше эмоциями, чем фактами. Е.И. Машбиц выступает в защиту компьютерного обучения. Приведем некоторые из высказываний оппозиции и замечания Е.И. Машбица.
1. Компьютер – суррогат учителя, немыслящий помощник, который может натаскивать, поощрять и упражнять обучаемого при выполнении только рутинных заданий. Учитель даже в большом классе значительное лицо; он незаменим.
Однако, как отмечалось выше, в настоящее время не ставится вопрос о том, чтобы заменить учителя. Альтернативе учитель или компьютер противопоставляется другая: учитель с компьютером или учитель без него. При такой постановке вопроса ответ однозначен. Утверждение же о том, что компьютер может использоваться при выполнении только рутинных заданий, нетрудно опровергнуть. К настоящему времени накоплен большой опыт, свидетельствующий о возможности применения компьютера при решении творческих задач.
2. Компьютеризация – зло, которое приводит к дегуманизации преподавателя, учащихся и учения. Занятия обезличиваются, обучающий утрачивает возможность преподносить материал так, как считает необходимым, а обучаемые не могут проявить свою индивидуальность.
Эта точка зрения также несостоятельна. Проанализировав все доводы за и “против”, психолог Л.Н. Проколиенко убедительно показала, что компьютер создает исключительно большие возможности для самовыражения учащегося, становления его личности.
3. Нет очевидных доказательств того, что компьютерное обучение более эффективно, чем традиционное. Приводятся многочисленные сведения о том, что некоторые программы отнюдь не обеспечивают достижения педагогических целей, вызывают у учащихся скуку.
Тут надо сказать, что многочисленные факты выпуска на рынок западных стран малоэффективных программ – лишь свидетельство издержек начального периода использования компьютера. Так в США и Великобритании (за исключением относительно небольшого числа научных центров, которые созданы при крупных компьютерных фирмах и в университетах) составлением обучающих программ нередко занимаются люди, не имеющие серьезной подготовки в области психологии обучения и дидактики, а иногда и методики обучения.
Исключительно важен вопрос, какую роль будет играть преподаватель при компьютерном обучении. Останется ли он центральной фигурой учебного процесса, если будет использовать компьютер? Ответить на это можно так. От того, что преподаватель пользуется учебником, написанным специалистами, учебными пособиями и техническими средствами, изготовленными также не им самим, его роль не уменьшается. И в компьютерном обучении от преподавателя зависит, когда и как использовать обучающую программу, как приспособить ее к определенному контингенту учащихся или применить без изменений и т.д.
Работа преподавателя с выбранной компьютерной программой не предполагает следование четкой инструкции ее использования. Преподаватель волен в своем творчестве. Он имеет право использовать фрагменты программы, в соответствии с конструированием занятий по своей методике. В разделе “Особенности методики” мы подробнее рассмотрим возможности работы преподавателя с применением компьютерных средств.
Основу компьютеризации обучения составляют два направления:
- овладение компьютерной грамотностью;
- применение компьютера, как средства обучения.
Компьютеризация по второму направлению призвана повысить эффективность учебного процесса, уменьшить разрыв между требованиями, которые общество предъявляет подрастающему поколению, и тем, что действительно дает обучение.
Одно из наиболее плодотворных применений компьютера в образовании – использование его как средства управления учебной деятельностью учащихся. Именно в этом качестве он может наиболее существенно повысить эффективность обучения.
Известно, как важна индивидуализация обучения. Но при традиционной классно-урочной системе возможности индивидуализации обучения очень ограничены: предоставить каждому учащемуся персонального преподавателя ни одно общество не в состоянии. На практике же выходит, что то объяснение, которое доступно для одних учащихся, для других – недостаточно, а третьим, наоборот, кажется до скучного подробным. По этому и получается, что слабоуспевающие в решении задач не всегда получают помощь в необходимом объеме, а более способных нередко приходиться “притормаживать”.
Между тем компьютер может обеспечить индивидуализацию обучения в массовом порядке, да еще при выборе обучающего воздействия (объяснение, подсказка, похвала), учесть историю обучения каждого конкретного ученика. Компьютер осуществляет, так называемое, рефлексивное управление, то есть строит модель учащегося, которая учитывает особенности его познавательных процессов – восприятия, мышления, памяти, и оказывает помощь учащемуся с учетом его индивидуальных возможностей.
Исключительно огромны возможности компьютера в проблемном обучении, при котором учащийся выступает, как исследователь, самостоятельно открывающий нечто новое. При этом оттачиваются ум и воля, он учится преодолевать трудности, принимать нешаблонные решения.
Компьютер помогает активизации учащихся. Это происходит отчасти благодаря тому, что современная техника открывает большие возможности наглядности (сочетание зрительной наглядности со слуховой, применение мультипликации и т.д.). Вместе с тем появляются принципиально новые возможности, позволяющие учитывать уровень развития познавательных процессов учащихся при постановке учебных задач и вопросов, при оказании им помощи.
Е.И. Машбиц выделяет следующие сильные стороны использования компьютера в процессе обучения:
- новизна работы с компьютером вызывает у учащихся повышенный интерес к работе с ним и усиливает мотивацию учения;
- цвет, мультипликация, музыка, звуковая речь расширяют возможности представления информации;
- компьютер позволяет строить индивидуализированное обучение на основе модели учащегося, учитывающей историю его обучения и индивидуальные особенности памяти, восприятия, мышления;
- с помощью компьютера может быть реализована личностная манера общения, что создает более благоприятную обстановку; это особенно важно для учащихся с замедленным темпом обучения;
- компьютер активно включает учащихся в учебный процесс, позволяет им сосредоточить внимание на наиболее важных аспектах изучаемого материала, не торопит с решением; у него всегда хватит терпения, он никогда не повышает голоса;
- намного расширяются наборы применяемых учебных задач, используются задачи на моделирование различных ситуаций, постановку диагноза; компьютер дает учащимся возможность наглядно убедиться в том, к чему приводят его решения;
- возможность пользоваться большим объемом ранее недоступной информации.
Подводя итог вышесказанному, очевидны преимущества использования компьютерных средств в обучении. Во-первых, это способствует увеличению скорости передачи информации, что очень важно в условиях постоянного увеличения объема информации, передаваемой обучающимся в процессе образования; во-вторых, это автоматизация рутинной работы учителя по обслуживанию процесса обучения, такой как передача информации по организации и сопровождению учебного процесса, учет, контроль и анализ знаний учащихся; в-третьих, это демонстрация и моделирование различных процессов и объектов, которые невозможно воспроизвести в реальных условиях, активизация интереса к процессу обучения, что улучшает его качество за счет повышения уровня восприятия учащимися изучаемого материала и добавления нового средства в дидактический процесс, который изменяет традиционную схему обучения по отдельному предмету "ученики - учебник - учитель" на "ученики - учебник - компьютерные средства (КС) - учитель". Новый элемент в цепочке традиционного обучения является вспомогательным ресурсом. И в заключение, это организация самостоятельной работы учащегося при самоподготовке и выполнении домашних заданий. В этом случае компьютерные средства дополняют функции учебника и выполняют роль компьютерных средств обучения (КСО). Используемые в КСО дидактика и методическое обеспечение учебного процесса должны и могут способствовать более эффективному и мотивированному усвоению учебного материала по сравнению с традиционными (печатными) изданиями. Компьютерные средства обучения должны формировать активную познавательную деятельность, развивать позитивное отношение к обучению и предоставлять рациональный поэтапный контроль усвоения изученного материала.
Место компьютера в учебном процессе во многом определяется типом обучающей программы. Некоторые предназначены преимущественно для закрепления умений и навыков. Место таких программ определить не трудно: их можно использовать после усвоения определенного теоретического материала в рамках традиционной методики обучения.
Другие программы ориентированны преимущественно на усвоение новых понятий в режиме, близком к программированному обучению. Большинство их обладает относительно ограниченными дидактическими возможностями. Компьютер здесь используется как средство программированного обучения, несколько более совершенное, чем простейшее обучающее устройство, но не допускающее развернутого диалога, содержащее, как правило, фиксированный набор обучающих воздействий.
Большими возможностями обладают обучающие программы, которые реализуют проблемное обучение, особенно “интеллектуальные” обучающие программы (своим названием они обязаны тому, что при их разработке используются идеи “искусственного интеллекта”). Многие из них генерируют обучающие воздействия (учебные тесты, задачи, вопросы, подсказки). Такие системы, как правило, учитывают не только правильность ответа, но и способ решения, могут его оценивать, а некоторые – совершенствовать стратегию обучения с учетом накапливаемого опыта. Имеются системы, которые могут обсуждать с учащимися не только правильность решения, но и выбор стратегии решения, причем в языке, близком к естественному. По мнению педагогов и психологов, знакомившихся с протоколами диалогов, создается такое впечатление, что общались ученик и учитель.
Следующий тип обучающей программы предполагает моделирование и анализ конкретных ситуаций. Такие программы особенно полезны в трудовом и профессиональном обучении, поскольку способствуют формированию умений принимать решения в различных ситуациях, в том числе в экстремальных.
Наконец, программы, обучение по которым строится в виде игры. Они способствуют повышению мотивации учения (хотя следует отметить, что соревновательные мотивы, желание, во что бы то ни стало, победить иногда преобладает тут над познавательными мотивами, что вряд ли педагогически оправдано). Игра стимулирует инициативу и творческое мышление, способствует формированию умений совместно действовать (особенно, в кооперативных играх), подчинить свои интересы общим целям. Кроме того, игра позволяет выйти за рамки определенного учебного предмета, побуждая учащихся к приобретению знаний в смежных областях и практической деятельности. Игры создают предпосылки для формирования у обучаемых всевозможных стратегий решения задач и структуры знаний, которые могут быть успешно применены в различных областях. Немаловажно и то, что обучаемый может свободно принимать решения – как правильные, так и неправильные – и при этом видеть, к чему это приводит. Но необходимо воспитывать и волевые усилия, готовность к выполнению даже малоинтересных, но необходимых функций.
При характеристике различных обучающих программ необходимо учитывать, какие именно функции обучающего и обучающегося автоматизируются. Н.Ф.Талызина и Т.В.Габай выделили следующие типы таких функций:
1) создание положительных мотивов, объяснение, показ и фиксация формируемой деятельности и входящих в нее знаний;
2) организация и контроль деятельности учащихся;
3) передача машине рутинной части учебной деятельности;
4) составление и предъявление учебных заданий, соответствующих различным этапам процесса усвоения, а также индивидуальным особенностям ученика и состоянию его деятельности в данный момент.
Таким образом, существующие на современном этапе компьютерные средства обучения по сложности реализации можно классифицировать на следующие виды: электронные версии печатных изданий, информационно-справочные, контролирующие, обучающие, интегрированные. Применение информационных технологий и компьютерных средств позволяет улучшить качество образования, как процесса за счет:
1. сокращения времени доступа к информационным ресурсам, сопровождающим обучение;
2. повышения надежности, объективности и скорости средств контроля и анализа знаний учащихся;
3. активизация восприятия учащимися изучаемого материала и добавления компьютерного моделирования и демонстрации в дидактический процесс.
4. улучшение качества самоподготовки;
5. совершенствование стратегий и технологий образовательного процесса.
Появление компьютера делает возможным обучение на дому. Вряд ли было бы оправданно игнорировать такую возможность, особенно учитывая вечернюю и заочную формы обучения.
Наибольший эффект имеют в обучении математике демонстрационные программы и программы – тренажеры, в которых образная составляющая понятий выдвинута на первый план. Подобные программные продукты дают, во-первых, возможность интерактивной работы, когда обучаемый сам становится участником события. Во вторых, в процессе обучения программированию учащиеся создают наглядные образы геометрических понятий (точка, фигура, преобразование и т.п). При этом многие понятия, известные из математики или представляемые пока интуитивно, более глубоко раскрывают свою сущность и становятся понятными именно на основе своего образного восприятия. Формирование математических понятий, таким образом, возможно проводить и по такой схеме: интуитивное представление – программа – графическое отображение (построение) – математический термин.
Компьютерные средства обучения называются интерактивными, если они обладают способностью «откликаться» на действия учащегося и преподавателя, «вступать» с ними в диалог. Компьютер можно использовать на всех этапах процесса обучения: при объяснении (введении) нового материала, закреплении, повторении, контроле знаний, умений и навыков. При этом на различных этапах урока он выполняет различные функции: преподавателя, рабочего инструмента, объекта обучения, сотрудничающего коллектива, досуговой (игровой) среды.
В функции преподавателя компьютер представляет:
- источник учебной информации (частично или полностью заменяющий преподавателя);
- наглядное пособие нового уровня с возможностями мультимедиа и телекоммуникациями);
- индивидуальное информационное пространство;
- тренажер;
- средство диагностики и контроля.
В функции рабочего инструмента компьютер выступает как:
- средство подготовки тестов, их хранение;
- текстовой редактор;
- графопостроитель, графический редактор;
- вычислительная машина больших возможностей;
- средство моделирования.
Функцию объекта обучения компьютер выполняет при:
- программировании, обучении компьютера заданным процессам;
- создании программных продуктов;
- применении различных информационных сред.
Сотрудничающий коллектив воссоздается компьютером как следствие коммуникации с широкой аудиторией (компьютерные сети), телекоммуникации в Internet.
Досуговая среда организуется с помощью:
- игровых программ;
- компьютерных игр по сети;
- компьютерного видео.
Работа учителя с компьютерными технологиями включает следующие функции:
- организация учебного процесса на уровне группы в целом, предмета в целом (график учебного процесса, внешняя диагностика, итоговый контроль);
- организация внутригрупповой активизации и координации (расстановка рабочих мест, инструктаж, управление внутригрупповой сетью и т.п.);
- индивидуальное наблюдение за учащимися, оказание индивидуальной помощи, индивидуальный «человеческий» контакт с учащимся. С помощью компьютера достигаются идеальные варианты индивидуального обучения, использующие визуальные и слуховые образы;
- подготовка компонентов информационной среды (различные виды учебного, демонстрационного оборудования, программные средства и системы, учебно-наглядные пособия и т.д.), связь их с предметным содержанием определенного учебного курса.
Один из остро дискуссионных вопросов касается того, в каких учебных предметах и на каких этапах обучения целесообразно использовать компьютер. Уместен вопрос: нужно ли это учащимся? Вряд ли можно дать однозначный ответ, однако напомним скептикам: было время, когда умножение и деление изучали не в школе, а только в университете, да и то не в любом.
Теоретическим фундаментом для построения эффективного компьютерного обучения в нашей стране могут стать психологические теории и концепции советских ученых П.Я.Гальперина и Н.Ф.Талызиной, Д.Б. Эльконина и В.В. Давыдова, А.М. Матюшкина и Т.В. Кудрявцева и др. Разумеется существующие теории строились безотносительно к компьютерному обучению и нуждаются в определенной доработке. Передача обучающих функций машине требует более глубокого исследования этих функций.
Наиболее разработана теория П.Я. Гальперина и Н.Ф. Талызиной, авторы которой уделяли внимание проблемам автоматического управления учебной деятельностью.
В связи с компьютеризацией обучения многие положения и понятия педагогической психологии и дидактики требуют уточнения. Так, для компьютерного обучения необходима такая трактовка метода обучения, которая допускает его операциональное описание и тем самым его технологизацию. Метод обучения реализуется, прежде всего: а) в системе обучающих воздействий; б) в способе включения учащихся в учебную деятельность; в) в «поле самостоятельности» учащегося (что характеризуется допустимыми отклонениями от нормативного способа решения учебных задач, при которых учащимся не оказывается помощь; г) в организационных формах обучения и модальности обмена информацией между обучающим (обучающим устройством) и обучаемым.
Возьмем для примера такой этап обучения, который, по мнению разработчиков обучающих программ, наиболее прост: изложение учебного материала. Но эта простота мнимая. Здесь недостаточно, как это часто делается, переложить текст учебника, снабдив его примерами и иллюстрациями, разбив на части и выделив основные положения. Чтобы успешно реализовать данный этап, необходимо, во-первых, проанализировать деятельность обучающего и обучаемого в их взаимодействии и, во-вторых, выявить то новое, что вносит компьютер во взаимодействие между ними. Анализ в терминах «говорит», «показывает» (применительно к деятельности учителя) и «смотрит», «слушает», «запоминает» (применительно к деятельности учащегося) малопродуктивен. Он не открывает пути организации взаимодействия учащегося с компьютером. Представляется плодотворной трактовка изложения учебного материала как педагогически направленного (то есть с учетом возрастных и индивидуальных особенностей обучаемых) осуществления (развертывания перед учащимися, воспроизведения) фрагмента учебной деятельности с включением (явным или неявным) учащихся в эту деятельность.
Воспроизведение учебной деятельности характеризуется следующими параметрами:
а) уровнем воспроизведения (предметно-содержательный, предметно-операциональный, рефлексивный); третий уровень – рефлексивный – не ограничивается изложением содержания изучаемых объектов и способов оперирования ими; он раскрывает, как бы выносит наружу процесс выработки основных интеллектуальных средств – гипотез, приемов анализа условий, поиска решения, способов контроля своих действий; для этого уровня характерно воспроизведение двух относительно самостоятельных деятельностей: предметной и деятельности, объектом которой является собственная деятельность;
б) содержанием, дополнительным к содержанию учебных курсов;
в) умственными действиями, необходимыми для усвоения содержания учебной деятельности;
г) включенностью учащихся в процесс воспроизведения учебной деятельности (имеется в виду также характер включенности: явная или неявная).
На этапе изложения учебного материала компьютер представляет собой мультимедийный источник учебной информации, частично или полностью заменяющий учителя. [8]
Применение компьютера на данном этапе эффективно, потому что:
1. Во первых, любая информация, представленная на компьютере воспринимается учащимися с огромным интересом. Это позволяет активизировать познавательную деятельность учащихся.
2. Во вторых, объяснение нового материала на компьютере происходит индивидуально для каждого учащегося. При желании он может вернуться на несколько шагов назад и просмотреть объяснение заново.
3. При чтении электронного учебника встречаются термины, понятия, выделенные цветом, так называемые гиперссылки. Гиперссылки – это прямая связь между различными частями информационного ресурса. Если ученик встретил незнакомое понятие, термин, теорему, то ему не нужно обращаться к справочнику или к дополнительной литературе, достаточно щёлкнуть кнопкой «мыши» на выделенном фрагменте. При этом происходит открытие того раздела учебника или справочника, в котором эти понятия даются более широко. Этот механизм является самым важным отличием электронных изданий от полиграфических.
4. Во многих электронных учебниках присутствует анимация (интерактивная модель). Она представляет собой картинку, которая «оживает» при нажатии на соответствующую кнопку мыши. Анимация позволяет более наглядно продемонстрировать теорему, понятие, свойство. Она дает возможность ученику увидеть то, что без компьютера он мог только представить, вообразить.
Очевидно, что компьютер обеспечивает разгрузку учителя от рутинных операций, создает реальные возможности для сосредоточения на творческих аспектах деятельности. Учитель, избавленный от необходимости контролировать каждый шаг в решении разнообразных учебных задач и в то же время получивший доступ к данным, которые раскрывают историю обучения каждого ученика, может больше внимания уделить индивидуальной работе с учащимися – как с отстающими, так и с особо одаренными, а также воспитательной работе.
Использование технологии Flash.
Технология Flash в последнее время сильно набрала популярность в областях отличных от WEB-дизайна, и часто не имеющих к WEB вообще никакого отношения. Одна из таких областей – разработка учебных пособий и демонстраций.
Сначала несколько слов об особенностях технологии Flash, которые позволяют рекомендовать ее в качестве инструмента оформления учебных материалов.
Технология Flash, прежде всего, – это технология векторной анимации. Такой подход дает большие преимущества перед традиционной покадровой анимацей (avi, mpeg). Векторная графика – чистое математическое описание каждого объекта на экране - в отличие от растровой графики, которая представляет собой, в простейшем, не сжатом виде, массив из точек разного цвета, очень нетребовательна к ресурсам для воспроизведения, занимает очень мало места, не искажается при масштабировании и поворотах. Анимация выполняется не в каждом кадре, а только в ключевых. Недостающие кадры не хранятся непосредственно в файле, а дорисовываются компьютером по заранее заданному закону. Это позволяет достичь невероятно малого размера результирующих файлов. Кроме того, фирма Macromedia (или сторонние производители) выпускает программные проигрыватели *.swf файлов почти для всех известных платформ и операционных систем.
В отличие от традиционных векторных редакторов и форматов векторной графики, Flash изначально ориентирован на экранный просмотр, а не на печать (сглаженные линии, округлый текст, плавные цветовые переходы). И это приближает качество картинки к фотографическому. Но главные козыри у Flash скрыты от глаз, просматривающих Flash-ролики.
Это собственный язык программирования. Этот язык – фирменная разработка Macromedia и носит название Action Script. Это объектно-ориентированная среда программирования, которая, поддерживает почти все нововведения объектно-ориентированного подхода. Средствами этого языка можно управлять любым элементом ролика и менять любые его свойства. Следствием внедрения в ролики языка программирования стала интерактивность, т.е. возможность ролика меняться в зависимости от действий пользователя.
Итак, перейдем к использованию Flash в создании учебных материалов по различным предметам, отличным от информатики.
В частности, Flash целесообразно использовать на занятиях по математики при обучении исследованию функций. На занятиях, посвященных исследованию функций преподавателю, как правило, приходится рисовать на доске множество различных графиков и дополнительных построений к ним. Это занимает много времени и достаточно утомительно. Применение Flash в таких случаях экономит время на уроке. Векторный подход к рисованию может повысить точность изображения (графики функций, касательные, площади криволинейных трапеций и пр.). Повысить наглядность позволяет анимация. В нужное время масштабируемый и динамично прорисовывающийся график гораздо наглядней статичной картинки на доске. При помощи интерактивности и Action Script появляется возможность варьировать параметры кривых и других элементов чертежа.
Трудно переоценить преимущества векторной графики в занятиях геометрией. Снова экономиться время за счёт готовых чертежей, демонстрируемых с компьютера. Анимация особенно пригодиться при изучении преобразований, в стереометрии. Решение задач на построения становится более наглядным.
И, в заключение, несколько слов о перспективах. Технология Flash давно вышла за рамки одной программы. Регулярное обновление версий делает Flash современным в любой момент времени. Ее используют в массе инструментальных средств. Одним из таких средств стала программа «Macromedia Director», симбиоз Flash и PowerPoint с уклоном в сторону обучающих средств. Эта программа специально предназначена для разработки именно обучающих средств с использованием инструментария и возможностей Flash. [16]
В последнее время встает вопрос: как использовать компьютерные программные средства в обучении и нужны ли они, ведь раньше спокойно обходились и без них. Но прогресс не стоит на месте, а значит, и отказываться от новых внедрений нецелесообразно. Наиболее значимой чертой формирующейся системы образования XXI века называют применение мультимедийных, информационных технологий в процессе отбора, накопления, систематизации и передачи знаний.
Современные компьютерные технологии предоставляют огромные возможности для развития процесса образования. Еще К. Д. Ушинский отмечал, что детская природа требует наглядности. Сейчас это уже не схемы, таблицы и картинки – они статичны, а более близкая детской природе игра, пусть даже и научно-познавательная. Каждый обучаемый получает возможность самостоятельно работать с учебной информацией, что позволяет ему детально разобрать новый материал по своей схеме, что позволяет реализовывать принципы дифференцированного и индивидуального подхода к обучению.
Мультимедиа – особый вид компьютерной технологии, объединяющей в себе как традиционную статическую (текст, графику), так и динамическую информацию (речь, музыку, видео-фрагменты, анимацию и т.д.).
Используя системы мультимедиа, позволяющие объединить возможности компьютера и знания учителя, стало возможным создание мультимедийных пособий, которые более наглядно, красочно и с мобильным доступом информации предстанут перед учениками. Содержание пособий включает в себя теоретическую часть, изложенную в более компактном варианте и задания для самопроверки.
В обращении пособия просты, что позволяет ученику легко вернуться к той информации, которую он не понял. Нажать кнопки клавиатуры гораздо быстрее и проще, чем перелистывать страницы учебника назад. Такие пособия проявляют у учеников большой интерес к учебе и желание изучать предмет в более углубленной форме, что, несомненно, сказывается на их уровне знаний в лучшую сторону. Учителям мультимедийные технологии открывают возможности отказаться от свойственных традиционному обучению рутинных видов деятельности преподавания.
Благодаря новым мультимедиа технологиям, стало возможным использовать компьютерные программы как иллюстративный материал, проводить тестирования и контрольные работы, решать творческие задачи, участвовать в дистанционных уроках, сочетать традиционные домашние задания с заданиями, для выполнения которых используются компьютеры, также позволяют взглянуть ученику на предмет с другой стороны и проявить себя в новой деятельности.
Внедрение информационных технологий в образование дает возможность выбора оптимального набора технологий для организации учебного процесса. При выборе необходимо учитывать их соответствие индивидуальным качествам обучаемых и специфическим особенностям конкретных предметных областей.
При работе с мультимедийными технологиями учащиеся с самого начала вовлечены в активную познавательную деятельность, так как потоки данных превращаются в изображения, благодаря которым у исследователя могут неожиданно возникать новые решения. Не всегда есть возможность провести эксперимент с реальными объектами или даже с их моделями. Тогда встает необходимость оперировать с образами, то есть проводить мысленный эксперимент, который характеризуется логической корректностью и активностью воображения. Графические средства не только отражают этапы мысленного экспериментирования, но и существенно облегчают процесс его протекания, так как создаются особые условия для формирования образов. Следовательно, компьютерная графика служит средством поддержки и развития мысленного экспериментирования.
Рассмотрим технологию Flash, которая и позволяет создавать мультимедийные пособия подобного рода. Она является сравнительно молодой и стремительно развивающейся, именно поэтому сочетает в себе большинство современных инструментов и механизмов, используемых при создании анимации. С появлением этой технологии, появилась возможность значительно повысить уровень эффективности преподавания за счет использования его простого и удобного интерфейса и, в принципе, ни чем не ограниченных возможностей в области анимации при разработке учебных пособий.
Flash работает с компактной векторной графикой, позволяя рисовать, оживлять и озвучивать любое действие, персонажа, программу. Непоколебимыми плюсами векторной графики являются простота, независимость от разрешения, малый объем конечного файла.
Целесообразно использовать Flash в создании учебных пособий к урокам геометрии при изучении темы «Движение». На занятиях, посвященных изучению понятия движения и его видов учителю, как правило, приходится рисовать на доске множество различных фигур и пытаться изобразить процесс их преобразования. Применение Flash в таких случаях экономит время на уроке, предоставляя готовые чертежи, повышает наглядность по сравнению со статичной картинкой на доске.
Таким образом, при помощи технологии Flash и было разработано мультимедийное пособие для учащихся 8–9 классов по теме «Движение».
школьный урок геометрия мультимедийный
Глава II. Мультимедийное пособие по теме «Движения на уроках геометрии» и методика его применения в обучении
§ 1. Задачи как средство изучения геометрических преобразований при изучении темы «Движение»
Как уже отмечалось, геометрия возникла из практики и находит свое применение на практике, и потому в преподавании геометрии необходимо связывать ее с реальными наглядно представимыми вещами. По мнению Г. Фройденталя, обучение геометрии может иметь смысл, если только используются связи геометрии с привычным пространством. Если педагог упустит это, то он упустит незаменимую возможность: геометрия является одной из лучших возможностей систематизировать реальную действительность.
При традиционном обучении геометрии многие учащиеся испытывают затруднения, цели обучения часто не достигаются, и одной из причин этого, по мнению многих методистов, является преобладание аналитических методов изучения. Психологически обоснованно, что при изучении систематического курса геометрии, особенно на первых этапах, целесообразно опираться на наглядно-действенное мышление и практическую деятельность учащихся и отдавать предпочтение конструктивному подходу в качестве возможного пути совершенствования преподавания систематического курса геометрии. Средством реализации конструктивного подхода может являться система конструктивных задач, обеспечивающая возможность изучения геометрических преобразований и их применения.
Геометрические преобразования отражают общие закономерности явлений природы. Такие преобразования как осевая, центральная симметрия, параллельный перенос, поворот – есть обобщение наблюдаемых в природе явлений. Понятие движения взято из реальной действительности и является отражением свойств реальных предметов. Благодаря этому изучение геометрических преобразований предполагает возможность широкого использования задач прикладного характера и практического содержания.
В школьных учебниках геометрии прикладных задач немного, причем в большинстве своем они рассчитаны на среднего ученика и не учитывают различие стилей мышления учащихся. В нашей работе мы постарались увеличить число прикладных задач и сейчас рассмотрим метод обучения через задачи и как средство изучения и применения геометрических преобразований выбрали систему задач практического содержания. Такой подход позволяет укрепить межпредметные связи геометрии с другими дисциплинами, наполнить содержание предметного материала геометрии реальными образами.
Математические задачи, решаемые при помощи движений
Существенным элементом структуры познавательного педагогического процесса являются методы обучения. Под методом обучения будем понимать упорядоченный способ взаимосвязанной деятельности учителя и учащихся, направленный на достижение целей обучения [26]. Система методов обучения состоит из общих методов обучения, разработанных дидактикой, и из специальных методов обучения математике, отражающих основные методы познания, используемые в математике.
Для обучения учащихся 8-9 классов геометрическим преобразованиям могут быть использованы различные методы обучения. Наиболее целесообразно в классах, непосредственно предшествующих профильным, и профильных классах использовать метод обучения через задачи. Сущность данного метода состоит в том, что математические задачи выступают как средство обучения и позволяют организовать процесс обучения таким образом, чтобы каждому учащемуся, независимо от его интересов и задатков, дать возможность обучаться по своей индивидуальной траектории.
Задачи делятся на воспроизводящие, которые способствуют выработке и закреплению определенного навыка или умения, и творческие, помогающие выявить и развить способности детей. Именно творческие задачи помогают самовыразиться учащимся, реализовать свои индивидуальные задатки.
Целесообразность введения элементов профилирования в 8-9 классах с помощью системы прикладных задач обосновывается тем, что многие учащиеся с гуманитарными наклонностями, встретившись с задачей математического или физического содержания, не проявляют интереса к ее решению. В то же время, задача исторического, художественного или лингвистического содержания может стать для них более интересной и привлекательной. В этом случае учащимся будет легче установить связи между величинами задачи и выразить их на математическом языке.
В соответствии с мнением Я.И. Груденова, изучение математических положений можно подразделить на три этапа: введение, усвоение и закрепление. На этапе введения учащиеся знакомятся с формулировками и доказательствами предложений. При усвоении происходит запоминание материала, и школьники учатся применять математические предложения в простейших случаях. Закрепление сводится к повторению формулировок и отработке навыков применения к решению задач. Проверка знаний по теме может включаться как элемент в перечисленные этапы или выделяться отдельно.
На протяжении всех этапов изучения материала учащиеся решают математические задачи. На вводном этапе задачи играют роль подготовительных упражнений. При усвоении, закреплении и проверке теории они используются в качестве упражнений в применении знании и отработке практических навыков. Например, перед построением отрезков, симметричных относительно оси, учащимся необходимо восстановить в памяти определение построения точек, симметричных друг другу относительно прямой. Упражнение, предназначенное для учащихся, ориентированных на гуманитарные области знаний, может представлять собой тест на знание данного определения: «Чтобы построить две точки, симметричные друг другу относительно прямой, нужно...». Учащимся необходимо вписать в пропуски соответствующий текст.
В упражнениях для учащихся естественнонаучного (прикладного) направления требуется на основании данного определения сформулировать правило построения произвольных фигур, симметричных друг другу относительно прямой. При выполнении задания учащимися математического направления предлагается самостоятельно попытаться сформулировать новое определение по аналогии с симметрией относительно прямой, не используя дополнительные источники информации.
Включение в учебный процесс задач различного предметного содержания может оказать положительное влияние не только на формирование геометрических умений и навыков у всех учащихся класса, но и на развитие и поддержание интереса к предмету математики у учащихся, склонных к нематематическим видам деятельности.
Эффективность применения рассмотренного метода обучения через задачи во многом зависит от наличия комплекса средств обучения. Основным средством обучения является учебник, теоретический и практический материал которого, в большинстве своем, имеет два уровня сложности — обязательный и предназначенный для учащихся, интересующихся математикой.
Межпредметные связи изучаемого материала по геометрии в 8-9 классах целесообразно устанавливать с материалом тех предметных областей, которые соответствуют наиболее распространенным направлениям профильного обучения в старших классах. В дополнение к традиционному учебнику следует использовать дидактические материалы, которые содержат упражнения нескольких различных уровней сложности. К проверочным упражнениям по геометрии должны быть применены и требования дифференциации их по предметной направленности. Данные требования могут быть учтены при включении в контрольную работу хотя бы одной задачи прикладного характера, учитывающей различия стилей мышления школьников.
Кроме названных средств обучения при проведении дифференцированного обучения успешно могут быть использованы такие средства как справочная и дополнительная литература, разнообразные средства наглядности, компьютер и т.д.
Основной формой организации обучения геометрии является урок. Выясним, какую направленность он приобретает в условиях уровневой дифференциации с элементами профилирования. При планировании вида учебной работы учитель чаще всего руководствуется ее дидактической целью. Если целью работы является усвоение или проверка знаний и умений, то предпочтение следует отдать индивидуальной форме выполнения задания. Работа в группе более эффективна на этапах введения и закрепления материала. Чаще всего индивидуальная работа требует меньших затрат времени, чем групповая работа. Некоторые творческие задания удобнее выполнять группе учащихся. Это задания, предполагающие проведение теоретических и практических исследований, например лабораторные работы. Разнообразие организационных форм может обеспечиваться включением в учебный процесс игровой, художественной и других видов деятельности.
Одним из самых доступных путей повышения эффективности урока, активизации учащихся на уроке является соответствующая организация самостоятельной учебной работы. Она занимает исключительное место на уроке, так как ученик приобретает знания только в процессе личной самостоятельной деятельности. По мнению психологов (ПЯ. Гальперин, Н.А. Менчинская, Н.Ф. Талызина и др.), самостоятельная работа, в конечном счете, приводит школьника либо к получению совершенного нового, ранее не известного ему знания, либо к углублению и расширению сферы действий уже полученных знаний.
Использование того или иного вида самостоятельной работы зависит от содержания материала, этапа его изучения, уровня овладения материалом учащимися и других факторов. Основополагающим признаком применения видов самостоятельных работ при дифференцированном обучении может быть выбран характер познавательной деятельности.
Воспроизводящие самостоятельные работы по образцу необходимы для запоминания способов действий в конкретных ситуациях (признаков понятий, факторов и определений), формирование умений и навыков и их прочного закрепления. Так, решение задач на любой тип геометрических преобразований по данному образцу способствует закреплению определенных конкретных преобразований и их основных свойств. Строго говоря, деятельность учеников при выполнении работ этого типа не совсем самостоятельна, поскольку их самостоятельность ограничивается простым воспроизведением, повторением действий по образцу. Однако роль таких работ велика. Роль учителя состоит в том, чтобы для каждого ученика определить оптимальный объем работы.
При изучении геометрических преобразований на этапе закрепления вместе с учащимися 8-9 классов полезно рассмотреть ряд задач таких, как «На рисунке изображены два симметричных произвольных треугольника. Построить ось симметрии».
Для самостоятельного решения целесообразно предложить аналогичную задачу: «На рисунке изображены два симметричных прямоугольника. Построить ось симметрии данных прямоугольников».
Целесообразность решения заданий такого вида обусловлена тем, что навыки и умения по теме «Геометрические преобразования» отрабатываются на основных фигурах геометрии, рассматриваются наиболее распространенные положения фигур при преобразованиях. Отсюда следует необходимость решения этих заданий всеми учащимися класса, независимо от их интересов и будущих профессиональных намерений.
Самостоятельные работы реконструктивно-вариантного типа позволяют на основе полученных ранее знании и данной учителем общей идее найти самсчггоятельно-конкретные способы решения задач.
Так, при изучении центральной симметрии учащимся целесообразно предложить задачу следующего вида

Отрезок AB’ является образом отрезка АВ при симметрии, центр которой не указан
Как построить образ точки К при симметрии, отображающей отрезок АВ на отрезок А ‘В’ с помощью а) циркуля, б) транспортира и линейки ?
В данном случае учитель должен дать некоторые указания к решению задачи:
а) воспользоваться тем, что центральная симметрия сохраняет расстояние между фигурами;
б) использовать свойство центральной симметрии не изменять ориентацию фигуры.
Указания помогут учащимся сориентироваться при решении задачи, но само решение будет принадлежать школьнику. Решение задания такого типа целесообразно предложить на уроке геометрии для различных групп учащихся. Учащимся, которые склонны к гуманитарной области знаний, мы предлагаем решить задачу с условием под буквой «а». Учащимся естественнонаучного направления - под буквой «б», математического направления — под буквами «а» и «б».
Самостоятельные работы данного типа приводят школьников «к осмысленному переносу знаний в типовые ситуации, учат анализировать условие задачи, формируют приемы и методы познавательной деятельности, способствуют развитию внутренних мотивов к познанию, создают условия для развития мыслительной активности школьников. Реконструктивно-вариативные работы формируют основания для дальнейшей творческой деятельности ученика.
Самостоятельные работы эвристического типа данного вида формируют умения и навыки поиска ответа за пределами известного образца. Ученик сам определяет путь решения задачи и находит его. Значительный интерес вызывает у учащихся решение задач на построение фигур. С большим интересом учащиеся решают задачи на построение соответственных точек и самостоятельно могут предложить различные способы построения. Наличие нескольких способов решения этих задач будут вызывать повышенную активность учащихся. В этом и будет состоять часть эвристической самостоятельной работы.
Поиску различных вариантов решения способствуют лабораторные работы, а также задачи следующего вида:
Отрезки АВ и A1B1 симметричны относительно прямой р. Построить точку, симметричную точку К, К принадлежит АВ относительно оси р.

Учащиеся могут предложить такие варианты решения данной задачи:
1) через точку провести прямую, перпендикулярную прямой s. Точка пересечения этой прямой с отрезком А1B1 является искомой;
2) на отрезке A1B1 от точки А1 отложить отрезок А1К1 равный отрезку АК. Точка К1 является искомой.
Самостоятельные работы целесообразно предлагать всем учащимся, независимо от их интересов. Разный уровень заданий будет проявляться в формулировании условия для каждой группы учащихся.

1. Постройте точки А’ и B’ симметричные данным точкам А и В относительно оси р. Постройте точку, симметричную точке С.
Постройте отрезки A’B’, A’C’ и B’С’ симметричные данным отрезкам АВ, АС и ВС относительно оси p. Воспользуйтесь предыдущей задачей.

3. Постройте фигуру. F’ симметричную F относительно оси р. Отметьте две точки на сторонах данной фигуры, соедините их и постройте отрезок, симметричный данному относительно оси p.

Творческие самостоятельные работы являются венцом системы самостоятельной деятельности школьников, которая позволяет учащимся получать принципиально новые для них знания, закрепляет навыки самостоятельного поиска знаний. Задачи такого типа - одно из самых эффективных средств формирования творчески развитой личности.
Для развития навыков творческой самостоятельности в применении геометрических преобразований 1-2 раза в учебном году учащимся можно предложить написать домашнее сочинение по данной теме. Темы сочинений целесообразно предложить непосредственно при изучении геометрических преобразований. Данная работа будет способствовать осмыслению школьниками темы и ее своевременному повторению.
План написания сочинения по теме целесообразно предложить учащимся заранее:
Что вы знаете о данном геометрическом преобразовании?
Приведите примеры из жизненного опыта, иллюстрирующие данное геометрическое преобразование: в природе, в быту, в технике.
Постройте произвольную фигуру при данном геометрическом преобразовании.
Темы сочинений для 8-9 классов:
- Симметрия (осевая и центральная) и ее использование в практической деятельности человека.
-Симметрия в архитектуре и строительстве.
- Гармония и красота.
- Поворот.
- Параллельный перенос и его применение в практической деятельности человека.
- Движение в природе.
Самостоятельные работы могут выполняться индивидуально, фронтально или в группах. Фронтальные работы могут быть организованы только на этапе обсуждения решения задачи. Индивидуальные и групповые самостоятельные работы применяются на всех этапах выполнения задания и изучения материала. Если целью работы является усвоение или проверка качества знаний и умений, то наиболее эффективна будет индивидуальная работа. На этапах введения и закрепления материала предпочтение отдается групповой форме работы.
Методические приемы обучения должны увеличивать долю самостоятельной деятельности учащихся, поощрять их инициативу. Большое внимание при этом необходимо уделять домашним заданиям, которые ученики выполняют самостоятельно. По результатам выполнения школьниками домашней работы можно судить о том, насколько они овладели изучаемым материалом.
Время, отводимое для решения домашнего задания, ставит перед учителем задачу - правильно определять объем этой работы. Это не так просто сделать в связи с неоднородностью класса, что ведет за собой необходимость в составлении индивидуальных домашних заданий.
На уроках при изучении темы «Геометрические преобразования плоскости» в 8-9 классах целесообразно использовать дифференцированно-групповую форму работы, которая предполагает организацию деятельности по овладению знаниями и умениями разных групп учеников с учетом их учебных возможностей. Такая форма работы наиболее приемлема, так как школьники с разной степенью развития познавательного интереса к математике обучаются в одном классе.
Рассмотрим, как дифференцированно-групповая форма работы может быть включена в процесс обучения. В процессе формирования знаний она используется в комплексе с фронтальной формой работы. Учитель сначала излагает материал всем учащимся, независимо от их интересов (это тот общеобразовательный минимум, который должен быть усвоен всеми школьниками). Затем дальнейшая работа осуществляется по группам, в каждую из которых входят учащиеся трех направлений — гуманитарного, естественнонаучного (прикладного) и математического. Школьники с различной степенью познавательного интереса к геометрии работают в группе совместно, что ведет к тому, что учащиеся вместе решают общую задачу, в классе царит здоровый дух соревнования. Учащиеся математического направления углубляют и расширяют свои знания по теме, а школьники, относящиеся к гуманитарному и естественнонаучному направлениям, повторяют материал вторично или уточняют отдельные моменты темы, а также еще раз аргументируют основные положения.
Так, на уроке введения понятия «симметрии» учитель вместе со всем классом вводит понятие данного геометрического преобразования. Обращаясь к учебной таблице, школьники вместе с учителем рассматривают предложенные предметы из окружающего мира, геометрические фигуры, находят их отличительные и сходные признаки. Убедившись, что учащиеся поняли материал, преподаватель делит класс на три группы, каждой из которых дается задание - придумать и нарисовать в тетради различные симметричные фигуры. По истечении 'времени представитель из каждой группы выходит к доске и рисует свои фигуры. Члены групп помогают своим представителям с объяснением симметричности данных фигур. Тем самым в ходе такой фронтальной беседы еще раз повторяется понятие о симметрии и ее видах, учитель добивается понимания материала каждым из школьников.
Такое сочетание форм обучения вызвано тем, что в начале разбора темы инициатива принадлежит учащимся, интересующимся математикой. Учащиеся с другими познавательными наклонностями не всегда успевают за ходом коллективного рассуждения. Поэтому работа в группе школьников с различной степенью познавательного интереса к геометрии позволяет ликвидировать этот пробел.
Задачи прикладного характера, решаемые при помощи движений
Особенностью темы «Геометрические преобразования» является то, что она имеет широкий спектр прикладной направленности, что обеспечивает ей широкую область приложений в различных сферах человеческой деятельности. Методическое значение геометрических преобразований в систематическом курсе геометрии, в первую очередь, заключается в том, что они могут облегчить изложение и усвоение всего курса геометрии
В основу методики изучения геометрических преобразований, как одного из центральных понятий, в основной школе следует положить следующие условия:
- исходя из того, что геометрические преобразования являются важнейшими понятиями современной геометрии, сделать эти понятия центральными понятиями основного курса геометрии;
- показывать внутрипредметные и межпредметные связи геометрических преобразований;
- применять геометрические преобразования к доказательству теорем и решению задач, если это упрощает рассуждения;
- объем изучаемых геометрических преобразований может изменяться в зависимости от программы курса геометрии.
Учитывая вышесказанное, рассмотрим роль упражнений на геометрические преобразования в условиях дифференцированного подхода к обучению учащихся.
Выясним, каким условиям должны удовлетворять задачи этой темы, способствующие усвоению материала.
Г.И. Саранцевым отмечается, что система задач должна удовлетворять принципам полноты, сравнения, постепенного нарастания сложности, разнообразия, непрерывного повторения.
Чтобы задачи удовлетворяли принципу полноты, они должны включать в себя все необходимые типы задач. Принцип постепенного нарастания сложности состоит в предшествовании простых упражнений сложным. Принцип сравнения требует чередования задач на прямые и обратные операции. Принципы разнообразия и непрерывного повторения заключаются необходимости разнообразия задач на повторение ранее изученного материала.
К содержанию прикладных задач С.С. Варданян предъявляет следующие требования: реальность, практическая ценность, межпредметный характер, профессиональная ценность, соответствие школьным программам, доступность языка, отражение личного опыта учащегося.
В соответствии с целями обучения геометрическим преобразованиям, а также дидактическими особенностями этой темы сформулируем требования к задачам по теме «Геометрические преобразования:
1. Список задач темы «Геометрические преобразования» для каждого из выше перечисленных направлений и профилей должен включать в себя:
- общие для всех учащихся упражнения, являющиеся необходимыми для усвоения темы и входящие в базовую подготовку;
- задачи, иллюстрирующие применение геометрических преобразований для учащихся, выбравших для себя различных направлении и профилей обучения.
2. Задачи темы «Геометрические преобразования» для профилей обучения должны содержать дополнительную информацию, необходимую для применения ее в будущей профессиональной деятельности.
3. При добавлении задач к теме «Геометрические преобразования» следует учитывать психолого-педагогические особенности подростков, склонных к определенным видам деятельности. Для учащихся классов различного профиля должны быть качественные различия в методических подходах к обучению, форме обучения, системах упражнении, степени иллюстраций различных положений.
4. Для каждого профиля и направления обучения должна быть разработана система задач по теме «Геометрические преобразования», которая будет способствовать усвоению вопросов данной темы на уровне, необходимом каждому учащемуся.
Содержание задач должно содержать только те сведения из других предметов, которые уже знакомы учащимся. Целесообразно использовать также факты, не требующие специальных знаний. При подборе задач к теме «Геометрические преобразования» мы придерживались дидактических принципов и выделенных нами требований к содержанию материала.
Тема «Геометрические преобразования» традиционна для курса геометрии 8-9 классов, основными программными целями изучения которой являются формирование представлений о геометрических преобразованиях, развитие умений учащихся использовать преобразования при решении несложных задач, применять в практической деятельности.
В школьных учебниках геометрии прикладных задач немного. В большинстве своем они рассчитаны на среднего ученика и не учитывают интересов учащихся с высокими и низкими познавательными способностями к математике. Этот недостаток необходимо исправить, так как данная тема располагает к увеличению числа прикладных задач. Такое увеличение позволит не только укрепить межпредметные связи геометрии с другими учебными дисциплинами и жизнью, но и наполнить содержание материала реальными образами. При составлении прикладных задач на геометрические преобразования для учащихся различных направлений класса необходимо учитывать требования к содержанию. Задачи для учащихся разных групп учащихся должны отличаться сложностью и наличием действий для решения. Сложность задачи может возрасти при рассмотрении комбинаций геометрических фигур. Действия для решения задачи могут состоять в дополнении задачи рисунком или чертежом и т.д.
Таким образом, возможность изучения геометрических преобразований в 8-9 классах в условиях уровневой дифференциации с элементами профилирования обеспечивается тем, что они позволяют придавать задачам различную практическую направленность, не меняя их сущности, учитывая различия в познавательных интересах учащихся класса. В то же время, использование на уроках геометрии упражнений гуманитарного, прикладного и математического содержания способствует правильному выбору учащимися класса профиля обучения на старшей ступени школы и успешному обучению. Для иллюстрации сказанного рассмотрим систему прикладных задач к теме «Геометрические преобразования плоскости» для учащихся 8-9 классов с учетом дифференциации в обучении с элементами профилирования.
Целесообразность предлагаемых задач состоит в том, что они предназначены для усвоения основных умений и навыков по теме всеми учащимися класса независимо от их интересов и склонностей. Данные задания являются интересными всем школьникам и составляют основу для дальнейшего изучения геометрии в старших классах по выбранному профилю обучения.
Даны точки А и В. Постройте точку С, симметричную точке В относительно точки А.
Даны две пересекающиеся прямые а и b и точка С, не лежащая на них. Постройте фигуры, в которые переходят прямые а и b при симметрии относительно точки С.
Может ли четырехугольник иметь центр симметрии и когда? Ответ объясните.
Дан параллелограмм АВСD. Постройте точку, симметричную точке А относительно прямой ВС.
Докажите, что любая прямая, проходящая через центр параллелограмма, делит его на две равные части.
Постройте образ A1B1 хорды АВ при ее повороте вокруг центра окружности на 45° против часовой стрелки. Сравните длины А1B1 и АВ.
Докажите, что при вращении правильного шестиугольника вокруг его центра на 120° он отображается сам на себя.
Начертите прямую а и отметьте точку О вне ее. Постройте образ прямой а при повороте вокруг точки О на 45° против часовой стрелки.
Постройте образ угла АВС, полученный поворотом вокруг центра О на 60° по часовой стрелке.

10. Прямоугольник ABCD при повороте на 170° против часовой стрелки вокруг центра D отображается на прямоугольник A1B1C1D1, АС -> А1С1, Чему равен острый угол между этими прямыми.
11. При параллельном переносе точка А переходит в точку А1, а точка В - в точку B1. Чему равна длина отрезка A1B1, если АВ = 7см? Объясните ответ.
12.Что можно сказать о прямых АА1 и BB1 из задания 11, если они различны? Ответ объясните.
13.Докажите, что при параллельном переносе прямоугольник переходит в прямоугольник.
14.При параллельном переносе точки А и В переходят соответственно в точки а1 и B1, не лежащие на прямой АВ. Пересекаются ли прямые АА1 и BB1?
15.Существует ли параллельный перенос, при котором точка (4;2) переходит в точку (2;4), а точка (1;0) в точку (0;1)?
16.Начертите параллелограмм АВСD и отметьте на стороне ВС произвольную точку М.Постройте образ этого параллелограмма при переносе на вектор АМ.
17. Докажите, что при симметрии относительно точки прямая переходит в параллельную ей прямую (или в себя).
18 .Прямые а и b пересекаются под углом а. При некотором движении а->a1 и b->b1. Чему равен угол между прямыми а1 и b1?
19. Даны две прямые х = 4 и у = 3. Укажите координаты точки на оси Оу, при повороте вокруг которой одна прямая отображается на другую.
20. Докажите, что при движении параллельные прямые переходят в параллельные, пересекающиеся - в пересекающиеся.
Задачи, предназначенные для всех учащихся класса, целесообразно рассматривать в процессе объяснения и усвоения темы. Спектр задач расширяется за счет включения упражнений, иллюстрирующих приложение геометрических преобразований в различных областях знаний. На этапе закрепления темы «Геометрические преобразования» учащимся предлагаются различные системы задач, которые учитывают индивидуальное направление развития личности школьника, ее интересы, запросы и возможности.
В предложенной системе задачи дифференцированы по уровням овладения материалом и прикладной направленности содержания. Дифференциация заключается в том, что предлагается несколько вариантов задач на усвоение некоторого понятия или выработке определенного умения. Варианты упражнений, которые различаются прикладной направленностью, обозначены разными буквами: для учащихся группы гуманитарного направления — «г», математического — «м», естественнонаучного — «е». Задачи, стоящие под разными буквами, отличаются не только содержанием, но и степенью сложности.
Для иллюстрации сказанного рассмотрим систему задач прикладного характера к теме «Геометрические преобразования плоскости», составленную с учетом ее использования в условиях дифференциации обучения в предпрофильных классах.
Осевая симметрия.
№1 «г». Восстановите фигуру по сохранившимся частям и осям симметрии.



«е». Постройте прямую (ось симметрии), относительно которой симметричны две данные фигуры.

 б)
б)
а)


в) г)
«м». Дана произвольная фигура F и прямая а. Постройте фигуру, симметричную данной, относительно прямой а.
Центральная симметрия.
№ 1 «г». Восстановите фигуру по сохранившимся частям и центру симметрии.

 б)
б)
а)
«е». Постройте точку (центр симметрии), относительно которой симметричны две данные фигуры.


«м». Постройте произвольную геометрическую фигуру. Отметьте на плоскости точку О. Постройте фигуру центрально-симметричную данной, взяв за центр симметрии отмеченную точку О.
Поворот.
№1 «г». Постройте образ отрезка при повороте на 60° по часовой стрелке вокруг выбранной вне отрезка точки.
«е». С помощью кальки постройте образ фигуры, изображенной на рисунке, при повороте плоскости вокруг точки О:
а) на 50° по часовой стрелке;
в) на 180° против часовой стрелки.

«м». Земельный участок квадратной формы был огорожен. От изгороди остались два столба на параллельных сторонах участка и столб в центре квадрата. Требуется восстановить границу участка.
Параллельный перенос.
№1 «г». На рисунке изображены пары фигур. В каких парах одна фигура может быть отображена на другую параллельным переносом в указанном отображении?

а)
 б)
б)

 г)
г)
в)
«е» Даны две окружности R я S и отрезок МN. Постройте отрезок, равный и параллельный отрезку MN, концы которого лежат на данных окружностях.

«м» Отрезок данной длины перемещается параллельно самому себе так, что один его конец скользит по окружности О (r). Докажите, что другой конец отрезка описывает при этом окружность, равную данной.

Приведенные выше задачи к каждому разделу темы «Геометрические преобразования плоскости», целесообразно предоставлять учащимся в форме самостоятельной работы, условия которой состоят в следующем: самостоятельная работа состоит из 9 задач и считается выполненной в том случае, если решены три любые задания из девяти предложенных. Условные обозначения задач - «г», «е», «м» - из этических соображений целесообразно не указывать.
Целью такой работы является формирование у учащихся умений самостоятельно приобретать и применять знания в соответствии со своими возможностями, интересами, устремлениями. В результате выполнения самостоятельных работ такого плана учитель может судить о познавательных интересах и способностях учащихся класса
Итоговая работа по теме «Геометрические преобразования плоскости» состоит из пяти заданий. Первые три - содержат основные вопросы по теме, которые составляют общеобразовательный минимум и знание которых необходимо продемонстрировать всем учащимся независимо от их интересов. Первые четыре задания рекомендовано решить учащимся группы естественнонаучного направления. Всю работу - учащимся группы математического направления.
Реализация идеи геометрических преобразований в обучении способствует формированию мировоззрения учащихся, что крайне необходимо при подготовке учащихся 8-9 классов к выбору профиля обучения в 10-11 классах.
Например, в ходе изучения осевой и центральной симметрии учащиеся получают представление о симметрии в окружающем мире, а также развивается их пространственное и конструктивное мышление. Школьники учатся применять знания о данном геометрическом преобразовании в практической деятельности, которая им наиболее интересна. В результате изучения видов симметрии учащиеся должны овладеть умениями строить ось и центр симметрии, распознавать симметричные фигуры, проводить оси и центры симметрии часто встречающихся фигур (квадрата, прямоугольника, круга), строить в простых случаях фигуры, симметричные данным относительно прямой и точки (точку, отрезок, треугольник, окружность).
В результате можно сделать вывод о том, что увеличение упражнений разнообразного содержания при обучении геометрическим преобразованиям в 8-9 классах обеспечивает усвоение дополнительного теоретического и практического материала на геометрические преобразования (понятий, теорем); способствует овладению школьниками методом геометрических преобразований; ориентирует ученика на поиск различных решений; усиливает прикладную направленность курса; придает деятельности школьников исследовательскую направленность.
§ 2. Общее описание мультимедийного пособия
В современном мире появились новые технические возможности. Более предпочтительными для пользователя становятся динамические изображения, нежели статические иллюстрации. Этим фактом, в частности, диктуется необходимость применения компьютерных средств в образовании. Компьютер помогает повысить активность учащихся в процессе обучения. Пассивное обучение малоэффективно, так как, чтобы освоить некоторое понятие учащемуся необходимо самостоятельно открыть, исследовать его.
Используя возможности flash-технологии, школьный учитель может создавать электронные учебники, виртуальные лабораторные работы, демонстрации, интерактивные мультимедиа-презентации. Кроме того, интерактивное дидактическое пособие, разработанное при помощи программы Macromedia Flash, является компьютерным программным средством, не требующим никаких специальных и дополнительных программных или технических средств. Файл пособия запускается при помощи программы Internet Explorer, которая имеется на большинстве персональных компьютеров, а маленький размер файла позволяет размещать его на странице Интернета. Таким образом возможно реализовать использование данного пособия не только в классе, но и на удалённых компьютерах.
Этим и обусловлен выбор формы пособия – flash–фильм, просматривая который, пользователь имеет возможность либо наблюдать за происходящими изменениями, либо изменять картинку самостоятельно, выделяя закономерности и приходя к определенным умозаключениям.
Выбор темы flash-фильма обусловлен труднодоступностью изображения материала, связанного с введением понятия движения и его видов. Раздел «Движение» способствуют представлению о различных фигурах не как о чем-то неподвижном, а как об изменяющемся и преобразующемся одно в другое – это процесс, который носит динамический характер и для более глубокого усвоения и осмысления требует динамической иллюстрации. Интерактивное пособие позволяет показать учащимся фигуры в движении, что невозможно сделать с помощью статических изображений мелом на доске. Изучение темы «Геометрические преобразования» необходимо для изучения последующего курса математики, развития мышления школьников, обеспечения учащихся некоторыми умениями и методами, необходимыми им в повседневной жизни. Это вызывает необходимость в повышении уровня осмысления материала, что становится возможным при использовании flash-технологии.
Предложенный flash-фильм призван выполнять роль наглядного пособия. Способ подачи материала с опорой на визуальное мышление, предложенный в этом пособии, мог бы облегчить восприятие учащимися довольно сложного для представления понятия движения и его видов. Данное пособие в большей степени является демонстрационным. В конце пособия включен тест для самопроверки полученных учащимися знаний.
Интерактивное пособие разрабатывалось с учётом требований, предъявляемых компьютерным программным средствам, использующимся в учебном процессе: педагогических, дидактических, методических и эргономических.
Предложенный продукт может быть использован на занятии, проводимом объяснительно-иллюстративным методом как в качестве наглядной демонстрации свойств объектов, так и в качестве первичного закрепления введенных понятий. При этом возможно использование пособия учениками самостоятельно, в качестве дополнительного источника знаний, связанных с разделом «Движение».
Объем flash-ролика составляет 1 МБ.
Системные требования:
- Pentium;
- CD ROM x 4;
- Windows 95/98/2000/XP;
- Macromedia Flash Player 5/7.
Данное пособие можно использовать на различных этапах урока и этапах изучения раздела «Движение». Просмотр представленного flash-фильма целесообразно организовывать как на уроках изучения нового материала в качестве вспомогательного демонстрационного пособия, так и на уроках закрепления, при этом просматривая лишь его фрагменты. Кроме того, пособие можно использовать в качестве дополнения к учебнику для самостоятельного просмотра учениками.
Flash-фильм состоит из трех частей: объяснение теоретического материала, его закрепления и представления тестовых заданий для проверки усвоения материала. Части в свою очередь разделены на сцены, материал которых соответствует изложению в учебнике Л. С. Атанасяна и др. Геометрия 7 – 9 класс по теме «Движение». Далее рассмотрим особенности каждой из сцен мультимедийного пособия.
Общей чертой всех сцен является постепенное появление текста (определений) в верхней части экрана, сопровождающегося также постепенно появляющимися изображениями к понятиям в нижней части. Условно мультфильм разбит на два раздела: первый – об осевой и центральной симметрии, а второй – понятие движения, параллельный перенос и поворот – это связано с последовательностью подачи материала в учебнике. Ведь симметрии изучают по учебнику Л.С. Атанасяна в 8 классе, а материал второго блока – уже в 9 классе. Для удобства комментирования пособия и усвоения материала после каждого понятия делаются паузы.
Просмотр фильма начинается с мотивационной сцены «Вместо вступления», где рассказывается о симметрии в окружающем мире. Если flash-фильм планируется показывать полностью, то рекомендуется начать именно с этой первой сцены (она же первая в содержании пособия). Изучив эту сцену, с помощью кнопки «Начать просмотр» сразу можно перейти к изучению теоретического материала.

Блок сцен «Осевая симметрия»

Цель данной сцены – ввести понятие двух точек, симметричных относительно прямой a, показать ось симметрии. В следующей сцене рассматриваются различные случаи выполнимости или невыполнимости условий определения и итог – при невыполнении хотя бы одного из пунктов определения точки несимметричны. Все наблюдения отражаются в постепенно заполняющейся таблице.

Далее переходим к сцене, в которой динамически отражена последовательность действий при построении точки, симметричной данной относительно прямой.

После чего учащемуся предлагается самостоятельно построить точку, симметричную данной относительно прямой, перетаскивая нужные элементы из правой части рабочего поля.

Следующие две сцены рассматривают построение отрезка, симметричного данному относительно прямой, если отрезок параллелен оси симметрии и перпендикулярен ей.


После чего учащийся может попробовать сам построить отрезки, симметричные данным, перетаскивая элементы из поля на чертеж.


В следующей сцене вводится определение фигуры, симметричной данной относительно прямой. Фигуру также предложено построить в сцене, следующей за данной.


В завершение этого блока сцен – примеры фигур, обладающих осевой симметрией в геометрии и в природе.

Блок сцен «Центральная симметрия».
Цель этой сцены – ввести понятия двух точек, симметричных относительно точки O, показать центр симметрии.

Далее рассматриваем пример, когда условие определения не выполняется и точки несимметричны.

Затем по аналогии с предыдущим блоком сцен предлагается сначала алгоритм действий для построения точки, симметричной данной относительно точки O

и учащийся старается построить таковую самостоятельно в следующей сцене.

После пример построения отрезка, симметричного данному относительно точки в двух случаях: отрезок и центр симметрии не лежат на одной прямой

отрезок и центр симметрии лежат на одной прямой.

Дальше учащийся пробует сам построить отрезок, симметричный данному относительно точки в разных вариантах его расположения.


Цель следующей сцены – ввести определение фигуры, симметричной данной относительно точки, сразу после которой предлагается построить ученику фигуру самостоятельно на основании раннее изученных построений симметричных относительно точки отрезков и точек.


Этот блок сцен, так же, как и предыдущий завершает демонстрация фигур обладающих уже центральной симметрией в геометрии и в природе.

Описанные выше сцены направлены на подведение к понятию отображения плоскости на себя и понятию движения.
Сцена «Движение».
Цель данной сцены – ввести понятие движения плоскости, показав сохранение расстояний на примерах осевой и центральной симметрий. Также поясняем понятие движения на примере осевой симметрии, представляя ее как поворот плоскости на 180˚ вокруг оси a.

Блок сцен «Параллельный перенос».
Здесь даем определение параллельного переноса на вектор a и указываем, что параллельный перенос является движением, то есть отображением плоскости на себя, сохраняющим расстояния.

Дальше, как и в предыдущих двух блоках идут задачи на построение.
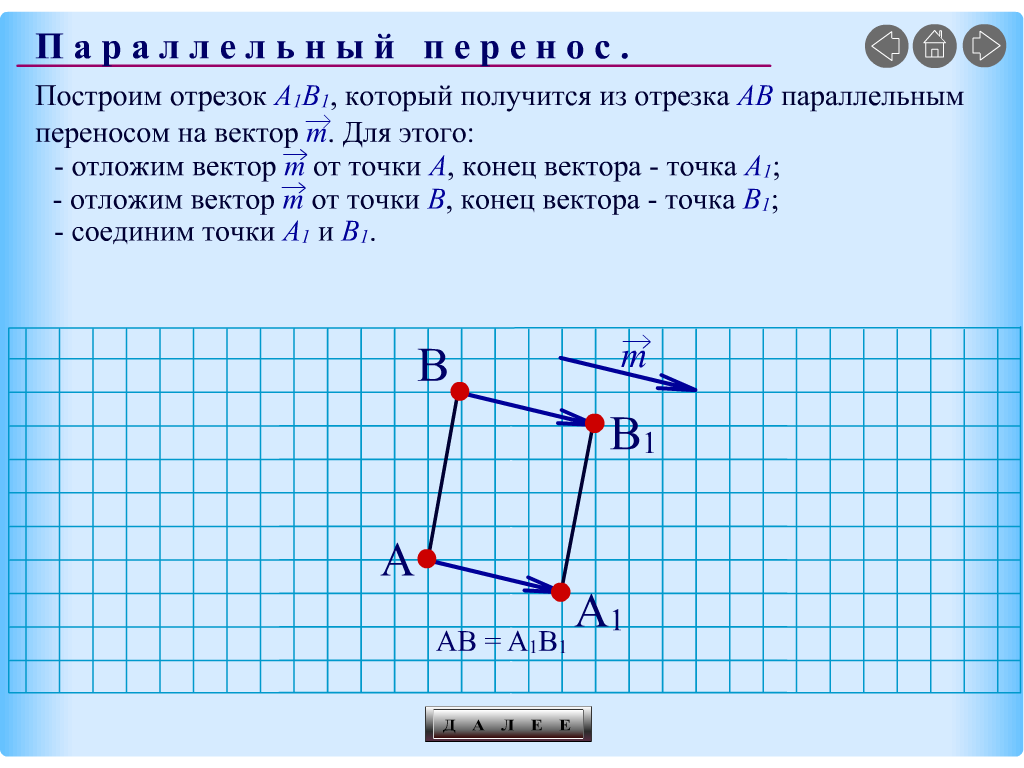

Выполняется параллельный перенос отрезка на вектор перпендикулярный и параллельный отрезку, затем параллельный перенос фигуры на заданный вектор.

И в завершении предложено построить образ данных фигур при параллельном переносе на данный вектор, перетаскивая векторы на поле и фигуры в нужном направлении вектора.



Сцена «Поворот».
Далее рассматриваем еще один вид движения – поворот. Даем определение поворота плоскости вокруг точки O на угол α, указываем центр поворота и показываем, что поворот является движением, то есть отображением плоскости на себя, сохраняющим расстояния.

И в этом блоке сцен за определением следуют сцены на выполнение движения отрезков и фигур – поворот отрезка вокруг данной точки по часовой стрелке

и против часовой стрелки.

И поворот фигуры вокруг данной точки на данный угол.

Сцена «Композиция движений» (закрепление).
Цель данной сцены – повторить изученные виды движения. Изначально дан треугольник, движения которого могут наблюдать учащиеся, задавая их в правой части окна с помощью кнопок напротив названия вида движения (сверху вниз).
Осевая симметрия:
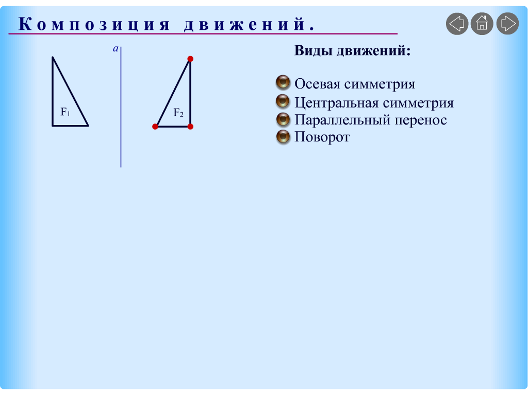
Центральная симметрия

Параллельный перенос

Поворот

Затем учащиеся могут убедиться в том, что последовательное выполнение движений – есть движение.

Далее представлены две задачи и пара тестовых заданий для закрепления материала. Предлагается обсудить эти задания всем классом, а затем уже индивидуально перейти к заданиям теста, представленного в пособии.
Задача 1

Задача 2
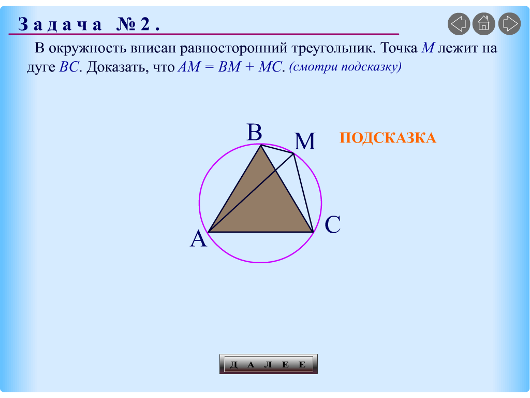


Тестовые задания
Тестовая часть мультимедийного пособия содержит 10 вопросов, в каждом из которых по 4 варианта ответа. Сначала идет блок, состоящий из пяти практических заданий. Первые четыре на определение преобразования плоскости и последнее на определение точки, симметричноц данной.


Блок тестовых заданий продолжают 5 теоретических вопросов вида: вставить пропущенное слово или слова с вариантами ответов.





Предложенные тесты полностью охватывают объем требований программы.
При работе с данным мультимедийным дидактическим пособием контроль рекомендуется проводить с помощью консультантов, выбранных из продвинутых учеников этого же класса или старшеклассников. Контроль может носить обучающий характер, если при выполнении заданий теста учащиеся задают вопросы учителю и консультантам и, получая пояснения, выполняют их. Также можно проводить и формальный контроль снова прибегнув к помощи консультантов, которые вместе с учителем, наблюдая за ходом выполнения заданий учащимися, будут заполнять соответствующие ведомости успеваемости по каждому из учеников, отмечая количество вопросов, на которые ученик верно ответил. В соответствии с ведомостью выставляют оценки по следующей системе: правильное выполнение 9-10 заданий – «5», 7-8 заданий – «4», 5-6 заданий – «3», меньше 5 заданий – это «2» .
§3. Методика применения пособия в процессе обучения по теме «Движения»
Методические требования к проведению занятий опираются на выявленные выше психолого-педагогические требования. Их реализация предусматривает проведение занятий с учащимися под руководством учителя с использованием компьютерного программного средства как основного организатора деятельности учащихся на уроке либо как вспомогательного. В первом случае функция учителя заключается в организации проведения занятий, осуществлении контроля за деятельностью учащихся, обеспечении им необходимой помощи в работе, объяснении учащимся соответствующего домашнего задания.
Мультимедийная программа позволяет обеспечивать организацию деятельности обучаемого, самоконтроль.
В деятельности учителя и учеников на занятии можно условно выделить три этапа
|
№ |
Название этапа. |
Деятельность учителя. |
Деятельность учащихся. |
|
1. |
Организация работы. |
Рассаживает учеников за компьютеры, включает компьютеры, осуществляет запуск программы. |
Рассаживаются по местам за компьютеры. |
|
2. |
Работа с пособием. |
Объясняет, какие действия необходимо выполнить для начала работы с пособием, наблюдает за работой учеников, следит, чтобы они работали индивидуально, помогает им, контролирует их деятельность. |
Работают с пособием индивидуально, обращаются в случае необходимости к учителю. |
|
3. |
Постановка домашнего задания. |
Задает домашнее задание, объясняет, как его надо выполнять. На следующем уроке проверяет выполненное учениками домашнее задание. |
Записывают домашнее задание. Выполненное домашнее задание приносят и сдают учителю на следующем уроке. |
Рассмотрим подробнее каждый из этапов.
Первый этап – организация работы. Учителю необходимо обратить внимание на то, чтобы учащиеся сидели за отдельными компьютерами, что позволит каждому из учеников работать с пособием в том темпе, в котором будет удобнее.
Второй этап – непосредственная работа с пособием. Пособие состоит из нескольких блоков, которые в свою очередь подразделяются на части:
Теоретическая часть (объяснение учебного материала).
Практическая часть (решение учеником задач).
Проверочная часть (тест).
В первой части (теоретической) составляется ориентировочная основа действий. Здесь ученик знакомится с учебным материалом. Программа последовательно предоставляет ученику объяснение по шагам, что дает возможность в случае, если ученик не понял какой-либо шаг в объяснении материала, еще раз просмотреть его. Затем аналогично, по шагам, происходит объяснение процесса решения типовых заданий.
Затем ученик переходит ко второй (практической) части. В этом блоке ученик выполняет задания, процесс решения которых демонстрировался в предыдущем блоке. Прочитав задание, ученик приступает к его выполнению.
Программа не оценивает деятельность ученика, однако предусматривает возможность фиксации операций каждого ученика в ходе его работы. После выполнения практической части в пособии, учитель приостанавливает деятельность учеников. Они выносят полученные чертежи через локальную сеть к главному компьютеру на проектор. После чего все вместе обсуждают правильность построения чертежа, исправляют ошибки, если они есть. Затем продолжают работу с пособием.
Домашнее задание состоит из заданий, аналогичных представленным в мультимедийном пособии. После проверки учителем домашнего задания, ученик, если допустил ошибки, выполняет работу над ошибками, а затем выполняет самостоятельную работу, которая состоит из аналогичных заданий, которые выполнялись учеником и за компьютером, и дома. Проверив эту самостоятельную работу, учитель выставляет за нее оценку. Ниже рассмотрим применение мультимедийного пособия на уроках геометрии в качестве наглядного вспомогательного средства изучения темы.
Основной дидактической целью пособия является визуализация ключевых и наиболее сложных для восприятия учащимися понятий и представлений, связанных с изучением раздела «Движение», а именно:
введение понятия движения;
рассмотрение видов движений: осевой и центральной симметрии, параллельного переноса и поворота;
построение фигур, симметричных относительно прямой;
построение фигур, симметричных относительно точки;
осуществление параллельного переноса на заданный вектор;
поворот фигуры на заданный угол по часовой или против часовой стрелки.
Данное пособие можно использовать при изучении раздела «Движение» или «Геометрические преобразования» по различным учебникам по геометрии курса средней школы 7-9 классов. Из анализа учебников мы сделали вывод о том, что пособие не может быть создано одновременно к нескольким учебникам из-за разных подходов к изучению темы. Таким образом, мультимедийное пособие предлагается как дополнение к учебнику Л. С. Атанасяна и др. «Геометрия 7-9». Необходимо сказать, что в настоящее время общеобразовательные школы в большинстве своем перешли на преподавание геометрии именно по этому учебнику.
Первые сцены могут быть показаны отдельно еще в 8 классе при изучении осевой и центральной симметрии, а затем в 9 классе с целью повторения изученного ранее для подведения к понятию отображения плоскости на себя и движения.
Для организации просмотра фильма в соответствии с учебниками других авторов возможно вызывать сцены в произвольном порядке, соответствующем методике изложения материала, а переход от одной сцены к другой при таком порядке просмотра осуществляется возвратом к содержанию с последующим переходом к нужной сцене.
Данное пособие состоит из трех частей: объяснения теоретического материала, осуществления движений на чертеже (или применения материала) и тестовых заданий для проверки и закрепления изученных знаний.
Один из главнейших принципов, который реализовывается в данном пособии, является принцип наглядности.
Элементы управления и навигации данного мультимедийного пособия реализованы так, чтобы пользоваться им было максимально просто.
Таким образом, учитель экономит время на объяснении учащимся того, как обращаться с этим пособием.
Пособие может быть использовано в качестве наглядной демонстрации движения тел на первом уроке изучения темы, так и в качестве закрепления введенных понятий на последующих уроках.
Также фильм может быть предложен ученику для самостоятельного изучения пропущенной темы, так как демонстрационные сцены фактически повторяют объяснение учителя, традиционно проводимое с помощью мела и доски.
Как сказано выше, работа с пособием может осуществляться на лабораторном занятии, где каждый ученик самостоятельно изучает предложенный в мультимедийном пособии материал, выполняет указанные построения, отвечает на вопросы теста, а затем все учащиеся вместе закрепляют в беседе с учителем основные понятия темы.
Для этого необходимо проведение урока в компьютерном классе.
Но если учитель построил объяснение нового материала в виде лекции, то в качестве иллюстративного материала для сопровождения объяснений послужит предложенное пособие.
Рассмотрим пример поурочного планирования изучения данного раздела с указанием возможностей использования мультимедийного пособия «Движение на уроках геометрии» на отдельных уроках для учащихся 9-х классов.
|
Тема урока. |
Количество часов. |
Комментарии к использованию мультимедийного пособия. |
|
§ 1. Симметрия. |
3 ч. |
|
|
П.1.Определение осевой и центральной симметрии. Основные свойства симметрий. |
1 ч. |
На этапе введения определения осевой симметрии рекомендуется просмотр блока сцен «Осевая симметрия», где помимо наглядного введения определения продемонстрирован процесс построения точки, отрезка и фигуры, симметричной данной относительно прямой. Аналогично на этапе введения определения центральной симметрии с блоком сцен «Центральная симметрия». |
|
П.2. Применение симметрий к решению задач различного практического содержания. Симметрия в природе, архитектуре, технике. |
2 ч. |
На этапе актуализации знаний на последнем часе изучения этого параграфа рекомендуется повторно просмотреть часть пособия, описанную в пункте 1. На этапе обобщения изученной темы – просмотр сцены «Фигуры, обладающие осевой/центральной симметрией в геометрии и в природе». |
|
Самостоятельная работа. |
1 ч. |
|
|
§ 2. Движение. |
2 ч. |
|
|
П.1. Понятие движения. Свойства движения. |
1 ч. |
Изучению этой темы посвящен блок сцен «Движение», переход к которым осуществляется из сцены «Содержание» нажатием кнопки «Движение». Перед просмотром этого блока сцен рекомендуется повторно просмотреть предыдущую часть пособия. |
|
П.2. Решение задач с помощью движения. Движение в природе. |
1 ч. |
|
|
§ 3. Поворот. |
2 ч. |
|
|
П.1. Определение поворота. Основное свойство поворота – поворот как центральная симметрия. |
1 ч. |
На этапе введения определения поворота рекомендуется просмотр сцены «Поворот», переход к которой осуществляется из сцены «Содержание» нажатием кнопки «Поворот». |
|
П.2. Решение задач различного прикладного содержания с помощью поворота. |
1 ч. |
|
|
§ 4. Параллельный перенос. |
3 ч. |
|
|
П.1. Определение параллельного переноса и его основные свойства. |
1 ч. |
На этапе введения определения поворота рекомендуется просмотр сцены «Параллельный перенос», переход к которой осуществляется из сцены «Содержание» нажатием кнопки «Параллельный перенос». |
|
П.2. Решение задач с помощью параллельного переноса. Геометрические узоры – орнаменты, бордюры, паркеты. |
2 ч. |
На этапе обобщения и систематизации изученного материала в качестве подготовки к проведению контрольной работы возможен быстрый просмотр ключевых вопросов темы. |
|
Контрольная работа. |
1 ч. |
Таким образом, просмотр данного flash-фильма можно осуществлять как на различных этапах изучения раздела «Движение», так и на различных этапах в рамках одного урока. Так как ключевые понятия данного раздела достаточно сложны для представления учащимися, то особенно важно на начальном этапе создать наглядную динамическую иллюстрацию. Поэтому особенно эффективно использовать данное пособие при введении новых понятий, что способствует более глубокому пониманию и осмыслению материала, созданию визуального представления. Также возможен просмотр сцен фильма на этапах закрепления и актуализации опорных знаний школьников.
Кроме того, учащиеся могут использовать мультимедийное пособие для самостоятельного просмотра после изучения на уроке как дополнение к учебнику с целью повторения или устранения пробелов в знаниях и умениях, связанных с понятием движения и его видов.
Следует отметить, что необходимо постепенно отойти от наглядной интерпретации и перейти к работе со статическими чертежами, то есть уделить внимание формированию умений решения геометрических задач и задач прикладного характера.
Рассмотрим фрагмент урока по теме «Параллельный перенос» с использованием мультимедийного пособия «Движения на уроках геометрии». В ходе этого урока учащиеся знакомятся с параллельным переносом, с применением параллельного переноса при решении задач, а также доказывают, что параллельный перенос есть движение – описывается процесс, который носит динамический характер и для более глубокого усвоения и осмысления требует динамической иллюстрации.
Согласно логике построения данного урока с целью подготовки к изучению нового материала следует в начале повторить и актуализировать знания учащихся, связанных с понятиями осевой и центральной симметрий. Затем удобно ввести определение параллельного переноса с использованием наглядной динамической иллюстрации. Затем закрепить увиденное на экране при построении чертежей в тетради, в решении задач с применением параллельного переноса. В конце урока необходимо обобщить изученные вопросы.
Фрагмент урока:
|
Деятельность учителя |
Деятельность учащихся |
|
II. Повторение и актуализация ранее изученного с целью подготовки к изучению нового материала: |
|
|
- Какие точки называются симметричными относительно прямой? - Какая фигура называется симметричной относительно данной прямой? - Какие точки называются симметричными относительно данной точки? - Какая фигура называется симметричной относительно точки? Задача (рисунок на доске):
- Отрезки AB
и
|
- Две точки A
и
- Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой a также принадлежит этой фигуре.
- Две точки A
и
- Фигура называется симметричной относительно точки O, если для каждой точки фигуры симметричная ей точка относительно точки O также принадлежит этой фигуре. Один из учеников выполняет построения на доске, остальные – в тетрадях.
|
|
III. Изучение нового материала. Введение понятия параллельного переноса |
|
|
Учитель объявляет новую тему урока. Далее учитель организует просмотр группы сцен «Параллельный перенос» фильма, комментируя происходящее на экране. После окончания просмотра необходимо записать определение параллельного переноса в тетрадь и каждому из учеников следует привести в тетради пример параллельного переноса отрезка (фигуры) на данный вектор. |
Ученики смотрят flash-фильм на проекторе, внимательно слушают учителя. |
Таким образом, предлагаемое мультимедийное пособие позволяет визуализировать представления о различных ключевых понятиях и закономерностях, связанных с понятием движения и его видов. За счет возможности демонстрации отдельных сцен пособия, данный flash-фильм можно использовать как на различных этапах изучения раздела «Движение», так и на различных этапах одного урока. Кроме того, показ составляющих частей фильма можно организовать в произвольном порядке, что обеспечивает возможность применения пособия независимо от используемого преподавателем учебника по геометрии.
§ 4. Опытная проверка разработанных материалов
Условия проведения экспериментальной проверки.
Проверка проводилась в ГОУ СОШ «Школа здоровья» № 1849 в 9 «А» классе. Учитель математики Сафронова Юлия Владимировна работает в школе 10 лет, имеет 12 разряд. Работает с интересом, в работе использует современные методики.
В классе 20 человек. Обучение геометрии ведется по учебнику Л.С. Атанасяна и др. «Геометрия 7-9». Состав класса неоднороден: большинство учащихся освоили курс геометрии на базовом уровне, два ученика продвинутого уровня, но есть и такие учащиеся, которые базового уровня не достигли. Учащиеся в течение урока ведут себя неактивно, так как в основном относятся к изучению геометрии без интереса.
Обучение школьников проводилось с применением мультимедийного пособия на ряду с традиционными формами обучения.
Цели экспериментальной проверки:
1. Проверить доступность материала, представленного в пособии.
Как показала опытная проверка, материал вполне доступен ученикам. После заслушивания объяснений учителя и просмотра соответствующих сцен мультимедийного пособия ученики правильно отвечали на поставленные вопросы, определяли вид перемещения, могли строить образы фигур при осевой и центральной симметрии, когда ось совпадала с линейкой клетчатой бумаги. После этого они учились строить фигуру симметричную данной, когда ось не совпадала ни с одной из линеек клетчатой сетки бумаги. При этом обнаружилось, что некоторые ученики не вполне владеют угольником и линейкой для построения образа точки.
2. Проанализировать проявление или отсутствие интереса к разработанному пособию у школьников.
В ходе применения разработанного пособия было замечено повышение активности учащихся на уроке при просмотре отдельных сцен пособия, особенно при работе с пособием самостоятельно, выполняя построения и обсуждая полученные результаты с одноклассниками. Ученики задавали вопросы по заданиям и рисункам пособия. Из чего можно сделать вывод о проявлении интереса к разработанному пособию у школьников.
3. Выяснить, позволяет ли данное пособие действительно увеличить объем материала как теоретического, так и задачного.
Учителем было высказано мнение о том, что предоставление в пособии задач на построение экономит время на выполнение аналогичных чертежей в тетради учениками и учителем на доске, что позволит осуществить разбор большего количества задач за отведенное на изучение данного раздела время.
4. Получить отзывы школьников и учителей относительно эффективности разработанного пособия.
Учитель Сафронова Ю.В. ознакомилась с представленными мультимедийным дидактическим пособием «Движения на уроках геометрии» и отметила следующее:
- доступность изложения теоретического и задачного материала пособия;
- изложение материала от простого к сложному;
- целесообразность использования данного дидактического пособия с целью расширения кругозора учащихся и повышения их интереса к предмету;
- удачным в использовании пособия, на ее взгляд, является возможность широкого применения наглядных методов обучения;
- возможность использования flash-фильма как на различных уроках геометрии (урок изучения нового материала, урок закрепления и обобщения изученного), так и на разных этапах одного урока (этап актуализации знаний, изложения нового материала, этап первичного закрепления);
Было высказано замечание о необходимости дополнительных заданий на построение образов фигур не только в отдельных видах движения, но и при их композиции.
Кроме того, Сафронова Ю.В., отметила возможность проведения лабораторных работ по геометрии с использованием предложенного мультимедийного пособия.
5. Проверить эффективность применения пособия как при фронтальной работе с классом, так и при групповой и индивидуальной работе.
В основном пособие применялось при фронтальной работе с классом. Вместе с тем ученики, которые недостаточно освоили материал, на уроке имели возможность работать с ним дополнительно в условиях домашней работы, что положительно повлияло на результаты обучения. Наиболее продвинутые ученики имели возможность работать с индивидуальным заданием повышенной сложности. Таким образом, и эта категория школьников получала развитие их представлений, знаний и умений.
Заключение
Цель дипломной работы – на основе анализа психолого педагогической, методической и учебной литературы разработать дидактическое пособие по теме «Движения на уроках геометрии» для учащихся 8-9 классов, содержащее динамические иллюстрации, изучение которых позволит учащимся получить более глубокое представление о понятие движения и его видов. Для достижения данной цели были решены следующие задачи:
1. Изучены психолого-педагогические основы использования компьютерных изображений как средства наглядности в обучении школьников, в частности, установить роль и виды компьютерной наглядности в обучении, требования, предъявляемые компьютерным средствам обучения.
Для реализации первой задачи были изучены психолого-педагогические основы применения наглядности в обучении школьников. В результате чего был сделан вывод о том, что наглядный материал выступает как внешняя опора внутренних действий, совершаемых ребенком под руководством учителя в процессе овладения знаниями. Понятия и абстрактные положения доходят до сознания учащихся легче, когда они подкрепляются конкретными примерами и образами. А знание учителем форм сочетания слова и средств наглядности, их вариантов и эффективности дает возможность творчески применять наглядные средства в соответствии с поставленной дидактической задачей и особенностями учебного материала.
2. Проанализировано содержание учебников, дидактических материалов, рабочих тетрадей различных авторов по геометрии по теме «Движение».
Для реализации второй задачи был проведен анализ учебной, научно-методической литературы по геометрии. В результате было отобрано содержание материала, которое наиболее рационально можно представить в пособии, и разработано поурочное планирование темы «Движение» с рекомендациями по использованию мультимедийного пособия на различных этапах изучения раздела и на различных этапах в рамках одного урока.
3. Разработано мультимедийное дидактическое пособие по теме «Движения на уроках геометрии»;
4. Разработаны методические рекомендации по использованию мультимедийного дидактического пособия.
Для реализации третьей и четвертой задач было создано мультимедийное дидактическое пособие по теме «Движения на уроках геометрии» и разработаны методические указания к его использованию.
5. Экспериментально проверена эффективность использования мультимедийного дидактического пособия «Движения на уроках геометрии».
Для реализации пятой задачи была проведена апробация разработанного мультимедийного пособия в школе на уроках геометрии в 9 классе, обучающихся по учебнику Л.С. Атанасяна и др. «Геометрия 7-9».
Необходимо заметить, что при изучении понятия движения и его видов мы наблюдаем на статических рисунках учебника процессы, которые носят динамический характер – и для более глубокого усвоения и осмысления данных понятий важно организовать их наглядную иллюстрацию. Это и обосновывает необходимость визуализации материала по данной теме, связанную со сложностью и абстрактностью ключевых изучаемых понятий.
В условиях технического прогресса и относительной доступности компьютерных средств нельзя не отметить бесспорное преимущество компьютерной графики и мультимедийных проектов в реализации принципа наглядности.
Изучение возможностей использования компьютерных средств в обучении, а также классификации компьютерных средств позволили определить выбор программного продукта для разработки представленного мультимедийного пособия, а анализ учебников школьного курса геометрии определил его структуру и содержание.
В результате в данной работе предложено мультимедийное пособие по теме «Движение», выполненное с помощью компьютерной программы Macromedia Flash. Пособие представляет собой информационно-обучающий анимированный ролик, предназначенный для использования как в качестве основного организатора деятельности учащихся на уроке, так и вспомогательного демонстрационного материала при изучении раздела «Движение» курса геометрии в 8-9 классах. Основной целью разработки является визуализация представлений о ключевых понятиях выбранной темы. Flash-фильм разделен на сцены, содержание которых соответствует различным вопросам раздела. Присутствуют методическое описание ролика, а также разработаны методические рекомендации к его использованию.
Предложенное пособие является лишь дополнительным средством обучения, и может использоваться на усмотрение преподавателя полностью или частично наряду с традиционными формами обучения. Также оно может применяться при домашнем и дистанционном обучении.
Таким образом, использование компьютерных технологий в изучении наглядной геометрии позволяет добиться качественно более высокого уровня наглядности предлагаемого материала.
Библиография
Азевич, А.И. Двадцать уроков гармонии [Текст]: Гуманитарно-математический курс / А.И. Азевич – М.: Школа-Пресс, 1998. – 160 с.: ил.
Александров, А.Д. О геометрии [Текст] / А.Д. Александров // Математика в школе. - 1980. - N3. - с.56-62.
Александров, А.Д. Геометрия [Текст]: 8-9 кл.: Учеб. пособие для учащихся школ и классов с утлубл. изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик – М.: Просвещение, 1991.
Арнхейм, Р. Визуальное мышление [Текст]: Хрестоматия по общей психологии / Р. Арнхейм.- М.: Изд-во МГУ, 1981.
Атанасян, Л.С. Геометрия [Текст]: 7–9 кл.: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев – М., Просвещение, 2006.
Басова, Н. В. Педагогика и практическая психология [Текст]: Учеб. пособие / Н.В. Басова. – Ростов н/Д: Феникс, 2000. – 416 с.: ил.
Бахман, Ф. Построение геометрии на основе понятия симметрии [Текст] / пер. с немец. Р.И. Пименова, под ред. И.М. Яглома, Ф. Бахман. – М., Наука, 1969.
Беспалов, Б.И. Действие: Психологические механизмы визуального мышления [Текст] / Б.И. Беспалов. - М.: Изд-во Моск.ун-та, 1984.
Башмаков, М.И. Развитие визуального мышления на уроках математики [Текст] / М.И. Башмаков, Н.А. Резник // Математика в школе. – 1991. – №1.
Болтянский, В.Г. Геометрия [Текст] / В.Г. Болтянский, И.М. Яглом. – М., 1955.
Болтянский, В.Г. Геометрия [Текст]: пробный учебник для 6-8 кл. / В.Г. Болтянский, М.Б. Волович, А.Д. Семушин. – М.: Просвещение, 1979. - 272 с.
Болтянский, В.Г. К вопросу о перестройке общего математического образования [Текст]: повышение эффективности обучения математике в школе: Кн. для учителя: Из опыта работы / В.Г. Болтянский, Г.Д. Глейзер, Р.С. Черкасов. - М.: Просвещение, 1989.
Бурмистрова, Т.А. Программы общеобразовательных учреждений. Геометрия [Текст] / Т.А. Бурмистрова. - М.: Просвещение, 2008. - 126 с.
Вейль Г. Симметрия [Текст]: Перевод с англ. Б.В. Бирюкова и Ю.А. Данилова. Под ред. Б.А. Розенфельда / Г. Вейль. – М., Наука, 1968.
Волков, К.Н. Психологи о педагогических проблемах [Текст]: Кн. для учителя, под ред. А.А. Бодалева / К.Н Волков. – М., Просвещение, 1981.
Вульф Г.В. Симметрия и ее проявления в природе. [Текст] / Г.В. Вульф. - М., 1950. - 239с.
Выготский, Л.С. Педагогическая психология [Текст] / Л.С. Выготский. – М., 1991.
Высоцкий, И. Н. Компьютер в образовании [Текст] / И.Н. Высоцкий // Информатика и образование. - 2000. - № 1. - С. 86-87.
Гальперин, П.Я. Введение в психологию [Текст]: Учеб. пособие для вузов / П.Я. Гальперин. – М.: Кн. дом «Университет», 1999. – 332с.
Гальперин, П.Я. Психология мышления и учение о поэтапном формировании умственных действий: Исследования мышления советской психологии [Текст] / П.Я. Гальперин.— М., 1966
Глейзер Г.И. Каким быть школьному курсу геометрии [Текст] // Математика в школе. / Г.И. Глейзер. - 1991. - №4.
Гусев, В.А. Практикум по решению математических задач. Геометрия [Текст] / В.Н. Литвиненко, А.Г. Мордкович. - М.: Просвещение, 1985.
Давыдов, В.В. Виды обобщения в обучении: логико-психологические проблемы построения учебных предметов [Текст] / В.В. Давыдов. - М., Педагогика, 1972.
Дорофеев, Г.В. Математика [Текст]: учеб. для 6 кл. общеобразоват. учреждений / Г.В. Дорофеев, И.Ф. Шарыгин. – М., Просвещение, 2006. – 302 с.: ил.
Еленина, А.М. Сборник вопросов и упражнений по геометрическим преобразованиям [Текст] / А.М. Еленина. - Красноярск, 1969.
Желудев, И.С. Симметрия и ее приложения [Текст]: 2-е изд. переработ, и дополн. / И.С. Желудев. - М.: Энергоатомиздат, 1983.
Зинченко, Т.П. Когнитивная и практическая психология [Текст] / Т.П. Зинченко. - М.: Московский психолого-социальный институт, 2000.Изучение геометрии в 7, 8, 9 классах [Текст]: Методические рекомендации к учебнику: Книга для учителя/ Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. – М., Просвещение, 2003.
Карпова, Т.Н. Наглядное обучение математике в педвузе – сочетание научности и доступности: психология, интуиция, опыт [Текст]: Непрерывное педагогическое образование / Т.Н. Карпова, Е.И. Смирнов. – Ярославль, 1995.
Колягин, Ю.М. Методика преподавания математики в средней школе. Частные методики [Текст] / Ю.М. Колягин, Г.Л. Луканкин, Е.Л. Мокрушин и др. - М., Просвещение, 1977.
Краснова, Г.А. Технологии создания электронных обучающих средств [Текст]/ Г.А. Краснова, М.И. Соловов, М.И. Беляев.- М., МГИУ, 2001, 224 с.
Крутецкий, В.А. Вопросы психологии способностей школьников [Текст] / В.А. Крутецкий.- М.: Просвещение, 1964.
Машбиц, Е.И. Компьютеризация обучения: проблемы и перспективы [Текст]/ Е.И. Машбиц.-М.: Изд. “Знание”, 1986.
Машбиц, Е. И. Психолого-педагогические проблемы компьютеризации обучения: Кн. для учителя [Текст]/ Е.И. Машбиц. – М.: Просвещение, 1988.
Мироненко, В.В. Хрестоматия по психологии: Учебное пособие для студентов пед. институтов [Текст]/ В.В.Мироненко; Под ред. А.В.Петровского.- М., “Просвещение”, 1997
Мишин, В.И. Методика преподавания математики в средней школе: Частная методика: Учебное пособие для студентов пед. ин-тов по физ.-мат. спец. [Текст]/ В.И. Мишин. – М.: Просвещение, 1987.
Немов, Р.С. Психология [Текст]: Учеб. для студ. высш. пед. учеб. заведений: в 3 кн. / Р.С. Немов. – 4-е изд. – М.: Владос, 2001. – Кн.2: Психология образования. – 608с.
Обухова, Л.Ф. Возрастная психология: Учеб. пособие [Текст]/ Л.Ф. Обухова. – М.: Пед. общество России, 2000. – 448с.
Педагогика [Текст] /Под ред. П. И. Пидкасистого. – М., 1998.
Погорелов, А.В. Геометрия [Текст]: учеб. для 7–9 кл. общеобразоват. учреждений. / А.В. Погорелов. – 4 изд. – М., Просвещение, АО «Московские учебники», 2003. – 224 с.: ил.
Подласый, И.П. Педагогика [Текст] /И.П. Подласый – М., 1999.
Роберт, И.В. Современные информационные технологии в образовании [Текст] /И.В. Роберт.- М.: Школа – пресс, 1994.- 102 с.
Рубинштейн, С.Л. Основы общей психологии. Психология мышления. – М., 1981.
Рысь, Ю.И.. Психология и педагогика: Учеб. пособие для студ. вузов [Текст] / Ю.И. Рысь, В.Е. Степанов, В.П. Ступницкий. – М.: Академический проект; Изд-во науч.-образоват. лит. РЭА, 1999. – 308 с.
Саранцев, Г.И. Методика обучения математике в средней школе [Текст]: Учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г.И. Саранцев.– М.: Просвещение, 2000.
Саранцев, Г.И. Решаем задачи на геометрические преобразования [Текст] Г.И. Саранцев. - 3-е изд. перераб. доп. - М.: АО «СТОЛЕТИЕ», 1997. – 192 с., ил.
Талызина, Н.Ф. Пути и возможности автоматизации учебного процесса, [Текст] / Н.Ф. Талызина, Т.В. Габай.- М.: Просвещние, 1977.
Талызина, Н.Ф. Управление процессом усвоения знаний: Психол. основы [Текст]/ Н.Ф. Талызина.– 2-е изд., доп.и испр. – М.: Изд-во МГУ, 1975.
Фридман, Л.М. Психологическая наука – учителю [Текст]/ Л.М. Фридман, К.Н. Волков. – М.: Просвещение, 1985.
Фридман, Л.М.Психологический справочник учителя [Текст]/ Л.М. Фридман, И.Ю. Кулагина. - М.: Просвещение, 1991.
Фридман, Л.М. Психолого-педагогические основы обучения математики в школе [Текст]/ Л.М. Фридман. – М.: Просвещение, 1983.
Холодная, М.А. Когнитивные стили как проявление своеобразия индивидуального интеллекта. Киев, 1990
Холодная, М.А. Психология интеллекта: парадоксы исследования. Томск: Изд-во Томского ун-та; М.: Барс, 1997
Шарыгин, И.Ф. Геометрия [Текст]: 7-9 кл.: учеб. для общеобразоват. учеб. завед. – 4 изд., доп. - М.: Дрофа, 2000. – 368 с.: ил.
Шлыкова, О.В. Культура мультимедиа [Текст]: Учебное пособие для студентов/ МГУКИ – М., ФАИР-ПРЕСС, 2004.
 симметричны относительно точки O,
точка
симметричны относительно точки O,
точка
 симметрична точке C
относительно точки O,
причем
симметрична точке C
относительно точки O,
причем

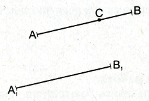
 и перпендикулярна к нему.
и перпендикулярна к нему.