Изучение геометрии на уроках математики в 5-6 классах

Дипломная работа

По теме:

Изучение геометрии на уроках математики в 5-6 классах

Оглавление:

Введение

Глава 1. Роль изучения геометрии в формировании общего образования школьников

§1. Развитие геометрии как школьного предмета

1.1 История российского геометрического образования до начала ХХ века

1.2 Основные этапы развития геометрического образования в советской школе 1917-1991)

§2. Роль изучения геометрии

§3. Психолого-педагогическая характеристика детей 11-13 лет

§4. Анализ действующих учебников математики на предмет содержания геометрического материала

Глава 2.Методическая разработка материалов для проведения уроков по геометрии в 5-6 классах

§1. Система упражнений пропедевтики и развития интереса к математике

1.1 Упражнений развития графической культуры

1.2 Упражнения на развитие наглядно-образное мышление

1.3 Система упражнений на развитие пространственных представлений

§2. Задачи для кружковой работы

2.1 Задачи по геометрии, решаемые методами оригами

2.2 Задачи на геоплане

2.3 Геометрия на клетчатой бумаге

2.4 Задачи на разрезание треугольника

§3. Материалы для проведения уроков

3.1 "Цепочки" задач по теме «Точки и прямые плоскости»

3.2 Разработка урока по теме «Угол»

Заключение

Библиография

Введение

В разное время высказывались различные мнения о преподавании геометрии и ее месте в системе школьного образования. Недостатки в освоении геометрии могут приводить к серьезному ущербу всего миропонимания.

Геометрические образы сопровождают человека в течение всей его жизни, начиная с первых лет. Первичные геометрические сведения у человека появляются до того, как он способен их формально-логически осмыслить. Чем богаче и разностороннее мир ребенка, тем большее количество таких первоначальных знаний он получает до начала обучения в школе. По наблюдениям многих учителей и специалистов-психологов при неверном обучении ранняя способность оперировать геометрическими образами и синтезировать геометрические знания может в дальнейшем не только не развиваться, но даже резко ослабевать. Поэтому одной из главных задач преподавания геометрии является задача планомерного, систематического развития геометрического, образного мышления, восприятие геометрии не только как школьного предмета, но и как феномена человеческой культуры.

Геометрическое образование должно начинаться с первых шагов пребывания ученика в школе — на уроках труда, природоведения, рисования, а в средних классах — географии и черчения. В настоящее время, в связи с постоянно растущей урбанизацией жизни и значительной формализацией процесса труда, едва ли не единственным источником приобретения опыта в геометрических образах является школа. В связи с этим появляется необходимость в разработке концепции, которая могла бы ликвидировать дефицит геометрического опыта и методически правильно подготовить учащегося к усвоению стандартного курса геометрии.

Геометрическая деятельность является первичной интеллектуальной деятельностью человечества в целом и каждого человека в отдельности. Геометрия - это «не только раздел математики, школьный предмет, это, прежде всего, феномен общечеловеческой культуры, являющийся носителем собственного метода познания мира».

В настоящее время изучение систематического курса геометрии начинается с 7 класса средней школы. Однако со многими геометрическими фигурами посредством практической деятельности дети знакомятся намного раньше. Это происходит уже на занятиях в детском саду и на уроках рисования, труда, математики в начальной школе.

К сожалению, в современной школе начальная часть геометрического образования развита недостаточно. Вследствие этого, школьники, при переходе в 7 класс, встречаются с трудностями, возникающими при изучении систематического курса геометрии: во-первых, происходит знакомство с новой терминологией, во-вторых, учащимся приходится работать с совершенно новыми объектами, восприятие которых требует развитого абстрактного мышления, в-третьих, от учащихся требуется не только свободное владение математическим языком, но и умение самостоятельно доказывать какие-либо утверждения.

В большинстве школ элементы геометрии в 5-6 классах изучаются в рамках одного предмета: математики. В связи с этим возникает вопрос о совершенствовании методики изучения элементов геометрии в курсе математики 5-6 классов.

Цель дипломной работы: Показать возможность непрерывного изучения геометрии на уроках математики, а также на кружках, составить задачный материал для данной работы.

Для достижения поставленной цели были определены следующие задачи:

- проанализировать действующие учебники 5-6 классов, методическую, педагогическую и психологическую литературу по теме дипломной работы;

- разработать систему упражнений для проведения уроков математики и кружковой работы.

При подготовке дипломной работы использовались следующие методические исследования:

- анализ литературы по теме дипломной работы;

- изучение способности детей 5-6 классов воспринимать наглядный геометрический материал;

- апробация разработанного задачного материала.

Данная работа состоит из двух глав. В первой главе рассматриваются периоды развития геометрии как учебного предмета и ее роль в формировании развития школьников; вопросы общей и возрастной психологии и педагогики: выявляются особенности развития психических процессов при изучении элементов геометрии у детей данного возраста (приводится психолого-педагогическая характеристика). Далее анализируются различные учебники математики с точки зрения содержания в них геометрического материала (Виленкин Н.Я. и др. Математика 5. Виленкин Н.Я. и др. Математика 6. «Математика 5» под ред. Г.В. Дорофеева и И.Ф. Шарыгина. «Математика 6» под ред. Г.В. Дорофеева и И.Ф. Шарыгина. Мордкович А.Г., Зубарева И.И. «Математика 5», «Математика 6»).

Во второй главе приводится методическая разработка пропедевтического курса геометрии и развития интереса к предмету геометрии. В этот раздел вошли системы упражнений на развитие графической культуры, наглядно-образного мышления и пространственных представлений. Составлен материал для кружковой работы. В этот пункт вошли такие разделы, как: задачи, решаемые методами оригами, задачи на геоплане, геометрия на клетчатой бумаге и задачи на разрезание треугольника. Также приведен материал для проведения уроков: цепочка заданий по теме «Точки и прямые на плоскости» и несколько упражнений по теме «Углы»,

После второй главы приводиться заключение, библиография.

Глава 1. Роль изучения геометрии в формировании общего образования школьников

§1. Развитие геометрии как школьного предмета

Приобретение любого познания всегда полезно для ума, ибо он сможет отвергнуть бесполезное и сохранить хорошее. Ведь ни одну вещь нельзя ни любить, ни ненавидеть, если сначала ее не познать. Леонардо да Винчи

Ушедший век многое привнес в теорию и методику обучения и воспитания учащихся в процесс их математического образования.

Мы привыкли думать, что геометрия – древнейшая наука и про ее преподавание все известно. Однако, это не так. Прежде всего, следует сказать, что, несмотря на то что геометрия – действительно древнейшая наука, ее современная методологическая основа сформировалась сравнительно недавно: в конце XIX – начале XX веков.

Условно последние десятилетия развития методики преподавания геометрии в школе можно разделить на следующие периоды.

Период использования в школе учебников А.П. Киселева – вплоть до начала 60-х годов XX века.

Период внедрения в школьную геометрию новых разделов: элементов теории множеств, геометрических преобразований, векторной алгебры и т.д. – В.Г. Болтянский, А.И. Фетисов, И.М. Яглом и др.

"Колмогоровский период" (1965-1980) – характеризуется очень серьезным подходом к осмыслению всей структуры школьной математики в целом и геометрии в частности.

"Период традиционных современных учебников" для массовой школы – Л.С. Атанасян и др., А.В. Погорелов, И.Ф. Шарыгин, А.Д. Александров и др. Появление этих учебников было связано с желанием авторов вернуться к более традиционному (чем у А.Н. Колмогорова) подходу к изучению школьного курса геометрии.

1.1 История российского геометрического образования до начала ХХ века

Развитие геометрии в XVIII веке:

в России начала развиваться система государственного образования, сложилась номенклатура учебных дисциплин, в рамках которой геометрия постепенно выделилась в самостоятельный учебный предмет, что вызвало создание соответствующих учебников.

Четкой концепции предмета, критериев отбора содержания и методов его изложения еще не существовало. Авторы порой руководствовались личным опытом и собственными вкусами. Ни один из созданных в это время курсов не был ни систематическим, ни логическим.

Существенное влияние на авторов учебников по геометрии оказывали западные традиции и непререкаемый в ту пору научный авторитет Евклида, что приводило к использованию в обучении геометрии самих "Начал", их адаптированных вариантов, переводных и оригинальных учебников, написанных в традициях Евклида. В целом же в XVIII веке вопрос об учебнике геометрии не был решен, что объяснялось не только колоссальным влиянием научного авторитета Евклида и возможностью использования его "Начал" в качестве учебного пособия, но и сравнительно небольшим по современным меркам числом учебных заведений, отсутствием острой потребности в массовом учебнике.

Зародились два направления в преподавании геометрии практическое (прикладное) и теоретическое. Основным для XVIII века было практическое направление, что объясняется изначальным появлением системы профессионального образования, а затем уже общего и необходимостью пропаганды геометрических знаний, которые долгое время были под запретом. В последней четверти XVIII века эти направления начали сближаться и само образование сделало шаг от элитарного профессионального к массовому общему.

В преподавании основное внимание уделялось геометрии плоских фигур, рассматриваемых в пространстве, и меньше внимания – стереометрии. Свойства фигур и тел изучались лишь в контексте вычисления площадей и объемов, применения этих свойств на практике. Вопрос о развитии у учеников пространственных представлений не ставился, хотя авторов учебников можно отнести к наивным фузионистам.

Основной метод преподавания – догматический. На первый план выдвигалось заучивание и воспроизведение готовых фактов, что в лучшем случае развивало лишь память. Этот вывод подтверждается и отсутствием в историко-методической литературе по математике сведений о существовании каких – либо задачников по геометрии. Неизвестен и ответ на вопрос об организации контроля за усвоением геометрических знаний.

Развитие геометрии в XIX веке:

сложилась система среднего образования, в рамках которой геометрия была самостоятельным учебным предметом, за исключением начальных учебных заведений. В гимназиях преподавалась элементарная геометрия: от начальных понятий до конических сечений, в неполных средних (городских и уездных училищах) – сокращенный законченный курс планиметрии с элементами стереометрии (поверхности и объемы тел без доказательств).

Содержание курса окончательно сформировалось и состояло из двух разделов: планиметрии (линии и фигуры) и стереометрии (тела). Курс не был систематическим в современном понимании этого слова, но являлся последовательным курсом элементарной геометрии в традициях Евклида, выстроенным на дедуктивной основе. Хотя в начале курса аксиомы полностью или частично приводились, но их значение как основ для построения геометрической теории не рассматривалось в школьных учебниках. Под аксиомами понимали очевидные истины. Таким образом, гимназические курсы геометрии в XIX веке не были аксиоматическими, но по содержанию были шире современных в части элементарной геометрии. Они еще не содержали элементов аналитической геометрии, но в них уже нашла отражение теория пределов. Однако можно утверждать, что к концу века образовался серьезный разрыв между геометрией как учебным предметом и геометрией как развивающейся наукой.

Курсы геометрии содержали логические пробелы в формулировках определений и в доказательствах. Определения подменялись описаниями, имелся дуализм в определении некоторых понятий. Так, с одной стороны, линия определялась как граница поверхности, а с другой – как результат движения точки. Вольно трактовалось и понятие обратной теоремы.

Определенное влияние на содержание школьных учебников геометрии этого периода оказывали западные авторы, прежде всего французские (Даламбер, Лежандр, Дистервег и др.), что привело к некоторому усилению позиций сторонников метрической геометрии. Однако подлинно метрической школьная геометрия еще не стала. Углы по-прежнему измерялись дугами окружности. Под измерением площадей и объемов понимали сравнение с фигурой, имеющей единичную площадь или объем. Этим объясняется крайне малое число задач на вычисление в школьных курсах и доминирование задач на построение и доказательство.

Курс геометрии стал теоретическим, практические приложения свелись к рассмотрению в большем или меньшем объеме измерений и построений на местности и соответствующих им инструментов (даже в училищах различных типов).

В XIX веке серьезное внимание уделялось вопросам преподавания, закрепления знаний и контроля за их усвоением, что и привело к появлению задачников по геометрии. Впервые был поставлен вопрос о самостоятельной деятельности учащихся при изучении геометрии, учете их психологических особенностей, хотя под последними понимали только внешние проявления психических процессов, типы восприятия. В связи с этим при усвоении школьниками начальных понятий геометрии встал вопрос о создании подготовительных курсов геометрии. Широкому распространению передовых идей в преподавании геометрии способствовали появившиеся в средние века педагогические журналы. Однако основным видом деятельности учителя по-прежнему оставались передача учащимся готовых геометрических знаний и проверка их усвоения.

1.2 Основные этапы развития геометрического образования в советской школе (1917-1991)

Советский период развития школьного геометрического образования:

преподавание геометрии в советской школе впитало в себя содержательные и в меньшей степени методические традиции российской школы благодаря как непосредственному использованию на практике учебника А.П. Киселева и его последующих редакций на протяжении почти 40 лет, так и возвращению к курсу геометрии в духе Евклида в учебниках А.В. Погорелова, Л.С. Атанасяна.

Фактология школьного курса, в целом сложившаяся к середине XIX века, практически не изменилась, курс оставался раздельным и последовательным, хотя объем содержания по сравнению с учебником А.П. Киселева уменьшился, что привело в середине 90-х годов к появлению принципа минимизации содержания.

Основные изменения содержания касались последовательности изучения отдельных тем курса; ведущего метода доказательства: на основе равенства фигур (Киселев, Атанасян, Александров), с помощью преобразований (Колмогоров, Болтянский, частично Александров); появления новых разделов (векторы, координаты, движения); включения стереометрических сведений или использования пространственных фигур в курсе планиметрии; использования теоретико-множественной терминологии и символики; аксиоматизация курса. У Киселева и его последователей аксиомы не являлись основой для построения школьного курса. На аксиоматической основе были построены учебники Колмогорова, Погорелова, Атанасяна и Александров, хотя со временем их "аксиоматизм" начал ослабевать. В целом курс носил теоретический характер, его практическая направленность реализовалась на уровне примеров, носила второстепенный характер. Он ориентировался на построение школьной геометрии как адаптированного слепка науки, а не учебного предмета, приоритетной оставалась информативная функция знаний, а не развивающая.

Борьба за появление пропедевтических курсов геометрии в 70-е годы завершилась включением в курс математики для 4-5 (5-6) классов большого объема геометрических фактов в рамках "геометрии без доказательств", что создало предпосылки к появлению в последующем самостоятельных курсов геометрии для 5-6 (1-6) классов.

Ориентация политики государства на развитие промышленности, создание материально-технической базы социализма, укрепление связи образования с производством выделила в качестве приоритетного естественно-техническое направление образования, в котором геометрии принадлежала одна из ведущих ролей. Преобладание технических вузов требовало от большинства выпускников школы твердых знаний по геометрии, сделав успешную сдачу вступительного экзамена одним из ведущих мотивов изучения геометрии. Это, в свою очередь, привело к появлению третьей после школьной и высшей математики – математики для поступающих.

Ведущими целями преподавания являлись формирование у учащихся геометрических знаний и умений, развитие логического мышления. Самостоятельная, познавательная деятельность школьников сводилась к решению разнообразных задач. Психологи характеризуют такое построение процесса обучения как направленное на формирование мышления эмпирического типа.

Стержневыми направлениями многочисленных методических исследований являлись поиск форм и средств эффективного обучения отдельным вопросам школьной геометрии, обучению решению задач различной тематики и типов. Несмотря на все усилия исследователей, педагогов-практиков, в 80-е годы появились многочисленные публикации, свидетельствовавшие о снижении результативности школьного геометрического образования. Это могло быть вызвано несовершенством методики, низкой квалификацией учителей, поскольку эффективность реализации локальных инноваций в массовой школе целиком зависит от профессиональных возможностей педагога, его интересов; изменением мотивации учебной деятельности; несоответствием содержания и методов обучения уровню психического развития школьников. Наметилась тенденция превращения школьной геометрии в учебный предмет "в себе".

Развитие детской психологии, внедрение развивающих моделей в начальное обучение (Занков, В.В. Давыдов, Эльконин), начало профильной и уровневой дифференциации старшего звена школы вступали в противоречие со стабильным содержанием и методами преподавания геометрии в 6-8 (7-9) классах средней школы, существовавшими в рамках предметно-центрической концепции обучения, где, в частности, ученик рассматривается как объект обучения, и требовали не только поиска новых моделей обучения, но и определения целей и поиска адекватного им содержания курса геометрии для 7-9 классов, превращения ученика в субъект учебного процесса, что нашло свое отражение в высказываниях и публикациях А.Д. Александрова, Н.М. Бескина, Г.Д. Глейзера, И.Ф. Шарыгина и других, однако на технологическом уровне проблемы начали решаться лишь в 90-е годы.

Изменение преподавания школьной геометрии в СССР в 60-80-е годы частично совпадали с общемировыми тенденциями включения в школьные курсы элементов современной математики и реализации лозунга "Евклид должен уйти!", а также возвращения к традициям Евклида на новом уровне и более умеренному подходу к связям школьных курсов и современных течений в математике.

§2. Роль изучения геометрии

Ни тридцать лет, ни тридцать столетий

Не оказывают никакого влияния на ясность

И красоту геометрических истин.

Льюис Кэрролл

В ряду учебных дисциплин, составляющих в совокупности школьный курс математики, геометрия играет особо важную роль. Эта роль определяется и относительной сложностью геометрии по сравнению с другими предметами математического цикла, и большим значением этого предмета для изучения окружающего мира. Геометрия, являясь неотъемлемой частью математического образования, имеет целью обще-интеллектуальное и общекультурное развитие учащихся. Развитие учащихся средствами геометрии направлено на достижение научных, прикладных и общекультурных целей математического образования, где общекультурные цели обучения геометрии в первую очередь предполагают всестороннее развитие мышления детей. Геометрия, как учебный предмет, обладает уникальными возможностями для решения главной задачи общего математического образования – целостного развития и становления личности средствами математики.

Уникальность геометрии как учебного предмета заключается в том, что она позволяет наиболее ярко устанавливать связи между естественными представлениями об окружающих предметах и их абстрактными моделями; формировать мыслительные операции различных видов и уровней; учитывать индивидуальные особенности протекания психических процессов учащихся.

Одной из важнейших задач школы является воспитание культурного, всесторонне развитого человека, воспринимающего мир как единое целое. Каждая из учебных дисциплин объясняет ту или иную сторону окружающего мира, изучает ее, применяя для этого разнообразные методы.

Геометрия – это раздел математики, являющийся носителем собственного метода познания мира, с помощью которого рассматриваются формы и взаимное расположение предметов, развивающий пространственные представления, образное мышление учащихся, изобразительно-графические умения, приемы конструктивной деятельности, т.е. формирует геометрическое мышление.

§3. Психолого-педагогическая характеристика детей 11-13 лет

При описании психических процессов детей 11-13 лет будем опираться на психические особенности младших школьников, поскольку дети 5-6 классов близки к младшему школьному возрасту.

Рассмотрим психические процессы младших школьников.

Познавательное развитие в младшем школьном возрасте.

- Внимание

- Восприятие

- Память: произвольная и непроизвольная

- Воображение

- Мышление

Внимание

Внимание - характеристика психической деятельности, выражающаяся в сосредоточенности и в направленности сознания на определённый объект. Под направленностью сознания понимается избирательный характер психической деятельности, осуществление в ней выбора данного объекта из некоторого поля возможных объектов.

Процесс обучения невозможен без достаточной сформированности такой функции деятельности человека, как внимание. У детей преобладает непроизвольное внимание. Ребенок в большей степени реагирует на яркие, эмоциональные признаки информации, чем на ее содержание, он обращает внимание на то, что ему непосредственно интересно. В ходе учебной деятельности ребенок учится направлять и устойчиво сохранять внимание на нужных, а не просто внешне привлекательных предметах.

Школьник младших классов может сосредоточенно заниматься одним делом 10—20 мин. По сравнению с дошкольниками у младших школьников в 2 раза увеличивается объем внимания, повышается его устойчивость переключение и распределение. Во втором и третьем классе многие учащиеся уже обладают произвольным вниманием, концентрируя его на любом материале, объясняемом учителем или имеющемся в книге.

Восприятие

Развитие отдельных психических процессов происходит на протяжении всего младшего школьного возраста. К семи годам у ребенка отмечаются достаточно развитый процесс восприятия (наблюдается высокая острота зрения и слуха, ориентирование на различные формы и цвета), но восприятие младшего школьника в учебной деятельности сводится лишь к узнаванию и называнию формы и цвета.

Восприятие - сложная система процессов приёма и преобразования информации, обеспечивающая организму отражение объективной реальности и ориентировку в окружающем мире.

У первоклассников присутствуют недостатки дифференцированности восприятия, так как еще не сформирована способность к систематическому анализу самих воспринимаемых свойств и качеств предметов. Возможность ребенка анализировать и дифференцировать воспринимаемые предметы связана с формированием у него более сложного вида деятельности, чем ощущение и различение отдельных непосредственных свойств вещей. Этот вид деятельности, называемый наблюдением, особенно интенсивно складывается в процессе школьного учения. На занятиях ученик получает, а затем и сам развернуто формулирует задачи восприятия тех или иных предметов и пособий. Благодаря этому восприятие становится целенаправленным. Такое восприятие, синтезируясь с другими видами познавательной деятельности (вниманием и мышлением), приобретает форму целенаправленного и произвольного наблюдения.

Память: произвольная и непроизвольная

В процессе становления в младшем школьном возрасте находится память. Память приобретает ярко выраженный познавательный характер. Изменения в области памяти связаны со следующими явлениями:

- ребенок начинает осознавать особую, мнемоническую задачу. Он отделяет эту задачу от всякой другой. Такая задача в дошкольном возрасте либо вовсе не выделяется, либо выделяется с большим трудом;

- в младшем школьном возрасте идет интенсивное формирование приемов запоминания. От наиболее примитивных приемов (повторение, внимательное длительное рассмотрение материала) в более старшем возрасте ребенок переходит к группировке, осмыслению связей разных частей материала.

В младшем школьном возрасте существуют следующие особенности памяти:

- наглядный материал запоминается лучше; чем словесный;

- название предметов запоминаются лучше, чем абстрактные понятия;

- абстрактный материал, обобщающий ряд фактов, запоминается лучше, чем абстрактный материал, не подкрепленный фактами.

Память в процессе обучения развивается в двух направлениях — произвольности и осмысленности.

Соотношение непроизвольной и произвольной памяти в процессе развития внутри учебной деятельности различно. В первом классе эффективность непроизвольного запоминания значительно выше, чем произвольного, так как у детей еще не сформированы особые приемы осмысленной обработки материала и самоконтроля. Обе формы памяти — произвольная и непроизвольная — претерпевают в младшем школьном возрасте такие качественные изменения, благодаря которым устанавливается их тесная взаимосвязь и взаимопереходы. Важно, чтобы каждая из форм памяти применялась детьми в соответствующих условиях (например, при заучивании какого-либо текста наизусть используется преимущественно произвольная память). Усвоение учебного материала может происходить и с помощью непроизвольной памяти, если она опирается на средства логического освоения этого материала. Тем самым развивается смысловая память, и ее совершенствование в этом возрасте позволит в дальнейшем освоить достаточно широкий круг мнемонических приемов, т.е. рациональных способов запоминания (деление текста на части, составление плана, приемы рационального заучивания и др.)

Воображение

Воображение - психическая деятельность, состоящая в создании представлений и мысленных ситуаций, никогда в целом не воспринимавшихся человеком в действительности. Воображение основано на оперировании конкретными чувственными образами или наглядными моделями действительности, но при этом имеет черты опосредствованного, обобщённого познания, объединяющие его с процессом мышления. Характерный для воображения отход от реальности позволяет определить его как процесс преобразующего отражения действительности.

Специфика учебной деятельности помогает развить у детей такую важную психическую способность, как воображение. Большинство сведений, сообщаемых школьникам учителем и учебником, имеет форму словесных описаний, картин и схем. Школьники каждый раз должны воссоздавать себе образ действительности (поведение героев рассказа, события прошлого, ландшафты и т. д.). В процессе школьных занятий развивается воссоздающее (репродуктивное) воображение, и уже воссоздающее воображение перерабатывает образы действительности. Дети изменяют сюжетную линию рассказов, представляют события во времени, изображают ряд объектов в обобщенном, сжатом виде (этому во многом способствует формирование приемов смыслового запоминания). Постепенное совершенствование воссоздающего, или репродуктивного, воображения в младшем школьном возрасте создает условия для развития у школьников творческого (продуктивного) воображения. Формированию этой предпосылки помогают занятия по труду, на которых дети осуществляют свои замыслы, изготавливая какие-либо предметы. Этому во многом способствуют и уроки рисования, требующие от детей создать замысел изображения, а затем искать наиболее выразительные средства его воплощения.

Мышление

Как известно, важнейшим психическим процессом является мышление. "Мышление – "это социально обусловленный, неразрывно связанный с речью психический процесс поисков и открытия существенно нового, процесс опосредованного и обобщенного отражения действительности в ходе ее анализа и синтеза".

Мышление возникает на основе практической деятельности из чувственного познания и далеко выходит за его пределы.

В психологии распространена следующая классификация видов мышления:

- наглядно-действенное (связанное с практической деятельностью);

- наглядно-образное (основанное на зрительном восприятии);

- отвлеченное (теоретическое).

В начальной школе у детей интенсивно развивается наглядно-образное мышление. Однако к 11 годам наглядные образы чаще заменяются словесными формулировками.

Мышление в младшем школьном возрасте приобретает абстрактный и обобщенный характер. Выполнение интеллектуальных операций школьниками связано с трудностями.

В развитии мышления наблюдаются две основные стадии:

Мыслительная деятельность младших школьников еще во многом напоминает мышление младшего школьника. Анализ учебного материала производится по преимуществу в наглядно-действенном плане. Дети опираются при этом на реальные предметы или их прямые заместители, изображения. Учащиеся пятых классов зачастую судят о предметах весьма односторонне, схватывая какой-либо единичный внешний признак. Умозаключения детей опираются на наглядные предпосылки, данные в восприятии. Обоснование вывода осуществляется не на основе логических аргументов, а путем прямого соотношения суждения воспринимаемыми сведениями.

Большинство обобщений, осуществляемых детьми на этой стадии, фиксирует, конкретно воспринимаемые признаки и свойства, лежащие на поверхности предметов и явлений;

К пятому классу изменяется характер мышления младших школьников. Учащиеся овладевают родовидовыми соотношениями между отдельными признаками понятий, т.е. классификацией.

В основе суждений младших школьников о признаках и свойствах предметов и явлений лежат чаще всего наглядные изображения и описания. Но вместе с тем эти суждения являются результатом анализа текста, мысленного сопоставления его отдельных частей, мысленного выделения в этих частях главных моментов, их объединения в целостную картину, наконец, обобщения частностей в некотором новом суждении, теперь уже отделенном от прямых его источников и ставшем абстрактным знанием. Следствием такой умственной аналитико-синтетической деятельности является абстрактное суждение или обобщенное знание. По мере того как ребенок учится классифицировать определенные предметы и явления, появляются все более сложные формы умственной деятельности, которая становится относительно самостоятельным процессом работы над учебным материалом, независящим непосредственно от восприятия. Постепенно растет количество суждений, в которых наглядные моменты сведены до минимума и объекты характеризуются по более или менее существенным связям.

Свойство детского ума воспринимать все конкретно, буквально, неумение подняться над ситуацией и понять ее общий, абстрактный или переносный смысл - одна из основных трудностей детского мышления, ярко проявляющаяся при изучении таких абстрактных дисциплин как математика и грамматика. При переходе в среднюю школу у ребенка значительно повышается удельный вес чтения как источника мыслей. Появляются новые учебные предметы, способствующие развитию отвлеченного мышления. Изучение такого максимально абстрактного предмета, как математика, хорошо показывает, как высоко поднимается уровень абстрактного мышление школьников данного возраста. Так, многим ученикам 5-6 класса легче дается решение «абстрактных» текстовых задач, чем задач с большим количеством конкретно-чувственных деталей, где основные существенные зависимости между величинами маскируются. К таким задачам относятся и задачи геометрического содержания.

Трудность обобщения (как одной их операций мышления) - одна из основных трудностей, возникающих при изучении математики. По словам В.А. Крутецкого, неспособные дети с большим трудом обобщали предложенный математический материал. Они с трудом перебирались от одной ступени к другой, причем каждая ступень должна была закрепляться значительным количеством упражнений. Отметим, что зачастую это происходит вследствие того, что многие младшие школьники не могут выделить общие и существенные свойства какого-либо предмета или явления. Так, узнав о способе нахождения площади прямоугольника (произведение длин его смежных сторон), многие школьники применяют этот способ для нахождения площадей других геометрических фигур, например треугольника. Итак, выделение существенного - это одна сторона процесса абстракции (позитивная). Отвлечение от несущественного - другая ее сторона (негативная). Многочисленные наблюдения и исследования показывают, что негативная сторона процесса протекает труднее, чем позитивная: отвлечение от несущественного происходит с большим трудом, чем выделение существенного. Однако трудности возникают и при другом мыслительном процессе: переходе от абстрактного к конкретному.

Типичными становятся ошибки в геометрической иллюстрации к задаче, в построении чертежей. Поэтому развитие отвлеченного мышления у пятиклассников в ходе усвоения понятий вовсе не означает, что их наглядно-действенное и наглядно-образное мышление перестает теперь развиваться или вообще исчезает.. Наоборот, эти первичные и исходняе формы всякой мыслительной деятельности по-прежнему продолжают изменяться и совершенствоваться, развиваясь вместе с отвлеченным мышлением и под его влиянием. Любое, даже наиболее развитое мышление всегда сохраняет связь с чувственным познанием, т.е. с ощущением, восприятием и представлением. Весь свой материал мыслительная деятельность получает только из одного источника – из чувственного познания. Известно, что усвоение материала будет более эффективным, если опираться на особенности соотношения конкретного и абстрактного мышления детей. В соответствии с этим на уроках "умственная деятельность должна подкрепляться конкретной материальной деятельностью". Значительное место, особенно при изучении геометрического материала, должны занимать упражнения, в которых требуется начертить, измерить, найти на рисунке и предмете, вырезать, составить фигуру и др. Это позволит стимулировать у учащихся развитие наглядно-действенного мышления и на его основе в дальнейшем – образного мышления.

С точки зрения формальной логики мышление характеризуется тремя основными формами: понятиями, суждениями, умозаключениями. Процесс формирования некоторого понятия – постепенны процесс, в котором можно выделить несколько последовательных стадий. Первая стадия представляет собой процесс "видения", который создает в сознании ребенка особую форму отражения реальной действительности – восприятия. "Чувственное восприятие объекта есть начальная, простейшая ступень в его познании – первая ступень в формировании соответствующего уму понятия". Далее в результате отвлечения от чувственного восприятия в сознании детей создается новая форма представление о данном объекте. На следующей ступени познания через род и видовое отличие формируется понятие. На данном этапе ребенок знакомится со свойствами объекта, рассматривает его с точки зрения уже известных ему понятий, выделяет объем и содержание понятия.

Если говорить об особенностях геометрического материала, то специфика его такова, что в возрасте 11-12 лет сформировать в сознании ребенка многие геометрические понятия очень трудно.

Геометрическое мышление в своей основе является разновидностью чувственного, образного мышления, что функционально присуще правому полушарию головного мозга. По мере развития геометрического мышления происходит возрастание логической составляющей и соответственно роли левого полушария. Отсюда важность геометрии в непосредственно физиологическом смысле и особенно для детей в возрасте 8-12 лет с доминирующим развитием правого полушария. А таких детей, как известно не меньшинство.

"Занятия геометрией способствуют развитию интуиции, воображения и других важнейших качеств, лежащих в основе любого творческого процесса". Итак, формирование геометрических представлений, несомненно связано, с развитием воображения. "основная тенденция, возникающая в развитии детского воображения – это переход ко все более правильному и полному отражению действительности, переход от простого произвольного комбинирования представлений к комбинированию логически аргументированному". Если ребенок 3-4 лет удовлетворяется для изображения самолета двумя палочками, положенными крест-накрест, то в 7-8 лет ему уже нужно внешнее сходство с самолетом. Школьник 11-12 лет часто сам конструирует модель и требует от нее еще более полного сходства с настоящим самолетом. С каждым годом возрастает реализм детского воображения. Однако воображение ребенка, оканчивающего начальную школу, характеризуется также другой чертой: наличием элементов репродуктивности, простого воспроизведения. И не секрет, что зачастую в 5 классе ребенок однотипно изображает геометрические фигуры и, в связи с этим, испытывает трудности при решении задач. Однако с возрастом элементов репродуктивности, простого воспроизведения в воображении школьника становится все меньше и меньше и все в большей степени появляется творческая переработка представлений. Образы воображения приобретают уже более обобщенный характер. С каждым годом обучения в школе развитие воображения все в большей степени базируется на освоении технических приемов действий в той или иной области творческой деятельности. Геометрическая деятельность не является исключением.

Известно, что воображение становится более "тусклым" в связи с тем, что у детей отсутствуют какие-либо практические умения. А геометрический материал предоставляет хорошую почву для развития этих умений. Именно благодаря геометрическим занятиям , ученики 5 класса дают действительно творческую переработку полученных ими впечатлений, комбинируя их таким образом, что возникают новые сочетания, которых не было в их непосредственном опыте. Такая «эмансипация» воображения детей младшего школьного возраста от непосредственных впечатлений является следствием расширения их опыта, благодаря практическим и лабораторным работам, а также широкому использованию наглядности.

Таким образом, можно сделать вывод, что в 5-6 классах учащиеся уже способны к восприятию довольно абстрактного геометрического материала, но при его изучении необходимо активно использовать наглядность и применять лабораторные и практические работы. Кроме того, важно не только развивать мышление (как отвлеченное, так и наглядно-образное), но и стремиться к формированию обобщенного воображения. В курсе математики 5-6 класса элементы наглядной геометрии развивают логическое мышление учащихся, их пространственные представления и практические навыки.

§4. Анализ действующих учебников математики на предмет содержания геометрического материала

Как показали исследования психологов, возраст детей от 7-12 лет наиболее благоприятен для формирования геометрических представлений. Детям этого возраста присуще яркость восприятия, наглядная образная память, большой интерес к окружающему миру, богатое воображение, способность легко усваивать материал и др.

Ещё в дошкольном возрасте ребёнок встречается с различными линиями, фигурами, поверхностями, формами, под влиянием которых у него формируются геометрические представления. Геометрические представления в этом возрасте носят случайный и хаотичный характер, они не всегда правильные, преимущественно «плоскостные». В начальной школе продолжается процесс накопления детьми представлений о пространстве, необходимых для усвоения элементарных понятий, а затем учащиеся приступают к дальнейшей стадии обобщения и конкретизации свойств и отношений предметов и явлений материального мира по разным признакам: временным, количественным, пространственным.

Обучение в начальной школе ставит своей целью упорядочить эти пространственные представления. Исходя из возрастных особенностей младших школьников, большое значение приобретает наглядность, использование аудиовизуальных средств и применение готовых моделей, изготовленных из картона, пластилина. На уроках учащихся учат находить знакомые им фигуры в окружающей обстановке, видеть их в сложных конфигурациях.

На уроках математики в начальной школе имеют большое значение практические работы: изготовление геометрических фигур, их вычерчивание, вырезание, получение прямого угла перегибанием бумаги, упражнения на формирование навыков работы с наиболее употребляемыми чертёжными инструментами (линейка, угольник, циркуль). Большое внимание уделяется приёму сопоставления и противопоставления фигур.

В начальной школе учащиеся должны уметь:

1 класс:

- изображать прямую, кривую, отрезок, многоугольник;

- находить длину отрезка в см;

- начертить отрезок заданной длины;

- увеличить или уменьшить отрезок на заданное количество см;

- различать углы прямые и непрямые, прямоугольники и квадраты;

- распознавать эти фигуры, называть их и изображать на клеточной бумаге;

2 класс:

-делить отрезок на равные части;

- распознавать и изображать ломаную, окружность, круг, многоугольник;

- измерять длину ломаной.

Характер работ по формированию пространственных представлений во втором классе усложняется, добавляются задачи на деление геометрических фигур на части, упражнения на составление фигур. В 3 классе идёт формирование представления о площади прямоугольника и квадрата. Учащиеся должны знать, что у прямоугольника все углы прямые, а противоположные стороны равны. Учащиеся должны уметь складывать различные фигуры из 2-3 элементарных частей.

Среди задач большинство таких, в которых геометрические фигуры используются для пересчитывания, задачи на деление фигур на части, задачи, связанные с формированием навыков чтения геометрических чертежей с использованием буквенных обозначений; задачи на выяснение геометрической формы предметов и их частей; задачи, развивающие глазомер.

Таким образом, к окончанию начальной школы пространственные представления учащихся становятся более осознанными, полными. Учащиеся, как правило, уже почти свободно ориентируются в пространстве, отмечают направления, определяют положение предметов по отношению к другим предметам, к сторонам горизонта. У них накоплен определённый запас геометрических представлений, терминов. Они могут узнавать пространственный объект в окружающей действительности и находить его графическое изображение. Учащиеся уже могут воспроизвести несложные представления в памяти, в воображении и словесно их описать, а также воспроизвести представления графически в виде предметной модели.

Уроки труда, рисования, математики содержат определённую систему предметов, методов и средств, создающих в уме школьника многообразную категорию пространственных представлений и отношений. Всё это определяет содержание пропедевтической работы учителя по развитию геометрических представлений учащихся начальных классов.

Программа по математики начальных классов уделяет особое внимание развитию конструктивных навыков учащихся, которые будут эффективны лишь при целенаправленном и систематическом их формировании на протяжении всех лет обучения в школе. При правильной постановке преемственности в их развитии, при строгом учёте психологических возрастных особенностей учащихся.

Министерством образования и науки РФ к использованию в образовательном процессе на 2008/2009 учебный год рекомендованы учебники по математике для 5-6 классов следующих авторских коллективов:

Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд,

И.И. Зубарева, А.Г. Мордкович,

С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин,

В.Г. Дорофеев, С.Б. Суворова, И.Ф. Шарыгин,

Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, «Математика: 5 класс», «Математика: 6 класс», Математика 5 класс

Глава 1. Натуральные числа

§1. Натуральные числа и шкалы

Отрезок. Длина отрезка. Треугольник

С практической точки зрения вводится понятие отрезка, как линии, которая соединяет две точки, эти точки называются концами отрезка.

С помощью рисунка вводится понятие лежать между

Сообщается, что отрезки можно сравнивать с помощью измерения и вводятся единицы измерения длины отрезков, которые детям уже известны, фактически идет повторение.

На основе рисунка вводится не только понятие треугольника и его составляющих частей, но понятие многоугольника, по количеству вершин.

Плоскость. Прямая. Луч

Понятие плоскости вводится интуитивно, на основе жизненных примеров: поверхность стола, школьной доски, оконного стекла. Сообщается, что плоскость не имеет края, она безгранично простирается во всех направления.

На основе уже известного понятия отрезка вводится новое понятие- прямая: если отрезок продолжить в обе стороны, то получится прямая. Сообщается, что прямая не имеет концов, неограниченно продолжается в обе стороны.

Сообщается аксиома: через две точки проходит единственная прямая.

Вводится понятие пересечения двух прямых на примере, по рисунку.

Понятие луча вводится на примере по рисунку. Точка О делит прямую на две части, каждую их которых называют лучом. Точка О называется началом лучей. Объясняется как обозначать лучи.

По рисунку вводится понятие дополнительных лучей.

§4. Площади и объемы

Площадь. Формула площади прямоугольника

Сначала на конкретной фигуре вводится понятие квадратного сантиметра и вычисляется ее площадь. Затем вводится понятие для площади произвольной фигуры.

Затем приведена словесная формулировка для нахождения площади, а потом уже составляется формула. Весь этот материал известен школьника из начальной школы.

Вводится понятие равных фигур, те, которые можно совместить наложением.

Вводятся некоторые свойства площадей (без доказательств):

Площади равных фигур равны. (их периметры тоже равны)

Площадь всей фигуры равна сумме площадей ее частей

После знакомства с понятием прямоугольника на его основе вводится понятие квадрата, как прямоугольника, у которого все стороны равны. Затем, вводится формула площади квадрата, после чего объясняется название квадрат числа.

Единицы измерения площадей

Со стандартными единицами измерения и с тем в чем измеряется площадь ученики уже знакомы. На основе знаний об единицах измерения длин отрезков объясняется как переводить одни квадратные единицы в другие.

Площади полей уже известными единицами измерения неудобно измерять. Аналогично вводятся новые единицы измерения: гектар и ар.

Прямоугольный параллелепипед

На основе примеров из жизни: спичечный коробок, деревянный брусок, кирпич - вводится понятие прямоугольного параллелепипеда. Затем вводятся элементы прямоугольного параллелепипеда: грани, ребра, вершины и их количество.

Сообщается, что длину, ширину и высоту параллелепипеда называют его измерениями. После этого вводится понятие куба, как прямоугольного параллелепипеда, у которого все измерения равны.

Объемы. Объем прямоугольного параллелепипеда

Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем больше объема второго сосуда. А если заполнить второй сосуд не удастся, то объем первого сосуда меньше объема второго.

Далее структура пункта и введение новых понятий полностью повторяет пункт "Площадь. Площадь прямоугольника".

§5. Обыкновенные дроби

Окружность и круг

Сначала объясняется как с помощью циркуля построить окружность: установим ножку циркуля с иглой в точку О, а ножку с грифелем будем вращать вокруг этой точки. Тогда грифель опишет замкнутую лини, такую линию называют окружностью. Затем на основе готового чертежа вводятся все элементы окружности: круг, радиус, диаметр (и их связь), полукруг, полуокружность, дуга окружности.

§8. Инструменты для вычислений измерений

Угол. Прямой и развернутый угол. Чертежный треугольник

Сразу вводится стандартное (полноценное) определение угла: углом называют фигуру, образованную двумя лучами (стороны угла), выходящими из одной точки (вершина угла).

Затем объясняется правило записи названия угла и приводится несколько вариантов (одной или тремя буквами). Вводится значок для обозначения угла.

По рисунку для точек вводится понятие лежать внутри и вне угла.

Когда рассматривалась тема о площади прямоугольника, сообщалось, что фигуры равны, если их можно совместить наложением. Сообщается, что это применимо для всех фигур и углов в том числе.

Ранее было введено понятие дополнительных лучей, на основе этого понятия вводится понятие развернутого угла: два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла составляют прямую линию, на которой лежит вершина угла.

С помощью практического объяснения вводится понятие прямого угла: согнем два раза пополам лист бумаги, а потом развернем его. Линии сгиба образуют 4 развернутых угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.

Далее проводится «знакомство» с новым чертежным инструментом: чертежный треугольник, как инструмент для построения прямых углов. И приводится план построения прямого угла:

Расположить чертежный треугольник так, чтобы вершина его прямого угла совпадала с точкой О, а одна из сторон пошла по лучу ОА;

Провести вдоль второй стороны треугольника луч ОВ.

В результате получим прямой угол АОВ.

Измерение углов. Транспортир

Проводится «знакомство» с новым инструментом, предназначенным для измерения углов.

Шкала транспортира располагается на полуокружности. Центр этой полуокружности отмечен на транспортире черточкой.

Штрихи транспортира делят полуокружность на 180 долей.

Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 1/180 доле развернутого угла. Такие углы называют градусами.

Вводится понятие градуса и его обозначение. Дети уже знаю, что прямой угол равен половине развернутого, на основе этого определения вводится градусная мера для прямого угла.

Также вводятся градусные меры для острого и тупого углов: если угол меньше 90 градусов, то его называют острым углом, а если больше, то - тупым.

Математика 6 класс

Глава 2. Рациональные числа

§9. Координаты на плоскости

Перпендикулярные прямые

Сразу дается определение перпендикулярных прямых: две прямые, образующие при пересечении прямые углы, называют перпендикулярными (с понятие прямых углов учащиеся знакомы по материалу 5 класса).

Вводится стандартное обозначение для перпендикулярных прямых и алгоритм построение перпендикулярных прямых с помощью чертежного треугольника и транспортира (с этими инструментами учащиеся знакомы на основе материала 5 класса).

Параллельные прямые

Сообщается, что для прямых существует два варианта взаимного расположения: они либо пересекаются, либо не пересекается. Рассматривается случай, когда прямые не пересекаются, такие прямые называются параллельными.

Вводится стандартный символ для обозначения параллельных прямых.

С помощью рисунков поясняется, что отрезки (лучи), лежащие на параллельных прямых, называют параллельными отрезками (лучами).

Далее рассматриваются признак параллельных прямых: если две прямые в плоскости перпендикулярны третьей, то они параллельны. Данный факт поясняется на примере прямоугольника.

С помощью рисунка дается пояснение как с помощью треугольника и линейки можно построить прямую, параллельную данной.

Далее, без каких либо пояснений, сообщается аксиома: через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.

И.И. Зубарева, А.Г. Мордкович, Математика 5 класс

Глава 1. Натуральные числа

§3. Язык геометрических рисунков

Математический язык – это не только язык чисел, букв и символов. Это еще и язык рисунков и чертежей. При изображении геометрических фигур соблюдаются некоторые правила.

На основе рисунка вводятся точки, прямые и отрезки и их обозначения.

§4. Прямая. Отрезок. Луч

Выполните задания и ответьте на вопросы:

Отметьте две точки – А и В. Проведите отрезок АВ.

Сколько существует отрезков, соединяющих точки А и В?

Отметьте две точки – С и Д. Проведите через них прямую. Сколько прямых можно провести так, чтобы они проходили через обе эти точки?

Начертите две пересекающиеся прямые. Обозначьте точку их пересечения буквой А.

Могут ли эти прямые иметь еще и другие точки пересечения?

Сколько общих точек могут иметь две пересекающиеся прямые?

Выводы:

Две точки могут быть концами единственного отрезка;

Через две точки можно провести единственную прямую;

Две прямые могут пересекаться только в одной точке.

Понятие луча вводится по рисунку.

§5. Сравнение отрезков. Длина отрезка

На основе устного упражнения учащиеся могут сделать вывод, что отрезки равны, если при наложении их можно совместить; отрезки равны, если они имеют одинаковую длину.

Понятие длины отрезка учащимся предлагается сформулировать самостоятельно.

§6. Ломаная

На основе рисунка сообщается какую линию называют ломаной. Вводятся ее элементы (вершины, звенья).

Вывод об обозначении ломаных учащимся предлагается сделать самостоятельно.

§8. Координатный луч

Рассматривается задача: шляпа, которую ветер сорвал со старухи Шапокляк, упала в десяти метрах от нее и покатилась со скоростью 3 м/с. С какой скоростью должна бежать Крыска Лариска, чтобы догнать шляпу через 10 с?

Приводится два способа: с помощью рисунка и без. И объясняется преимущество первого способа.

Затем, с помощью последовательно добавления элементов на рисунок вводится понятие координатного луча и координаты точки.

§11. Прямоугольник

Так как с этой фигурой учащиеся знакомы с начальной школы, то предлагается по рисунку ответить на вопросы:

Почему прямоугольник получил такое название

Как "зовут" этот прямоугольник?

Что обозначено буквами а и в?

Что такое периметр прямоугольника, как его найти?

Запишите выражения для периметра прямоугольника

Что такое диагональ прямоугольника?

Как найти площадь прямоугольника

Запишите выражение для площади прямоугольника

Глава 2. Обыкновенные дроби

§23. Окружность и круг

Проводится аналогичная работа, как и с прямоугольником.

Глава 3 Геометрические фигуры

§27. Определение угла. Развернутый угол

На основе рисунка вводится понятие дополнительного и противоположного лучей. Предлагается ученикам самостоятельно сформулировать определение угла, а затем, вводится определение: угол – это фигура, образованная двумя лучами, имеющими общее начало.

Далее вводится определение развернутого угла: развернутый угол – это угол, образованный дополнительными лучами.

§28. Сравнение углов наложением

Ученикам уже известно, что равные фигуры можно совместить так, что они совпадут. На основе рисунка показывается, что этот способ работает и для углов.

§29. Измерение углов

Ставится проблема: длины отрезков можно измерить с помощью линейки, а для углов такой способ не подойдет, значит, нам не хватает каких-то знаний, умений.

Вводится новый измерительный прибор (транспортир). Вводится понятие градуса и градусной меры угла. После чего вводятся виды углов.

§30. Биссектриса угла

Сообщается, что равные углы на геометрических чертежах принято отмечать равным количеством дуг.

Вырежем из бумаги угол и перегнем так, чтобы его стороны совместились. Проведем по линии сгиба луч. Этот луч называется биссектрисой угла. Сравните углы, на которые биссектриса разделила наш угол. Ответ обоснуйте.

Далее ученикам на основе изображения биссектрисы угла предлагается сформулировать определение.

Сравните определение с таким определением: биссектриса угла – это луч с началом в вершине угла, делящий угол на два равных угла.

§31. Треугольник

Сначала ученикам с помощью угольника предлагается построить различные треугольники. Затем вводятся виды треугольников.

§32. Площадь треугольника

Как найти площадь прямоугольника ученикам уже известно. На основе различных конфигураций прямоугольника учащимся предлагается вычислить площади.

Вводится понятие высоты треугольника. И с его помощью учащимся предлагается самостоятельно вывести формулу площади прямоугольника.

§33. Свойство углов треугольника

На основе практической деятельности (работы с прямоугольником), заполнение таблиц, учащие могут сделать вывод, что сумма углов треугольника равна 180 градусам.

§34. Расстояние между двумя точками. Масштаб

Учащиеся уже знают, что расстояние между двумя точками измеряется по соединяющей их прямой, что еще раз разбирается на примере: Настя живет в 7 минутах ходьбы от школы, а Костя идет от дома до школы 5 минут. Можно ли утверждать, что Костя живет ближе к школе, чем Настя? Могут ли Костя и Настя жить в одном доме? Может ли Костя жить дальше от школы, чем Настя?

§35. Расстояние от точки до прямой. Перпендикулярные прямые

Маша и Саша собирали грибы в лесу. После того как корзинки наполнились, ребята решили отправиться домой. Для этого им надо было выйти на шоссе, так как с тяжелой корзинкой идти по лесу довольно трудно. Но тут у них возник спор: – в какую сторону идти, чтобы быстрей выйти из леса.

Подумайте, как выглядит кратчайший маршрут, по которому надо было двигаться, чтобы добраться от точки О до шоссе, и изобразите его.

Под каким углом к краю шоссе проходит отрезок, который вы изобразили? Какой чертежный инструмент удобно было использовать для проведения этого отрезка?

Затем вводятся определения перпендикуляра, расстояния и взаимно перпендикулярных прямых.

§36. Серединный перпендикуляр

На основе изображения, на котором отмечены равные элементы, учащимся предлагается самостоятельно дать определение серединного перпендикуляра.

После все рассуждений вводится полное определение и свойство точек серединного перпендикуляра.

§37. Свойство биссектрисы угла

Учащимся с помощью рисунка предлагается ответить на вопросы, после которых они смогут сформулировать свойство биссектрисы.

Глава 5. Геометрические тела

§50. Прямоугольный параллелепипед

Даны две группы рисунков, которые учащимся предлагается классифицировать самостоятельно, а затем проверить себя:

Изображены тела, поверхность которых составлена из плоских фигур – многоугольников. Эти многоугольники называются гранями, а сами тела – многогранниками.

Тела ограничены не только плоскими поверхностями. Это круглые тела: цилиндр, шар и конус.

Далее аналогичная работа проводится другими группами рисунков:

Предметы имеют форму различных многогранников

Предметы имеют форму прямоугольного параллелепипеда.

Затем, вводятся основные элементы параллелепипеда.

§51. Развертка прямоугольного параллелепипеда

Рассматривается задача: на поверхности прозрачного куба находится паук, который пристально смотрит сквозь него на сидящую на другой грани куба муху. Всем понятно естественное для паука желание поймать муху, однако для этого ему нужно как можно скорее до нее добраться, а то ведь муха может и улететь. Другими словами, пауку необходимо двигаться к ней по кратчайшему маршруту. Изобразите простым карандашом путь, которым, по вашему мнению, должен двигаться паук. Подумайте, как проверить, является ли в действительности предложенный вами маршрут самым коротким.

§52. Объем прямоугольного параллелепипеда

Прямоугольный параллелепипед с измерениями 5 см, 6 см и 4 см, изготовленный из деревянного бруска, покрасили зеленой краской, а затем распилили на одинаковые кубики с ребром 1 см. Сколько среди этих кубиков окажется таких, у которых:

Окрашено 3 грани?

Окрашено только 2 грани?

Окрашена только 1 грань?

Не окрашено ни одной грани?

Чтобы ответить на последний вопрос, можно было найти число всех кубиков, а затем вычесть из него число кубиков, у которых окрашена хотя бы одна грань, т.е. сумму чисел, найденных в первых трех заданиях.

Рассматривается сводная таблица для длины, площади и объема. Затем вводится формула для вычисления объема.

Замечание: главная особенность рассмотренного учебника состоит в том, что учащиеся самостоятельно "добывают" все необходимые знания с помощью устных и практических заданий. Затем только сверяются с данными в учебнике.

3. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин «Арифметика: 5 класс», «Арифметика: 6 класс», Арифметика 5 класс

Глава 2. Измерение величин

Прямая. Луч. Отрезок

В данном разделе порядок рассмотренных понятий построен от самого сложного (понятие плоскости) к самому простому (отрезок).

Понятие плоскости вводится на интуитивном, бытовом уровне: поверхность стола или поверхность воды на пруду (в безветренную погоду) может служить примером части плоскости.

Если согнуть лист бумаги, то линия сгиба будет частью прямой лини. Коротко – частью прямой.

Рассматривается несколько вариантов для обозначения прямой.

Сообщается, что через любые две точки можно провести только одну прямую, значит две различные прямые могут пересекаться только в одной точке. А что если прямые не пересекутся, как бы их не продолжали? Такие прямые называются параллельными.

Вводится значок для обозначения параллельных прямых. По рисунку объясняется как с помощью линейки и угольника провести параллельные прямые.

Если на прямой отметить точку, то она разделит прямую на две части (в отличие от учебника Н.Я. Виленкина понятия дополнительного луча не вводится), каждая из которых называется лучом. Сообщается об обозначениях луча.

Часть прямой, ограниченная точками называется отрезком.

Измерение отрезков

Понятия единицы измерения и единичного отрезка вводятся с помощью задачи: ученик 5 класса и его сестра - десятиклассница решили подсчитать число шагов от школы до дома. Получилось, что одно и тоже расстояние равно 300 шагам брата и 250 шагам сестры. Очевидно, что разные результаты получились из-за того, что сестра измеряла расстояние большими шагами, чем брат.

В таких случаях говорят, что были использованы различные единицы измерения длины. Отрезок, длина которого принята за единицу измерения, называют единичным отрезком.

На примере объясняется измерение с недостатком и с избытком.

Длину отрезка называют расстоянием между его концами.

Метрические единицы длины

Окружность и круг. Сфера и шар

Окружность - замкнутая линия, которую описывает ножка циркуля с карандашом. Центр окружности-т точка, в которую установили острие циркуля.

Радиус, хорда и диаметр определяются как отрезки, соединяющие различные точки окружности.

Круг - часть плоскости, находящаяся внутри окружности.

Сфера - все точки пространства, удаленные от данной точки на одно и тоже расстояние.

Шар - часть пространства, находящаяся внутри сферы.

Традиционная последовательность материала и его изложение.

Углы. Измерение углов

Понятие угла и его составляющих (вершина, стороны) вводится по рисунку на конкретном примере. Угол- часть плоскости, ограниченная лучами, выходящими из одной точки.

Понятие равных углов так же вводится по рисунку. Два угла называются равными, если они совмещаются наложением.

Далее рассматриваются все виды углов: развернутый, прямой, острый тупой.

Ели на прямой отметить точку, то образуется два луча, выходящих из одной точки. Эти точки тоже делят плоскость на две части, каждую из которых называют развернутым углом.

Прямой угол вводится на основе развернутого при помощи практических представлений: перегнем лист бумаги так, чтобы лучи совпали, и расправим лист. Тогда линия сгиба, разделит каждый из развернутых углов на два равных угла, каждый из которых называют прямым углом.

Сообщается, что углы измеряют и строят с помощью транспортира.

Острый и тупой угол вводятся традиционно, как угол, меньший и больший 90, соответственно.

Прямые, пересекающиеся под прямым углом, называют перпендикулярными. Вводится традиционный значок для обозначения перпендикулярных прямых.

Треугольник. Прямоугольник

Ученикам уже знакомы все виды углов, на основе этого вводятся виды треугольников. Кроме этого, вводится равнобедренный и равносторонний треугольники.

Все понятия вводятся традиционно и последовательно.

Прямоугольник

Вначале вводится стандартное определение прямоугольника: прямоугольник - четырехугольник, у которого все углы прямые. Определяются вершины и стороны прямоугольника.

Так как определение параллельных прямых было уже введено ранее, то сообщается, что прямоугольника противоположные стороны равны и параллельны.

Понятие квадрата вводится на основе прямоугольника, как частный случай: прямоугольник, у которого все стороны равны, называют квадратом.

Площадь прямоугольника. Единицы площади

Вводится понятие единичного квадрата и сообщается, что его площадь принимают за единицу измерения площадей, вводятся основные единицы измерения площадей.

Формула площади прямоугольника вводится по рисунку на конкретном примере.

Сообщается формула площади квадрата и дается объяснение названия второй степени числа, как квадрата числа.

Вводятся единицы измерения площадей земельных участков

Прямоугольный параллелепипед

Понятие прямоугольного параллелепипеда вводится на конкретных примерах: классная комната, коробка конфет, кирпич.

По рисунку вводятся все основные составляющие параллелепипеда.

Понятие куба вводится, как частный случай прямоугольного параллелепипеда, у которого все ребра равны.

На рисунке изображена коробка, имеющая форму прямоугольного параллелепипеда, если ее разрезать по вертикальным ребрам и развернуть, то получится развертка прямоугольно параллелепипеда, тоже изображена на рисунке.

Объем прямоугольного параллелепипеда. Единицы объема

Все понятия, связанные с данным пунктам вводятся аналогично и в той же последовательности, как и площадь прямоугольника.

Арифметика 6 класс

Глава 5

Длина отрезка

Ранее уже вводилось понятие длины отрезка, но только в том случае, когда его длина выражалась рациональным числом. В этом пункте дано понятие длины произвольного отрезка, которая может выражаться как рациональным, так и иррациональным числом.

Итог: произвольный отрезок АВ имеет длину а – положительное число. Верно и обратное утверждение: если дано положительное число а, то можно указать отрезок АВ, длина которого равна этому числу.

Длина окружности. Площадь круга

Вводится число пи и обосновывается причина использования его приближенного значения, постоянное число, равное отношению длины окружности к длине ее диаметра.

Формула длины окружности получается на основе определения числа пи, а формула площади круга приводится без доказательства.

Далее рассматривается пример на использование полученных формул.

Координатная ось

Ранее вводилось понятие координатной оси. Но там рассматривались только рациональные точки, т.е. точки, имеющие рациональные координаты х, и ось была «дырявая» - без иррациональных точек. Однако координата х произвольной точки координатной оси есть, вообще говоря, действительное число, т.е. оно может быть рациональным или иррациональным. Этот вопрос и был выяснен на основании общего понятия длины отрезка, введенного ранее. Теперь координатная ось перестала быть «дырявой» - каждой ее точке соответствует действительное число (взаимно однозначное соответствие между точками оси х и действительными числами).

Декартова система координат на плоскости

Декартова система координат вводится на основе двух осей координат, расположенных под прямым углом, ось х и ось у (позднее сообщается, что можно обозначить оси и другими буквами), с точкой пересечении О., являющейся начальной точкой для каждой из осей.

Затем вводятся координаты точки на конкретном примере, по рисунку, и координатные четверти.

4. В.Г. Дорофеев, С.Б. Суворова, И.Ф. Шарыгин, Математика 5 класс

Глава 1. Линии и углы

§1. Линии

Разнообразный мир линий

На интуитивном уровне вводится понятие линии: если мы ведем карандашом по поверхности, то рисуем линию. Объясняется происхождение термина линия ( от латинского слова linea – лен, льняная нить, веревка).

Сообщается, что существует множество видов линий и рассматриваются следующие из них: замкнутая и не замкнутая ( на основе того можно линию обвести карандашом или нет); самопересекающаяся линия и линия без самопересечений.

На основе рисунка вводятся такие понятия как внутренняя и внешняя области и граница.

Главные линии: прямая и окружность

Понятие линий и их видов учащимся уже знакомо. На интуитивном уровне и вводится понятие прямой. Рассматриваются ее свойства как линии и возможности ее получения.

Далее, аналогичным способом вводится понятие окружности и круга, и их составляющие элементы.

Части прямой. Ломаная

Учащиеся знакомятся с понятием луча: точка О на прямой АВ делит ее на две части – лучи ОА и ОВ.

Если несколько, не лежащих на одной прямой, точек соединить отрезками, то мы получим ломаную. Вводятся элементы ломаной: вершины, стороны (звенья).

Длина линии

Отрезки можно сравнивать друг с другом. Если отрезки расположены на одном листе бумаги, то это легко сделать с помощью циркуля. Но это не всегда удобно. Другой способ – сравнить длины отрезков. Длину можно найти, если измерить отрезок, а для этого нужны единицы измерения. Вводятся единицы измерения. Сообщается, что для измерения длин отрезков используется линейка.

§2. Углы

Как обозначают и сравнивают углы

Проведем на плоскости два луча АВ и АС с общим началом в точке А. Часть плоскости, ограниченная этими лучами, называется углом.

Углы так же как и отрезки можно сравнивать. Для этого используется наложение одного угла на другой.

Вводится понятие биссектрисы, как луча, который делит угол на два равных угла.

Далее вводятся виды углов в сравнении с прямым, но не используя градусную меру.

Измерение углов

Вводится понятие градуса, и уже через градусную меру рассматриваются виды углов.

Учащиеся знакомятся с новым измерительным прибором- транспортиром.

Глава 3. Многоугольники

§1. Прямоугольники и треугольник

Ломаные и многоугольники

Замкнутая ломаная линия без самопересечений, которой четыре вершины называется четырехугольником. Четырехугольник это один из видов многоугольников.

Вводятся элементы фигуры: вершины, стороны, углы, диагональ.

Прямоугольники

Четырехугольники бывают различных видов, среди них один, уже хорошо знакомый ребятам – прямоугольник. Прямоугольник – это четырех угольник, у которого все углы прямые.

У прямоугольника противоположные стороны равны, а две другие (смежные) стороны могут быть различны.

Если же у прямоугольника все стороны равны, то он называется квадратом. Т.о., всякий квадрат является прямоугольником.

Треугольники и их виды

Самым простым многоугольником является треугольник.

Далее рассматриваются все виды треугольников:

Равнобедренный (равные стороны называются боковыми, а третья сторона - основанием), а треугольник, у которого все стороны равны, называется равносторонним.

Вид треугольника определяется не только числом равных сторон, но и величиной углов: прямоугольный, тупоугольный, остроугольный (виды углов ученикам уже знакомы).

§2. Площади

Площадь прямоугольника

Отрезки и углы дети уже умеют сравнивать, причем двумя способами: геометрическим- наложением и арифметическим – с помощью измерения. Ставится вопрос о сравнении прямоугольников, на который дает ответ понятие площади.

Вводятся единицы измерения площади и определение площади, а далее формулы площади для прямоугольника и квадрата.

Единицы площади

Вводятся новые единицы измерения, предназначенные для измерения площадей земельных участков: ар и гектар.

Глава 5. Многогранники

§1. Геометрические тела

Предметы и их форы

Математики изучают не предметы, а их формы. Вместо предметов они рассматривают геометрические тела: цилиндр, шар, конус и т.д.

Происходит знакомство с элементами многогранников.

Изображение геометрических тел

Параграф носит повествовательный характер. Учеников знакомят с основными правилами изображения геометрических тел.

§2. Параллелепипед и пирамида

Прямоугольный параллелепипед

Многогранники могут иметь самую различную форму. Среди них выделяют прямоугольный параллелепипед. Вводятся все элементы прямоугольного параллелепипеда.

Среди всех параллелепипедов выделяется один, уже хорошо известный ученикам – куб.

Пирамида

Важным и интересным семейством многогранников являются пирамиды. Вводятся элементы пирамиды. И рассматривается простейший вид пирамиды.- треугольная.

Развертки

Изображена фигура и сообщается, что если ее вырезать и сложить, то получится куб. И наоборот, разрезав куб по некоторым ребрам, мы можем развернуть его на плоскости. При этом мы получим развертку куба.

Математика 6 класс

Глава 2. Прямые на плоскости и в пространстве

Пересекающиеся прямые

Напоминаются уже известные свойства прямой: бесконечна, незамкнутая, через две точки можно провести только одну прямую.

На рисунке изображены две пересекающиеся прямые. Они делят плоскость на четыре угла. У этих углов общая вершина – точка пересечения прямых.

Вводится понятие вертикальных углов и объясняется, что они равны, т.к. каждый из этих углов дополняет один и тот же угол до развернутого угла.

Далее вводится понятие перпендикулярных прямых. Если одну пару вертикальных углов составляют острые углы, то другую – тупы. Но может оказаться так, что все четыре угла между собой равны, тогда каждый из них равен 90. В этом случае прямые называют перпендикулярными. Объясняется происхождение термина и вводится стандартный символ для обозначения перпендикулярных прямых.

На основе рисунка сообщается, что перпендикулярные прямые можно построить с помощью угольника или с помощью транспортира.

Параллельные прямые

Случай, когда прямые пересекаются был рассмотрен в предыдущем пункте, а если прямее не пересекаются, для них существует свой термин, они называются параллельными.

Вводится символ для обозначения параллельных прямых и поясняется история его происхождения.

Далее приводится подробный план построения параллельных прямых с помощью угольника и линейки. Но предварительно свойство, характеризующее параллельные прямые и которое позволяет выполнить построение с помощью циркуля и линейки: если провести несколько параллельных прямых и прямую их пересекающую, эта прямая пересечет каждую из этих параллельных прямых под одним и тем же углом.

На основе рисунка вводится свойство параллельных прямых: если прямые перпендикулярны одной и той же прямой, то они параллельны.

На примере куба рассматривается следующий случай взаимного расположения прямых в пространстве. Вводится определение скрещивающихся прямых.

Расстояние

Рассматривается расстояние между точками, от точки до прямой, между параллельными прямыми и от точки до плоскости.

Глава 5. Окружность

Прямая и окружность

На основе серии рисунков вводится взаимное расположение прямой и окружности.

С помощью рисунка сообщается свойство касательной: касательная перпендикулярна радиусу, проведенному в точку касания.

Далее на основе этого свойства приводится подробный прян построения касательной к окружности.

Две окружности на плоскости

Объяснение видов взаимного расположения двух окружностей на плоскости проводится аналогично предыдущему пункту.

Построение треугольника

Сначала приводится подробное построение треугольника со сторонами 3, 4, 5 см с помощью циркуля и линейки.

Далее приводится попытка построения треугольника со сторонами 1, 2, 4 см. Такое построение не возможно осуществляется вывод и сообщается неравенство треугольника.

Круглые тела

Рассматривается цилиндр, шар и конус. Знакомство осуществляется по следующему плану:

Историческая справка (происхождение термина)

Составляющие элементы

Глава 7. Симметрия

Осевая симметрия

Проводится практическая работа. Возьмите лист бумаги. Перегните его по некоторой прямой и проткните иглой. Развернув лист, вы увидите две точки, расположенные по разные стороны от этой прямой. Эти точки симметричные относительно прямой – линии сгиба.

Если через полученные точки провести прямую, то можно убедиться, что она перпендикулярна линии сгиба, а точки находятся от нее на одинаковом расстоянии (важное свойство симметрии).

Затем, рассматривается алгоритм для построения точки, симметричной данной. С помощью этих знаний можно строить фигуру, симметричную данной.

Если фигуры симметричны, то они равны!

Аналогом осевой симметрии в пространстве является симметрия относительно плоскости – зеркальная симметрия.

Ось симметрии фигуры

Говорят, что фигура симметрична относительно некоторой прямой, если при перегибании по этой прямой части фигуры совпадают. Именно эта линия сгиба и называется осью симметрии фигуры.

Построения циркулем и линейкой

Задача: пусть дан отрезок АВ. Требуется построить прямую, ему перпендикулярную и проходящую через его середину.

Выполняется построение, после вводится специальное название – серединный перпендикуляр.

Центральная симметрия

Ведутся аналогичные рассуждения (см. центральную симметрию).

Глава 12. Многоугольники и многогранники

Сумма углов треугольника

Ученикам в классе предлагается начертить по треугольнику. С помощью транспортира измерить все углы и найти их сумму. У всех должно получится 180 градусов. Затем этот же факт объясняется с помощью рассуждений: с помощью прямых, параллельных основанию.

Параллелограмм

Рассматриваются и поясняются свойства параллелограмма. Кроме этого выполняется построение параллелограмма с помощью циркуля и линейки.

Правильные многоугольники

Многоугольник, у которого равны все стороны и все углы, называют правильным.

Рассматриваются некоторые свойства правильных многоугольников. Например, все вершины правильного многоугольника лежат на одной окружности. Этот факт можно использовать для построения.

Далее рассматриваются правильные многогранники.

Площади

Две фигуры, имеющие одинаковые площади, называют равновеликими. Затем, вычисляются площади данных квадрата и прямоугольника.

Если фигуры составлены из одинаковых частей, или, как говорят, равносоставлены, то они имеют равные площади.

Призма

В этом пункте учащиеся знакомятся еще с одним семейством многогранников – призмами. Вводятся все составляющие элементы на основе треугольной и прямоугольной призм.

Выводы

Геометрическая линия наиболее полно представлена в УМК Г.В. Дорофеева, И.Ф. Шарыгина. Подробно рассматриваются многие темы. Особенно такие, как: «Линии», «Треугольник», «Симметрия». Изучение происходит не только на ознакомительном уровне. Изучаются свойства фигур.

Многие задания имеют практическую направленность, что еще раз подтверждает эффективность курса. Авторы показывают учащимся возможности применения геометрических знаний в реальной жизни.

К каждой теме подобрано достаточно много заданий по изучаемому материалу. Предлагаются задания двух уровней сложности. Задания второго уровня чаще носят исследовательский характер.

Предлагаются задания в рабочих тетрадях. Это задания такого характера как: построить, начертить, измерить, вычислить. Некоторые задание предлагаются для развития глазомера. В дидактических материалах есть обучающие и проверочные задания по всем темам курса. Авторы отдельное внимание уделяют интеллектуальному развитию ребенка. На это направлены знания, представленные в дополнительных разделах. Авторы, познавательный материал предлагают для дополнительного изучения, тем самым, подталкивая учащегося к самостоятельной деятельности.

геометрия школьник учебник пропедевтика

Глава 2. Методическая разработка материалов для проведения уроков по геометрии в 5-6 классах

Наши первые учителя – наши руки, ноги, глаза. Заменить все это книгами, это значит научить нас не рассуждать, а пользоваться разумом других людей; это значит научить нас многое принимать на веру и никогда ничего не знать. Руссо

§1. Система упражнений пропедевтики и развития интереса к математике

Программа по математике указывает на важность формирования у учащихся навыков логического мышления, развития пространственных представлений, воображения и творческого мышления.

В решении этих задач особое место принадлежит геометрии, так как ее изучение неразрывно связано с осуществлением таких операций, как абстрагирование, конкретизация и применение полученных знаний на практике. Школьному курсу геометрии традиционно отводится важная роль в развитии учащихся - развитие пространственных представлений.

Из всех трех видов мышления целенаправленное внимание в курсе математики уделяется словесно-логическому, понятийному мышлению. Именно поэтому в более комфортных условиях находятся учащиеся с научным складом мышления. Это и является причиной победы некоторых учащихся на математических олимпиадах, с одной стороны, и неуспеваемости учащихся с художественным и практическим складом мышления, с другой. Хорошо, если учащиеся художественного типа мышления реализуют себя в творчестве, посещая художественные и музыкальные школы, кружки, но на уроках математики такие учащиеся испытывают большие затруднения. В основе их неуспеваемости лежат психологические проблемы.

В настоящее время в качестве одного из главных критериев математического развития личности многие психологи рассматривают уровень развития пространственного мышления, который характеризуется умением оперировать пространственным образом. Математика является одним из тех предметов, при изучении которого важное место отводится зрительному каналу поступления информации.

1.1 Упражнения, направленные на развитие графической культуры

Характеристика заданий:

- задания на развитие тонкой моторики руки;

- задания на наблюдательность, внимательность и аккуратность;

- навыки работы с циркулем и линейкой.

Учимся чертить правильно.

1. Начертите по линейке и линии тетради несколько линий так, чтобы они не пересекались.

2.Возьмите угольник и обрисуйте его. Рядом повторите то же самое, не обрисовывая, а используя только одну сторону линейки.

3. Возьмите циркуль и начертите окружность

а) любого радиуса.

б) радиуса 2 см.

4. Дорисуйте окружность

5. Начертите кусок орнамента в тетради и продлите его по всей длине страницы.

6. Придумайте соседу по парте орнамент и обменяйтесь рисунками.

7. Какая из фигур, приведенных на рисунке, лишняя? Почему?

1.2 Упражнения на развитие наглядно-образное мышление

Характеристика заданий:

-умение находить заданные простые геометрические фигуры разной величины и в разных положениях;

- подготовка к правильному обозначению геометрических фигур;

- развитие мысленных образов;

Фигуры, вычерчиваемые одним росчерком

1. Попробуйте начертить каждую из предложенных фигур, не отрывая карандаш от бумаги и не проводя по одной линии дважды.

2. Фигуру, показанную на рисунке, нужно обвести, не отрывая карандаш от бумаги и не обводя одно и то же ребро дважды. Если допустить, что линии могут пересекаться, то задача решается просто. Решение весьма усложняется, если пересечение линий запрещено:

3. Фигуру, изображенную на рисунке, обвести, не отрывая карандаш от бумаги и не обводя одно и тоже ребро дважды. Пересечение линий возможно:

4. Говорят, что Магомет описывал одним росчерком состоящий из двух рогов Луны знак, представленный на рисунке. Попробуйте это сделать

5. На озере семь островов, которые соединены между собой мостами так, как показано на рисунке. На какой остров должен доставить катер путешественников, чтобы они могли пройти по каждому мосту и только один раз? С какого острова катер должен снять этих людей?

6. Возьмите лист бумаги и нанесите на него девять точек так. чтобы они расположились в форме квадрата, как показано на рисунке. Перечеркните теперь все точки четырьмя прямыми линиями не отрывая карандаш от бумаги:

7. Сколько различных квадратов с вершинами в данных точках можно начертить:

8. Не отрывая карандаша от бумаги и не проводя никакую линию дважды, нарисуй следующие фигуры

9. Каждую из фигур на рисунке нарисуй, не отрывая карандаша от бумаги и не проводя одну линию дважды. Для каждой фигуры найди все точки, с которых можно начинать рисунок

10. Попробуй нарисовать такую фигуру, как на рисунке, не отрывая карандаша от бумаги и не проводя им по одному и тому же месту дважды.

11. Проложи дорожки

а) От каждого из двух домиков положи (нарисуй) дорожки к гаражу, колодцу и к станции так, чтобы они не пересекались.

б) Попробуй сделать то же самое для трех домиков (третий домик находится правее второго).

12. Положите 12 спичек так, чтобы получилось 5 квадратов. Переложите 3 спички так, чтобы получилось 3 равных квадрата.

В геометрии очень важно уметь смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать (задания №13-18 перерисовать в тетрадь и записать ответ).

13. На отрезке АВ взяты точки К и М . Сколько получили разных отрезков? На первый взгляд кажется, что их три: АК, КМ и MB. Но если внимательно рассмотреть этот рисунок 1, то можно найти еще три отрезка: AM, KB и АВ. Сколько отрезков изображено на рисунке 2?

1. 2.

14. Прямоугольник ABCD разделен на части прямыми КМ и ОР. Сколько получилось разных прямоугольников? Четыре? Нет! Найдите на этом рисунке девять прямоугольников

15. Сколько четырехугольников на рисунке?

16. Сколько треугольников на рисунке?

17. Найдите 27 треугольников в фигуре на рисунке

18. Найдите звезду на рисунке

1.3 Система упражнений на развитие пространственных представлений

Характеристика заданий:

- задания на развитие пространственного мышления;

- задания на развитие умения увидеть по чертежу на плоскости объемное тело;

- первичные навыки развертывания поверхности геометрических тел;

1.Указать число кубиков, из которых состоит фигура:

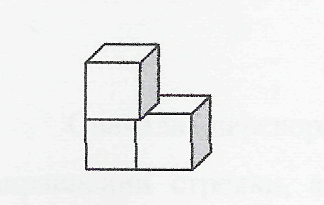
2. Сколько граней у неотточенного шестигранного карандаша?

Куб находится на рабочем столе. Сколько граней можно покрасить не переворачивая?

3. Сколько разных красок понадобится, если противоположные грани куба раскрасить одним цветом, а соседние разными?

4. Заштрихуйте грань, противоположную данной;

5. Достройте рисунок так, чтобы получился куб:

6. Сначала переворачивается без скольжения 2 раза на 90° фигура слева в направлении стрелки, а затем переворачивается один раз на 90° фигура справа в направлении стрелки:

7. Найдите получившееся объединение фигур:

8. Определите количество квадратов, которое содержат фигуры:

9. Сколько одинаковых квадратов надо взять, чтобы из них можно было сложить в два раза больший квадрат ?

Сколько одинаковых кубиков надо взять, чтобы получился в три раза больший куб?

10. Обозначим нижнюю грань куба буквой Н, верхнюю буквой В, боковые Б. Расставьте на развёртках куба буквы в соответствии с уже намеченными:

11. Какие буквы совместятся с буквой А при склеивании развёртки изображённой на рисунке:

12. Какие из заготовок на рисунке не могут быть развёртками куба и почему?

13. Мысленно сверните куб из развёрток, представленных на рисунках, и определите, какая грань является верхней, если нижняя грань закрашена:

14. Четыре грани кубика окрашены не засыхающей краской так, как показано на рисунке. Какой след оставит кубик на листе бумаге, если его переворачивать без скольжения вправо из положения слева три раза на 90°?

§2. Задачи для кружковой работы

2.1 Задачи по геометрии, решаемые методами оригами

Слово "оригами" происходит от двух японских слов: "ори" – сложенный, "ками" – бумага, и может быть переведено как "сложенная бумага". Складывание фигурок из бумаги имеет многовековую историю и своими корнями тесно связано с культурой Востока.

Неопределяемыми понятиями геометрии являются: точка, прямая и плоскость. В традиционном школьном курсе геометрии решаются задачи на построение при помощи циркуля и линейки. В решении таких задач с помощью линейки можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; прямую, проходящую через две данные точки. При помощи циркуля можно описать окружность данного радиуса и отложить отрезок на данной прямой от данной точки.

Возможности перегибания листа бумаги включают в себя не только "геометрию линейки", но и "геометрию циркуля", что обеспечивает возможность решения большого разнообразия серьезных, а порой и забавных задач. Как правило, решение задач методами перегибаний (оригами) проще и нагляднее. Некоторые задачи, решаемые методами оригами, при помощи циркуля и линейки просто не имеют решения!

Наглядность и относительная простота освоения оригами могут помочь и при изучении геометрии. Такой подход оживляет и заметно облегчает освоение целого ряда абстрактных, и потому сложных для освоения многим учащимся геометрических понятий, делает их изучение более ясным и доступным, убеждает в правильности классических утверждений, теорем и побуждает к дальнейшим исследованиям. Ученики учатся понимать то, о чем говорят сами, и то, что говорят другие, учатся мыслить.

Условные знаки и приемы складывания

Деление отрезка на равные части

Из произвольного листа бумаги при помощи сгибов можно получить квадрат. Если на этом листе бумаги дан отрезок, который требуется разделить, то всегда сначала можно построить квадрат со стороной равной этому отрезку, а затем разделить сторону квадрата.

В задачах этого раздела происходит деление на равные части стороны квадрата (прямоугольника) при этом подразумевается, что длина заданного отрезка равна стороне квадрата.

Методом перегибания точно разделить сторону квадрата на три равные части.

Разделить сторону квадрата на 11 равных частей

Разделить прямоугольник ABCD на 9 равных прямоугольников, не используя измерительных приборов, как на рисунках 1 и 2.

Вариант 2

Прямой угол

Методом складывания разделить один из углов квадрата на три равных угла

Геометрия листа произвольной формы

Из произвольного листа бумаги получите с помощью сгибов квадрат

Из произвольного листа бумаги получить равносторонний треугольник

На листе бумаги проведены прямая, а также даны центр окружности и некоторая точка на ней (сама окружность не нарисована). Как с помощью перегибаний найти точки пересечения воображаемой окружности с проведенной прямой?

О- центр окружности

А- лежит на окружности

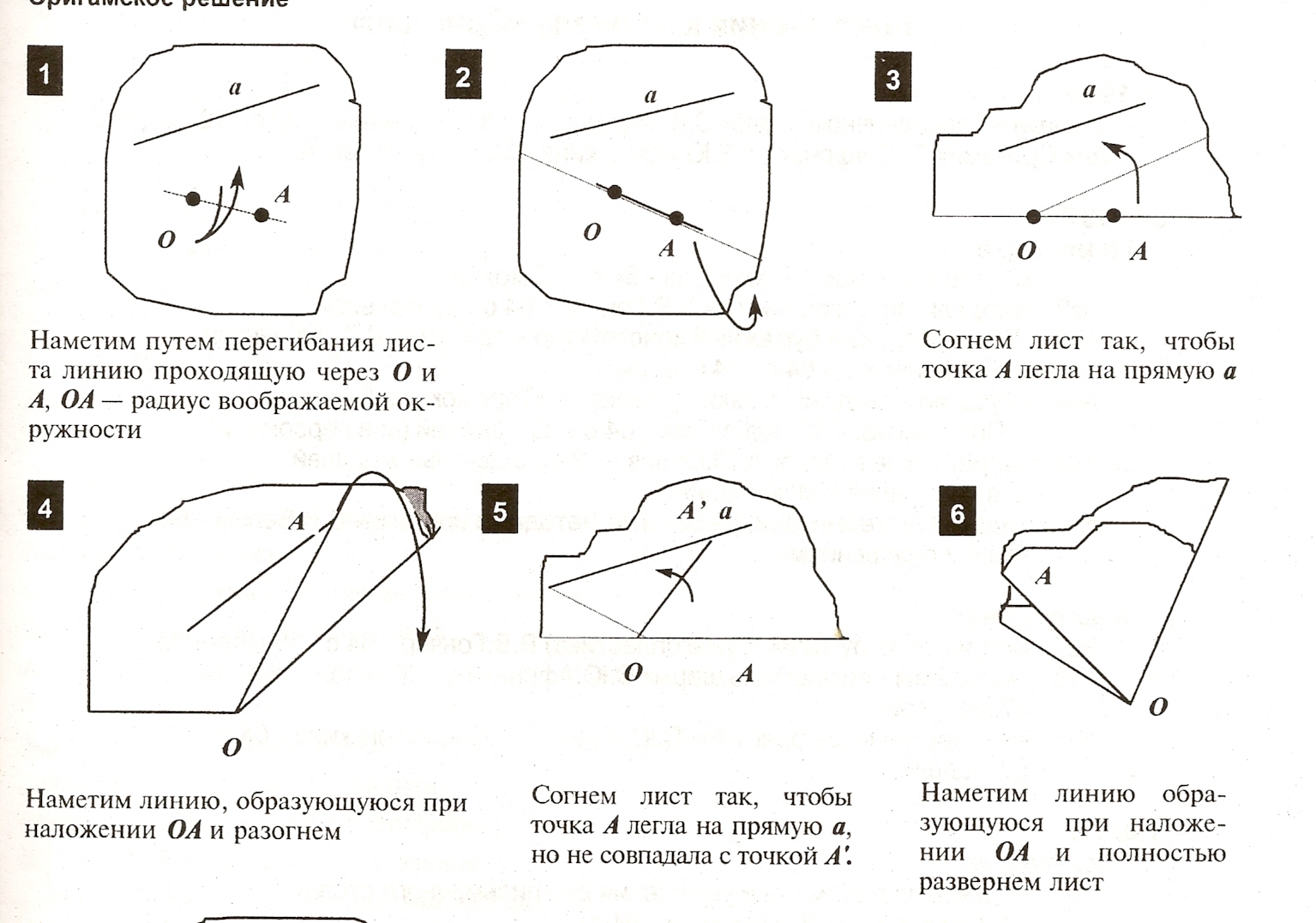
2.2 Задачи на геоплане

Что такое геоплан?

Геоплан представляет собой плоскую поверхность с закрепленными на ней тонкими стержнями, располагающимися в форме квадратной сетки или каким-либо другим способом (в виде окружности, многоугольника). Построение фигур осуществляется на геоплане при помощи эластичных шнуров (резиновых нитей или колец), которые фиксируются между стержнями.

Главное достоинство геоплана состоит в возможности быстрого построения геометрических фигур. При этом не требуются ни бумага с карандашом, ни доска с мелом и не нужно ничего стирать: любую конфигурацию можно быстро изменить или построить заново.

Как строить фигуры на геоплане

Строить (изображать) на геоплане можно различные геометрические фигуры: отрезки, углы, ломаные, треугольники, квадраты, ромбы, прямоугольники, параллелограммы, трапеции, всевозможные многоугольники, а также различные конфигурации, образованные линиями. Можно иллюстрировать или устанавливать свойства геометрический фигур: равенство сторон, углов, площадей, периметров.

Даже незначительные перемещения эластичных нитей по полю геоплана способны изменить (преобразовать) начальную ситуацию: упростить или усложнить ее, рассмотреть частный или более общий случай.

Для чего решать задачи на геоплане

Решение задач на геоплане развивает геометрическую зоркость, умение видеть (распознавать) на чертеже геометрические фигуры или их отдельные элементы, устанавливать их свойства. Работа с геопланом учит наблюдать, анализировать чертеж, проводить опыт, пользоваться здравым смыслом, прикидкой. Все эти умения необходимы каждому человеку. А, кроме того, решать задачи на геоплане это увлекательно!

Как изготовить геоплан самому

Геоплан можно смастерить самому в школьной мастерской или дома. Для этого необходимо подобрать деревянную доску, фанерку или картонку подходящего размера, нанести на нее квадратную сетку и вбить тоненькие гвоздики без шляпок в ее узлах. Желательно, чтобы расстояние между двумя соседними гвоздиками по вертикали или горизонтали было равно 1 дм. В качестве эластичных шнуров можно использовать обычные резиновые жгутики с маленькими петельками или шайбочками на концах, а также тоненькие резиночки со связанными концами (кольца).

При решении задач можно воспользоваться и бумажным прототипом геоплана – обычной ученической тетрадью с наколотой шилом или набитой тонким гвоздиком квадратной сеткой на всех ее листах.

Отрезки

Два отрезка, длиной по 5 дм каждый, постройте на геоплане таким образом, чтобы они пересекались в точке, делящей их на четыре отрезка длиной 1 дм, 2 дм, 3 дм, 4дм.

На четвертой части геоплана (5х5 дм) разместите десять отрезов длиной 1 дм, 1 дм, 1 дм, 2 дм, 2 дм, 3 дм, 3 дм, 4 дм, 4 дм и 5 дм таким образом, чтобы никакие два из них не имели общей точки.

Постройте три отрезка с общим концом так, чтобы длина первого из них равнялась 2 дм, второго – 3 дм, а длина третьего была бы больше длины первого, но меньше длины второго. Найдите два решения.

Выберите точку и постройте на вашем геоплане три самых маленьких по длине попарно неравных отрезка с концами в этой точке.

Постройте самый короткий и самый длинный отрезки геоплана так, чтобы их общая точка делила один из них на две равные по длине части.

Постройте отрезок, являющийся диагональю прямоугольника со сторонами 4 дм и 6 дм. Постройте еще два отрезка, пересекающие первый и разбивающие его на три равные по длине части.

Ломаные

Постройте ломаную из пяти звеньев, длиной по 3 дм каждое, так, чтобы расстояние между ее концами равнялось 9 дм; было больше 9 дм; было меньше 9 дм.

Из отрезков длиной, равной длине диагонали прямоугольника со сторонами 2 дм и 1 дм, постройте ломаную, состоящую из трех, пяти, семи звеньев, так, чтобы расстояние между ее концами равнялось 1 дм.

Постройте ломаную, состоящую из шести звеньев, таким образом, чтобы ее длина была больше 18 дм, но меньше 19 дм.

Постройте ломаную в виде буквы русского алфавита, состоящую из двух, трех, четырех звеньев.

Постройте ломаную в виде буквы М русского алфавита Переместите одну из ее вершин таким образом, чтобы образовалась ломаная в виде другой буквы русского алфавита.

Турист в течении дня несколько раз изменял направление своего движения. До обеда он прошел 4 км на север, затем повернул на восток и двигался 2 км, а далее прошел некоторое расстояние в направлении на северо-восток, больше двух км, но меньше 3 км, и, наконец, км на восток. После обеда он начал двигаться на юг и прошел км, затем повернул на запад и двигался 3 км, а далее он прошел в направлении на юго-запад такое же расстояние, какое он прошел в направлении на северо-восток до обеда. В результате турист оказался в пункте, отстоящем от начальной точки движения на расстоянии 2 км в направлении на восток. Выберите подходящий масштаб и постройте ломаную, изображающую маршрут туриста.

*В данных задачах речь идет лишь о незамкнутой простой ломаной, т.е. о такой, у которой конец последнего звена не совпадает с началом первого и несоседние звенья не пересекаются.

Углы

Постройте углы величиной 45, 90, 135, 180 градусов таким образом, чтобы все они имели общую вершину и каждый меньший по величине угол содержался внутри большего.

Постройте смежные углы таким образом, чтобы величина одного из них была бы больше 135 градусов.

Изобразите на геоплане несколько слов, состоящих из букв русского алфавита, в написании которых встречаются лишь прямые углы.

Постройте острый угол, величина которого равна 45 градусов. Выберите внутри его точку и постройте еще один угол таким образом, чтобы стороны обоих углов были соответственно перпендикулярными.

Постройте два угла, стороны которых попарно параллельны, таким образом, чтобы при пересечении этих сторон образовался прямоугольник, имеющий площадь 6 дм².

Постройте два угла, стороны которых попарно перпендикулярны, таким образом, чтобы при пересечении этих сторон образовался отрезок, имеющий длину 2 дм.

Треугольники

Постройте треугольник, у которого длина первой стороны больше 2 дм, но меньше 3 дм, длина второй стороны больше 3 дм, но меньше 4 дм, длина третьей стороны больше 4 дм, но меньше 5 дм.

Четырех угольники

Постройте четырехугольник, все стороны которого имеют длину, равную диагонали прямоугольника размером 3х1 дм. Найдите несколько решений.

Постройте четырехугольник, все стороны которого имеют различные длины от 4 до 5 дм.

Постройте квадрат со стороной 6 дм. Постройте все различные квадраты, вершины которых лежат на сторонах исходного квадрата.

Постройте прямоугольник, площадь которого равна 12 дм², четырьмя различными способами.

Постройте шесть квадратов, площади которых равны 4 дм², 16 дм², 64 дм², таким образом, чтобы каждый меньший по площади квадрат содержался внутри каждого большего.

Постройте два прямоугольника, имеющих: а)равные периметры и равные площади; б)равные площади и разные периметры.

2.3 Геометрия на клетчатой бумаге

Рекомендации по проведению уроков

Начинать обучать школьников желательно с пятого класса.

Преподавание должно вестись непринужденно, почти в импровизационном стиле. Эта видимая легкость на самом деле требует от учителя большой и серьезной подготовки.

Занятия лучше проводить в нестандартной форме.

Необходимо использовать на уроках как можно больше наглядного материала: различных карточек, картинок, наборов фигур, иллюстраций к решению задач, схем.

При разборе темы нужно стараться добиваться понимания, а не зазубривания.

Урок №1

Цель: развивать комбинаторные навыки (рассмотреть различные способы построения линии разреза фигур, правила, позволяющие при построении этой линии не терять решения), развивать представления о симметрии.

Задачи 1-4 решаем на уроке, задача 5 – на дом.

Квадрат содержит 16 клеток. Разделите квадрат не две равные части так, чтобы линия разреза шла по сторонам клеток. (Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе). Сколько всего разрезаний имеет задача?

Указание. Найти несколько решений этой задачи не так уж сложно. На рисунке некоторые из них показаны, причем решения б) и в) одинаковы, так полученные в них фигур можно совместить наложением (если повернуть квадрат в) на 90 градусов).

Но найти все решения и ни одно решение не потерять уже труднее. Заметим, что ломаная, делящая квадрат на две равные части симметрична относительно центра квадрата. Это наблюдение позволяет шаг за шагом рисовать ломаную с двух концов. Например, если начало ломаной в точке А, то конец ее будет в точке В. Убедитесь, что для данной задачи начало и конец ломаной можно нарисовать двумя способами.

При построении ломаной, чтобы не потерять какое-либо решение, можно придерживаться такого правила. Если следующее звено ломаной можно нарисовать двумя способами, то сначала нужно заготовить второй такой же рисунок и выполнить этот шаг на одном рисунке первым, а на другом вторым способом. Аналогично нужно поступать, когда способов не два, а три. Указанный порядок действий помогает найти все решения.

Прямоугольник 3х4 содержит 12 клеток. Найдите пять способов разрезания прямоугольника на две равные части так, чтобы линия разреза шла по сторонам клеток (способы разрезания считаются различными, если части, полученные при одном способе разрезания, не равны частям, полученным при другом способе).

Прямоугольник 3х5 содержит 15 клеток и центральная клетка удалена. Найдите пять способов разрезания оставшейся фигуры на две равные части так, чтобы линия разреза шла по сторонам клеток.

Квадрат 6х6 разграфлен на 36 одинаковых квадратов. Найдите пять способов разрезания квадрата на две равные части так, чтобы линия разреза шла по сторонам квадрата.

Задача 4 имеет более 200 решений. Найдите хотя бы 5 из них.

Урок №2

Цель: продолжать развивать представления о симметрии (осевой, центральной).

Разрежьте фигуры, изображенные на рисунке, на две равные части по линиям сетки, причем в каждой из частей должен быть кружок.

Фигуры, изображенные на рисунке, надо разрезать по линиям сетки на четыре равные части так, чтобы в каждой части был кружок. Как это сделать?

Разрежьте фигуру, изображенную на рисунке, по линиям сетки на четыре равные части и сложите из них квадрат так, чтобы кружочки и звездочки расположились симметрично относительно всех осей симметрии квадрата.

Разрежьте данный квадрат по сторонам клеток так, чтобы все части были одинакового размера и формы и чтобы каждая содержала по одному кружку и звездочке.

Разрежьте квадрат 6х6 из клетчатой бумаге, изображенный на рисунке, на четыре одинаковые части так, чтобы каждая из них содержала три закрашенные клетки.

Урок №3

Цель: научиться разрезать прямоугольник на две равные части, из которых можно сложить квадрат, другой прямоугольник. Научиться определять, из каких прямоугольников, разрезав их, можно составить квадрат.

Дополнительные задачи 7-8 (эти задачи можно рассмотреть в начале урока для разминки).

Прямоугольник 4х9 клеток разрежьте по сторонам клеток на две равные части так, чтобы из них затем можно было сложить квадрат.

Можно ли прямоугольник 4х8 клеток разрезать на две части так, чтобы из них можно было составить квадрат?

Из прямоугольника 10х7 клеток вырезали прямоугольник 1х6 , как показано на рисунке. Разрежьте полученную фигуру на две части так, чтобы из них можно было сложить квадрат.

Из прямоугольника 8х9 клеток вырезали закрашенные фигуры, как показано на рисунке. Разрежьте полученную фигуру на две равные части так, чтобы из них можно было сложить прямоугольник 6х10.

На клетчатой бумаге нарисован квадрат размером 5х5 клеток. Покажите, как разрезать его по сторонам клеток на 7 различных прямоугольников.

Разрежьте квадрат 13х13 на 5 прямоугольников по сторонам клеток так, чтобы все десять чисел, выражающих длины сторон прямоугольников, были различными целыми числами.

Разделите фигуры, изображенные на рисунке, на две части. (Разрезать можно не только по линиям клеток, но и по их диагоналям.)

Разрежьте фигуры, изображенные на рисунке, на четыре равные части.

2.4 Задачи на разрезание треугольника

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абул-Вефа, знаменитого персидского астронома Х века, жившего в Багдаде. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них той или иной новой фигуры лишь в начале ХХ века. Одним из основоположников этого увлекательного раздела геометрии был знаменитый составитель головоломок Генри Э. Дьюдени.

В наши дни любители головоломок увлекаются решением задач на разрезание прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берется за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Поскольку здесь не требуется глубокое знание геометрии, то любители иногда могут даже превзойти профессионалов-математиков.

Вместе с тем, задачи на разрезание не являются несерьезными или бесполезными, они не так уж и далеки от серьезных математических задач.

Задачи на разрезание помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

Можно ли провести разрез произвольного треугольника так, чтобы получить два треугольника?

Можно ли провести разрез треугольника так, чтобы получить три треугольника?

Можно ли провести два разреза треугольника, чтобы получить три треугольника?

Можно ли проведением двух разрезов треугольника получить четыре треугольника?

Можно ли провести два разреза треугольника так, чтобы получить пять треугольников?

Как нужно провести два разреза треугольника, чтобы получить шесть треугольников?

Можно ли двумя разрезами разбить треугольник на семь треугольников?

Можно ли двумя разрезами разбить треугольник на восемь треугольников?

Какое количество треугольников можно получить при проведении трех разрезов данного треугольника?

Сколько треугольников изображено на рисунке? Назовите их.

Сколько углов вы видите на рисунке? Назовите их.

Сосчитайте сколько треугольников изображено на рисунке?

Схема рассуждений

Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре увеличивается число искомых треугольников (принцип нарушается при переходе от случая «в» к случаю «г», но в случае «г» усложняется «геометрический фон», т.е. появляются такие взаимопроникающие треугольники, которые состоят, например, из треугольника и четырехугольника, а в случае «в» все взаимопроникающие треугольники можно рассматривать состоящими только из треугольников).

Оценка выполнения задания

Случай «а»

Если учащийся увидел большой треугольник, состоящий из двух маленьких, т.е. всего три треугольника, то он получает 1 балл.

Если учащийся не видит какой-либо из трех треугольников, то он получает 0 баллов.

Случай «б»

На данном рисунке изображен большой треугольник, состоящий из трех маленьких, всего четыре треугольника. Такое решение оценивается в 1 балл.

Случай «в»

Схема рассуждений и ход решения

1. Сосчитаем все маленькие треугольники, их всего шесть

Сосчитаем треугольники, состоящие из двух маленьких, их всего три

Сосчитаем треугольники, состоящие из трех маленьких, их всего шесть

Треугольник, состоящий из шести маленьких треугольников – 2

Всего получилось 16 треугольников

Оценка выполнения задания

Учащиеся сосчитали (увидели) все взаимопроникающие треугольники, подсчет вели с помощью алгоритма – 2 балла.

Задача решалась без применения алгоритма (какие треугольники учащийся увидел, такие и сосчитал, но нашел больше семи треугольников – 1 балл).

Учащийся при решении насчитал меньше семи треугольников, т.е. не увидел взаимопроникающих треугольников, - оценка 0 баллов.

Случай «г»

Схема рассуждений и ход решения

Сосчитаем треугольники в «нижней» части рисунка, их всего шесть, причем все они состоят только из треугольников.

Добавляем «верхнюю» часть, получаем треугольники, состоящие из треугольников и четырехугольника.

Всего получилось: (3+2+1)+(3+2+1)=12 треугольников.

Оценка выполнения задания

Учащийся подсчитал все треугольники с помощью алгоритма (выбор алгоритма значения не имеет) – оценка 3 балла.

Учащийся применил для решения алгоритм, не позволяющий выделить все имеющиеся на рисунке треугольники – оценка 2 балла.

Учащиеся, не увидевшие взаимопроникающих треугольников, получают 1 балл.

Учащиеся, увидевшие на рисунке меньше семи треугольников, получают 0 баллов.

Сосчитайте число треугольников, изображенных на рисунке.

Ответы: а) 13 треугольников; б) 27 треугольников; в) 47 треугольников; г) 27 треугольников; д) 32 треугольника; е) 48 треугольников.

Начертите треугольник. Пересеките его двумя прямыми так, чтобы на рисунке оказалось:

а) Пять треугольников

Схема рассуждений

Надо получить пять треугольников. Один треугольник уже есть, он построен по условию задачи. Если из любой вершины провести прямую, пересекающую противоположную сторону, то получим еще два треугольника. В одном из полученных треугольников через вершину, лежащую на стороне исходного треугольника, проведем прямую, пересекающую противоположную сторону этого треугольника, получим еще два треугольника.

б) Восемь треугольников

Схема рассуждений

Чтобы получилось семь треугольников (один уже есть), достаточно провести прямые через две вершины, пересекающие противоположные им стороны исходного треугольника.

Оценка выполнения задания

Верное решение оценивается в 3 балла. Попытки, близкие к верному решению, - 1 балл и неверно решенная задача – 0 баллов.

§3. Материалы для проведения уроков

3.1 "Цепочки" задач по теме "Точки и прямые плоскости"

Задачи направлены на развитие математических способностей учащихся.

В этом разделе содержатся задачи, которые интересны и полезны для учащихся любого возраста.

В предлагаемых задачах прекрасно работает "математическая интуиция" и "математическое воображение", которые в среднем школьном возрасте как бы полностью открыты, ничем не загромождены (знания и опыт часто заслоняют эти очень важные качества). Интуитивное предвидение верных фактов, комбинаций и даже методов – это одно из огромных достоинств предлагаемых ниже задач.

Сначала рассмотрим задачи, для решения которых фактически не требуется никаких теоретических знаний.

Методические рекомендации: данные задачи можно использовать для устной работы при проведении урока на этапе актуализации знаний.

Есть одна точка. Проведите через эту точку прямую. Сколько прямых можно провести через данную точку? Какая фигура при этом получится плоская или пространственная?

Есть три точки. Как они могут быть расположены? Сколько через них можно провести прямых? Почему? (Эта задача может быть сформулирована для любого числа точек).

На листе бумаги отметили пять точек и провели всевозможные прямые, каждая из которых проходит через какие-либо две из этих точек. Как расположить точки, чтобы оказались проведенными: а) пять прямых; б) шесть прямых?

На листе бумаги отметили n точек и провели всевозможные прямые, каждая из которых проходит через какие-либо из этих точек. Оказалось, что проведено шесть прямых. Возможно ли, что n=3; n=4; n=5; n=6? Для тех случаев, когда это возможно, сделайте чертежи.

На полу классной комнаты отметим мелом точу А.

Сколько прямых задают эта точка А и точки, являющиеся вершинами углов в классной комнате? Сделайте чертежи, обозначьте вершины углов класса и выпишите все получившиеся прямые.

Представьте себе, что на каждой стене класса отмечена точка (сколько таких точек отмечено?). Мысленно соедините эти точки прямыми. Сколько образовалось прямых?

Сколько получится прямых, если добавить к точкам на стенах класса точку А, отмеченную на полу классной комнаты?

Ниже приведем систему творческих задач, решение которых требует нестандартного подхода.

Методические рекомендации: задачи из данной группы можно использовать как дополнительный материал на уроке для тех детей, которые раньше всех справятся с заданием на урок. За выполнение этих заданий можно поставить оценку в журнал.

Могут ли шесть прямых пересекаться в восьми точках?

Могут ли семь прямых пересекаться в восьми точках? Сколько точек пересечения может быть у семи прямых?

Как расположить пять точек и две прямые, чтобы на каждой прямой было по три точки?

Можно ли шесть деревьев посадить в четыре ряда так, чтобы в каждом ряду было по три дерева?

3.2 Разработка урока по теме "Угол"

Учащимся предлагается рассмотреть заранее заготовленные рисунки. Перед учащимися ставятся вопросы:

– Назовите лучи, изображенные на рисунках.

– Назовите начало каждого луча.

– Что можно сказать о лучах на рисунке 2? (Они имеют общее начало – точку А).

– Что можно сказать о лучах на рисунке 1? (Начало лучей в разных точках).

– Показать область плоскости, на которые ее делят лучи на рисунке 2.

– Можно ли указать определенные части плоскости, на которые ее делят лучи на рисунке1? (Нет).

По "рис.3" предлагаются вопросы:

– Назовите лучи, имеющие общее начало и лежащие в одной области плоскости. (ОА и ОВ, ОА и ОС, ОС и ОD, ОD и ОВ)

– Назовите пары лучей, имеющие общее начало. (ОА и ОВ, ОА и ОС, ОС и ОD, ОD и ОВ, ОD и ОА, ОВ и ОС)

– Покажите области, на которые делят ее пары лучей.

3. После такой подготовительной работы дается понятие угла. По рис. 1, 2 предлагается указать угол, выясняется, каких признаков угла недостает на рис.1.

4. Вводится обозначение угла по рис.2 (А – вершина, АВ и АС – стороны, чтение угла).

5. Под руководством учителя всеми учащимися проводится практическая работа: “Из листа бумаги вырезать угол”. Учащиеся приготавливают лист бумаги, чертежные инструменты, ножницы. Выясняется последовательность построения угла, выбирается начало (вершина), проводятся два произвольных луча из вершины. Учащиеся строят угол. Вырезают. Учитель, выполняя у всех на глазах эту же работу, предлагает задание учащимся:

– Покажите угол.

– Что представляет собой оставшаяся часть? (Выясняется, что тоже угол – обе фигуры часто называют плоским углом.)

Делается вывод: получили две фигуры, каждая есть угол. Учащимся указывается обозначение угла.

6. Предлагается начертить в тетради произвольный угол, назвать его, сделать подпись под чертежом. (Эту же работу выполняет ученик, вызванный к доске). После выполнения задания учащиеся сверяют его с чертежом на доске. Еще раз в памяти детей восстанавливается понятие угла, его обозначение, чтение.

7. Учащиеся самостоятельно по рис.3 записывают множество образовавшихся углов. Ответ сверяют с плакатом, на котором записан ответ. При проверке самостоятельной работы учащиеся выясняют пропущенные углы, а затем дается разъяснения, особенно для углов АОD и ВОС.

8. Проводятся устные упражнения, выясняется, является ли фигура на "рис.5" углом.

9. Выполняются упражнения с записью в тетрадях и на классной доске.

10. Задание на дом.

На следующих уроках для закрепления понятия угла проводится такая работа:

По готовым чертежам надо записать множество углов, полученных пересечением прямых.

По плакату с изображением различных геометрических фигур предлагается назвать углы каждой фигуры.

Проводится особая подготовка к выполнению упражнения: “Начертить два угла так, чтобы их общей частью был: а) угол; б) четырехугольник; в) луч; г) отрезок "рис.10". С этой целью были выполнены следующие упражнения:

а) Начертить ВDE и провести прямую MN так, чтобы общей частью угла и прямой был: а) отрезок; б) точка; в) луч "рис.11"

Попутно с ответами учащимся предлагается определить, будет ли решением отрезок М_>1>N_>1>, точка А, стороны DB и DE, угол BDE (рис.11).

Упражнение это выполняется в тетрадях и на классной доске со всеми комментариями.

б) Начертить угол МКЕ и провести луч АD так, чтобы их общую часть составляли: отрезок, точка, луч.

Это упражнение учащиеся выполняют самостоятельно в тетради, затем сверяют с чертежом на доске.

Проводится практическая работа по определению областей данного угла (работа выполняется на отдельном листке бумаги). Разделите данный угол двумя отрезками на две области, на три области, на четыре области.

Заключение

Изучив психолого-педагогическую и методическую литературу по поставленной проблеме, мы сделали следующие выводы:

- в 5-6 классах учащиеся уже способны к восприятию довольно абстрактного геометрического материала, но при его изучении необходимо усилить практическое применение;

- изучение геометрического материала в 5-6 классах позволяет обобщить и систематизировать знания, полученные в начальной школе на основе практической деятельности;

- знакомство с геометрическими понятиями в курсе математики 5-6 классов носит пропедевтический характер по отношению к дальнейшему изучению геометрии и имеет практическую направленность.

Исследуя структуру пропедевтического курса геометрии, мы пришли к выводу, что формирование начальных геометрических представлений может проходить в рамках одного предмета - математики, однако с целью углубления и расширения интеллектуального уровня учащихся и развития их пространственных представлений можно изучать элементы геометрии отдельным блоком.

Анализ различных учебников математики 5-6 классов показал, что геометрический материал тесно связан с арифметическим и алгебраическим. Однако в большинстве учебников недостаточно внимания уделяется рассмотрению свойств геометрических фигур, геометрическому смыслу решаемых задач. Однако следует отметить, что, дополнять базисный учебный план различными темами по геометрии, нежелательно, потому что перегрузка геометрическим содержанием может происходить за счет сокращения арифметического материала курса. Увеличивая объем содержания геометрического материала, необходимо помнить о важности формирования у учащихся вычислительных навыков, навыков решения текстовых задач, уравнений. Поэтому, на наш взгляд, не следует чрезмерно пересыщать уроки математики в 5-6 классах геометрическим содержанием. Зная о высоком развивающем значении геометрии, а также о трудностях, которые могут возникнуть у учащихся при изучении систематического курса, мы пришли к выводу о необходимости совершенствования методики обучения элементам геометрии в 5-6 классах, уделяя внимание, прежде всего практическим работам.

Библиография:

1. Белим, С.Н. Задачи по геометрии, решаемые методами складывания (оригами) [Текст] – М.: Аким, 1998]

   Гусев, В.А. Психолого-педагогические основы обучения математике [Текст] / В.А. Гусев. – М.: Вербум, Академия, 2003. – 432 с.

   Екимова, М.А. Задачи на разрезание [Текст] – М.: МЦНМО, 2005.-120 с.:ил

   Зайкин, М.И. Развивай геометрическую интуицию [Текст]: 5-9 кл.: Кн. для учащихся / М.И. Зайкин.— М.: Просвещение: Владос, 1995.— 112 с.: ил.

5.Зубарева, И.И. Рабочая тетрадь №1 [Текст]: 5 кл.: Учеб. Пособие для общеобразоват. Учреждений / И.И. Зубарева. – 2-е изд. – М.: Мнемозина, 2006.- 64 с.: ил.

6. Зубарева, И.И. Рабочая тетрадь №2 [Текст]: 5 кл.: Учеб. Пособие для общеобразоват. Учреждений / И.И. Зубарева. – 2-е изд. – М.: Мнемозина, 2006.- 68 с.: ил.

7. Зубарева, И.И. Рабочая тетрадь №1 [Текст]: 6 кл.: Учеб. Пособие для общеобразоват. Учреждений / И.И. Зубарева. – 2-е изд. – М.: Мнемозина, 2006.- 94 с.: ил.

8. Зубарева, И.И. Рабочая тетрадь №2 [Текст]: 6 кл.: Учеб. Пособие для общеобразоват. Учреждений / И.И. Зубарева. – 2-е изд. – М.: Мнемозина, 2006.- 98 с.: ил.

9. Зубарева, И.И. Математика [Текст]: 5 кл.: Учеб. Для общеобразоват. Учреждений / И.И. Зубарева, А.Г. Мордкович.-6-е изд., стереотип.-М.: Мнемозина, 2007.- 270 с.:ил.

10. Зубарева, И.И. Математика [Текст]: 6 кл.: Учеб. Для общеобразоват. Учреждений / И.И. Зубарева, А.Г. Мордкович.-6-е изд., стереотип.-М.: Мнемозина, 2007.- 270 с.:ил.

11. Зубарева, И.И. Математика [Текст]: 5-6 кл.: Методическое пособие для кчителя / И.И. Зубарева, А.Г. Мордкович.-2-е изд.-М.: Мнемозина, 2005.- 104 с.: ил.

12. Игнатьев, Е.И. В царстве смекалки [Текст] / Е.И. Игнатьев.- М.: Столетие, 1994.- 192 с.6.

13. Кордемский, Б.А. Математическая смекалка [Текст] / М.И. Зайкин. – М.: Наука: Гл. ред. Физ. Мат. Лит., 1991.- 576 с

14. Математика [Текст]: Учеб. Для 5 кл. общеобразоват. Учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Швацбурд; 18-е изд.- М.: Мнемозина, 2006.-142 с.:ил.

15. Математика [Текст]: Учеб. Для 6 кл. общеобразоват. Учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Швацбурд; 18-е изд.- М.: Мнемозина, 2006.-142 с.:ил.

16. Математика [Текст]: Учеб. Для 5 кл. общеобразоват. Учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин; 2-е изд.-М.: Просвещение, 2000.-255 с.: ил.

17. Математика [Текст]: Учеб. Для 6 кл. общеобразоват. Учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин; 2-е изд.-М.: Просвещение, 2001.-270 с.: ил.

18. Методика обучения геометрии [Текст]: Учеб. Пособие для студ. Высш. Пед. Учеб. Заведений / В.А. Гусев, В.В. Орлов, В.А. Панчищина и др.; Под ред. В.А. Гусева.-М.: Академия .-2004.-368 с.

19. Математика [Текст]: Учеб. Для 5 кл. общеобразоват. Учреждений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.; Под ред. Г.В. Дорофеева, И.Ф. Шарыгина.-М.: Просвещение.-1994.-272 с.: ил.

20. Математика. Анализ данных. Доли [Текст]: Рабочая тетрадь для 5 кл. общеобразоват. Учреждений /Е.А. Бунимович, К.А. Краснянская, Л.В. Кузнецова, И.А. Лурье, С.С. Минаева, Л.О. Рослова, С.Б. Суворова.- М.: Просвещение.-1994.- 96 с.

21. Математика [Текст]: Учеб. Для 6 кл. общеобразоват. Учреждений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.; Под ред. Г.В. Дорофеева, И.Ф. Шарыгина.-М.: Просвещение.-2002.-208 с.: ил.