Применение занимательного задачного материала для активизации познавательной деятельности учащихся при обучении решению текстовых задач

Введение

Эффективность обучения, в частности обучения математике, во многом зависит от того, насколько учащиеся заинтересованы в изучаемом предмете. Поэтому проблема развития познавательного интереса учащихся привлекает внимание, как исследователей, так и практиков. Познавательный интерес взаимосвязан со многими сторонами учебного процесса. Он выступает одновременно как результат, обусловленный способом организации учебной деятельности, так и как средство повышения эффективности обучения.

Успешность обучения школьников напрямую зависит от степени заинтересованности в предмете. Достижения же учеников способствуют развитию познавательного интереса. Следовательно, успешность в обучении постоянно взаимодействует с познавательным интересом учащегося, эти явления постоянно влияют друг на друга. Чтобы развить этот интерес, нами предлагаются старинные текстовые занимательные задачи, которые способствуют активизации познавательной деятельности на уроке математики с помощью своего занимательного, необычного, а иногда сложного для понимания содержания условия задачи, и сопровождение некоторых задач историческим материалом.

Целью дипломной работы является рассмотрение возможности применения занимательного задачного материала для активизации познавательной деятельности учащихся при обучении решению текстовых задач.

Для достижения поставленной цели были поставлены следующие задачи:

анализ психолого-педагогической литературы с целью выявления психологических особенностей школьников 11 – 15-летнего возраста;

анализ учебной литературы различных авторских коллективов для 5 – 8 классов;

составление банка старинных занимательных текстовых задач по некоторым темам основной школы;

составление методических рекомендаций по их использованию.

Дипломная работа состоит из введения, двух глав, заключения, списка литературы и приложения.

В первой главе «Теоретические основы организации познавательной деятельности учащихся при обучении решению текстовых задач» рассматриваются психолого-педагогические особенности детей 11 – 15-летнего возраста, дан сравнительный анализ современных учебников для общеобразовательных школ, говорится о приемах решения текстовых задач и об активизации познавательной деятельности на этапе поиска решения задачи. А также говориться о роли и месте текстовых задач в обучении математике.

Во второй главе «Применение занимательного задачного материала на уроках математики» представлены старинные текстовые задачи по некоторым темам школьного курса. Ко многим задачам помимо стандартного приведены старинные способы решения, а также исторические сведения.

Глава 1. Теоретические основы организации познавательной деятельности учащихся при обучении решению тестовых задач

§1. Психолого-педагогические особенности детей 11-15-летнего возраста

Одна из основных трудностей профессии учителя состоит не только в необходимости знать досконально учебный материал уроков, в умении правильно выбрать и применить методы и приемы преподавания. Столь же важно и умение использовать в своей работе знания о возрастных особенностях учащихся данного возраста, знание возрастной и педагогической психологии.

Далее мы подробнее рассмотрим психолого-педагогические особенности подросткового возраста.

Подростковый возраст — стадия онтогенетического развития между детством и взрослостью (от 11 до 15 лет), которая характеризуется качественными изменениями, связанными с половым созреванием и вхождением во взрослую жизнь. [27]

Л.С. Выгодский перечислил несколько основных групп наиболее ярких интересов подростка, которые он назвал доминантами [30; 145]:

- эгоцентрическая доминанта (интерес подростка к собственной личности);

- доминанта дали (установка подростка на обширные, большие масштабы, которые для него наиболее субъективно приемлемы, чем ближние, текущие, сегодняшние);

- доминанта усилия (тяга подростка к сопротивлению, преодолению, к волевым напряжениям, которые иногда проявляются в упрямстве, хулиганстве, борьбе против воспитательного авторитета, протесте и других негативных проявлениях);

- доминанта романтики (стремление подростка к неизвестному, к рискованному, к приключениям, к героизму).

В подростковом возрасте ведущую роль играет общение со сверстниками в контексте собственной учебной деятельности подростка. Присущая детям этого возраста деятельность включает в себя такие ее виды, как учебная, общественно-организационная, спортивная, художественная, трудовая. При выполнении этих видов полезной деятельности у подростков возникает осознанное стремление участвовать в общественно необходимой работе, становиться общественно значимым. Он учится строить общение в различных коллективах с учетом принятых в них норм взаимоотношений, рефлексии собственного поведения, умения оценивать возможности своего «Я». Это наиболее сложный переходный возраст от детства к взрослости, когда возникает центральное психическое, личностное новообразование человека – «чувство взрослости». Специфическая социальная активность подростка заключается в большей восприимчивости к усвоению норм, ценностей и способов поведения, которые существуют в мире взрослых и в их отношениях.

Как отмечает В.А. Караковский [5; 176], младшему подростку особенно присущи потребность в достойном положении в коллективе сверстников и семье; стремление обзавестись верным другом; стремление избежать изоляции как в классе, так и в малом коллективе; повышенный интерес к вопросу о «соотношении сил» в классе; стремление отмежеваться от всего подчеркнутого детского; отсутствие авторитета возраста; отвращение к необоснованным запретам; восприимчивость к промахам учителей; переоценка своих возможностей, реализация которых предполагается в отдаленном будущем; отсутствие адаптации к неудачам; тенденция предаваться мечтаниям; боязнь осквернения мечты; повышенный интерес к спорту и т.д. Наряду с этим младший подросток характеризуется повышенной утомляемостью, ярко выраженной эмоциональностью, иногда резкостью в суждениях (до грубости). К концу периода младшего подростничества учащиеся начинают осознавать необходимость самостоятельного выбора дальнейшей программы образования, что предполагает сформированность достаточно устойчивых интересов и предпочтений, ориентацию в различных сферах труда и общественно полезной деятельности.

Показательно для подросткового возраста и отношение к авторитету. Если в младшем школьном возрасте авторитет учителя не менее значим, чем авторитет семьи, то для подростка проблема авторитета взрослого не самоочевидна. С одной стороны, позиция подростка «я - взрослый» как бы противопоставляет его взрослым, с другой их авторитет остается важным фактором его жизни. Сохранению авторитета взрослого (учителя) способствует следующее: «1) неизменность общественного положения подростка, он был и остается учеником, школьником; 2) его полная материальная зависимость от родителей, которые наряду с учителями выступают в роли воспитателя; 3) отсутствие у подростка умения... действовать самостоятельно». [5; 178]

В этом возрасте главная ценность – система отношений со сверстниками, взрослыми, подражание осознаваемому или бессознательно следуемому «идеалу», устремленность в будущее (недооценка настоящего). Отстаивая свою самостоятельность, подросток формирует и развивает на основе рефлексии свое самосознание, образ «Я», соотношение «реального» и «идеального Я». На основе интеллектуализации психических процессов происходит их качественное изменение по линии все большей произвольности, опосредованности.

Эта эпоха отрочества соотноситься с макрофазой индивидуализации, которая, по А. В. Петровскому, «характеризуется поиском средств и способов для обозначения своей индивидуальности…» [5; 177]

Поэтому, учителю на уроках не обойтись без учета важных особенностей возраста: тенденция к утверждению своей исключительности, «индивидуальности» и эмоциональное удовлетворение от исследовательской деятельности. Благоприятной ситуацией учения для подростков является ситуация успеха, которая обеспечивает им эмоциональное благополучие. Страх перед неуспехом, боязнь поражения порой приводит подростков к поиску благовидных причин, чтобы не пойти в школу или уйти с урока. Поэтому надо обеспечить ему эту ситуацию успеха, с использованием дифференцированного подхода.

Все трудности, противоречия и преимущества непосредственно связаны с особенностями развития психических процессов подростков: ощущение, восприятие, память, внимание, мышление.

Ощущение

Очень важно, что ребёнок ощущает, когда «прикасается» к тому, о чём до этого только слышал. В этот момент главное, чтобы возникло ощущение лёгкости восприятия и понимания нового предмета, что ничего сложного, например, в обыкновенных дробях, десятичной записи числа, или решении задач не «по действиям», а с помощью составления уравнения нет. Таким образом, если ученика не пугать контрольными, то ощущение в момент их написания не будет стрессовым, и как следствие, оценка за работу будет гораздо выше, понимание пройденной темы останется более глубоким.

Вообще, в психологии ощущением называют «результат сознательной деятельности, дифференциации, выделения отдельных чувственных качеств внутри восприятия»[29; 177].

Во время уроков ощущение от предметов, объектов, действий происходит на 90% за счет зрительной информации. Зрение даёт информацию о цвете, размере, объёме, отдалённости предмета. Поэтому важно, при обучении математике, использовать принцип наглядности, а именно – использовать таблицы и схемы, модели предметов, раздаточный материал, постоянно приводить примеры из окружающего мира, связанные со свойствами изучаемых объектов, и т.д.

Кроме зрительного восприятия, ведущую роль играет слуховое восприятие, то есть ощущение, вызванное раздражением слуховых рецепторов. Чем меньше постороннего шума на уроке математики, из-за обсуждения школьниками посторонних тем, не связанных с темой урока, а тем более, шума, следствием которого является плохое поведение на уроке, тем больше шансов понять тот или иной материал гораздо быстрее и качественнее. Здесь, также стоит отметить, что голос учителя на уроке, его интонация, громкость дают разные ощущения и восприятия от преподаваемого материала.

Восприятие

Известно, что прием и переработка человеком поступившей через органы чувств информации завершается появлением образов предметов или явлений. Процесс формирования этих образов называется – восприятием. Итак, «восприятие – целостное отражение предметов, ситуаций и событий, возникающее при непосредственном воздействии физических раздражителей на рецепторные поверхности органов чувств» [28]

Одну и ту же информацию дети воспринимают по–разному, в зависимости от своих интересов, потребностей, способностей и т. п. Восприятие зависит от прошлого опыта, от содержания психической деятельности человека.

Восприятие обладает рядом свойств:

1) целостность, т. е. восприятие есть всегда целостный образ предмета;

2) константность – благодаря ей окружающие предметы воспринимаются как относительно постоянные по форме, цвету, величине.

3) осмысленность – восприятие тесно связано с мышлением, с пониманием сущности предмета.

4) избирательность – проявляется в преимущественном выделении одних объектов над другими.

В зависимости от того, в какой степени целенаправленна будет деятельность ребенка, восприятие разделяют на непреднамеренное и преднамеренное.

Непреднамеренное восприятие может быть вызвано как особенностями окружающих предметов (их необычность, яркость), так и соответствием этих предметов интересам. В непреднамеренном восприятии нет заранее поставленной цели.

Преднамеренное восприятие с самого начала регулируется задачей – воспринимать тот или иной предмет, явление, ознакомиться с ним.

Стоит отметить, что в начале подросткового периода формируется преднамеренное восприятие. Ученики начинают постепенно воспринимать те явления, предметы, которые необходимы для достижения поставленной цели, даже если эти предметы и явления не столь их интересуют. Восприятие начинает становиться более избирательным, целенаправленным, анализирующим.

Память

Память - это психический процесс запечатления, сохранения и воспроизведения прошлого опыта [32] .

Процесс запоминания у подростков приобретает целенаправленный характер. Их память становится продуктивной и точной, у них развиваются навыки преимущественно смыслового запоминания, и в связи с этим проявляется резко отрицательное отношение к механической памяти - «зубрежке». Такое пренебрежение может сопровождаться отрицательным отношением вообще к необходимости серьезно работать над запоминанием, заучиванием учебного материала.

По времени хранения материала у подростков преобладает кратковременная и долговременная память.

Кратковременная память: в среднем время удержания информации в памяти составляет несколько минут. Чтобы продлить его, надо повторять информацию, так как новая информация немедленно вытесняет первую. Результаты экспериментов [32] показывают, что объем кратковременной памяти - 7 ± 2 структурные единицы (объем измеряется в тех единицах, в которых предъявляется материал). Поскольку объем памяти ограничен, необходимо:

создать приоритетность информации;

организовать информацию в блоки, сжать ее в меньшее число оперативных единиц.

Долговременная память не ограничена ни объемом, ни временем хранения. Чтобы лучше сохранить информацию, надо повторить ее через 15 - 20 минут, затем через 8-9 часов, и наконец, через 24 часа. Наилучшее время для запоминания - с 8 до 12 утра. Информация в долговременной памяти не пропадает, а лишь затрудняется доступ к ней.

По типу запоминаемого материала подростки обладают двигательной, эмоциональной и образной памятью. Последняя в свою очередь делится на зрительную и слуховую.

Внимание

Внимание – это особое свойство человеческой психики. Оно не существует самостоятельно, вне мышления, восприятия, работы памяти. Нельзя быть просто внимательным – можно быть внимательным, выполняя какие-либо действия. Поэтому вниманием называют избирательную направленность сознания на выполнение определенной работы. Формы проявления внимания многообразны. Оно может быть направлено на работу органов чувств (зрительное, слуховое внимание), на процессы запоминания, мышления, на двигательную активность.

Внимание обладает определенными особенностями, которые во многом являются характеристикой человеческих способностей и возможностей. Основные свойства внимания: объем, сосредоточенность (концентрация), распределяемость, устойчивость, колебание, переключаемость.

Объем внимания измеряется тем количеством объектов, которые воспринимаются одновременно. Объем внимания зависит не только от генетических факторов и от возможностей кратковременной памяти человека, но и от жизненного опыта, от поставленной цели, от особенностей воспринимаемых объектов. Объединенные по смыслу объекты воспринимаются в большем количестве, чем не объединенные. У ребенка объем внимания равен 2 - 4 объектам.

Концентрация внимания выражается в степени сосредоточенности на объекте. Чем меньше круг объектов внимания, чем меньше участок воспринимаемой формы, тем концентрированнее внимание. Концентрация внимания обеспечивает углубленное изучение познаваемых объектов, вносит ясность в представление человека о том или ином предмете, его предназначении, конструкции, форме.

Распределение внимания выражается в умении одновременно выполнять несколько действий или вести наблюдение за несколькими процессами.

Устойчивость внимания характеризуется длительностью сосредоточенности, умением не отвлекаться в течение определенного периода времени. Необходимым условием устойчивости внимания является разнообразие впечатлений или выполняемых действий. И об этом не стоит забывать учителю при подготовке к уроку.

Свойством, противоположным устойчивости, является отвлекаемость. Отвлекаемость внимания выражается в колебаниях внимания, которые представляют собой периодическое ослабление внимания к конкретному объекту или деятельности. Следует учесть, что колебание внимания происходит даже при очень сосредоточенной работе.

Переключение внимания состоит в перестройке внимания, в переносе его с одного объекта на другой.

Различают три вида внимания: непроизвольное, произвольное и послепроизвольное.

Непроизвольное внимание – это сосредоточение внимания на предмете в силу его каких-то особенностей. Здесь отсутствуют усилия ребенка направленные на сосредоточение. Внимание привлекает так называемый раздражитель. Новизна раздражителя также вызывает непроизвольное внимание. Большое значение в возникновении непроизвольного внимания имеют интеллектуальные, эстетические и моральные чувства. Предмет, вызвавший у ребенка интерес, удивление, восхищение, восторг продолжительное время приковывает его внимание.

Произвольное внимание – это сознательно регулируемое сосредоточение на объекте. Здесь ученик сосредотачивается не на том, что ему интересно и приятно, а на том, что ему надо сделать. Произвольно сосредотачиваясь на объекте, ребенок прилагает некие волевые усилия, которые и поддерживают внимание в течение процесса деятельности. Произвольное внимание возникает, когда ученик ставит перед собой цель деятельности, достижение которой требует сосредоточенности. Важным условием поддержания внимания является психическое состояние ученика. Утомленному ребенку очень сложно сосредоточить внимание. Значительно ослабляет произвольное внимание эмоциональное возбуждение, вызванное посторонними причинами.

Если говорить о подростках, то их внимание характеризуется несколько большим объемом, по сравнению с младшими школьниками. Ребята уже в состоянии воспринимать достаточно большое количество объектов одновременно. Стоит отметить, что внимание становится более устойчивым, но, в то же время, для этого возраста характерна частая отвлекаемость. Также внимание обладает специфичной избирательностью. В этот период происходит становление произвольного внимания.

Мышление

Любое проявление понимания связано с двумя универсальными субъектно-личностными факторами - мышлением и языком. Если говорить о мыслительной деятельности людей, то она совершается с помощью мыслительных операций (анализ, синтез, сравнение, абстрагирование, обобщение, конкретизация). Чем большим числом операций владеет человек, тем быстрее и осознаннее он воспринимает новый материал.

«Мышление – это движение мысли, раскрывающее связь, которая ведёт от отдельного к общему и от общего к отдельному. Мышление – это опосредованное – основанное на раскрытии связей, отношений, опосредований – и обобщённое познание объективной реальности» [29; 310].

Человек много знает об окружающем его мире. Он знает химический состав далеких звезд, ему знаком мир элементарных частиц, он познает законы высшей нервной деятельности, он знает о существовании рентгеновских лучей, ультразвуков, хотя не имеет возможности воспринимать все это. Человек отражает в сознании не только предметы и явления, но и закономерные связи между ними. Например, люди знают закономерную связь между температурой и объемом тела, им известно отношение между сторонами прямоугольного треугольника, они понимают связь между господствующими ветрами, широтой, высотой местности над уровнем моря, отдаленностью от моря, с одной стороны, и климатом — с другой.

Что у данной фигуры три угла или, что потолок белый, доказывать не надо. Это воспринимается человеком непосредственно, с помощью анализаторов. А вот что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов — этого никто не способен видеть непосредственно, как бы внимательно он ни вглядывался в прямоугольный треугольник и каким бы острым зрением ни обладал. Такого рода познание не является непосредственным показанием наших анализаторов, а является, как говорят, опосредованным познанием.

Мышление представляет собой опосредованное сознание, то есть, например, мы не видели, как решали задачу и получили ответ, но мы видим решение и ответ, значит, мы делаем вывод, что задача решена. Или, например, человек, сидящий в комнате, хочет узнать, какова температура снаружи. Для этого есть разные возможности — почувствовать эту температуру своим кожным анализатором непосредственно (выйдя на улицу) или посмотреть на термометр, прикрепленный снаружи у окна. В последнем случае человек о температуре узнает опосредованно. Воспринимая одно, человек судит о другом. Иначе говоря, опосредованное познание предмета или явления осуществляется посредством восприятия другого предмета или явления, закономерно связанного с первым.

Вообще говоря, мы мыслим с помощью понятия явлений окружающего мира. Возникает понятийное мышление не сразу, а появляется только к 13-15 годам. Значит, у подростков оно находится на стадии развития, и этому виду мышления надо уделять огромную роль. В качестве средств понимания многие исследователи предлагают использовать определённую организацию учебного материала: индивидуальные задания; различные интерпретации, раскрывающие смысл понятия; перевод с одного языка на другой (с русского на язык математики, то есть язык символов); системы вопросов; диалог и др.

Подростки в основном находятся на эмпирическом уровне мышления, они практически не задают вопросов учителю, отвечают формально, заученно. Возраст учеников таков, что они часто слушают и даже внимательно, но не слышат, не могут самостоятельно увидеть проблему, и организовать полноценный диалог становится проблематичным.

Учитывая специфику школьного предмета математики: высокую абстрактность его понятий, которая выражается в преобладании синтаксиса изложения (формы) в ущерб семантике, большую роль для организации обучения, нацеленного на понимание (в узком смысле), имеют два фактора - содержательный анализ учебного материала и диалог. Умение проводить содержательный анализ составляет первый уровень теоретического мышления - аналитический. Он состоит в умении находить закономерные связи, внутренние отношения, то есть раскрывать сущность вещей, закономерности их развития, выделять генетическую основу рассматриваемых объектов, устанавливать связи единичных явлений внутри некоторого целого.

Мышление человека, и в частности школьника, наиболее ярко проявляется при решении задач. Любая мыслительная деятельность начинается с вопроса, который ставит перед собой человек, не имея готового ответа на него. Иногда этот вопрос ставят другие люди, но всегда акт мышления начинается с формулировки вопроса, на который надо ответить, задачи, которую надо решить, с осознания чего-то неизвестного, что надо понять, уяснить.

§2. Текстовые задачи в обучении математике

1. Место и роль текстовых задач в курсе алгебры современной школы

Обучение математике через решение задач означает такую организацию учебного процесса, при которой через задачи, через их решение реализуется триединая цель обучения (обучающая, развивающая и воспитательная цели).

Под обучающей функцией, понимаются те задачи которые направлены на формирование у школьников системы знаний, умений и навыков. Эти знания, умения и навыки могут быть предусмотрены программой или служить ее расширению и углублению на различных этапах ее усвоения.

Под воспитательными функциями задач понимают:

1) возбуждение и поддержание интереса к математике;

2) воспитание у школьников ответственного отношения к математике;

3) воспитание потребности умения учится математике.

Развивающие функции задач:

1) формирование умений эффективно в изучении математики при использовании методов научного познания, такие как: наблюдение, сравнение, противопоставление, анализ, синтез, обобщение и др.;

2) овладение элементарной логической грамотностью;

3) овладение умением выполнять умозаключения индуктивного и дедуктивного характера;

4) умение правильно ставить мыслительный и/или практический опыт, выдвигать гипотезы, проверять их;

5) умение осуществлять выбор средств и методов для достижения поставленной цели, учитывая конкретные условия;

6) умение переводить простейшие ситуации жизненного характера на математический язык.

В соответствии с этим задачи в процессе обучения выступают как средство организации и управления учебно-познавательной деятельностью школьников на различных ее этапах: репродукция, эвристика, исследование.

Задачи играют большую роль и в формировании мышления. Советский психолог О.К. Тихомиров так охарактеризовал связи между решением задач и мышлением «мышление психологически выступает как деятельность по решению задач».[6] Таким образом, можно утверждать, что решение текстовых задач позволяет более эффективно формировать мышление школьников.

Задачи в школьном курсе также выступают как средство связи теории с практикой, что соответствует одному из дидактических принципов обучения, а именно принципу прикладной направленности обучения.

Каждая задача в определенном месте учебного процесса может выполнять различные функции. Например, одна и также задача может выполнять функцию мотивации при введении нового математического понятия. Также эта задача может служить демонстрацией логики рассуждений и образцом оформления условия и решения. Эту же задачу можно применять для отработки навыка в решении задач под руководством учителя, а также при самостоятельном решении ее учеником. Задача может нести функции контроля знаний и умений. Задача может развивать творчество учащихся, если задача предполагает несколько способов решения.

2. Этапы решения текстовой задачи

В школьном образовании текстовые задачи всегда занимали особое место. Ещё задолго до нашей эры в Древнем Египте, Вавилоне, Китае, Индии были известны разнообразные методы решения текстовых задач.

Текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т.п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь его количественные и функциональные характеристики. [4; 7] Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи. Задачи в обучении выступают в процессе обучения и средством стимулирования и мотивации учебно-познавательной деятельности школьников. В своей работе мы рассматриваем текстовые задачи, которые могут способствовать активизации познавательной деятельности учащихся на уроке, для этого были подобраны задачи с необычным содержанием, задачи в стихах, нестандартные методы решения задач.

Существуют различные методы решения текстовых задач: арифметический, алгебраический, геометрический, логический и др.

Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами. [4; 14]

Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Одну и ту же задачу можно также решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений, в основе составления которых лежат различные соотношения между данными и искомыми. [4; 15]

Решить задачу геометрическим методом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. [4; 15]

Решить задачу логическим методом – это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения. Примерами таких задач могут служить задачи «на переправы», классическим представителем которых является задача о волке, козе и капусте, или задачи «на взвешивание». [4; 16]

Решение любой текстовой задачи состоит из нескольких этапов: [4]

Анализ содержания задачи.

Поиск пути решения задачи и составление плана ее решения.

Осуществление плана решения задачи.

Проверка решения задачи.

Формулировка окончательного ответа на вопрос задачи.

Дополнительная работа над решенной задачей.

Рассмотрим некоторые этапы решения задачи.

1. Анализ содержания задачи.

Основная цель ученика на первом этапе — это понять задачу. Ученик должен четко представить себе: о чем эта задача? Что в задаче известно? Что нужно найти? Как связаны между собой данные (числа, величины, значения величин)? Какими отношениями связаны данные и неизвестные, данные и искомое? Что является искомым: число, отношение, некоторое утверждение?

Можно выделить следующие возможные приемы выполнения первого этапа решения текстовой задачи.

1. Представление жизненной ситуации, описанной в задаче, мысленное участие в ней. С этой целью полезно после чтения задачи предложить учащимся представить себе то, о чем говорится в задаче, и предложить нарисовать словесную картинку.

2. Разбиение текста на смысловые части и выделение на этой основе необходимой для поиска решения информации.

Например: «Один человек выпьет кадь пития в 14 дней, а с женою ту же кадь в 10 дней. И ведательно есть, в колико дней жена его особенно выпьет ту же кадь?»

3. Переформулировка текста задачи: замена описания данной в ней ситуации другой, сохраняющей все отношения и зависимости и их количественные характеристики, но более явно их выражающие.

Цель переформулировки — опустить несущественные детали, уточнить и раскрыть смысл существенных элементов.

Рассмотрим на примере простой задачи: «Утром в магазине было 30 книжных шкафов. К концу рабочего дня осталось 12 шкафов. Сколько шкафов продали за день?» — удобнее искать, если текст ее будет сформулирован так: «Было 30 шкафов. Осталось 12 шкафов. Сколько шкафов продали?»

4. Очень важно при работе над задачей научить учащихся выделять основные (опорные) слова, которые связаны с действием, соответствующим сюжету.

2. Поиск пути решения задачи и составление плана ее решения

Цель ученика на втором этапе — выделить величины, данные и искомые числа, входящие в задачу, установить связи между данными и искомым и на этой основе выбрать соответствующее действие.

Использование различных методических приемов при обучении решению текстовых задач способствует развитию кругозора учащихся, правильному пониманию математического смысла различных жизненных ситуаций, активизирует их познавательную активность. На данном этапе используются различные способы моделирования.

1. Предметное моделирование.

Рассматривается, например, задача: «У Лены было 6 карандашей, а у Тани 4 карандаша. Сколько карандашей у обеих девочек?» К доске выходят две девочки. У одной из них в руке 6 карандашей, у другой — 4 карандаша. Такое воспроизведение уточняет представления детей, возникшие при восприятии ими задачи.

2. Графические модели (это рисунки и чертежи, которые помогают понять задачу, организовать поиск ее решения).

Рисунок может быть таким, что по нему, не выполняя арифметического действия, легко дать ответ на поставленный в задаче вопрос, например: Задача Л. Эйлера¹ «Крестьянка принесла на рынок некоторое число яиц. Первому покупателю она продала половину того, что имела, и еще пол-яйца; второму – половину того, что у нее осталось, и еще пол-яйца; третьему – половину нового остатка и еще пол-яйца; четвертому – половину того, что осталось, и еще пол-яйца. После этого у нее ничего не осталось. Сколько яиц было у нее вначале?»

Решение:

Что было у крестьянки перед встречей с четвертым покупателем? Что-то, половина чего была продана, после чего осталось пол-яйца. Но, значит, пол-яйца были второй половиной того, что у нее было. Значит, перед встречей с четвертым покупателем у крестьянки было одно яйцо. Нарисуем его в виде одной клетки. Перед встречей с третьим покупателем у нее было это яйцо и те пол-яйца, которые она продала третьему, и все это составляло половину того, что она имела. Значит, пририсуем пол-яйца и удвоим полученное – эти три яйца были у крестьянки перед встречей с третьим покупателем. Аналогично, пририсовав к трем яйцам пол-яйца и удвоив полученное, будем иметь семь яиц, имевшиеся у нее перед встречей со вторым покупателем. Проделав еще раз эту операцию, узнаем, сколько было у нее яиц в самом начале.

текстовый задача математика познавательный

Ответ: 15 яиц.

Заметим, что полученный ответ следует проверить: 1-му покупателю продано 152 + 0,5 = 8 яиц, после чего осталось 7 яиц, 2-му покупателю продано 72 + 0,5 = 4 яйца, после чего осталось 3 яйца, 3-му покупателю продано 32 + 0,5 = 2 яйца, после чего осталось 1 яйцо, 4-му покупателю продано 12 + 0,5 = 1 яйцо, после чего не осталось ничего.

3. Схематическая модель — это краткая запись задачи (в методической литературе рассматриваются различные виды краткой записи). Например: «Средний из трех братьев старше младшего на два года, а возраст старшего брата превышает сумму лет двух остальных братьев четырьмя годами. Найти возраст каждого брата, если вместе им 96 лет»

Схематическая запись: Первому брату x – лет, второму 2+x, а третьему x+2+x+4

3. Осуществление плана решения задачи

Выбрав какой-нибудь метод решения, учащиеся переходят к его выполнению, т. е. к третьему этапу решения задачи.

Выполнение плана решения задачи представляется учеником устно или письменно (целиком или фрагментарно). Иногда выполняемые записи или построения сопровождаются устным комментарием.

4. проверка решения задачи

Способов проверки решения задачи много:

Самый элементарный – прикидка ответа (установление границ искомого числа). Прикидка позволяет заметить неправильность рассуждения, несоответствие между величинами, но для многих задач она не применима.

Самый полезный, универсальный – составление и решение обратной задачи. Этот способ проверки развивает мышление, способность рассуждать, но является громоздким и отнимает много времени.

Самый надежный способ проверки – решение задачи другим способом. Во второй главе приведено множество задач, решенных двумя способами.

6. Дополнительная работа над решенной задачей.

Эффективным средством формирования творческой активности и мышления учащихся, дающим возможность более полно реализовать обучающие, развивающие и воспитывающие функции задач, является дополнительная работа над уже решенной задачей:

изменение условия задачи;

постановка нового вопроса;

сравнение содержания данной задачи и ее решения с содержанием и решением другой задачи;

анализ выполненного решения;

обоснование правильности решения;

составление задач по аналогии.

Таким образом, практическая ценность обучения школьников решению текстовых задач разнообразными методами в современных условиях заключается совсем не в том, что это обучение раз и навсегда вооружит их примерами решения различных задач, возникающих на практике и в дальнейшем обучении, а в том, что оно обогатит их опыт мыслительной деятельности. Использование на уроках математики старинных занимательных задач способствует развитию мышления и речи, развитию сообразительности и памяти.

§3. Активизация познавательной деятельности учащегося. Познавательный интерес

Обучение – самый важный и надежный способ получения систематического образования. Оно отражает все существенные свойства педагогического процесса (двусторонность, направленность на всестороннее развитие личности, единство содержательной и процессуальной сторон).

Будучи сложным и многогранным, специально организуемым процессом отражения в сознании учащегося реальной действительности, обучение есть не что иное, как специфический процесс познания, управляемый педагогом. Именно направляющая роль учителя обеспечивает полноценное усвоение учащимися знаний, умений и навыков, развитие их умственных сил и творческих способностей.

Проблема активизации познавательной деятельности учащихся одна из актуальных задач педагогики.

Познавательная деятельность – это единство чувственного восприятия, теоретического мышления и практической деятельности. Она осуществляется на каждом жизненном шагу, во всех видах деятельности и социальных взаимоотношений учащихся (производительный и общественно полезный труд, ценностно-ориентационная и художественно-эстетическая деятельность, общение), а также путем выполнения различных предметно-практических действий в учебном процессе (экспериментирование, конструирование, решение исследовательских задач и т.п.). Но только в процессе обучения познание приобретает четкое оформление в особой, присущей только человеку учебно-познавательной деятельности или учении.

Обучение всегда происходит в общении и основывается на вербально-деятельностном подходе. Слово одновременно является средством выражения и познания сущности изучаемого явления, орудием коммуникации и организации практической познавательной деятельности учащихся. 

Обучение, как и всякий другой процесс, связано с движением. Оно, как и целостный педагогический процесс, имеет задачную структуру, а, следовательно, и движение в процессе обучения идет от решения одной учебной задачей к другой, продвигая учащегося по пути познания: от незнания к знанию, от неполного знания к более полному и точному. Обучение не сводится к механической «передаче» знаний, умений и навыков, т.к. обучение является двусторонним процессом, в котором тесно взаимодействуют педагоги и учащиеся: преподавание и учение.

Отношение учащихся к учению преподавателя обычно характеризуется активностью. Активность – это такое качество деятельности, которое характеризуется высоким уровнем мотивации, осознанной потребностью в усвоении знаний и умений, результативностью, она определяет степень (интенсивность, прочность) «соприкосновения» обучаемого с предметом его деятельности.

В структуре активности выделяются следующие компоненты: · готовность выполнять учебные задания; · стремление к самостоятельной деятельности; · сознательность выполнения заданий; · систематичность обучения; · стремление повысить свой личный уровень и другие.

С активностью непосредственно сопрягается еще одна важная сторона мотивации учения учащихся – это самостоятельность, которая связана с определением объекта, средств деятельности, её осуществления самим учащимся без помощи взрослых и учителей. Познавательная активность и самостоятельность неотделимы друг от друга: более активные школьники, как правило, и более самостоятельные; недостаточная собственная активность учащегося ставит его в зависимость от других и лишает самостоятельности.

По мнению Т.И. Шамовой [36] познавательная активность – одно из ведущих качеств личности, проявляющееся в направленности и устойчивости познавательных интересов, стремлении к эффективному овладению знаниями и способами деятельности, в мобилизации волевых усилий на достижение учебно-познавательной цели. Здесь в комплексе появляются эмоциональные, интеллектуальные и нравственно-волевые процессы. Это качество деятельности личности формируется главным образом в процессе познания, которое по своей природе связано с целенаправленной активностью субъекта. В данном случае активность выступает как средство и условие достижения цели. И, наконец, приведение субъекта в активное состояние является результатом его взаимодействия с внешней средой.

В педагогических целях целесообразно понимать, что познавательная активность носит индивидуальный характер. Именно потому, что мышление, например, есть мышление данного определенного индивида, всегда остается его мышлением, определяемым его индивидуальностью и теми отношениями, в рамках которых он живет.

С учетом тенденций преобразования школы и общества Т.И. Шамова предлагает различать уровни познавательной активности, во-первых, по отношению ученика к учению, которое проявляется в интересе к содержанию усваиваемых знаний и самому процессу деятельности, во-вторых, по стремлению проникнуть в сущность явлений и их взаимосвязей, а также овладеть способами деятельности, а, в-третьих, по мобилизации учеником нравственно-волевых усилий на достижение цели деятельности.

Опираясь на эти показатели, она выделила три основных уровня познавательной активности и предложила следующие характеристики:

Первый уровень – воспроизводящая активность – характеризуется стремлением ученика понять, запомнить и воспроизвести знания, овладеть способом их применения по образцу. Критерием этого уровня активности может служить стремление ученика понять изучаемое явление, которое проявляется на уроке в обращении к учителю с вопросом, в практической деятельности по выполнению заданий учителя (работа с печатным материалом, дидактическими средствами обучения, решение задачи и т.д.), в систематическом выполнении домашней работы. Этот уровень активности отличается неустойчивостью волевых усилий школьника. Характерным показателем первого уровня активности является отсутствие у учащихся интереса к углублению знаний, проявляющееся, например, в отсутствии вопросов типа «почему?». При организации воспроизводящей деятельности учитель пользуется объяснительно-иллюстративным методом преподавания, что и обеспечивает воспроизводящую активность ученика.

Второй уровень – интерпретирующая активность. Она характеризуется стремлением ученика к выделению смысла изучаемого содержания, проникновению в сущности явления, стремлением познать связи между явлениями и процессами, овладеть способами применения знаний в измененных условиях. Критерием оценки сформированности этого уровня активности будет являться наличие у школьника стремления узнать у учителя или из другого источника причину возникновения явления, проявляющегося в постановке вопросов типа «почему?», умение объяснить самому природу возникновения явлений, объяснить их взаимосвязь, умение применить знания в измененной ситуации, где образец нужно узнать и для этой цели необходимо самому привести предварительные преобразования с учебным материалом. Характерным показателем второго уровня познавательной активности является большая устойчивость волевых усилий, которая проявляется в том, что ученик стремиться довести начатое дело до конца, при затруднении не отказывается от выполнения задания, а ищет пути решения. На этом уровне активности ученик проявляет эпизодическое стремление к самостоятельному поиску ответа на заинтересовавший его вопрос. Сущность деятельности педагога, стремящегося развивать познавательную активность школьников на втором уровне, связана с использованием информационно-поисковых методов обучения, что и обеспечивает частично-поисковый характер деятельности ученика.

Третий уровень – творческий уровень активности – характеризуется интересом и стремлением ученика не только проникнуть глубоко в сущность явлений и их взаимосвязей, но и найти для этой цели новый способ. На этом уровне активности учащиеся проявляют стремление применить знания в новой ситуации, т.е. произвести перенос знаний и способов деятельности в условия, которые до сих пор школьнику не были известны. Критерием оценки сформированности третьего уровня познавательной активности может служить интерес ученика к теоретическому осмыслению изучаемых явлений и процессов, к самостоятельному поиску решения проблем, возникших в процессе практической и познавательной деятельности. Характерная особенность этого уровня активности – проявление высоких волевых качеств ученика, упорство и настойчивость в достижении цели, широкие и устойчивые познавательные интересы. Данный уровень активности обеспечивается возбуждением высокой степени рассогласования между тем, что ученик знал, что уже встречалось в его опыте, и новой информацией, новым явлением. Педагогическим средством, позволяющим включить указанный механизм в действие, является организация исследовательской деятельности учащихся.

Понятие познавательной активности тесно связано с понятием активизации учебно-познавательной деятельности, которая рассматривается как процесс создания определенных условий обучения, способствующих повышению познавательного потенциала школьника.

Познавательный интерес

Познавательный интерес выступает как ценнейший мотив учебной деятельности школьников, и это наиболее существенное его проявление. Он усиливает и углубляет другие познавательные мотивы, с которыми он переплетается и взаимодействует: возможность получать знания, узнавать новое, успехи в учении и др.

Также познавательный интерес взаимодействует и с моральными мотивами, главным образом с чувством долга и ответственности. Познавательный интерес выступает не только как мотив и средство обучения, но и как устойчивое качество личности. Пытливость, любознательность, готовность к познавательной деятельности, “жажда знаний” - все это различные выражения познавательной направленности личности, в основе которой лежит познавательный интерес, определяющий активное отношение к миру и к процессу его познания. Познавательный интерес определяет активность в учении, инициативу в постановке познавательных целей. Он определяет поисковый, творческий характер любого вида познавательной деятельности, благоприятствует формированию способностей к творчеству в самых разных видах деятельности.

Г. И Щукина так определяет познавательный интерес: «Познавательный интерес – это избирательная направленность личности, обращенная к области познания, к ее предметной стороне и самому процессу овладения знаниями». [37]

Особое значение, которое учёные придают познавательному интересу, связано с его важностью для обучения. Важность состоит в том, что познавательный интерес является одним из главных мотивов обучения. Так по данным Г. И. Щукиной познавательный интерес фигурирует среди других мотивов обучения как центральный. [37]

Г. И. Щукина сформулировала признаки, отличающие познавательный интерес от других мотивов учения:

1. Познавательный интерес — наиболее предпочитаемый школьниками мотив среди других мотивов учения.

2. Познавательный интерес как мотив учения «раньше и более осознаётся школьниками».

3. Познавательный интерес как мотив носит «бескорыстный характер».

4. Познавательный интерес, «создавая внутреннюю среду развития, существенно меняет силу деятельности, влияет на её характер протекания и результат».

5. Познавательный интерес, развивается в кругу других мотивов и взаимодействует с ними.

Большую роль для формирования интереса к изучению математики играет личность учителя, причем наиболее важной чертой в этом является его увлечённость предметом и преподаванием, желание учителя поверить в возможности ученика, готовность прийти ему на помощь. Учитель должен быть сдержан и терпелив и никогда не допускать грубости по отношению к ученику.

Благотворно влияет на формирование интереса поощрение учителя, его похвала.

Поэтому, задача учителя: сформировать познавательный интерес как устойчивый мотив познавательной деятельности, что составляет прочную основу и направленности личности и её отношение к учению, к духовным ценностям.

Учение – основа развития познавательных интересов учащихся. В учебном процессе, организующем и направляющем познавательную деятельность школьника, заключены важнейшие условия и возможности прямого и косвенного влияния на познавательный интерес. Эти влияния, выступающие как стимулы познавательного интереса систематически и повседневно формируют не только ситуативный интерес, но и содействуют становлению его как самого значимого мотива познавательной деятельности.

Стимуляция познавательных интересов в учебном процессе имеет разные источники и, чтобы управлять формированием интереса, учитель должен ясно осознавать, что именно способствует их возникновению и укреплению.

По мнению Г.И. Щукиной существует три важнейших источника стимуляции познавательных интересов [37]:

1) Содержание учебного материала вызывает удивление перед новыми открытиями, уважение к науке и её представителям, понимание значимости науки для жизненной и общественной практики.

2) Организация познавательной деятельности – рациональная организация обучения рождает удовлетворение собственным продвижением, стремление к преодолению трудностей.

3) Отношения, которые складываются в учебном процессе между учителем и учащимися – учение с учителем, товарищами, в результате чего складываются многозначительные отношения, сопутствуют возникновению иного строя моральных и интеллектуальных переживаний, являющихся также сильными побудителями познавательного интереса. Здесь возникают коллективные сопереживания, радость за успех товарища, стремление оказать ему помощь.

Повышение интереса на уроках математики может достигаться следующим образом:

1) Обогащение содержания материалом по истории науки.

2) Решение задач повышенной трудности и нестандартных задач.

3) Подчеркивание силы и изящества методов вычислений, доказательств, преобразований и исследований.

4) Разнообразие уроков, нешаблонное их построение, включение в уроки элементов, придающих каждому уроку своеобразный характер, использование Т.С.О., наглядных пособий, разнообразие устного счета.

5) Активизация познавательной деятельности учащихся на уроке с использованием форм самостоятельной и творческой работы.

6) Использование различных форм обратной связи: систематическое проведением опросов, кратковременных устных и письменных контрольных работ, различных тестов, математических диктантов наряду с контрольными работами, предусмотренными планом.

7) Разнообразие домашнего задания.

8) Установление внутри и межпредметных связей, показом и разъяснением применения математики в жизни и в производстве.

Развитие познавательного интереса на уроках математики.

Интерес к учебному предмету – направленность личности на процесс овладения знаниями, избирательно обращенная к определенному учебному предмету (к предмету математика). Интерес к учебному предмету выступает как разновидность, частный случай познавательного интереса, базирующегося на специфической человеческой потребности в новых впечатлениях, новой информации. Выделение интереса к учебному предмету как особого вида познавательного интереса обусловлено спецификой учебной деятельности в среднем и старшем звеньях школы.

Любой уровень динамики развития познавательного интереса имеет свой основной признак, отличающий его от других уровней. Выделим четыре уровня развития познавательного интереса к урокам математики: любопытство, любознательность, склонность к математическим дисциплинам, устойчивый интерес к обучению.

Раскроем основные диагностические признаки и проявления интереса к учебной деятельности у учащихся на каждом уровне.

1.Любопытство. Эпизодический интерес к внешней стороне задач и занимательному материалу. Интересующий предмет непостоянен. Проявляется у учащихся в виде наблюдения различного рода мероприятий, возможно кратковременное участие в них, если они чем-либо вызывают положительные эмоции. Вне яркого, занимательного материала интерес отсутствует. Низкий познавательный интерес к уроку математики.

2.Любознательность. Положительная реакция на содержательную сторону задачи и занимательного материала вообще. Диапазон интересов сужается. Интерес концентрирован на одном объекте. Обучаемые стремятся к познанию содержательной стороны объекта: интересуются условиями, содержанием предмета. Однако интерес к математике ситуативен. Учащиеся оживляются, задают вопросы, включаются в деятельность, но интерес не устойчив, быстро угасает. Средний познавательный интерес к уроку математики.

3.Склонность к математическим дисциплинам. Стремление к открытию, новые пути реализации полученных решений. Проявляется у обучаемых в активном стремлении участвовать в различных видах деятельности: выполнять долговременные поручения и дополнительные задания, посещать факультативы и клубы. Высокий познавательный интерес.

4.Устойчивый интерес к математике. Потребность в апробировании теоретических знаний на основе имеющейся базы. Интерес к математике имеет профессиональную направленность. Учащиеся положительно оценивают собственные способности, стремятся совершенствовать собственные умения и навыки. Высший познавательный интерес к урокам математики.

Поэтому, можно сделать вывод, о том, что формирование положительных мотивов учения в качестве одной из самых главных в обучении математике, т.к. высокий уровень мотивации учебной деятельности на уроке и интереса к учебному предмету – это первый фактор, указывающий на эффективность современного урока.

В моей работе был рассмотрен один из факторов побуждения учащихся к активизации познавательной деятельности - занимательность учебного материала. Занимательные текстовые старинные задачи интересны не только формулировкой, но и методами решения, некоторые решения очень необычны, такие как решение с конца или метод ложных положений. Проанализировав учебную литературу, мы пришли к выводу, что можно дополнить представленный задачный материал старинными занимательными задачами. Эти задачи были отнесены к определенным разделам изучения. Они могут использоваться как при изучении нового материала, так и при закреплении. На уроке, где закрепляется и повторяется материал, ученики как правило, теряют интерес и внимание, ведь нового они ничего не узнают. Поэтому в учебный материал таких уроков можно и нужно включать старинные занимательные текстовые задачи, которые представлены в следующей главе.

§4. Анализ учебно-методической литературы

С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин (5, 6, 7, 8 кл.)

В данных учебниках используются специальные символы для обозначения типа задания. Излагаемый материал учебника представлен в виде тем, все из которых начинаются с определения, введения какого-то понятия, изложения правила, каких-либо свойств, просто объяснительного текста по новой теме. В учебнике имеется достаточное число сложных задач. Для каждого нового действия, приема решения задач в учебнике имеется достаточное число упражнений, которые не перебиваются упражнениями на другие темы. А упражнения для повторения ранее пройденного материала помещены в конце учебника отдельным пунктом.

В учебниках имеется множество нестандартных развивающих старинных задач, которые находятся в основном в разделах «Дополнительные задачи», либо «Занимательные задачи», и при введении и нового материала не используются; также имеются исторические справки, такие как: обозначение дробей и записи чисел, вавилонский способ записи дробей без знаменателей, исторические сведения о выдающихся математиках разных веков, использование комплексных чисел, решения квадратных уравнений в древние времена и т.д.

Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварбурд (5, 6, 8 класс) Знакомство с новым материалом в учебнике разбито на части, после каждой из которых учащимся предлагается решить несколько заданий на новую тему. После изложения нового материала учащимся предлагается ответить на ряд вопросов, проверить, как они поняли и усвоили материал параграфа.

Практическая часть учебника представлена различными типами заданий, отмеченных каждый своим специальным символом. Задания располагаются по возрастанию от легких к сложным.

Излагаемый материал учебника представлен в виде тем, которые начинаются с ввода каких-то понятий, определений и правил. Зачастую введение нового материала начинается с постановки проблемной ситуации – учащимся предлагаются задания, в процессе выполнения которых они самостоятельно или с помощью учителя приходят к новым определениям, правилам или новым свойствам.

Исторических задач в учебнике нет, но в каждом встречаются после определенных параграфов рассказы об истории возникновения и развития математики. Например, говорится о достоинствах монет, о появлении дробей, о записи десятичных дробей в XV веке, что такое фигурные числа и т.д.

И.И. Зубарева, А.Г. Мордкович (5, 6 классы)

В данных учебниках к подаче нового материала предпринят подход, называемый методом целесообразных задач, суть которого состоит в том, что учащимся предлагается система заданий, в процессе выполнения которых они получают возможность самостоятельно или с помощью учителя познакомиться с новым свойством, сформулировать правило, «придумать» новый термин и, даже порой, найти путь доказательства некоторого утверждения.

Кроме самой структуры ознакомления с новым материалом несомненным преимуществом этого учебника является наличие заданий на проверку истинности высказываний.

Практическая часть учебника представлена различными типами заданий, отмеченными каждый своим специальным символом. Задания на повторение ранее пройденного материала, которые позволяют проверить усвоение учениками минимума по соответствующей теме, содержатся в конце параграфа.

Учебники содержат множество увлекательных текстовых задач, задач современного характера (упоминается мотоцикл «Харлей Дэвидсон» и т.п.), также есть задачи с участием сказочных персонажей (Вини-Пух, Карлсон, кот Матроскин и т.п.)

А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская (7, 8 классы)

Комплект состоит из двух частей – учебника и задачника. В данных учебниках используются специальные символы для обозначения типа задания. Излагаемый материал учебника представлен в виде тем, все из которых начинаются с определения, введения какого-то понятия, изложения каких–либо свойств, алгоритма решения, замечания, после чего всегда приводятся примеры помогающие лучшему пониманию новой темы. Стиль изложения учебников легкий, доступный; в то же время изложение характеризуется четкостью, алгоритмичностью. Решение практически всех текстовых задач оформлено в виде трех этапов:

Первый этап. Составление математической модели.

Второй этап. Работа с математической моделью.

Третий этап. Ответ на вопрос задачи.

А также рассматриваются виды математических моделей: словесная, алгебраическая, графическая и геометрическая модели.

Задачники полностью соответствуют структуре изложенных тем в учебнике.

Г.В. Дорофеев. С.Б. Суворова, Е.А. Бунимович и др. (5, 6, 7, 8)

Введение нового материала начинается с примеров, которые дают четкое и наглядное представление будущего определения или понятия, подлежащего изучению. После каждого параграфа дается достаточное количество примеров на изученную тему. Также имеются пункты - проверь себя, для тех, кому интересно, вопросы для повторения и задания для самопроверки. В учебниках имеется небольшое количество старинных задач, которые находятся в разделах для тех, кому интересно, дополнительные задачи, также имеется сведения из истории математики.

Все представленные выше комплекты в большей или меньшей мере содержат материал, способствующий развитию познавательного интереса учащихся. Во второй главе нами будут предложены текстовые занимательные старинные задачи, дополняющие задачный материал действующих учебников по некоторым темам.

Глава 2. Применение занимательного задачного материала на уроках математики

Во второй главе представлены текстовые старинные занимательные задачи - это задачи с интересным содержанием или интересными способами решения. Элемент занимательности облегчит обучение. 

Данные задачи разделены по следующим разделам:

задачи, которые решаются с помощью различных действий с обыкновенными и десятичными дробями;

задачи, решение которых может быть осуществлено с конца;

задачи, решаемые с помощью составления линейных уравнений;

задачи, решаемые с помощью составления систем линейных уравнений;

задачи, решаемые с помощью составления квадратных уравнений;

задачи по теме «Алгебраические дроби» (8класс).

Ко всем задачам приведены решения, причем многие из этих решений относятся к старинным методам и, как правило, не представлены в современных учебных пособиях. Однако, на наш взгляд, как было сказано в первой главе, демонстрация учащимся таких методов способствует развитию интереса к математике, даже тех учеников, которые увлечены гуманитарными науками, так как приводиться краткая историческая справка к той или иной задаче.

1. Задачи, которые решаются с помощью различных действий с обыкновенными и десятичными дробями

В этом разделе подобраны задачи, которые решаются с помощью различных действий с обыкновенными и десятичными дробями. Для решения учащиеся предварительно должны уметь:

выполнять арифметические действия с натуральными числами, обыкновенными и десятичными дробями;

решать текстовые задачи арифметическим способом; составлять графические и аналитические модели реальных ситуаций;

составлять алгебраические модели реальных ситуаций и выполнять простейшие преобразования буквенных выражений;

переходить от одной формы записи чисел к другой; представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной;

решать текстовые задачи, включая задачи, связанные с отношением величин и дробями;

решать уравнения методом отыскания неизвестного компонента действия.

В этом разделе представлены исторические задачи, которые мы рекомендуем для закрепления нового материала. Первую задачу лучше дать после изучения темы «умножение и деление смешанных дробей», вторую задачу после темы «нахождение дроби от числа», третью - «задачи на совместную работу», четвертую после изучении главы «обыкновенные и десятичные дроби», пятую после изучения темы «отношения и пропорции».

Лев съел овцу одним часом, а волк съел овцу в два часа, а пес съел овцу в три часа. Ино хочешь ведати, сколько бы они все три – лев и волк и пес – овцу съели вместе вдруг и сколько бы они скоро ту овцу съели сами, сочти ми?

Решение: За один час лев, волк и пес вместе съели бы овцы. Действительно, (овцы)

Тогда одна овца ими вместе будет съедена за часа.

Задача взята из математической рукописи XVII в.

Сам составитель решал эту задачу так: за 12 часов лев съедает 12 овец, волк – 6, а пес – 4. Всего же они съедят за 12 часов 22 овцы. Следовательно, в час они съедят овцы, а одну овцу все вместе – в часа.

Некто пришел в ряд, купил игрушек для малых ребят: за первую игрушку заплатил часть всех своих денег, за другую остатка от первой покупки, за третью игрушку заплатил остатка от второй покупки, а по приезде в дом нашел остальных в кошельке денег 1 руб. 92 коп. Спрашивается, сколько денег в кошельке было и сколько за вторую игрушку денег заплачено?

Решение:

- остаток;

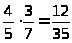(денег) – за первую игрушку;

- остаток от второй игрушки;

(денег) – стоит вторая игрушка;

(денег) – осталось в кошельке;

(руб.) было в кошельке;

(руб.) – стоила 1 игрушка;

(руб.) стоила 2 игрушка;

(руб.) стоила 3 игрушка.

3. Один человек выпьет кадь пития в 14 дней, а с женою ту же кадь в 10 дней. И ведательно есть, в колико дней жена его особенно выпьет ту же кадь?

Решение: Решение этой задачи очень простое. Человек выпивает в день кади, а вместе с женой - кади. Следовательно, жена выпивает в день кади. Таким образом, всю кадь жена выпьет за 35 дней.

4. Некий человек нанял работника на год, обещав ему дать 12 рублей и кафтан. Но тот по случаю, поработав 7 месяцев, восхотел уйти и попросил достойную плату с кафтаном. Ему дали по достоинству 5 рублей и кафтан. Какой цены был оный кафтан?

Решение: За год работник должен был получить 12 рублей и кафтан, то есть за каждый проработанный месяц ему должны начислять 1 рубль и стоимости кафтана. За проработанные 7 месяцев работник должен был получить 7 рублей и стоимости кафтана, а получил 5 рублей и кафтан. Следовательно, стоимости кафтана соответствуют 2 рублям. Таким образом, цена кафтана была (рубля).

5. Древнеримская задача (II в.)

Некто, умирая, завещал: «Если у моей жены родится сын, то пусть ему будет дано имения, а жене – остальная часть. Если же родиться дочь, то ей , а жене ». Родилась двойня – сын и дочь. Как же разделить имение?

Решение: Имение нужно разделить между сыном, женой и дочерью пропорционально числам 4:2:1 (1 - так как дочери достанется в 2 раза меньше чем матери, 2 – так как матери достанется в 2 раза меньше чем сыну, а сыну - следовательно 4, так как у сына по условию в два раза больше чем матери). Меньше всего дочке (1 доля), потом маме (2 доли), а потом сыну (4 доли), значит всего долей 7, получается так: , , .

2. Задачи, решение которых может быть осуществлено с конца

Учащиеся должны уметь:

те же пункты что и в первом разделе;

приводить дроби к общему знаменателю;

находить дробь от числа и число по его дроби.

Эти задачи могут применяться на уроках итогового повторения в 6 -8 классах. Задачи такого характера заставляют учащихся искать нестандартные пути решения, развивают мышление и интерес к предмету.

1. Назови мне число, которое, умноженное на три, сложенное с произведения, разделенное на 7, уменьшенное на частного, уменьшенного на само себя, уменьшенное на 54, после извлечения квадратного корня, прибавления 8 и деления на 10 будет равняться 2.

Решение: Индийские математики пользовались арифметическим приемом, который они широко применяли. Это – «правило обращения», или «правило инверсии». Суть его заключается в следующем: если нужно найти число, которое после ряда операций приводит к некоторому известному числу, то для этого необходимо над этим последним числом произвести в обратном порядке все обратные операции.

Решение данной задачи заключается в том, что, начиная с числа 2, производят обратные действия в обратном порядке:

Число 28 и есть искомое.

2. Найти число, которое, будучи умножено на 3, а затем разделено на 5, увеличено на 6, после чего из него извлечен корень квадратный, отнята единица и результат возведен в квадрат, дает 4.

Решение:

Следуя «правилу обращения», получим:

; 2+1=3; 32=9; 9-6=3; ;

Число 5 и будет искомым. «Правило обращения», которым пользовались индийские ученые, стало широко известно и за пределами Индии. Позднее им стали пользоваться сначала в странах Арабского халифата, а потом и в Европе.

3. Французская задача XVII в.

Трое имеют по некоторой сумме денег каждый. Первый дает из своих денег двум другим столько, сколько есть у каждого. После него второй дает двум другим столько, сколько каждый из них имеет. Наконец, и третий дает двум другим столько, сколько есть у каждого. После этого у всех троих, оказывается, по 8 экю². Спрашивается, сколько денег было у каждого вначале.

Рассуждения удобно начать с конца и решение представить в виде следующей таблицы:

I	8
II	8
III	8

4. Одна женщина отправилась в сад собрать яблоки. Чтобы выйти из сада, ей нужно было пройти 4 двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину собранных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся яблок. Так же она поступила и с третьим стражником; а когда она поделилась яблоками со стражником у четвертых дверей, то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?

Решение:

Стандартное решение.

Ответ: 160 яблок, женщина собрала в саду.

Решение с конца.

1) 10 яблок – это половина того, что осталось перед 4-ой дверью, , значит, 20 яблок осталось перед четвертыми дверями.

2) 20 яблок – это половина того что осталось перед 3-ей дверью, , значит, 40 яблок осталось перед третьими дверями. 

3) 40 яблок – это половина того что осталось перед 2-ой дверью, , значит, 80 яблок осталось перед второй дверью.

4) 80 яблок – это половина того что осталось перед 1-ой дверью, , значит, 160 яблок было перед первой дверью.

5. Чешская задача

По преданию, основательница чешского государства принцесса Либуша обещала отдать свою руку тому, кто сумеет решить задачу: «Если бы я дала первому жениху половину слив из этой корзины и еще одну сливу, второму жениху половину оставшихся слив и еще одну сливу, а оставшиеся сливы поделила пополам и половину их и еще три сливы дала бы третьему жениху, то корзина опустела бы». Сколько слив в корзине?

Решение:

Стандартное решение.

Пусть первоначально в корзине было x слив. Первый жених получил бы слив

Второй

Третий

Так как

То

,

Ответ: у принцессы Либуши первоначально было 30 слив.

Решение с конца:

1) После того как принцесса Либуша отдала третьему жениху половину слив и еще 3, у нее ничего не осталось, следовательно 3 сливы и были половиной того что осталось перед встречей с третьим женихом.

3+3=6 слив, было перед третьим женихом.

2) Так как перед встречей со вторым женихом осталось 6 слив и еще одна, что являлось половиной того что было перед встречей со вторым женихом, то

слив, осталось перед вторым женихом.

3) Перед встречей с первым женихом осталось 14 слив и еще одна, что являлось половиной того что было у принцессы первоначально, т.е.

слив, первоначально.

3. Задачи, решаемые с помощью составления линейных уравнений

Задачи, представленные в данном разделе имеют довольно сложную формулировку и поэтому они могут быть использованы скорее на уроках обобщения, закрепления и в качестве индивидуальных домашних заданий, нежели на уроках введения нового материала.

Учащиеся должны уметь:

использовать символический язык алгебры, выполнять тождественные преобразования простейших буквенных выражений, применять приобретенные навыки в ходе решения задач;

решать линейные уравнения, применять данные умения для решения задач.

1. Задача из арифметики Л.Ф. Магницкого³

У некоторого человека были для продажи вина двух сортов. Первое ценою 10 гривен⁴ ведро, второе же – по 6 гривен. Захотелось ему сделать из тех двух вин, взяв по части, третье вино, чтобы ему цена была по 7 гривен. Какие части надлежит из тех двух вин взять к наполнению ведра третьего вина ценою 7 гривен?

Решение:

Стандартное решение.

Пусть для составления одного ведра требуемой смеси нужно взять ведер первого сорта и ведер второго сорта. Первая часть вина стоит 10x гривен, а вторая гривен.

Составим уравнение:

,

откуда

x=, .

Итак, нужно взять ведра вина по 10 гривен и ведра вина по 6 гривен за ведро.

Старинный способ решения:

Запишем цены вин каждого сорта и цену смеси так:

Вычислить прибыль 7-6=1 и убыток 10-7=3 на каждом ведре и запишем результат по линиям:

Таким образом, 3 части из четырех приходиться на более дешевое вино и 1 часть – на более дорогое.

2. Найти число, если известно, что от прибавления к нему его и вычитания от полученной суммы ее трети получается число 10.

Решение задачи сводиться к решению уравнения:

Ответ: число 9

Задача из Акмимского папируса (VI в.)

Некто взял из сокровищницы . Из того, что осталось, другой взял , оставил же он в сокровищнице 150. Сколько было в сокровищнице первоначально?

Решение:

4. Требуется число 100 разделить два раза так, чтобы большая его часть от первого деления была вдвое более меньшей части от второго деления и чтобы большая часть от второго деления была втрое более меньшей части от первого деления.

Решение: Обозначим меньшую часть от второго деления через x, тогда большая часть от первого деления будет 2x. Найдем теперь меньшую часть от первого деления. Она будет равна (100- 2x). Следовательно, большая часть второго деления равняется (300-6x). Ясно, что обе части от второго деления должны составить 100, то есть:

,

откуда x=40

Следовательно, результат первого деления: меньшая часть равна 20, большая часть – 80.

Результат второго деления: меньшая часть равна 40, большая часть – 60.

5. Задача из «Греческой Антологии»⁵

- Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

- Вот сколько, - ответил философ, - половина изучает математику, четверть – музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины.

Решение:

Задача сводится к уравнению:

Следовательно, школу Пифагора посещают 28 человек, что и нужно было найти.

6. Задача из «Греческой Антологии»

Здесь погребен Диофант. И камень могильный

При счете искусном расскажет нам,

Сколь долог был его век.

Велением бога он мальчиком был шестую часть своей жизни;

В двенадцатой части затем, прошла его светлая юность.

Седьмую часть жизни прибавим – перед нами очаг Гименея.

Пять лет протекли, и прислал Гименей ему сына.

Но горе ребенку! Едва половину он прожил

Тех лет, что отец, как скончался несчастный.

Четыре года страдал Диофант от утраты такой тяжелой

И умер, прожив для науки. Скажи мне,

Скольких лет достигнув, смерть воспринял Диофант?

Решение: Условие задачи приводит к уравнению

Следовательно, Диофант умер в 84 года.

7. Задача из трактата «Начала искусств вычисления»⁶

Пятая часть пчелиного роя сидит на цветке кадамба, одна треть на цветках силиндхата. Утроенная разность двух последних чисел направилась к цветкам кутая. И осталась еще одна пчелка, летающая взад и вперед, привлеченная ароматом жасмина и пандануса. Спрашивается, сколько всего пчел?

Решение: Задача сводиться к уравнению

Следовательно, всего было 15 пчел.

8. Некто сказал своему другу: «Дай мне сто рупий, и я буду вдвое богаче тебя», на что последний ответил: «Если ты мне дашь только 10 рупий, я стану вшестеро богаче тебя». Спрашивается, сколько было у каждого?

Решение: Пусть у первого было рупий, а у второго рупий. Ясно, что первое условие будет выполнено. Имея в виду второе условие, находим

Следовательно, у первого было 140-100=40 рупий, у второго 70+100=170 рупий.

9. Купец, будучи должен 753 руб., попросил у того же заимодавца еще 303 руб. Последний согласился удовлетворить его просьбу на условии, чтобы весь долг был уплачен в течении 8 месяцев и притом так, чтобы должник, внеся к концу первого месяца некоторую сумму на покрытие части долга, ежемесячно увеличивал свой взнос на половину, т.е. уплатил бы во второй месяц полторы таких суммы, в третий месяц две таких же суммы, в четвертый две с половиной и т.д. Обсудив эти условия, купец согласился на них. Спрашивается, какую сумму должен он внести в первый месяц и сколько в каждый из следующих месяцев?

Решение:

Пусть к концу первого месяца купец должен внести x руб., тогда

(рублей)

2–ой месяц 48+24=72

3-ий месяц 48+48=96

4-ый месяц 48+48+24=120

5-ый месяц 48+48+48=144

6-ой месяц 48+48+48+24=168

7-ой месяц 48+48+48+48=192

8-ой месяц 48+48+48+48+24=216

10. Задача из «Курса алгебры» А.Н. Страннолюбского.

Два работника прожили у хозяина равное время; один из них получал по 15, а другой по 10 рублей в неделю. При окончательном расчете оказалось, что первый работник должен получить более второго именно на ту сумму, которую он забрал в течение работы, а забрал он сперва 4 руб., потом 3 руб., и наконец 7 рублей. Сколько продолжалась работа?

Решение:

Пусть x - число недель, в течении которых продолжалась работа, (15-10) разница в полученных деньгах, тогда:

(недели)

11. Отец завещал своего имения сыну и дочери; из оставшегося затем капитала 2500 руб. должны были пойти на уплату долга, а 3000 руб. в пользу вдовы. Как велик был оставленный отцом капитал и по скольку должны получить сын и дочь?

Решение: Обозначим оставленный отцом капитал через x, тогда

(руб.)

Сыну завещал

Дочери завещал

12. Некто на вопрос о возрасте двух его сыновей отвечал: «Первый мой сын втрое старше второго, а обоим им вместе столько лет, сколько было бы мне 29 лет тому назад; мне теперь 45 лет». Найти лета обоих сыновей.

Решение: Обозначим лета второго сына через x, тогда

4 года второму сыну

А первому (лет)

13. Задача Магницкого

Спросил некто учителя: «Скажи, сколько у тебя в классе учеников, так хочу отдать тебе в учение своего сына». Учитель ответил: «Если придет еще учеников столько же, сколько имею, и пол столько, и четвертая часть, и твой сын, тогда у меня учеников 100». Спрашивается, сколько было у учителя учеников?

Решение:

I способ (стандартное решение)

Пусть было x учеников. Составим уравнение

; (учеников)

II способ

Эту задачу Магницкий решает «фальшивым правилом» (или методом «двух ложных положений»), которому в своей «Арифметике» отводит особое место.

Далее по формуле

Искомое число учеников:

Ответ: 36 учеников.

Метод «двух ложных положений» Сущность этого метода покажем на примере решения уравнения:

(1)

Для решения этого уравнения предположим, что искомое . Подставив x1 в уравнение (1), получим:

(2)

где n1 – первая ошибка правой части уравнения (1). Теперь предположим, что x=x2, тогда, подставив x2 в уравнение (1), получим:

(3)

Вычтем почленно из уравнения (2) уравнение (3) и получим:

(4)

Теперь обе части уравнения (2) умножим на x2 , а обе части уравнения (3) на x1 и затем почленно вычтем полученные уравнения:

(5)

Из уравнения (4) найдём a, а из уравнения (5) найдём b. Так как из исходного уравнения (1) , то получим:

Получили следующее правило, которое арабский автор сформулировал следующим образом:

«Возьми для неизвестного число, которое ты хочешь, назови его первое положение и поступай согласно условию задачи. Если оно подходит к условию, то это и есть неизвестное. Но если оно отклоняется в ту или иную сторону, назови разницу первым отклонением. Затем возьми другое число и назови вторым положением; если оно не удовлетворяет условию, то оно даёт второе отклонение. После этого умножай первое положение на второе отклонение и назови первым результатом; потом второе положение умножай на первое отклонение, это есть второй результат. Если оба отклонения в одно и то же время больше или оба меньше, дели разность двух результатов на разность двух отклонений; если дело обстоит иначе, дели сумму двух результатов на сумму отклонений, частное и есть искомое число».

14. Задача Этьенна Безу⁷

По контракту работникам причитается по 48 франков за каждый отработанный день, а за каждый неотработанный день с них взыскивается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?

Решение: если x – число дней, отработанных работниками, то

Ответ: 6 дней отработали работники в течение 30 дней.

15. Каков возраст братьев?

Средний из трех братьев старше младшего на два года, а возраст старшего брата превышает сумму лет двух остальных братьев четырьмя годами. Найти возраст каждого брата, если вместе им 96 лет.

Решение: Первому брату x – лет, второму 2+x, а третьему x+2+x+4

Получим

Первому 22 года, второму 22+2=24 года.

Третьему 22+24+4=50 лет.

4. Задачи, решаемые с помощью составления систем линейных уравнений

В данном разделе представлены задачи, решение которых осуществляется с помощью составления систем уравнений. Для решения таких задач учащиеся должны уметь:

составлять буквенные выражения и формулы по условиям задач;

осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое;

выражать из формул одну переменную через остальные;

выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями;

выполнять тождественные преобразования рациональных выражений;

решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы.

Данные задачи подходят для изучения параграфа «Системы линейных уравнений». 1 и 2 задачи подходят для проверки полученных знаний учащимся при изучении данной темы. Первую задачу можно давать для проверки как домашнее задание, и на следующем уроке со всем классом разобрать эту задачу, причем это будет делать не учитель, а ученик у доски. Задача под номером два может пойти как самостоятельная работа (проверка знаний, умений, навыков по пройденной теме), она систематизирует и обобщает весь пройденный материал по данной теме. Задачи под номерами 3, 4, 7 могут быть использованы при введении нового материала, в частности задача № 3 позволяет сразу активизировать познавательную деятельность учащихся из-за нестандартного изложения, но, в то же время, она проста для понимания и интересна ученикам. Задачи под номерами 5, 6 лучше использовать при закреплении изученного материала.

1. Задача Евклида⁸

Мул и осёл под вьюком, по дороге с мешками шагали. Жалобно охал осел, непосильною ношей придавлен. Это подметивший мул обратился к сопутчику с речью: «Что ж, старина, ты заныл и рыдаешь, будто девчонка? Нес бы вдвойне я, чем ты, если б отдал одну ты мне меру, если ж бы ты у меня лишь одну взял, то мы бы сравнялись». Сколько нес каждый из них, о геометр, поведай нам это.

Решение: I способ

Если x – груз мула, то (x-1) груз осла, увеличенный на 1, а следовательно, первоначальный груз осла был (x-2). С другой стороны, в два раза больше, чем груз осла, уменьшенный на 1, т.е. . Т.о.,

.

Отсюда, груз мула и груз осла 7-2=5.

II способ (через систему линейных уравнений)

Обозначив через x поклажу осла, а через y – поклажу мула, сводим задачу к системе уравнений с двумя неизвестными

Или

Груз мула y=7, груз осла x=5.

2. Задача Диофанта⁹ (из трактата «Арифметика»)

Найти три числа так, чтобы наибольшее превышало среднее на данную часть наименьшего, чтобы среднее превышало меньшее на данную часть наибольшего и чтобы наименьшее превышало число 10 на данную часть среднего числа.

Решение: Исходя из условий задачи, составим систему

подставим 3-е уравнение в 1-е, получим

в первое уравнение вместо y подставим (3z-30), и рассмотрим только первое уравнение

Подставим z в 3 уравнение и найдем y

И найдем x из второго уравнения

Ответ: , ,

3. Задача Китая, из трактата «Девять отделов искусства счета»

5 волов и 2 барана стоят 11 таэлей¹⁰, а 2 вола и 8 баранов стоят 8 таэлей. Сколько стоят отдельно вол и баран?

Решение: пусть x цена вола, а y – цена барана

Решение задачи сводиться к рассмотрению следующей системы уравнений

Следовательно, один вол стоит 2 таэля, а один баран таэля.

4. Задача из рассказа А.П. Чехова «Репетитор»

Купец купил 138 аршин¹¹ черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное – 3 рубля?

Решение: I способ условие задачи сводится к системе

63 – аршин синего сукна, 75 аршин черного сукна.

II способ Пусть синего сукна было x аршин, тогда черного аршин.

X=63 (аршина) – синего

138-63=75 (аршин) – черного.

Ответ: синего 63 аршина, черного 75 аршин.

5. Задача Леонардо Пизанского¹²

Один говорит другому: «Дай мне 7 динариев¹³, и я буду в 5 раз богаче тебя». А другой говорит: «Дай мне 5 динариев, и я буду в 7 раз богаче тебя». Сколько у каждого?

Решение: условие задачи сводиться к системе

Следовательно, первый имел динария, а второй - динария.

6. Задача из сказки «1001 ночь» (ночь 458)

Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другая расположилась под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: «Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один ин нас слетел к вам, то нас с вами стало бы поровну». Сколько голубей сидело на ветвях и сколько под деревом?

Решение: если x и y – число голубей на дереве и под деревом, то по условию имеем

Ответ: 5 голубей на дереве и 3 голубя под деревом.

7. Задача Адама Ризе¹⁴

Трое торгуют¹⁵ лошадь за 12 флоринов¹⁶, но никто в отдельности не располагает такой суммой. Первый говорит двум другим: «Дайте мне каждый по половине своих денег, и я куплю лошадь». Второй говорит первому и третьему: «Дайте мне по одной трети ваших денег, и я приобрету лошадь». Наконец, третий говорит первым двум: «Дайте мне только по четвертой ваших денег, и лошадь будет моя». Теперь спрашивается, сколько денег было у каждого?

Решение: Пусть x, y, z – количество флоринов соответственно у первого, второго и третьего покупателей. Составим систему

Выразим в первом уравнении и подставим во второе уравнение

Теперь поставим x в первое уравнение, получим

Подставим x и z в третье уравнение и найдем y

Зная y, найдем x и z.

Ответ: , , – количество флоринов соответственно у первого, второго и третьего покупателей.

5. Задачи, решаемые с помощью составления квадратных уравнений

Для решения представленных здесь задач учащиеся должны предварительно уметь:

решать неполные квадратные уравнения;

решать полные квадратные уравнения;

решать приведенные квадратные уравнения;

находить ошибки в решенных уравнениях и исправлять их;

делать проверку.

1. Задача Бхаскары¹⁷:

На две партии разбившись,

Забавлялись обезьяны.

Часть восьмая их в квадрате

В роще весело резвилась.

Криком радостным двенадцать

Воздух свежий оглашали.

Вместе сколько, ты скажешь,

Обезьян там было в роще?

Решение: если обозначим число всех обезьян через x, то задача сводится к решению квадратного уравнения

Прибавляя к обеим частям квадрат 32, будем иметь

После извлечения квадратного корня найдем

В данном случае, говорит Бхаскара, отрицательные единицы первой части таковы, что единицы второй части меньше их, а потому последнее можно считать и положительными и отрицательными, и получаем двойное значение неизвестного: 48 и 16.

Стандартное решение квадратного уравнения:

2. Задача Бхаскары

Сколько обезьян в стае, если квадрат пятой части, уменьшенной тремя, спрятался в пещере, и только одна осталась на виду, взобравшись на дерево?

Решение: задача сводиться к решению квадратного уравнения

и

В заключении Бхаскара делает такое замечание: «Так как есть число отрицательное, то годится только первое решение».

Но комментатор Бхаскары Кришна Бхатта говорил, что если бы по условию вопроса было сказано: одна пятая часть стаи вычитается из трех, то второе решение, а не первое удовлетворяло бы условию.

3. Задача Магавиры¹⁸:

Найти число павлинов в стае, которой, умноженная на себя, сидит на мандариновом дереве, а квадрат остатка вместе с 14 другими павлинами – на дереве тамала.

Решение: задача сводиться к решению квадратного уравнения

, где x – число павлинов в стае.

Отсюда , а не подходит по смыслу задачи.

6. Задачи по теме «Алгебраические дроби» (8 класс)

1. Один путник идет от града в дом, а ходу его будет 17 дней, а другой путешественник от дому во град тот же путь творяше, может пройти в 20 дней, оба же сии человека пойдоша во един и тот же час от мест своих, и ведательно есть, в колико дней сойдуться? (Магницкий)

Решение: Пусть x – км весь путь, тогда км/дн – скорость первого, км/дн – скорость второго

км/дн – скорость сближения

дн

Ответ: встретятся через дней.

2. Задача Ньютона

Некий торговец каждый год увеличивает на одну треть свое состояние, уменьшенное на 100 фунтов, которые ежегодно затрачивает на свою семью. Через три года обнаруживает, что его состояние удвоилось. Спрашивается, сколько у него было денег вначале?

Решение Ньютона. «Чтобы решить вопрос, заметьте, что в нем содержатся в скрытом виде некоторые предложения, которые все должны быть выявлены и выражены».

Словесно	Алгебраически
У торговца имеется состояние, из которого он в первый год затрачивает 100 фунтов	или
Остаток он увеличивает на одну треть	или или
В третий год он опять тратит 100 фунтов и остаток также увеличивает на одну треть, причем оказывается вдвое богаче, чем был в начале	или =2х

Таким образом, вопрос выражается уравнением

приведя которое, мы найдем x

Умножьте уравнение на 27, и вы получите 64х-14800=54х,

Вычтите из обеих сторон 54х, и останется 10х-14800=0 или 10х=14800; разделив на 10, вы найдете, что х=14800. Т.о., состояние торговца вначале, а также его последующая прибыль, или доход, были равны 14800 фунтов.

3. Обмен зайцев на кур.

Крестьянин менял зайцев на кур: брал за всяких двух зайцев по три курицы. Каждая курица снесла яйца – третью часть от числа всех куриц. Крестьянин, продавая яйца, брал за каждые 9 яиц по столько копеек, сколько каждая курица снесла яиц, и выручил 72 копейки. Сколько было кур и сколько зайцев?

Решение: обозначим за x количество кур, которое выменял крестьянин.

Каждая курица снесла, как сказано в условии, яиц и общее число яиц у крестьянина составляет штук.

Каждые 9 яиц крестьянин продал по копейки, то есть одно яйцо за и выручил поэтому копеек, что по условию равно 72 копейки. Из равенства

Находим

Итак, крестьянин выменял 18 кур, а зайцев было у него штук.

Заключение

Практическая ценность обучения школьников решению текстовых задач разнообразными методами в современных условиях заключается совсем не в том, что это обучение раз и навсегда вооружит их примерами решения различных задач, возникающих на практике и в дальнейшем обучении, а в том, что оно обогатит их опыт мыслительной деятельности. Отдельный метод решения задач может быть забыт учащимися. Но развивающиеся в процессе обучения продуктивное мышление и речь, сообразительность и память помогут им не только восстанавливать утраченное, если потребуется, но и находить решения новых встающих перед ними задач.

Таким образом, в современных условиях цели обучения школьников решению текстовых задач должны включать обогащение опыта мыслительной деятельности школьников различными методами рассуждений, воспитание у них умения ориентироваться в различных по своей природе взаимоотношениях величин.

Целью данной дипломной работы было рассмотрение возможности применения занимательного задачного материала для активизации познавательной деятельности учащихся при обучении решению текстовых задач.

Для достижения этой цели была изучена психолого-педагогическая литература по проблеме развития познавательного интереса подросткового возраста. Одним из способов развития познавательного интереса традиционным является использование старинных занимательных задач на уроках математики. Также были выявлены психологические особенности школьников, которые необходимо знать и учитывать учителю при работе с учениками 5 - 8 классов.

Проанализировав содержание учебников по математике для 5 - 8 класса, мы пришли к выводу о возможности дополнения и разнообразия предлагаемого там задачного материала старинными занимательными задачами. Подобные задания способствуют активизации познавательной деятельности учащихся, а также развивают интерес к математике не только детей, увлеченных этим предметом, но и детей, ориентированных на гуманитарные науки, за счет ярко выраженных здесь межпредметных связей (ко многим задачам приводятся исторические справки, есть задачи в стихах и т. п.). Последнее обстоятельство способствует также и расширению мировоззрения учащихся.

Во второй главе диплома приведены старинные текстовые задачи к некоторым разделам программы 5–8 классов, а также методические рекомендации по их использованию. Ко всем задачам приведены решения.

Таким образом, цель дипломной работы, на наш взгляд, достигнута, задачи, поставленные в начале работы, выполнены.

Библиография

1) Алгебра: учеб. для учащихся 8 кл. с углубл. изучением математики [Текст] / [Н.Я. Виленкин, А.Н. Виленкин, Г.С. Сурвилл и др.]; под ред. Н.Я. Виленкина.– 7-е изд., дораб.– М.: Просвещение, 2005.– 303с.: ил.

2) Баврин, И.И. Старинные задачи [Текст] : Кн. для учащихся. / И.И. Баврин, Е.А. Фрибус.– М.: Просвещение, 1994.– 128 с.: ил.

3) Глейзер, Г.И. История математики в школе [Текст] / . М.: Просвещение, 1964. 376 с. ил.

4) Демидова, Т.Е. Теория и практика решения текстовых задач [Текст] : Учеб. пособие для студ. высш. пед. учеб. заведений / Т.Е. Демидова, А.П. Тонких.– М.: Академия, 2002.– 288с.

5) Зимняя, И.А. Педагогическая психология [Текст] : Учебник для вузов. / И.А. Зимняя.– 2-е изд., доп., испр. и преобр. М.: Логос, 1999.– 384 с.

6) Зубарева, И.И. Математика. 5 кл. [Текст] : Учеб. для общеобразоват. учреждений / И.И. Зубарева, А.Г. Мордкович.– 6-е изд., стер.– М.: Мнемозина, 2007.– 270с.: ил.

7) Зубарева, И.И. Математика. 6 кл. [Текст] : Учеб. для общеобразоват. учреждений / И.И. Зубарева, А.Г. Мордкович.– 7-е изд., испр.– М.: Мнемозина, 2008.– 264с.: ил.

8) Математика [Текст] : Учеб. для 5 кл. общеобразоват. учреждений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.; под ред. Г.В. Дорофеева, И.Ф. Шарыгина.– М.: Просвещение, 1994.– 272 с.: ил.

9) Математика. 6 класс [Текст] : Учеб. для общеобразоват. учреждений: В 2 ч. Ч. 1 / Г.В. Дорофеев, С.Б. Суворова, И.Ф. Шарыгин и др.; под ред. Г.В. Дорофеева, И.Ф. Шарыгина.– 6-е изд.– М.: Дрофа, 2002.– 208 с.: ил.

10) Математика. 6 класс [Текст] : Учеб. для общеобразоват. учреждений: В 2 ч. Ч. 1 / Г.В. Дорофеев, С.Б. Суворова, И.Ф. Шарыгин и др.; под ред. Г.В. Дорофеева, И.Ф. Шарыгина.– 6-е изд., перераб.– М.: Дрофа, 2002.– 224 с.: ил.

11) Математика. Арифметика. Алгебра. Анализ данных. 7 класс [Текст] : Учеб. для общеобразоват. учеб. заведений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.; под ред. Г.В. Дорофеева.– 2-е изд.– М.: Дрофа, 1998.– 288 с.: ил.

12) Математика [Текст] : Учеб. для 5 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков и др.– 5-е изд.– М.: Мнемозина, 1997.– 384с.: ил.

13) Математика [Текст] : Учеб. для 6 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков и др.– 11-е изд., стереотип.– М.: Мнемозина, 2003.– 304с.: ил.

14) Методика и технология обучения математике. Курс лекций [Текст] : пособие для вузов / под ред. Н.Л. Стефановой, Н.С. Подходовой.– М.: Дрофа, 2005.– 406 с.: ил.

15) Мордкович, А.Г. Алгебра. 7 кл. [Текст] : Учеб. для общеобразоват. учреждений / А.Г. Мордкович.– 3-е изд., доработ.– М.: Мнемозина, 2000.– 160 с.: ил.

16) Мордкович, А.Г. Алгебра. 7 кл. [Текст] : Задачник для общеобразоват. учреждений / А.Г. Мордкович.– 3-е изд., доработ.– М.: Мнемозина, 2000.– 160 с.: ил.

17) Мордкович, А.Г. Алгебра. 8 кл. [Текст] : Учеб. для общеобразоват. учреждений / А.Г. Мордкович.– 3-е изд., доработ.– М.: Мнемозина, 2001.– 233 с.: ил.

18) Мордкович, А.Г. Алгебра. 8 кл. [Текст] : Задачник для общеобразоват. учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.– 3-е изд., доработ.– М.: Мнемозина, 2001.– 239 с.: ил.

19) Муравин, К.С. Алгебра. 8 кл. [Текст] : Учеб. для общеобразоват. учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев.– 3-е изд., стереотип.– М.: Дрофа, 2000.– 208 с.: ил.

20) Нагибин, Ф.Ф. Математическая шкатулка [Текст] / Ф.Ф. Нагибин.– Ярославль: Просвещение, 1964.– 168 с.

21) Немов, Р.С. Психология [Текст] : В 3 кн.: Учеб. для студ. высш. пед. учеб. заведений / Р.С. Немов.– 4-е изд. М.: Владос, 2003.– Кн. 2: Психология образования.– 608 с.

22) Никольский, С.М. Арифметика [Текст] : Учеб. для 5 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.– 2-е изд.– М.: Просвещение, 2000.– 255с.: ил.

23) Никольский, С.М. Арифметика [Текст] : Учеб. для 6 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.– 2-е изд.– М.: Просвещение: Моск. учебники, 2001.– 270 с.: ил.

24) Никольский, С.М. Алгебра [Текст] : Учеб. для 7 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.– 2-е изд.– М.: Просвещение, 2000.– 285с.: ил.

25) Никольский, С.М. Алгебра [Текст] : Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.– М.: Просвещение, 2000.– 287с.: ил.

26) Олехник, С.Н. Старинные занимательные задачи [Текст] / Ю.В. Нестеренко, М.К. Потапов.– 2-е изд., испр.– М.: Наука. Гл. ред. физ-мат. лит., 1988.– 160 с.

27) Планея: Психологический словарь, [Электронный документ] (http://www.pbi.ru/dic/v/v_39.htm). 19.10.09

28) Психологический словарь, [Электронный документ] (http://psi.webzone.ru/st/081500.htm). 17.09.09

29) Рубинштейн, С.Л. Основы общей психологии [Текст] / С.Л. Рубинштейн.– СПб.: Питер, 2000.– 712 с.: ил.

30) Столяренко, Л.Д. Педагогическая психология [Текст].– 2-е изд., перераб., и доп.– Ростов н/Д.: Феникс, 2003.– 544с.– (Учебники и учебные пособия)

31) Талызина, Н.Ф. Педагогическая психология [Текст] : Учеб. для студ. сред. пед. учеб. заведений / .– 3-е изд., стереотип.– М.: Академия, 1999.– 288 с.

32) Тихомиров, О.К. Психология мышления [Текст] / О.К. Тихомиров.– М.: Академия, 2005.– 288 с.

33) Фридман, Л.М. Психология детей и подростков [Текст] / Л.М. Фридман.– М.: Просвещение, 2003.

34) Фридман, Л.М. Сюжетные задачи по математике. История, теория, методика [Текст] : Учеб. пос. для учителей и студентов педвузов и колледжей / Л.М. Фридман.– М.: Шк. пресса, 2002.– 208 с.– (Б-ка журн. «Математика в шк.». Вып. 15)

35) Чистяков, В.Д. Старинные задачи по элементарной математике [Текст] / В.Д. Чистяков. 3-е изд., испр.– Минск.: Вышейш. шк., 1978.– 272 с. ил.

36) Шамова, Т.И. Активизация учения школьников [Текст] / Т.И. Шамова.– М.: Педагогика, 1982.– 208 с.: ил.

37) Щукина, Г.И. Проблема познавательного интереса в педагогике [Текст] / Г.И. Щукина.– М.: Педагогика, 1971.– 352 с.

38) http://www.ukraina.com/index2.php?option=com_content&task=view&id= 43&pop=1&page=0&Itemid=32. 07.11.2009

1 Леонард Эйлер (1707 - 1783)   российский и швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, 
астрономии и ряда прикладных наук.
Эйлер   автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.

2 Экю (фр. Ecu) — французские золотые и серебряные монеты Средних веков.

3 Русский математик и педагог Леонтий Филиппович Магницкий (1669 - 1739) в 1703 г. Опубликовал В Москве свою знаменитую книгу «Арифметика, сиреч наука числительная». Эта книга была до середины XVIII в. основным учебником по математике в России. «Арифметика» Магницкого поистине была энциклопедией математических знаний и сыграла большую роль в распространении математических знаний в России. [2;49]

4 Гривна – С середины XI в. в Киевской Руси в качестве основной денежной единицы ходят гривни – серебряные слитки, а также их рубленные части – рубли. [38]

5 «Греческая антология» - сборник задач, составленных в стихотворной форме, главным образом гекзаметром, которым, как известно, написаны знаменитые поэмы Гомера «Илиада» и «Одиссея». Особенно в большом ходу эти задачи были в X – XIV вв.[35;114]

6 Трактат «Начала искусства вычисления» опубликован в 1593 г. В нем важнейшие правила, вероятно, для лучшего запоминания даются в стихотворной форме. По-видимому, это сочинение в свое время было принято как учебное руководство в школах по элементарной математике. Содержание книги дает хорошую картину состояния китайской математики вплоть до конца XVI в. [35;118]

7 Французский математик Этьенн Безу (1730 - 1783) занимался исследованием свойств систем алгебраических уравнений высших степеней и установил теорему о делении многочлена на линейный двучлен (теорема Безу) [2;44]

8 Евклид древнегреческий математик 300 г. до н.э, написавшего 13 книг, объединенных общим названием «Начала». [2;14]

9 Диофант Александрийский (II – III вв. н.э.) был последним великим математиком античности. До нас дошли два его сочинения – «Арифметика» и «О многоугольных числах». Творчество Диофанта оказало большое влияние на развитие алгебры, математического анализа и теории чисел. [2;19]

10 Таэль – денежно весовая единица Восточной Азии, применяющаяся с древних времен Китая; ныне вышла из употребления

11 Аршин – старорусская единица измерения длины, 0,7112 метра

12 Леонардо Пизанский (1180 - 1240)имел прозвище Фибоначчи, т.е. «сын Боначчо» (Боначчо - добродушный). Основные достижения Леонардо Пизанского изложены в его сочинениях «Книга абака» и «Практика геометрии». [2;35]

13 Динар – единица валюты различных стран, большинство из которых арабоговорящие или бывшие частью Османской империи

14 Адам Ризе. В XVI в. немецкие алгебраисты назывались коссистами, так как алгебру они именовали coss – от итальянского слова cosa – вещь (неизвестная). Одним из знаменитых коссистов был Адам Ризе (1489 - 1559). В 1524 г. он написал учебник по алгебре. Ризе свел 90 правил для решения квадратных уравнений с одним неизвестным к 24. [2;36]

15 Торгуют – т.е. покупают

16 Флорин – золотая монета, которую впервые начали чеканить во Флоренции в 1252 году, отсюда и название монеты.

17 Бхаскара (Бхасхара Ачарья) (1114 — ум. позднее 1178), индийский математик и астроном. Труд «Венец учения» («Сиддханта-широмани», 4 книги, в т. ч. «Лилавати» и «Биджаганита»), содержащий методы решения ряда алгебраических и теоретико-числовых задач, астрономические сведения. [2]

18 В IX в. в Индии жил математик и астроном Магавира. В своем «Кратком курсе математики» он установил двузначность квадратного корня, ставил вопрос об извлечении корня из отрицательного числа, решал задачи, приводящие к системам линейных уравнений с несколькими неизвестными. [2;27]