Элементы истории математики при преподавании темы "Тригонометрия" в общеобразовательной школе
ДИПЛОМНАЯ РАБОТА
По теме
«Элементы истории математики при преподавании темы «Тригонометрия» в общеобразовательной школе»
Введение
Использование учителем математики исторических сведений не является обязательным при изложении материала урока. Однако, как указывает К. А. Малыгин «...экскурсы в историческое прошлое оживляют урок, дают разрядку умственному напряжению, поднимают интерес к изучаемому материалу и способствуют прочному его усвоению»1. Тем более что материал по истории математики весьма обширен и интересен, так как развитие математики тесным образом связано с решением насущных задач, возникавших во все периоды существования цивилизации.
Рассказав об исторических причинах возникновения тригонометрии, показав, как плоды деятельности великих ученых оказали влияние на развитие этой области математики и на решение конкретных задач, учитель возбудит у школьников интерес к изучаемому предмету и покажет его практическое значение. Очевидно, каждый учитель математики полагает, что использование исторических сведений повышает интерес учащихся, имеет большое мировоззренческое и общекультурное значение. И, тем не менее, учителя крайне редко излагают на уроке математики исторические сведения, или используют в системе упражнений задачи с историческим содержанием. Здесь сказывается нехватка учебного времени, отсутствие разработанной методики, желание больше уделить внимание закреплению.
Проблема использования исторического материала на уроках математики интересовала многих ведущих ученых, педагогов и методистов, таких как: Г. И. Глеизер, Д. Я. Стройк, Н. Я. Виленкин, Я. И. Перельман, К. А. Рыбников, А. П. Юшкевич и другие. Увлечь учащихся, заставить их заинтересоваться изучаемым предметом - вот первейшая и главная задача использования элементов истории математики на уроках.
Целью исследования является, во-первых, выявить целесообразно ли ознакомление учащихся с историческим материалом при преподавании тригонометрии в общеобразовательной школе, во-вторых, показать, как сочетается изучение определенных разделов программы по тригонометрии с изложением соответствующего исторического материала. Для этого необходимо было рассмотреть само содержание исторического материала и выбрать те его части, которые разумно использовать на уроках тригонометрии, предложить формы его изложения, и определить объем материала, который можно предоставить учащимся для самостоятельного изучения и использования на внеурочных занятиях.
Исходя из целей, в ходе нашего исследования, мы ставим перед собой следующие задачи:
выявить возрастные особенности старшего школьного возраста
рассмотреть понятие мотивации в процессе обучения;
познакомиться с историко-генетическим методом в преподавании математики;
показать историю развития тригонометрических понятий;
сформулировать дидактические принципы и требования к отбору историко-научного материала для включения в процесс обучения тригонометрии;
разработаем примерное планирование уроков с использованием исторического материала;
рассмотреть формы и примеры использования исторического материала на уроках геометрии и тригонометрии в средней школе;
В первой главе дипломной работы рассмотрены психолого-педагогические основы, которые имеют непосредственное отношение к преподаванию тригонометрии в средней школе.
Во второй главе изложен историко-математический материал, связанный с возникновением и развитием тригонометрических понятий.
В третьей главе изложены методические особенности использования исторического материала при изучении курса тригонометрии в общеобразовательной школе и показали примеры использования исторического материала на уроках.
Завершается дипломная работа заключением и библиографией.
Глава 1. Психолого-педагогические основы преподавания тригонометрии в средней школе
1.1 Возрастные особенности старшего школьного возраста
«Учение выступает как вид деятельности, целью которого является приобретение человеком знаний, умений и навыков» - так пишет в своих трудах известный психолог и педагог Р.С. Немов. «Учение в школе - это организованный процесс. Особенности учебной деятельности состоят в том, что она прямо служит средством психологического развития индивида». Эти слова справедливы и в отношении математики, ведь учение не может быть успешным, если учитель не знает психологических особенностей своих учеников.
Перед учителями во все времена стоит вопрос, как сделать свои уроки интересными, познавательными и развивающими. Как привлечь внимание учеников, сделать их не пассивными слушателями, но равноправными участниками образовательного процесса. Для лучшего понимания своих учеников учителя всегда должны учитывать психологические аспекты, о которых речь идет ниже.
В подростковом возрасте начинает формироваться мировоззрение, как основной мотив и регулятор поведения. Перед учителем возникает цель развития в ученике целостного, интеллектуально развитого индивида. А при формировании научности мировоззрения необходимо помнить, что оно зависит от активности самого подростка, его самостоятельности в приобретении знаний.
Значительные изменения претерпевают в подростковом возрасте и познавательные процессы. Учебная деятельность, включающая в себя процесс усвоения знаний и способов их использования, позволяет подросткам устанавливать более широкие связи между имеющимися и вновь приобретаемыми знаниями, более сознательно контролировать свою мыслительную деятельность и управлять ею. Постепенно у них формируется умение самостоятельно оперировать предположениями и критически оценивать их. Но, зачастую, взрослые, учителя безапелляционно отвергают наивные, односторонние, далеко еще не зрелые заключения, создавая своей бестактностью предпосылки для конфликтов и недоразумений. Конечно же, таких столкновений учителя допускать не должны.
Нравственные и социальные качества старшеклассников формируются ускоренными темпами. Этому способствует не только сензитивный период зрелости, но и новая обстановка: изменение характера деятельности, положение в обществе, интенсивность общения. Появляется острое желание выразить свою индивидуальность; у некоторых молодых людей это стремление приобретает гипертрофированные формы. Любым способом им хочется обратить на себя повышенное внимание окружающих. Здесь могут помочь терпимость и заинтересованная помощь взрослых.
Далеко не последнюю роль в учебной деятельности подростка играет мотивационный момент. Мотивы обучения могут быть связаны с его результатами. В таком случае от учащихся требуется немалое волевое усилие как при положительной мотивации (похвала, хорошая отметка), так и тем более при отрицательной (плохой балл аттестата и т.п.). Также мотивы учения могут содержаться как в самом процессе учебной деятельности, так и в целях учения: стремление расширить свой кругозор, проявить свои способности, желание учиться дальше и т.д. В таких случаях усилению мотивации будут способствовать проблемные методы обучения, своевременная информация о достигнутом и т.п.
1.2 Мотивация как двигатель обучения
Современными исследователями мотивация рассматривается не просто как необходимое условие, но как движущая сила, способствующая достижению успеха. В педагогических пособиях «мотивация» определяется как «общее название для процессов, методов, средств побуждения учащихся к продуктивной познавательной деятельности, активному освоению содержания образования»2. В психологии термин «мотивация» является объяснительным конструктором, используемым для описания и объяснения причин поведения людей, его направленности и механизма осуществления. Как и интеллект, мотивацию нельзя наблюдать непосредственно, но она может быть выявлена косвенно на основе некоторых когнитивных, поведенческих и эмоциональных показателей [1;7-8].
Известный американский когнитивный психолог Роберт Стернберг, описывая причины, мешающие людям с высоким уровнем интеллекта достигать высоких результатов и добиваться успеха, в качестве основной причины указывает на недостаток мотивации: «Практически в любой окружающей обстановке... мотивация имеет не меньшую роль в достижении успеха, чем умственные способности» (Stenberg. 1996, р. 251) [ 1; 6].
Успешность учения во многом зависит от мотивации, от того личностного смысла, который учение имеет для учащегося. Мотивация учения является проблемой, которая остро стоит и перед подростками, и перед учителями, и перед родителями. Если в первый класс ребенок приходит любознательным, желающим получить новые впечатления и выполнять задания учителя, то по мере его обучения в школе, особенно в подростковом возрасте, учителя все чаще сталкиваются с негативным отношением учащихся к школе, к урокам, со скукой, апатией, депрессией или агрессией. Отсутствие необходимой мотивации учения часто ведет к стойкой неуспеваемости, которая способствует появлению отклонений в поведении школьника [2; 27].
Из всех отдельных видов человеческой мотивации мотивация достижения имеет непосредственное отношение к учебному процессу. Т. О. Гордеева определяет мотивацию достижения как мотивацию, направленную на возможно лучшее выполнение любого вида деятельности, ориентированной на достижение некоторого результата (так называемой продуктивной деятельности) [1; 8]. Она указывает, мотивация достижения является надежным предиктором успеваемости в школе и вузе, а также успешности в бизнесе и других профессиях.
По свидетельству А. Анастази и С. Урбины, в свою очередь ссылающихся на внушительный список англоязычных работ, имеет место растущее признание роли мотивации учащихся в школьном обучении [1; 5].
Особый интерес к проблематике мотивации достижения показал, что она является одной из фундаментальных мотиваций человека, без которой невозможно его полноценное развитие. В современном индустриальном обществе ситуации, связанные с деятельностью достижения, преобладают в учебной и профессиональной деятельности. Следует отметить, что мотив достижения является главным «возрастным» мотивом учебной деятельности подростков [2; 37]. Мотивация достижения проявляется в стремлении прилагать усилия и добиваться, возможно, лучших результатов в области, которую субъект считает важной и значимой. В качестве деятельности достижения могут выступать интеллектуальная, спортивная, любая профессиональная, в том числе учебная деятельность. Мотивация достижения имеет наибольшее значение в активности, направленной на достижение определенного результата, который может быть оценен в соответствии с предметными, индивидуальными или социальными нормами. Однако наиболее исследована мотивация достижения в области решения интеллектуальных задач, где испытуемыми выступают главным образом школьники и студенты [1; 8-9].
Успешное выполнение продуктивной деятельности требует не только развитых способностей, но и таких важных мотивационных характеристик, как интерес к выполняемому делу, вара в свои способности достичь успешного результата, умение справляться с трудностями, адекватно реагировать на неудачи и проявлять настойчивость (Dweck, 1999) [1; 6-7].
Учение является одним из основных видов деятельности школьников, поэтому многими психологами исследовались мотивы учебной деятельности как значимые в этот период психологического развития. Все мотивы учения, с точки зрения исследователя Л. И. Божович, подразделяются на две большие категории [3]. Одни из них непосредственно связаны с содержанием учебной деятельности и процессом познания (познавательные); другие - с более широкими взаимоотношениями ребенка с окружающей средой (социальные). Кроме того, выделяют собственные, внутренние мотивы, учебной деятельности учеников и внешние мотивы, мотивы-стимулы. Первые связаны с процессами познания и социального взаимодействия, а также некоторыми личностными образованиями, такими как самоуважение и самооценка. Вторые с внешним стимулированием, использованием системы поощрений, наказаний и т.д. [2; 28]
Оптимальный вариант функционирования мотивации достижения включает доминирование у субъекта в структуре мотивации интереса к деятельности, сопровождающегося удовольствием от ее осуществления, а также ощущением компетентности и контроля. В исследовании М. Чиксентмихайи, основанное на тысячах интервью с людьми, описывающими то, что делает их счастливыми, показало: наибольшее счастье приносит людям не зарабатывание денег или признание (внешняя мотивация), а деятельность, удовлетворяющая их самих и сопровождающаяся увлеченностью, когда внимание человека чем-то захвачено (внутренняя мотивация). Например, один ученик может быть сильно мотивирован выполнением домашнего задания по тому, что оно представляет для него интерес, другой - потому, что хочет заслужить похвалу родителя, третий в первую очередь ориентируется на мнение учителя или признание со стороны сверстников [1; 250-253]. Первый случай, когда работа, выполняемая учеником важна для него и интересна сама по себе, как мы указывали выше, является оптимальным для продуктивности деятельности школьников.
Интересно, что большинство психологов склоняются к мнению, что внешняя мотивация уменьшает внутреннюю. Регулярное длительное подкрепление (в виде оценок, замечаний, системы наказаний и т.д.) воспринимается как внешний контроль и дает возможность ученикам снять с себя ответственность за происходящее, что негативно сказывается на внутренней мотивации. Более того, наличие корыстного подкрепления при наличии интереса к деятельности смещает акценты с содержания самой деятельности на ее результат. Поэтому учителю следует обязательно включать задания, не связанные с получением конкретного результата [2; 28].
Особое место среди мотивов учебной деятельности занимает познавательный интерес, появление которого тесно связано, во-первых, с наличием положительных эмоций, связанных с умственным трудом, когда ребенок воспринимает учебу не только как свой долг, но и как радостный приятный процесс. Во-вторых, для развития познавательного интереса необходима такая среда, которая бы стимулировала, любознательность ребенка, давала бы ему пищу для ума, заставляла задавать вопросы [2; 43].
Щукина Г. И., изучавшая проявления познавательного интереса у подростков, показала, что он как устойчивая черта личности встречается лишь у отдельных учащихся. При этом развитие познавательного интереса не имеет четко выраженных возрастных градаций и закономерностей. У большинства школьников по мере обучения интересы не становятся более устойчивыми, широкими, теоретическими. Можно сказать, что в старших классах аморфных интересов оказывается больше, чем в младших. Исключением является избирательное отношение к школьным предметам, связанными с профессиональной направленностью. Кроме того, она показала, что одним из ключевых факторов появления и развития познавательного интереса является качество и уровень преподавания, подчас личная увлеченность предметом учителя [2; 43].
Традиционно успешную учебную деятельность связывает с наличием у школьников внутренней познавательной мотивацией и познавательного интереса. Отчасти это так, на наличие у ученика только познавательного интереса без каких-либо социальных мотивов может привести к отсутствию у него чувства ответственности за учение. Подчас это выражается в стремлении к «чистому» творчеству, пренебрежение к отработке учебных навыков, выполнение технических подсчетов, правильному оформлению решения задач, а также в невнимании повторения пройденного, не выполнении домашних заданий и т.д. Поэтому для успешной учебной деятельности также необходим баланс внутренних социальных и познавательных мотивов. При этом грамотно построенная система внешних стимулов может способствовать появлению в перспективе внутренней мотивации [2; 29-30].
Исходя из всего выше изложенного, мы можем говорить о том, что в ходе учебного процесса, мотивационная сфера учащихся имеет большое значение и непосредственно влияет на деятельность школьников. Таким образом, задачей учителя, помимо реализации основных целей обучения, является увеличение и стимулирование интереса учащихся к изучаемому предмету.
Как известно, использование на уроках элементов истории математики повышает интерес учащихся, имеет большое мировоззренческое и общекультурное значение. Знакомя учащихся с ними, мы как бы кратко повторяем путь развития математики как науки и ее связь с историей развития цивилизации, что, несомненно, заинтересует учащихся и сделает более мотивированным процесс обучения.
1.3 Об историко-генетическом методе
Вопросы использования элементов истории математики в преподавании рассматривались многими известными учеными-математиками и деятелями в области математического образования. Среди наиболее известных исследований по этой теме, включающих отбор историко-математического материала и рекомендации по его использованию на уроках математики в школе, можно отметить работы:
В этих, как и в большинстве работ, авторы сходятся во мнении, если учитель знает историю математики, знает как происходило становление и развитие основных математических понятий и идей, то он будет лучше понимать внутреннюю логику учебных тем, сможет дидактически более грамотно вводить математические понятия. Учитель не только должен знать, как происходило развитие основных математических понятий и идей, но и понимать, что учащиеся в своем обучении кратко повторяют этот путь и сталкиваются с теми же трудностями, с какими сталкивались ученые, стоявшие у истоков формирования того или иного математического понятия. Учителю необходимо не только быть знакомым с историей науки, но параллельно, неразрывно с излагаемым материалом, обращать внимание на то, какие методические идеи и находки подсказывает ему история науки, следовать с историко-генетическому метод.
В основе историко-генетического метода лежит следующее наблюдение: изучая математику, учащиеся кратко повторяют путь человечества, который оно прошло, добывая математические знания. Если мы знаем этот путь, знаем историю математики, то можем, используя это знание, координировать учебный процесс, делая его более эффективным, а математику, преподносимую учащимся, более понятной. Поясним эту идею следующим высказыванием американского профессора М. Клайна: «Нет никакого сомнения, что затруднения, которые встретили великие математики, являются теми же камнями преткновения, какие встречают студенты, и что никакие попытки смазать эти трудности с помощью логической словесности не достигнут цели. И если нужны были 1000 лет, чтобы первоклассные математики добрались до понятия отрицательных чисел, и потребовалось еще 1000 лет, чтобы математики признали отрицательные числа, то можно быть уверенным, что учащиеся испытают затруднения с отрицательными числами. Больше того, учащимся придется преодолеть эти трудности почти тем же путем, каким это преодолели математики, постепенно привыкая к новым понятиям, оперируя с ними и используя все интуитивные средства, которые учитель сможет им привести»([10] с. 7).
Для того чтобы лучше разъяснить суть историко-генетического метода, рассмотрим кратко главные этапы его становления. Началом его проникновения в преподавание математики можно считан, появление в 1685 г. «Исторического и практического трактата по алгебре» Дж. Валлиса. Исторический подход к изложению предмета и метода алгебры, реализованный в трактате, вызывал у читателей большую заинтересованность и тем самым способствовал ускоренному постижению смысла излагаемого материала, логики выводов и доказательств. Таким образом, впервые было замечено, что если к математическим понятиям, терминам и символам подойти с позиции исторического развития, то они перестанут казаться искусственными и оторванными от жизни. Станет, виден их глубокий жизненный смысл, их естественность и необходимость. «Трактат по алгебре» Валлиса можно считать первым курсом алгебры, построенном на историко-генетических началах.
В XVIII в., т.е. спустя почти двести лет, французский математик А.К. Клеро, следуя за педагогической идеей Валлиса, уделил большое внимание историческому методу в процессе обучения математике. Он считал очень продуктивной методику, которая учит искать и делать открытия, потому что при таком изложении математических утверждений указывается, каким образом люди пришли к открытию.
В середине XIX столетия англичанин В.Г. Спенсер опубликовал книгу «Геометрия путем изобретения», в которой излагал для детей геометрию не обычным дидактическим способом, а знакомил читателей с геометрическими представлениями, постепенно и как бы только подготавливая к ее изучению. Такая методика также дала положительные результаты.
В конце XIX — начале XX столетий историко-генетический метод стал широко популяризироваться деятелями математического образования. В 1904 г. французский математик А. Пуанкаре писал: «Зоологи считают, что за короткий период развития эмбриона животного он воспроизводит историю своих предшественников всех эпох. Кажется, что-то же самое происходит в развитии ума. Задача воспитания - дать уму ребенка пройти то, что изведали его предки, пройти быстро определенные этапы, но не опустить ни одного из них. Для достижения этой цели история науки должна служить поводырем».
В России одним из активных пропагандистов историко-генетического метода был русский исследователь истории математики и математического образования В.В. Бобынин. Приведем цитату из его работы 1886 г. «Философское, научное и педагогическое значение истории математики»: «Умственное развитие молодых поколений управляется теми же законами и вследствие этого проходит в существенных чертах те же самые фазы развития, которые имели место в соответствующих ступенях умственного развития всего человечества... преподавание каждой науки должно идти тем же путем, которым шла при своем развитии сама наука...» ([10] с. 8). Такой метод В.В. Бобынин называет генетическим, понимая под этим «метод, развивающий в преподавании положения и выводы науки именно таким образом, как они развивались в действительности» ([10] с. 8). В качестве основного педагогического значения истории математики Бобынин указывает именно на значение ее для генетического метода преподавания. Фактически о том же говорит и русский психолог и педагог П.Ф. Каптерев: «Наиболее удобная в педагогическом отношении форма изложения есть генетическая, когда сообщается история происхождения знания, показывается, как знание возникло и развивалось» ([10] с. 8).
Определенного рода повторяемость общего пути умственного развития человечества в формировании индивидуального сознания, которую на опыте собственной педагогической деятельности подмечали многие преподаватели XIX в., в середине XX столетия стала предметом психологических исследований. Психолог В.В. Давыдов считает, что учащиеся присваивают культурные формы в процессе учебной деятельности, осуществляя при этом мыслительные действия, адекватные тем, посредством которых исторически вырабатывались продукты духовной культуры, т.е. школьники как бы воспроизводят реальный процесс создания людьми понятий, образов, ценностей и норм. Отсюда В.В. Давыдов делает важный вывод о том, что обучение в школе всем предметам необходимо строить так, чтобы оно «в сжатой сокращенной форме воспроизводило действительный исторический процесс рождения и развития... знаний» ([11] с. 152). Таким образом, историко-генетический метод действительно может играть большую роль в преподавании математики, так как именно он позволяет учащимся пройти тот путь, который проходило человечество, добывая математические знания.
Историко-генетический метод побуждает каждый раз обосновывать введение того или иного понятия, рассказывая, какие задачи практики привели к его открытию, и как оно впервые использовалось. С его помощью учитель может предвидеть трудности, возникающие при усвоении учащимися школьной программы и преодолевать их, используя исторический опыт.
Историко-генетический метод способен подсказать учителю решение и некоторых чисто методических проблем, например, как лучше спланировать изучение данного учебного материала, какой методической разработке отдать предпочтение, в какой последовательности изучать те или иные темы. «Вообще, мы можем ожидать больший успех делая то, что нам подсказывает генетический принцип, чем следуя чисто формальной концепции математики» ([12] с.91). Этот метод может оказать учителю большую помощь при реализации в учебном процессе эвристических приемов: чтобы подвести учащихся к открытию математического факта, учитель должен кратко пройти вместе с ними тот путь, который привел людей к установлению этого факта.
Однако преподаватели прекрасно понимают, что попытка воспроизвести весь исторический путь познания математической истины, повторяя все детали ошибок и заблуждений первооткрывателей, приведет к отказу от тех преимуществ, которые предоставляют дидактике современные обобщающие идеи, концепции и методы науки, и, как следствие, к разрушению логической структуры курса. Поэтому историко-генетическому методу противопоставляется другой метод преподавания - логический.
При логическом изложении не должно быть ничего лишнего, никаких нарушающих стройность предмета исторических случайностей. Однако и ходе преподавания стало очевидным, что логический метод также не лишен недостатков. В своей строго логической форме, без указаний на происхождение понятий и выхода теории в практику, математическая дисциплина принимает слишком искусственный характер, «...мы видим, как вопросы могут быть разрешены, но перестаем понимать, как и почему они были поставлены» ([10] с. 8). По этой причине логическое изложение не заинтересовывает даже способных учащихся так, как могло бы.
Вот почему уже много лет не угасает интерес к историко-генетическому методу. Однако очевидно, что этот метод эффективен лишь в том случае, когда в процессе изложения научных понятий правильно найдено соотношение логического и исторического подхода в преподавании. Говоря об историко-генетическом методе, мы, безусловно, не имеем в виду его крайние формы - повторение в преподавании развития математического знания со всеми нюансами и тонкостями. Для методически правильной организации обучения учителю, прежде всего, необходимо знать общие законы развития математической науки, пути формирования и становления математических понятий и идей.
В конце XIX в. история математики как наука лишь зарождалась и поэтому не могла решить поставленных перед нею задач. Только в наше время, когда, благодаря исследованиям таких историков математики, как Г.Г. Цейтен, Б.Л. Ван-дер-Варден, Г. Вилейтнер, И.Я. Депман, А.П. Юшкевич, Б.А. Розенфельда и др., накоплен и систематизирован колоссальный историко-математический материал, стало возможным на основе этих данных делать обобщения, говорить об общих законах развития математического знания, прослеживать пути формирования математических понятий от их зарождения до современного состояния.
Исторические справки и сведения, эвристические идеи выводов формул и доказательств теорем, яркие несложные примеры, несомненно, заинтересуют учащихся и сделают более эмоциональными уроки математики, и главное, позволят им в случае необходимости даже через несколько лет снова вывести уже забытую формулу или теорему. Отметим также, что основные этапы эвристического рассуждения, реализуемого на уроке, могут быть подсказаны учителю данными истории математики и осуществлены с помощью историко-генетического метода.
Историко-генетический метод преподавания нельзя сводить только к использованию отдельных историко-математических сведений на уроках математики. Реализуя этот метод в своей работе, учитель повторяет вместе с учащимися путь развития науки, ведет их по пути новых открытий. Отдельные историко-математические сведения, которые он использует, - это лишь вершина айсберга, каким является метод. Разумеется, учителю необходимо знать и отдельные частные сведения, которые он может непосредственно рассказывать на уроке. Но если учитель знает основные этапы развития математических понятий и идей и знает конкретно, какой фрагмент этих сведений он хочет изложить учащимся, то подобрать нужный историко-математический материал ему будет несложно.
Историко-математические сведения, излагаемые учителем, могут быть самыми разными и нести самую разнообразную смысловую нагрузку, однако наиболее эффективным их использование будет лишь в том случае, если они излагаются в системе, единым методом и если их использование позволяет сделать изложение материала более последовательным, понятным, целостным и интересным.
преподавание тригонометрия школа математика
Глава 2. История развития тригонометрических понятий
Термин «тригонометрия» дословно означает «измерение треугольников». Его ввёл в употребление в 1595г. немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. Тригонометрия - раздел математики, который изучает зависимости между углами и сторонами треугольников, а также свойства тригонометрических функций синуса, косинуса, тангенса, котангенса, секанса и косеканса. К концу 17 века почти все эти функции были уже, по существу, известны. Правда, самого понятия тригонометрических функций, как и их обозначений, тогда ещё не существовало. Вместо них говорили о длинах некоторых хорд, касательных, секущих в окружности определённого радиуса. В тригонометрии изучались три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т. е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через её центр (сферическая тригонометрия).
Изучение свойств тригонометрических функций началось при исследовании свойств сферической геометрии. Древние астрономы, наблюдая за движением небесных светил, обрабатывали измерения, необходимые для ведения календаря, определения время начала сева и сбора урожая и дат религиозных праздников. По звёздам определялся курс корабля в море или направление движения каравана в пустыне. Наблюдения за звёздным небом с незапамятных времён вели и астрологи. Естественно, все измерения, связанные расположением светил на небосводе, являются косвенные. Прямые — осуществлялись только на поверхности Земли. Но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами. И тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева или размеры острова в море, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие, а поскольку звёзды и планеты представлялись точками на небесной сфер то сначала стала развиваться именно сферическая тригонометрия. Её считали разделом астрономии.
Отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы и астрологи Междуречья научились предсказывать положения Луны и Солнца, достигнув в этом больших успехов. От них мы унаследовали систему измерения углов в градусах, минутах и секундах, основанную на секундах в принятой ими шестидесятеричной системе исчисления. Первые по-настоящему важные достижения в математике, в частности в тригонометрии, принадлежат древнегреческим учёным.
2.1 О тригонометрических таблицах
В Древней Греции тригонометрия как часть астрономии достигла значительного развития. Древнегреческие ученые впервые поставили перед собой задачу решения прямоугольного треугольника, т. е. определения его элементов по двум данным элементам, из которых хотя бы один — сторона треугольника. Для решения этой задачи вначале составляли таблицы длин хорд, соответствующих различным центральным углам круга постоянного радиуса. Первые тригонометрические таблицы хорд были составлены астрономом-математиком Гиппархом из Никеи (II в. до н. э.). Гиппарх был основоположником приложения математики к географии, кроме того, он составил звездный каталог, довольно точно определил расстояние от Земли до Луны и ввел географические координаты — широту и долготу. Сочинения Гиппарха до нас не дошли. Но многие из них вошли в «Альмагест» — знаменитое сочинение древнегреческого астронома Клавдия Птолемея.
Альмагест — классическое сочинение, в котором изложена античная теория движения небесных тел, геоцентрическая система мира. Эта система просуществовала до XVI в., когда появились труды Н. Коперника с изложением новой гелиоцентрической системы мира. «Альмагест» содержит элементы прямолинейной и сферической тригонометрии, описание астрономических инструментов, звездный каталог таблиц хорд и др. Таблица хорд Птолемея составлена в шестидесятеричной системе счисления через полградуса от 0 до 180° и играла такую же роль, как таблица синусов (т. е. полухорд), так как синус есть половина хорды окружности единичного радиуса, стягивающей дугу, соответствующую двойному углу.
Таблицы синусов были введены индийскими астрономами, которые рассматривали и линию косинуса. Техника тригонометрических вычислений (применявшихся для решения прямоугольных треугольников) получила значительное развитие в Индии. Так, для синуса 3°45' Бхаскара в своих таблицах указывает значение которое дает семь верных десятичных знаков. Дальнейшего развития тригонометрические таблицы достигли в трудах ученых стран ислама, которые ввели понятие линии тангенса. Абу-л-Вафа (X в.) пользовался также величиной, обратной косинусу (секансом) и синусу (косекансом), и составил таблицу синусов через каждые 10'. Самые точные таблицы в начале XV в. были составлены ал-Каши. Большой точности таблицы тригонометрических функций составил Региомонтан (1436—1476) и другие европейские ученые XVI—XVIII вв.
В России первые тригонометрические таблицы были изданы в 1703 г. под названием «Таблицы логарифмов, синусов и тангенсов к научению мудролюбивых тщателей». В издании этих таблиц участвовал Л. Ф. Магницкий.
2.2 О тригонометрических функциях и о развитии тригонометрии
Индийские
ученые
положили
начало учению о тригонометрических
величинах, которые они рассматривали
в пределах первой четверти круга. Синус
и косинус встречаются в индийских
астрономических сочинениях уже в IV
— V
вв. Заменив хорду синусом, индийцы
вначале называли синус «ардхаджива»,
т. е. половина хорды («джива» — хорда,
тетива лука), а позже просто «джива».
Это слово было, как полагают, искажено
арабами в «джайб», означающее по-арабски
пазуха, выпуклость. Слово «джайб» было
переведено в XII
в. на латынь соответствующим словом
sinus.
Косинус индийцы называли «котиджива»,
т.е. синус остатка (до четверти окружности).
В XV
в. Региомонтан, как и другие математики,
применял для понятия «косинус дуги (х)»
латинский термин sinus
complementi,
т.е. синус дополнения, имея в виду
 .
От
перестановки этих слов и сокращения
одного из них (cosinus)
образовался термин «косинус», встречающийся
в 1620г. у английского астронома Э. Гунтера,
изобретателя логарифмической линейки.
.
От
перестановки этих слов и сокращения
одного из них (cosinus)
образовался термин «косинус», встречающийся
в 1620г. у английского астронома Э. Гунтера,
изобретателя логарифмической линейки.
В IX — X вв. ученые стран ислама (ал-Хабаш, ал-Баттани, Абу-л-Вафа и др.) ввели новые тригонометрические величины: тангенс и котангенс, секанс и косеканс. В частности, ал-Баттани установил, что в прямоугольном треугольнике острый угол можно определить отношением одного катета к другому. Происхождение названий двух тригонометрических функций, тангенса и секанса (термины, введенные в 1583 г. немецким математиком Т. Финком), связано с геометрическим их представлением в виде отрезков прямых. Латинское слово tangens означает касающийся (отрезок касательной), secans — секущий (отрезок секущей). Термины «котангенс» и «косеканс» были образованы в средние века по аналогии с термином «косинус». Все три термина вошли во всеобщее употребление в первой половине XVII в. Сферическая тригонометрия, непосредственно применявшаяся в астрономии, начала развиваться раньше плоской как часть астрономии и самостоятельно не существовала. Выдающийся ученый Насир ад-Дин ат-Туси (1201 — 1274), уроженец иранского города Туc, первый открыл путь к отделению тригонометрии от астрономии и выделению ее в самостоятельную дисциплину. Его труд «Китаб аш-шакл ал-кита» (книга о фигуре из секущих), называемый также «Трактатом о полном четырехугольнике», является первым в мире сочинением, специально посвященным тригонометрии. В нем достаточно полно изложено то, что было установлено раньше, а также отдельные исследования самого автора. Тригонометрический труд ат-Туси, как полагают некоторые ученые, оказал влияние на европейских математиков, в частности на Региомонтана.
В XV в. Региомонтан сыграл в Европе примерно ту же роль, какую играл Насир ад-Дин в странах ислама за двести лет до него. Труд Региомонтана «Пять книг о треугольниках всех видов» в свою очередь - имел большое значение для дальнейшего развития тригонометрии. Другие работы в области тригонометрии принадлежат Копернику, Виету, Кеплеру. Таким образом, процесс накопления тригонометрических знаний привел к тому, что, начиная примерно с XIII в., накопленный материал стал подвергаться систематизации, составляя отдельную, все более самостоятельную область математики - тригонометрию. Принципиально новый этап в развитии тригонометрии состоял в установлении связей этой науки с алгеброй. Начало этому было положено в конце XVI в. Франсуа Виетом (1540—1603). Виет, французский математик, известный главным образом своими открытиями в алгебре, выпустил в 1579 г. в Париже обширные математические таблицы («Canon mathmaticus»), содержащие главным образом тригонометрические таблицы, в которых радиус круга принимала за 100 000. Уже в «Каноне» и особенно в XIX главе «Восьмой книги» Виет формулирует без доказательств всю систему утверждений сферической тригонометрии. Указанные теоремы косинусов Виет формулирует в предложениях 15 и 16 этой главы следующим образом:
«XV. Если в каком-либо сферическом треугольнике даны три стороны, то можно найти и углы.»
«XVI. Если в каком-либо сферическом треугольнике даны три угла, то можно найти стороны.»
Полная аналогия между этими двумя предложениями указывает на то, что Виету была совершенно ясна связь между обеими теоремами косинусов и, весьма возможно, он знал, что вторая из них может быть получена из первой с помощью полярного треугольника. Он вывел среди многих других тригонометрических формул, выражения для синусов и косинусов кратных дуг. С тех пор установление связей между тригонометрией и алгеброй посредством взаимных интерпретаций прочно вошло в практику математических исследований.
Следующий этап обогащения содержания тригонометрии состоял в установлении более общей трактовки тригонометрических функций на базе математического анализа. Содержание тригонометрии, равно как и средства ее аналитического выражения, достигли состояния, близкого к современному, более 200 лет тому назад, во второй половине XVIII в. Сущность произведенных в то время преобразований состояла в радикальной перестройке тригонометрии на алгебраическо-аналитической основе, позволяющей ей сделаться важной частью математического анализа. Решающая роль в этом принадлежит Леонарду Эйлеру (1707—1783).
Свой современный вид сферическая тригонометрия, как и тригонометрия, приняла в трудах великого Леонарда Эйлера, уроженца Базеля, работавшего в Петербурге и Берлине. Если до Эйлера тригонометрия имела дело со значениями тригонометрических функций, то тригонометрия Эйлера имеет дело с тригонометрическими функциями, которые он связал с помощью известной формулы, носящей его имя, с экспоненциальной функцией благодаря этому из тригонометрических формул исчез sinus totus полный (наибольший) синус, т. е. радиус круга, место которого в этих формулах теперь заняла единица. Он создал тригонометрию как науку о функциях, дал ей аналитическое выражение.
Эйлеру принадлежит мысль рассматривать тригонометрические функции как безмерные числа, называя их общим термином: «трансцендентные количества, получающиеся из круга». Эйлер ввел в тригонометрию символику, практически совпадающую с привычной для нас, получил ряд новых соотношений, установил связь тригонометрических функций с показательными, дал правило знаков функций для всех четвертей, получил обобщенную формулу приведения и освободил тригонометрию от многих ошибок, которые допускались почти во всех европейских учебниках математики (тупые углы не имеют функций и т.п.). Тем самым в развитии тригонометрии был сделан очень важный шаг. Тригонометрические функции оказались просто одним из классов аналитических функций.
Примерно в то же время, в 1770 г., появился и удержался до нашего времени термин «тригонометрические функции». Его ввел Г.С. Клюгель в работе «Аналитическая тригонометрия» Эти функции сразу получили широкое применение и стали важной частью аппарата математического анализа. Почти одновременно тригонометрия стала применяться в традиционной области ее использования, в геометрии. Таким образом, к XIX в. тригонометрия, не теряя теоретической целостности, приобрела разнообразные интерпретации, проникла во многие разделы математики.
В современной структуре математических наук тригонометрия определяется как та их часть, где исследуют один из классов аналитических функций, называемых тригонометрическими, а также их приложения. Эти функции чаще всего вводятся с помощью специальной конструкции - порождающей окружности. В качестве своих аргументов они могут иметь как действительные, так и комплексные величины, что придает им высокую степень общности. Их специфические свойства: периодичность, четность или нечетность и др. позволяют с помощью формул (например, формул приведения) существенно упрощать и облегчать операции с ними.
2.3 История преподавания тригонометрии в школе
Проблема преподавания тригонометрии, как и математики в целом, могла быть решена лишь при условии освоения достижений мировой математической науки. В России этому немало способствовал Л. Эйлер, являясь почетным членом Санкт- Петербургской Академии Наук. Тригонометрические исследования Эйлера явились основой первого русского учебника по тригонометрии, коим являлась книга М.Е. Головина «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789г.).
Однако согласно программам 1804г., которые своим названием «Математика чистая и прикладная, и физика» подчеркивали направление преподавания, перед тригонометрией ставилась определенная цель - решение треугольников. Ярым противником формальной школы был М.В. Остроградский. В своем конспекте по тригонометрии он выступает как сторонник определения тригонометрических функций на первом этапе их изучения как отношения сторон в прямоугольном треугольнике, но с последующим обобщением их определения и распространением его на углы любой величины.
Реформы графа Д. Толстого (см. приложение) отражаются и на изложении тригонометрии. 3-е издание учебника Ф. Семашко появляется в 1886 г., в момент рассвета «толстовской» школы. В предисловии автор пишет: «В настоящее время программы всех учебных заведений требуют рассмотрения тригонометрических величин из круга; согласно этим программам я переделал теоретическую часть науки». Комиссия преподавателей средних школ высказалась по этому вопросу следующим образом:
«1. В курсе тригонометрии необходимо изучать теорию круговых функций с применением ее к решению треугольников; ни в коем случае не ограничивать курс решением треугольников.
2. Приложения тригонометрии к геодезии не считать необходимым».
Министерство народного просвещения очень быстро откликнулось на это постановление. Но, таким образом, тригонометрия вступила на путь формального изложения, которое характеризуется следующими особенностями: отсутствием пропедевтического курса; определением тригонометрических функций как отношений «тригонометрических линий» к радиусу; недостаточным использованием понятия функциональной зависимости и, в частности, изучением изменений тригонометрических функций в без применения их графиков неудовлетворительным развитием теории функций.
Под влиянием общественного мнения в 1906 г. изменена программа курса тригонометрии, основная идея которой используется и в наши дни. Тригонометрия была разделена на два концентра. Первый концентр (6 кл.) содержал материал, необходимый для решения прямоугольных и косоугольных треугольников с помощью таблиц тригонометрических величин. Второй концентр (7 кл.) давал теорию гониометрических функций (включая понятия об обратных функциях), тригонометрические уравнения и неравенства, необходимые для приближенного вычисления значений тригонометрических функций.
В связи с построением пропедевтического курса пересматривается вопрос об определениях тригонометрических функций. На первом этапе вводятся определения синуса, косинуса и тангенса через стороны прямоугольного треугольника. Во второй части широко используются графики тригонометрических функций, подробно рассматривается вопрос о вычислении приближенных значений функций и о составлении таблиц. Таким образом, преподавание тригонометрии приобретало новое направление, теоретически более обоснованное и рассчитанное на более широкое использование приложений.
В настоящее время тригонометрию изучают в старших классах школы. Материал соответственно разделен на три части, которые изучаются в разные периоды времени обучения. Впервые тригонометрические выражения появляются в курсе планиметрии, после теоремы Пифагора или непосредственно перед ней. Используются они преимущественно для решения плоских треугольников. При этом отрабатываются первоначальные навыки работы с таблицами тригонометрических функций. Ученики усваивают определения синуса, косинуса и тангенса острого угла.
Во второй раз тригонометрические функции определяются с помощью производящей окружности. Постепенно переходят к рассмотрению тригонометрических функций любого аргумента, выраженного в радианах, и соотношений между ними. Школьников обучают строить графики функций, рассматриваются некоторые свойства.
В третьей части изучаются решения тригонометрических уравнений и неравенств. Рассматривается приложение тригонометрических функций в физике при изучении гармонических колебаниях.
Глава 3. Использование историко-научного материала при преподавании тригонометрии
3.1 Формы использования исторического материала при преподавании на уроках
Говоря о формах изложения учащимся исторического материала, следует отметить, что нет и не может быть единого правила, руководствуясь, которым можно было бы ознакомить с элементами истории математики учащихся всех возрастов и классов. Форма изложения учащимся исторического материала в школе, в первую очередь, зависит от возрастных психологических особенностей учащихся. Основная форма введения исторического материала на уроках математики представляет собой сообщение о исторических сведениях. Не на каждом уроке, но все же достаточно часто и систематически следует делать исторические отступления и сравнения, а также приводить примеры решения исторических задач.
Необходимо упоминание о том, что приемы решения треугольников, конечно без соответствующих понятий и названий, встречались уже в древнейших цивилизациях. В качестве примеров здесь можно приводить задачи, связанные с солнечными часами и гомонами. Приведем вариант объяснения этих задач на уроке.
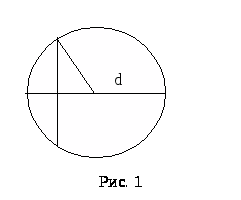
«Ученики, исторически тригонометрия изначально была теснее всего связана с астрономией, в которую долгое время входила в качестве самостоятельного раздела. Задачи, теперь относящиеся к геометрии, встречаются довольно рано в математике разных цивилизаций. Например, в Вавилоне не позднее второго века до н.э. решалась, следующая задача: Вычислить длину хорды S круга, исходя из величины диаметра d и высоты а сегмента, отсеченного этой хордой (рис.1). Задачи такого типа были связаны с использованием солнечных часов, основным элементом которых был так называемый гномон. При решении этой задачи использовали соотношение сторон прямоугольного треугольника, позднее получившее название теоремы Пифагора:
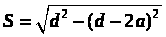

Древние вавилоняне умели вычислять высоту предмета по известной длине его тени. И в Египте и в Вавилоне пользовались гномоном для наблюдения за движением Солнца. Гномон - это вертикальный шест, который устанавливали на ровной горизонтальной площадке. Длина тени, отбрасываемая шестом, зависит от положения солнца и меняется в течение дня. Самой длинной тень будет в момент восхода Солнца. В полдень, когда длина тени наименьшая, ее направление совпадает с направлением истинного меридиана. Используя гномон, в древности решали многие практические задачи. Одной из них, была следующая: если L -длина гномона, то по длине l, отбрасываемой им в данный момент, определить угловую высоту h солнца над горизонтом.
По длине тени определяли точное время. Фиксировали линию, отбрасываемую концом гномона в течение дня, затем делили ее на двенадцать равных частей, получали дневные часы. Поскольку длина линии тени менялась в зависимости от продолжительности светового дня, то в разное время года была разная величина часа. Так, зимний час, был короче летнего. Изучая линию тени, люди научились определять момент солнцестояния, находить длину солнечного года и решать другие практические задачи.»
Учитель должен согласовать объем исторических сведений с материалом урока, он не должен перегружать урок, отвлекать учеников от изучаемой темы. Преподаватель математики на своих уроках сможет давать учащимся более углубленные и систематические знания о развитии изучаемых понятий.
История тригонометрии в гораздо большем объеме может излагаться на внеклассных занятиях.. Формы внеклассной работы могут быть самые различные: факультативные занятия, математические кружки, занятия по решению исторических задач, доклады, как самих учащихся, так и учителя, математические вечера и викторины, выпуск стенных газет, ведение исторического календаря и т.п.. Следует отметить, что при занятиях в математическом кружке учащихся смогут подготовить самостоятельные выступления лишь по тем вопросам истории, которые связаны с изучением частных вопросов математики, а не касаются более широких, обобщающих тем. Учащиеся под руководством преподавателя могут разработать доклады и подготовить выступления о деятельности какого-либо математика, или же, предварительно образовав группу из нескольких человек могут подготовить выступление, осветив более широкие темы, такие как «история измерения углов и дуг», «Тригонометрические функции в Индии», « Тригонометрия - автономная ветвь математики» и т.д..
Довольно занимательным для учащихся может стать участие в создании школьной математической стенной газеты. Задачей создания в школе математической газеты является общее повышение математической культуры в школе. На страницах газеты могут найти свое место небольшие статьи по вопросам математики, выходящие за рамки школьной программы; образцы наиболее интересных в методическом отношении задач; исторические справки, исторические задачи; биографии выдающихся современных или живших ранее математиков; математические софизмы и парадоксы; и прочее. Таким образом, газета может в значительной мере отражать интересы учащихся, в частности по истории математики.
Необходимо привить учащимся способность работать с учебной, справочной и популярной литературой, а также искать необходимую информацию в Интернете. На первых порах возможно только знакомство с наиболее интересными задачами или математическими фактами, имеющими свое историческое значение, в дальнейшем смогут разрабатывать более серьёзные вопросы, готовить развернутые доклады и сообщения, самостоятельно искать и готовить для них материал.
3.2 Основные принципы и требования к отбору историко-научного материала для включения в процесс обучения математике
Рассмотрим принципы отбора и конкретные требования, предъявляемые к историко-научному материалу.
Среди принципов отбора историко-научного материала для включения в содержание образования Л.Я. Зорина [12] называет следующие:
создание мотивации к познанию. Историко-научный материал привлекается для создания учащихся мотивации, убежденности в необходимости новых знаний;
формирование научного мировоззрения. Историко-научный материал привлекается, чтобы убедить учащихся в познаваемости мира; показать эволюцию идей и понятий, проходящих через всю науку;
- раскрыть кризисные ситуации в науке, показать, как они возникают, как, преодолеваются;
формирование научного мышления в процессе обучения. Историко-научный материал необходим, чтобы проиллюстрировать новый этап, в научном мышлении, связанный с введением нового метода исследования, нового метода рассуждений, познакомить учащихся с историей так называемых случайных открытий, историей несостоявшихся открытий; дать представления об общих исканиях, стремлениях, и в особенности, заблуждениях, через которые человеку нужно пройти по пути к истине;
формирование творческого мышления в процессе обучения. Историко-научный материал помогает раскрыть, истолковать возникновения научных проблем, внесших коренные изменения в дальнейшее развитие мира науки, ход решения проблемы, метода решения проблемы;
 формирование
нравственных качеств учащихся.
Историко-научный материал помогает
раскрыть учащимся необходимые качества
творческой личности.
формирование
нравственных качеств учащихся.
Историко-научный материал помогает
раскрыть учащимся необходимые качества
творческой личности.
Рассмотрим конкретные правила отбора историко-научного материала для использование его в процессе обучения. Выделяются следующие требования:
Органическое включение историко-научного материал в курс математики, т.е. историко-научный материал привлекается в зависимости от цели и содержания изучаемого вопроса, требующего использования исторических сведений [13];
Целенаправленность в изложении историко-научного материала в курсе математики, его использование отвечать целям и интересам успешного изучения учебного материала. Иначе говоря, исторические сведения не должны быть использованы сами по себе, а должны подчиняться учебной функции, которая служит доминантой в процессе обучения [14].
Доступность в изложении историко-научного материала в курсе математики. При сообщении историко-научного материала надо помнить, что общее отвлеченное дается всегда труднее, чем частное и наглядное, и вводить это общее и отвлеченное лишь постепенно, осторожно, не обременяя учащихся непосильным материалом [14].
Эмоциональность в изложении историко-научного материала в математике. Эмоциональное изложение позволит стимулировать познавательную деятельность школьника.
Приведем примерное планирование исторического материала.
Тематическое планирование По учебнику А.Г. Мордковича
Глава1. Тригонометрические функции (28 часов)
|
Название параграфа |
Исторически материал |
Литература |
|
Введение (длина дуги окружности). (1ч) |
О происхождении тригонометрии; Предпосылки возникновения науки; Что означает слово тригонометрия; Тригонометрия как часть астрономии. |
Рыбников А.А. «История математики» Учебник – М.Изд-во МГУ,1994 История математики с древнейших времен до начала 19 столетия. В трех томах. Под редакцией А.П. Юшкевича Изд-во «Наука»1970 «Энциклопедия для детей, том 11- математика» Изд-во «Аванта плюс»М.1998 |
|
Числовая окружность. (2ч) |
||
|
Числовая окружность на координатной плоскости. (2ч) |
||
|
Синус и косинус. (3ч) |
Появление терминов синус и косинус; Тригонометрические функции в Индии. |
Г.И. Глейзер «История математики в школе». Пособие для учителей.-М.:Просвещение, 1982 РыбниковА.А. «История математики» Учебник-М.,Изд-во МГУ,1994 |
|
Тангенс и котангенс. (1ч) |
Тень и рождение тангенса, Учения о солнечных часах. |
1. Г.И. Глейзер «История математики в школе». Пососбие для учителей.-М.:Просвещение,1982 |
|
Тригонометрические функции числового аргумента. (2ч) |
||
|
Тригонометрические функции углового аргумента. (2ч) |
||
|
Формулы приведения. (2ч) |
Кто установи формулы приведения. |
«История неевклидовой геометрии. Развитие понятий о геометрическом пространстве» Розенфельд Б.А.,М., «Наука»,1976 Г.И.Глейзер «История математики в школе».Пособие для учителей-М.:Просвещение,1982 |
|
Функция y=sin x, ее свойства и график. (2ч) |
Первый график появившийся в печати, Леонард Эйлер. Современный вид тригонометрии. |
«История неевклидовой геометрии. Развитие понятия о геометрическом пространстве». Розенфельд Б.А. М., «Наука»,1976 |
|
Функция y=cos x, ее свойства и график. (2ч) |
||
|
Периодичность функции y= cos x, y = sin x. (1ч) |
Джон Валлис, первые доказательства периодичности |
1.Г.И.Глеизер «История математики в школе». Пособие для учителей-М.: Просвещении е,1982 |
|
Как построить график функции y=mf(x),если известен график функции y=f(x). (1ч) |
||
|
Как построить график функции y=f(kx), если известен график функции y=f(x). (2x) |
||
|
График гармонического колебания. (1ч) |
||
|
Функции y=tgx, y=ctgx, их свойства и графики. (2ч) |
На основе приведенного планирования приведем примеры конспектов урока с использованием элементов истории математики при преподавании тригонометрии по учебнику Мордкович А.Г. Алгебра и начала анализа.10-11 кл.
Конспект урока по алгебре,10 класс.
Тема урока: « Введение. Длина дуги окружности».
Тип урока: урок изучения нового материала.
Вид урока: беседа, практическая работа.
Цель учения (для учащихся): изучить и закрепить понятие числовой окружности.
Цель: повторить геометрический материал о вычислении длин дуг окружностей; ввести понятие числовой окружности.
Триединые дидактические цели урока:
Образовательная - повторить геометрический материал о вычислении длин дуг окружностей, ознакомить учащихся с новой математической моделью - единичной окружностью, ввести понятия – единичная окружность, четверти окружности, открытые дуги.
Развивающая – развивать логическое мышление, умение анализировать, сравнивать, обобщать.
Воспитательная – воспитывать у учащихся интерес к изучению математики, развивать культуру устной и письменной математической речи.
Технология организации проведения учебного занятия:
Подготовительный этап;
Проведение занятия;
Подведение итогов.
Алгоритм проведения учебного занятия:
организационный момент;
постановка целей урока;
устное повторение;
изучение нового материала;
подведение итогов;
домашнее задание.
Обоснование выбора методов, средств и форм обучения:
Оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
- обязательный учет характера учебного материала;
- использование элементов истории;
- выбор исследовательского метод, как наиболее преемственного для понимания темы «Введение. Длина дуги окружности».
Условия достижения результатов:
взаимосвязь тригонометрии с другими науками;
соблюдение преемственного обучения;
опора на полученные ранее знания;
активное взаимодействие учащихся в классе.
Основные принципы проведения урока:
наглядность;
доступность;
систематичность;
связь с предыдущим (непрерывность).
Литература
Вид доски на начало урока: на доске изображена числовая окружность
Ход урока:
|
Этапы |
Содержание |
Примечание |
|
Организационный момент. |
Здравствуйте, садитесь |
|
|
Постановка урока |
Сегодня мы продолжаем знакомство с большим разделом алгебры - тригонометрические функции, и хочется чтобы вы понимали какой многовековой опыт несет за плечами наука тригонометрия. Поэтому хочу несколько слов сказать о истории этой науки и предпосылках ее возникновения. |
|
|
Изучение нового материала. 1) Сведения из истории тригонометрии. |
Термин «тригонометрия» дословно означает «измерение треугольников». Она возникла, прежде всего, из практических нужд. Древние астрономы наблюдали за движением небесных светил. Учёные обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звёздам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звёздным небом с незапамятных времён вели и астрологи. Естественно, все измерения, связанные расположением светил на небосводе, — измерения косвенные. Прямые — осуществлялись только на поверхности Земли. Но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами. И тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева или размеры острова в море, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие, с этим вы знакомились на уроках геометрии, изучая соотношения между сторонами и углами треугольника. Всё это очень интересно и в дальнейшем на следующих уроках я расскажу о великих ученых, которые внесли, неоценимы вклад в историю тригонометрии, и расскажу историю возникновения основных тригонометрических терминах. Пока же вернемся изучению тригонометрических функций и для введения этих функций нам понадобиться числовая окружность. Отнеситесь к этому очень внимательно, поскольку, как показывает опыт, учащийся, хорошо овладевший понятием «числовая окружность», свободно и непринужденно работающий с ней, без труда будет обращаться с тригонометрическими функциями. Для облегчения восприятия материала вспомним некоторые знакомые вам понятия. |
Слушают |
|
Устное повторение |
Вспоминаем с учащимися понятие: дуга окружности, длина дуги окружности, формулу для нахождения длины дуги окружности. |
Учащиеся отвечают на вопросы учителя |
|
Изучение нового материала 2) ввод понятий |
1) единичная окружность (после введения понятия) «… Следует отметить, что к записи формул при единичном радиусе стали приходить со времен Леонарда Эйлера(1707-1783) Эйлер усовершенствовал как символику, так и содержание тригонометрии. Одна из его заслуг: в отличие от своих предшественников он исключил из своих формул R –целый синус, принимая R=1 и упрощая, таким образом, записи и вычисления. 2) 1,2,3,4 четверти окружности 3) открытые дуги |
слушают |
|
Практическое задание |
1.
Выполняют упражнение на нахождение
длин различных дуг, выражая их в долях
числа
2. Показать учащимся прием нахождения на единичной окружности точек, соответствующих числам 1,2,3,4,5, и т.д.(примеры2,3 из учебника Мордковича А.Г.) 3. Выполнить №1,2,6,7,8 |
1.Решают с учителем (как вариант в диалоговой форме, либо кто-то у доски, но также в диалоговой форме в решении принимает участие весь класс. 2.Конспекти-руют и принимают активное участие в разборе задачи. 3.Решают по очереди у доски |
|
Дом задание Итоги |
№3,4,5. Повторение пройденного материала, знать основные понятия. |
Записывают домашнее задание. |
Конспект урока по алгебре,10 класс.
Тема урока : «Синус и косинус».
Тип урока: урок изучения нового материала.
Вид урока: лекция, практическая работа.
Цель учения (для учащихся): актуализировать определения синуса и косинуса, изучить их свойства.
Цель: ознакомить учащихся с определением синуса и косинуса, составить таблицу знаков синуса и косинуса по четвертям окружности, изучить свойства синуса и косинуса и формулы приведения, приучить к работе со справочной и дополнительной литературой.
Триединые дидактические цели урока:
Образовательная – ввести название для декартовых координат точек числовой окружности: абсцисса точки М(t)-cos (t), ордината точки М (t) – sin(t).
Развивающая – развивать внимание, логическое мышление, умение анализировать, обобщать и систематизировать.
Воспитательная – развитие познавательного интереса, воспитание информационной культуры.
Технология организации проведения учебного занятия:
Подготовительный этап;
Проведение занятия;
Подведение итогов.
Алгоритм проведения учебного занятия:
организационный момент;
постановка целей урока;
изучение нового материала;
практические задания;
подведение итогов;
домашнее задание.
Обоснование выбора методов, средств и форм обучения:
Оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
- обязательный учет характера учебного материала;
- использование элементов истории;
- выбор исследовательского метод, как наиболее преемственного для понимания темы «Синус и Косинус».
Условия достижения результатов:
взаимосвязь тригонометрии с другими науками;
соблюдение преемственного обучения;
опора на полученные ранее знания;
активное взаимодействие учащихся в классе.
Основные принципы проведения урока:
наглядность;
доступность;
систематичность;
связь с предыдущим (непрерывность).
Ход урока:
|
Этапы |
Содержание |
Примечание |
|
Организационный момент |
Здравствуйте, садитесь |
|
|
Постановка целей урока |
Постановка целей урока |
|
|
Изучение нового материала. Ввод понятий |
На предыдущем уроке мы с вами познакомились с понятием числовая окружность, и знаем, что каждая точка числовой окружности имеет в системе хоу свои координаты. Это позволяет нам с вами сформулировать определение. |
Слушают и конспектируют |
|
Введение определений синус и косинус на числовой окружности |
Далее вводим определение синуса и косинуса. |
|
|
Введение таблицы знаков
|
Составляем таблицу знаков синуса и косинуса по четвертям окружности. Вводим
равенство, связывающее
|
|
|
Сведения из истории тригонометрии |
Мы
с вами ввели определение синуса и
косинуса, составили таблицу знаков
синуса и косинуса по четвертям
окружности, ввели равенство, связывающее
тригонометрических функций. При том надо отметить только в 1748г. Леонард Эйлер впервые трактует синус, косинус и т.д. как тригонометрические функции, а много веков до него их рассматривали как тригонометрические линии, обязательно связанные с окружностью. К
примеру древнегреческие ученые не
знали наших тригонометрических
функций, вместо синуса они пользовались
хордой. Начало учения о тригонометрических
величинах было положено в Индии.
Заменив хорду синусом, индийцы вначале
называли синус «ардхаджива», т. е.
половина хорды («джива» — хорда, тетива
лука), а позже — просто «джива». Это
слово было, как полагают, искажено
арабами в «джайб», означающее по-арабски
пазуха, выпуклость. Слово «джайб» было
переведено в XII
в. на латынь соответствующим словом
sinus.
Косинус индийцы назйвали «котиджива»,
т.е. синус остатка (до четверти
окружности).В XV
в. Региомонтан, как и другие математики,
применял для понятия «косинус дуги
(х)» латинский термин sinus
complementi,
т. е. синус дополнения, имея в виду
- о индийском математике Ариабхатте и его трактате ; - о развитии тригонометрии в странах Востока -тень рождения тангенса Для подготовки рекомендую( но не настаиваю) взять в школьной библиотеке книги-Глейзер «История математик в школе»,РыбниковА.А. «История математики», энциклопедию Аванта плюс (том 11) |
Учащиеся слушают Распределяют между собой доклады, записывают литературу |
|
Практическое задание |
Разобрать
с учащимися пример 1, показывающий
способы вычисления значений
|
Разбирают с учителем пример. |
|
Домашнее задание Итоги |
Повторение пройденного материала, подготовить доклад на предложенные темы, определения из учебника заучить |
Записывают д/з |
Заключение
Раздел тригонометрии занимает важное место в процессе изучения математики в общеобразовательной школе и очень важно, чтобы элементы истории при преподавании были актуальными, познавательными и развивающими. Проведя анализ психолого-педагогической литературы, мы выяснили, что среди мотивов учебной деятельности познавательный интерес занимает особое место. Для успешной учебной деятельности необходим баланс внутренних, социальных и познавательных мотивов. При этом грамотно построенная система внешних стимулов может способствовать появлению в перспективе внутренней мотивации при изучении тригонометрии.
Анализ историко-генетического метода показал его эффективность при изучении тригонометрии. Следует отметить что при этом излагаемые учителем историко-математические сведения должны быть последовательны, понятны, целостны и вызывать интерес к изучаемому предмету у учеников.
Проследив исторические этапы формирования и развития тригонометрии в отдельную ветвь математики, а также показав эволюцию преподавания тригонометрии в школе, мы изложили основные принципы и требования к отбору историко-научного материала для включения в процесс преподавания тригонометрии.
Современная школьная программа указывает на необходимость знакомства учеников с фактами из истории математики и биографиями великих математиков. Но в программе нет конкретных указаний, какие сведения из истории, когда и как сообщать школьникам. В дипломной работе разработано примерное планирования уроков с включением в них историко-математического материала.
Таким образом, результаты дипломной работы показали, что какая бы ни была форма сообщения исторических фактов — краткая беседа, экскурс, лаконичная справка, решение задачи, показ и разъяснение рисунка, использованное для этого на уроке время потрачено эффективно. Рассказ о исторических причинах возникновения тригонометрии, ее развитии и практическом применении побуждает у школьников интерес к изучаемому предмету, формирует их мировоззрение и повышает общую культуру. Представленные в работе конспекты уроков показывают, что всегда можно найти как время, так и нужное место для сообщения ученикам сведений по истории математики.
Библиография.
Гордеева,Т.О. Психология мотивации достижения.[тескт]/ Т.О. Гордеева.-М.:Смысл:Академия,2006г.-336 с.
Методика и технология обучения математике: Курс лекции: пособие для ВУЗов [текст] /под ред. Н. С. Стефановой, Н. С. Подходовой.-М.:Дрофа,2005г.-416с.:ил.
Божович,Л.И. Избранные психологические труды: Проблема формирования личности [текст]/ Л.И. Божович; под.ред. Фельдштейна Д.И.-М.:Междунар.пел.акад.,1995.-209с.
Меморандум американских математиков.-пер. с англ.[текст]/ Математика в школе.-1964г.-№4.
Азевич А. И. Двенадцать уроков гармонии: Гуманитарно-математически курс.-М.: Школа-Пресс,1998г.-160с.:ил.(Библиотека журнала «Математика в школе». Вып.7).
Баврин И.И., Фрибус Е.А. Старинные задачи: Кн. Для учащихся.-М.: Просвещение,1994.-128с.:ил.
Волошинов А.В. Математика и искусство.-2-е изд.,дораб. и доп.- М.: Просвещение,2000-399с.:ил.
Гиндикин С.Г. Рассказы о физиках и математиках.-2-е изд.-М.: Наука,Гл.ред. физ.-мат.лит.;1985-192с.(Библиотека «Квант» вып.14)
Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики: Мат. анализ. Теория вероятности. старин.и занимат. задачи:Кн. Для учащихся 10-11 кл.общеобразоват.учреждений.-М.: Просвещение,1997.-269с.:ил.
Белобородова С.В.Об историко-генетическом методе.//Математика в школе.-1999.-№6.-с.7-10.
Давыдов В.В. Теория развивающего обучения.-М.: ИНТОР,1996.-544с.:ил.
Зорина Л.Я. Вопросы конструирования содержания среднего образования.М.,НИИОП,1980.
Бондаревский В.Б. Воспитание интереса к занятиям и потребности к самообразованию.М.1985.
Барсуков А.Н. Математика в школе.1956№2
Мордкович А.Г. Алгебра и начала анализа.10-11 кл.: В двух частях.Ч1:Учеб.для общеобразоват. Учреждений.-3-е изд., испр.-М.: Мнемозина,2002.
Мордкович А.Г и др. Алгебра и начала анализа.10-11кл.:Задачник для общеобразоват. учреждений.-М.: Мнемозина,2000.
Розенфельд Б.А. История неевклидовой геометрии. Развитие понятия о геометрическом пространстве.М., «Наука»,1976
Глейзер Г.И. История математики в школе.-пособие для учителей.М.Просвещение,1981
Приложение
Толстой Дмитрий Андреевич (1823, Москва - 1889, Петербург), государственный деятель.
Происходил из аристократического графского рода. В 1843 с отличием окончил Царскосельский лицей и, увлекшись наукой, исследовал распространение в России различных религий, за что был награжден премией Академии наук и пожалован бриллиантовым перстнем от Николая I. В 1853 был назначен директором канцелярии Морского министерства. В 1861 стал управляющим департаментом Министерства народного просвещения. Либеральные воззрения Толстой не шли дальше отмены крепостного права, он оставался противником реформ 60 - 70-х гг. - судебной, земской и др., видя в них угрозу самодержавной власти.
В 1865 Толстой был назначен обер-прокурором Синода. В 1866, после покушения Д.Д. Каракозова, когда было решено обратить серьезное внимание на воспитание юношества, усилив контроль за системой народного образования, Толстой добавил к своей должности обязанности министра народного просвещения, что, по мнению К.Д. Ушинского, позволило "давить народное просвещение тяжестью двух министерств". В 1871 Толстой провел реформу среднего образования, направленную на уничтожение какой бы то ни было самостоятельности мысли учащихся. Вводил изучение мертвых языков вместо общеобразовательных предметов; реорганизовал реальные гимназии в училища, сократив в них срок обучения, и проводил в жизнь сословный принцип: церковноприходская школа для "народа", реальное училище для купцов и промышленников, классическая гимназия и ун-т для дворян. Толстой выступал также противником высшего образования женщин.
Вот почему либерально-демократическими кругами реформа Толстой расценивалась как реакционная. Хотя за время пребывания Толстого у власти число средних и высших учебных заведений увеличилось почти втрое, а низших - более чем в 20 раз, М.Т. Лорис-Меликов писал о нем: "Личность эта, стоявшая в продолжение пятнадцати лет во главе одной из важнейших отраслей государственного управления, сотворила больше зла Для России, чем все остальные деятели, даже вместе взятые". В 1880, во время подготовки либеральных реформ, Толстой был отправлен в отставку. Убийство народовольцами Александра 2 похоронило надежды на новый правительственный курс и привело в 1882 Толстого на пост министра внутренних дел для наведения "твердого порядка". Толстой провел реорганизацию Министерства внутренних дел и создал охранные отделения, где провокация стала нормой агентурной работы. Однако деятельность Г.П. Судейкина показала опасность подобной тактики.
Толстой наряду с К.П. Победоносцевым являлся наиболее ярким, прямолинейным и просвещенным выразителем узко дворянских интересов, подготовив проекты "контрреформ" - восстановления предварительной цензуры (1882), отмены автономии ун-тов (1884), введения земских начальников (1889) и др. Как человек, известный рядом серьезных исследований ("История финансовых учреждений России со времени основания государства до кончины императрицы Екатерины II", "Римский католицизм в России", биографический словарь "Люди екатерининского времени" и др.), Толстой был назначен президентом Академии наук. Будучи тяжело болен, до конца жизни оставался на своих постах, боясь прихода на свое место людей с либерально-демократическими убеждениями.
Использованы материалы кн.: Шикман А.П. Деятели отечественной истории. Биографический справочник. Москва, 1997 г.
1 Малыгин К.А. Элементы историзма в преподавание математики в средней школе / К.А. Малыгин. – М.: Учпедгиз.1956 – С. 3.
2 Подласый И.П. Педагогика: Новый курс: учеб. Для студ. Пед. Вузов: в 2 кн. / И.П. Подласый. – М.: Гуманист: Владос, 2000. – кн.1: Общие основы. Процесс обучения. – С.36
 .
. Таблицы
значений
Таблицы
значений и
и
