Использование разнообразных форм уроков при изучении темы "Квадратные уравнения" в 8 классе

ГОУ СПО "Кунгурское педагогическое училище"

ПЦК преподавателей естественно-математических дисциплин

Выпускная квалификационная работа

по методике математики

Использование разнообразных форм уроков при изучении темы "Квадратные уравнения" в 8 классе

Исламовой Энзиры Таузифовны

Специальность 050201

Математика

Группа М-51

отделение: очное

Руководитель: Л.Г. Янкина

преподаватель математики

2008

Оглавление

Введение

Глава 1. Теоретические аспекты обучению решения уравнений учащихся 8 класса

1.1 Основные направления изучения линии уравнений в школьном курсе алгебры

1.2 Методика изучения квадратных уравнений

1.3 Характеристика разнообразных форм уроков

Глава 2. Разработка и практическое использование различных форм уроков математики

2.1 Разработка уроков по теме "Неполные квадратные уравнения"

2.2 Разработка уроков по теме "Полные квадратные уравнения"

2.3 Разработка уроков по теме "Приведенные квадратные уравнении

Заключение

Литература

Введение

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т.д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. При изучении любой темы уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся [12,241].

Автором данной работы выбрана тема "Использование разнообразных форм уроков при изучении темы "Квадратные уравнения" в 8 классе", так как она актуальна в современном мире; это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.

Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений.

Исходя из вышесказанного, автор, выбирая тему, руководствовался ее значимостью и сложностью при обучении учащихся решению квадратных уравнений разного вида.

Цель работы: разработка и апробация уроков по теме "Квадратные уравнения" в 8 классе. Исходя из данной цели, были поставлены следующие задачи:

  • изучить научно-методическую литературу, касающуюся изучению уравнений;

  • проанализировать школьные учебники и выделить в них место уравнений.

  • подобрать, систематизировать дополнительный материал по данной теме для разработки уроков.

Объект исследования работы: процесс обучения школьников решению квадратных уравнений.

Предмет: методические условия усвоения решения квадратных уравнений при использовании разных форм уроков.

Контингент: учащиеся 8-го класса Иштеряковской средней школе.

Гипотеза: если на уроках использовать различные формы уроков, то это способствует лучшему усвоению решения квадратных уравнений разного вида.

Глава 1. Теоретические аспекты обучению решения уравнений учащихся 8 класса

1.1 Основные направления изучения линии уравнений в школьном курсе алгебры

Уравнение как общематематическое понятие многоаспектно. Можно выделить главные области возникновения и функционирования понятия "уравнение" как:

  • средства решения текстовых задач;

  • особого рода формулы, служащей в алгебре объектом изучения;

  • формулы, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением [12,268].

Каждое из этих представлений оказалось в том или ином отношении полезным.

Названным областям относятся три основных направления изучения линий уравнений в школьном курсе алгебры.

1. Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время, ведущее положение в приложениях математики занимает математическое моделирование. (Математическое моделирование заключается в конструировании по определенным правилам некоторой формальной системы, которая отображает через совокупность математических операций над величинами определенную гипотезу о структуре или воспитания). Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании [2,246].

2. Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах:

  • выделение и изучение наиболее важных классов уравнений, и их систем;

  • изучение обобщенных понятий, относящихся ко всей линии в целом.

Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений.

3. Направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией, причем эта связь - двусторонняя. Основная идея, реализуемая в процессе установления взаимосвязи этих линий, - это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений.

Например, введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х2 = b, где b-неотрицательное рациональное число, но и любых квадратных уравнений с рациональными коэффициентами и неотрицательным дискриминантом [5,36].

Линия уравнений тесно связана также и с функциональной линией. Одна из важнейших таких связей - приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.). С другой стороны, функциональная линия оказывает существенное влияние, как на содержание линии уравнений, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений и их систем [12,269].

Характеризуя уравнение, нужно учитывать разные стороны этого понятия. Уравнение представляет собой некоторую запись, составленную по определенным правилам (синтаксический подход). Заменяя в записи буквы (переменные) конкретными числами, переходят к верным или неверным равенствам (логический подход). Стоящие в левой и правой частях уравнения, выражения задают функции, значения которых связаны знаком "=" (функциональный подход). Действия над уравнениями производятся по некоторым правилам (операционный подход). Задание "решить уравнение" предполагает отыскание всех его корней (целевой подход).

На практике понятие уравнения может быть введено посредством выделения его в результате решения задач алгебраическим методом. В этом случае существенным является подход к понятию уравнения, при котором уравнение представляет косвенную форму задания некоторого неизвестного числа, имеющего в соответствии с сюжетом конкретную математическую интерпретацию (модельный подход). Указанный способ введения понятия уравнения соответствует прикладному аспекту понятия уравнения, отраженному в следующем определении: "Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Корнем уравнения называется то значение неизвестного, при котором уравнение обращается в верное равенство".

Существует другой вариант определения уравнения: "Равенство с переменной называется уравнением. Значение переменной, при котором равенство переменной обращается в верное числовое равенство, называется корнем уравнения". Это определение характеризует уравнение как предикат особого вида, а корень уравнения - число из множества истинности этого предиката. Термин "уравнение" несет в себе признаки знакового компонента, а термин "корень уравнения" учитывает смысловой компонент.

Можно встретить и третий вариант определения, роль которого проявляется при изучении графического метода решения уравнений: "Уравнение - это равенство двух функций".

Классификация уравнений тесно связана с конкретными функциями, изучаемыми в школьном курсе математики. В соответствии с этим в школьном курсе алгебры выделяются определенные виды уравнений:

В отношении формирования понятия равносильности и его применения учебные пособия можно разделить на две группы. К первой относятся те пособия, в которых использовании е равносильных преобразований явно основано на введении и изучении понятия равносильности; ко второй - те, в которых применение равносильных преобразований предшествует определению понятия равносильности [9,102].

Методика работы над понятием при указанных подходах существенно отличается.

В школьном курсе математики можно выделить три этапа, связанных с рассмотрением этого вопроса.

Во-первых, в начальном курсе математики и в начале изучения алгебры решаются простейшие модели. Используемые преобразования получают индуктивное обоснование. По мере накопления опыта индуктивные рассуждения чаще заменяются такими, где равносильность используется, но сам термин не вводится.

Во-вторых, выделяется понятие равносильности и сопоставляется его теоретическое содержание с правилами преобразований, которые выводятся на его основе.

В-третьих, на основе понятия равносильности происходит развертывание и общей теории, и теории отдельных классов уравнений. Это характерно для старших классов при изучении курса "Алгебры и начала анализа", а также имеет место и в начальной школе в классах углубленного изучения математики [17,172].

В процессе решения уравнений также используется понятие логического следования, которое изучается позже понятия равносильности и является дополнением к нему. Методика работы с понятием логического следования имеет много общих черт с методикой изучения равносильности и равносильных преобразований. Нередко в практике работы учителей логическое следование применяется как прием, упрощающий процесс решения, если сохранение равносильности может быть достигнуто сравнительно "дорогой ценой" [14, 111].

Среди неравносильных преобразований есть преобразования, не являющиеся логическим следованием. Например, переход к рассмотрению частного случая (пример: переход от уравнения и рассматривать как практические приемы, позволяющие сосредоточить внимание на отдельных шагах процесса решения уравнения).

Можно выделить три основных типа таких преобразование:

  1. Преобразование одной из частей уравнения.

  2. Согласованное преобразование обеих частей уравнения.

  3. Преобразование логической структуры.

Преобразования первого типа используются при необходимости упрощения выражения в какой-то из частей уравнения. Например, решая уравнение можно пытаться заменить выражение в левой части более простым. В данном случае соответствующее преобразование приводит к уравнению , неравносильному исходному за счет изменения области определения. Возможность получения при такой замене уравнения, неравносильного данному, приходится учитывать при изучении некоторых типов уравнений, например тригонометрических или логарифмических.

В классе дробно-рациональных уравнений с этим явлением приходится сталкиваться гораздо реже. Здесь это связано с возможностью потери корней при сокращении дробей. Наконец, в классе целых алгебраических уравнений рассматриваемый тип преобразований всегда приводит к уравнениям, равносильным данным.

Преобразования второго типа состоят в согласованном изменении обеих частей уравнения в результате применения к ним арифметических действий или элементарных функций. Преобразования второго типа сравнительно многочисленны. Они составляют ядро материала, изучаемого в линии уравнений.

Приведем примеры преобразований этого типа.

  1. Прибавление к обеим частям уравнения одного и того же выражения.

  2. Умножение (деление) обеих частей уравнения на одно и того же выражения.

  3. Переход от уравнения а = b к уравнению f (a) =f (b), где f - некоторая функция, или обратный переход.

К третьему типу преобразований относятся:

  • преобразования, осуществляемые на основе свойств арифметических операций. К ним можно отнести переход от уравнения к совокупности уравнений после предварительного разложения на множители; переход от уравнения к системе после приравнивания суммы квадратов выражений к нулю; почленное сложение, умножение, деление уравнений, неравенств и т.д.

  • преобразования, осуществляемые при помощи логических операций. Примерами их являются выделение из системы одного из компонентов, замена переменных.

Таким образом, владение содержанием линии уравнений позволяет расширить список выполнимых преобразований.

В итоге изучения материала линий уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.

С началом систематического курса алгебры основное внимание уделяется внимание способам решения линейных и квадратных уравнений, которые становятся специальным объектом изучения.

Далее рассмотрим различные виды квадратных уравнений и методику их изучения.

1.2 Методика изучения квадратных уравнений

С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для изучения данной темы по программе для общеобразовательных учреждений отводится 26 часов [8, 151]. Основная цель - выработать умения решать квадратные уравнения и решать задачи, сводящиеся к ним.

Квадратным уравнением называется уравнение вида bx + c = 0, где х - переменная, а, b и с - некоторые числа, причем а . Числа а, b и с - коэффициенты квадратного уравнения [1, 98].

Умение решать квадратные уравнения служит базой для решения других типов уравнений и их систем (дробных рациональных, иррациональных, высших степеней).

Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:

  • формулу нахождения дискриминанта;

  • формулу нахождения корней квадратного уравнения;

  • алгоритмы решения уравнений данного вида.

В результате изучения данной темы учащиеся должны уметь:

  • решать неполные квадратные уравнения;

  • решать полные квадратные уравнения;

  • решать приведенные квадратные уравнения;

  • находить ошибки в решенных уравнениях и исправлять их;

  • делать проверку.

Решение каждого уравнения складывается из двух основных частей:

  • преобразования данного уравнения к простейшим;

  • решения уравнений по известным правилам, формулам или алгоритмам.

При изучении темы "Квадратные уравнения" рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А.Г. Мордкович, С.М. Никольский, Ю.Н. Макарычев, М.И. Башмаков (Приложение 6)

Можно сделать следующие выводы:

1) во всех современных школьных учебниках алгебры методическая линия изучения квадратных уравнений одинакова.

2) в учебнике под ред.М.И. Башмакова дается историческая справка, а в других учебниках этого нет.

3) в учебниках алгебры С.М. Никольского и Ю.Н. Макарычева при изучении темы "Квадратные уравнения" рассматриваются прямая и обратная теорема Виета.

Обучение решению уравнений начинается с простейших их видов, и программа [5,131] обусловливает постепенное накопление как их видов, так и "фонда" тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. В курсе математики старших классов учащиеся сталкиваются с новыми классами уравнений, систем или с углубленным изучением уже известных классов. Однако это мало влияет на уже сформированную систему знаний, умений и навыков; они дополняют ее новым фактическим содержанием.

Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы "Квадратные уравнения":

I этап - "Решение неполных квадратных уравнений".

II этап - "Решение полных квадратных уравнений".

III этап - "Решение приведенных квадратных уравнений".

На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах2 = 0, ах2 + с = 0, где а ≠ 0 и с≠ 0, ах2 + bх = 0, где а ≠ 0 и

b ≠ 0. Рассмотрим решение несколько таких уравнений:

1. Если ах2 = 0. Уравнения такого вида решаются по алгоритму:

1) найти х2;

2) найти х.

Например, 5х2 = 0. Разделив обе части уравнения на 5 получается: х2 = 0, откуда х = 0.

2. Если ах2 + с = 0, с ≠ 0 Уравнения данного вида решаются по алгоритму:

1) перенести слагаемые в правую часть;

2) найти все числа, квадраты которых равны числу с.

Например, х2 - 5 = 0, Это уравнение равносильно уравнению х2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два и - . Таким образом, уравнение х2 - 5 = 0 имеет два действительных корня: x>1> =, x>2> = - и других действительных корней не имеет.

3. Если ах2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:

1) вынести общий множитель за скобки;

2) найти x>1>, x>2>.

Например, х2 - 3х = 0. Перепишем уравнение х2 - 3х = 0 в виде х (х - 3) = 0. Это уравнение имеет, очевидно, корни x>1> = 0, x>2> = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х (х - 3) = 0 получится число, не равное нулю.

Итак, данные примеры показывают, как решаются неполные квадратные уравнения:

1) если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0;

2) если уравнение имеет вид ах2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x>1 >= 0; x>2> = - ;

3) если уравнение имеет вид ах2 + с = 0, то его преобразуют к виду

ах2 = - с и далее х2. = - В случае, когда - < 0, уравнение х2 = - не имеет действительных корней (значит, не имеет корней и исходное уравнение ах2 + с = 0). В случае, когда - > 0, т.е. - = m, где m>0, уравнение х2 = m имеет два корня = , = - , в этом случае допускается более короткая запись = . Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.

На втором этапе осуществляется переход к решению полного квадратного уравнения. Это уравнения вида ах2 + bx + c = 0, где a,b,c - заданные числа, а ≠ 0, х - неизвестное.

Любое полное квадратное уравнение можно преобразовать к виду , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Дискриминант уравнения равен: D = p2 - 4q. Рассматриваются следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.

1. Если D < 0, то квадратное уравнение ах2 + bx + c = 0, где а ≠ 0 не имеет действительных корней. Например, 2х2 + 4х + 7 = 0. Решение: здесь а = 2, b = 4, с = 7. D = b2 - 4ас = 42 - = 16 - 56 = - 40. Так как D < 0, то данное квадратное уравнение не имеет действительных корней.

2. Если D = 0, то квадратное уравнение ах2 + bx + c = 0, где а ≠ 0, имеет два равных корня, которые находятся по формуле .

Например, 4х - 20х + 25 = 0. Решение: а = 4, b = - 20, с = 25. D = b2 - 4ас = (-20) 2 - = 400 - 400 = 0. Так как D = 0, то данное уравнение имеет два равных корня, которые находятся по формуле . Значит,

3. Если D > 0, то квадратное уравнение ах2 + bx + c = 0, где а ≠ 0 имеет два корня, которые находятся по формулам: ; (1)

Например, 3х2 + 8х - 11 = 0. Решение: а = 3, b = 8, с = - 11. D = b2 - 4ас = 82 - (-11) = 64 + 132 = 196. Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:

.

Составляется алгоритм решения уравнения вида ах2 + bx + c = 0.

  1. Вычислить дискриминант D по формуле D = b2 - 4ас.

2. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.

3. Если D = 0, то квадратное уравнение имеет два равных корня, который находятся по формуле

4. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня:

; .

Это алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому алгоритму не решают.

Математики - люди практичные, экономные, поэтому пользуются формулой:

. (2)

Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно - записать сразу формулу (2) и с ее помощью делать необходимые выводы [1,98].

На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х2 +px + q = 0 (3), где p и q - данные числа. Число p - коэффициент при х, а q - свободный член.

Дискриминант уравнения равен: D = p2 - 4q. Приведенные квадратные уравнения получаются из полного квадратного уравнения следующим образом:

Где и .

Рассматривают 3 случая:

1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле

.

(Приложение 1) (4)

2. D = 0, тогда уравнение (3) имеет единственный корень, или, как говорят, два совпадающих корня:

3. D < 0, то уравнение не имеет корней. Обычно в случае приведенного квадратного уравнения (3) вместо D рассматривается выражение , имеющее тот же знак, что и D. При этом формулу корней приведенного квадратного уравнения (4) записывают так:

Отсюда следует, что:

  1. если то уравнение (3) имеет два корня;

  2. если то уравнение имеет два совпадающих корня;

  3. если то уравнение не имеет корней.

Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения [23,17].

Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. (Приложение 2)

Иначе говоря, если x>1 >и x>2> - корни уравнения х2 +px + q = 0, то

x>1> + x>2 >= - p,

x>1> x>2> = q. (5)

Данные формулы называют формулами Виета в честь французского математика Ф. Виета (1540-1603), (Приложение 3) который ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.

Например, приведенное уравнение х2 - 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема, обратная теореме Виета.

Теорема, обратная теореме Виета. Если для чисел x>1>, x>2, >p, q справедливы формулы (5), то x>1> и x>2> - корни уравнения х2 + px + q = 0 [2,49].

Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.

Например. Напишем приведенное квадратное уравнение, корнями которого являются числа 1 и - 3.

По формулам Виета

p = x>1> + x>2 >= - 2, q = x>1> x>2 >= - 3.

Следовательно, искомое уравнение имеет вид х2 + 2х - 3 = 0.

Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего, требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной - только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета.

Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители

Таким образом, неполные и приведенные квадратные уравнения имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев. Обычно они изучаются перед выводом корней общего квадратного уравнения. В целом можно сказать, что освоение темы "Квадратные уравнения" поднимает учащихся на качественно новую ступень овладения содержанием школьной математики.

Важную роль в учебном процессе играют формы организации или виды обучения, в качестве которых выступают устойчивые способы организации педагогического процесса.

Основной формой организации учебно-воспитательной работы с учащимися является урок.

1.3 Характеристика разнообразных форм уроков

Урок - логически законченный, целостный, ограниченных определенными рамками времени отрезок учебно-воспитательного процесса, где представлены все основные элементы этого процесса (цели, содержание, средства, методы, формы организации). Урок представляет собой форму организации деятельности учителя и учащихся.

Урок - это занятие с классом учеников, продолжительностью 40-45 минут. Количество таких занятий определяет учебный план школы, а их содержание - Госстандарт и школьные программы [2,65].

Понятие урок имеет характерные черты (основные характеристики), позволяющие рассматривать его с разных позиций. Иначе, урок состоит из компонентов:

  • цель;

  • содержание;

  • средства и методы обучения;

  • организация учебной деятельности.

Главную роль среди основных характеристик урока играют цели урока: образовательные, воспитательные и развивающие. В соответствии с целью урока отбирается содержание обучения, и, прежде всего содержание урока.

На разных уроках ставится разная дидактическая цель и дидактические задачи не могут иметь одинаковые объем и значение, поэтому различают:

урок обычный, на котором решается лишь одна дидактическая задача (изучение нового материала, или закрепление изученного, или контроль);

урок комбинированный (смешанный), где последовательно решаются несколько дидактических задач;

урок синтетический, на котором решаются одновременно несколько дидактических задач.

В практике обучения наиболее часто проводятся комбинированные уроки. Структура такого урока включает:

  1. Организационный момент.

  2. Проверка знаний и умений учащихся.

  3. Изучение нового материала.

  4. Закрепление изученного материала.

Выделяют четыре основных типа уроков:

  • урок по ознакомлению с новым материалом;

  • урок по закреплению изученного материала;

  • урок проверки знаний, умений и навыков;

  • урок по систематизации и обобщению изученного материала.

Кроме рассмотренной классификации получила распространение классификация по способам проведения уроков (урок-лекция, урок-практикум, урок-презентация, урок - контрольная работа, комбинированный урок, урок - игра и т.д.) [22,64].

Урок - лекция. Материал лекции должен быть интересным, сопровождаться показом наглядных пособий, содержать много примеров из опыта учителя и школьников. Лекция проводится в течение 20 минут, в остальное время урока можно провести самостоятельную работу по проверке усвоения материала или провести этап закрепления и систематизации знаний.

Как правило, это уроки, на которых излагается значительная часть теоретического материала изучаемой темы.

По характеру изложения и деятельности учащихся лекция может быть информационной, объяснительной, лекцией-беседой и т.д.

Лекционная форма проведения уроков целесообразна при:

изучении нового материала, мало связанного ранее изученным;

рассмотрении сложного для самостоятельного изучения материала;

подаче информации крупными блоками;

применении изученного материала при решении практических задач.

Структура лекции определяется выбором темы и цели урока. Другими словами, лекция строится на сочетании этапов урока: организации; постановки цели и актуализации знаний, сообщение знаний учителем и усвоения их учащимися; определении домашнего задания.

Структура данного типа урока может быть такова:

1) повторение материала, необходимого для сознательного усвоения новых математических знаний;

2) изучение нового материала;

3) первичное закрепление изучаемого материала;

4) задание на дом.

Последовательность структурных элементов урока может быть и другой, но в любом случае основная часть урока данного типа посвящается работе над новым материалом [21,95].

Урок - практикум. Основное место на уроках данного типа занимает выполнение учащимися различных тренировочных упражнений и творческих работ. Предлагаются упражнения в определенной системе. Большое место на этих уроках отводится самостоятельной работе учащихся.

Структура этих уроков, как правило, следующая:

  1. воспроизведение учащимися знаний, умений и навыков, которые потребуются для выполнения заданий;

2) самостоятельное выполнение учащимися различных упражнений;

3) проверка выполнения работы и подведение итогов;

4) задание на дом.

С целью развития знаний, умений и навыков на таких уроках иногда включаются элементы нового. Кроме этого, с помощью специальных упражнений проводится подготовительная работа к изучению к следующих тем. Но эти дидактические цели подчиняются основной цели урока - закреплению изученного материла [8,25].

Контрольные уроки. Основное место на таких уроках отводится устной и письменной проверке усвоения изученного материла. Проверка, как правило, сочетается с закреплением знаний, умений и навыков. Самостоятельные письменные работы занимают от 15 до 30 минут, остальное время отводится на закрепление ранее изученного. В конце урока, если проверка проводилась в устной форме, учитель, как правило, дает краткую характеристику знаниям, умениям и навыкам учащихся, указывает на достижения, недостатки и пути их преодоления. Если проверка проводилась в письменной форме, то последующий урок посвящается анализу результатов контрольной работы, исправлению типичных ошибок, повторению и закреплению тех разделов, которые оказались хуже усвоенными [22,35].

Урок - путешествие. Урок проводится в форме воображаемого путешествия. Этапами урока являются остановки по пути следования. Экскурсоводом (инструктором) может быть учитель или заранее подготовленный ученик.

Урок построен в виде практических исследований, работы с изображениями, наглядными пособиями, бесед и докладов о событиях математики.

По окончанию путешествия составляют отчет об "увиденных" событиях.

Урок - презентация. Преимущество компьютерной презентации состоит в облегчении труда преподавателя, упорядочивании и сохранности наглядного материала, необходимого для конкретного занятия.

Презентации дают возможность подать в привлекательном виде тщательно подготовленную информацию. Главная дидактическая функция презентации обусловлена тем, что реализуемая в ней последовательность представления визуальных компонентов определяет порядок восприятия учебного материала. Презентация обеспечивает методически выверенное распределение внимания. Компьютерная презентация помогает упорядочить весь материал, выстроить его, следуя логике изложения и хранить его в одном файле. Сохранение наглядных материалов и возможность их корректирования тоже является важным моментом для преподавателя.

Возможны различные виды уроков с применением информационных технологий:

уроки-беседы с использованием компьютера как наглядного средства; уроки постановки и проведения исследований;

уроки практической работы;

уроки - зачеты;

интегрированные уроки и т.д.

Компьютер можно использовать на различных этапах процесса обучения: при объяснении нового материала, закреплении, повторении, контроле знаний, умений и навыков.

Урок - соревнование. Основу урока соревнования составляют состязания команд при ответах на вопросы и решении чередующихся заданий, предложенных учителем.

Формы проведения таких уроков самая различная. Это поединок, бой, эстафета, соревнования, построенные по сюжетам известных игр: "КВН", "Брейн-ринг", "Счастливый случай", "Звездный час" и др.

Урок - экскурсия проводится с целью накопления непосредственных восприятий и наблюдений учащимися объектов и явлений, связанных с изучением материала по математике. Проводя экскурсии, предусмотренные программой, в природу и на производство (например, в сад, на ферму, строительную площадку и т.п.), учитель организует наблюдения за количественными изменениями, сбор числового материла и т.п.

Экскурсия может явиться началом работы по теме программы. Цель ее - вызвать у учащихся интерес к изучению темы, содействовать накоплению материала, необходимого для последующей работы по теме.

Экскурсия может быть организована в процессе работы над темой. Ее назначение - содействовать частичной проверке уже полученных знаний и умений, а также дополнить материал, необходимый для дальнейшей работы по теме. Она может подвести итог работы по теме или нескольким темам. Цель такой экскурсии - закрепить и расширить знания учащихся, обобщить материал, полученный на уроке или ряде уроков.

Таким образом, существует многообразие форм уроков [11, 32].

Далее рассмотрим применение вышеперечисленных форм уроков при обучении математике.

Глава 2. Разработка и практическое использование различных форм уроков математики

Для того чтобы доказать или опровергнуть, что использование различных форм уроков способствует улучшению качества знаний школьников по теме "Квадратные уравнения", были разработаны и проведены разнообразные формы уроков в 8 классе МОУ “Иштеряковская средняя общеобразовательная школа". При изучении темы были выбраны такие формы уроков, как:

  • урок - лекция;

  • урок - презентация;

  • урок - практикум;

  • урок - игра "Звездный час";

  • урок - программирование;

  • контрольный урок.

2.1 Разработка уроков по теме "Неполные квадратные уравнения"

Урок - лекция по теме "Неполные квадратные уравнения"

Тип урока: изучение новой темы.

Цели урока: ввести понятие квадратного и неполного квадратного уравнения; показать решения неполных квадратных уравнений; формировать умение решать неполные квадратные уравнения; развивать математическую речь, мышление, внимание; воспитывать интерес к предмету, самостоятельность. Ход урока: 1. Организационный момент. 2. Сообщение темы и цели урока.

У нас сегодня урок - лекция, учимся решать неполные квадратные уравнения.

3. Актуализация знаний

3.1 Устный счет

4,8: 2

2,4

3 - 0,4

2,6

1,4 + 4,9

6,3

+ 0,8

3,2

: 0,13

20

: 3

2,1

: 0,4

8

: 0,1

200

+ 5,9

8

0,2

1,8

: 0,2

1000

: 20

0,4

3.2 Повторение вопросов теории

Что такое уравнение?

Что значит решить уравнение?

Что такое корень уравнения?

3.3 Итог

Итак, мы вспомнили, что такое уравнение, корень, немного посчитали устно. А сейчас открываем тетради, записываем сегодняшнее число и тему урока "Неполные квадратные уравнения".

4. Работа по теме урока

4.1 Историческая справка

Квадратные уравнения умели решать еще вавилоняне. Это было связано с решением задач о нахождении площадей земельных участков, а также с развитием астрономии. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения.

4.2 Объяснение нового материала

(Учитель, объясняя тему урока, делает на доске короткие записи в виде схем, которые остаются на доске во время всего этого урока. Эти записи нужны, чтобы дети хорошо усвоили тему).

Квадратным уравнением называется уравнение вида bx + c = 0, где х - переменная, а, b и с - некоторые числа, причем а . Числа а, b и с - коэффициенты квадратного уравнения. Число D =называют дискриминантом квадратного уравнения. Если в квадратном уравнении хотя бы один из коэффициентов равен нулю, то такое уравнение называют неполным квадратным уравнением.

Неполные квадратные уравнения бывают трех видов:

Рассмотрим решение каждого из этих видов (составляется таблица по решению неполных квадратных уравнений).

единственный корень уравнения равный

нулю

один из корней уравнения всегда равен нулю

корни противоположны по знаку и равные по модулю

  1. Закрепление.

5.1 Выполнение заданий № 504, 505, 508 - устно по цепочке (при выполнении заданий учитель обращает внимание школьников на вид уравнений и способам их решения, используя таблицу).

5.2 Выполнение задания №509 - у доски.

5.3 Выполнение задания №510 - с комментированием.

5.4 Выполнение задания №511 (а, б) - самостоятельно (взаимопроверка)

6. Подведение итогов.

Какие уравнения называются квадратными?

Какие квадратные уравнения называются неполными?

Сколько корней имеет неполное квадратное уравнение вида:

1) 2) 3)

7. Домашнее задание: №511 (в, г), теория.

Урок - игра по теме "Решение неполных квадратных

уравнений"

Тип урока: закрепление.

Цели урока: повторить и закрепить умение решать неполные квадратные уравнения, развивать математическую речь, логическое мышление, сообразительность, внимание, воспитывать интерес к предмету, самостоятельность.

Оборудование: жетоны, карточки с заданиями.

Ход урока:

1. Организационный момент (класс делится на две команды, выбирают капитана, название команды, в конце урока капитаны оценивают своих игроков).

2. Сообщение темы и цели урока.

Сегодня на уроке мы с вами повторим решение неполных квадратных уравнений, задач. Урок мы проведем в виде игры. Я вас разделю на две команды, причем у каждой команды должен быть капитан и название команды. Даю три минуты, для того чтобы выбрать капитана и придумать название своей команды.

3. Работа по теме урока (открывается доска, на которой написаны названия игр).

3.1 Представление команд.3.2 "Заполни квадрат" (упражнение на развитие памяти и внимания).

Итак, первый этап игры называется "Заполни квадрат". Обеим командам дам таблицу (на обратной стороне доски висит таблица с буквами). Вам нужно за 10 секунд запомнить, что записано в клетке и записать в свой квадрат, угадать слово. За правильно выполненное задание команда получает 1 жетон.

Н

Е

Н

Л

У

А

Н

О

Ы

П

Е

П

Н

В

Р

Е

Я

3.2 "Отвечай-ка" (повторение теории).

Сейчас команды будут отвечать на вопросы.

Вы сначала подумайте, а потом поднимите руку. Итак, слушайте внимательно. За правильный ответ - 1 жетон.

1) Какое уравнение называется неполным?

2) Приведите пример неполного квадратного уравнения?

3) Назовите коэффициенты уравнения .

4) Назовите виды неполных квадратных уравнений?

5) Что такое уравнение?

6) Что значит решить уравнение?

3.3 "Посчитай-ка" (за правильный ответ - 2 жетона)

Итак, мы с вами повторили теорию, а сейчас необычное задание. Вы командой решаете данное задание: найдите сумму, разность и произведение корней неполного квадратного уравнения. На работу вам 3 минуты. (Ответ: корни: 0 и 1; 0+1=1; 0-1=-1; 0*1=0).

3.3.1 Проверка (за правильный ответ - 2 жетона).

3.4 "Соображай-ка" (3 жетона)

Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.

3.5 "Решение уравнений" (каждой команде учитель раздает карточки с заданиями, учащиеся решают вместе и выносят ответы на доску.

За каждое правильно решенное задание команда получает по одному жетону).

На работу вам 10 минут.

Решить неполные квадратные уравнения:

3.5.1 Проверка ответов.

4. Итог урока

Что мы повторили?

Сейчас посмотрим, какая команда набрала больше жетонов (за первое место грамота). Теперь капитаны каждой команды должны оценить работу каждого члена команды.

Урок-практикум по теме "Неполные квадратные

уравнения"

Тип урока: закрепление и проверка знаний.

Цель: закрепить и проверить знания по теме "Неполные квадратные уравнения", развивать математическую речь, внимание, воспитывать самостоятельность, интерес к предмету.

Оборудование: карточки с заданиями для самостоятельной работы, листочки для математического диктанта.

Ход урока:

  1. Организационный момент.

  2. Сообщение темы и цели урока.

  3. Актуализация знаний.

3.1 Математический диктант (на листочках).

  1. Какое уравнение называют квадратным уравнением?

  2. Какое уравнение называют неполным квадратным уравнением?

  3. Какие виды неполных квадратных уравнений бывают?

  4. Сколько корней может иметь неполное квадратное уравнение ?

  5. Сколько корней может иметь неполное квадратное уравнение ?

  6. Сколько корней может иметь неполное квадратное уравнение ?

3.2 Проверка математического диктанта (меняются листочками).

  1. Работа по теме урока.

4.1 Решение неполных квадратных уравнений.

4.1.1 Решение у доски:

а)

б)

4.1.2 Самостоятельная работа (по вариантам). На работу 4 минуты. Кто решит первым запишет свой ответ на доске.

1 вариант:

2 вариант: .

4.1.3 Проверка самостоятельной работы: сверка с доской.

4.2 Докажите, что:

а) числа 5 и - 5 являются корнями квадратного уравнения ;

б) числа о и - 7 являются корнями квадратного уравнения

Под буквой а решает 1 ученик с обратной стороны доски, под б - 2 ученик, остальные решают самостоятельно в тетрадях.

4.2.1 Проверка: самопроверка.

5. Самостоятельная работа на 1 вариант.

Решаем до конца урока и сдаем тетрадь на проверку.

1. Найти корни уравнения:

а) ;

б) .

2. Решите уравнение:

а) ;

б) .

3. Какие из следующих уравнений являются неполными? В Случае неполного уравнения найдите его корни.

а) ;

б) ;

в) ;

г) .

4. Найдите сумму корней неполного уравнения .

6. Итог урока.

Баллы по заданиям: за каждое правильно решенное задание 1 балл.

Итоговая шкала оценок:

9б. - "5"

7-8 б. - "4"

5-6 б. - "3"

Менее 5 б. - "2"

Анализ уроков по теме "Неполные квадратные уравнения"

В связи с тем, что по тематическому планированию изучение темы "Квадратные уравнения", начинается с рассмотрения вопроса о неполных квадратных уравнениях, были разработаны и апробированы уроки именно по этой теме: урок - лекция, урок - игра и урок - практикум.

Цели и задачи уроков выполнены. Все учащиеся были хорошо подготовлены к урокам. Они с интересом работали на уроках, этому служит эмоциональная речь учителя, приветливое отношение, поддержка отстающих. Ученики внимательны, сосредоточены.

Изучение всех тем начинается с организационного момента. Все этапы урока взаимосвязаны, каждый этап заканчивался микрообобщением. Время было распределено рационально.

В этапе объяснения нового материала используется историческая справка, что способствует развитию познавательного интереса, при закреплении темы используется игра, которая состоит из нескольких этапов. В процессе игры у детей формируются общеучебные умения и навыки, в частности умения контроля и самоконтроля, формируется такие черты характера, как взаимопонимание, ответственность, честность.

Также был разработан и проведен урок - практикум. Урок начался с повторения ранее изученного материала, необходимый для выполнения самостоятельной работы. Дети были активны, практически все знали ответы на задаваемые вопросы, отвечали правильно без затруднений и подсказок. Умеют привести примеры неполных квадратных уравнений каждого вида.

Выполняя задания по ранее изученному материалу, было видно, что ученики поняли тему. Задания выполняли быстро без ошибок, объясняя каждый момент решения.

Самостоятельная работа была напечатана на листочках. Данная работа не вызвала трудностей.

Самостоятельную работу писали 12 человек. После проверки самостоятельной работы, получились следующие результаты:

Оценка

Количество человек

%

"5"

10

83

"4"

2

17

"3"

-

-

Таким образом, с заданием справились все, отрицательных оценок нет. Были допущены ошибки при вычислениях.

2.2 Разработка уроков по теме "Полные квадратные уравнения"

Урок-программирование по теме " Полные квадратные уравнения" (уравнения общего вида)

Тип урока: изучение новой темы.

Цели урока: ввести понятие полного квадратного уравнения, научить учащихся решать полные квадратные уравнения, развивать математическую речь, внимание, самостоятельность.

Оборудование: карточки с пропущенными словами или формулами, алгоритм решения полных квадратных уравнений.

Ход урока:

1. Организационный момент.

2. Сообщение темы и цели урока.

  1. Актуализация знаний.

3.1 Опрос теории.

  1. Что называют квадратным трехчленом?

  2. Что называют дискриминантом квадратного уравнения?

  3. Приведите пример квадратного уравнения, дискриминант которого:

а) больше нуля;

б) равен нулю;

в) меньше нуля.

4) Назовите коэффициенты a, b и c квадратного трехчлена (трехчлены заранее записаны на доске):

а) ;

б) ;

в) .

4. Работа по теме урока.

4.1 Изучение нового материала. Учащиеся самостоятельно изучают тему, для этого учитель раздает карточки с текстом (приложение 6), где учащиеся должны заполнить пустые строчки и записать в тетрадь, то что необходимо для решения данного вида уравнения. На работу дается 20 минут. Потом вместе с учителем проверяют.

Полное квадратное уравнение - это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля. Это уравнения вида ах2 + bx + c = 0, где a,b,c - заданные числа, а ≠ 0, х - неизвестное.

Любое полное квадратное уравнение можно преобразовать к виду , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассмотриваются следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.

1. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет действительных корней.

Например, 2х2 + 4х + 7 = 0. Решение: здесь а =., b = …, с = …. D = ….

Так как D < 0, то данное квадратное уравнение не имеет корней.

2. Если D = 0, то квадратное уравнение ах2 + bx + c = 0 имеет два равных корня, которые находятся по формуле .

Например, 4х - 20х + 25 = 0. Решение: а =.., b = ……., с = …. …. D = …. Так как D = 0, то данное уравнение имеет … корни. Эти корни находятся по формуле . Значит, х = ……….

3. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два различных корня, которые находятся по формулам: ; . Например, 3х2 +8х - 11 = 0. Решение: а =.., b = ……, с = …….

D = ………

Так как D > 0, то данное квадратное уравнение имеет … корня. Эти корни находятся по формулам: => =…….

4.2 Проверка и составление алгоритма решения полного квадратного уравнения.

Составляется алгоритм решения уравнения вида ах2 + bx + c = 0.

1. Вычислить дискриминант D по формуле D = b2 - 4ас.

2. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.

3. Если D = 0, то квадратное уравнение имеет два корня, которые находятся по формуле

4. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня:

; .

5. Закрепление.

5.1 Выполнение задания № 533 (устно)

5.2 Выполнение задания №534 (самостоятельно по вариантам) - ответы на обратной стороне доски.

1 вариант - а, г, е.

2 вариант - б, з, е.

6. Итог урока.

Какие уравнения называются полными? И как они решаются?

7. Домашнее задание: учить теорию, № 535, 536 (а-в).

Урок - "Математическая эстафета" по теме " Решение полных квадратных уравнений"

Цели урока: закрепить умение решать полные квадратные уравнения; рассмотреть различные задания, решающиеся с помощью квадратного уравнения; проверить умение учащихся решать полные и неполные квадратные уравнения.

Тип урока: закрепление.

Оборудование: 3 таблицы с заданиями.

1. Организационный момент (выбирают жюри, учащиеся объединяются в две команды)

2. Сообщение темы и цели урока.

Сегодня у нас необычный урок, мы с вами проведем математическую эстафету.

3. Работа по теме урока.

Наша эстафета состоит из 3-х этапов. На каждом этапе вы получаете одинаковое количество заданий. Задания будут усложняться. Решив уравнения одной сложности, получаете задания другой сложности, т.е. переходите на 2 этап. Победит та команда, которая первой пройдет все этапы.

Итак, начнем.

3.1 I этап. Задания 1-ой сложности. Решаете вместе, чтобы было быстрее. Ответы записать в таблицу и сдать на проверку жюри. За каждое правильное решение команда получает по 1 балл.

Уровень 1

Примеры

Ответы

3.2.2 этап - задания 2-ой сложности с ответами. За каждое правильное решение команда получает - 2 балла (жюри проверяет решение). На этом этапе ответы даны, нужно решить данные уравнения и получить правильный ответ.

2 уровень

Ответы

(х+8) (х-9) =-52

(-4;

5)

(х+1) (х+2) = (2х-1) (2х-10)

(;

8)

(1; - 2)

()

Нет корней

3 этап - на 3 этапе учащиеся решают не командой, а работают индивидуально (в тетрадях). Кто первым справится с заданием, тот ученик выносит ответы на доску. Класс оценивает этого ученика, после того, как большинство учащихся справится с заданием.

(х-1) (х-2) = (3х+1) (х-2)

3. Итог урока. Жюри проводит итог, объявляет результаты. Команды, которая набрала большее количество баллов, получают отметку "5", другая команда получает отметку "4".

4. Домашнее задание: учитель раздает карточки с заданиями.

Тест по теме "Полные квадратные уравнения"

Тип урока: урок - контроля.

Цель урока: проверить знания по теме "Полные квадратные уравнения", развивать самостоятельность, внимание, навыка самооценки, воспитывать интерес к предмету.

Ход урока:

1. Орг. момент.

2. Сообщение темы и уели урока.

Проверим, как вы усвоили тему "Полные квадратные уравнения".

3. Работа по теме урока.

Тест решаете до конца урока и сдаете на проверку.

Тест по теме "Полные квадратные уравнения"

Вариант 1.

1. Полное квадратное уравнение - это уравнение вида:

А) , где а; Б) ах +bx+0=0;

В) , где а; Г) , где а.

2. Если в квадратном уравнении D = 0, то уравнение имеет:

А) 1 корень Б) 3 корня

В) не имеет корней Г) 2 корня

3. Какой из предложенных многочленов является квадратным трехчленом?

А. Б.

В. Г.

4. Какое из чисел - 2, - 1, 3, 5 являются корнем уравнения

?

А. - 1 Б. - 2 В.3 Г.5

5. Чему равна сумма корней уравнения ?

А. Б. - В. Г.

6. Какое из предложенных квадратных уравнений не имеет корней?

А. Б.

В. Г.

7. Чему равна сумма квадратов корней уравнения

?

А.4 Б.18 В.16 Г.6

8. Какое из чисел 9, - 1, 6, является корнем уравнения .

А) 9 Б) В) - 1 Г) 6

9. При каких значениях параметра квадратное уравнение имеет только один корень?

А. Нет таких значений Б.

В. Г.

10. Если в полном квадратном уравнении D<0, то уравнение имеет:

А) один корень Б) два корня

В) не имеет корней Г) четыре корня

Вариант 2.

1. Полное квадратное уравнение - это уравнение вида:

А) , где а , b; Б) ах +bx+0=0;

В) , где а; Г) , где а.

2. Если в квадратном уравнении D > 0, то уравнение имеет:

А) 1 корень Б) 3 корня

В) не имеет корней Г) 2 корня

3. Какой из предложенных многочленов является квадратным трехчленом?

А. Б.

В. Г.

4. Какое из чисел - 2, - 1, 3, 5 являются корнем уравнения?

А. - 2 Б. - 1 В.3 Г.5

5. Чему равна сумма корней уравнения ?

А. Б. - В. Г.

6. Какое из предложенных квадратных уравнений не имеет корней?

А. Б.

В. Г.

7. Чему равна сумма квадратов корней уравнения

?

А.4 Б.18 В.9 Г.1

8. Какое из чисел 9, - 1, 6, является корнем уравнения

.

А) 9 Б) В) - 1 Г) 6

9. При каких значениях параметра квадратное уравнение имеет только один корень?

А. Нет таких значений Б.

В. Г.

10. Если в полном квадратном уравнении D<0, то уравнение имеет:

А) один корень Б) два корня

В) не имеет корней Г) четыре корня

Критерии оценок:

"5" - 9-10 б.

"4"-7-8 б.

"3" - 5-6 б.

4. Подведение итогов.

5. Домашнее задание: решить тест противоположного варианта.

Анализ уроков по теме "Полные квадратные уравнения"

Так как на втором этапе внимание уделяется на решение полных квадратных уравнений, автором были разработаны и апробированы различные по форме уроки по данной теме.

При изучении нового материала был использован урок - программирование. Урок изучения нового материала начинается с организационного момента. Все учащиеся были хорошо подготовлены к уроку. При изучении темы была связь предыдущего материала с новым. На данном уроке каждый ученик получил карточку с текстом, где учащиеся сами должны были заполнить текст, найти пути решения полных квадратных уравнений. Данный урок был полезным для учащихся, каждый из них старался находить различные пути решения, все учащиеся были вовлечены в работу. Данный урок смог заинтересовать учащихся, что способствовало лучшему усвоению темы.

Для закрепления темы по решению полных квадратных уравнений была проведена "Математическая эстафета", с целью: закрепить умение решать полные квадратные уравнения, также решать различные задания, решающиеся с помощью квадратного уравнения. Урок начался с организационного момента. Класс делился на две команды, выбрали капитанов. Учащиеся двух команд на каждом этапе получали одинаковое количество заданий. Решив уравнения одной сложности, команда получала задание другой сложности. В игру включались все учащиеся. Всем данный урок очень понравился, так как такой урок проводился впервые. Они были заинтересованы и задания выполняли без затруднений и подсказок учителя. Победила та команда, которая первой прошла все этапы. В конце урока жюри подводила итоги. Ученики той команды, которая набрала большее количество баллов, получили отметку "5". Команда, которая набрала меньшее количество - отметка "4".

Также по теме "Полные квадратные уравнения" автором был разработан тест, который состоял из 10 вопросов. Тест решали 12 человек. И получились следующие результаты:

Отметка

Количество человек

%

"5"

9

75

"4"

3

25

"3"

-

-

Таким образом, тест показал высокий уровень знаний теоретического и практического материала учащихся. Проведенные автором уроки повлияли на успеваемость положительно. Учащиеся знают алгоритм решения полного квадратного уравнения, умеют находить дискриминант и корни квадратного уравнения. Было видно, что ученики поняли тему. Задания выполняли быстро без ошибок, объясняя каждый момент решения (Приложение 4).

2.3 Разработка уроков по теме "Приведенные квадратные уравнении

Урок - презентация по теме "Приведенные квадратные уравнения

Тип урока: изучение новой темы.

Цели: повторить понятие квадратного уравнения; ввести понятие приведенного квадратного уравнения; формировать умение распознавать квадратные уравнения и приводить к ним.

Ход урока:

Организационный момент.

Актуализация знаний.

    1. Устный счет.

4,8: 2

2,4

3 - 0,4

2,6

1,4 + 4,9

6,3

+ 0,8

3,2

: 0,13

20

: 3

2,1

: 0,4

8

: 0,1

200

+ 5,9

8

0,2

1,8

: 0,2

1000

: 20

0,4

    1. Устный опрос.

Какие уравнения называются квадратными? (Квадратное уравнение , a - старший коэффициент; b - второй коэффициент; c - свободный коэффициент (свободный член уравнения)).

Чему равен дискриминант квадратного уравнения?

Как найти корни полного квадратного уравнения?

Какие уравнения называются неполными?

Сколько корней имеет полное квадратное уравнение, если

а) D = 0; D < 0

б) D > 0

Сообщение темы и цели урока.

Объяснение нового материала.

Далее учитель объясняет новую тему.

Приведенное квадратное уравнение получается из квадратного уравнения по схеме:

(Ученики делают записи в тетрадь)

Например, приведенными квадратными уравнениями являются уравнения:

Таким образом, приведенное квадратное уравнение можно рассматривать как частный случай полного квадратного уравнения , где а = 1, b = p, c = q. Дискриминант уравнения равен: D = b

Обычно в случае приведенного уравнения вместо дискриминанта D рассматривается выражение . При этом формулу корней приведенного уравнения записывают так: .

5. Закрепление.

5.1 Решите уравнение:

1) (учитель решает у доски, учащиеся в тетрадях).

2) (1 ученик у доски, остальные в тетрадях).

3) ; (самостоятельно).

6. Итог урока.

Какие уравнения называются неполными, полными, приведенными?

Приведите примеры неполных, полных, приведенных квадратных уравнений.

Чем они отличаются?

7. Домашнее задание: теория, решить уравнения:

Урок - практикум по теме "Решение квадратных и приведенных квадратных уравнений"

Цели урока: отработка общих умений и навыков при решении квадратных уравнений; развитие внимания, навыков самоконтроля и самооценки.

Оборудование: карточки для самостоятельной работы, портрет ученого.

Ход урока:

1. Организационный момент (1 мин)

2. Сообщение темы и цели - повторим, то, что необходимо знать при решении квадратных уравнений; проверим свои умения решать квадратные уравнения в самостоятельной работе.

3. Разминка (6 мин)

3.1 Игра "Заполни квадрат". (Упражнение на развитие памяти и внимания). За 10 секунд запомнить, что записано в клетках квадрата, и записать в свой квадрат.

А

Р

У

Е

Н

В

Е

И

Н

Расшифруйте слово. Зашифровано слово "УРАВНЕНИЕ"

3.2 Историческая справка. Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 4000 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развитие математики, был французский математик Виет. Имя этого математика нам скоро встретится.

4. Повторение (фронтальный опрос 6 мин)

4.1 Вычислите:

а) - 4*1* (-4), - 4*2*5, - 5*6*4;

б) (-10) 2, 3 2, (-7) 2

Это нужно уметь при нахождении дискриминанта D.

4.2 Игра "Срочная радиограмма". Класс делится на две команды: девочки - мальчики. В двух конвертах - отдельные слова. Задача: составить одно математическое предложение из имеющихся слов. Трудность состоит в том, что одного слова не хватает.

"Если ДИСКРИМИНАНТ больше нуля, то уравнение имеет два различных корня";

"Если квадратное уравнение записано в СТАНДАРТНОМ виде, то можно находить дискриминант".

5. Тестовые вопросы (5 мин)

На доске 8 квадратных уравнений. Эти задания на слух, повторяются только два раза. Залог успеха - огромное внимание.

  1. 2х2 - 8х +4 = 0; 5.5х2+ 6х = 0;

  2. 3х2 + 4х - 1 = 0;

  3. 6. х2 - 8х + 12 = 0;

  4. 4х2 - 8 = 0; 7.3х2 = 0;

  5. х2 - 10х + 100 = 0; 8.14 - 2х2 + х = 0

а) Выпишите номера полных квадратов уравнений.

б) Выпишите коэффициенты а, b, c в уравнении 8.

в) Выпишите номер неполного квадратного уравнения, имеющего один корень.

г) Выпишите коэффициенты a, b, c в уравнении 5.

д) Найдите дискриминант в уравнении 6.

е) Найдите дискриминант в уравнении 4 и сделайте вывод о количестве корней.

Проверяем, оцениваем себя сами:

нет ошибок - "5"

1 - 2 ошибки - "4"

3 - 4 ошибки - "3"

6. Игра " Следствие ведут знатоки " (10 мин)

Прежде чем доверить расследование серьезного дела, необходимо пройти проверку.

а) Сможете ли вы отыскать ошибку в решении уравнения?

- х2 + 6х + 16 = 0,х2 - 6х + 16 = 0,a = 1, b = - 6, c = - 16.

D = b2 - 4ac = ( - 6) 2 - 4 * 1 * ( - 16) = 36 +64 = 100

Ошибку ищем по этапам, с самого начала. Ошибка: - 16, отсюда дискриминант равен 38.

7. Самостоятельная работа (12 мин)

Выполнив самостоятельную работу, узнаете, можете ли вы решать квадратные уравнения без ошибок.

Первые два уравнения можно проверить (решения на оборотной стороне доски).

1. х2 + 2х - 25 = 0.

  1. 9х2 - 6х + 1 = 0.

  2. 3х2 + 8х - 3 = 0.

8. Подведение итогов урока.

Обобщающий урок по теме "Квадратные уравнения" в форме игры "Звездный час"

Цели урока:

  • закрепить практические и теоретические знания и умения учащихся при выполнении заданий по теме "Квадратные уравнения";

  • развивать самостоятельность, активность, внимание;

  • воспитывать интерес к предмету.

Оборудование: звездочки, таблицы с цифрами.

Ход урока:

1. Организация класса

а) Приветствие

б) Проверка готовности рабочих мест

2. Сообщение темы и цели урока

Сегодня у нас особенный урок, мы проведем с вами "Звездный час" по теме "Квадратные уравнения", тем самым еще раз проверим свои знания и умения.

3. Закрепление материала

3.1 Знакомство с правилами игры.

Итак, представим, что мы с вами в студии. Вы игроки, а я ведущая. У вас у каждого на партах лежат таблички с цифрами от 1 до 5.

1

2

3

4

5

Итак, послушайте условия игры.

Я буду задавать всем вопросы, а соответственно поднимать табличку с тем номером, который соответствует правильному ответу. А так же у каждого из вас лежат на партах листочки. За каждый правильный ответ, когда я вам скажу, вы будете на нем чертить звездочку. А в конце игры мы их подсчитаем и оценим работу каждого из вас.

3.2 Проведение игры.

Итак, начинаем игру. Сейчас мы будем работать с вами по 1 таблице

Таблица №1

1

2

3

4

5

Д =

Итак, сверху вы видите номера ответов, а под ними соответствующие ответы. Я задаю вопрос, вы 5 секунд, думаете и поднимаете таблички с правильными ответами.

  1. Какой вид имеет квадратное уравнение.

  2. Назовите формулы корней квадратного уравнения.

  3. Назовите неполное квадратное уравнение.

  4. Назовите, чему равен дискриминант квадратного уравнения.

Хорошо с этим заданием вы справились хорошо, почти все учащиеся поднимали таблички с правильными ответами. А кто ошибался, он еще раз увидел правильные формулы и надеюсь, так же доучит материал.

А теперь мы все переходим во второй тур. Во втором туре мы выясним знание правил по данной теме. Работать будем со второй таблицей.

Таблица №2

1

2

3

4

5

Теорема обратная теореме Виета

Квадратное уравнение

Теорема Виета

Неполное квадратное уравнение

Приводимое квадратное уравнение

Я буду говорить вам правило, а вы поднимайте соответствующую карточку.

1) Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Верно, следующий вопрос, слушайте и поднимайте таблички.

2) Если в квадратном уравнении хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется….

Верно, приведите пример квадратного уравнения.

3) Уравнение вида , где х переменная, а, в, с - некоторые числа, причем, а  0 называется….

Верно, приведите пример квадратного уравнения

4) Если для чисел x>1>, x>2, >p, q справедливы формулы

x>1> + x>2 >= - p,

x>1> x>2> = q,

то x>1> и x>2> - корни уравнения х2 + px + q = 0.

Верно, скажите, сколько корней имеет неполное квадратное уравнение каждого вида.

Молодцы.

5) Как называются полные квадратные уравнения, у которых все три коэффициента отличны от нуля и в которых первый коэффициент равен 1.

Хорошо и с этим заданием вы справились.

4. III тур. Самостоятельная работа.

Вам в этом туре необходимо решить квадратные уравнения, которые написаны на доске. (7 мин)

1. х2 - 2х - 10 = 0.

  1. 9х2 + 12х + 4 = 0.

  2. 3х2 - х +10 = 0.

  3. х2 - 3х - 4 = 0.

Вы самостоятельно решаете эти уравнения в тетради, а потом мы проверим (диктую ответы, дети сами проверяют).

Хорошо давайте проверим.

Итак, ребята, если вы правильно решили все 4 уравнения, то получите 4 звездочки; если 3, то 3 звездочки; если 2, то 2 звездочки; если 1, то 1 звездочку.

5. Подведение итогов

Итак, вот и подходит к концу наша игра. В ходе игры мы повторили теоретический и практический материал, и теперь мы можем подвести итог игры. Подсчитайте свои звездочки.

Кто набрал от 20 до 25 звезд, получают "5"

Кто набрал от 20 до 15 звезд, получают "4"

Кто набрал 15 звезд и меньше, получают "3"

Контрольная работа по теме "Квадратные уравнения"

Цели урока: проверить знания и умения решения учеников по теме "Квадратные уравнения".

Оборудование: карточки с заданиями.

Ход урока:

1. Организационный момент

2. Сообщение темы и цели урока.

3. Работа по теме урока.

Вариант I

1. Имеет ли корни уравнение:

а) ;

б) ?

  1. Решите уравнение:

а) ;

б) ;

в) ;

г) ;

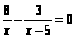  1. Сократите дробь .

  2. Один из корней уравнения равен 5. Найдите другой корень и коэффициент .

  3. Площадь квадрата на 8см2 меньше площади прямоугольника. Сторона квадрата в три раза меньше одной стороны прямоугольника и на 2 см больше второй его стороны. Найдите длину стороны квадрата.

  4. Поезд должен был пройти 840 км в определенное время. На половине пути он был задержан на 30 мин из-за технической неисправности. Чтобы прибыть во время, ему пришлось увеличить скорость на 2 км/ч. Сколько времени поезд находился в пути?

Вариант II

1. Имеет ли корни уравнение:

а) ;

б) ?

2. Решите уравнение:

а) ;

б) ;

в) ;

г) ;

3. Сократите дробь

.

4. Один из корней уравнения равен 12. Найдите другой корень и коэффициент .

  1. Периметр прямоугольника равен 32 см, а его площадь равна 60см2. Найдите длину меньшей стороны прямоугольника.

  2. Из города А в город В выехали велосипедист и мотоциклист. Скорость велосипедиста на 10 км/ч меньше скорости мотоциклиста, поэтому он затратил на весь путь на 6 ч больше. С какой скоростью ехал мотоциклист, если расстояние между городами 120 км?

4. Подведение итогов.

Анализ уроков по теме "Приведенные квадратные уравнения"

При проведении уроков по теме "Приведенные квадратные уравнения" были использованы: при изучении новой темы - урок - презентация, т.е. на уроке использовался мультимедийный проектор. Урок начался с повторения ранее изученного материала. Ученики были активны и заинтересованы, т.к. такие уроки проводятся в школе очень редко. При закреплении и повторении был разработан урок - практикум, с использованием игровых моментов. Здесь даже пассивные, несмелые дети активно включались в работу, применяя на практике свои знания и умения. Особенно учащимся нравились задания, в которых надо исправить ошибки. В ходе игры выяснилось, что ученики хорошо различают квадратные уравнения. При выполнении практического задания трудностей не возникло.

Также автором разработан и проведен обобщающий урок по всей теме в форме игры "Звездный час", целью которого являются: закрепить практические и теоретические знания и умения, учащихся при выполнении заданий по теме "Квадратные уравнения"; развивать самостоятельность, активность и внимание. И можно сделать вывод о том, что учащиеся теорию знают хорошо и умеют ее применять на практике.

В конце изучения темы "Квадратные уравнения" была проведена комплексная контрольная работа. После проверки контрольной работы получились следующие результаты:

Оценка

Количество человек

%

"5"

4

33

"4"

5

42

"3"

3

25

Контрольная работа показала средний уровень знаний по данной теме (Приложение 5).

Сравнив результаты трех этапов, можно увидеть, что на первом и третьем этапах преобладающей отметкой является "5", результаты показали высокий уровень знаний. А на третьем этапе уровень знаний хуже, чем в предыдущих этапах. Этому повлияло то, что контрольная работа была комплексная, где включались решения квадратных уравнений различных видов. По результатам контрольной работы видно, что учащиеся умеют:

  • решать неполные квадратные уравнения;

  • решать полные квадратные уравнения;

  • умеют использовать формулы для решения квадратных уравнений;

  • решать приведенные квадратные уравнения;

  • умеют находить ошибки в решенных уравнениях и исправлять их;

  • делать проверку.

Также контрольная работа выявила недочеты в работе по определенным моментам, и определил пути их устранения. В связи с этим рекомендуется провести определенную работу по отработке и коррекции знаний учащихся, и обратить внимание на некоторые ее моменты, а именно:

  • закрепить умения в решении задач;

  • устранить пробелы в знаниях по теме "Сложение и вычитание отрицательных чисел";

  • развивать вычислительные навыки.

Таким образом, проведенный в 8 классе комплекс уроков показал, что использование разных форм уроков способствует лучшему усвоению решения квадратных уравнений разного вида.

Заключение

Материал, связанный с уравнениями, составляет значительную часть школьного курса математики. На изучение темы "Квадратные уравнения" по программе дается всего 16 ч. В процессе выполнения данной работы были созданы конспекты уроков с использованием разнообразных форм уроков именно по теме "Квадратные уравнения".

При применении их в образовательный процесс были достигнуты достаточно высокие результаты обучения. Ученики 8 класса показали достаточно высокие результаты при выполнении самостоятельных и контрольных работ. На уроках учащиеся были заинтересованными и активными.

Задачи, которые были поставлены в начале работы, решены: изучена методическая литература по данной теме; созданы и апробированы на практике конспекты уроков, проанализированы результаты применения его на практике, цель достигнута.

Гипотеза, которая была поставлена в начале работы, нашла своё подтверждение, то есть автором в данной работе было доказано, что при использовании разнообразных форм уроков при изучении темы "Квадратные уравнения", повысится успеваемость учащихся и поэтому существует необходимость применения на уроках алгебры.

При выполнении данной работы понадобились не только те знания, которые имеются у самого автора, но и необходимая работа с дополнительной литературой, составление конспектов уроков.

Данную выпускную квалификационную работу можно использовать в педагогической деятельности, она может стать методическим пособием для студентов Кунгурского педагогического училища, как при подготовке докладов, сообщений на эту тему, так и при проведении пробных уроков или преддипломной практики. А также ею могут воспользоваться учителя математики, преподающие в средней школе, которые стремятся вызвать интерес к урокам математики.

Литература

  1. Алимов, Ш.А. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. - 10-е изд. - М.: Просвещение, 2003.

  2. Бантова, М.А. Методика преподавания математики в начальных классах/ Бантова М.А., Бельтюкова А.М. и др. Ё Учеб. пособие для учащихся школьных отд-ний пед. училищ. Изд.2-е. - М.: Просвещение, 1998.

  3. Башмаков, М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений/ М.И. Башмаков. - М.: Просвещение, 2004.

  4. Бекаревич, А.Б. Уравнения в школьном курсе математики/ А.Б. Бекаревич. - М., 1968.

  5. Бурмистрова, Т.А. Программы общеобразовательных учреждений/ Т.А. Бурмистрова. - М.: Просвещение, 1994.

  6. Глейзер, Г.И. История математики в школе VII - VIII классы/ Г.И. Глейзер. - М., 1997.

  7. Зильзерберг, Н.И. Урок математики: Подготовка и проведение/ Н.И. Зильзерберг. - М., 2002.

  8. Иванова, Т.А. Как подготовить уроки - практикумы/ Т.А. Иванова/ Математика в школе. - 2001.

  9. Колягин, Ю.М. Методика преподавания математике в средней школе/ Ю.М. Колягин. - М.: Просвещение, 2001.

  10. Кузнецова, Г.М. Программы для общеобразоват. Школ, гимназий, лицеев: Математика 5-11 кл. / Г.М. Кузнецова. - М.: Дрофа, 2002.

  11. Лягущенко, Е.И. Методика обучения математике в 5 кл. / Е.И. Лягущенко. - Минск, 2001.

  12. Маркушевич, Л.А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л.А. Маркушевич, Р.С. Черкасов. / Математика в школе. - 2004. - №1.

  13. Мордкович, А.Г. Алгебра 8 кл.: Учеб. для общеобразоват. учреждений/ А.Г. Мордкович. - М.: Мнемозина, 2003.

  14. Мордкович, А.Г. Алгебра.8 кл.: Метод. пособие для учителя/ А.Г. Мордкович. - М.: Мнемозина, 1999.

  15. Мишин, В.И. Методика преподавания математики в средней школе/ В.И. Мишин. - М., 2201.

  16. Никольский, С.М. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - 2-е изд. - М.: Просвещение, 2003.

  17. Оганесян, В.А. Методика преподавания математики в средней школе/ В.А. Оганесян. - М.: Просвещение, 2000.

  18. Сабинина, Л.В. Методика в понятиях и терминах. Ч.1. /Л.В. Сабинина. - М.: Просвещение, 1998.

  19. Саранцев, Г.И. Методика обучения математике в средней в школе/ Г.И. Саранцев. - М., 2002.

  20. Стефанова, Н.Л. Методика и технология обучения математике. Курс лекций: пособие для вузов/ Н.Л. Стефанова. - М.: Дрофа, 2005.

  21. Столяр, А.А. Общая методика преподавания математики/ А.А. Столяр. - М., 1999.

  22. Темербекова, А.А. Методика преподавания математики: Учеб. пособие для студ. высш. Учеб. Заведений/ А.А. Темербекова. - М.: Гуманит. изд. центр ВЛАДОС, 2003.

  23. Шаталова, С. Способы решения квадратных уравнений / С. Шаталова // Математика в школе. - 2004. - №42.