Формирование познавательной потребности у учащихся средствами информационных технологий

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

"Поволжская государственная социально-гуманитарная академия"

Факультет математики, физики и информатики

Кафедра педагогики

Дипломная работа

Формирование познавательной потребности у учащихся средствами информационных технологий

Самара

2010

Содержание

Введение

1. Теоретические основы формирования познавательной потребности учащихся на уроках математики средствами информационных технологий в процессе обучения

1.1 Понятие и уровни познавательной потребности учащихся

1.2 Использования информационных технологий на уроках

2. Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий

2.1 Особенности изучения темы "Интеграл" в школьном курсе математики

2.2 Экспериментальная работа по формированию познавательной

потребности учащихся средствами информационных технологий на примере изучения темы "Интегралы"

2.3 Результаты экспериментальной работы

Заключение

Список литературы

Приложение

Введение

Актуальность исследования. В условиях изменения социально-экономических ориентиров общества и реформирования школы меняется образовательная парадигма, и развитие личности рассматривается как ключевая цель, достижению которой подчинены все компоненты системы образования. Гуманизация школьного образования предполагает решение следующих задач: развитие самостоятельности учащихся и их способности к самоорганизации; формирование готовности к сотрудничеству и толерантности к чужому мнению; формирование умения вести диалог и находить содержательные компромиссы; выявление и развитие потенциала познавательной потребности каждого обучающегося. Основная характеристика личности как субъекта деятельности - потребность, рассматривается учеными в качестве системообразующего свойства личности.

Затруднение в деятельности учителей по формированию познавательной потребности в учебном процессе состоит в том, что многие учебные пособия еще не в полной мере содействуют успешному развитию познавательной потребности учащихся. В них в основном дано содержание учебного материала, недостаточное количество заданий, требующих от каждого обучаемого наблюдения примеров; нахождения сходства и различия между сопоставляемыми явлениями; раскрытия существенных признаков, характеризующих сущность понятий, правил, законов; формулирования новых выводов. Правила, законы, выводы часто даются в готовом виде и требуют только заучивания.

Формированию познавательной потребности можно формировать различными способами в учебном процессе школы и самостоятельно. Одним из таких способов, которые эффективно способствуют сегодня формировать познавательные потребности являются информационные технологии.

Стремительно развивающиеся информационные технологии приносят глубокие изменения во все области жизни. В нашей стране и за рубежом интенсивно идет поиск новых моделей образования, при этом в качестве движущей силы модернизации всех образовательных процессов рассматривается развитие инновационных подходов к организации обучения на основе широкого и активного использования информационных технологий.

Информатизация образования рассматривается как одно из основных направлений государственной образовательной политики. В настоящее время нет необходимости убеждать учителей в важности разработки и внедрения в педагогическую практику наиболее совершенных технологий обучения, обеспечивающих повышение качества учебного процесса, способствующих активизации познавательной потребности учащихся, развитие их умственных способностей.

Использование информационных технологий повышает эффективность процесса обучения, экономит учебное время, позволяет работать ученику в таком темпе, при котором он лучше усваивает учебный материал, т.е. создает условия для приобретения учащимися знаний.

Опрос, проведенный среди учителей школ показал, что больше половины из них не используют компьютерные средства в процессе обучения. В ходе опроса выяснилось, что имеются отдельные попытки создания и использования разнообразных обучающих компьютерных средств для преподавания математики, среди которых: видеолекции, электронный учебный материал по отдельным темам математики, компьютерные обучающие программы на базе готовых программных оболочек, сетевые учебно-методические комплексы, банки тестовых тренировочных и контрольных заданий по математическим дисциплинам, лабораторные работы с применением интегрированных прикладных математических пакетов, таких как Mathematica, Maple, MathCad, MathLab и других, видеоконференции и форумы.

Степень научной разработанности проблемы.

Наиболее проницательные педагоги прошлого неоднократно отмечали, что, несмотря на огромную роль преподавателя, основные цели образования достигаются, прежде всего, как результат собственных усилий обучающихся.

Познавательная потребность относится к достаточно широко изученным проблемам в психологии и педагогике. Однако, являясь предметом изучения в трудах В.А.Крутецкого, А.К.Марковой, А.М.Матюшкина, В.И.Орлова, С.Л.Рубинштейна, Ф.И.Харламова, Т.И.Шамовой, Г.И.Щукиной и других, в новых условиях она приобретает новое звучание, вызывает еще больший интерес.

Появились новые технологии в учебной деятельности, повышающие уровень познавательной потребности ученика с использованием информационных технологий. Вопросы использования компьютерных технологий в обучении поднимают О.Белоконева, Е.Глебова, С.А.Дьяченко, Е.В.Коротаева.

Примерами новаторских разработок служат интегрированные уроки О.А.Александровой, О.В.Галяндиной, Н.М.Керусенко, В.Н.Гребнева. Заслуживает внимания опыт С.З.Валиевой, которая в своей работе использует электронный учебник-справочник "Алгебра" для подготовки старшеклассников к ЕГЭ.

Актуальность данной проблемы и послужило поводом для выбора темы дипломной работы.

Объект исследования: формирование познавательной потребности школьников в учебном процессе.

Предмет исследования: использование информационных технологий на уроках математики как средство формирования познавательной потребности учащихся.

Цель исследования: теоретически обосновать проблему формирования познавательной потребности у учащихся через использование информационных технологий на уроках математики, смоделировать и апробировать средства информационных технологий учителя математики по формированию познавательной потребности у учащихся.

Гипотеза исследования. Формирование познавательной потребности у учащихся в процессе обучения математике будет успешным, если:

- на основе анализа педагогической, психологической и методической литературы будут определены основные понятия по теме исследования и раскрыта их сущность;

- выявлены средства, такие как информационные технологии, способствующие эффективному формированию познавательной потребности у школьников;

- на основе системно-структурного подхода смоделированы средства взаимодействия учителя математики с учащимися по формированию у них познавательной потребности с помощью использования информационных технологий.

Задачи исследования:

На основе теоретического анализа педагогической, психологической, методической литературы по проблеме формирования познавательной потребности у учащихся через использование информационных технологий выделить ключевые понятия и раскрыть их сущность.
Выявить средства способствующие формированию познавательной потребности у школьников, такие как информационные технологии.
Определить результативность экспериментальной работы путем сравнительного анализа формирования познавательной потребности у школьников средством использования информационных технологий.

Новизна исследования определяется тем, что в нем:

- раскрыты основные понятия по проблеме формирования познавательной потребности у школьников в процессе обучения;

- определены основные средства, такие как информационные технологии, способствующие формированию познавательной потребности у школьников;

- выявлены и экспериментальным путем проверены средства взаимодействия учителя математики с учащимися по использованию информационных технологий на уроках математики по формированию у последних познавательной потребности.

Теоретическая и практическая значимость исследования: теоретически углублена проблема формирования познавательной потребности у учащихся с помощью использования информационных технологий; созданы и апробированы на практике педагогические средства деятельности учителя математики со школьниками по использованию информационных технологий на уроках математики по формированию у последних познавательной потребности.

База исследования: опыт деятельности учителя математики; опытно-экспериментальная работа проводилась в Муниципальном Образовательном учреждении средней общеобразовательной школы №1 г. Абдулино Оренбургской области совместно с учителем математики высшей категории Н.В.Николаевой. Выборку составили 20 учеников 11 "А" класса.

Методы исследования. Для проведения исследования нами применялся следующий комплекс методов: организационные методы (сравнительный способ); эмпирические методы (констатирующий и формирующий эксперимент, анкетирование, тестирование); методы обработки научных результатов (качественный и количественный способ).

Структура дипломной работы: структура соответствует логике научного поиска и содержит: введение, две главы, заключение, список литературы, приложение.

1.1 Понятие и уровни познавательной потребности учащихся

Люди не могут жить без потребностей. Познавательная потребность есть у всех. У одних потребность выражается в научной страсти, а у других в любви к кроссвордам и детективам и т.д.

Потребность – объективная нужда организма в определенных условиях, обеспечивающих его жизнь и развитие. Все потребности характеризуются, прежде всего, предметным содержанием, т.е. направленностью на определенный объект. Тот предмет, на который направлена потребность и есть непосредственный побудитель деятельности. Для потребности характерна периодическая актуализация их.

Потребности человека не остаются неизменными: одни потребности усложняются, другие отмирают и возникают новые потребности.

В основе изменения потребности лежит, с одной стороны, изменение круга предметов, удовлетворяющих потребность, с другой – изменение способа из удовлетворения.

Энциклопедический словарь дает следующее определение потребности: "Потребность – это внутреннее состояние, выражающее зависимость живого организма от конкретных условий активности личности" [30, 209].

В педагогическом словаре дается следующее определение потребности: "Потребности – это нужда в чем-либо, объективно необходимом для поддержания жизнедеятельности и развития человеческой личности, общества в целом" [18, 116].

Педагогическое значение потребности вытекает из их роли в развитии личности. Поэтому только такое педагогическое воздействие приведет к желаемому результату, которое правильное учитывает потребность ребенка, подростка и которое так или иначе направлено на воспитание этих потребностей, через разнообразные мотивы деятельности ребенка.

Понятие познавательной потребности проделало к настоящему времени длинный путь, на котором было и полное отрицание потребности как самостоятельной и "возвеличивание" ее как центральной в иерархии нужд человека. Начиная с 50-х годов, было показано, что познавательная потребность не "обслуживает" другие потребности, а является независимой потребностью индивида, имеющей собственные задачи в структуре поведения. Целый ряд аспектов познавательной потребности, а именно ее структура, динамика, связь с другими потребностями остается предметом серьезных дискуссий. Спорным является и само определение сущности познавательной потребности.

Познавательная потребность и ее формирование в психолого-педагогической литературе изучены недостаточно. В последнее время интерес к этой проблеме усилился, во-первых, в связи с исследованием закономерностей всестороннего развития личности, составной частью которого является развитие познавательной потребности, во-вторых, в связи с исследованием мотивационной регуляции мыслительной деятельности, и в частности мотивационной обусловленностью творческого мышления.

О.К.Тихомировой была подчеркнута важность анализа потребностей в выработке новых знаний, которые наряду с потребностями в поиске знаний относятся к собственно интеллектуальным познавательным потребностям [58, 34]. Однако на пути решения данной проблемы встают трудности, прежде всего методического характера.

Познавательная потребность по В.С.Юркевич стоит на трех китах: активности, потребности в самом процессе умственной деятельности и удовольствии от умственного труда [36].

Познавательная потребность в том случае, если она вызвана именно познавательной потребностью может быть не связана с конкретно-практическими целями индивида (возможностью награды, социального успеха и т.д.) и в этом смысле познавательная потребность "бескорыстна". Это позволяет отделить познавательную потребность, направляемую именно потребностью в познании, от деятельности, мотивированной другими потребностями: "потребностью в достижениях", "потребностью в успехах" и т.д.

Часто приходится слушать, что к концу начальной школы угасает потребность к учению вообще, отсюда теряется интерес к учению, а учение является поддерживающим звеном формирования познавательной потребности. Ну а угасание приводит к неудовлетворению учебной деятельности. Всякая деятельность начинается с потребностей.

Потребность по А.Н.Леонтьеву – это направленность активности ребенка, психическое состояние создающее предпосылку деятельности [42]. Однако сама по себе потребность не определяет характера деятельности, это объясняется тем, в самом "потребностном" состоянии предмет и удовлетворения жестоко не записан: одна и та же потребность может быть удовлетворена разными предметами, разными способами. Предмет ее удовлетворения определяется только тогда, когда человек начинает действовать – это приводит, как говорят психологи, к "опредмечиванию" потребности. Но без потребности не пробуждается активность ребенка, у него не возникают мотивы, он не готов к постановке целей.

По Л.И.Божовичу всякому ребенку свойственна потребность в новых впечатлениях, переходящая в не насыщаемую познавательную потребность [11]. Если у школьника не актуализирована эта широкая познавательная потребность, создающая готовность к учебной деятельности, то он не переходит и к другим – более активным формам поведения. Например, к постановке целей, если же учителю не удается опереться на имеющиеся у школьников познавательные потребности и использовать их для самостоятельной постановки целей учащимися, то ему ничего не остается, как ставить перед учениками готовые цели.

В тех случаях, когда потребность в общей познавательной активности не находят выражения в формах самостоятельности учебной деятельности школьника, возникают в работе с учеником трудности: его не реализованные потребности могут найти выход в упрямстве, конфликтности и других нежелательных формах поведения.

И, наконец, учителю важно специально использовать вопрос о содержании учебной деятельности, в которой реализуется потребность. Так называемая не насыщаемая потребность, может по-разному удовлетворится в учебной деятельности – это зависит от условий учебной работы, требований учителя. В одних случаях познавательная потребность может удовлетворяться уже получением хороших отметок, в других – при правильно организованной учебной деятельности – ориентацией школьника на внутреннее содержание учебной деятельности, способы выполняемых действий. В ходе самой учебной деятельности – в зависимости от условий ее организации, ее общей атмосферы, типа общения с учителем – потребности учения формируются, перестраиваются, совершенствуются. В процессе учебной деятельности изменяется не только собственно показательный компонент потребностей, но и социальные установки учения – потребность включения в общественно значимую работу, другому человеку, потребность самоусовершенствования и т.д. Все это создает основу для становления специфически человеческой потребности в деятельности, в созидании.

Познавательная потребность в наиболее типичной форме первично выступает как ситуативно-возникающая познавательная потребность, порождаемая условиями конкретной задачи, особенностями общения межличностного взаимодействия. Ситуативно-порождаемая познавательная потребность возникает в условиях таких интеллектуальных задач, в процессе решения которых возникает проблемная ситуация, требующая от субъекта "открытия" нового знания или способа действия, обеспечивающего решение поставленной задачи. Познавательная потребность, таким образом, рождается в ситуациях задачи, условия которой выступают первично как субъективно известные и привычные. Лишь в самом процессе решения обнаруживается несоответствие используемых привычных способов действия требованиям задачи, составляющим ее "скрытые" условия, невозможность ее решения с помощью известных способов. Обнаруживаемые таким образом требования задачи выступают как "новые", предъявляемые и интеллектуальной задачей к мыслительной деятельности. Новые требования мыслительной задачи выступают как источник ситуативного порождения познавательной потребности и условие возникновения поисковой познавательной активности, направленной на обнаружение неизвестного. Ситуативно-порождаемая познавательная потребность, таким образом, возникает на основе новых требований "предъявляемых" к познавательной деятельности возникающей проблемной ситуацией. Можно также сказать, что познавательная потребность возникает в условиях проблемной ситуации. Потребности нужно развивать и укреплять, чтобы вызвать в ребенке стремление к развитию своих возможностей, к самовоспитанию способностей.

Дальнейшие исследования показали, что стремление к познанию, или, иначе говоря, познавательная потребность, в наибольшей мере ответственно за уровень развития умственных способностей. Именно благодаря высокоразвитой потребности в познании (в настоящее время имеется несколько понятий для обозначения стремления к умственной деятельности: умственная активность, познавательная потребность, интеллектуальная активность) у детей развиваются способности, причем тем в большей мере, чем лучше. В.С.Юркевич в своей работе выделяет главные характеристики познавательной потребности [35].

1. Познавательная потребность – это, прежде всего потребность в новой информации, однако сама новая информация может выступать в самых различных формах: в новом стимуле (новый цвет предмета, неожиданный звук, необычная форма), в новом знании о предмете (его назначение, устройство и т.д.), и наконец, в новой системе представлений о мире (научные знания, наука в целом). И самые элементарные и самые сложные способы удовлетворения познавательной потребности в целом характеризуют одну и ту же познавательную потребность, однако в зависимости от этих способов различаются уровни развития познавательной потребности.

Если познавательная потребность младенца удовлетворяется новой погремушкой, новым необычным звуком (уровень потребности во впечатлениях), то дошкольнику, чтобы удовлетворить свою страсть к познанию, уже нужны детские книжки, фильмы и рассказы взрослых. Возраст от двух до пяти лет – возраст " почемучки", когда ребенок самым активным образом пытается понять окружающий его мир. Это начальный этап другого уровня – любознательность. В дальнейшем своем развитии, у подростка или старшего школьника, познавательная потребность выходит на более высокий уровень – целенаправленной деятельности, когда учащийся стремится к специальной области знаний и на этой основе возникают, развиваются, укрепляются его интересы и склонности.

Не вдаваясь в анализ каждого из уровней, можно подчеркнуть, что, появляясь с рождения ребенка и будучи неотъемлемой характеристикой жизни каждого человека, познавательная потребность принципиально меняется с возрастом, последовательно усложняясь, при этом более сложные уровни познавательной потребности идут на смену более элементарным. С возрастом различия между детьми и соответственно взрослыми людьми в сложности способов удовлетворения познавательной потребности резко увеличиваются. У каждого человека, ребенка или взрослого, в той или иной мере представлены разные уровни удовлетворения познавательной потребности, однако один из уровней является ведущим, и именно от него зависит общей уровень интеллектуального развития.

2. Именно из факта существования разных способов удовлетворения познавательной потребности вытекает факт "не насыщаемости" познавательной потребности.

Человеку нужны новое знание, новые стимулы чуть ли не в каждый момент жизни, без этого человек буквально заболевает.

Познавательная потребность – одна из немногих, которую невозможно полностью удовлетворить. Она проявляется всегда (исключая время сна, конечно), либо в более сложной (разные виды познания), либо в самой упрощенной форме.

3. Познавательная потребность независима от задач приспособления к конкретной ситуации и направлена, прежде всего, на сам процесс познания. "Бескорыстие" познавательной потребности, ее ориентация главным образом на процесс, а не на результат – важнейшая характеристика этой потребности. Ученик, по-настоящему любящий математику, радуется каждой новой задаче и совсем не будет рад, если ему вдруг дадут готовое решение. Но не только у математически одаренных детей проявляется это потребность "поломать голову". Удовольствие от самого процесса познания, в какой бы форме оно не было, знакомо каждому человеку, и это есть характернейшая особенность познавательной потребности.

4. Тесно связана с этой особенностью – ориентацией на процесс познания – и другая особенность познавательной потребности, а именно тесная связь с положительными эмоциями.

Ученик, по-настоящему любящий математику, радуется. Именно чувство удовольствия, радости и отличает умственную деятельность, выполняемую на основе познавательной потребности, от познавательной деятельности, направляемой другими потребностями.

Ученик старательно занимается, чтобы заслужить похвалу или, чтобы не ругали дома. К познавательной потребности это не относится. Но вот тот же ученик, придя из школы, хватается за книжку о животных и, забыв обо всем, читает, пока не закончит. Т.е. школьник занимается по собственной охоте, ему это нравится, вызывает яркие положительные эмоции. Это и есть познавательная потребность.

Радость в момент познавательной деятельности инициируемой именно познавательной потребностью, сейчас можно регистрировать. Целый ряд физиологических показателей свидетельствуют о том, что в момент интеллектуального напряжения вместе с участком мозга, занятым умственной работой, всегда возбуждается и центр положительных эмоций (при условии, что умственное напряжение вызвано именно потребностью в познании, а не какой-либо другой потребностью, скажем страхом не выполнить задание). У некоторых людей эта связь настолько прочна и сильна, что лишение интеллектуальной деятельности приводит их к тяжелому состоянию. Факт связи познавательной потребности с положительными эмоциями важен, во-первых, для диагностики характера познавательной деятельности, во-вторых, для разработки необходимой стратегии и тактики развития познавательной потребности. Конкретное содержание процесса развития познавательной потребности с выделением уровней ее развития обычно не являлось предметом специального исследования. Проблема уровней развития познавательной потребности наиболее детально разрабатывалась В.С.Ильиным, выделившим четыре ее уровня (ориентировочно-ознакомительная потребность, любознательность, потребность – помысел, страсть), а В.С.Юркевич выделившей три уровня: потребность во впечатлениях, любознательность, целенаправленная познавательная потребность [82; 36].

В.С.Юркевич охарактеризовала уровни следующим образом, на первом уровне познавательной потребности главную роль играет так называемая потребность во впечатлениях, которая выражается в стремлении индивида к новым стимулам, в его реакции на новые впечатления, поступающие к нему извне. В начальном уровне познавательной потребности еще нет стремления к получению нового знания - это потребность именно в новых стимулах. Наиболее ярко уровень потребности выражен у младенцев и детей раннего дошкольного возраста, сохраняя определенное значение и в дальнейшем. Следующий уровень – любознательность, на котором наблюдается уже личностный отбор той информации, которая к нему поступает и которую он сам способен получить. Познавательная потребность на этом уровне гораздо более целенаправленна, возникают и укрепляются интересы, разнообразные формы личностного отношения к знанию. Только на этом уровне появляется потребность в знании. Однако на этом уровне познавательная потребность еще недостаточно определена и связана с социальными задачами, носит стихийно-эмоциональный и нередко узкоиндивидуальный характер. Особенно ярко выражена любознательность у подростков, можно сказать, что возрастом любознательности является весь школьный возраст. В этом возрасте любознательность формируется, переживает "расцвет" и сменяется следующим этапом познавательной потребности. Третий уровень – это уровень целенаправленной познавательной потребности, сама потребность не стихийна, а отражает жизненные ценности личности. Именно этот этап познавательной потребности проявляется как устойчивое стремление индивида к той или иной области знаний, как становление склонности его определенной деятельности. Есть определенные основания считать, что предыдущие уровни познавательной потребности не утрачиваются полностью, а как бы снимаются, последующим включаясь в него в качестве одного из компонентов этого, более развитого уровня познания.

В.С. Юркевич выделяет две формы познавательной потребности:

- потребность в познании может проявляться в форме усвоения уже готовых знаний (потребность в усвоении впечатлений, интеграции, систематизации их и потребность в накоплении знаний);

- потребность в исследовательской деятельности с целью получения нового знания. Первая - наименее активная форма познавательной потребности. В результате этой формы усваивается, но не создаётся новое знание. Вторая - более активная форма, прямо направленная на получение новых знаний. Учащиеся, обладающие той или другой формой познавательной потребности, заметно различаются. Школьники с потребностью в усвоении знаний склонны к запоминанию фактического материала, у них нередко обнаруживается особенно чёткая система в его хранении. Школьники с исследовательской потребностью старается сами доходить до правильного ответа, с интересом решают незнакомые задачи, любят " хитрые " вопросы. Эти формы отличаются именно степенью участия различных потребностей. Познавательная потребность способствует интенсивному развитию интеллектуальных процессов (восприятия, мышления, воображения). Формирование познавательной потребности положительно сказывается на развитие мотивации и личности: формируется тип мотивации, где ведущим мотивом становится познавательная потребность, формируется личность высокой интеллектуальной активности, обладающая жаждой непрестанного поиска и раздумий, повышается быстрота и точность восприятия учебного материала, логичность мышления, стремление проникнуть в глубину изучаемого вопроса, повышается потребность в заданиях, требующих самостоятельности, творческого подхода в задачах повышенной трудности, знания становятся большими по объему. Переход познавательной потребности на следующий уровень связан с дальнейшим развитием личности школьника, его мотивационной сферой, с расширением и углублением качества знаний. Это придает новые качества, которыми она обладала на первом и втором уровне. В классных коллективах, где познавательная потребность достигает такого уровня развития, встречаются отдельные учащиеся, у которых она перерастает в страсть, в жажду раздумий над предметом. Это обычно учащиеся с выдающимися способностями. Познавательная потребность развивается разными путями, в том числе и информационными технологиями.

1.2 Использования информационных технологий на уроках математики

В настоящем постиндустриальном обществе роль информационных технологий (ИТ) чрезвычайно важна, так как использование ИТ может обеспечить существенную экономию учебного времени. В отработанных моделях такого использования время, затрачиваемое на освоение ИТ, окупается за счет эффективности учебного процесса по дисциплинам, где ИТ применяется, в дополнение к этому идет освоение новых, приоритетных моделей деятельности. ИТ занимают сегодня центральное место в процессе интеллектуализации общества, развития его системы образования и культуры.

Информационные технологии (ИТ, от англ. information technology, IT) — широкий класс дисциплин и областей деятельности, относящихся к технологиям управления и обработки данных, в том числе, с применением вычислительной техники [59]. В прошедшее время под информационными технологиями чаще всего понимают компьютерные технологии. В частности, ИТ имеют дело с использованием компьютеров и программного обеспечения для хранения, преобразования, защиты, обработки, передачи и получения информации. Специалистов по компьютерной технике и программированию часто называют ИТ-специалистами.

Согласно определению, принятому ЮНЕСКО, ИТ — это комплекс взаимосвязанных, научных, технологических, инженерных дисциплин, изучающих методы эффективной организации труда людей, занятых обработкой и хранением информации; вычислительную технику и методы организации и взаимодействия с людьми и производственным оборудованием, их практические приложения, а также связанные со всем этим социальные, экономические и культурные проблемы [65]. Сами ИТ требуют сложной подготовки, больших первоначальных затрат и наукоемкой техники. Их введение должно начинаться с создания математического обеспечения, формирования информационных потоков в системах подготовки специалистов.

Их широкое использование в самых различных сферах деятельности человека диктует целесообразность наискорейшего ознакомления с ними, начиная с ранних этапов обучения и познания. Система образования и наука являются одним из объектов процесса информатизации общества. Информатизация образования в силу специфики самого процесса передачи знания требует тщательной отработки используемых ТИ (технологий информатизации) и возможности их широкого тиражирования. Кроме того, стремление активно применять современные информационные технологии в сфере образования должно быть направлено на повышение уровня и качества подготовки специалистов. "Отработка" применяемых в сфере образования ИТ должна ставить своей целью реализацию следующих задач:

поддержку и развитие системности мышления обучаемого;
поддержку всех видов познавательной деятельности человека в приобретении знаний, развитии и закреплении навыков и умений;
реализацию принципа индивидуализации учебного процесса при сохранении его целостности.

Итак, основными задачами современных информационных технологий обучения являются разработка интерактивных сред управления процессом познавательной деятельности, доступа к современным информационно-образовательным ресурсам (мультимедиа учебникам, различным базам данных, обучающим сайтам и другим источникам). По мнению Т.Е.Булгаковой основными задачами современных информационных технологий обучения являются разработка интерактивных сред управления процессом познавательной деятельности, доступа к современным информационно-образовательным ресурсам (мультимедиа учебникам, различным базам данных, обучающим сайтам и другим источникам) [16, 87].

Классификация информационных технологий зависит от критерия классификации. В качестве критерия может выступать показатель или совокупность признаков, влияющих на выбор той или иной информационной технологии. Примером такого критерия может служить пользовательский интерфейс (совокупность приемов взаимодействия с компьютером), реализующийся операционной системой. ИТ разделяются на две большие группы: технологии с избирательной и с полной интерактивностью. ИТ с избирательной интерактивностью принадлежат все технологии, обеспечивающие хранение информации в структурированном виде. Сюда входят банки и базы данных и знаний, видеотекст, телетекст, интернет и т.д. Эти технологии функционируют в избирательном интерактивном режиме и существенно облегчают доступ к огромному объему структурируемой информации. В данном случае пользователю разрешается только работать с уже существующими данными, не вводя новых [16, 87]. ИТ с полной интерактивностью содержит технологии, обеспечивающие прямой доступ к информации, хранящейся в информационных сетях или каких-либо носителях, что позволяет передавать, изменять и дополнять ее. По степени использования в информационных технологиях компьютеров различают компьютерные и бескомпьютерные технологии. В области образования информационные технологии применяются для решения двух основных задач: обучения и управления. Соответственно paзличают компьютерные и бескомпьютерные технологии обучения, компьютерные и бескомпьютерные технологии управления образованием. В обучении информационные технологии могут быть использованы, во-первых, для предъявления учебной информации обучающимся, во-вторых, для контроля успешности ее усвоения. С этой точки зрения информационные технологии, используемые в обучении, делятся на две группы: технологии предъявления учебной информации и технологии контроля знаний. К числу бескомпьютерных информационных технологий предъявления учебной информации относятся бумажные, оптотехнические, электроннотехнические технологии. Они отличаются друг от друга средствами предъявления учебной информации и соответственно делятся на бумажные, оптические и электронные. К бумажным средствам обучения относятся учебники, учебные и учебно-методические пособия; к оптическим - эпипроекторы, диапроекторы, графопроекторы, кинопроекторы, лазерные указки; к электронным телевизоры и проигрыватели лазерных дисков. К числу компьютерных информационных технологий предъявления учебной информации относятся:

- технологии, использующие компьютерные обучающие программы;

- мультимедия технологии;

- технологии дистанционного обучения.

Компьютерные технологии, наиболее часто применяемые в учебном процессе, можно разделить на две группы:

1) сетевые технологии, использующие локальные сети и глобальную сеть Internet (электронные вариант методических рекомендаций, пособий, серверы дистанционного обучения, обеспечивающие интерактивную связь с учащимися через Internet, в том числе в режиме реального времени);

2) технологии, ориентированные на локальные компьютеры (обучающие программы, компьютерные модели реальных процессов, демонстрационные программы, электронные задачники, контролирующие программы, дидактические материалы).

Курс математики в старших классов должен быть наиболее тесно связан с курсом информатики. Некоторые задачи из рассматриваемых тем следует доводить до составления программы решения с помощью компьютера. Применение ЭВМ в обучении математики – один, наверное, из самых современных приемов активизации познавательной деятельности учащихся как на уроке, так и во внеурочное время. ЭВМ занимает особое место в учебном процессе. Специалисты считают, что только молодые могут воспринять концепции и логику компьютерного мышления. Дети легко постигают азы машинной графики, без особых усилий осваивают язык символов, выполняя упражнения, играя в основанные на зрительных эффектах электронные игры, требующие живости, гибкости мышления, хорошей непосредственной реакции. Компьютер меняет сам характер мышления, заставляя проникать в самую суть явлений, вырабатывает внимание, характер. Возможности современных компьютеров просто поразительны. Компьютеры в качестве учителя малоэффективны, это уверенно подтвердил опыт. Компьютеры необходимы как помощники учителя, в этой роли они неоценимы. Учить надо с компьютером, но не одним компьютером. Особенно полезен компьютер в качестве базы для наглядного обучения, тренажера, для контроля. Применение компьютера на уроках математики позволяет в ряде случаев более наглядно изложить отдельные вопросы программы. Например, при помощи программы Advanced Grapher в считанные секунды можно получить несколько разноцветных графиков, на получение которых "вручную" необходимо потратить немало времени (рис. 1-3).

Рис.1

Рис.2

Рис.3

Данная программа применяется при изучение таких тем, как: линейная функция, квадратичная функция, преобразование графиков функций, исследование показательной и логарифмической функций и построение их графиков, графическое решение уравнений, графики обратных функций, графики тригонометрических функций, интеграл и площадь криволинейной трапеции.

Например, на интегрированных с информатикой уроках, пользуясь услугами локальной сети, возможно, например, построение графиков тригонометрических функций с помощью редактора электронных таблиц EXCEL. На уроке математики, проходящем в кабинете информатики, можно организовать работу учащихся, например, с использованием мультимедийных учебных пособий из серии "Математика не для отличников", которые по сути являются идентичными электронными версиями печатных учебников, а для проверки знаний используется тест. Учащиеся сначала решают задачу, а затем набирают ответ в числовом или аналитическом виде, или выбирают его из числа предложенных программой. Если же ответ неверен, то программа лишь констатирует этот факт, но она не в состоянии провести анализ ошибок.

Самое главное, что выгодно отличает "Курс математики для школьников и абитуриентов Л.Боревского", электронное пособие "Математика для абитуриентов" и современный учебно-методический комплекс ЗАО "Просвещение – МЕДИА" "Все задачи школьной математики" - это интерактивное решение задач с помощью компьютера, при котором обеспечивается поэтапный (пошаговый) контроль за работой обучаемого. Это снимает сразу две проблемы:

- программа проверяет каждый шаг ученика, указывая на его текущие ошибки и подсказывая выход из трудной ситуации;

- немедленная реакция компьютера на ошибочный шаг позволяет тут же поправить ученика, избежать невольного запоминания ошибочных ходов.

Именно в этом заключается неоспоримое преимущество использования компьютера в педагогике: мы получаем индивидуального бесстрашного наставника персонально для каждого ученика.

По окончании решения программа выдает четкие рекомендации по дальнейшей работе над задачей и даже открывает в электронном учебнике тот материал, который необходимо дополнительно проработать.

Такое пошаговое контролируемое решение отвечает важному педагогическому принципу: не проверять уже имеющиеся знания, а обучать новым методам решения.

Услугами сети Интернет учащиеся чаще пользуются в домашних условиях при подготовке к семинарам, в работе над выполнением творческих заданий, а учитель может пополнить свою методическую копилку. Например, много полезной информации для преподавателя можно получить с Российского образовательного портала (school.edu.ru) , крупнейшего в данный момент в России сайта, посвященного математическому образованию школьников. На "странице учителя" можно найти сведения о проходящих методических и научных конференциях и семинарах, прочитать интересные статьи и др. Воспользовавшись информационно - поисковой системой "Задачи" (zadachi.mccme. ru) можно получить по указанию темы перечень задач разного уровня сложности. И таких примеров можно привести много. Но интегрированные уроки и применение Интернет-технологий - дело не ежедневное. Интернет только входит в учебный процесс. Сейчас он используется в основном как источник современной информации. Для учителя Интернет представляет интерес и с точки зрения профессионального роста.

Информационные технологии в обучении предполагают дистанционное обучение. Современное дистанционное обучение строится на использовании следующих основных элементов:

Среды передачи информации (почта, телевидение, радио, информационные коммуникационные сети);
Методов, зависимых от технической среды обмена информацией.

В настоящее время перспективным является интерактивное взаимодействие с учащимся посредством информационных коммуникационных сетей, из которых массово выделяется среда интернет-пользователей. В 2003 году инициативная группа ADL начала разработку стандарта дистанционного интерактивного обучения SCORM, который предполагает широкое применение интернет-технологий. Введение стандартов способствует как углублению требований к составу дистанционного обучения, так и требований к программному обеспечению. В настоящее время имеются отечественные разработки программного обеспечения, которые достаточно широко применяются как отечественными, так и зарубежными организациями, предоставляющими услуги по дистанционному обучению.

Дистанционное обучение претендует на особую форму обучения (наряду с очной, заочной, вечерней, экстернатом).

Использование технологий дистанционного обучения позволяет:

Снизить затраты на проведение обучения (не требуется затрат на аренду помещений, поездок к месту учебы, как учащихся, так и преподавателей и т. п.);
Проводить обучение большого количества человек;
Повысить качество обучения за счет применения современных средств, объемных электронных библиотек и т.д.
Создать единую образовательную среду (особенно актуально для корпоративного обучения).

Дистанционное обучение занимает всё большую роль в модернизации образования. Согласно приказу 137 Министерства образования и науки РФ от 06.05.2005 "Об использовании дистанционных образовательных технологий", итоговый контроль при обучении с помощью ДОТ (дистанционных образовательных технологий) можно проводить как очно, так и дистанционно. Госдума РФ рассматривает проект поправок к закону об образовании, связанных с дистанционным обучением.

На уроках математики компьютер может использоваться с самыми разными функциями и, следовательно, целями: как способ диагностирования учебных возможностей учащихся, средство обучения, источник информации, тренинговое устройство или средство контроля и оценки качества обучения. Возможности современного компьютера огромны, что и определяет его место в учебном процессе. Его можно подключать на любой стадии урока, к решению многих дидактических задач, как в коллективном, так и в индивидуальном режиме.

Специфика и возможности компьютерного урока таковы, что отнести его строго к определенной группе по тенденциям развития образовательных технологий нельзя. Приход ЭВМ в школу способен облегчить труд учителя, особенно рутинного характера, например использование презентации, созданные в Power Point, это своего рода мини-конспекты урока. Компьютер - хранитель информации, накопленной учителем за годы работы, и получена она с его помощью может быть в любой момент времени.

Вводить компьютерные компоненты можно в уроки любых предметов. Все дело заключается в целесообразности, наличии соответствующих качественных программ, условиях использования.

Урок с применением компьютера будет способствовать формированию познавательной потребности у того учителя, который:

сохраняет человеческие приоритеты в обучении;
имеет доброе, доверительное отношение к машине и ее педагогическим возможностям;
умеет бережно и в то же время смело обращаться с персональным компьютером;
интеллектуально развит, эрудирован, способен оценивать педагогические возможности компьютерных программ;
методически гибок;
дисциплинирован, точен, владеет упорядоченным логизированным мышлением.

Таким образом, без профессионального роста в освоении информационных технологий не обойтись.

Первый шаг, который делает учитель, обращаясь к компьютерной технологии обучения, состоит в изучении педагогических программных средств по своему предмету и оценке их достоинств и недостатков. К сожалению, еще не встречалось ни одного мультимедийного учебного пособия по математике, которое бы полностью соответствовало школьной программе: используется нетипичная терминология. Отличные от школы, системы аксиом, или громоздкая система ввода информации (очень "закрученный" редактор формул, что не ускоряет, а, наоборот замедляет процесс решения).

Ознакомление с программной продукцией целесообразно начинать с изучения средств, создающих компьютерную среду. К этим программам относятся программные инструкции, советы, рекомендации по самому широкому кругу вопросов. С ними учитель может проводить и классные, и внеклассные занятия, освобождая себя от многократного повторения учащимся одних и тех же прописных истин, от налета субъективности в оценке учебных успехов учащихся, помогая осваивать им технологию самообучения.

Компьютерную среду создают также справочно-информационные материалы. Их назначение состоит в том, чтобы обеспечить на уроке большую наглядность и доказательность, использовать эти программы для наведения разного рода справок и для самопроверки, для предоставления образца выполнения какого-либо задания на конкретном предметном материале.

Справочно-информационные материалы призваны облегчить многим детям освоение школьной программы, они носят поддерживающий и сопровождающий, нередко и мотивирующий характер.

Одной из основных проблем при изучении геометрии в школе является проблема наглядности, связанная с тем, что изображения даже простейших геометрических фигур, выполненные в тетрадях или на доске, как правило, содержат большие погрешности. Современные компьютерные средства позволяют решить эту проблему. Стереометрия - это одна из немногих, если не единственная область школьной математики, в отношении которой не приходится агитировать за ИТ. Современная трехмерная графика позволяет создавать модели сложных геометрических тел и их комбинаций, вращать их на экране, менять освещенность. Поэтому полный интерактивный курс стереометрии, предложенный компанией "Физикон", призван помочь учителю более успешно справиться с решением стоящих перед ним задач, а его использование на уроках геометрии в 10-11 классах сделает доступным сложный учебный материал более широкому кругу учащихся.

На уроках алгебры и начал анализа использование мультимедийного пособия "Функции и графики" прекрасно иллюстрирует построение графиков элементарных и более сложных функций и преобразование графиков.

Таким образом, компьютер как бы соединяет в себе ряд традиционных ТСО, которые всегда использовались, в основном, для усиления наглядности. Это активизирует познавательный процесс у обучаемых, развивает мышление (наглядно-действенное, наглядно-образное), повышает результативность учебного процесса, в том числе и познавательную потребность. Использование ИТ на уроках математики позволяет реализовать такие развивающие цели обучения, как развитие познавательной потребности, формирование мышления, развитие умений осуществлять экспериментально-исследовательскую деятельность (например, за счет реализации возможностей компьютерного моделирования), формирование информационной культуры, умений осуществлять обработку информации.

Элементы компьютерной среды, помогающие учителю в изучении математики, представлены следующими программами:

- графический редактор "Paint" входит в стандартный комплект программных средств компьютера. Он служит для создания, просмотра и редактирования графических изображений. Созданное изображение может быть распечатано на принтере или записано в виде файла для его дальнейшего использования;

- графический редактор "Adobe Illustrator" является более мощным средством для создания и обработки рисунков, он имеет дело с так называемым векторным изображением;

- с помощью редактора электронных таблиц Microsoft Excel можно строить графики функций и выполнять несложные вычисления;

- программа 3D See Builder поможет выполнить задачи на построение сечений;

- school. еdu. ru. - Российский образовательный портал;

- zadachi.mccme.ru - информационно- поисковая система <Задачи>;

- matematica.agava.ru - сайт разнообразных математических задач для поступающих в вузы с решениями;

- school. msu.ru - учебно- консультационный сайт для учащихся и преподавателей средних школ;

- мультимедийные учебные пособия: "Алгебра не для отличников", "Геометрия не для отличников", "Тригонометрия не для отличников", "Teach Pro Математика. Решение уравнений и неравенств", "Teach Pro Математика. Тригонометрия. Функция", Л.Боревский "Курс математики 2000", "Математика абитуриенту", "Все задачи школьной математики. Алгебра 7-9, Алгебра и начала анализа 10-11, итоговая аттестация выпускников", "Открытая математика. Планиметрия", "Открытая математика. Стереометрия", "Открытая математика. Функции и графики".

Создание приложений учебного назначения в соответствии с современными требованиями даже с помощью инструментальных систем отдельными преподавателями и малыми творческими коллективами не дает желаемых результатов, т.к. создание качественного продукта требует участия специалистов различных отраслей информационных технологий. Поэтому для их производства необходимо организовывать стабильные технологические цепочки (издательские лаборатории).

Конечно же, основой для реализации такого программного обеспечения служит подготовленный преподавателем сценарий компьютерной поддержки курса, обеспечивающий информационную, дидактическую и методическую составляющую курса.

Применение современных информационных технологий значительно повышает эффективность самообразования. В электронный вид переведены многие, всемирно известные, энциклопедии и словари, существует большое количество электронных книг и учебников.

Компьютер позволяет повысить самостоятельность работы учащихся, которая необходима для перевода знаний извне во внутреннее достояние школьника, учитель может варьировать формы контроля над усвоением учебного материала. Это можно проиллюстрировать использованием компьютера при изучении темы "Применение определенного интеграла к вычислению площадей" на уроках математики. Подходящим программным средством в качестве компьютерной поддержки темы может использоваться электронные таблицы EXCEL. Разработка в ней задачи интегрирования позволяет, во-первых, освоить многие операции, изучаемые в программном средстве по предмету информационных технологий, и, во-вторых, закрепить материал по интегрированию в приложении к вычислению площадей. Тем самым значительно сокращаются затраты учебного времени по общим предметам. Кроме того использование специализированных программ таких как MATLab, МВТУ и другие позволяют упростить процесс вычисления и решения некоторых сложных дифференциальных и интегральных задач.

Современный этап применения компьютерной технологии обучения в учебном процессе заключается в использовании компьютера как средства обучения не эпизодически, а систематически с первого до последнего занятия при любом виде обучения. Основная проблема при этом заключается в методике компьютеризации курса, который предстоит освоить обучаемому. Возможна либо полная перестройка и ориентация на создание новых компьютеризованных курсов, либо реализация методики с частичной компьютерной поддержкой курса. Другими словами речь идет о форме компьютерной поддержки процесса обучения. В настоящее время практика использования компьютерных технологий в образовании обнаруживает две тенденции:

- применение промышленных универсальных компьютерных программ, предназначенных для решения широкого круга практических и научных задач из различных предметных областей, и адаптированных к учебным дисциплинам;

- применение обучающих программ, специально разработанных для целей обучения и реализующих соответствующие методики, заложенные в них разработчиками. На сегодняшний день существует широкий спектр программ от простейших, контролирующих до сложных мультимедийных продуктов.

2.1 Особенности изучения темы "Интеграл" в школьном курсе математики

Выбор темы "Интеграл" неслучаен. Тема "Интеграл" изучается в рамках программы 11 класса общеобразовательной школы.

Существует большое количество программ по математике, каждая из которых имеет свои особенности в изложении того или иного вопроса. В связи с этим каждая школа работает по определенной программе, в соответствии с которой разрабатывается учебный комплект, в который входят учебные пособия, книга для учителя и дидактические материалы.

В таблице 3 представлены программы по изложению темы "Интеграл" основных авторов, по которым ведется обучение математике сегодня в школах: Ш.А.Алимова, А.Н.Колмогорова, А.Г.Мордкович, С.М.Никольского.

Таблица 3 Тематическое планирование темы "Интеграл" по программам разных авторов

Автор программ

Изложение темы

Кол-во часов

А.Н.Колмогоров

11 класс

Площадь криволинейной трапеции

Формула Ньютона-Лейбница

Применение интеграла

Контрольная работа

Зачет

Ш.А.Алимов

11 класс

Первообразная. Правила нахождения

Формула Ньютона–Лейбница Площадь криволинейной трапеции и интеграл

Вычисление интеграла.

Применение интеграла к решению практических задач

Урок обобщения и систематизации знаний

Контрольная работа

А.Г.Мордкович

11 класс

Первообразная и неопределенный интеграл

Определенный интеграл

Зачет

Контрольная работа

Учебно-тренировочные занятия по теме "Первообразная и интеграл" к ЕГЭ

С.М.Никольский

11 класс

Площадь криволинейной трапеции

Определенный интеграл.

Формула Ньютона-Лейбница

Применение определенных интегралов в геометрических и физических задачах

Контрольная работа

На основе этих программ этими авторами написаны действующие учебники. В учебниках, традиционно применяемых в школьном обучении, как правило, используются следующие подходы к введению понятия определенного интеграла.

Интеграл как предел интегральных сумм.

Этот подход предполагает введение операции интегрирования как независимой операции; при этом интеграл определяется как предел последовательности, составленной из интегральных сумм. Начинается изучение в этом случае с рассмотрения конкретных задач, например, задачи о площади под кривой; задачи о работе силы и др. Затем, обобщив полученные результаты, переходят к определению интеграла как предела интегральных сумм.

Хотя данное определение громоздко, но идея метода наглядна (геометрическая интерпретация – площадь криволинейной трапеции). Вместе с определением интеграла получают и способ его вычисления. Но на практике для вычисления интеграла используют формулу Ньютона – Лейбница, которую при данном подходе необходимо доказать.

Интеграл как приращение первообразной.

Этот подход предполагает введение операции интегрирования как операции, обратной дифференцированию. При этом формула Ньютона – Лейбница практически служит определением интеграла.

При этом подходе не требуется специально выводить формулу Ньютона – Лейбница, с помощью которой доказываются многие свойства интеграла. Однако в этом случае идея метода суммирования отходит на второй план. Недостаток этого подхода состоит в том, что появляются затруднения при изучении приложений интеграла. В итоге все – таки приходится рассматривать интеграл как предел интегральных сумм, чтобы получить единый, достаточно общий метод решения задач геометрии, механики, электродинамики и других разделов физики. Это рассмотрение можно провести либо сразу после введения понятия интеграла, объяснив учащимся, что не всегда возможно найти первообразную данной функции, либо непосредственно при изучении приложений интеграла, рассмотрев этот метод на одной из задач.

М. И. Башмаков дает следующее определение интеграла: "Пусть дана положительная функция f, определенная на конечном отрезке [a; b] [7]. Интегралом от функции f на отрезке [a; b] называется площадь её подграфика".

В учебнике Мордковича А. Г. "Алгебра и начала анализа" при введении понятия "Определенный интеграл" рассматриваются задачи, приводящие к данному понятию, а именно задача о вычислении площади криволинейной трапеции, задача о вычислении массы стержня и задача о перемещении точки [45]. Все три задачи при их решении приводятся к одной и той же математической модели. При чем говорится о том, что многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Далее дается математическое описание этой модели, которая была построена в трех рассмотренных задачах для непрерывной на отрезке [a; b] функции y=f(x):

разбивают отрезок [a; b] на n равных частей;
составляют сумму

S_>n>=f(x_>0>)Δx_>0>+f(x_>1>) Δx_>1>+…+f(x_>k>) Δx_>k>+…+f(x_>n-1>) Δx_>n-1>;

3) вычисляют .

Автор учебника поясняет, что в курсе математического анализа доказано, что этот предел существует. Его называют определенным интегралом от функции y=f(x) по отрезку [a; b].

В учебнике А. Н. Колмогорова "Алгебра и начала анализа" при введении интеграла рассматривается задача о вычислении площади криволинейной трапеции [33]. Автор приводит в учебнике два способа вычисления площади криволинейной трапеции: с помощью теоремы о площади криволинейной трапеции и с помощью интегральных сумм. Второй способ сводится к определению интеграла. С помощью интегральных сумм выводятся также формулы для вычисления объемов тел, работы переменной силы, а также нахождения массы стержня и центра масс.

Среди применений интеграла в данном учебнике выводится формула для нахождения работы переменной силы, формула вычисления массы стержня и центра масс. Все формулы выводятся одним способом: с помощью интегральных сумм. Для самостоятельного решения учащимся предлагается задача о нахождении кинетической энергии стержня и несколько задач на уже рассмотренные формулы. Причем задачи делятся на несколько уровней сложности, в том числе задачи повышенной трудности.

Проведём анализ некоторых школьных учебников алгебры и начал анализа. Как мы видим из таблицы, не у всех анализируемых авторов программы совпадают. Например, в учебнике А.Н.Колмогорова "Алгебра и начала анализа" при введении интеграла рассматривается задача о вычислении площади криволинейной трапеции. Автор приводит в учебнике два способа вычисления площади криволинейной трапеции: с помощью теоремы о площади криволинейной трапеции и с помощью интегральных сумм. Второй способ сводится к определению интеграла. С помощью интегральных сумм выводятся также формулы для вычисления объемов тел, работы переменной силы, а также нахождения массы стержня и центра масс.

Наиболее углублено тема "Интеграл" рассмотрена в учебнике А.Г.Мордковича [45]. В учебнике А.Г.Мордковича "Алгебра и начала анализа" при введении понятия "Определенный интеграл" рассматриваются задачи, приводящие к данному понятию, а именно задача о вычислении площади криволинейной трапеции, задача о вычислении массы стержня и задача о перемещении точки. Все три задачи при их решении приводятся к одной и той же математической модели. Причем говорится о том, что многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Далее дается математическое описание этой модели, которая была построена в трех рассмотренных задачах для непрерывной на отрезке [a; b] функции y=f(x):

разбивают отрезок [a; b] на n равных частей;
составляют сумму

S_>n>=f(x_>0>)Δx_>0>+f(x_>1>) Δx_>1>+…+f(x_>k>) Δx_>k>+…+f(x_>n-1>) Δx_>n-1>;

3) вычисляют .

После чего автор учебника возвращается к трем рассмотренным ранее задачам и результат, полученный при их решении, переписывает следующим образом:

где S – площадь криволинейной трапеции, ограниченной графиком функции y=f(x);

где m – масса неоднородного стержня с плотностью p(х);

где s – перемещение точки, движущейся по прямой со скоростью v=v(t).

В учебнике в физических приложениях интеграла приводятся те же задачи, что и при введении понятия интеграла, а именно задачи о массе стержня и перемещении точки. Этим автор учебника и ограничивает изучение приложений интеграла в физике.

В учебнике С.М.Никольского "Алгебра и начала анализа" рассмотрение задачи о вычислении площади криволинейной трапеции приводит к понятию интегральных сумм и пределу от них, после чего вводится определение определенного интеграла [47]. Теоретическое обоснование применения определенного интеграла рассматривается в таких физических задачах, как задачи на работу силы, работу электрического заряда, на вычисление массы стержня переменной плотности, давления жидкости на стенку и центра тяжести. Среди приложений интеграла в физике рассматриваются следующие задачи (вместе с теоретическим их обоснованием): задачи о работе силы, работе электрического заряда, задача о массе стержня переменной плотности, задача о давлении жидкости на стенку, задача о нахождении центра тяжести системы материальных точек. Однако, автор учебника приводит очень скупую систему упражнений, при чем не использует в практических задачах и половины тех формул, которые были ранее выведены.

В учебнике Ш.А.Алимова "Алгебра и начала анализа" перед введением понятия интеграла рассматривается задача о нахождении площади криволинейной трапеции, где вычисление площади сводится к отысканию первообразной F(х) функции f(x) [2]. Разность F(b)- F(a) называют интегралом от функции f(x) на отрезке [a; b]. Далее автор рассматривает вычисление площади криволинейной трапеции с помощью интегральных сумм, говорит о том, что такой способ приближенного вычисления интеграла требует громоздких вычислений и им пользуются в тех случаях, когда не удается найти первообразную функции. В качестве примеров применения интеграла приведены задачи о вытекании воды из бака и нахождении работы силы. Задачи для самостоятельного решения однотипны и их очень мало.

К учебнику А.Н.Колмогорова предполагается дидактический материал, авторами которого являются Б.М.Ивлев, С.М.Саакян, С.М.Шварцбурд [17,33]. В данном пособии содержатся самостоятельные и контрольные работы, проверочные работы, материал для итогового повторения и программированного контроля и карточки-задания для зачетов. Все они даны в соответствии с действующим учебником "Алгебра и начала анализа" под редакцией А.Н. Колмогорова.

2.2 Экспериментальная работа по формированию познавательной потребности учащихся средствами информационных технологий на примере изучения темы "Интегралы"

Экспериментальная работа проводилась в 11 "Б" классе МОУ СОШ №3 г. Абдулино Оренбургской области совместно с учителем по математике высшей категории Н.В. Николаевой. Выборку составили 20 учеников.

Для проверки выдвинутой нами гипотезы мы продумали и организовали педагогический эксперимент, который осуществлялся в три этапа: констатирующий, формирующий, контрольный. На констатирующем этапе нами была подобрана система методик, и по ним было проведено исследование по выявлению степени сформированности познавательной потребности у школьников. На основе анализа результатов констатирующего среза были выделены группы учащихся по уровню сформированности познавательной потребности, которые мы учитывали при организации уроков с использованием информационных технологий.

В школе, где я проходила практику, ведется преподавание по программе А.Н. Колмогорова. Исследуемая тема отражена в третьей главе учебника А.Н.Колмогорова и состоит из двух параграфов (§7 "Первообразная" и §8 "Интеграл"), что составляет 11 уроков.

При изучении темы "Интеграл" в 11 классе использовались следующие информационные технологии: интерактивная доска, мультимедийная презентация, проектор (таблица 4).

Таблица 4

№	Название темы урока	Количество часов	Применяемые ИТ
1	Интеграл. Площадь криволинейной трапеции. Вводный урок	2	Мультимедийный проектор (Power Point)
2	Формула Ньютона-Лейбница	4	Мультимедийный проектор (Power Point)
3	Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.	1	Мультимедийный проектор (Power Point), Интерактивная доска
5	Применение интегралов к решению физических задач.	1	Мультимедийный проектор (Power Point)
6	Обобщающий урок	1	Интерактивная доска, Мультимедийный проектор (Power Point)
7	Контрольная работа. Зачет	2

На уроках использовались различные формы учебной работы: фронтальная, дифференцированно-групповая, индивидуальная и индивидуализированная (самостоятельная работа, домашние задания, тесты, зачеты). Чаще всего в своей работе я проводила комбинированные уроки, которые строятся на совокупности логических не обусловленных звеньев процесса обучения. Использование познавательной потребности способствует повышению успеваемости (в особенности за счет уменьшения неудовлетворительных оценок и увеличения количества хороших оценок). Сильным ученикам особенно нравятся задания, которые требуют большего напряжения и дают дополнительную информацию, слабые же получают удовлетворение от успеха, поскольку им приходится работать со значительно более доступным материалом, чем прежде. Повышается интерес к предмету.

Рассмотрим несколько уроков.

Для начала нами был проведен вводный урок с применением электронной презентации, в котором были даны основные понятия темы (см. приложение 1). Приведем фрагмент урока по теме 1.

Урок 1.

Тема: Интеграл. Площадь криволинейной трапеции. Вводный урок

Цель: сформировать представления о криволинейной трапеции и интеграле, сформировать умения самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи:

Обучающая: создать условия для формирования представления о площади криволинейной трапеции и интеграле.

Развивающая: развивать познавательную потребность учащихся.

Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данный урок носит ознакомительный характер, ученики знакомятся с понятиями "площадь криволинейной трапеции", "первообразная", "интеграл", получают понятие об интеграле как площади криволинейной трапеции. Тема рассчитана на 2 часа.

План урока:

Организация начала урока.
Постановка проблемы урока.
Актуализация ЗУН, необходимых для творческого применения знаний.
Формирование новых понятий и способов действий
Обобщение и систематизация знаний и способов деятельности
Усвоение образца комплексного применения ЗУН
Применение знаний умений и навыков в новых условиях
Подведение итогов урока

Ход урока:

1. Организация начала урока. Проверка присутствующих,

2. Постановка проблемы урока. Постановка целей и задач урока.

3. Актуализация ЗУН, необходимых для творческого применения знаний.

Проиллюстрируем фрагмент урока. Чтобы заитересовать учащихся даются исторические сведения об интеграле (Слайд 2).

Формирование новых понятий и способов действий.

Определение криволинейной трапеции. Площадь криволинейной трапеции. Если на [а;b] ([а;b] ?Ох) функция у=f(х) – непрерывная, не меняет знак (график не пересекает ось абсцисс), тогда фигура, ограниченная графиком функции f, отрезком [а;b] и прямыми х = а, х = b, называется криволинейной трапецией (слайд 8).

Если f - непрерывная и неотрицательная на отрезке [а;b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а;b], т.е.

Введение понятия "интеграл".

Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции. Для простоты будем считать функцию f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.

Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x_>0> = а<x_>1> < x_>2> < … <x_>n-1> < x_>n> = b и пусть

где k = 1, 2, ..., n — 1, n. На каждом из отрезков [x_>k-1>; x_>k>] как на основании построим прямоугольник высотой F(x_>k-1>). Площадь этого прямоугольника равна:

а сумма площадей всех таких прямоугольников равна:

В силу непрерывности функции f объединение построенных прямоугольников при большом n, т. е. при малом Δx, "почти совпадает" с интересующей нас криволинейной трапецией. Поэтому возникает предположение, что Sn≈S при больших n. (Коротко говорят: "S_>n> стремится к S при n, стремящемся к бесконечности"— и пишут: S_>n>→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) S_>n> при n→∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до b и обозначают , т. е.

при n→∞

(читается: "Интеграл от а до b эф от икс дэ икс"). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой

Полный конспект урока см. приложение 1.

В теме "Применение интегралов" мы изучили площадей криволинейных трапеций с помощью интегралов. В процессе проведения опытно-экспериментальной работы нами был разработан план урока для 11 класса на тему: "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью MS Excel" с применением интерактивных досок и информационных технологий (урок 7). Приведем фрагмент урока по теме 7 (см. приложение 1).

Тема урока: Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.

Цель: Обеспечить закрепление понятия интеграл, способы его вычисления, применение интеграла для вычисления площадей.

Задачи:

Обучающая: сформировать навыки планирования ответа, умение считать и писать в быстром темпе, навыки самоконтроля

Развивающая: развивать познавательную потребность учащихся.

Содержание урока: Данная тема рассчитана на два часа и состоит из двух частей: часть 1 – "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. В процессе изучения данной темы учащиеся узнают о физическом приложении интеграла.

План урока:

Организация начала урока.
Постановка проблемы урока.
Актуализация ЗУН, необходимых для творческого применения знаний
Контроль и самоконтроль знаний, умений и навыков по теме интеграл
Формирование новых понятий и способов действий
Обобщение и систематизация знаний и способов деятельности
Усвоение образца комплексного применения ЗУН
Применение знаний умений и навыков в новых условиях
Подведение итогов урока

Задание 2. Вычисление определенного интеграла с помощью таблицы Excel.

Для численного вычисления определенного интеграла методом трапеций используется формула:

Методику вычисления определенного интеграла в Excel с использованием приведенной формулы рассмотрим на примере.

Пусть требуется вычислить определенный интеграл

Величина интеграла, вычисленная аналитически равна 9. Для численного вычисления величины интеграла с использованием приведенной формулы выполните следующие действия:

табулируйте подинтегральную функцию в диапазоне изменения значений аргумента 0 – 3 (см. рис.).

в ячейку С3 введите формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2+C2, которая реализует подинтегральную функцию.
Скопируйте буксировкой формулу, записанную в ячейке С3 до значения аргумента х = 3. Вычисленное значение в ячейке С17 и будет величиной заданного интеграла - 9.

Вычислите интегралы, работая парами.

Это можно проиллюстрировать использованием компьютера при изучении темы "Применение определенного интеграла к вычислению площадей" на уроках математики. Подходящим программным средством в качестве компьютерной поддержки темы может использоваться электронные таблицы EXCEL. Разработка в ней задачи интегрирования позволяет, во-первых, освоить многие операции, изучаемые в программном средстве по предмету информационных технологий, и, во-вторых, закрепить материал по интегрированию в приложении к вычислению площадей. Тем самым значительно сокращаются затраты учебного времени по общим предметам. Программная разработка в EXCEL состоит из набора изучаемых функций; степенных, показательных, тригонометрических, для которых предлагается ввести соответствующие числовые коэффициенты и пределы интегрирования. В соседний столбец для каждой функции выведены формулы для вычисления первообразных с указанными коэффициентами и пределами интегрирования. После выбора функций значения интегралов и соответствующих им площадей рассматриваются автоматически. На графики выводятся подынтегральная функция и первообразная. Таким образом, имеется возможность графически и численно проанализировать характер функций и влияние на значение площади, то есть выполнить компьютерное моделирование. Поскольку первообразные находятся учащимися "ручным" способом и в электронную таблицу вводятся предварительно выведенные формулы, то работа с компьютером не сводится к механическим операциям и предполагает углубленное знакомство со свойствами функций и приобретения навыков их интегрирования. При этом представляется возможным дифференцировать темпы работы, обеспечить ее вариативность.

Так, например, нами применялись устные коллективные разминки, занимающие не более 5 минут, развивающие быстроту реакции, внимательность, умение четко и конкретно мыслить. В такие разминки следует включать вопросы, требующие однозначного, быстрого хорового ответа и направленные на актуализацию опорных знаний, и на проверку домашнего задания, и на отработку каких либо математических понятий и определений.

Для этого нами был проведен интегрированный урок.

Мотивируя применение интегрированных уроков необходимо отметить, что разнообразие занимательных форм (игры-путешествия, состязания, конкурсы, шарады, загадки) на уроках создаёт положительный эмоциональный фон деятельности, располагает к выполнению тех заданий, которые учащиеся считают трудными и непреодолимыми.

Творческие задания представляют собой один из путей, с помощью которого происходит у детей формирование познавательного интереса.

Познавательная деятельность учащихся в обучении, какой бы характер она не носила, какой бы активной она ни была, всегда должна направляться и организовываться учителем.

Тема: "Применение интеграла при решении физических задач" (см. приложение 1)

Цель: продолжить формирование умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Задачи урока:

Обучающие: способствовать формированию знаний, умений по данной теме;

Развивающие: умственная деятельность (выполнять операции анализа, синтеза, делать выводы, выделять существенные признаки объектов);

Воспитательные: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данного урока нет в тематическом планировании, но нами предлагается использовать данную разработку изучении темы 7. Учащиеся знакомятся с примерами применения интеграла в физике и геометрии.

План урока:

Организация начала урока.
Постановка проблемы урока.
Актуализация ЗУН, необходимых для творческого применения знаний
Формирование новых понятий и способов действий
Обобщение и систематизация знаний и способов деятельности
Усвоение образца комплексного применения ЗУН
Применение знаний умений и навыков в новых условиях
Подведение итогов урока

Ход урока:

Организация начала урока.
Постановка проблемы урока. На прошлом уроке мы ознакомились с геометрическими задачами, которые решаются при помощи интеграла. Но интеграл применим не только в математике, другие области науки также используют его и сегодня мы с вами проверим это на примере такой науки как физика.
Актуализация ЗУН, необходимых для творческого применения знаний

Физические величины, вычисляемые с помощью интеграла, можно разделить на два типа, в зависимости от того, как они естественно определяются. К первому типу относятся "первичные" величины (длина пути, масса, количество электричества, количество теплоты и т. п.), т. е. такие величины, для которых другие, связанные с ними ("вторичные") величины (соответственно скорость, линейная плотность, величина тока, удельная теплоемкость и т. п.) определяются как производные этих величин. Ко второму типу относятся такие, которые определяются естественным образом как интегралы от "первичных" по отношению к ним величин (например, площадь, работа). Для первого типа величин интегральная формула для их вычисления может и должна быть доказана, опираясь на известное из предыдущего материала определение "вторичной" величины как производной от данной "первичной". Для второго типа интегральная формула появляется по определению.

4. Формирование новых понятий и способов действий

При введении понятия интеграла как предела интегральных сумм довольно наглядным и понятным для учащихся является пример задачи о давлении жидкости на стенку.

Задача. Бассейн высоты H наполнен водой. Вычислить давление воды на прямоугольную стенку бассейна с основанием прямоугольника, равным а.

Разделим высоту Н на n равных частей (Δh). Стенка разделится на "элементы". Так как кубометр воды весит тонну, то давление столба жидкости высоты h_>i> м, имеющего сечение 1 м², равно h_>i> тоннам.

Давление же воды на элемент, находящийся на глубине h_>i>, равно произведению h_>i> на площадь элемента: h_>i>a Δh. Обозначим произведение h_>i>a через F(h_>i>). Тогда величина давления на всю стенку приближенно равна

P_>n>≈ F_>1>(h_>1>)Δh_>1>+…+F_>n>(h_>n>) Δh_>n>.

Данную сумму называют интегральной суммой функции F(h) на отрезке [0; H]. При этом предполагается, что функция F(h) непрерывна на отрезке [0; H] и может принимать любые значения. Если и высоты "элементов" стремятся к нулю, то точное выражение суммы равно . Его называют определенным интегралом от функции F(h) на отрезке [0; H] и обозначают .

Далее понятие определенного интеграла обобщается на произвольную непрерывную функцию F(x) и произвольный отрезок [a; b].

Рассмотрим несколько задач с физическими моделями, где интеграл определяется как приращение первообразной.

1. Задача о перемещении точки.

Пусть v=v(t) скорость прямолинейного движения точки, заданная на некотором промежутке времени [t_>1>; t_>2>]. При этом пусть v(t)>0. Как выразится длина пути, пройденного точкой за данный промежуток времени?[5]

Обозначим координату движущейся точки в момент t через S(t). Тогда, так как движение при v>0 происходит только в положительном направлении (или иначе, т. к. S(t) – функция возрастающая, ввиду того, что ), то искомое расстояние будет выражаться числом S(t_>2>)-S(t_>1>). С другой стороны S(t) есть первообразная функции v(t) (). Таким образом вычисление длины пути, пройденного точкой за данный промежуток времени, сводится к отысканию первообразной S(t) функции v(t), т. е. к интегрированию функции v(t).

Разность S(t_>2>)-S(t_>1>) называют интегралом от функции v(t) на отрезке [t_>1>; t_>2>] и обозначают так:

Импульс силы.

Пусть на тело массой m в течение времени t действует какая-то сила F(t). Найти количество движения тела при заданной зависимости силы от времени за промежуток времени [t_>1>; t_>2>].

Как известно из физики второй закон Ньютона в импульсном представлении выражает уравнение

ΔР=FΔt.

Произведение P=mv(t) массы на скорость называется "количеством движения". Так как скорость тела зависит от времени, то за промежуток времени [t_>1>; t_>2>] искомое количество движения может быть найдено так: Р(t_>2>)-Р(t_>1>). С другой стороны Р(t) есть первообразная функции F(t). Таким образом вычисление количества движения тела за данный промежуток времени, сводится к отысканию первообразной Р(t) функции F(t).

Разность P(t_>2>)-P(t_>1>) называют интегралом от функции F(t) на отрезке [t_>1>; t_>2>] и обозначают так:

Величина называется также "импульсом силы" за время [t_>1>; t_>2>]. Словесная формулировка результата: изменение количества движения равно импульсу силы.

Количество электричества.

Представим себе переменный ток, текущий по проводнику. Вычислим количество электричества, протекающего за интервал времени [a; b] через сечение проводника. Если бы сила не менялась со временем, то изменение количества электричества q равнялось бы произведению I(b-a). Пусть задан закон изменения I=I(t) в зависимости от времени. Тогда количество электричества, протекающего за интервал времени [a; b], равно q(b)-q(a). С другой стороны на малом промежутке времени можно считать силу тока постоянной и равной I(t), а dq=I(t)dt, следовательно, вычисление количества электричества за данный промежуток времени, сводится к отысканию первообразной функции I(t).

Разность q(b)-q(a) называют интегралом от функции I(t) на отрезке [a; b] и обозначают так:

Вытекание воды из сосуда

Данная задача проста и наглядна в своей постановке для учащихся.

Представим себе сосуд, из которого вытекает вода. В момент времени t поток воды вычисляется по формуле q=q(t). Найдем объем воды, вытекающей из сосуда за промежуток времени [t_>1>; t_>2>]. Объем воды, находящейся в сосуде, обозначим через V. Этот объем со временем меняется, т. е. V есть функция времени t.

Рассмотрим промежуток времени [t_>1>; t_>2>]. Очевидно, что за это время из сосуда вытечет V(t_>2>)-V(t_>1>) воды. С другой стороны, поток воды – это величина, характеризующая скорость изменения количества воды в сосуде, т.е. dV=q(t)dt. Следовательно, вычисление объема воды, вытекающей из сосуда за промежуток времени [t_>1>; t_>2>], сводится к отысканию первообразной функции q(t).

Разность V(t_>2>)-V(t_>1>) называют интегралом от функции q(t) на отрезке [t_>1>; t_>2>] и обозначают так:

Все вышерассмотренные модели – это наиболее часто встречающиеся в школьном курсе физики законы и формулы, поэтому они не требуют от учащихся дополнительных знаний по физике, а, следовательно, удовлетворяют как принципу научности, так и принципу доступности материала.

Зачетное занятие было проведено нами в форме обобщающего урока по теме "Первообразная. Интеграл", проведенный с помощью мультимедийной презентации.

Обобщающий урок по теме "Первообразная. Интеграл".

Цель: обобщить и систематизировать знания по теме "Первообразная. Интеграл"

Задачи:

Обучающие: обобщение и систематизация знаний учащихся, закрепление основных понятий базового уровня.

Развивающие: развитие познавательных потребностей учащихся, логического мышления и внимания, формирование потребности в приобретении знаний.

Воспитательные: воспитание сознательной дисциплины и норм поведения, воспитание ответственности, умения принимать самостоятельные решения.

Оборудование: мультимедийный проектор, презентации.

План урока

Организация начала урока.
Обобщение и систематизация знаний и способов деятельности
Подведение итогов урока

Ход урока

1. Организация начала урока.

Проверка домашнего задания с места (фронтально).

Сегодня на уроке мы должны обобщить все знания и умения по теме "Первообразная и интеграл" с целью подготовки к контрольной работе. Начнём повторение мы с устной работы, затем проведём групповую работу, которая откроет нам некоторые исторические факты. Вспомним вычисление площадей фигур, а также повторим, где используют интеграл в физике. В заключении урока проведём самостоятельную работу по перфокартам.

Устная работа (фронтально).

1)На экране спроецирована таблица для устного счёта. Для функций, указанных в таблице, составить хотя бы одну первообразную. (Таблица в презентации).

2) Устное повторение теоретического материала (фронтально):

- Дайте определение первообразной.

- Как читается основное свойство первообразной?

- Какие правила нахождения первообразной существуют?

- Что называется неопределённым интегралом?

- Что называется криволинейной трапецией?

- Как выглядит формула Ньютона – Лейбница?

- В чём состоит геометрический смысл определенного интеграла?

- В чём состоит физический смысл определенного интеграла?

3)Верно ли? На слайде для каждой функции f(x) записана первообразная F(x), но в записи первообразной есть ошибка. Найдите ошибку и прокомментируйте.

f(x)=(8x-5)², F(x)=(8x-5)³/3+C

Ответ: не хватает перед первообразной множителя 1/8так, как функция f(x) сложная.

f(x)=sin(5+4x), F(x)= -1/5cos(5+4x)+C

Ответ: перед первообразной должен быть множитель1/4, а не 1/5так, как коэффициент к=4.

Ответ: не хватает перед первообразной множителя 2.

2. Обобщение и систематизация знаний и способов деятельности

1а) Групповая работа над темой. На экране через проектор с компьютера проецируются портреты математиков: 1 - Лейбница, 2 - И. Бернулли, 3 - Ферма, 4 – Я. Бернулли, 5 - Ньютона. Класс делится на пять групп. Каждая группа получает карточку со своим заданием: найти значение постоянной С. На этой же карточке дана историческая справка о вкладе конкретного учёного в развитие теории интегрального исчисления. Вычислив значение С, каждая группа связывает это число с номером портрета математика. Представитель от группы зачитывает историческую справку для других. (Портреты в презентации, задания для групп в приложениях 1 и 2).

1б) Продолжим групповую работу. Установить соответствие.

На экране три функции f,g,h и три графика первообразных для данных функций. Для каждой функции записать первообразную и найти график этой первообразной. Решают все на месте в тетрадях также группами, затем озвучивают результаты.

1. f(x)=sinx, 2. g(x)=cosx, 3. h(x)=cos2x

Решение:

F(x)= -cosx+C, G(x)=sinx+C, H(x)=0,5 sin2x+C

2) Устно. Первообразная тесно связана с интегралом. Мы с вами вспоминали формулу Ньютона – Лейбница. Вы знаете, что определённый интеграл используют для вычисления площадей плоских фигур, и в первую очередь для вычисления площади криволинейной трапеции.

Посмотрим на экран и выясним являются ли фигуры криволинейными трапециями.

Физкультминутка

3) Работа у доски. Три ученика выходят к доске и получают карточки с заданием вычислить площадь фигуры. Остальные учащиеся на местах решают две задачи на нахождение площади фигур, затем правильность решения проверяется с помощью проектора.

Задание классу.

Учебник №360(г), №364(г).

Задание 1 ученику - №365(в),

Задание 2 ученику - №365(г),

Задание 3 ученику - №361(б).

4) Работа у доски.

Определённый интеграл используют и в других дисциплинах. Например, на уроках физики с помощью определённого интеграла можно вычислить работу переменной силы, массу, центр масс, электрический заряд, перемещение и количество теплоты.

Задача 1.Сила упругости пружины, растянутой на 6 см, равна 4,2 Н. Какую работу надо произвести, чтобы растянуть пружину на 6см?

Решение:F=kx;

4,2=k*0,06;

k=420:6;

k=70, F=70x

5) Контролирующая самостоятельная работа по перфокартам.

В каждом варианте 6 заданий. К каждому заданию 4 варианта ответов, только один из них правильный. У каждого ученика на парте лежит контрольный талон. Решив задание в тетради, уч – ся выбирает номер верного ответа и зачёркивает его в контрольном талоне. После выполнения всех 6 заданий в каждом контрольном талоне будет зачёркнуто 6 чисел. Ученики сдают талоны учителю, который при помощи шаблона с прорезями быстро проверяет работы, накладывая шаблон на талон.

Контрольный талон

Фамилия, имя Класс вариант
1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25

Шаблон для проверки

1 вариант

		Х
	Х		X

Х				X
			X

2 вариант

X
	Х		X
		X
		X
		X

Знак "Х" означает места прорезей в шаблоне.

Оценка результатов:

6 крестиков верных – "5";

5 крестиков верных – "4";

4 крестика верных – "3";

3 и меньше – "2".

6) Индивидуальное проблемное задание для тех, кто быстро справился с самостоятельной раньше других:

При каком положительном значении параметра а площадь фигуры, ограниченной линиями y= 1/x², y=0, x=1, x=a равна 7/8?

3. Подведение итогов урока

Подводится итог урока. Цель нашего урока была обобщить знания по теме "Первообразная. Интеграл." Давайте посмотрим как мы работали. На экран с помощью проектора выводится таблица. Поднимите руку, если вы

- знаете таблицу первообразных;

- умеете пользоваться таблицей для нахождения первообразной сложной функции;

- легко находите площадь криволинейной трапеции;

- умеете применять интеграл для решения физических задач.

Те, кто поднял руку на все вопросы, готовы к выполнению контрольной работы. Остальным надо подготовиться лучше. Выставляются оценки за работу на уроке. Задаётся домашнее задание.

Для развития познавательной потребности нами предлагается во внеклассной форме работы использование различных видов уроков для развития познавательной потребности учащихся. Мы, например, использовали урок-КВН (см. приложение 1).

Урок КВН по теме "Интеграл"

Цель: обобщение изученного материала по теме, формирование умений применять математические задания к решению практических задач.

Задачи:

Развивающие: развитие познавательной потребности, творческих способностей.

Воспитательные: воспитание интереса к предмету, воспитание чувства коллективизма и взаимовыручки.

КВН проводится интерактивно с помощью сайта школы.

На экране ЭВМ написано:

I команда

II команда

(Ниже ведётся запись полученных очков).

Правила игры.

Класс разбивается на две команды.

Выбираются капитаны команд.

Капитаны назначают консультантов.

Для участия во всех видах работы ученики вызываются к доске капитанами команд.

Ход урока.

1 этап. Разминка – ведется на бумажном носителе.

На экране ЭВМ написаны задания.

II этап. Блиц – турнир – проводится с помощью ЭВМ (желательно применение проектора).

III этап. Домашнее задание.

К доске приглашаются по 1 ученику от каждой команды.

1. С помощью интеграла вывести формулу объёма конуса.

2. С помощью интеграла вывести формулу объёма шара.

IV этап. Конкурс капитанов.

V этап. Конкурс болельщиков – задания проектируются на доску с помощью проектора, а также дублируются на сайте школы.

VI этап. Конкурс эрудитов - задания проектируются на доску с помощью проектора, а также дублируются на сайте школы

1. Вычислите:

2. Вычислите:

Решение 1.

Пусть

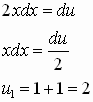
Решение 2.

Пусть

VII этап. Конкурс консультантов. (дополнительный) – проводится при помощи Mathcad.

VIII этап. Подведение итогов.

Выигравшая команда объявляется победительницей, а многие учащиеся получают оценки.

Итак, применение информационных технологий в преподавании темы "Интегралы":

Содействует воспитанию аккуратности, организованности, дисциплины;
Формирует умения работать коллективно, в группе, паре, самостоятельно;
Прививает интерес к предмету посредством применения современных информационных технологий;
Способствует развитию интеллектуальных качеств личности школьника: самостоятельность, гибкость, способности видеть проблему, обобщать, переключаться с одного вида работы на другой;
Развивает эмоции учащихся, создавая эмоциональные ситуации удивления, сопереживания;
Развивает познавательный интерес, создавая игровые ситуации.

2.3 Результаты экспериментальной работы

Для исследования сформированности познавательной потребности школьников нами был подобран комплекс методов: "Познавательный интерес", "Познавательная потребность", "Мое учение".

Для выявления познавательного интереса была применена методика "Познавательного интереса", целью которой является установление характера и силы познавательного интереса (см. приложение 2). Анализ результатов данной методики приведены в таблице 5.

Таблица 5 Анализ результатов констатирующего и контрольного срезов изучения уровня познавательного интереса

Из таблицы 4 видно, что произошла динамика в характере и силе познавательного интереса у учащихся к учебе. У учеников увеличился интерес к учебе, приблизительно 1,25 раз. Наиболее наглядно, полученные данные можно увидеть на диаграмме 1.

Диаграмма 1 Уровень познавательного интереса

Для изучения познавательной потребности была применена методика "Познавательная потребность", целью которой является установление интенсивности познавательной потребности у учащихся (см.приложение 2, анкета 2). Анализ полученных данных помещен в таблицу 6.

Таблица 6 Анализ результаты изучения познавательной потребности школьников

Как мы видим, из таблицы 6, произошла динамика роста познавательной потребности:

Увеличилась умственная работа школьников, при задании на сообразительность учащиеся предпочитают самостоятельный поиск ответа (+6%), стали больше читать дополнительной литературы (+10);
На 16% увеличилось эмоциональное отношение учащихся к интересным занятиям, связанным с умственной работой.
Учащиеся стали чаще задавать вопросы, что свидетельствует о возросшем интересе к учебному материалу.

Этот факт наглядно демонстрируют диаграммы 2-3.

Диаграмма 2 Частота умственной работы

Диаграмма 3 Отношение школьника к вопросу на сообразительность

Для выявления отношения школьников к учению, предметную направленность их познавательных интересов, изучить некоторые особенности процесса самостоятельной деятельности учащихся мы воспользовались методикой "Мое учение" (см. приложение 2, анкета 3). Результаты этого исследования представлены в таблице 7.

Таблица 7 Сравнительный анализ результатов методики "Мое учение" (в %)

Этап	I	III	IV	V
1	2	3	1	2	3
Констатирующий	92	0	8	20	68	12	76	24
Контрольный	96	0	4	12	80	8	64	36

Этап	VI	VII
1	2	3	1	2	3	4	5	6
Констатирующий	60	4	12	0	24	60	28	12	68
Контрольный	24	76	0	8	0	20	56	24	24

Из таблицы 7 видно, что на 4 % увеличилось число учащихся, которым интересно учиться в школе; на 12 % возросло число учеников, чувствующих себя всегда спокойно при выполнении самостоятельных работ и 44 % учеников научились правильно распределять время при выполнении самостоятельных работ.

В процессе опытно-экспериментальной работы выявлены два наиболее значимых направления использования информационных технологий в образовании: как средства обучения и как инструментов познания. Первый подход таит в себе ряд проблем, связанных с усвоением уже готовой информации, при котором отсутствует творческая компонента усвоения. Другой подход – использование компьютерных средств как инструментов познания является наиболее продуктивным подходом к обучению, Инструментами познания являются различные компьютерные средства, предназначенные для организации и облегчения процесса познания. Именно с таким подходом связывается дальнейшее развитие использования информационных технологий в обучении. В этом случае учащийся под управлением преподавателя проходит путь познания самостоятельно, а не является потребителем уже готовых знаний, что способствует более глубокому и осознанному усвоению материала, развитию умений разрабатывать учебные компьютерные программы.

Экспериментальная проверка показала, что разработанная методика обучения учащихся 10-11 классов способствует повышению у учащихся уровня знаний в области интегрального исчисления; уровня познавательной потребности; готовности к использованию информационных технологий в будущем.

Использование компьютера в качестве средства обучения путем применения прикладных программ в качестве формализмов представления знаний способствует более быстрому и более полному усвоению материала, чем при использовании всех имеющихся в настоящее время обучающих компьютерных программ.

Сравнительный анализ контрольного констатирующего среза показали, что произошла динамика роста, хоть и не значительная. Таким образом, наша гипотеза подтвердилась.

Заключение

Итак, познавательная потребность – это, прежде всего потребность в новой информации, однако сама новая информация может выступать в самых различных формах: в новом стимуле (новый цвет предмета, неожиданный звук, необычная форма), в новом знании о предмете (его назначение, устройство и т.д.), и наконец, в новой системе представлений о мире (научные знания, наука в целом). И самые элементарные и самые сложные способы удовлетворения познавательной потребности в целом характеризуют одну и ту же познавательную потребность, однако в зависимости от этих способов различаются уровни развития познавательной потребности.

В классных коллективах, где познавательная потребность достигает такого уровня развития, встречаются отдельные учащиеся, у которых она перерастает в страсть, в жажду раздумий над предметом. Это обычно учащиеся с выдающимися способностями.

Современный этап применения информационной технологии обучения в учебном процессе заключается в использовании компьютера как средства обучения не эпизодически, а систематически с первого до последнего занятия при любом виде обучения. Основная проблема при этом заключается в методике компьютеризации курса, который предстоит освоить обучаемому. Возможна либо полная перестройка и ориентация на создание новых компьютеризованных курсов, либо реализация методики с частичной компьютерной поддержкой курса. Другими словами речь идет о форме компьютерной поддержки процесса обучения. В настоящее время практика использования информационных технологий в образовании обнаруживает две тенденции:

- применение промышленных универсальных информационных программ, предназначенных для решения широкого круга практических и научных задач из различных предметных областей, и адаптированных к учебным дисциплинам;

Использование информационных технологий в обучении позволяет у большинства детей со склонностями к техническим наукам развить устойчивый интерес к данным предметам. При этом решается ещё одна задача образовательного процесса - его гуманизация. Каждый ребенок находит себе задание по своим силам, уровню подготовки и интереса.

Для исследования познавательной потребности нами была подобрана система методов. Данное исследование проводилось в три этапа: констатирующий формирующий и контрольный.

По результатам проведенных методик мы увидели, что произошла динамика роста познавательной потребности: приблизительно на 4,5% увеличилась умственная работа школьников, при задании на сообразительность, учащиеся предпочитают самостоятельный поиск ответа, стали больше читать дополнительной литературы, так же приблизительно на 4,5% увеличилось эмоциональное отношение к интересным занятиям, связанным с умственной работой. Учащиеся стали чаще задавать вопросы, что свидетельствует о возросшем интересе к учебному материалу, таким образом, наша гипотеза подтвердилась.

Список литературы

Азевич А.И. Несколько компьютерных программ. //Математика в школе. – 2002. - №10. – С.41-43.
Алимов Ш. А. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк./ Ш. А. Алимов, Ю. М. Колягин, Ю.В. Сидоров и др. - М.: Просвещение, 1993. – 254 c.
Анастази А. Психологическое тестирование. Кн. 2: Пер. с англ./Под ред. Туревича К.М., Лубовского В.И. – М.: Педагогика, 1982. – 365 с.
Аут К.Х., Виленкин Н.Я. О роли основных принципов дидактики в преподавании школьного курса математики. //Математика в школе. – 1987. - №1. - С.41-47.
Ахметгалив А. Мотивация деятельности на уроках математики. //Математика в школе. – 1996. - №2. – С.57-62.
Барчунова Ф. Развитие познавательного интереса к геометрии учащихся VI–VII классов. //Математика в школе. – 1974. - №6. – С.21-28.
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1992. – 351 с.
Белова О.Е. Об использовании компьютерных технологий в процессе изучения темы "Определенный интеграл и его приложения" //Математическая и методическая подготовка студентов педвузов и университетов в условиях модернизации системы образования: Материалы XXII Всероссийского семинара преподавателей математики педвузов и университетов – Тверь: Изд-во ТГУ, 2003.
Белова О.Е. Особенности методической системы обучения интегральному исчислению студентов педвузов на основе использования информационных технологий //Вестник КрасГУ (Гуманитарные науки). – Красноярск: ИЦ КрасГУ, 2006. – Вып.3. – С.81–84.
Берман Г. Н. Сборник задач по курсу математического анализа: Уч. пособие. - СПб.: Изд-во "Профессия", 2001. – 432 с.
Божович Л.И. Проблемы развития мотивационной сферы ребенка. В кн.: Изучение мотивации поведения детей и подростков /Под ред. Л.И. Божович, Л.В. Благонадежной – М., 1972.
Бокуть Л.В. Компьютерные технологии для эффективной познавательной деятельности. //Минск: Материалы международной научно - метод. конф. "Высшее техническое образование: проблемы и пути развития", - 2004. - С.166-167.
Будунов Г. М. Компьютерные технологии в образовательной среде: "за" и "против". – М.: АРКТИ, 2005. – 234с
Виленкин, Н. Я., Куницкая, Е. С., Мордкович, А. Г. Математический анализ. Интегральное исчисление: Уч. пособие для студентов-заочников II курса физико-математических факультетов педагогических институтов. - М.: Просвещение, 1979. – 175 с.
Виштынецкий Е.И. Применение информационных технологий в сфере образования и обучения [Электронный ресурс] Режим доступа: http://www.snfpo.ru/help/articles/a1.htm
Выготский Л.С. Собрание сочинений: В 6 томах. Том 4. Детская психология /Под ред. Эльконина Д.Б. – М.: Педагогика, 1984. – 432 с.
Гальперин П.Я., Котик Н.Р. К психологии творческого мышления //Вопросы психологии. – 1982. - №5. – С. 23-26.
Гузеев В.В. Инновационные идеи в современном образовании //Школьные технологии. – 1997. – №1. - С.47-52.
Давыдов В.В. Теория развивающего обучения. - М.: Педагогика, 1986.-240 с.
Дразкин И.Е. Опыт системы преподавания математики. //Математика в школе. – 1996. - №6. – С.35-39.
Дружинин В.Н. Психология общих способностей.–СПб.: Питер, 1999.–368 с.
Дьюи Д. Психология и педагогика мышления. /Пер. с англ. Николаевой Н.М., под ред. Виноградова Н.Д. – М.: Совершенство, 1997. – 208 с.
Задачи как средство обучения алгебре и началам анализа в X классе [Текст]: Уч. Пособие //Сост. Е. С. Канин. – Киров: Редакционно-издательский совет Кировского ГПИ имени В. И. Ленина, 1985. – 92 c.
Задачник по курсу математического анализа: Уч. пособие для студентов заочн. отделений физ.-мат. фак-тов пединститутов. Ч. I //Под ред. Н. Я. Виленкина. – М.: Просвещение, 1971. – 343 с.
Захарова И.Г. Информационные технологии в образовании: Учебное пособие для студ. высш. пед. учеб. заведений. - М.: Издательский центр "Академия", 2003. – 192 с.
Зельдович, Я. Б. Высшая математика для начинающих и её приложения к физике: Уч. пособие для физико-математических средних школ и проведения факультативных занятий. – М.: Наука, 1970. – 560 с.
Интернет в гуманитарном образовании: Учеб. Пособие для студ. вузов /Под ред. Е.С.Полат. — М.: Гуманит. Изд. Центр ВЛАДОС, 2001. — 272 с.
Капустина Т.В. Компьютерная система "Mathematica 3.0" //Математика в школе. - 2003. - №7. – С. 35-37.
Кастро К., Альфтан Т. Компьютеры во внешкольном образовании //Перспективы: вопросы образования. - М., 1991. - № 2. – С. 45-49.
Кларин М.В, Инновационные модели обучения в зарубежных педагогических поисках. Пособие к спец. курсу для вузов, институтов усовершенствования учителей, повышения квалификации работников образования. - М.: Арена, 1994. – 128 с.
Когаловский М.Р. Перспективные технологии информационных систем. – М.: Мастерство, 2001. –256 с.
Кождаспирова Г.М., Коджаспиров А.Ю. Педагогический словарь. – М.: ACADEMIA, 2000.
Колмогоров, А. Н. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. – М.: Просвещение, 1998. – 365 c.
Косов Б.Б. Творческое мышление восприятие и личность. – М.: "Институт практической психологии", Воронеж: НПО "МОДЕК", 1997 –47 с.
Краткий психологический словарь /Ред.-сост. Л.А.Карпенко; /Под общ. ред. А.В.Петровского, М.Г.Ярошевского. - 2-е изд. - Ростов н/Д: Феникс, 1998. - 512 с.
Кривоногов В.В. Нестандартные задания по математике: 5-11 классы. – М.:Издательство "Первое сентября", 2003. – 224с
Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение, 1968 – 432с.
Кузьмина В.Г. Активизация познавательной деятельности учащихся. //Математика в школе. – 1996. - №4. – С.12-16.
Кухарь А.В. Некоторые пути формирования познавательного интереса у учащихся IV–V классов. //Математика в школе. – 1985. - №5. – С.20-26.
Леонтьев А.Н. Избранные психологические произведения: В 2 т. – Т II. – М., 1983. – 467 с.
Математика 10-11 классы: методическое пособие для учителя / И.И.Зубарева, А.Г. Мордкович. – 3-е изд., испр. – М.: Мнемозина, 2008. –104с.
Математика 10-11 классы: развернутое тематическое планирование. Линия Г. В. Дорофеева / авт.-сост. Т.Н. Видеман. – Волгоград: Учитель, 2009.– 71 с.
Математика. 11 класс: Поурочные планы по учебнику Н.Я. Виленкина, В.И. Жохова. II полугодие /Авт.- сост. Л.А. Тапилина, Т.Л. Афанасьева. – Волгоград.: Учитель, 2005. – 144 с.
Мигунова Н.П. Некоторые приемы активизации познавательной деятельности учащихся. //Математика в школе. – 2000. - №6. – С.10-15.
Мордкович А. Г. Алгебра и начала анализа [Текст]: Учеб. для 10-11 кл. общеобразоват. учреждений. Ч. I. – М.: Мнемозина, 2003. – 375 с.
Никольский С. М. Алгебра и начала анализа [Текст]: Учеб. для 11 класса общеобразоват. учреждений/ С. М. Никольский, М. К. Потапов. - М.: Просвещение, 2003.
Нифагин В.А., Бокуть Л.В. Обучение математическому моделированию на основе электронных пособий. //Минск: Материалы II-й международной научно-метод. конф. "Дистанционное обучение - образовательная среда XXI века", 2002. - С.122-123.
Новые педагогические и информационные технологии в системе образования: Учебное пособие для студентов пед. вузов и системы повышения квалификации пед. кадров / Е.С. Полат, М.Ю. Бухаркина, М.В. Моисеева, А.Е. Петров; Под ред. Е.С. Полат. – М.: Издательский центр "Академия", 2003. – 272 с.
Овечкина О.И. Приемы активизации познавательной деятельности. //Математика в школе. – 1993. - №5. – С.4-8.
Программы для общеобразовательных учреждений. Математика. – МОРФ. – 63 с.
Ретинская И.В., Шугрина М.В. Отечественные системы для создания компьютерных учебных курсов //Мир ПК. — 1993. — № 7.- С 12-14
Роберт И.В. Современные информационные технологии в образовании: дидактические проблемы; перспективы использования. М.: Школа-Пресс. 1994.— 205 с
Рубинштейн С.Л. Основы общей психологии. В 2 т. – Т 1 –М.,1989. – 720 с.
Скатецкий В.Г. Организационно-методические связи преподавания математики на факультетах нематематического профиля // Высшая школа. 1999, № 2, С. 45-49.
Старцева Н.А. Применение электронных пособий на уроках математики //Информационные технологии в образовании. Сб. научно - методических материалов. - Новосибирск: НГУ, 2004. – С.23 -26
Тихомирова О.К. Познавательная потребность. //Сб. "Проблемы формирования социогенных потребностей". Тбилиси, 1974, с. 102—105.
Хохлова Н.М. Информационные технологии. - М.: Приор-издат, 2007.–192 с.
Хрестоматия по общей психологии. Психология мышления /Под ред. Ю.Б.Гиппенрейтер, В.В.Петухова. – М., МГУ, 1987. –276 с.
Хуторской А.В. Интернет в школе: Практикум по дистанционному обучению. - М.:ИОСО РАО, 2000. - 304 с.
Черников Б.В. Информационные технологии управления: учебник. – М.:ИД "ФОРУМ" : ИНФРА – М, 2009. – 352 с.
Черняк А.А., Черняк Ж.А., Доманова Ю.А. Высшая математика на базе MATHCAD. Общий курс. - С-Пб: БХВ-Петербург, 2004. -54 с.
Яковлева Е.А. Развитие творческого потенциала у школьников. //Вопросы психологии. – 1997. - №2. - С.37-42.

Приложение 1

Урок 1

Тема: Интеграл. Площадь криволинейной трапеции.

Задачи урока:

Обучающая: создать условия для формирования представления о площади криволинейной трапеции и интеграле.

Развивающая: развивать познавательную потребность учащихся.

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данный урок носит ознакомительный характер, ученики знакомятся с понятиями "площадь криволинейной трапеции", "первообразная", "интеграл". Тема рассчитана на 2 часа.

План урока:

1.Организация начала урока.

2.Постановка проблемы урока.

3.Актуализация ЗУН, необходимых для творческого применения знаний.

4.Формирование новых понятий и способов действий

5.Обобщение и систематизация знаний и способов деятельности

6.Усвоение образца комплексного применения ЗУН

7.Применение знаний умений и навыков в новых условиях

8.Подведение итогов урока

Ход урока:

Сообщение учащимся темы и целей урока: Тема нашего сегодняшнего урока: Интеграл. Площадь криволинейной трапеции (Слайд 1).

Исторические сведения об интеграле (Слайд 2):

Введение понятия "интеграл".

Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x_>0> = а<x_>1> < x_>2> < … <x_>n-1> < x_>n> = b и пусть , где k = 1, 2, ..., n — 1, n. На каждом из отрезков [x_>k-1>; x_>k>] как на основании построим прямоугольник высотой F(x_>k-1>). Площадь этого прямоугольника равна:

а сумма площадей всех таких прямоугольников равна:

, т. е.

при n→∞

Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 - х2 и у = 0

Решение:

1. Построим криволинейную трапецию:

у = 4 - х2

- квадратичная функция, график – парабола, ветви направлены вниз.

у = 0 - ось абсцисс.

2. Найдём [а;b]:

4-х2 = 0;

х2 = 4

х = -2 или х = 2, т. е. а = -2 b = 2

3. Найдём площадь криволинейной трапеции по формуле:

S = F(b) – F(а)

Домашнее задание (Слайд 10).

Урок 2

Задачи:

Развивающая: развивать познавательную потребность учащихся.

Содержание урока: Данная тема рассчитана на два часа и состоит из двух частей: часть 1 – "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel". Вторым часом нами был проведен интегрированный урок (физика + математика) по теме "Применение интеграла при решении физических задач"

Оборудование: интерактивная доска, рабочий листок для каждого ученика, тесты, подготовленные страницы флипчарта, лото компьютер с установленной программой MS Office 2003.

План урока:

Организация начала урока.
Постановка проблемы урока.
Актуализация ЗУН, необходимых для творческого применения знаний.
Контроль и самоконтроль знаний, умений и навыков по теме интеграл
Формирование новых понятий и способов действий
Обобщение и систематизация знаний и способов деятельности
Усвоение образца комплексного применения ЗУН
Применение знаний умений и навыков в новых условиях
Подведение итогов урока

Ход урока:

Каждый из учащихся до урока получает рабочий листок ученика (см. в конце плана урока), на котором записаны этапы урока. Это может позволить учащимся работать в удобном им ритме. Именно в нём учащийся выполняет задания, и после урока лист сдаётся. Часть заданий можно проверить с помощью компьютера или интерактивной доски на уроке. Учащиеся могут выполнять задания в любой удобной для них последовательности. Выбор заданий самостоятельной работы (лото) также произволен, по договорённости с членами группы, которая может формироваться произвольно. Варианты самостоятельной работы можно составить различными по степени трудности для учёта индивидуальных особенностей учащихся. На уроке предусмотрена работа в парах и группах. Объём выполненной работы на уроке и степень самостоятельности оценивается учителем по рабочему листу ученика.

Необходимые для выполнения на уроке задания разнообразны по форме подачи условия (текст, лото, тест, игровые моменты), позволяют развивать творческую и мыслительную деятельность учащихся сформировать:

Умение применить знания на практике
Умения чётко и ясно излагать свои мысли

I. Организационный момент.

Сегодня мы заканчиваем изучение темы "Интеграл". Мы познакомились с понятием интеграл, узнали о его применении для вычисления площадей фигур. На сегодняшнем уроке мы ещё раз пролистаем страницы применения этого математического понятия. А также научимся вычислять определенный интеграл с помощью компьютерных программ.

II. Актуализация знаний

Карточка №1 Найти пары чисел а и в, при которых функция f(x) удовлетворяет условиям

f(x)= ах²–в, = 6, f ' (3) = 48

Решение:

f ' (x)=2ах; 6а = 48; а = 8,

===

=6, в=18

Карточка №2 Вычислить интеграл, используя его геометрический смысл.

Решение: у=,

у 0

у²=2х – х², (х-1)²+ у²=1

Это уравнение окружности с центром (1;0) и радиусом R=1. Площадь круга данного радиуса S_>кр>= R²= . Учитывая, что у 0

= =

Карточка №3

При каком значении а (1/2< а <18) S_>1>S_>2>?

Решение:

S_>1>=

S_>2=>

По условию S_>1> S_{>2 ,}> значит lna+ln2 ln18-lna_>
,>

2 lna 9; а² 9; -3 а 3

Учитывая условие 1/2< а <18, получаем 1/2< а <3.

Как вы считаете, что нужно знать, чтобы вычислить площади фигур?
Дайте определение первообразной функции, неопределенного интеграла.

Дайте определение определенного интеграла. Запишите формулу, по которой он вычисляется? Чье имя носит эта формула? (Можно сообщить заранее подготовленную историческую справку о И. Ньютоне и Г. Лейбнице. (см. Слайд 1 – слайд демонстрируется на компьютере, дфомируется с помощью MS Power Point)

Предложите способ вычисления указанных интегралов (устно) (Слайд 2).

Задание 2 Вычисление определенного интеграла с помощью таблицы Excel. Данное задание дается с целью уяснения учащимися сущность метода численного решения задачи и овладеть первичными навыками составления, ввода, трансляции, отладки, исполнения и оформления задачи в табличном редакторе.

Для численного вычисления определенного интеграла методом трапеций используется формула:

Пусть требуется вычислить определенный интеграл

табулируйте подинтегральную функцию в диапазоне изменения значений аргумента 0 – 3 (см. рис.).

в ячейку С3 введите формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2+C2, которая реализует подинтегральную функцию.
Скопируйте буксировкой формулу, записанную в ячейке С3 до значения аргумента х = 3. Вычисленное значение в ячейке С17 и будет величиной заданного интеграла - 9.

Вычислите интегралы, работая парами. Выбирая соответствующую ответу букву, вы прочтете фамилию французского математика, который дал определение интеграла как предела интегральных сумм. (ответ: Огюстен Луи Коши. 1789-1857).

Дайте определение криволинейной трапеции (Слайд 3). Среди фигур, изображенных на рисунке, выбрать криволинейную трапецию. /Ответ:1,3,5/

Вспомните, как вычисляется площадь криволинейной трапеции. Запишите формулу для площади. Как можно вычислить площади фигур в случаях 2,4,6?

Работа в группах (по 4 человека) Задание: вычислить площади криволинейных трапеций – игра "Лото". (см. Слайд 4).

Справившиеся с заданиями учащиеся могут приступить к выполнению заданий IV и V в рабочем листе урока.

Задание IV. Вычислить площадь фигуры, ограниченной графиком функции

у=|-х²-4х -3|, осью ОХ.

Решение: -х²-4х -3 0, координаты вершины х_>0>= -2;у_>0>=1

Площадь заштрихованной фигуры

S= = -(=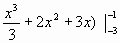1

Задание V.

При каком значении а числа S_>1,>S_>2>, S_>3>образуют три последовательных числа арифметической прогрессии. Найти разность этой прогрессии.

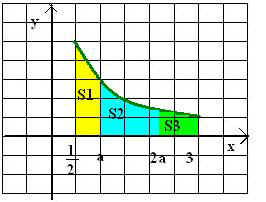
Решение:

S_>1>=2 -

S_>2>= -

S_>3>= -

Согласно свойству арифметической прогрессии

2S_>2>= S_>1>+ S_>3,>т.е.

2( - )= 2 - + - ; =; а=

S_>1>=; S_>2>=

Разность прогрессии

d= S_>2>- S_>1>=-

Подведение итогов урока. Выяснить наличие вопросов, которые появились при решении рассмотренных на уроке задач, а также учитель просит ребят оценить свою работу на уроке, на сколько она была плодотворной, что было на уроке удачным, а что нет.

Слайд 1 - Познай секреты математики:

"Интеграл. Вычисление площадей с помощью определённого интеграла"

"Закодируй ответ"

Определите фамилию французского математика, который дал определение определенного интеграла как предела интегральных сумм.

"Да, много решено загадок

от прадеда и до отца,

и нам с тобой продолжить надо

тропу, которой нет конца"

(В. Ноздрёв, профессор)

"Лото" Вычисли площадь криволинейных трапеций.

IV.Вычислите площадь фигуры, ограниченной графиком функции

у=|-х²- 4х-3| и осью ОХ.(рисунок)

При каком значении а числа S_>1,>S_>2,>S_>3>образуют три последовательных члена арифметической прогрессии. Найти разность этой прогрессии.<рисунок>

Слайд 2

1. (ответ: 1/4)

2. (ответ )

3. (ответ: 1-ln2)

4. (ответ: 2+ln3)

можно расположить за "шторкой" на интерактивной доске. После обсуждения методов решения, "шторку" открыть.

Слайд 3

Слайд 4

Ответы к Слайду 4

1
1
2
4,5
4ln2
6-2
0,5

1	1	2
4,5	4ln2	6-2	0,5

Правила игры "Лото". Учитель готовит 5-6 больших карт, разделенных на прямоугольники с записанными на них ответами, и соответственное количество карточек с примерами. Большие карты раздаются группам играющих. Дается время, в течение которого ребята, разделив по своему усмотрению карточки, выполняют задания (можно всей группе решать одно и то же задание, затем сверять). Найдя на большой карте ответ, который считает правильным группа, накрывают им задание. Выигрывает та группа, которая раньше всех накрыла все клетки своих карт. Чтобы проверить правильность решения, учитель переворачивает карточки и тогда, если все ответы верны, должна получиться картинка, которую предварительно рисуют на всех маленьких карточках (сначала рисуют картинку, потом пишут задания, а затем их разрезают).

Урок 3

Интегрированный урок (физика + математика) по теме "Применение интеграла при решении физических задач"

Задачи:

Обучающие: способствовать формированию знаний, умений по данной теме;

Оборудование: компьютер, мультимедиа проектор, экран.

Содержание урока: данного урока нет в тематическом планировании, но нами предлагается использовать данную разработку изучении темы 7.

План урока:

Организация начала урока.
Постановка проблемы урока.
Актуализация ЗУН, необходимых для творческого применения знаний
Формирование новых понятий и способов действий
Подведение итогов урока

Ход урока:

Организация начала урока.
Постановка проблемы урока. На прошлом уроке мы ознакомились с геометрическими задачами, которые решаются при помощи интеграла. Но интеграл применим не только в математике, другие области науки также используют его и сегодня мы с вами проверим это на примере такой науки как физика.
Актуализация ЗУН, необходимых для творческого применения знаний

4. Формирование новых понятий и способов действий

P_>n>≈ F_>1>(h_>1>)Δh_>1>+…+F_>n>(h_>n>) Δh_>n>.

Рассмотрим несколько задач с физическими моделями, где интеграл определяется как приращение первообразной.

1. Задача о перемещении точки.

Разность S(t_>2>)-S(t_>1>) называют интегралом от функции v(t) на отрезке [t_>1>; t_>2>] и обозначают так:

Импульс силы.

Как известно из физики второй закон Ньютона в импульсном представлении выражает уравнение

ΔР=FΔt

Разность P(t_>2>)-P(t_>1>) называют интегралом от функции F(t) на отрезке [t_>1>; t_>2>] и обозначают так:

Количество электричества.

Разность q(b)-q(a) называют интегралом от функции I(t) на отрезке [a; b] и обозначают так:

Вытекание воды из сосуда.

Данная задача проста и наглядна в своей постановке для учащихся.

Представим себе сосуд, из которого вытекает вода. В момент времени t поток воды вычисляется по формуле q=q(t). Найдем объем воды, вытекающей из сосуда за промежуток времени [t_>1>; t_>2>]. Объем воды, находящейся в сосуде, обозначим через V. Этот объем со временем меняется, т. е. V есть функция времени t.

Разность V(t_>2>)-V(t_>1>) называют интегралом от функции q(t) на отрезке [t_>1>; t_>2>] и обозначают так:

5. Самостоятельная работа.

Учащиеся самостоятельно прорешивают задачи с использованием свойств интеграла.

№1. Вычислите силу давления воды на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м.

Решение. Сила давления воды зависит от глубины х погружения площадки: P(x)=ax, где а – площадь площадки. Получаем

(т)

№2. Тело массой 1 движется с ускорением, меняющимся линейно по закону a(t)=2t-1. Какой путь пройдёт тело за 4 единицы времени от начала движения t=0, если в начальный момент его скорость равнялась 2?

Решение. Скорость тела в любой момент времени t вычисляется по формуле

v=v_>0>+at

Используя данные задачи, получаем:

№3. Тело брошено с поверхности Земли вертикально вверх с начальной скоростью v_>0>. Какова наибольшая высота, достигаемая телом?

Решение. Скорость тела в любой момент времени t движения равна разности начальной скорости и скорости gt, вызванной ускорением, определяемым силой тяжести: v=v_>0>-gt. Движение вверх будет происходить при v=v_>0>-gt>0, т. е. при . Таким образом, максимальная высота полета равна

№4. На прямой расположены материальная точка массы m и однородный стержень массы M и длины l. Точка удалена от концов стержня на расстояния c и c+l. Определить силу гравитационного притяжения между стержнем и точкой.

Решение. Разобьем отрезок [c; c+l] на большое число отрезков. Если отрезки эти малы, то массу каждого из них можно считать точечной и силу гравитационного притяжения между таким отрезком и массой m вычислять по закону всемирного тяготения. Если длина отрезка равна Δх, а расстояние его от начала координат равно х, то сила гравитационного притяжения равна

Δх

Суммируя полученные для каждого отрезка значения силы гравитационного притяжения, мы получим представление искомой силы в виде суммы тем более точное, чем мельче отрезки, на которые мы разбивали отрезок [c; c+l]. В пределе получим

6. Подведение итогов урока. Вывод о проблеме урока. Задание домашнего задания.

Урок-КВН по теме "Интеграл"

Задачи:

Развивающие: развитие познавательной потребности, творческих способностей.

Воспитательные: воспитание интереса к предмету, воспитание чувства коллективизма и взаимовыручки.

КВН проводится интерактивно с помощью сайта школы.

На экране ЭВМ написано:

I команда

II команда

(Ниже ведётся запись полученных очков).

Правила игры.

Класс разбивается на две команды.

Выбираются капитаны команд.

Капитаны назначают консультантов.

Для участия во всех видах работы ученики вызываются к доске капитанами команд.

Ход урока.

1 этап. Разминка – ведется на бумажном носителе.

На экране ЭВМ написаны задания.

Докажите, что функция F(х) является первообразной для функции f(х) на промежутке

F(х) = + 3х – 5,

f(х) = 3( + 1)

Найдите общий вид первообразной для функции:

f(х) = 2х3 – 6 + х – 1

Вычислите интеграл:

а) ;

б) .

Найдите первообразную функцию f(х) = 4 – , график которой проходит через точку (–3; 10).

Решение:

F'(х) = (х3 +3х – 5)' = 3 + 3 = 3( +1)

F'(х) = f(х).

F(х) является первообразной f(х)

3. а)

б)

Консультанты каждой команды собирают тетради и передают консультантам другой команды для проверки. Побеждает та команда, у которой больше сумма очков.

II этап. Блиц – турнир – проводится с помощью ЭВМ (желательно применение проектора). Найдите ошибку: (с классом)

8. Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по закону

S = 0,5 + 3t + 2(м),

где t – время движения в секундах.

Найти U тела через 7 сек.

U (7) = 10 м/сек.

III этап. Домашнее задание.

К доске приглашаются по 1 ученику от каждой команды.

1. С помощью интеграла вывести формулу объёма конуса.

2. С помощью интеграла вывести формулу объёма шара.

Решение:

Рисунок 1

Дано: АВ = R

ОВ = H.

Вывести формулу V конуса.

Вывод: При вращении прямоугольного треугольника ОАВ вокруг оси ОХ, содержащей катет

ОВ получается конус. Треугольник ОАВ является частным случаем криволинейной трапеции, ограниченной графиком функции y=f(х) (прямой ОА), прямыми х = 0 и х = Н, осью абсцисс. V тела вращения вычисляется по формуле

Найдём уравнения прямой ОВ:

Вывод: V конуса равен произведения площади основания на высоту.

Решение 2:

Рисунок 2

Дано: полукруг (О;R)

Вывести формулу V шара.

Вывод: При вращении полукруга вокруг оси ОХ, получаем тело вращения шар.

Полукруг является частным видом криволинейной трапеции, ограниченной графиком функции у=f(х) и прямыми х = – R, х = R, у = 0.

Уравнение окружности имеет вид

+ =

= –

Подставим в формулу:

Вывод: V шара радиуса R равен 4/3 .

IV этап. Конкурс капитанов.

1. Вычислите площадь фигуры, ограниченной графиками функций

2. Вычислите площадь фигуры, ограниченной линиями

В процессе решения задач капитанами, учащиеся решают задачи капитанов из противоположных команд и готовят для него вопросы по теме заданий. По результатам решения задачи и ответов на вопросы, капитаны получают соответствующие баллы.

Решение задания 1.

1. Найдём абсциссы точек пересечения графиков данных функций:

2. Постройте графики данных функций с применением ИКТ.

х	3	4	7	12	19	28
у	0	3	6	9	12	15

х	0	2
у	1	2

1). Чему равен путь, пройденный точкой, движущейся прямолинейно, за отрезок времени от t1=1с до t2 = 4с, если скорость точки U(t) = (2t? – 3t) м/с?

Чему равно ускорение этой точки в момент времени t = 2с?

2). Тело движется прямолинейно со скоростью U(t) = (3 – 2t)

Найти путь, пройденный телом за первые 5 сек.

Чему равно ускорение тела в момент t = 5 c?

Решение 1.

Решение 2.

1. Вычислите:

2. Вычислите:

Решение 1.

Пусть

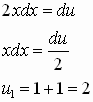
Решение 2.

Пусть

VII этап. Конкурс консультантов. (дополнительный) – проводится при помощи Mathcad.

1. Исследуйте функцию f(х) = – х? + 3х? – 4 и постройте её график.

2. Исследуйте функцию f(х) = х? - 3х? + 4 и постройте её график.

VIII этап. Подведение итогов.

Выигравшая команда объявляется победительницей, а многие учащиеся получают оценки.

Приложение 2

Методы исследования

Анкета 1. Познавательный интерес.

Цель: выявить уровень развития познавательных интересов учащихся.

Порядок проведения: учащимся предлагается заполнить следующую анкету, выбрав один из предложенных вариантов ответа на вопрос.

1. Связаны ли интересы ученика с выбором будущей профессии?

а) связаны очень тесно;

б) связаны, но мало сопровождаются соответствующей организацией деятельности;

в) никак не связаны.

2. Обращается ли ученик к серьезным источникам: пользуется ли научной литературой, работает ли со словарем и так далее?

а) постоянно;

б) иногда;

в) очень редко.

3. Ставит ли перед собой задачи, выполнение которых невозможно в один присест и требует кропотливой работы в течение многих дней и даже месяцев?

а) большинство занятий подчинено этому принципу;

б) ставит такие задачи, но редко выполняет;

в) не ставит долговременных задач.

4. В какой мере, занимаясь любимым делом, может делать "черную", неинтересную работу (например, выполнять длительные вычисления при решении задач)?

а) делает всегда столько, сколько нужно;

б) делает периодически;

в) не любит выполнять неинтересную для него работу.

5. Способен ли при необходимости заниматься продолжительное время интеллектуальной деятельностью, жертвуя развлечениями, а иногда и отдыхом?

а) всегда, когда это нужно;

б) только изредка;

в) не способен.

Анализ: за каждый ответ а) начисляется 2 балла, за ответ б) - 1 балл, за в)- 0 баллов. Затем суммируют набранные учеником баллы. Результат:

от 8 до 10 баллов - показатель высокого уровня развития познавательного интереса;

от 4 до 7 баллов - показатель среднего уровня;

3 и ниже баллов - низкий уровень развития познавательного интереса.

Анкета 2. Познавательная потребность

Цель – изучение познавательной потребности учащегося

Ход проведения.

Учащимся предлагается анкета с пятью вопросами. Их просят внимательно прочитать возможные варианты ответа и отметьте у себя в бланке ответов вариант ответа, которое наиболее всего подходит им.

№ п/п	Вопрос	Возможные ответы	Балл
1	Как часто ученик подолгу занимается какой-нибудь умственной работой (час-полтора — для младшего школьника, несколько часов - подряд— для подростков)?	а) часто б) иногда в) очень редко	5 3 1
2	Что предпочитает школьник, когда задан вопрос на сообразительность?	а) помучиться, но самому найти ответ б) когда как в) получить готовый ответ от других	5 3 1
3	Много ли читает школьник дополнительной литературы?	а) постоянно, много б) иногда много, иногда ничего не читает в) мало или совсем ничего не читает	5 3 1
4	Насколько эмоционально ученик относится к интересному для него занятию, связанному с умственной работой?	а) очень эмоционально б) когда как в) эмоции ярко выражены (по сравнению с другими ситуациями)	5 3 1
5	Часто ли задает вопросы?	а) часто б) иногда в) очень редко	5 3 1

Интенсивность познавательной потребности определяется суммой баллов: 17-25 баллов – потребность выражена сильно, 12-16 баллов – умеренно, меньше 12 баллов – слабо.

Анкета 3. Мое учение.

Цель: выявить отношение школьников к учению, предметную направленность их познавательных интересов, изучить некоторые особенности процесса самостоятельной деятельности учащихся.

Методика представляет собой проективный тест, заданный в форме неоконченных предложений.

Порядок проведения: учитель раздает листы, объявляет цель работы и дает инструкцию учащимся, внимательно читая текст, указать (дописать) то, что отражает особенности их учебной деятельности.

I. Учиться в школе мне:

а) интересно;

б) неинтересно;

в) не знаю.

II. Мои любимые предметы: _______________________________.

III. При выполнении самостоятельной работы я:

а) сразу же приступаю к делу, работаю всегда быстро, даже если допускаю при этом ошибки;

б) сначала стараюсь понять задание, тщательно анализирую его, но потом действую уверенно;

в) очень долго думаю над заданием, не решаюсь приступить к его выполнению, чувствую себя неуверенно.

IV. При выполнении самостоятельных работ всегда волнуюсь, так как ___.

V. Чувствую себя всегда спокойно, так как ____________________________.

VI. Трудности у меня:

а) бывают всегда;

б) иногда;

в) не встречаются.

VII. Чаще всего я:

а) не понимаю цель работы;

б) не понимаю задание;

в) не понимаю, как его выполнить;

г) не умею контролировать ход своей работы;

д) не знаю, как проверить результаты работы;

е) не умею правильно распределить время.

VIII. Я очень дорожу всегда помощью ___________________________________.

IX. Если бы я был учителем, то таким как я ученикам, при выполнении заданий ____________________________________________________________.

Коротко о себе: 1) учусь на 4-5;

а) имею 3;

б) не успеваю по некоторым предметам;

в) увлекаюсь _______________________;

г) хочу стать _______________________.

Анализ: обработка первых двух вопросов дает возможность выявить самооценку отношения учащихся к учению. Остальные ответы характеризуют индивидуальные особенности процесса самостоятельной деятельности. На основе их анализа можно выделить:

а) учащихся, которые приступая к решению задачи, действуют импульсивно, торопятся, не всегда замечают ошибки, а, следовательно, требуют внимания учителя на начальном этапе работы;

б) учащихся, которые действуют взвешено, спокойно, уверенно;

в) "тугодумы" - у которых затянут ориентировочный этап, заметны нерешительность и робость.

В связи с этим анализируются и сопоставляются данные, характеризующие эмоциональное состояние учащихся при выполнении заданий, типичные затруднения.