Формирование мотивации учебной деятельности при изучении математических предложений
Федеральное агентство по образованию
Государственное образовательное
учреждение высшего профессионального
образования
Вятский
государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и методики преподавания математики
Выпускная квалификационная работа
Формирование мотивации учебной деятельности при изучении математических предложений
Выполнил:
студент V курса математического факультета
Потемкина Наталья Владимировна
Научный руководитель:
кандидат педагогических наук, доцент кафедры математического анализа и МПМ И.В. Ситникова
Рецензент:
Доцент кафедры математического анализа и МПМ М.В. Крутихина
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой М.В. Крутихина
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение. 3
Анализ литературы. 5
Анализ психолого-педагогической литературы 5
1.2 Анализ учебно-методической литературы. 8
2. Этап мотивации учебной деятельности в психолого-педагогической литературе. 10
Психологические характеристики отдельных сторон мотивационной сферы учения. 10
Пути формирования мотивации учения. 12
Реализация этапа мотивации учебной деятельности. 22
Мотивация изучения математических понятий. 22
3.2 Мотивация изучения теорем. 27
3.3 Мотивация изучения алгоритмов. 32
Заключение. 40
Библиографический список. 41
Введение
Совершенствование системы обучения, стимулируемое социальным заказом общества, постоянно усложняет и требования к психологическому развитию выпускников школы. Сегодня уже не достаточно овладеть школьниками суммой знаний, важное значение придается задаче научить школьников учиться, а психологически это означает – научить их хотеть учиться.
Формирование мотивации учения в школьном возрасте без преувеличения можно назвать одной из центральных проблем современной школы, делом общественной важности. Ее актуальность обусловлена обновлением содержания обучения, постановкой задач формирования у школьников приемов самостоятельного приобретения знаний и познавательных интересов, осуществления в единстве идейно-политического, трудового, нравственного воспитания школьников, формирования у них активной жизненной позиции, введением всеобщего обязательного образования. Социальный заказ нашего общества школе состоит сегодня в том, чтобы повысить качество обучения и воспитания, изжить формализм в оценке результатов труда учителя и учащихся.
Следовательно, актуальность темы обусловлена следующим:
Мотивация выполняет важные функции в обучении: побуждает поведение, направляет и организует его, придает ему личностный смысл и значимость;
Недостаточное использование мотивации в школе при изучении математических предложений.
Объект исследования: методика изучения математических предложений.
Предмет исследования: этап мотивации введения математических предложений.
Гипотеза: мотивационный этап при введении математических предложений способствует формированию у учащихся положительных мотивов учения и познавательных интересов учебной деятельности.
Цель: рассмотреть особенности организации этапа мотивации учения при введении математических предложений.
В соответствии с целью поставлены следующие задачи:
анализ психолого-педагогической и учебно-методической литературы;
рассмотреть психологические характеристики мотивационной сферы учения;
рассмотреть различные пути формирования мотивации учения;
проследить реализацию этапа мотивации учебной деятельности при изучении математических понятий, теорем и алгоритмов;
проведение опытной работы по формированию мотивации учения при введении математических предложений.
1. Анализ литературы
1.1 Анализ психолого-педагогической литературы.
Сегодня в практике вопрос о мотивации без преувеличения может быть назван центральным.
Рассмотрим отношение к мотивации учения в психолого-педагогической литературе.
Среди основных задач стоящих в настоящее время перед каждым учителем, нет другой, более важной и в тоже время более сложной, чем задача формирования у учащихся положительной устойчивой мотивации к учебной деятельности, такой мотивации, которая побуждала бы их к упорной, систематической учебной работе. Ведь очевидно, что без такой мотивации деятельность ученика в учебно-воспитательном процессе будет неэффективной.[14]
В книге Марковой А.К. «Мотивация учения и ее воспитание у школьников» [14] отмечено, что мотивационная сфера состоит из нескольких аспектов: потребность, мотив и цель. Дано определение мотива, в общем, и мотива в обучении.
Мотив – направленность активности на предмет, внутренне психическое состояние человека, прямо связано с объективными характеристиками предмета, на который направлена активность. Если потребность характеризует готовность к деятельности, то наличие мотива придает активности новый, более действенный характер. В обучении мотивом является направленность учащихся на отдельные стороны учебного процесса. Фактически сюда входит направленность ученика и на овладение знаниями, и на получение хорошей отметки, и на похвалу родителей, и на установление желаемых отношений со сверстниками. Иными словами, учебное поведение побуждается всегда несколькими мотивами.
Марковой рассмотрены функции и виды мотивов.
Мотивация выполняет несколько функций: побуждает поведение, направляет и организует его, придает ему личностный смысл и значимость. Наличие нескольких функций мотивации показывает, что мотивация не только предшествует поведению, но и постоянно предшествует поведению на всех его этапах, во всех его звеньях.
Все мотивы разделены на группы:
социальные;
познавательные;
творческие или социально-познавательные.
В данной книге рассмотрена глава «Пути формирования мотивации учения». В которой указываются некоторые советы для лучшей организации мотивации на уроке.
Мотивационное влияние может оказывать не всякий учебный материал, а лишь такой, информационное содержание которого соответствует наличным и вновь возникающим потребностям ребенка.
Содержание каждого урока каждой темы должно быть глубоко мотивированно, однако не с помощью создания сиюминутных, скоропроходящих интересов или ссылок на практическую значимость в будущей жизни (хотя и это иногда не следует упускать), а главным образом тем, что это содержание должно быть направлено на решение серьезных проблем научно-теоретического познания явлений и объектов окружающего мира, на овладение методами такого познания.
В данном источнике также рассмотрены этапы изучения темы учебной программы. Первым рассмотрен мотивационный этап.
Следующий источник, посвященный проблеме мотивации – «Психология ведения урока», Скороходовой Н.Ю.[22]
В данной книге мотивации посвящен целый раздел: «Мотивация на уроке».
Дается определения мотива и мотивации:
Мотив – побуждение к активности в определенном направлении.
Мотивация – процессы, определяющие движение к поставленной цели, а также факторы (внешние и внутренние), которые влияют на активность или пассивность поведения.
Изучение мотивации позволяет ответить на три основных вопроса:
1. Что заставляет приступать к выполнению определенных действий? Какие потребности личности вызывают ее активность?
2. Почему человек проявляет настойчивость при попытках достичь цели? Каковы особенности настойчивой личности, умеющей упорно стремиться к цели? (внутренние факторы мотивации.)
3. Какие внешние условия побуждают мотивы личности и позволяют ей сохранять движение к определенной цели? (Внешние функции мотивации.)
Перечислены основные направления работы по развитию внутренней мотивации учеников с использованием системы стимулирования. Внутренняя мотивация предполагает развитие собственных мотивов школьника, в первую очередь – самоуважения в деятельности, познавательных и социальных мотивов. Внешней мотивацией часто называют использование внешних стимулов, подход «кнута и пряника».
В книге приведена схема влияния учителя на мотивацию достижения у учеников на уроке (схема Хекхаузена), и в конце каждого раздела приводятся советы учителю. Подробно описано развитие познавательного мотива (интереса к предмету и любознательности) и социальных мотивов (организация сотрудничества).
Плюсом является то, что в книгу включена тема «ошибки в мотивировании». Это позволяет на основе анализа действии учителя во время пресечь возможные ошибки.
При неправильном мотивировании проявляются аффективные реакции, например, отказ от деятельности, агрессивное самоутверждение или пассивность и уныние.
1.2 Анализ учебно-методической литературы по математике.
Один из рассмотренных источников – «Общая методика преподавания математики» Саранцева Г.И.[19], в котором рассмотрены основные положения методики.
В данной книге мотивация рассматривается как этап при формировании математических понятий и теорем. Также указаны типы упражнения, рекомендуемые на данном этапе.
В книге Груденова Я.И. «Совершенствование методики работы учителя математики»[5] мотивация не упоминается как таковая. Рассмотрены этапы изучения математических предложений: введение, усвоение и закрепление. Введение может рассматриваться как мотивационный этап. Я.И. Груденовым рассмотрены три способа введения математических предложений:
учащиеся подготавливаются к самостоятельному формулированию определения, аксиомы, к «открытию» теоремы.
учащиеся готовятся к сознательному восприятию, к пониманию нового математического предложения, формулировка которого им сообщается затем в готовом виде.
учитель сам формулирует новое математическое предложение, без предварительной подготовки, а затем сосредоточивает усилия учащихся на их усвоении и закреплении.
Первый и второй способ формируют мотивацию учебной деятельности. В книге именно эти способы введения рассмотрены подробней.
При осуществлении первых двух способов используется эвристический метод, в классе создается проблемная ситуация, которая способствует самостоятельному «открытию» учащимися новых знаний. Это повышает их интерес к занятиям, способствует развитию творческих способностей, но требует определенной затраты учебного времени.
В учебном пособии Е.И. Лященко: «Лабораторные и практические работы по методике преподавания математики»[13], приведено содержание лабораторных и практических работ по методике преподавания математики в средней школе.
Во второй главе: «лабораторные работы по методике преподавания математики», отдельно рассмотрены лабораторные работы по логико-математическому анализу определений, теорем и алгоритмов. К каждой лабораторной работе указаны ее тема, цели, средства обучения, основное содержание, задания для самостоятельной работы, отдельные образцы оформления результатов самостоятельной работы, литература. В каждой работе выделен мотивационный этап, но наиболее полно он представлен при рассмотрении теорем. В книге много примеров, что помогает лучше понять методику.
Итак, изучив некоторую литературу по теме «формирование мотивации при изучении математических предложений», можно сделать вывод, что мотивация важна в обучении, но в то же время полно она раскрывается не во многих книгах. В основном идет упоминание о мотивации, говориться о ее роли, но ее сущность полностью не раскрывается.
2. Этап мотивации учебной деятельности в психолого-педагогической литературе.
2.1 Психологические характеристики отдельных сторон мотивационной сферы учения.
Совершенствование системы обучения, стимулируемое социальным заказом общества, постоянно усложняет и требования к психологическому развитию выпускников школы. Сегодня уже не достаточно овладеть школьниками суммой знаний, важное значение придается задаче научить школьников учиться, а психологически это означает – научить их хотеть учиться.
Поэтому учителю надо поставить перед собой задачу – какие именно характеристики мотивации следует формировать для возникновения нового – сознательного и целенаправленного отношения ученика к внутренним сторонам учения как общественно значимой деятельности, к содержанию своего учебного труда.
Итак, рассмотрим строение мотивационной сферы учения у школьников, т. е. того, что определяет, побуждает учебную активность ребенка.
Всякая деятельность начинается с потребностей. Потребность – это направленность активности ребенка, психическое состояние, создающее предпосылку деятельности. Одна и та же потребность может быть удовлетворена разными способами. Но без нее не пробуждается активность ребенка, у него не возникают мотивы, он не готов к постановке целей.
Всякому ребенку свойственна потребность в новых впечатлениях, переходящая в ненасыщаемую познавательную потребность. На нее учитель должен прежде всего опереться, актуализировать ее, сделать более четкой осознанной у большинства учащихся. Необходимо и обеспечить переход от потребностей к деятельности. В одних случаях познавательная потребность может удовлетворяться уже получением хороших отметок, в других – при правильно организованной учебной деятельности – организацией школьника на внутреннее содержание учебной деятельности, способы выполняемых действий. В процессе учебной деятельности появляются и социальные установки учения – потребность включения в общественно значимую практику, отдачи обществу, другому человеку, потребность самосовершенствования и т. д.
Другой важный аспект мотивационной сферы – мотив, т. е. направленность активности на предмет, внутреннее психическое состояние человека, прямо связанное с объективными характеристиками предмета, на который направлена активность. В обучении мотивом является направленность учащихся на отдельные стороны учебного процесса. Фактически сюда входит направленность ученика и на овладение знаниями, и на получение хорошей отметки, и на похвалу родителей, и на установление желаемых отношений со сверстниками. Иными словами, учебное поведение побуждается всегда несколькими мотивами.
Особенность мотива как одной из сторон мотивационной сферы состоит в том, что он прямо связан со смыслом, личностной значимостью этой деятельности: если изменяется мотив, ради которого школьник учится, то это принципиально перестраивает и смысл всей его учебной деятельности, и наоборот.
Но возникновение мотивов учения недостаточное условие для эффективной учебной деятельности, если у школьника не сформировано умение ставить самостоятельные цели в учебной работе. Цель – это направленность активности на промежуточный результат, представляющий этап достижения предмета потребности. Для того чтобы реализовать учебный мотив, например, овладеть приемами самообразования, надо поставить и выполнить много промежуточных целей в учебном труде: научиться видеть отдельные результаты своей учебной деятельности, подчинить им этапы сегодняшней учебной работы, поставить цели выполнения учебных действий, цели их самопроверки и т. д. Кроме того надо чтобы учащиеся учились осознавать цели своих действий и соотносить их с мотивами учебной деятельности, в которую эти действия включены; учебная цель может оставаться одной и той же (например, овладение приемами самообразования), а смысл учебной деятельности будет меняться в зависимости от ее мотива (стать всесторонне развитым человеком, поступать в вуз и т. д.).
Существует еще одна сторона мотивационной сферы учебной деятельности, о которой часто говорят в школе, – интерес к учению. Он тесно связан с уровнем сформированности учебной деятельности и в этом плане есть выражение и проявление состояния других сторон мотивационной сферы – мотивов и целей. В качестве основной черты интереса называют эмоциональную окрашенность, связь с эмоциональными переживаниями ребенка. Конечно, эта особенность важна, но не она все таки является главной. По-видимому, связь интереса с положительными эмоциями имеет значение на первых порах возникновения любознательности ученика (в новой теме, в новом учебном предмете), но для поддержания устойчивости интереса необходима сформированность учебной деятельности, а также связанные с ней способности к самостоятельной постановке учебных целей и их разрешению.[14]
Мы остановились на особенностях нескольких видов побуждений – потребностей, мотивов, целей, интересов. Главная же направленность мотивационной сферы – мотивы, т. е. направленность активности на предмет.
2.2 Пути формирования мотивации учения.
Формирование у учеников мотивов, придающих дальнейшей учебе ребенка значимый для него смысл, в свете которого его собственная учебная деятельность становилась бы для него сама по себе жизненно важной целью (например, престижных или выполнение требований родителей и т. д.), является крайне необходимым, без чего дальнейшая учеба школьника может оказаться просто невозможной. Надеяться на то, что такие мотивы возникнут сами по себе не приходиться. Поэтому важно обеспечить такое ее формирование, которое поддерживало бы эффективную и плодотворную учебную деятельность каждого ученика на протяжении всех лет его пребывания в школе, и было бы основой для его самообучения и самосовершенствования в будущем.
Рассмотрим пути и методы формирования положительной устойчивой мотивации к учебной деятельности.
1. Важную роль в мотивации учения играет содержание учебного материала.
Мотивационное влияние может оказывать не всякий учебный материал, а лишь такой, информационное содержание которого соответствует наличным и вновь возникающим потребностям ребенка.
При разработке тематических планов, планов отдельных уроков, при подборе учебного и иллюстративного материала учитель должен всегда учитывать характер потребностей своих учащихся, знать наличный уровень этих потребностей и их возможное развитие, с тем чтобы содержание учебного материала удовлетворяло наличным потребностям школьников и в наибольшей степени способствовало возникновению и развитию нужных для дальнейшей учебной деятельности новых потребностей.
Для этого содержание учебного материала должно быть вполне доступно учащимся, должно исходить из имеющихся у них знаний и опираться на них и на жизненный опыт детей, но в то же время материал должен быть достаточно трудным и сложным. Если содержание учебного материала не требует от учащихся работы по его осмыслению и усвоению, то такой учебный материал не будет удовлетворять, в частности, потребности учащихся в постоянном развитии психических функций (памяти, мышления, воображения), не будет развивать у учащихся ярких эмоций (положительных и отрицательных) и, следовательно, не будет удовлетворять потребности в эмоциональном насыщении, поэтому легкий, малосодержательный учебный материал не будет способствовать возникновению и развитию новых потребностей.
Информационно бедный материал также не обладает мотивационным эффектом, он не вызывает и не формирует положительных устойчивых мотивов учебной деятельности.
Учебный материал по содержанию обязательно опирается на прошлые знания учащихся, их жизненный опыт. Но в то же время он обязательно должен нести новую информацию, в свете которой могут быть осмыслены прошлые знания и опыт. Новое в знаниях должно показывать ограниченность прошлого знания и жизненного опыта, показывать знакомые объекты с новой стороны, с новой точки зрения, показать, что одних жизненных наблюдений совершенно не достаточно для установления подлинной сущности явления.
Нужно также учитывать возможности учащихся в усвоении научных понятий. Но сейчас возможности учащихся в овладении основами современной научной мысли, научной картины мира все еще не используются в полной мере. Содержание обучения, ориентированное на формирование научно-теоретического стиля мышления, диалектического обобщения знаний, способствует становлению у учащихся положительной мотивации, направленной на освоение научной картины мира, на овладение общими способами научного познания, общими приемами действий для такого познания.
Итак, содержание каждого урока, каждой темы должно быть глубоко мотивированно, однако не с помощью создания сиюминутных скоро проходящих интересов или ссылок на практическую значимость в будущей жизни, а главным образом тем, что это содержание должно быть направлено на решение серьезных проблем научно-теоретического познания явлений и объектов окружающего мира, на овладение методами такого познания. Только в этом случае у школьников будет создаваться перспектива на дальнейшее изучение знакомых, постоянно наблюдаемых явлений, будет создана основа для формирования содержательных мотивов учебной деятельности.[14]
2. Организация учебной деятельности – один из путей формирования мотивации.
Содержание учебного материала усваивается учащимися в процессе учебной деятельности. От того какова эта деятельность, из каких частей (отдельных учебных действий) она состоит, как эти части между собой соотносятся, т. е. какова структура учебной деятельности – от всего этого во многом зависит результат обучения, его развивающая и воспитывающая роль. Успешность учебной деятельности зависит также от того, на что она направлена, какие цели осуществляют учащиеся при этом, направлены ли эти цели на овладение учебным материалом как самостоятельной целью, или же учебная деятельность служит для них лишь средством для достижения целей, не связанных с содержанием обучения. Отношение учащихся к собственной деятельности определяется в значительной степени тем, как учитель организует их учебную деятельность, какова ее структура и характер.
Изучение каждого самостоятельного этапа или темы учебной программы должно состоять из следующих трех основных этапов: мотивационного, операционально-познавательного и рефлексивно-оценочного.
Мотивационный этап.
На данном этапе ученики должны осознать, почему и для чего им нужно изучить данный раздел программы. Что именно им придется изучить и освоить, какова основная учебная задача предстоящей работы. Мотивационный этап обычно состоит из следующих учебных действий:
1) Создание учебно-проблемной ситуации, вводящих учащихся в предмет изучения предстоящей темы (раздела) программы. Учебно-проблемная ситуация может быть создана учителем разными приемами:
а) постановкой перед учащимися задачи, решение которой возможно лишь на основе изучения данной темы. Например, перед изучением темы «Квадратные уравнения» (7 класс, алгебра) учитель предлагает учащимся решить текстовую задачу, которая сводится к квадратному уравнению, тем самым демонстрируя необходимость изучения метод решения квадратных уравнений и научиться им пользоваться;[14]
б) беседой (рассказом) учителя о теоретической и практической значимости предстоящей темы (раздела) программы.
Рассмотрим, например, фрагмент из урока по теме «Площади поверхности тел» в 11 классе. На предыдущих уроках учащиеся уже изучили вывод формулы для вычисления площади боковой поверхности цилиндра. Теперь они должны найти формулу для определения площади поверхности сферического сегмента. Материал довольно однообразный, но учитель начинает не с формулы и не с повторения доказательства, а с сообщения ТАСС: «12 апреля 1961г. в Советском Союзе выведен на орбиту вокруг земли первый в мире космический корабль-спутник «Восток» с человеком на борту. Пилотом-космонавтом является летчик, майор Гагарин Юрий Алексеевич». Учащиеся, конечно, хорошо знают об этом событии. Но они не могут не знать о том, какой восторг в нашей стране и во всем мире оно вызвало. Учитель должен передать этот восторг своим чтением.
«По предварительным данным,- снова читает учитель,- период вращения корабля-спутника вокруг Земли – 89,1 мин; минимальное удаление от поверхности Земли равно 175 км, а максимальное расстояние – 302 км…».[3]
Теперь уже учащиеся удивлены: какое отношение имеет беспримерный подвиг Ю.А Гагарина к уроку геометрии и, в частности, к теме «Поверхность шара и его частей»? Их мысли можно прервать вопросом: «Какую часть поверхности Земли видел Ю.А. Гагарин, пребывая в апогее?» Вопрос вызывает у учащихся интерес, но через несколько минут самостоятельных размышлений они устанавливают, что их математически знаний пока не достаточно. Далее приходиться пока отложить задачу и заняться выводом нужной формулы. Но как только формула выведена, учащиеся снова возвращаются к задаче.
Задачу можно обогатить, предложив учащимся найти площадь поверхности Земли, которую видел Ю.А. Гагарин в течении всего своего полета.
в) рассказом учителя о том, как решалась проблема в истории науки.
2) Формулировка основной учебной задачи. Обсуждение основного противоречия (проблемы) в созданной учебно-проблемной ситуации завершается формулированием основной учебной задачи, которая должна быть решена в процессе изучения данной темы (раздела) программы. Формулировка основной учебной задачи обычно производится учителем как итог обсуждения проблемной ситуации. Учебная задача показывает учащимся тот ориентир, на который они должны направлять свою деятельность в процессе изучения данной темы. Тем самым учебная задача создает основу для постановки каждым учащимся перед собой определенных целей, направленных на изучение учебного материала.[14]
3) Самоконтроль и самооценка возможностей предстоящей деятельности по изучению данной темы. После того как основная учебная задача сформулирована, понята и принята учащимися, намечают и обсуждают план предстоящей работы. Учитель сообщает время, опущенное на изучение темы, сообщает, что нужно знать и уметь для изучения темы, что у учащихся наличествует, а что требует пополнения. Завершается обсуждение тем, что отдельные учащиеся дают самооценку своим возможностям по изучению темы, указывают, какой материал они повторят, и что еще сделают для подготовки к предстоящим урокам.
Операционально-познавательный этап.
На этом этапе учащиеся усваивают содержание темы (раздела) программы и овладевают учебными действиями и операциями, входящими в его содержание. Роль данного этапа в становлении мотивации учебной деятельности зависит главным образом от того, будет ли ясна учащимся необходимость всего содержания и отдельных его частей, всех учебных действий и операций для решения основной учебной задачи, поставленной на мотивационном этапе.
В осознании учащимися содержания темы призвано помочь моделирование. Оно должно вступать и как средство наглядного представления объектов и закономерностей (всеобщих отношений) изучаемого материала, и как средство наглядно-действенного представления тех действий и операций, которые нужно выполнить и освоить учащимся для выявления этих объектов и закономерностей, а также для решения широкого круга задач, основанных на этих закономерностях.
Например, при изучения раздела тригонометрических функций, чтобы их изучение в самом общем виде, как функции числового аргумента, стало для учащихся мотивированным, оправданным с точки зрения задач познания окружающего мира, эти функции целесообразно рассмотреть как математические модели количественных отношений, характеризующие многие явления действительности, и в первую очередь явления гармонических колебаний. Основная учебная задача при такой трактовке тригонометрических функций формулировалась как задача нахождения методов описания (выражения) общих зависимостей между величинами, характеризующих процесс гармонического колебательного движения.
Рефлексивно-оценочный этап.
Этот этап итоговый в процессе изучения темы, когда учащиеся учатся рефлексировать (анализировать) собственную учебную деятельность, оценивать ее, сопоставляя результаты деятельности с поставленными основными и частными учебными задачами (целями). Качественное проведение этого этапа имеет огромное значение в становлении мотивации учебной деятельности.
Работу по подведению итогов изучения пройденного раздела (темы) необходимо организовать так, чтобы учащиеся смогли испытать чувство эмоционального удовлетворения от сделанного, радость победы над преодоленными трудностям, счастье познания нового, интересного. Тем самым будет формироваться у учащихся ориентация на переживание таких чувств в будущем, что приведет к возникновению потребности в творчестве, познании, в упорной самостоятельной учебе, т. е. к появлению положительной устойчивой мотивации учебной деятельности.
Организация этого этапа должна быть проведена так, чтобы учащиеся смогли обозреть пройденный ими путь познания, выделить в нем наиболее значимые вехи и дороги, оценить их с точки зрения будущих задач обучения. целесообразно использовать не один и тот же постоянный прием подведения итогов, например устный опрос и контрольную работу, а разнообразные методы и приемы, дающие возможность проявить учащимся самостоятельность и инициативу.
3. Влияние коллективных форм учебной деятельности на мотивацию учения.
Различные формы коллективной деятельности учащихся играют значительную роль в становлении мотивации учения, что объясняется несколькими обстоятельствами.
Большое значение имеет включение всех учащихся в активную учебную работу, ибо только в процессе деятельности может формироваться нужная мотивация. Использование групповых форм обучения втягивает даже «глухих» учащихся, так как, попав в группу одноклассников, которые коллективно выполняют определенное задание, ученик не может отказаться выполнять свою часть работы, иначе подвергнется моральной критике своих товарищей, а их мнением, уважением он, как правило, дорожит, зачастую даже больше, чем мнением учителя. Кроме того, работая в микроколлективе, каждый ее член старается быть не хуже других, возникает здоровое соревнование, которое способствует интенсификации учебной работы, придает ей эмоциональную привлекательность, что также играет роль в становлении соответствующей мотивации.
Когда ученик, работая коллективно в группе учащихся, находясь в тесном общении с ними, наблюдает, какой большой интерес вызывает его деятельность у товарищей, какую ценность представляет для них эта работа, то он сам начинает ее ценить, начинает понимать, что учебная работа может представлять значимость сама по себе. А это способствует включению ученика в активную учебную работу, которая постепенно становиться его потребностью и приобретает для него признаваемую им ценность, что приводит к мотивации учения.
Для формирования устойчивой положительной мотивации учебной деятельности очень важно, чтобы каждый ученик почувствовал себя субъектом учебно-воспитательного процесса. Этому может способствовать личностно-ролевая форма организации учебного процесса. При данной форме организации каждый ученик выполняет определенную роль в процессе обучения. Это способствует становлению мотивации этой деятельности, которая приобретает для школьников признаваемую ценность.
Таким образом, различные формы коллективной деятельности дают возможность дифференцировать эту деятельность для разных категорий учащихся, дифференцировать задания так, чтобы сделать их посильными для каждого ученика. Это также важно для становления мотивации учения.
4. Значение оценки в становлении мотивации учебной деятельности.
Для формирования положительной устойчивой мотивации учебной деятельности важно, чтобы главным образом в оценке работы ученика был качественный анализ этой работы, подчеркивание всех положительных моментов, продвижений в освоении учебного материала и выявление причин имеющихся недостатков, а не только их констатация. Этот качественный анализ должен направляться на формирование у учащихся адекватной самооценки работы, ее рефлексии. Балльная оценка должна занимать в оценочной деятельности учителя второстепенное место. Особенно осторожно надо использовать в текущем учете неудовлетворительные отметки, а на первых порах обучения, по-видимому, лучше вовсе их не использовать. Вместо этого надо просто указывать на имеющиеся пробелы в работе. Такой анализ надо где-то фиксировать. При тематической форме учета и оценке работы учащихся это легко сделать.[14]
Итак, мы рассмотрели разные пути формирования положительной устойчивой мотивации учебной деятельности учащихся. Для становления такой мотивации следует использовать не один путь, а все пути в определенной системе, в комплексе, ибо не один из них, сам по себе, без других, не может играть решающей роли в становлении мотивации всех учащихся.
Реализация этапа мотивации учебной деятельности.
3.1 Мотивация изучения математических понятий.
Начальным этапом формирования понятий является мотивация. Сущность этого этапа заключается в подчеркивании важности изучения понятия, в побуждении школьников к целенаправленной и активной деятельности, в возбуждении интереса к изучению понятия. Мотивация может осуществляться как по средствам привлечения средств нематематического содержания (внешняя мотивация), так и в ходе выполнения специальных упражнений, объясняющих необходимость развития математических теорий (внутренняя мотивация). Например, появление обыкновенных дробей, как правило, мотивируется потребностями практики. Введение смежных углов можно мотивировать необходимостью изучения не только отдельных фигур, но и их объединений. Рассмотрение взаимного расположения прямой и окружности приводит к трем случаям, один из которых характерен тем, что окружность и прямая имеют одну общую точку. Указанный случай и обуславливает введение понятия касательной к окружности.[19]
Примеры:
1. Арифметическая (геометрическая) прогрессия может быть введена путем выполнения упражнений на запись числовых последовательностей, заданных определенными свойствами, либо на выявление свойств, которыми обладают указанные последовательности.
Например, при введении понятия арифметическая прогрессия можно предложить следующее задание:
Дана последовательность чисел: 4, 7, 10, 13, 16, ….
Ответьте на следующие вопросы:
Какая закономерность прослеживается между числами? (последующее число отличается от предыдущего на 3);
Попробуйте выразить 3-ий член, 4-ый член, n-ый член через первый;
Таким образом, обозначив первый член последовательности через а>1>, второй – а>2>, и так далее, а n-ый через а>n>, мы можем сделать соответствующие выводы: а>n>=a>n>>-1 >+ 3; разность между элементами равна 3, обозначим это число через d, тогда а>n>=a>n>>-1 >+ d, а>n>=a>1 >+ (n – 1)d. Рассмотренная числовая последовательность называется арифметической.
Определение: числовую последовательность, каждый член которой, начиная со второго, равен сумме предшествующего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.[17]
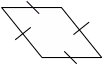
2. Ознакомление с существенными свойствами трапеции может осуществляться посредством предъявления учителем рисунка, на котором изображены различные четырехугольники, и выделения учащимися тех из них, у которых две стороны параллельны, а две другие нет.






а б в г
д е ж з

и
Рассматривая эти рисунки, учащиеся должны ответить на вопрос: «Какие из данных фигур имеют общие свойства?» Ребята замечают, что в четырехугольниках а, б, г, д, и две противоположные стороны параллельны, а две другие нет. После этого им сообщается, что такой четырехугольник называется трапецией.
Введение понятия трапеция может быть введено и путем выполнения упражнений на построение различных четырехугольников, в том числе и четырехугольников у которых две стороны параллельны, а две другие нет.
3. Рассмотрим подробнее мотивационный этап на примере введения понятия «правильный многоугольник».
Введение начинается с создания учебно-проблемной ситуации.
В начале урока учителем предлагаются на рассмотрение различные многоугольники, нарисованные на доске.




 а б в г
а б в г





























д е ж з
Урок начинается с фронтальной беседы. Учитель задает несколько вопросов, например:
Чем отличается фигура г) от других фигур? (не является выпуклой)
Что общего у многоугольников в), д), е), ж)? (все стороны равны)
Что общего у многоугольников е), ж), з)? (все углы равны)
Чем отличаются фигуры а) и д)?
Чем отличаются фигуры ж) и д)?
Выделите общее у многоугольников е) и ж).(стороны и углы равны)
Таким образом, были отмечены существенные свойства понятия. Далее учитель отмечает, что выпуклые многоугольники, у которых все стороны и углы равны, имеют специальное название. Предлагается ученикам назвать эти многоугольники, и обосновать ответ (это можно сделать, так как уже изучено понятие правильного треугольника). То есть ставиться цель – дать название таким многоугольникам.
Таким образом, после проделанной работы, учитель формулирует строгое определение: правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
4. На этапе мотивации можно предлагать задачи, разрешение которых и приводит к формированию определения. Рассмотрим на примере введения понятия «параллелограмм».
В начале урока ученикам можно предложить для решения одну из следующих задач:
В четырехугольнике известны длины a и b двух смежных сторон. Какой должна быть форма четырехугольника, чтобы по этим данным можно было определить его периметр?
В каких случаях для нахождения всех элементов четырехугольника достаточно знать две его смежные стороны и угол между ними?
Так же можно предложить задачу, привлекающую учеников своей фабулой. Например:
Собака и лиса устроили соревнования по бегу. Они договорились, что победителем будет тот из них, кто, пробежав по двум смежным сторонам поляны, имеющей форму четырехугольника, первым прибежит из одной вершину в противоположную. Известно две смежные стороны АВ и ВС поляны связаны соотношением ВС=2АВ. Какой формы должна быть поляна, чтобы можно было установить соотношение скоростей собаки и лисы, при котором собака победит лису?[7]
Решая задачу, школьники рассматривают различные формы четырехугольников, в том числе и параллелограмма. В процессе решения «лишние» четырехугольники отбрасываются, остается параллелограмм. Таким образом были рассмотрены существенные свойства параллелограмма, и была поставлена цель – построить четырехугольник, форма которого удовлетворяет поставленным в задаче условиям.
После того, как задача решена, учитель еще раз акцентирует внимание учащихся на свойствах полученного четырехугольника и отмечает, что он имеет свое название - «параллелограмм». Далее дается строгое определение параллелограмма: параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
3.2 Мотивация изучения теорем.
При введении теоремы можно условно выделить следующие этапы ее изучения:
мотивация изучения теоремы и раскрытие ее содержания (усмотрение геометрического факта и формулировка теоремы);
работа нал структурой теоремы;
мотивация необходимости доказательства теоремы;
построение чертежа и краткая запись содержания теоремы;
поиск доказательства, доказательство и его запись;
закрепление теоремы;
применение теоремы.
Для мотивации изучения теорем можно предложить такие приемы:
Прием 1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.
Мотивировать необходимость изучения свойства «Две различные прямые либо не пересекаются, либо пересекаются только в одной точке» можно, предложив предварительно учащимся решить дома следующие задачи:
На плане местности четыре населенных пункта отмечены точками А, В, С, К. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта К в пункт В (пути считаем прямолинейными). Если пересекутся, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересекаться в двух точках?
В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо не имеют ни одной. Отметив, что пути движения в данных задачах были отрезками, предлагается подумать над вопросом: измениться ли вывод, если вместо двух отрезков взять две прямые?
Ответы могут быть разными. Если ответы разные, то сразу можно предложить выяснить, могут ли две прямые иметь две общие точки, и тем самым перейти к доказательству теоремы, мотив изучения которой стал очевиден. Если же ответ один, то есть две различные прямые пересекаются в одной точке, то учитель говорит, что в этой задаче это действительно так. При решении других задач может быть по-другому: ведь вы не можете рассмотреть все конкретные жизненные ситуации и прорешать все задачи.[13]
С теоремой о сумме углов треугольника учащиеся могут ознакомиться, измеряя непосредственно углы треугольника. Обобщая результаты измерений, учащиеся приходят к выводу, что сумма углов треугольника равна 180°.[19]
Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач.
Для мотивации изучения теоремы «Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны» можно использовать следующую задачу:

А

 В
В
С
 М
М
Д рис.1
Картографам необходимо было нанести на карту два населенных пункта А и В (рис.1). Измерить расстояние между пунктами оказалось невозможно, так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С, от которой можно измерит расстояние и до пункта А и до пункта В. Измерили эти расстояния и построили на бумаге расстояния АС и СВ соответствующей длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за точку С, отложили отрезки СД и СМ, равные соответственно отрезкам СВ и СА, и соединили точки Д и М отрезком. Картографы считают, что расстояние ДМ равно расстоянию АВ (в соответствующем масштабе). Правы ли картографы?
По условию задачи известно, что АС = СМ, ВС = СД и, кроме того, АСВ = ДСМ как вертикальные углы.
Надо установить, что ДМ = АВ.
Откуда может следовать равенство этих отрезков?
Равенство отрезков ДМ и АВ может следовать из равенства треугольников АСВ и ДСМ.
Но в равных треугольниках соответственно равны все шесть элементов (по три угла и по три стороны), а здесь мы имеем только две стороны и угол между ними одного треугольника, соответственно равные двум сторонам и углу между ними другого треугольника.
Следует доказать, что если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника равны.[13]
Мотив изучения и необходимость доказательства теоремы показаны.
Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.
Например, перед доказательством теоремы «В равнобедренном треугольнике углы при основании равны» учащимся предлагается решить задачу:
В равнобедренном треугольнике АВС (АВ=ВС) вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников.
Так как третьего признака равенства по трем сторона у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем : «В равнобедренном треугольнике углы при основании равны», «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой», «Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны».[13]
Прием 4. Показ, как решалась данная проблема в истории науки.
Например, перед изучением второго признака равенства треугольников, можно привести историческую справку.
В
В
древние времена, для определения расстояния от берега до морских кораблей, Фалес Милетский (философ древней Греции) использовал следующий способ:
П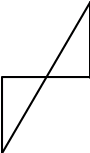
С Д А
Е
Рис 2
усть А – точка берега (рис.2), В – корабль на море. Для определения расстояния АВ восстанавливают на берегу перпендикуляр произвольной длины: АС⊥АВ; в противоположном направлении восстанавливают СЕ⊥АС так, чтобы точка Д (середина АС), В и Е находились на одной прямой. Тогда СЕ будет равна искомому расстоянию АВ.[4]После этой справки учитель задает вопрос, а прав ли Фалес, утверждая, что СЕ=АВ. Ответы учеников могут разделиться. Далее учитель вводит теорему: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны». Пользуясь данной теоремой, ученики без труда ответят, что треугольники АВД и СЕД равны, а значит и соответственные стороны АВ и СЕ равны.
Проследим мотивационный этап работы над теоремой на примере теоремы: «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой».
Один из приемов мотивации изучения данной теоремы – знание теоремы для решения задач.
М
С
В
ожно использовать другой прием, показав конструкцию строительной фермы (рис.3), где АС=СВ, АД=ДВ, ДМ=МВ; простейшую конструкцию стропил (рис.4) АВ=ВС и АК=КС, то есть наблюдение жизненных фактов.








М


А Д В
А К С
Рис 3.
Рис 4.
С целью мотивации изучения этой теоремы можно использовать решение практической задачи.
Ч
М
В
К
тобы повесить с помощью веревки перпендикуляр к данной прямой MN из данной на ней точки, поступают так: откладывают от этой точки О равные расстояния ОВ и ОА; прикрепляют к колышкам А и В концы веревки и, взяв веревку за середину С, натягивают ее; провешенная прямая СО и будет искомым перпендикуляром. Почему?(рис.5)



C




Р



М А О В N
Рис 5.
Рис 6.
Можно использовать решение учебно-практической задачи:
Чтобы разделить угол Р пополам с помощью только масштабной линейки, поступают так: 1) откладывают на сторонах угла Р (рис.6) равные отрезки РМ и РК; 2) соединяют точки М и К отрезком; 3) делят отрезок МК пополам, получают точку В; 4) проводят луч РВ. РВ – искомая биссектриса, разделившая угол пополам. Почему?[13]
3.3 Мотивация изучения алгоритмов.
Понятие «алгоритм» является основным, неопределяемым. Сущность его на содержательно-интуитивном уровне может быть описана следующим образом: алгоритм – понятное предписание, указывающее, какие операции и в какой последовательности необходимо выполнить с данными, чтобы решить задачу данного типа. Для описания общего метода решения класса однотипных задач в школе часто используются правила. Правило представляет собой свернутый алгоритм, отдельные шаги его являются блоками (системами операций в «сжатом» виде).
Для того чтобы правильно организовывать работу учащихся по овладению алгоритмами школьного курса математики, учителю необходимо овладеть умением выполнять логико-математический анализ алгоритмов (правил).
Логический анализ алгоритмов (правил) предполагает: а) проверку наличия у данного правила характеристических свойств алгоритма; б) выделение последовательности операций и логических условий в данном правиле; в) установление связи алгоритма с другими знаниями.
Логико-математический анализ алгоритма позволяет правильно осуществить отбор материала для работы с учащимися по овладению алгоритма.
Работа с учащимися по овладению алгоритмом обычно включает три основных этапа: 1) введение алгоритма; 2) усвоение алгоритма; 3) применение алгоритма.
Одной из целей первого этапа изучения алгоритма и является мотивация изучения алгоритма.
Основным средством, используемым на различных этапах формирования алгоритма, является система упражнений. Содержание ее определяется на основании логико-математического анализа конкретного алгоритма.
Можно выделить два способа введения алгоритмов: содержательный и формальный. Если алгоритм выполнения некоторой операции выявлен в процессе решения сюжетной задачи, то этот способ введения алгоритма называется содержательный. Если алгоритм вводят без рассмотрения сюжетной задачи, то этот способ введения алгоритма называется формальным.
Рассмотрим мотивировку введения алгоритма на примере введения способов операций и алгоритмов их выполнения в 5 – 6 классах.
Алгоритмы выполнения операций должны быть, где это возможно, мотивируемы. Способы мотивировок могут быть различные: словесно-логический, логико-математический, экспериментальный (эмпирический) и т. д.
В зависимости от способа введения алгоритма выполнения операций используют сюжетные задачи с различными целями:
При содержательном способе введения алгоритма, исходя из решения текстовой задачи, формулируют алгоритм выполнения операции;
При формальном введении алгоритма содержательное решение текстовой задачи служит мотивировкой введенного алгоритма.
Содержательный способ введения операции и алгоритма ее выполнения.
Изучение вопроса начинают с рассмотрения конкретных сюжетных задач, способ решения которых для ранее изученных чисел учащимся известен. Принимают соглашение, что для новых чисел задачу решают с помощью «той же операции». Здесь мы имеем содержательное введение операции на новом множестве чисел, как обобщение способа решения задачи. Далее возникает проблема - найти правило, то есть алгоритм выполнения операции для новых чисел. Решение задачи, точнее говоря, результат применения операции к данным числам в каждом случае находят, проводя содержательные рассуждения в соответствии с фабулой задачи, и иногда с использованием геометрической иллюстрации задачной ситуации. В соответствии с принятым соглашением и полученным результатом записывают равенство вида a*b=c. Меняя числовые данные в задаче, как правило, получают несколько таких равенств. Кроме основного равенства в процессе содержательного решения задачи могут быть получены некоторые вспомогательные равенства.
Таким образом, при содержательном введении алгоритма роль сюжетных задач сводиться к получению некоторых равенств, то есть к получению формальных объектов. Чтобы сформулировать правило выполнения операции с новыми числами, нужно провести синтаксический анализ полученных основных равенств, то есть рассмотреть какие объекты имеем в каждой части равенств, установить возможные между ними связи, а используя вспомогательные равенства, выяснить какие использованы ранее известные алгоритмы. При проведении этого анализа рассмотренные сюжетные задачи уже никакой роли не играют. Исходя из проведенного синтаксического анализа, формулируют правило выполнения введенной операции. Если при этом есть несколько принципиальных различных случаев выполнения операции, то такой анализ нужно проводить для каждого случая отдельно. Совокупность правил выполнения операции в различных случаях представляет алгоритм выполнения операции.
Следует заметить, что в школе при введении алгоритмов выполнение действий содержательным способом не всегда должное внимание уделяется приведению синтаксического анализа полученных равенств. Поэтому даже при использовании сюжетных задач нередко правила выполнения действий учитель формулирует сам. Проводить синтаксический анализ различных выражений необходимо учить учащихся не только при введении новых алгоритмов, нужны специально направленные на это упражнения.
Содержательный способ введения алгоритма возможен без содержательного введения операций. В этом случае учащимся уже должно быть известно, что задачу нужно решать с помощью рассматриваемой операции, то есть не нужно вводить соглашение о выполняемой операции. Что касается введения алгоритма, то изучение вопроса следует вести так же как и в рассмотренном выше случае.
Формальный способ введения алгоритма.
Здесь имеются различные возможности:
1) можно построить систему синтаксических упражнений, подводящих учащихся к применению алгоритма выполнения новой операции. Проводя анализ выполненных упражнений, учащиеся приходят к формулировке алгоритма;
2) алгоритмы вводит учитель сам, показывает его применение на примерах и т. д.
При этом способе введения алгоритма после формулировки его и приобретение учащимися некоторого умения применять алгоритм, следует рассмотреть сюжетные задачи с целью мотивировки введенного правила. В этом случае решение задачи нужно найти двумя способами: выполняя операцию по алгоритму и проведя содержательные рассуждения в соответствии с фабулой задачи. Совпадение результата решения задачи разными способами подтверждает целесообразность введения именно таких правил выполнения операции.
Различия в использовании содержательных задач при разных способах введения алгоритмов состоит в том, что при первом способе учащиеся проводят синтаксический анализ равенств, полученных при решении задачи, при втором способе такой анализ не проводиться, так как нас интересует результат выполнения операции по алгоритму и результат, полученный при содержательном решении задачи.
Следует заметить, что не всегда при формальном введении алгоритмов выполнения операций их мотивировку проводят содержательно, иногда мотивировку можно провести формальными средствами.
Первый способ введения алгоритмов выполнения операции наряду с основной целью – формулировкой алгоритма, позволяет развивать у учащихся умение проводить анализ, обобщение, сравнение, то есть способствует развитию мышления. Кроме того, в процессе изучения математики необходимо научить школьников переводить на математический язык содержание задачи, сформулированной в терминах естественного языка, а также осуществлять обратный перевод, то есть интерпретировать символические записи в терминах конкретной задачи. Эти умения связаны с обучением математическому моделированию. При содержательном введении алгоритмов можно показать учащимся, что переход от естественного языка к языку математических знаков:
а) совершенствует форму записи мыслей, делает ее более компактной и обозримой;
б) позволяет в самой структуре языка отражать структурные связи между изучаемыми объектами;
в) дает единую модель для решения разнообразных задач – в этом заключается универсальность математических методов.
Второй способ введения алгоритмов позволяет формировать у учащихся такой элемент алгоритмической культуры, как умение выполнять формальные предписания. Однако следует помнить, что это оперирование по формальному предписанию важно не само по себе, а для достижения определенных целей: познавательных, практических и тому подобное. За знаками, с которыми оперируют по данному алгоритму, стоит определенное внезнаковое содержание, которое отображается с помощью данных знаков. В случае алгоритма в математическом смысле мы отвлекаемся (в определенной мере) от этого содержания. Такое абстрагирование облегчает действия по алгоритму, так как исполнителю не приходиться отвлекать внимание на смысл операций и значение знаков, с которыми оперирует по алгоритму. При решении текстовых задач с использованием известных алгоритмов содержательному толкованию подвергаются лишь исходные данные решаемой задачи и результат ее решения по данному алгоритму. Здесь важно, что бы учащиеся умели устанавливать соответствия между формальными знаками, с которыми работает алгоритм, и отображаемым в них содержанием. Такие умения формируются у учащихся при содержательном введении операций и алгоритмов.
Все три аспекта важны в системе школьного обучения, поэтому при изучении операций и алгоритмов их выполнения следует использовать оба способа их введения.
При содержательном способе введения операций и алгоритмов их выполнения большую роль играет выбор сюжетных задач, которые называются ведущими. В качестве ведущих следует набирать такие задачи, которые удовлетворяют следующим требованиям:
1) при выборе фабулы задачи следует учитывать и использовать практический опыт учащихся;
2) меняя числовые данные в задаче, можно рассмотреть все возможные случаи вводимой операции;
3) содержательный способ решения задачи должен быть адекватным вводимому алгоритму.
Проведение анализа задач, использованных в качестве ведущих, в учебниках математики, с точки зрения высказанных требований, может способствовать улучшению изложения материала учебников.[16]
Рассмотрим содержательный способ введения на примере алгоритма сложения дробей с разными знаменателями.
В начале урока учитель предлагает ученикам для решения следующую задачу:
« Изобразите
в тетради такой же квадрат, как на
рисунке. Закрасьте ½ квадрата синим
цветом, ¼ - красным, 1/8 – желтым, 1/16 –
зеленым. Какая часть квадрата осталась
незакрашенной? Какая часть квадрата
закрашена?»[9]
Изобразите
в тетради такой же квадрат, как на
рисунке. Закрасьте ½ квадрата синим
цветом, ¼ - красным, 1/8 – желтым, 1/16 –
зеленым. Какая часть квадрата осталась
незакрашенной? Какая часть квадрата
закрашена?»[9]
Ребята без труда ответят на вопросы задачи. Далее учитель задает вопрос: «Как ответить на вопрос задачи, не пользуясь рисунком? С помощью каких действий?». Этот вопрос также не будет затруднительным, ученики без труда ответят, что нужно сложить ½ +1/4 +1/8 + 1/16. Но возникает проблема, как это сделать, так как пока изучено только сложение дробей с одинаковыми знаменателями. Таким образом перед учениками ставиться цель – научиться складывать дроби с разными знаменателями. После этого учитель вводит алгоритм сложения дробей с разными знаменателями:
приведем эти дроби к общему знаменателю;
выполним сложение по правилу сложения дробей с равными знаменателями.
После введения алгоритма и выполнения нескольких примеров на закрепление, без труда решается задача, предложенная в начале урока. Плюс задачи в том, что можно сразу проверить полученный результат с тем, который получился при закрашивании квадрата.
Рассмотрим другой способ введения алгоритма – формальный, на примере сложения десятичных дробей.
В начале урока ученикам предлагаются для решения различные несложные упражнения. Например,
Выполнить сложение: 1/7 + 5/7; 1/10 + 7/10.
Записать в виде обыкновенной дроби числа: 0,5; 0,07.
Представить числа в виде разрядных слагаемых: 457; 4,57; 56; 0,56.
Назвать числа, равные числу 4,7.
Сложить числа, представив их в виде суммы разрядных слагаемых и применив законы сложения: 286 + 37.
В
 ыполнить
сумму, называя каждый раз единицы каких
разрядов вы складываете: 5873
ыполнить
сумму, называя каждый раз единицы каких
разрядов вы складываете: 5873
 326
326
Далее вводиться сам алгоритм сложения десятичных дробей:
Уровнять число знаков после запятой в слагаемых;
Записать слагаемые друг под другом так, что бы запятая оказалась под запятой;
Сложить полученные числа, как складываются натуральные числа;
Поставить в полученной сумме запятую под запятыми в слагаемых.
После введения алгоритма может быть рассмотрена задача, например:
«В соревнованиях по тройному прыжку Юра сделал прыжки 2,48 м, 2,76 м и 3,42 м, а Саша – 2,54 м, 2,3 м и 3,56 м. Кто из мальчиков стал победителем?»[10]
Заключение
Данное исследование проводилось с целью рассмотреть особенности организации этапа мотивации при введении математических предложений.
Основные задачи, которые ставились перед началом исследования, были выполнены. Анализ психолого-педагогической и учебно-методической литературы показал, что сформированность мотивации является важным качественным показателем эффективности учебно-воспитательного процесса. Но в то же время данной теме уделяется мало внимания, в основном идет упоминание о мотивации, говориться о ее роли, но ее сущность полностью не раскрывается.
В работе рассмотрены психологические характеристики мотивационной сферы учения, а именно потребностей, мотивов, целей, интересов. Главная же направленность мотивационной сферы – мотивы, т.е. направленность учащихся на отдельные стороны учебного процесса.
Выделены различные пути и методы формирования положительной устойчивой мотивации к учебной деятельности. Для получения более эффективного результата следует использовать не один путь, а все пути в определенной системе. Рассмотрена реализация этапа мотивации учебной деятельности при изучении математических понятий, теорем и алгоритмов. По рассмотренным методическим рекомендациям было проведено опытное преподавание.
Гипотеза, выдвинутая в начале работы, подтвердилась в ходе проведения исследования. Действительно, мотивационный этап при введении математических предложений способствует формированию у учащихся положительных мотивов учения и познавательных интересов учебной деятельности.
Библиографический список
Брадис, В.М. методика преподавания математики в средней школе. Государственное учебно-педагогическое издательство министерства просвещения РСФСР. М, 1954г.
Волович, М.Б. Наука обучать. Технология преподавания математики. М. Linka-Press, 1995г.
Возняк, Г.М. Прикладные задачи в мотивации обучения. // Математика в школе. №2, 1990г.
Глейзер, Г.И. История математики в школе. Пособие для учителей. Под редакцией В.Н. Молодшего. М. «Просвещение», 1964г.
Груденов, Я.И.. Совершенствование методики работы учителя математики, М: Просвещение, 1990.
Груденов, Я.И. Изучение определений, аксиом, теорем. М. Просвещение, 1981.
Дробышева, И.В. Мотивация: дифференцированный подход. // Математика в школе. № 4, 2001г.
Дубнов, Я.С. Беседы о преподавании математики. М. «Просвещение», 1965г.
Дорофеев, Г.В., Петерсон, Л.Г. Математика. Учебник для 5 класса. Часть вторая. М. «Баланс», С-инфо, 1997.
Зубарева, И.И., Мордкович, А.Г. Математика. 5 класс. Учебник для общеобразовательных учреждений. М. «Мнемозина», 2003г.
Карелина, Т.М. О проблемных ситуациях на уроках геометрии. // Математика в школе. №6, 1999г.
Лоповок, Л.М. Тысяча проблемных задач по математике. Книга для учащихся. М. Просвещение, 1995г.
Лященко, Е.И. и др. Лабораторные и практические работы по методике преподавания математики. М. Просвещение, 1988.
Маркова А.К., Орлов А.Б., Фридман Л.М. Мотивация учения и ее воспитание у школьников, М. Педагогика, 1983.
Маркова А.К., Т.А. Матис, А.Б. Орлов. Формирование мотивации учения, М. Просвещение, 1990.
Методические разработки по методике преподавания математики в средней школе. М. МГПИ, 1980.
Мордкович, А.Д. Алгебра. 9 класс. Учебник для общеобразовательных учреждений. М. «Мнемозина», 2002 г.
Рогановский, Н.М. Методика преподавания математики в средней школе. Минск. Высшая школа, 1990г.
Саранцев, Г.И. Общая методика преподавания математики. Саранск. Типография «Красный Октябрь», 1999.
Саранцев, Г.И. Эстетическая мотивация в обучении математике. Саранск. Типография «Красный Октябрь», 2003г.
Саранцев, Г.И. Формирование математических понятий в средней школе. // Математика в школе. №6, 1998г.
Скороходова Н.Ю. Психология ведения урока. С.Пб. Речь, 2002.
Таймасханов, У.Д. Создание проблемных ситуаций. // Математика в школе. №5, 1994г.
Фридман, Л.М. Теоретические основы методики обучения математике. Пособие для учителей, методистов и педагогических высших учебных заведений. М. Издательство «Флинта», 1998г.
Приложение 1.
Урок геометрии в 10 классе.
Тема урока: «Параллельность прямой и плоскости».
Цели урока:
введение понятия параллельности прямой и плоскости;
введение признака параллельности прямой и плоскости и его доказательство.
Этап мотивации:
В начале урока ученикам предлагается рассмотреть все возможные случаи взаимного расположения прямой и плоскости в пространстве и привести примеры из окружающей нас действительности.
прямая лежит в плоскости (сформулируйте аксиому, в которой выражено свойство принадлежности прямой плоскости);
прямая и плоскость имеют только одну общую точку, то есть пересекаются;
прямая и плоскость не имеют ни одной общей точки.
Третий случай дает определение параллельности прямой и плоскости, попробуйте сформулировать его сами.
Определение: прямая и плоскость называются параллельными, если они не имеют общих точек.
Примеры:
натянутые троллейбусные провода параллельны плоскости земли;
линия пересечения стены и потолка параллельна плоскости пола, эта же линия параллельна плоскости стола.
Назовите различные пары прямых и плоскостей параллельных между собой на примере куба.
Далее идет изучение теоремы, сначала можно рассмотреть следующий пример:
На стол положим спицу а1, вторую спицу а2, расположим так, чтобы она была параллельна спице а1. Ставим перед классом вопрос: «Что можно сказать о взаимном расположении спицы а2 и поверхности стола?» После получения правильного ответа задаем еще один вопрос: «Какую теорему можно сформулировать?»
Теорема: «Если прямая не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости».
После введения теоремы идет ее доказательство.
Приложение 2.
Урок алгебры в 7 классе.
Тема урока: «Вынесение общего множителя за скобки».
Цель урока: ввести алгоритм для вынесения общего множителя за скобки.
Этап мотивации:
В начале урока проводиться актуализация знаний.
1 задание: раскрыть скобки
2(х + 3у – 10х2у);
5у2(1 – 4х);
- 3ху( - 5х + 3у2 – 1).
2 задание: найти НОД чисел
15 и 10;
35 и 14;
16, 12 и 8.
3 задание: выделить общий множитель
х2 и ху;
( - у2z) и ( - xz);
2х и 4у.
После этапа актуализации знаний для решения предлагается следующее упражнение: «Сократите дробь (х – у)/(ах – ау)».
Ученики замечают, что для того чтобы сократить дробь достаточно в знаменателе вынести а за скобки и дробь можно сократить на (х – у). После выполнения упражнения учитель отмечает, что при выполнении многих заданий и при решении задач бывает полезно выносить общий множитель за скобки.
Рассмотрим пример разложения многочлена на множители с помощью вынесения общего множителя за скобки.
Разложить на множители многочлен 10ху2 – 6ху.
Обычно в многочлене с целыми коэффициентами множитель выносимый за скобки, выбирают так, чтобы члены многочлена, оставшегося в скобках, не содержали общего буквенного множителя, а модули их коэффициентов не имели общих делителей. В данном примере общим множителем является одночлен 2ху или ( - 2ху). Вынесем, например, за скобки 2ху. Получим:
10ху2 – 6ху = 2ху*5у – 2ху*3 =2ху (5у – 3).
Таким образом при вынесении общего множителя за скобки мы пользуемся несложным алгоритмом:
Найти НОД коэффициентов всех слагаемых;
выделить общий множитель в каждом члене многочлена;
вынести общий множитель за скобки.
Далее предлагаются упражнения на отработку введенного алгоритма.