Статистические методы оценки значимости компонент педагогической системы учителя

Профессиональная деятельность учителя включает следующие компоненты, которые им реализуются в разной степени, что и определяет уровень и качество его работы:

1) исследовательский (умение находить, ставить и разрешать проблемные ситуации, формулировать цели и задачи, определять предмет и объект исследования, выбор методов исследования, их использования, делать выводы из результатов исследования);

2) информационный (умение воспринимать информацию, собирать и анализировать ее, систематизировать, конструировать, обобщать, визуализировать, вербализировать, трансформировать и транслировать информацию);

3) интеллектуальный (умение систематизировать, анализировать и обобщать учебный материал и результаты учебной деятельности, синтезировать, сравнивать, выделять главное и определяющее в учебном процессе);

4) прогностический (умение прогнозировать ход учебного процесса и его результат, осуществлять целеполагание с формулировкой целей, задач. гипотезы, умение выяснять условие реализации прогноза, осуществлять поиск резервов с учетом аудитории, закономерностей, проводить верификацию прогноза с учетом результатов практики и обратной связи);

5) креативный (умение осуществлять типизацию, включать воображение, умение ставить акценты и осуществлять модернизацию элементов учебного процесса);

6) аксиологический (умение выбирать объекты, формы и методы контроля, отбор значимых параметров учебного процесса, обладание способностью к самоорганизации);

7) диагностический (умение проводить диагностирование, выбирать оптимальные методы диагностирования, обрабатывать на основе современных математических методов результаты учебной деятельности);

8) коммуникативный (умение устанавливать контакты с аудиторией и коллективом, строить и реализовывать стратегию взаимодействия с обменом информацией);

9) проектировочный (умение осуществлять процедуру целеполагания, планировать и конструировать учебный процесс на основе его математического моделирования с учетом реальных условий его реализации);

10) управленческий (учение организовывать коллектив учащихся на выполнение поставленных целей, умение прогнозировать, проектировать, информировать, контролировать, отслеживать результаты деятельности и своевременно их корректировать, умение реализовывать мотивации).

Представлялось небезынтересным выявить наиболее важные с точки зрения ряда учителей (экспертов) компоненты их профессиональной деятельности, оценить степень согласованности их мнений (степень конкордации мнений).

Для этого была составлена матрица рангов для оценки значимости каждого из десяти указанных выше компонент профессиональной деятельности учителя и проведены необходимые математические операции с экспертными оценками значимости каждой из компонент.

Их результаты сведены в таблицу:

Факторы	X_>1>	X_>2>	X_>3>	X_>4>	X_>5>	X_>6>	X_>7>	X_>8>	X_>9>	X_>10>
Сумма рангов	7	8	20	48	35	25	16	32	47	37
Квадраты отклонений	110,25	420,25	56,25	420,25	56,25	6,25	132,25	20,25	380,25	90,25
Место факторов	1	2	4	10	7	5	3	6	9	8

Итак, по значимости учителя-эксперты расположили факторы-компоненты учебной деятельности в следующем порядке: исследовательский, информационный, диагностический, прогностический, аксиологический, коммуникативный, креативный, управленческий, проектировочный, прогностический. Естественно, другие эксперты могут дать другое место факторам, однако исследования предполагают демонстрацию общих методов проведения статистических оценок педагогической деятельности учителей.

Обращает на себя внимание тот факт, что сумма рангов у четвертого компонента (прогностический элемент) существенно выше, чем у остальных (исключение составляет лишь проектировочный элемент). Может показаться, что этот результат сомнителен, хотя его можно объяснить недостаточной подготовленностью учителей к решению соответствующих проблем. Для проверки «сомнительности», то есть в известном смысле аномальности, используем критерий получения аномальных результатов по результатам исследований. Согласно соответствующей процедуре упорядочим ряд из оценок суммы рангов в порядке возрастания результатов этих экспертных оценок:

то есть получим следующий ряд: 7 8 16 20 25 32 35 37 47 48.

Проверим нулевую гипотезу Н_>0>, альтернативную Н_>1>, для случая х_>10>, считая его максимально аномальным. Тогда критериальная статистика вычисляется по формуле:

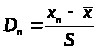, где .

Распределение и процентные точки получены К. Пирсоном и Н.В. Смирновым.

Для нашего случая , S = 13,01, D_>10> = 1,576.

По заданному уровню значимости () по таблице критических значений статистики D_>n> находим критическое значение : оно для =0,05 и объема выборки n = 10 равно 2,294.

Так как , то гипотеза H_>0> об аномальности оценки x_>10> не подтверждается, т.е. x_>10>уклоняется от среднего значения незначительно.

Исследуем согласованность мнений экспертов. С этой целью воспользуемся методами математической статистики и определим коэффициент конкордации, позволяющий выявить, хорошо ли согласуются ранжировки друг с другом. В рассматриваемом случае эксперты приписывают факторам разные номера, и совпадающих номеров нет. Тогда ранги равны приписываемым номерам и являются целыми числами. Коэффициент конкордации вычисляется по формуле:

где S – наблюдаемая сумма квадратов отклонений, k – количество экспертов, n – число членов выборки (факторов), тогда W = 0,821.

Проверим значимость W. Если ранжировки независимы, то величина имеет примерно F-распределение с числом степеней свободы (v_>1> = 9), 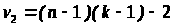, v_>2> = 34. Находим, что величина значима для уровня . Следовательно, можно утверждать, что существует неслучайная согласованность мнений экспертов: их мнения согласуются.

Представляет определенный интерес проанализировать согласованность и взаимную корреляцию оценок отдельных пар экспертов. Для этого вычислим коэффициенты ранговой корреляции Спирмена, определяемые следующим образом:

отсюда

Проанализируем для первых двух мнений экспертов. Первый эксперт проанализировал компоненты учебной деятельности в порядке возрастания их значимости следующим образом:

Соответственно, в порядке возрастания рангов можно записать:

1 2 3 4 5 6 7 8 9 10

Этим рангам соответствуют ранги 2-го эксперта:

1 2 3 4 5 8 6 7 9 10

Тогда для пары первый-второй эксперт .

По таблицам распределения Стьюдента для n = 10. и верхнее критическое значение коэффициента Спирмена, равное 0,745. Так как найденное значение меньше критического, то «нуль-гипотеза» (Н_>0>) отклоняется, и значит мнения первого и второго экспертов коррелированны.

Вообще говоря, можно было бы сделать вывод о корреляции мнений и по другому методу.

Дело в том, что если больше нуля, то корреляция положительная, а если меньше нуля – она отрицательная.

Для корреляции мнений 1-го и 3-го экспертов , , то есть мнения 1-го и 3-го экспертов коррелированны.

Для 1-го и 4-го экспертов , , то есть мнения 1-го и 4-го экспертов коррелированны.

Для 1-го и 5-го экспертов , , то есть мнения 1-го и 5-го экспертов коррелированны.

Помимо коэффициента ранговой корреляции Спирмена при статистической обработке результатов исследований пользуются коэффициентом ранговой корреляции Кендалла.

В соответствии с этим методом определения корреляции рассмотрим упорядоченные по Y ранги: 1, 2, 3, …, n и соответствующие им ранги X: q_>1>, q_>2>, q_>3>, …, q_>n>.

Коэффициент ранговой корреляции Кендалла вычисляется по формуле:

или по эквивалентной формуле:

где называется статистикой Кендалла, - сумма инверсий для рангов X.

Если , то корреляция положительная, а если - отрицательная.

Анализ корреляции мнений экспертов позволяет получить:

1-й - 2-й эксперты: ; ; – корреляция положительная.

1-й - 3-й эксперты: ; ; – корреляция положительная.

1-й - 4-й эксперты: ; ; – корреляция положительная.

1-й - 5-й эксперты: ; ; – корреляция положительная.

Таким образом, в результате использования статистических методов выявления значимости компонент учебного процесса, степени согласованности мнений экспертов и выявления корреляции между мнением 1-го эксперта и каждого последующего (по Спирмену и Кендаллу) получено согласованное заключение экспертов о том, что наиболее значимыми для успешного проведения учебного процесса являются умение учителя организовывать урок таким образом, чтобы он представлял собой для ученика цепь проблемных ситуаций с четко поставленными целями и задачами урока.

Урок должен быть логически завершенным с четкими выводами по результатам исследования того или иного физического явления. В этом отношении просматриваются особая роль физического эксперимента и компьютерных дидактических материалов.

Важным компонентом урока должна быть его информативность, опирающаяся на умение учителя собирать, анализировать, систематизировать, визуализировать и вербализировать учебную информацию. В этой работе нельзя переоценить значимость компьютерно-ориентированных технологий, тем более, что их роль в проведении диагностических операций и обработке результатов с использованием современных математических методов очень высока.

Нельзя не отметить, что экспертные оценки могут быть и иными, что вполне возможно и зависит от многих причин и условий проведения педагогического эксперимента, и, в первую очередь, от выбранной для обучения педагогической системы, ее системообразующего фактора и реализующей ее идеи педагогической технологии, традиций, целевой направленности и т.д.

Однако выявление уровня значимости набора компонент учебного процесса может быть в каждом конкретном случае проведено на основе строгих математических (в данном случае – статистических) методов, значимость которых велика как в естественнонаучных исследованиях, так и в педагогических.