Самоанализ деятельности учителя как основа управления процессом обучения математике
Содержание
Введение
Глава 1. Теория и технология самоанализа урока математики
1.1.Специфика урока математики в современной школе
1.2.Теория анализа урока
1.3.Технология самоанализа урока математики
Глава 2. Использование технологии самоанализа урока математики в учебном процессе
2.1.Подготовка учителя к работе с технологией
2.2. Система
упражнений, направленная на повышение
уровня компетентности учителя
математики
2.2.1. Система упражнений по повышению компетентности в постановке цели урока
2.2.2. Система упражнений по повышению компетентности учителя в отборе содержания учебного материала
2.2.3. Система упражнений по повышению компетентности учителя в выборе методов обучения
2.2.4. Система упражнений по повышению компетентности учителя в выборе форм обучения
2.2.5. Система упражнений по повышению компетентности учителя в подведении итогов урока
2.3. Опыт применения технологии самоанализа урока математики
Заключение
Библиографический список
Введение
Одной из главных форм процесса обучения был и остается урок. Современный урок отличается прежде всего тем, что учитель умело использует все возможности для развития личности ученика, её активного умственного роста, глубоко и осмысленного усвоения знаний, для формирования её нравственных основ. Совершенно очевидно, что для осуществления всех этих и многих других сложных задач не может быть раз и навсегда установленного типа урока, с застывшими навечно этапами и стандартной последовательностью их осуществления. Поэтому очень важно уделять большое внимание самоанализу как отдельного урока, так и всей деятельности учителя в целом с целью эффективного управления процессом обучения.
Повышение квалификации учителя математики во многом зависит от степени владения умениями анализировать свою деятельность и деятельность своих коллег. Анализ и самоанализ урока должны быть направлены на сопоставление выдвинутых образовательных, воспитательных и развивающих целей с достигнутым результатом.
Цель анализа заключается в выявлении методов и приемов организации деятельности учителя и учащихся на уроке. Основной же задачей при этом является поиск резервов повышения эффективности процесса обучения.
На основе анализа деятельности своих коллег и самоанализа, можно выделить направления совершенствования качества процесса обучения и поставить задачи по их реализации. Тем самым, учитель может повысить уровень своего мастерства в управлении процессом обучения. Такой анализ является необходимым в работе каждого учителя, как начинающего, так и учителя, имеющего опыт работы. Необходимость выявления особенностей самоанализа деятельности учителя математики как основы управления процессом обучения определяет актуальность исследования выпускной квалификационной работы.
Проблему исследования составляет поиск путей эффективного самоанализа урока математики как основы управления процессом обучения.
Объектом исследования является процесс обучения математике.
Предмет исследования – технология самоанализа урока математики.
Цель работы заключается в исследовании теоретических основ анализа урока и построении технологии самоанализа урока математики.
В основу исследования положена гипотеза: если разработать технологию самоанализа урока математики, на её основе подобрать систему упражнений по повышению компетентности учителя и применить ее на практике, то это будет способствовать управлению процессом обучения математике и росту мастерства учителя.
Для достижения поставленной цели и проверки сформулированной гипотезы потребовалось решить следующие задачи исследования:
провести анализ психолого-педагогической и математико-методической литературы с целью определения роли и места анализа деятельности учителя математики в процессе обучения;
раскрыть специфику урока математики в современной школе для ее использования в процессе самоанализа деятельности педагога;
выявить теоретические основы самоанализа урока;
разработать технологию самоанализа урока математики;
дать рекомендации, позволяющие использовать самоанализ для эффективного управления процессом обучения;
опытным путем убедиться в верности разрабатываемой технологии.
Для решения поставленных задач и проверки гипотезы применялись следующие методы исследования:
– изучение и анализ психолого-педагогической и математико-методической литературы по теме исследования;
– проведение опытной работы и экспериментальная проверка основных положений дипломного исследования;
– количественная интерпретация результатов педагогического эксперимента.
Теоретическая значимость результатов исследования определяется выделением основных принципов анализа и самоанализа урока и построением технологии анализа урока.
Практическая значимость результатов исследования заключается в разработке схемы поэтапного самоанализа урока, которая дает качественную и количественную информацию об эффективности проведенного урока математики, и разработке системы упражнений по каждому аспекту урока, которая направлена на устранение пробелов в необходимом блоке структуры урока.
Выпускная квалификационная работа состоит из введения, двух глав, заключения, библиографического списка.
Глава 1. Теория и технология самоанализа урока математики
1.1 Специфика урока математики в современной школе
Математика всегда считалась самой сложной наукой, что придавало ей больший интерес и привлекало внимание ученых-исследователей. В настоящее время роль математики в обществе не угасла, а лишь возросла.
Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, связанная с мышление человека, с овладением определенным методом познания и преобразования мира математическим методом.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И, наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, финансы, химия, информатика, техника, биология, психология и многие другие).
Таким образом, возрастает роль математической подготовки в общем образовании современного человека, и, в связи с этим, ставятся конкретные цели обучения математике в школе. В пояснительной записке к Программе для образовательных учреждений [12] четко определена цель обучения математике, которая определяется ролью математики в развитии общества в целом и формировании личности каждого отдельного человека. Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Г. И. Саранцев выделяет две группы целей обучения математике, которые, на наш взгляд, являются более полными и полностью удовлетворяют требованиям программы для общеобразовательных учреждений [13].
Первая группа целей математического образования включает в себя овладение системой математических знаний, умений и навыков, дающей представление о предмете математики, ее языке и символике, математическом моделировании, специальных математических приемах, об алгоритме и периодах развития математики, основными общенаучными методами познания и специальными эвристиками, используемыми в математике.
Вторую группу целей составляют: формирование мировоззрения учащихся, логической и эвристической составляющих мышления, алгоритмического мышления; воспитание нравственности, культуры общения, самостоятельности, активности; эстетического воспитания школьников; воспитания трудолюбия, ответственности за принятие решений, стремление к самореализации.
Основной организационной формой массового обучения математике в современной школе всегда был и остается урок, имеющий немало известных педагогических достоинств. Необходимо отметить специфичность математики и ее отличие от других предметов. А. Я. Хинчин в своей статье «О воспитательном эффекте урока математики» [22] говорит о том, что математика, в отличие от большинства других преподаваемых в школе дисциплин, имеет предметом своего изучения не непосредственно вещи, составляющие окружающий нас внешний мир, а количественные отношения и пространственные формы, свойственные этим вещам. Этой особенностью объясняются методические трудности, которые встают перед преподавателем математики, и которых почти не знают преподаватели других наук. Перед учителем математики стоит нелегкая задача – преодолеть в сознании учеников возникающее представление о «сухости», формальном характере, оторванности этой науки от жизни и практики.
Этой же особенностью математической науки объясняется специфика задач, которые встают перед учителем математики, если он хочет использовать преподавание своей науки в воспитательных целях. Стоящая перед ним задача труднее, чем в случае большинства других наук. Ибо математика – научная дисциплина, занятая изучением не самих вещей, а лишь отношений между ними и потому необходимо требующая поднятия на некоторую ступень абстракции.
Специфичность науки выделяет урок математики из всей системы уроков, которая предлагается в современном школьном учебно-воспитательном процессе. Урок математики обладает целым рядом специфичных особенностей. Для него характерны и являются наиболее существенными следующие признаки [9]: 1) содержание урока математики не является автономным, оно разворачивается с опорой не ранее изученное, подготавливая базу для освоения новых знаний, что связано со строгой логикой построения курса математики; 2) в процессе овладения системой математических знаний, в большей степени по сравнению с другими учебными предметами, уделяется внимание развитию у учащихся логического мышления, умений рассуждать и доказывать; 3) при обучении математике должны быть созданы условия для того, чтобы каждый ученик мог усвоить на уроке главное в изученном материале, поскольку без базовой математической подготовки невозможна постановка образования современного человека; 4) стремление к эффективному обучению школьников на уроках математики обусловлено и тем, что в школе математика служит опорным предметом для изучения смежных дисциплин; 5) в процессе обучения математике теоретический материал осознается и усваивается преимущественно в процессе решения задач, потому на уроках математики чаще всего теория не изучается в отрыве от практики.
Для достижения поставленных целей в изучении математики необходимо учитывать специфичность урока математики при его построении. Общая структура урока характеризуется следующими этапами: постановка цели урока; проверка домашнего задания; повторение пройденного; объяснение нового материала; применения знаний и умений; закрепление изученного; обобщение и систематизация новых знаний; контроль знаний и умений учащихся; постановка домашнего задания. В зависимости от типа урока математики один или несколько этапов урока являются определяющими. Выделим несколько типов современных уроков математики и для каждого определим ведущий его этап: урок ознакомления с новым материалом (этап объяснения нового материала); урок закрепления изученного (этап закрепления изученного); урок применения знаний и умений (этап применения знаний и умений); урок обобщения и систематизации знаний и умений (этап обобщения и систематизации знаний и умений); комбинированный урок; урок-зачет (этап применения, контроля знаний и умений) и т. д.
Каждому типу урока соответствует свое строение, свои цели, методы и формы. В зависимости от типа урока математики выполняется логическое построение содержания. И здесь очень важна роль учителя, его уровень компетентности, который должен постоянно расти. Для достижения высокого уровня мастерства учителя, который позволит повысить эффективность процесса обучения математике, очень важна роль самоанализа урока, поскольку анализ является основным методом познания чего-либо. Понятие комплексного анализа, его принципы и формы рассмотрены в следующем пункте.
1.2 Теория анализа урока
Выделим несколько определений анализа.
Анализ – рассмотрение, изучение, научное исследование чего-либо, мысленное расчленение объекта исследования на образующие элементы и изучение свойств последних [15].
Анализ – процедура мысленного, а часто также и реального расчленения предмета (явления, процесса), свойств предмета (предметов) или отношений между предметами на части (признаки, свойства, отношения) [21].
Наиболее точное, на наш взгляд, определение анализа дает С. В. Кульневич [8]. Анализ – логический прием познания, представляющий собою мысленное разложение предмета (явления, процесса) на части, элементы или признаки, их сопоставление и последовательное изучение с целью выявления существенных, т.е. необходимых и определенных качеств и свойств.
В разных источниках можно встретить разнообразные виды анализа современного урока. По мнению С. Г. Манвелова [9], наиболее распространенными типами анализа урока является: полный, комплексный, краткий и аспектный. Н. Ю. Ерофеева [2] в своей статье, посвященной диагностике и анализу учебного процесса, выделяет пять основных видов анализа современного урока: краткий, структурный, аспектный, полный и комплексный. С. В. Кульневич [8], предлагает три классификации анализа урока: по общим основаниям (педагогический, психологический, методический, сопоставительный, целевой, выборочный, анализ с точки зрения педагогического общения, физиолого-гигиенический); по времени педагогической деятельности (предваряющий, текущий, ретроспективный, комплексный ретроспективный); на основе усложнения видов анализа (краткий, структурный, поэлементный, системный, аспектный, полный, содержательной направленности, структурно-временной, комбинированный, дидактический, комплексный).
Так же как и анализ, самоанализ, на наш взгляд, имеет несколько видов: краткий, структурный, аспектный, полный и комплексный.
Проблему анализа и оценки эффективности деятельности учителя и учащихся на уроке целесообразно рассматривать в единстве с проблемой формализма и в учебно-воспитательном процессе, и в деятельности лиц, контролирующих его. В связи с этим возникает ряд вопросов. Во-первых: каковы основные принципы анализа деятельности учителя и учащихся и какое количество фактических данных необходимо для объективного и квалифицированного анализа; во-вторых: как помочь учителю выявить резервы повышения эффективности учебно-воспитательного процесса и не превращать анализ урока в пересказ его содержания.
Эффективность анализа современного урока зависит от соблюдения ряда принципов. Принципы педагогического анализа урока являются отражением объективных закономерностей и связей, присущих процессу обучения. Совокупность этих принципов представляет собой систему, в которой каждый из них так или иначе взаимодействует со всем большинством принципов. Поэтому нарушение одного из них может привести к нарушению других. Успех анализа урока достигается последовательным применением всей системы принципов и каждого из них в отдельности.
Вслед за В. П. Симоновым [16] на первое место поставим принцип оптимальности. Этот принцип тесно связан с научностью и целесообразностью требований. Это говорит о том, что в систему требований, которая предъявляются к уроку при его анализе, должны включаться только важные вопросы, а не второстепенные. Учитель должен четко понимать какие направления в его деятельности главные, генеральные, на что ему следует обратить внимание в первую очередь. Такие рекомендации, как обращать внимание, «не слышен ли шум с улицы, из других классов и коридора» или «где проходит урок: в классе, кабинете, лаборатории», не имеют отношения к анализу урока и его эффективности.
Второй принцип, который является не менее важным, чем первый, – это принцип объективности. По мнению Ю. А. Конаржевского [6] для анализа урока этот принцип играет особенно важную роль. Объективные свойства, связи, отношения внешнего мира отражаются человеком не механически. Он пытается как-то объяснить познанные факты, делает из них какие-то определенные выводы, стремится сформулировать свое собственное отношение к добытым в процессе познания фактам. Поэтому педагогическая действительность, хотя и существует независимо от субъекта анализа, определяя характер и общее направление деятельности руководителя, становится одновременно предметом его познания.
Эти субъективные моменты будут совпадать с объективным содержанием, если учитель будет достаточно подготовлен в теоретическом отношении и будет иметь набор знаний, необходимых для анализа урока. Если же таковые отсутствуют, то субъективные моменты будут противоречить объективному содержанию знания.
В процессе анализа урока необходимо исходить не из наших субъективных мнений о нем, а из него самого, необходимо не мышлению подчинять анализируемый урок, а мышление аналитика подчинять этому уроку.
В контексте анализа урока принцип объективности предусматривает следующее.
Необходимость при анализе урока исходить из него самого, из присущих ему свойств, связей, отношений, закономерностей развития, выводить из него самого логику его собственного движения, а не накладывать на него свои субъективные схемы.
Отчленение существенных черт урока от несущественных, обусловленных временными, преходящими факторами его развития. Отделение закономерного от незакономерного, является важным условием объективного подхода к анализу урока. Смещение существенного и несущественного, типичного и нетипичного при анализе урока ведёт к необъективной оценке.
Объективный подход к анализу урока требует учета не только качественной его определенности как некой целостности, но и его количественных характеристик.
Не только признание противоречий в развитии урока, но и анализ источника этих противоречий, логики их движения, учет их связи с другими противоречиями, показ их связи с другими обстоятельствами становления и развития анализируемого урока.
Этот принцип требует от учителя не анализа урока вообще, а конкретного анализа его составляющих, их взаимодействия и т.д.
Следующий принцип, который предложил В. А. Тестов для построения образовательных процессов обучения математике [19], подходит, на наш взгляд, и для анализа урока математики – принцип взаимосвязанности. Этот принцип предполагает рассмотрение совокупности устойчивых связей, обеспечивающих целостность изучаемого объекта. Анализ урока не может ограничиться изучением отдельных составляющих, их необходимо рассматривать в связи. Лишь через различные отношения внешние и внутренние составляющие урока, его элементы и подсистемы могут проявить свою сущность. Поэтому изучение структуры урока является единственным путем проникновения вглубь этого процесса. В теории анализа урока этот принцип, наряду с другими принципами, играет важную роль.
Принцип развития, по мнению Ю. А. Конаржевского [6], находится в тесной связи с принципом взаимосвязи и взаимодействия. Только в результате всеобщего изменения и развития объективной реальности возникают различные, в том числе и связи, между разного рода явлениями.
Исходя из этого принципа, учителю, ведущему педагогический анализ, необходимо рассматривать каждую ступень изучаемого процесса в неразрывной связи с ее внутренними, сущностными тенденциями и внешними условиями.
Применительно к анализу урока принцип развития можно сформулировать следующим образом: предметом анализа является ряд последовательных качественных и количественных изменений (предмета, явления, процесса), обладающих единой, общей и внутренней для них тенденцией к движению конечного определенного результата. Иными словами, рассматривать предмет анализа следует в процессе возникновения становления, изменения и развития.
Принцип развития предъявляет к построению процесса анализа урока целый ряд определенных требований: рассматривать урок в становлении и развитии, вскрывать его противоречивый характер, учитывать количественные и качественные изменения в ходе процесса учения, перехода учащихся и урока из одного состояния в другое, определять связь между прошлым, настоящим и будущим. Только такой путь может привести к установлению причины получения того или иного конечного результата, удовлетворительного или неудовлетворительного.
Анализ урока должен быть направлен на развитие учителя, его профессионализма, на включение его в режим творчества. В противном случае анализ урока теряет всякий смысл, приобретает формальный характер и становится никому не нужным.
Следующий принцип, который выделяет Ю. А. Конаржевский [6], является важным для самого учителя, который проводит урок. Конкретными инструментами воплощения в жизнь человекоцентристского принципа в анализе урока является уважение к человеку, доверие и доброжелательное отношение к нему.
Исходя из этого, принцип человекоцентризма конкретно в анализе урока выражается в следующем.
Посещение и анализ урока рассматривается не как контроль за работой учителя, а как услуги, которую ему оказывается в целях дальнейшего совершенствования его профессиональной подготовки.
Анализ урока – это инструмент, при помощи которого осуществляется признание результатов труда учителя.
Анализ урока – это канал для контакта с руководителем школы, это возможность для совместной работы руководителя и учителя по совершенствованию профессиональной деятельности последнего.
Анализ урока – это стимулятор педагогической производительности учителя, его прогресса.
Анализ урока – это канал, использование которого дает возможность руководителю школы формировать единство лично-профессиональных целей учителя и целей общешкольных, осуществлять мотивирование деятельности педагога, формировать его профессиональную уверенность.
Главная задача руководителя в анализе урока – постоянно формировать у учителя чувство успеха.
Очень важно в ходе анализа уроков подготавливать учителя к постепенному самоанализу уроков и рефлексированию своей деятельности.
Для эффективности анализа урока важен принцип активности, выделенный Ю. А. Конаржевским [6]. Применительно к анализу урока он требует активной позиции аналитика по отношению как к уроку, так и к его автору –учителю – с целью расширения сущности анализируемого процесса, его дальнейшего совершенствования, а если это необходимо, то и преобразования.
Если аналитик выступает в роли пассивного фиксатора, простого наблюдателя, созерцателя, он не принесет никакой пользы учителю. Анализируя урок, руководитель должен активно мыслить, стремиться вскрыть перед учителем сущность проведенного им урока, выявить присущие ему свойства и связи. Все это предполагает существенную переработку чувственных образов, полученных в результате непосредственного наблюдения урока, в результате его непосредственного восприятия, отделение общего от единичного, необходимого от случайного, формирование характеристик и черт урока, отражающих общие, необходимые и существенные его свойства, качества, характеристики.
В анализе урока этот принцип связан с учетом индивидуальных особенностей учителя, уровня его профессиональной подготовки, интересов, жизненного и социального опыта.
Требования этого принципа в анализе урока выражаются в следующем.
Индивидуальный подход к учителю в процессе анализа урока может осуществляться только на основе знания системы его работы, знания его личности.
Именно на основе этого необходимо индивидуализировать объем, частоту и форму аналитических контактов с педагогом, уровень его самостоятельности, дидактической и методической свободы, требовательности и стиля общения.
Опираясь на глубокий и действенный анализ урока, помочь учителю в создании индивидуальной творческой лаборатории, в формировании своего профессионального почерка.
В ходе индивидуального воздействия на учителя помогать ему укреплять и развивать те положительные свойства, качества, методические подходы, которыми он располагает. Поощрение желаемых видов индивидуального поведения действует всегда более плодотворно, чем подавление нежелательных. Опора на сильные стороны приносит больше пользы, чем бесконечный разбор недостатков.
На наш взгляд, выделенные принципы необходимо соблюдать, в том числе и при самоанализе урока математики. Также при анализе и самоанализе урока необходимо учитывать реальные возможности данной школы и кабинета, в котором проводится урок математики.
Самоанализ урока как основа контроля за эффективностью деятельности учителя и учащихся позволяет получать объективную информацию о реализации учебно-воспитательных задач учителем, об эффективности использования им методов обучения и воспитания.
Самоанализ может выступать в разных формах. О. В. Токмакова [20] предлагает две наиболее распространенные формы: «анализ типа фильтр» и «анализ через синтез». Первая форма характерна для анализа достаточно устойчиво функционирующих систем, так как анализ в этом случае является формальным, то есть выделяется то, что было хорошо и что плохо, не предусматривая при этом синтеза. Ясно, что данный тип не приемлем для анализа урока, так как самое важное при анализе урока, является определение резервов совершенствования деятельности учителя, которые он способен устранить. Вторая форма самоанализа предусматривает соединение анализа и синтеза, которое отчетливо выступает в сравнении. Однако, используя сравнение, необходимо иметь в виду, что сравнивать можно только то, что между собой связано и находится на одном уровне, в сравнении должна быть система параметров, эта система должна быть полной и к каждому параметру необходима оценочная шкала. Для анализа и самоанализа учебного занятия в системе развивающего обучения необходимо выяснить, какие параметры нужно сравнить в ходе анализа, какую систему параметров можно взять за основу, какой должна быть оценочная шкала для каждого из параметров.
М
ногие
руководители работу с педагогом над
учебным занятием проводят, сравнивая
реальное учебное занятие со своими
мыслями по нему (рис.
Для учебного занятия в системе развивающего обучения такая ситуация может оказаться губительной, так как нарушается принцип объективности анализа урока и первый принцип сравнения (сравнивать можно только то, что между собой связано прямой зависимостью и находится на одном уровне). Результатом такого анализа будет псевдокоррекция деятельности педагога, так как связь в этой схеме сравнения односторонняя.
Следовательно, для сравнения нужно выбирать какие-то иные объекты. Сравнение реального учебного занятия с проектом учебного занятия дает возможность для коррекции практической деятельности конкретного педагога (рис. 2).

П
роектируя
учебное занятие, педагогу необходимо
продумывать цели, содержание, формы
организации познавательной деятельности,
методы обучения и конечный результат.
За основу проекта учебного занятия был
выбран так называемый «дидактический
четырехугольник» (рис. 3). По «вершинам»
дидактического четырехугольника и
проводится сравнение двух систем:
реальной и желаемой.
Проект педагог показывает перед началом учебного занятия. Это представление может быть устным, а может быть и в форме технологической карты занятия. В обоих случаях необходимо раскрыть следующие аспекты.
Характеристика обучаемых.
Структура межличностных отношений: лидеры, аутсайдеры, наличие групп, типы взаимоотношений.
Особенности физиологического развития обучаемых: особенности высшей нервной системы (заторможенность, возбудимость), дефекты зрения, слуха, соматическая ослабленность, патологические изменения.
Особенности психического развития обучаемых: развитие интеллектуальной, волевой, эмоциональной и других сфер у отдельных учащихся.
Характеристика развития психических качеств: уровень сформированности познавательного интереса, потребности в знаниях, установка в классе на учение, недостатки в отношениях личности к себе, педагоге, семье, коллективу.
Особенности подготовленности обучаемых: обучаемость, обученность, степень обученности в классе, пробелы в фактических знаниях и умениях, уровень сформированности общеучебных умений и навыков, пробелы в навыках учебного труда, дефекты в привычках и культуре поведения.
Специфика дидактических и воспитательных воздействий образовательного учреждения.
Особенности влияния семьи, сверстников, внешкольной среды.
Анализ внешних связей учебного занятия (триединая дидактическая цель темы, место и роль учебного занятия в изучаемой теме, характер связи учебного занятия с другими занятиями темы).
Характеристика системы целей к учебному занятию (общедидактическая цель учебного занятия, триединая дидактическая цель учебного занятия, уровневая цель как прогнозируемый результат, способ постановки цели на учебном занятии, задачи предполагаемых этапов и структура учебного занятия).
Характеристика замысла учебного занятия (содержание учебного материала, система предметных и общеучебных умений и навыков, опыт творческой деятельности и характер образовательной среды на занятии, формы организации познавательной деятельности, методы обучения и формы их реализации, приёмы обучения).
Контроль и диагностика результатов обучения на учебном занятии (оценочная шкала, критерии выставления оценок на учебном занятии, формы и методы контроля результатов обучения).
Использование проекта повышает уровень эффективности анализа и самоанализа учебного занятия. Но при сравнении реального учебного занятия и его проекта корректируются только практические умения и навыки педагога. Связь в этой схеме сравнения (см. рис. 2) тоже односторонняя. Нет коррекции проекта, следовательно, нет повышения теоретического уровня профессиональной компетентности педагога. Рассмотрим схему (рис. 4) анализа развивающего учебного занятия, предложенную О. В. Токмаковой [20], в которой проект сравнивается с реальным занятием (корректируются практические умения и навыки), затем проект сравнивается с идеальным учебным занятием для конкретного педагога с учетом реальных условий (корректируются теоретические знания).
Эта схема характеризуется наличием двойных связей в сравнении, то есть коррекция двойная. Анализ и самоанализ учебного занятия в соответствии с заложенной в ней логикой выводит на повышение как практического, так и теоретического уровня профессиональной компетентности педагога. Тем более что при выборе шкал сравнения используются основополагающие дидактические утверждения. Именно с помощью этой схемы анализа учебного занятия можно выйти на настоящие причины недостаточных результатов учебного занятия или доказать его эффективность.
Реальное учебное занятие Проект учебного занятия
Идеальная система обучения
Следовательно, для анализа и самоанализа учебного занятия необходимо взять следующую систему параметров: цели урока, содержание образования, формы организации познавательной деятельности, методы обучения, результат образовательного процесса и выделить оценочную шкалу по каждому параметру. Оценочная шкала для каждого параметра представлена в дидактике.
Оценка правильности постановки триединой дидактической цели.
Триединая дидактическая цель, по мнению Ю. А. Конаржевского [6], несет в себе три функции обучения: познавательную, развивающую и воспитательную.
Познавательный аспект триединой дидактической цели по содержанию должен включать в себя следующие параметры:
объем и уровень усвоения предметных знаний для каждого обучаемого;
объем и уровень формирования предметных умений и навыков (способов деятельности) на занятии для каждого обучаемого;
конкретные общеучебные умения (слушать, работать с книгой, задавать вопросы, делать выводы, анализировать…) и средства работы над ними;
конкретные пробелы в знаниях, умениях и навыках (знаниях и способах деятельности) обучаемых.
Содержание воспитательного аспекта триединой дидактической цели включает определенные качества личности, основные мировоззренческие идеи, задачи гражданского, трудового, нравственного, эстетического и физического воспитания, саморазвития и профориентации.
Развивающий аспект по содержанию включает в себя четыре основных блока: речь, мышление, сенсорную и двигательную сферы.
Речевое развитие – это показатель интеллектуального и общего развития человека (обобщение и усложнение ее словарного запаса, смысловой функции речи, усиление ее коммуникативных свойств, овладение художественными образами, выразительными свойствами языка).
Мышление – это умение анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, ставить и решать проблемы. Овладение этими умениями и означает умение мыслить.
Сенсорная сфера. Речь идет о развитии глазомера, ориентировки в пространстве и во времени, точности и тонкости различения цвета, света и тени, формы, звуков и оттенков речи, эмоций, чувств.
Двигательная сфера. Ее развитие предусматривает овладение моторикой мелких мышц, умением управлять своими двигательными действиями, развивать двигательную сноровку, соразмерность движений.
Таким образом, развивающий аспект триединой дидактической цели включает в себя создание условий на учебном занятии для развития и формирования у школьников мышления, восприятия, воображения, развития речи, памяти, познавательных интересов, самостоятельности, интеллекта, воли, эмоций, адекватной двигательной реакции и умения управлять своими движениями.
Оценка правильности отбора содержания урока математики [20]:
соответствие содержания образования уровню современной науки, производства и основным требованиям общества;
учет единства содержательной и процессуальной сторон обучения;
структурное единство образования на разных уровнях его формирования с учетом развития и становления ребенка, предполагающее взаимную уравновешенность, пропорциональность и гармоничность компонентов образования.
Оценка правильности выбора форм организации познавательной деятельности на уроке математики [20]:
адекватность выбранных форм организации познавательной деятельности целям занятия, содержанию и методам обучения;
обеспечение включения каждого обучаемого в активную учебно-познавательную деятельность на занятии;
формирование знаний и способов деятельности должно идти по пути, самому короткому для конкретных обучаемых.
Оценка правильности выбора методов обучения на уроке математики [20].
Методы обучения выбираются в зависимости от характера содержания учебного материала, цели учебного занятия, уровня обученности детей и мастерства педагога.
Если содержание учебного материала характеризуется значимостью вводимого элемента, большим объемом опорных знаний, чем новых, достаточной связью элементов, то применима группа методов проблемного характера (метод проблемного изложения, частично-поисковый метод, исследовательский).
Если содержание учебного материала характеризуется вспомогательным значением изучаемых понятий и явлений, недостаточным количеством опорных знаний, абстрактным характером и трудной актуализацией связей, их множественностью, большим количеством фактического материала, то применяется группа методов репродуктивного характера (объяснительно-иллюстративный метод, репродуктивный метод).
Оценка оптимальности результатов обучения на учебном занятии:
достижение каждым обучаемым реально возможного для него в данный период уровня успеваемости, воспитанности и развитости, но не ниже удовлетворительного в соответствии с принятыми нормами отметок (то есть усвоение обязательных результатов обучения);
соблюдение педагогом и обучаемыми установленных для них норм времени на урочную и домашнюю работу, то есть временные затраты должны быть в соответствии с общепринятыми нормами;
минимально необходимые усилия, затрачиваемые обучаемыми и педагогом (интенсивность деятельности).
Признаки эффективной системы контроля на учебном занятии:
оптимальность сочетания контроля, взаимоконтроля и самоконтроля на учебном занятии для установления правильности выполнения задания и коррекции пробелов;
получение достоверной и своевременной информации о достижении всеми обучаемыми планируемых результатов обучения;
адекватность самооценки обучаемого оценке педагога;
получение всеми обучаемыми информации о реальных результатах учения.
Признаки самостоятельной работы на учебном занятии:
наличие цели самостоятельной работы;
наличие конкретного задания;
четкое определение формы выражения результата;
определение формы проверки результата самостоятельной работы;
выполнение самостоятельной работы каждым учащимся.
Данная схема анализа позволяет продиагностировать каждый этап урока в отдельности, увидеть в какой части урока были допущены ошибки, найти пробелы и недочеты, а также положительные моменты. Проанализировав учебное занятие, учитель может сравнить полученные результаты с тем, что он планировал и соотнести с тем, как должно быть, сделать выводы и спланировать свои действия по ликвидации недочетов.
Возможны различные способы анализа и самоанализа учителем урока математики. В данной работе нами подобраны две схемы: самоанализ деятельности учителя и программа самоанализа педагогического мастерства.
Самоанализ деятельности учителя (Ю. В. Завельский [3])
Первое, что должен сделать учитель, анализирующий свой урок, –определить его место в теме и в общем курсе, а так же задать себе вопрос, насколько ясным стало это место для учащихся после урока.
Попытаться соотнести поставленные цели урока для учащихся и для учителя с достигнутыми на уроке и определить причины успеха или неудачи.
Определить уровень формирования на уроке знаний (логичность подачи материала, научность, доступность, трудность) и умений (соответствие путей формирования специальных умений общепринятым умениям, прочность отработанных умений, степень их автоматизма).
Ответить на вопрос, что нового дал данный урок для развития ума, памяти, внимания, умения слушать товарищей, высказывать свои мысли и отстаивать свою точку зрения, для формирования интереса к математике.
Подумать, насколько оптимально был выстроен урок. Соответствовал ли он вашим интересам, темпераменту, уровню учебной подготовки и развития учащихся, специфике класса? Адекватна ли была организация деятельности учащихся обучающим, развивающим и воспитательным целям урока?
Попробовать оценить степень активности на уроке. Сколько раз и кто из них выступал на уроке, почему молчали остальные, как стимулировалась их работа, насколько были продуманы их действия при подготовке к уроку, что из этого получилось?
Каким был темп урока? Поддерживался ли интерес учащихся к уроку на всем его протяжении? Как была организована смена видов деятельности учащихся на уроке? Как был организован учебный материал, что было дано в виде «готовых знаний», до чего «додумались» сами учащиеся?
Ответить на вопрос, как в ходе урока была организована опора на предыдущие знания, жизненный опыт учащихся и насколько актуальным для них был учебный материал урока?
Очень важным для урока является та его сторона, которая связана с контролем за деятельностью учащихся. Надо постараться оценить, как эта работа была организована на уроке, как контролировалось домашняя работа учащихся? Весь ли труд учеников был проверен? Насколько быстро и эффективно это было сделано?
Попытаться охарактеризовать психологическую атмосферу урока, степень доброжелательности, взаимной заинтересованности всех участников урока, характер их общения.
Наконец, немаловажным является настроение учителя после урока. Изменилось ли оно по сравнению с тем, каким оно было до него? В чем причина этих изменений? Что теперь, после того, как урок прошел, целесообразно было бы изменить в нем? Что можно поставить себе в плюсы, а что в минусы?
Таблица 1
Программа самоанализа педагогического мастерства (Т. В. Машарова[10])
|
Показатели оценки деятельности учителя |
Баллы |
|
Создание общих условий эффективности учебно-воспитательного процесса. |
|
|
Обеспечение общих условий эффективности урока: |
|
|
представленные указания в планах урока (цели, задачи, основные этапы); |
1 |
|
учебные пособия, ТСО, способствующие быстрому вовлечению в урок; |
1 |
|
нет ненужных задержек и отступлений на уроке. |
1 |
|
Адаптация обучения к возможностям учеников: |
|
|
обучение соответствует возрастным особенностям учеников; |
1 |
|
учет в необходимых случаях индивидуальных особенностей учащихся; |
1 |
|
для учащихся разных уровней успеваемости даются групповые задания соответствующих уровней сложности. |
2 |
|
Преподавательская компетенция |
|
|
Владение учебным предметом и методами обучения: |
|
|
информация и демонстрация учебных пособий соответствуют теме точны, современны; |
1 |
|
учитель без затруднений использует не менее двух форм и методов обучения; |
1 |
|
применяются оригинальные методы и приемы обучения. |
2 |
|
Организация учебной деятельности в последовательности: выступление, достижение, закрепление, интерпретация: |
|
|
урок начинается со стимулирующего введения, привлечения внимания и обеспечения необходимой мотивации; |
2 |
|
новый материал представлен как ответ на поставленные вопросы на предыдущем занятии или во введении; |
1 |
|
итоги урока подводятся как соотношение результатов с ранее пройденным, с другими предметами, с жизнью. |
2 |
|
3. Техника объяснения |
|
|
Устное и письменное объяснение: |
|
|
ключевые моменты урока отражены на доске; |
1 |
|
записи на доске аккуратны и разборчивы; |
1 |
|
звучание, произношение, построение устной речи устной речи учителя правильное и профессиональное (литературная речь, речь специалиста). |
2 |
|
Разъяснение при непонимании материала учащимся: |
|
|
выделяются непонятные слова или фразы и заменяются общедоступными описательными выражениями; |
1 |
|
пояснения даются с помощью аналогий и примеров; |
2 |
|
новая учебная информация логически выводится из анализа имеющихся знаний. |
2 |
|
4. Учебное взаимодействие |
|
|
Контроль и коррекция деятельности учащихся: |
|
|
оценка действий ученика определяется личным отношением к нему учителя; |
1 |
|
учитель избегает прямых указаний и коррекции действий ученика; |
1 |
|
ученики побуждаются к самооценке и самоконтролю, оценке и коррекции деятельности друг друга. |
2 |
|
Использование предложений, инициативы и вопросов учащихся на уроке: |
|
|
вопросы и предложения учащихся применяются с благодарностью; |
1 |
|
тактично отмечаются слабые места, несовершенство в примерах и предложениях учащихся; |
1 |
|
идеи учеников разрабатываются и используются на уроке. |
2 |
|
5. Создание продуктивной атмосферы на уроке |
|
|
5.1. Стимулирование интересов учащихся: |
|
|
используются интересные и необычные аспекты, парадоксы, юмор; |
1 |
|
предлагаются проблемные и творческие задания; |
2 |
|
на уроке используется жизненный опыт учеников. |
2 |
|
5.2. Помощь учащимся в выработке положительной самооценки: |
|
|
в речи учителя нет сарказма, насмешек, упреков; |
1 |
|
конкретные ученики поощряются за конкретную работу; |
1 |
|
учитель поддерживает и одобряет школьников, сталкивающихся с затруднениями на уроке. |
1 |
|
6. Поддержание приемлемого поведения в классе |
|
|
6.1. Поддержание делового включения учащихся в урок: |
|
|
использование приемов активизации внимания учащихся; |
1 |
|
применение активных методов обучения; |
1 |
|
использование специальных способов активизации работы активных и пассивных учащихся. |
2 |
|
6.2. Воздействие при нарушении дисциплины: |
|
|
учитель не замечает мелкие непреднамеренные нарушения; |
1 |
|
немедленно и взвешенно реагирует на серьезные нарушения; |
1 |
|
по возможности не наказывает нарушителей дисциплины, а использует их для организации особых форм учебной работы. |
2 |
После урока проводится обработка результатов диагностики. Оценка производится по 36 позициям: 24 классическим (по 1 баллу) и 12 инновационным (по 2 балла). Максимально возможное число баллов 48. После подсчета количества баллов находится коэффициент мастерства как отношение числа набранных баллов к числу оцениваемых позиций (максимум – 1,3). По вычисленному коэффициенту определяется уровень мастерства педагога: 1,1 – 1,3 – педагог-мастер, 0,8 – 1 – высокий уровень мастерства, 0,5 – 0,8 – массовый уровень, менее 0,5 – непригоден к работе.
Владея теорией анализа урока математики, учитель может самостоятельно разработать технологию самоанализа урока с выходом на систему упражнений.
1.3 Технология самоанализа урока математики
На основе теоретического материала нами разработана технология самоанализа урока математики.
Целью технологии самоанализа урока является повышение эффективности процесса обучения школьников математике.
Содержанием технологии самоанализа является урок математики. Подготовка к уроку математики и его проведение является специфичным по сравнению с другими дисциплинами, и анализ позволяет использовать эту специфику для повышения эффективности процесса обучения.
Формой технологии самоанализа урока математики является индивидуальная работа с учителем.
Работа учителя заключается в подготовке к уроку, его проведении, в анализе проведенного урока с целью определения резервов своей деятельности, в подведении итогов самоанализа, в проведении необходимой самостоятельной работы, направленной на заполнение обнаруженных резервов.
Методом технологии самоанализа урока математики является анкетирование. На основе теоретического материала нами разработана схема самоанализа урока математики (Приложение 1).
Данная анкета предназначена для определения пяти основных компетентностей учителя математики при самоанализе урока: целевой, содержательной, методической, организационной и обобщающей.
Для определения компетентности учителя математики при самоанализе урока нами был использован индикативный подход. Каждая компетентность проверяется с помощью системы из трех индикаторов, которые дают качественную оценку проведенного урока математики. Для каждого индикатора также предлагается оценочная шкала в баллах от 0 до 2, которая позволяет дать количественную оценку уроку.
Целевую компетентность определяют три индикатора: уровень конкретности цели, соотнесение цели с задачами урока и уровень формирования познавательного интереса на уроке.
Для содержательной компетентности нами были выбраны три следующих индикатора: уровень конкретности при выделении основных дидактических единиц (теорем, свойств, правил и понятий), дифференциация содержания (по степени сложности, объему усвоения и видам помощи) и соответствие практической деятельности учащихся целям урока и этапам усвоения знаний.
Методическая компетентность определяют три индикатора: наличие само- и взаимоконтроля на уроке, соотнесение методов и содержания урока и соотнесение методов и цели урока.
При определении организационной компетентности нами использовались следующие индикаторы: обеспечение сотрудничества учащихся на уроке, уровень активности класса, соотнесение форм с целями, содержанием и методами обучения на уроке.
Обобщающую компетентность определяют индикаторы: достижение образовательной цели урока, достижение воспитательной цели урока и достижение развивающей цели урока.
При обработке результатов подсчитывается количество баллов по каждой компетентности анкеты. Максимальное количество баллов для каждой компетентности равно 6. Меньшее количество набранных баллов говорит о том, что учитель недостаточно компетентен в данном аспекте. Для повышения уровня компетентности необходимо выявить и проанализировать причины недочетов, а затем провести работу по их устранению.
Средством технологии самоанализа урока математики является анализ с выходом на систему упражнений. Проведенный урок математики анализируется по схеме самоанализа урока (Приложение 1), делается вывод, и учитель на основе вывода может самостоятельно разработать систему упражнений и заданий, которые помогут ему повысить уровень компетентности. Высокий уровень компетентности по каждому компоненту позволит, на наш взгляд, повысить уровень обучения математике. Нами в данной работе подобран ряд упражнений по каждому аспекту урока, которые направлены на устранение пробелов в необходимом блоке структуры урока.
Подводя итог, можно сказать, что самоанализ урока математики по данной технологии дает качественную и количественную информацию о проведенном уроке, позволяет учителю выявить в какой части урока есть недочеты и их причины. На основе самоанализа учитель может самостоятельно разработать технологию управления процессом обучения школьников математике, что будет способствовать повышению эффективности работы учителя математики. Данная технология самоанализа урока математики может быть применена на практике.
Использование этой методики на практике рассмотрено во второй главе выпускной квалификационной работы.
Глава 2. Использование технологии самоанализа урока математики в учебном процессе
2.1 Подготовка учителя к работе с технологией
В своей статье «Как подготовить современный урок» Ю. В. Завельский дает определение урока [4].
Урок – главная составная часть учебного процесса. Учебная деятельность учителя и учащихся в значительной мере сосредотачивается на уроке. Вот почему качество подготовки учащихся во многом определяется уровнем проведения урока, его содержательной и методической наполненностью, его атмосферой. Для того чтобы этот уровень был достаточно высоким, надо, чтобы учитель в ходе подготовки постарался сделать его своеобразным педагогическим произведением со своим замыслом, завязкой и развязкой.
Рекомендации, приведенные ниже, могут помочь учителю в подготовке такого урока.
При непосредственной разработке урока математики учитель должен определить:
цели урока, что необходимо для обеспечения целостности урока и направления внимания на наиболее значимые результаты;
дидактический аппарат – содержание, методы и средства обучения, необходимые для достижения поставленных целей;
структуру урока, что совместно с применяемым дидактическим аппаратом должно содействовать включению учащихся в целенаправленную учебную деятельность.
1. Для правильного и точного формулирования цели урока необходимо помнить правила её постановки, а также учитывать следующие моменты: программные требования, содержание материала, необходимый уровень знаний и умений учащихся, место урока в системе уроков по данной теме, подготовленность класса, свои возможности, тип и вид урока, конечный результат.
Правильная постановка цели урока, является важным этапом в его подготовке и первым шагом к достижению необходимого результата. В книге О. В. Токмаковой [20] выделены три правила постановки цели на уроке, которые, мне кажется, нужно учитывать:
педагог организует действия по принятию цели обучения;
цель формулируется так, чтобы ее содержание было конкретным и понятным, чтобы она четко ориентировала обучаемых на усвоение знаний и способов действия, на критерии описания явлений и на требования к результатам усвоения;
постановка цели на учебном занятии осуществляется обучаемыми самостоятельно или вместе с педагогом.
При постановке цели необходимо также учитывать тип планируемого урока. Урок является сложным педагогическим объектом, поэтому, как и всякие сложные объекты, уроки могут быть разделены на типы по различным признакам. Этим объясняется существование многочисленных классификаций уроков, в том числе и уроков математики. На мой взгляд, самой удачной является классификация С. Г. Манвелова [9], который разделяет уроки по трем параметрам: дидактической цели, способу проведения и этапам учебного процесса.
Цель любого урока должна содержать три дидактических аспекта: образовательный, воспитательный и развивающий, которые тесно взаимосвязаны, и в зависимости от конкретных условий их роль в организации и проведении урока различна. Образовательные цели изучения конкретного материала зафиксированы в общем виде в программе.
С. Г. Манвелов выделяет последовательность действий учителя по выявлению содержания и специфики постановки образовательных целей урока [9]:
определить содержание программных знаний и умений учащихся, формируемых на уроке;
выявить итоговые уровни их сформированности, зафиксированные в разделе «Требования к математической подготовке учащихся» стандарта и программы, а также в обязательных результатах обучения математике;
конкретизировать полученные сведения с учетом подготовленности класса и местом урока в системе уроков по изучаемой теме, разработанной при тематическом планировании.
Таким образом, к образовательным целям урока относят формирование программных знаний и умений на четко определенном уровне: ознакомительном, репродуктивном (добиться понимания и воспроизведения конкретного программного материала и т.п.) или итоговом (сформировать знания и умения в соответствии с требованиями к математической подготовке учащихся).
Постановка воспитательных целей урока осуществляется в рамках целостного подхода к процессу становления личности и охватывает все основные стороны воспитания учащихся: умственное, нравственное, трудовое, экономическое, экологическое, правовое, эстетическое и физическое.
Развивающие цели урока направлены на общее развитие учащихся, предполагающее, в частности, не только развитие их интересов, но и способностей. Наибольшую значимость для учителя имеют наиболее эффективные пути осуществления развивающей функции обучения. К ним относятся:
развитие интеллектуальной, волевой, эмоциональной сфер личности;
развитие умений учебно-познавательной деятельности (умений организации учебного труда, работы с книгой и другими источниками информации, развитие культуры устной и письменной математической речи и т.д.).
Приведем примеры формулировок развивающих целей урока:
развитие памяти учащихся;
развитие умений преодолевать трудности при решении математических задач;
развитие любознательности учащихся;
развитие познавательного интереса учащихся;
развитие умений искать ответы на возникшие вопросы с помощью учебника и т.д.
На уроке практически реализуются все три цели – образовательные, воспитательные и развивающие, причем комплексно. Одна из них, как правило, выступает основной, а другие, решая собственные задачи, в то же время помогают достижению главной, ведущей цели.
2. Содержание учебного материала – это тот фактический материал и теоретические положения, которые подлежат усвоению учащимися. Оно выступает в качестве своеобразной материальной основы урока, на базе которой осуществляется вся учебная деятельность.
Основные требования при отборе содержания учебного занятия:
содержание урока должно соответствовать требованиям учебных программ;
содержание урока должно быть методологически обосновано;
в содержании должна прослеживаться рациональная последовательность рассмотрения материала, его расположения, опора каждого следующего понятия на предыдущее;
содержание учебного материала должно быть доступно, просто, понятно;
выбор и подача материала должно нести воспитательную функцию;
содержание учебного материала должно быть направлено на развитие учащихся, формирование мировоззрения учеников;
содержание учебного материала должно содержать научную достоверность, научную глубину;
обязательна связь теоретического материала с практическим и наоборот;
необходима логичность построения учебного материала: соответствие общего и частного, однозначность терминологии.
3. Метод обучения – это путь, способ взаимодействия учителя и учащихся на основе комплексной последовательности приемов преподавания и учения, направленный при руководящей роли учителя на достижение целей обучения. Это способ взаимодействия учителя и учащихся, при помощи которого достигается овладение учащимися знаниями, умениями, навыками, формируется их мировоззрение, развиваются их познавательные силы и способности. Это способ взаимосвязанной деятельности учителя и учащихся, направленный на достижение целей обучения, воспитания и развития личности [15].
Выбор методов обучения на уроке является одним из важных и сложных этапов подготовки к уроку. При выборе метода, учителю необходимо учитывать цель урока, необходимый результат, содержание материала, знать и владеть основными методами обучения. Наряду с понятием «метод обучения» используется понятие «прием обучения». Принято считать, что метод обучения представляет собой совокупность приемов обучения. Планируя учебное занятие, необходимо предусмотреть использование различных приемов взаимосвязанной деятельности педагога и обучаемых.
Рассмотрим классификацию методов обучения по типу познавательной деятельности ([7], [11], [18]).
Объяснительно-иллюстративный метод обучения удобен для передачи большого количества информации, изложения и усвоения фактов, подходов, оценок, выводов и пр. Обучаемые, воспринимая информацию из уст педагога, остаются в рамках репродуктивного мышления. При использовании этого метода обучаемый получает информацию вербальным способом, причем эта информация сопровождается наглядным иллюстрированиями. Этот метод вбирает в себя в себя в качестве средств и форм проведения такие традиционные методы, как устное изложение, работу с книгой, лабораторную работу. Но при использовании всех этих разнообразных средств деятельность учащихся остается той же – восприятие, осмысление, запоминание.
Приемы объяснительно-иллюстративного метода обучения [20]:
интонационное выделение педагогом логически важных моментов изложения;
повторное, более краткое предъявление готового знания;
подробное резюмирование педагогом каждого отдельного законченного этапа изложения;
сопровождение обобщенных выводов педагога приведением конкретных примеров;
демонстрация наглядных пособий, таблиц, графиков с целью иллюстрирования отдельных выводов;
предъявление готового плана в ходе изложения;
предъявление переформулированных вопросов, текстов заданий, облегчающих понимание их смысла;
намек-подсказка, содержащая готовую информацию.
Репродуктивный метод основан на применении изученного по образцу, правилу, алгоритму и т. п. Репродуктивный метод может приобретать разные формы и осуществляться разными средствами. Это упражнения над натуральными предметами, над материалом учебника и учебных пособий, умственные упражнения (сравнение, умозаключение, классификация и т. д.). Упражнения могут быть индуктивные и дедуктивные, под непосредственным руководством и контролем учителя и в виде самостоятельной работы.
Приемы репродуктивного метода обучения [20]:
задание на составление кратких пояснений в ходе решения задач;
задание на воспроизведение наизусть (определения, правила, формулировки теоремы, доказательство и т.д.);
задание на заполнение таблиц вслед за педагогом;
организация усвоения стандартных способов действия с помощью ситуации выбора;
задание на приведение собственных приемов, очевидно подтверждающих правило, свойство и т.д.;
наводящие вопросы, побуждающие к актуализации знаний и способов действия.
Суть метода проблемного изложения заключается в том, что учитель ставит пред учащимися проблему и сам показывает путь её решения, вскрывая возникающие противоречия. Назначение этого метода состоит в том, чтобы показать образцы научного познания, научного решения проблем. Учащиеся при этом следят за логикой решения проблемы, получая эталон научного мышления и познания, образец культуры развертывания познавательных действий. И в рамках этого метода работают над непосредственным решением проблемы. Они становятся свидетелями научного поиска педагога.
Приемы метода проблемного изложения [20]:
контрдоводы педагога предлагаемому оппоненту в процессе изложения;
предъявление преднамеренно нарушенной логики изложения, доказательства и анализа педагогом полученных при этом результатов;
раскрытие педагогом причин и характера неудач, встречавшихся на пути решения задач;
обсуждение педагогом возможного результата, сделанного из неверных предположений;
фиксирование внимания на последовательности противоречий, возникающих в ходе решения задач;
интригующее описание педагогом излагаемого объекта с последующей постановкой вопроса;
направление педагогом ребят на мысленное решение логического задания, выдвинутого в ходе изложения;
риторические вопросы педагога в ходе изложения;
предъявление конфликтного приема.
Сущность частично-поискового метода заключается в организации активного поиска способа решения выдвинутых педагогом (или автором учебника) проблемы. Степень самостоятельности обучаемых, по сравнению с предыдущим методом обучения, увеличивается. Их деятельность приобретает продуктивный характер, но процесс мышления и поиска направляется и контролируется педагогом или специальными программами.
Приемы частично-поискового метода обучения [20]:
включение детей в доказательство выдвинутой педагогом гипотезы;
задание на решение нескольких задач, выделенных из трудной исходной, после чего они возвращаются к исходной задаче;
наводящие вопросы, помогающие выбору правильных путей решения задачи, одновременно указывающие на различные подходы к ней;
задание на поиск ошибок в рассуждениях, доказательстве теоремы, решении задачи;
задание на обобщение фактов, изложенных педагогом в специальной последовательности;
задание на выдвижение очередного шага рассуждения в логике, заданной педагогом.
Исследовательский метод. Педагог создает проблемную ситуацию, а все остальное – дело самих обучаемых: формулировка проблемы, поиска способа решения проблемы и ее непосредственное решение. Инициатива, самостоятельность, творческий поиск проявляется в исследовательской деятельности наиболее полно. Формы заданий при исследовательском методе могут быть различны. Это могут быть задания, поддающиеся быстрому решению в классе и дома, задания, требующие целого урока, домашнее задание на определенный, но ограниченный срок.
Приемы исследовательского метода обучения [20]:
задание на самостоятельное составление нестандартных задач;
задание с несформулируемым вопросом;
задание с избыточными данными;
задание на самостоятельное обобщение на основе собственных практических наблюдений;
задание на отыскание границ применяемости полученных результатов;
задание на определение степени достоверности полученных результатов;
задание «на мгновенную догадку», «на соображение».
4. Успешность обучения зависит не только от методов обучения, как бы осознанно и продумано они не подбирались учителем, но и от форм обучения, с помощью которых реализуются методы обучения.
К формам реализации методов обучения относятся: беседа, лекция, рассказ, семинар, практикум, самостоятельная работа, практическая работа, лабораторная работа, работа с учебником и книгой и т.д. Приведем примеры и сущность тех форм обучения, которые чаще всего используются на уроках математики [17].
Беседа – это вопросо-ответный метод обучения, при котором учитель опираясь на усвоение знаний и практический опыт, путем строго продуманной системы вопросов и ответов на них подводит учащихся к решению поставленных образовательных и воспитательных задач.
Лекция – это монологический способ изложения объемного материала используется, как правило, в старших классах и занимает весь или почти весь урок.
Рассказ учителя – это образное, живое, эмоциональное и последовательное изложение преимущественно фактического материала, осуществляемое в описательной или повествовательной форме.
Объяснение применяется в тех случаях, когда рассказ учителя и даже показ изучаемых объектов не могут обеспечить ясное понимание учащихся, когда необходимо доказать правильность каких-либо положений и объяснить их.
Работа с учебником и книгой – один из видов словесных форм обучения. Работа с учебником и книгой проводится на всех этапах процесса обучения, однако она требует от учащихся навыка и помощи со стороны учителя.
Практические работы проводятся после изучения крупных разделов, тем и носят обобщающий характер.
В свою очередь, каждая форма реализации методов обучения имеет несколько разновидностей.
При подготовке к уроку очень важно уделять внимание каждому аспекту урока без исключения. Готовясь к уроку, учитель пишет подробный план урока, в котором выделяет цели урока и ожидаемый результат. Затем учитель математики проводит урок, после этого анализирует данный урок по схеме самоанализа (Приложение 1), подсчитывает баллы и определяет уровень своей компетентности по каждому аспекту урока. Если в результате самоанализа урока получилось, что учитель недостаточно компетентен в каком-то аспекте, то учителю необходимо провести самостоятельную работу, направленную на повышение своего уровня компетентности.
2.2 Система упражнений, направленная на повышение уровня компетентности учителя математики
Для повышения компетентности учителя нами подобрана система упражнений по каждому аспекту урока, которая поможет учителю. При составлении системы упражнений использовались библиографические источники [1], [5], [14].
2.2.1. Система упражнений по повышению компетентности в постановке цели урока.
Изучить книгу С. Г. Манвелова «Конструирование современного урока математики» [9], составить опорный конспект, словарик и краткую аннотацию.
Разработать триединую дидактическую цель урока ознакомления с новым материалом по теме «Неравенства и системы неравенств высших степеней с двумя переменными».
Разработать триединую дидактическую цель урока-практикума по теме «Свойства определенного интеграла».
Разработать триединую дидактическую цель комбинированного урока по теме «Прямоугольник. Свойства и признаки».
Разработать структуры учебных занятий разных типов по данным темам.
Урок ознакомления с новым материалом по теме «Умножение положительных и отрицательных чисел». Цель: формирование знаний о правилах умножения чисел и умений применять их на практике; развитие умений сравнивать, выявлять закономерности, обобщать; воспитание графической культуры. Проанализируйте поставленную цель урока. Соответствует ли она типу урока и его теме?
Урок-практикум по теме «Применение нескольких способов разложения многочлена на множители». Цель: рассмотреть способы разложения многочлена на множители; развивать навыки самоконтроля; воспитать волю и настойчивость для достижения конечных результатов при разложении многочлена на множители. Проанализируйте поставленную цель урока. Соответствует ли она типу урока и его теме?
Комбинированный урок по теме «Прямоугольник». Цель: формирование знаний о прямоугольнике и других геометрических фигурах; развитие умений обобщать, абстрагировать и конкретизировать свойства изучаемых объектов и отношений; воспитание уважительного отношения к сверстникам. Проанализируйте поставленную цель урока. Соответствует ли она типу урока и его теме?
Урок-путешествие по теме «Применение подобия». Продумать цель и структуру урока.
Урок решения ключевых задач по теме «Решение треугольников». Продумать цель и структуру урока.
Урок с дидактической игрой по теме «Неравенство треугольника». Продумать цель и структуру урока.
2.2.2. Система упражнений по повышению компетентности
учителя в отборе содержания учебного материала.
Выбрать несколько математических понятий, изучаемых в школе. Исследовать, насколько трактовка этих понятий в школьных учебниках соответствует их современной научной трактовке.
Конкретизировать объем работы на уроке по теме «Интеграл».
Продумать содержание урока по теме «Признаки параллельности двух прямых» с учетом его типа: урок-лекция, урок-семинар, урок-соревнование, урок-зачет, урок-практикум.
Продумать систему использования наглядных пособий и дополнительной информации на каждом уроке по теме «Основное свойство дроби».
Составить задачи с практическим содержанием по теме «Определенный интеграл».
Определить содержание заданий на повторение при изучении темы «Определенный интеграл».
Разработать задания вариативного типа для закрепления темы «Определенный интеграл».
Разработать содержание заданий на углубление знаний по теме «Определенный интеграл».
Разработать систему упражнений, направленную на формирование у учащихся умений и навыков тождественных преобразований целых и дробных рациональных выражений, построенную по возрастающей сложности.
Разработать сценарий деловой игры по методическому решению проблемы «Тождественные преобразования целых рациональных выражений как основа для выполнения тождественных преобразований дробных и иррациональных выражений».
Составить систему задач, решаемых с помощью дифференциальных уравнений с учетом межпредметных связей: задачи, при составлении которых используется геометрический смысл производной; задачи, при составлении которых используется физический смысл производной;
Урок геометрии по теме «Практическое применение подобия треугольников». Поставить цель урока, выбрать тип и продумать содержание.
Составить несколько задач, формирующих умение выделять аналогичные элементы фигур и зависимости.
Разработать систему упражнений на готовых чертежах, способствующих усвоению условия и заключения задачи.
Составить несколько задач, способствующих формированию умения применять: 1) осевую симметрию; 2) центральную симметрию; 3) параллельный перенос.
Указать типы задач, которые целесообразно решать с помощью векторов.
Составить систему задач, формирующих умение осуществлять переход от одного способа задания функции к другому.
При решении
тригонометрических уравнений вида
 учащиеся часто механически используют
способ решения алгебраических уравнений
того же вида. Какие ошибки при этом
допускают учащиеся? Какие упражнения
могли бы предупредить появление такого
рода ошибок?
учащиеся часто механически используют
способ решения алгебраических уравнений
того же вида. Какие ошибки при этом
допускают учащиеся? Какие упражнения
могли бы предупредить появление такого
рода ошибок?
2.2.3. Система упражнений по повышению компетентности
учителя в выборе методов обучения.
Раскройте сущность проблемного обучения. Какими методами обучения обеспечивается эта дидактическая система?
Какие методы обучения, по вашему мнению, наиболее эффективны при изучении темы «Решение системы линейных уравнений способом сложения» на этапах: 1) проверки ранее усвоенного материала; 2) усвоение нового материала; 3) закрепление изученного?
Продумать урок изучения нового материала по теме «Теорема Пифагора и обратная к ней» с использованием следующих методов обучения: объяснительно-иллюстративный, репродуктивный, проблемного изложения, частично-поисковый, исследовательский.
Какие методы организации познавательной деятельности учащихся целесообразно использовать при изучении темы «Свойства функций»? В соответствии с выбранным методом подобрать необходимые модели и таблицы.
Продумать тип и метод обучения на уроке по теме «Пропорция».
Проанализировать различные методы подготовки учащихся к восприятию нового учебного материала по теме «Арифметическая прогрессии».
Выбрать наиболее эффективные методы закрепления и применения полученных знаний по теме «Арифметическая прогрессии».
Рассмотреть методику постановки и проверки домашнего задания на уроке.
Организовать и провести деловую игру на уроке по теме «Уравнения, неравенства, системы уравнений и неравенств».
Рассмотреть возможность использования на уроке элемента игры: математическое лото, кодирование известных изречений, «молчанка» (С. Г. Манвелов [9]), математические кроссворды и ребусы.
Подготовить вводную беседу по теме «Положительные и отрицательные числа», используя исторический материал.
Какое сочетание методов обучения обеспечивает усвоение учебного материала?
Продумать возможные пути создания проблемных ситуаций на уроках математики.
Чем отличается проблемный вопрос от обычного? Когда математическая задача становится проблемной?
Разработать примерный план урока по выбранной теме при условии, что новый материал на уроке будет изучаться проблемно.
2.2.4. Система упражнений по повышению компетентности
учителя в выборе форм обучения.
Охарактеризуйте конкретные формы проявления объяснительно-иллюстративного, репродуктивного, эвристического, исследовательского метода, метода проблемного изложения знаний в обучении математики.
Охарактеризуйте возможные пути создания проблемных ситуаций на уроках математики.
Продумать различные формы организации самостоятельной работы на уроке по теме «Векторы».
Разработать содержание устной работы при введении нового материала по теме «Векторы».
Выбрать оптимальное сочетание форм организации работы учащихся на уроке при изучении темы «Интеграл».
Какие из форм проверки домашнего задания являются наиболее эффективными (в соответствии с целями урока: опрос с места, опрос у доски, общий письменный опрос)?
Продумать формы организации проверки и контроля знаний, полученных учащимися на уроке по теме «Определенный интеграл».
Перечисляя
свойства расстояний, один из учеников
использовал следующую формулировку:
«Для любых точек А, В, С АВ
 АС+СВ», другой попытался поправить его,
утверждая, что «АС
АС+СВ», другой попытался поправить его,
утверждая, что «АС
 АВ+ВС». Как, на ваш взгляд, должен
реагировать на это учитель?
АВ+ВС». Как, на ваш взгляд, должен
реагировать на это учитель?
Составить карточки для самостоятельного изучения следующей теоремы: «Через данную точку можно провести одну и только одну плоскость, параллельную данной плоскости».
Получив
задание найти функцию, обратную данной
 ,
ученик выполнил его следующим образом:
,
ученик выполнил его следующим образом:
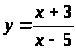 ,
,
 ,
,
 .
Ответ:
.
Ответ:
 .
Какова должна быть, по вашему мнению,
реакция учителя на допущенные учеником
ошибки?
.
Какова должна быть, по вашему мнению,
реакция учителя на допущенные учеником
ошибки?
С помощью
каких приемов можно сформировать у
учащихся умение использовать производную
для уточнения графика, например для
уточнения графика функции
 ,
построенного по точкам, в точке
,
построенного по точкам, в точке
 .
.
Какой должна быть, по вашему мнению, реакция учителя на следующее ошибочное определение, данное учеником: «Нечетная функция – это функция, не являющаяся четной»?
Как можно организовать работу по формулированию определений самими учащимися?
Какие виды самостоятельных работ проводятся на уроках алгебры и геометрии? Как сочетать коллективную, групповую и индивидуальную работу с учащимися на уроке математики?
Продумать возможности использования радио и телепередач для изучения математики.
Приступая к изучению вычитания положительных и отрицательных чисел, создать проблемную ситуацию, которая привела бы к постановке перед учащимися проблем: а) вычесть из меньшего положительного числа большее число, б) из нуля вычесть какое-то число.
2.2.5. Система упражнений по повышению компетентности
учителя в подведении итогов урока.
Привести различные варианты подведения итога урока по теме «Основное свойство дроби».
Разработать требования к системе упражнений (задач) на преобразование выражений, содержащих степень с дробным показателем.
Составить три итоговые контрольные работы по проверке умений учащихся выполнять тождественные преобразования, изученные в курсе алгебры VII, VIII и IX классов.
Составить тесты на определение обучаемости и обученности по теме «Системы линейных уравнений».
Составить самостоятельную работу на усвоение понятия «координаты вектора».
В проверку знаний входит не только определение того, что знают учащиеся, но и установление того, что не знают они, что и как надо восполнить. В соответствии с этими установками найдите наиболее подходящие формы тематического учета знаний учащихся.
Охарактеризовать традиционные и новые формы проверки знаний учащихся. Продумать способы рационального сочетания традиционных и новых форм проверки знаний учащихся по математике.
Познакомиться с различными видами тестов и исследовать возможность их использования для проверки математических знаний и умений учащихся.
Подобрать тесты для проверки знаний и умений учащихся по какой-либо конкретной теме. Каковы критерии оценок знаний, выявляемых с помощью тестов?
После изучения сложения на множестве рациональных чисел учащимся был задан вопрос: «Может ли сумма двух слагаемых чисел быть меньше одного из слагаемых?» Ученик Н. ответил: «Нет, не может. К одному числу прибавляем еще число, получится, конечно, большее». О чем говорят такие ошибки? Как избежать их?
Для проведения самостоятельной работы учитель может определить для себя какой-то промежуток времени, за который он должен выполнить все необходимые упражнения. При выполнении некоторых упражнений можно использовать темы своих текущих уроков, а результат применить на уроке. Так же учитель может разработать ряд собственных упражнений на основе данных.
После проведения самостоятельной работы необходимо проверить себя, чтобы узнать есть ли движение вперёд. Для этого необходимо снова провести самоанализ урока по схеме и подсчитать результаты. При достижении максимального результата по всем аспектам урока не нужно останавливаться на достигнутом, а необходимо продолжать работу по повышению уровня своего мастерства.
2.3 Опыт применения технологии самоанализа урока математики
В период прохождения педагогической практики нами была проведена опытная работа в 11 «А» классе школы № 27 г. Кирова.
Основная цель осуществлённой экспериментальной работы – проверить эффективность технологии самоанализа урока в управлении процессом обучения математике.
Задачи экспериментальной работы.
Составить психолого-педагогическую характеристику 11 «А» класса, сделать выводы о путях работы с данным коллективом.
Провести самоанализ текущих уроков, проанализировать результат и сделать выводы.
Провести проверку эффективности уроков и сделать выводы.
Сформулировать общие выводы о проделанной работе, соотнести полученные результаты с основной целью экспериментальной работы.
Приведём психолого-педагогическую характеристику 11 «А» класса школы № 27, основанную на наблюдениях классного руководителя (С. Е. Фомичева) и социометрическом исследовании класса (Приложение 2).
В 11 «А» классе 15 учащихся, из них 3 мальчика и 12 девочек. В данном составе класс учится с первого класса. После окончания 9 класса основной состав сохранился. В классе 6 отличников, 5 человек учатся на «4» и «5», у остальных по одной тройке по математике.
Подростки нормально общаются между собой, помогают друг другу в учебе, не бывает драк и серьезных конфликтов, нет разделения на «богатых» и «бедных». В классе царит дружественная атмосфера.
Есть дети со слабым здоровьем, которые часто болеют, пропускают занятия.
Дети все из благополучных семей. Отношения с родителями доверительные. Есть дети из неполных семей, которых воспитывает одна мама.
Помимо школы подростки занимаются в спортивных секциях (карате, лыжи, волейбол), художественных (Театр моды, СЮТ и других). Посещают спецкурсы по физике и математике, а также курсы дополнительного образования. Ведут очень активный образ жизни.
Очень активны вне школы и в учебной деятельности, всегда с удовольствием принимают участие во внеклассных мероприятиях, особенно где требуется проявить индивидуальность. Ребята очень предприимчивы, каждый ученик – это индивидуальность.
По данным социометрического исследования класса можно сказать, что коллектив разбит на 2 микрогруппы, различные по численности. В первой группе 13 человек, а во второй группе 2 мальчика. Психологический климат класса достаточно благоприятен для развития дружного, сплочённого коллектива; большинству ребят достаточно уютно находиться в обществе своих одноклассников. По мнению учащихся, класс дружный и сплочённый; ребята стараются помогать друг другу; взаимная ответственность развита высоко.
Можно сделать вывод, что в классе хорошая дружественная атмосфера, которая благотворно влияет на поведение детей на уроках математики и их ответственное отношение к предмету. В классе 74% детей учатся хорошо и отлично, в том числе и по математике, и только 26% ребят имеют по математике оценку «три». Можно сказать, что класс достаточно сильный и уровень обученности детей выше среднего, но его можно увеличить (по моему мнению), так как эти 26% ребят очень способны и они вполне могут учиться на «хорошо» по математике. А, значит, и уровень обучения может стать высоким.
В ходе педагогической практики было проведено 10 уроков. Рассмотрим характеристику двух проведенных уроков и проанализируем их по разработанной технологии самоанализа.
Урок алгебры до экспериментальной работы
Тема урока: «Первообразная».
Цели урока: сформировать условия для вторичного осмысления и развития уже введенных понятий, выработки умений навыков по их применению; развивать логическое мышление, внимание; воспитывать трудолюбие.
Структура урока:
Сообщение темы и цели практикума.
Проверка домашнего задания.
Актуализация опорных знаний и умений учащихся.
Решение задач на закрепление.
Проверочная работа.
Подведение итогов урока.
Постановка домашнего задания.
Основной метод урока: репродуктивный.
Формы, применяемые на уроке: устная работа, работа в парах, самостоятельная работа.
Подведение итогов: итоги проверочной работы представлены в таблице 1 Приложения 3.
Результат самоанализа урока
|
№ |
Компетентность |
Максимальное число баллов |
|
1 |
Целевая |
4 |
|
2 |
Содержательная |
4 |
|
3 |
Методическая |
4 |
|
4 |
Организационная |
3 |
|
5 |
Обобщающая |
3 |
Вывод. Компетентность учителя по каждому аспекту средняя 60%. Уровень обученности ребят по данному уроку средний 74%. Для определения уровня обученности ребят проводилась проверочная работа (Приложение 3).
В данном случае учителю необходимо обратить внимание на такие аспекты урока, как постановка цели, отбор содержания, выбор методов. Следует особое внимание уделить выбору форм и подведению итогов урока.
Мной была проведена самостоятельная работа, которая была направлена на повышение компетентности всех компонентов, с использованием вышеописанной системы упражнений. Особое внимание было обращено на выполнение упражнений по повышению компетентности в выборе форм и подведении итогов урока.
Было проведено еще 7 уроков, к каждому из которых была применена технология самоанализа. Каждому уроку предшествовала подготовка, после проведения урока проводился самоанализ по схеме (Приложение 1) и подводились итоги качественной и количественной оценки эффективности урока. Затем проводилась самостоятельная работа по повышению компетентности всех аспектов урока.
Урок алгебры после экспериментальной работы
Тема урока: «Свойства определенного интеграла».
Цели урока: воспитывать волю и настойчивость для достижения конечных результатов при вычислении определенного интеграла; развивать навыки самоконтроля; сформировать умения решения задач на свойства определенного интеграла.
Структура урока:
Сообщение темы и цели практикума.
Проверка домашнего задания.
Актуализация опорных знаний и умений учащихся.
Инструктирование по выполнению заданий практикума.
Выполнение заданий в группах.
Проверка и обсуждение полученных результатов.
Самостоятельная работа.
Постановка домашнего задания.
Резервные задачи.
Методы урока: репродуктивный.
Формы, применяемые на уроке: работа в группах, самостоятельная работа.
Подведение итогов: итоги самостоятельной работы представлены в таблице 1 Приложения 3.
Результат самоанализа урока
|
№ |
Компетентность |
Максимальное число баллов |
|
1 |
Целевая |
5 |
|
2 |
Содержательная |
5 |
|
3 |
Методическая |
5 |
|
4 |
Организационная |
4 |
|
5 |
Обобщающая |
4 |
Вывод. Компетентность учителя по каждому аспекту выше среднего 76%. Уровень обученности ребят по данному уроку выше среднего 85%. Для определения уровня обученности ребят проводилась проверочная работа (Приложение 3).
В данном случае уже заметен результат работы по технологии самоанализа урока. Если продолжать движение в намеченном направлении, то в деятельности учителя возможно достижение высокого уровня компетентности, а значит и роста эффективности обучения математике.
Составим сводную таблицу результатов проведённых уроков по математике с применением самоанализа, используя выделенные критерии эффективности (на основании своего мнения).
|
Результаты опытной работы |
||
|
Критерии
|
До опытной работы |
После опытной работы |
|
Компетентность
|
60% |
76% |
|
Уровень обученности учащихся |
74% |
85% |

Сформулируем общие выводы о проведении экспериментальной работы.
Соотнося основную цель опытной работы с её результатами, можно утверждать, что комплексный анализ урока является основой эффективного процесса обучения математике.
Каждый урок требует особой подготовки в постановке цели урока, отборе содержания, выборе методов и форм урока математики, а так же подведение итогов.
При анализе урока необходимо учитывать основные принципы, которые позволяют сделать анализ полным и объективным.
Для повышения уровня мастерства учителю необходимо работать над собой, над заполнение резервов в своей деятельности.
Заключение
В процессе теоретического исследования поставленной проблемы и опытной работы в соответствии с задачами и целью исследования получены следующие основные выводы и результаты.
1. В результате анализа различных точек зрения по проблеме самоанализа деятельности учителя как основы эффективного процесса обучения классифицированы принципы самоанализа урока: принцип оптимальности, принцип объективности, принцип взаимосвязанности, принцип развития, принцип человекоцентризма, принцип активности. Также классифицированы виды самоанализа урока математики: краткий, структурный, аспектный, полный и комплексный.
2. Разработана и предложена технология самоанализа урока математики, в основание которой легли теория анализа урока математики, компетентностный и индикативный подходы в оценке деятельности учителя.
3. На основе разработанной технологии самоанализа урока математики предложена система упражнений по повышению компетентности учителя в каждом аспекте урока.
4. В ходе опытно-экспериментальной работы показано положительное влияние технологии самоанализа и самостоятельной работы учителя, на управление процессом обучения школьников и рост мастерства учителя. Основанием для вывода об эффективности разработанной технологии явились количественные и качественные показатели использованных в ходе исследования тестов.
Зная основные составляющие самоанализа, умея правильно ставить цели анализа, зная его принципы и методы и умея использовать их при анализе своей деятельности, учитель может повысить уровень своего мастерства и добиться высоких результатов в управлении процессом обучения. Так как для эффективного управления процессом обучения, очень важно для учителя уметь анализировать свою деятельность, видеть достоинства, недостатки и находить пути их решения, делать выводы и применять это на практике.
Следует отметить, что деятельность учителя многогранна. В данной работе рассмотрена лишь одна из ее сторон – урок. В работе доказано, что самоанализ урока является основой эффективного управления процессом обучения. Дальнейшей же перспективой исследования является рассмотрение самоанализа всей деятельности учителя как основы управления процессом обучения математике.
Изложенное выше позволяет считать, что самоанализ урока математики позволяет управлять процессом обучения школьников и повышает уровень компетентности учителя. Таким образом, подтверждена выдвинутая гипотеза и решены задачи исследования.
Библиографический список
Автономова, Т. В. Практикум по методике преподавания математики в средней школе [Текст]: учебное пособие / Т. В. Автономова, В. И. Мишин: под ред. В. И. Мишина. – М.: Просвещение, 1993. – 192 с.
Ерофеева, Н. Ю. Анализ урока и профессиональной деятельности учителя [Текст] / Н. Ю. Ерофеева // Завуч. – 2000. – № 1. – С. 96-106.
Завельский, Ю. В. Как анализировать свой собственный урок [Текст] / Ю. В. Завельский // Завуч. – 2000. – № 4. – С. 92-93.
Завельский, Ю. В. Как подготовить современный урок [Текст] / Ю. В. Завельский // Завуч. – 2000. – № 4. – С. 94-96.
Килина, Н. Г. Сборник задач по методике преподавания математики [Текст]: учебное пособие / Н. Г. Килина. – Киров.: КГПИ, 1976. – 80 с.
Конаржевский, Ю. А. Анализ урока [Текст] / Ю. А. Конаржевский – М.: Педагогический поиск, 2000. – 336 с.
Крившенко, Л. П. Педагогика [Текст]: учебник / Л. П. Крившенко, М. Е. Вайндорф-Сысоев и др.; под ред. Л. П. Крившенко. – М.: Проспект, 2004.– 540 с.
Кульневич, С. В. Анализ современного урока [Текст]: практическое пособие / С. В. Кульневич, Т. П. Лакоценина; под ред. С. В. Кульневич. – Ростов-на-Дону: Учитель, 2003. – 224 с.
Манвелов, С. Г. Конструирование современного урока математики [Текст] / С. Г. Манвелов. – М: Просвещение, 2005. – 175 с.
Машарова, Т. В. Педагогические теории, системы и технологии обучения [Текст]: учебное пособие / Т. В. Машарова. – Киров: ВГПУ, 1997. – 160 с.
Пидкасистый, П. И. Педагогика [Текст]: учебник / П. И. Пидкасистый, В. И. Журавлев [и др.]; под ред. П. И. Пидкасистого. – М.: Педагогическое общество России, 1995. – 640 с.
Программа для общеобразовательных школ, гимназий, лицеев. Математика. 5-11 кл. [Текст] / Сост. Г. М. Кузнкцова, Н. Г. Миндюк. – М.: Дрофа, 2000. – 320 с.
Саранцев, Г. И. Методология методики обучения математике [Текст] / Г. И. Саранцев. – Саранск: Красный Октябрь, 2001. – 144 с.
Саранцев, Г. И. Сборник упражнений по методике преподавания математики в средней школе [Текст]: учебное пособие / Г. И. Саранцев. – М.: Просвещение, 1983. – 80 с.
Сахаров, В. Ф. Словарь-справочник по педагогике [Текст] / В. Ф. Сахаров, М. Г. Яновская. – Киров: ВГПУ, 2000. – 47 с.
Симонов, В. П. Директору школы об управлении учебно-воспитательным процессом [Текст]: учебное пособие / В. П. Симонов. – М.: Педагогическое общество России, 1999. – 340 с.
Сорокин, Н. А. Дидактика [Текст]: учебное пособие / Н. А. Сорокин. – М.: Просвещение, 1974. – 222 с.
Скаткин, М. Н. Дидактика средней школы [Текст]: учебное пособие / М. Н. Скаткин. – М.: Просвещение, 1982. – 319 с.
Тестов, В. А. Стратегии обучения математике [Текст] / В. А. Тестов. – М.: Технологическая Школа Бизнеса, 1999. – 304 с.
Токмакова, О. В. Управление процессом обучения [Текст]: учебное пособие / О. В. Токмакова – Киров: ВятГГУ, 2005. – 121 с.
Философский словарь [Текст] / Под ред. М. М. Розенталя. – М.: Политиздат, 1972. – 496 с.
Хинчин, А. Я. О воспитательном эффекте уроков математики [Текст] / А. Я. Хинчин // Математика в образовании и воспитании. – 2000. – С. 64 - 102.
Приложение 1
Анкета определения компетентности учителя при самоанализе урока математики
|
Содержание анализа |
Баллы |
|
|
1. Целевая компетентность |
||
|
Индикатор
1. Уровень |
цель неконкретна, нет ориентации на усвоение знаний, умений и навыков; |
0 |
|
цель четко сформулирована, ориентирует ребят на усвоение математических фактов, понятий и способов действия с ними; |
1 |
|
|
цель четко сформулирована, ориентирует ребят на усвоение математических фактов, понятий, способов действия с ними, а также на результат урока. |
2 |
|
|
Индикатор 2. Соотнесение цели и задач урока |
цель частично конкретизируется в задачах и не объясняется ребятам; |
0 |
|
цель полностью конкретизируется, но не все задачи объясняются ребятам; |
1 |
|
|
цель четко конкретизируется в задачах. |
2 |
|
|
Индикатор 3. Уровень формирования познавательного интереса |
не формируется; |
0 |
|
формируется с использованием только внешних стимулов (поощрение словом, порицание и др.); |
1 |
|
|
формируется с помощью активных приемов внутреннего стимулирования (проблемные вопросы и др.). |
2 |
|
|
2. Содержательная компетентность |
||
|
Индикатор 1. Выделение основных дидактических единиц |
выделены не полностью; |
0 |
|
выделены, но нарушена логическая последовательность; |
1 |
|
|
четко выделены в логичной последовательности. |
2 |
|
|
Индикатор 2. Дифференцирование содержания |
только на этапе применения; |
0 |
|
на двух и более этапах, но не по всем параметрам; |
1 |
|
|
на протяжении всего урока и по всем параметрам. |
2 |
|
|
Индикатор 3. Соответствие практической части целям урока и этапам усвоения знаний |
соответствует этапам усвоения знаний; |
0 |
|
соответствует основным целям урока и этапам усвоения знаний; |
1 |
|
|
соответствует основным целям урока и этапам усвоения знаний. Знания формируются с опорой на математические модели, графики, формулы на всех этапах урока. |
2 |
|
|
3. Методическая компетентность |
||
|
Индикатор 1. Само- и взаимоконтроль на уроке |
не осуществлялся или проходил без коррекции и оценки; |
0 |
|
осуществлялся, но результаты не доводились до ребят и не корректировались; |
1 |
|
|
осуществлялся, результаты доводились до всех ребят на этом же уроке и была проведена своевременная коррекция достижения цели. |
2 |
|
|
Индикатор 2. Соотнесение методов и содержания урока |
методы не соответствуют содержанию учебного материала; |
0 |
|
методы соответствуют содержанию учебного материала, но не соответствовали особенностям детей; |
1 |
|
|
методы соответствуют содержанию учебного материала и особенностям обучаемых. |
2 |
|
|
Индикатор 3. Соотнесение методов и цели урока |
методы не соответствуют содержанию триединой дидактической цели урока; |
0 |
|
методы соответствуют содержанию триединой дидактической цели урока, но не полностью; |
1 |
|
|
методы полностью соответствуют триединой дидактической цели урока. |
2 |
|
|
4. Организационная компетентность |
||
|
Индикатор 1. Сотрудничество ребят |
формы обеспечивают деятельность ребят по усвоению знаний, но не обеспечивают сотрудничество; |
0 |
|
формы обеспечили деятельность ребят по усвоению знаний и их сотрудничество, но не всех; |
1 |
|
|
формы обеспечили полное сотрудничество ребят на уроке. |
2 |
|
|
Индикатор 2. Уровень активности класса |
большая часть класса не включалась в активную работу; |
0 |
|
почти все ребята работали, но все-таки часть из них отвлекались и занимались посторонними делами; |
1 |
|
|
все без исключения активно работали. |
2 |
|
|
Индикатор 3. Соответствие форм цели, содержанию и методам урока |
формы не соответствуют целям урока, содержанию и методам обучения; |
0 |
|
формы частично соответствуют целям урока, содержанию и методам обучения |
1 |
|
|
формы полностью соответствуют целям урока, содержанию и методам обучения. |
2 |
|
|
5. Обобщающая компетентность |
||
|
Индикатор 1. Достижение образовательной цели урока |
не достигнута; |
0 |
|
частично достигнута; |
1 |
|
|
достигнута полностью. |
2 |
|
|
Индикатор 2. Достижение воспитательной цели урока |
не достигнута; |
0 |
|
частично достигнута; |
1 |
|
|
достигнута полностью. |
2 |
|
|
Индикатор 3. Достижение развивающей цели урока |
не достигнута; |
0 |
|
частично достигнута; |
1 |
|
|
достигнута полностью. |
2 |
Приложение 2
Результаты социометрического опроса
Таблица 1
|
№ п/п |
Фамилия |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1 |
Вахрушев |
+- |
+ |
+ |
|||||||||||
|
2 |
Мамаев |
+- |
+ |
+ |
|||||||||||
|
3 |
Пермяков |
+- |
+- |
+- |
|||||||||||
|
4 |
Банина |
+ |
+ |
+- |
|||||||||||
|
5 |
Бусыгина |
+- |
+- |
+- |
|||||||||||
|
6 |
Дьяченко |
+ |
+ |
+- |
|||||||||||
|
7 |
Ермакова |
+ |
+- |
+ |
|||||||||||
|
8 |
Кабакова |
+- |
+- |
+- |
|||||||||||
|
9 |
Кислицина |
+ |
+- |
+- |
|||||||||||
|
10 |
Макарова |
+- |
+- |
+- |
|||||||||||
|
11 |
Максютова |
+ |
+ |
+ |
|||||||||||
|
12 |
Рукавишникова |
+- |
+- |
+- |
|||||||||||
|
13 |
Савельева |
+- |
+- |
+ |
|||||||||||
|
14 |
Хохолкова |
+- |
+ |
+- |
|||||||||||
|
Кол – во полученных выборов |
1 |
1 |
5 |
3 |
6 |
2 |
3 |
3 |
2 |
5 |
1 |
4 |
2 |
4 |
|
|
Кол – во взаимных выборов |
1 |
1 |
3 |
1 |
3 |
1 |
1 |
3 |
2 |
3 |
0 |
3 |
2 |
2 |
Таблица 2
|
№ п/п |
Фамилия |
1 |
2 |
3 |
5 |
10 |
12 |
13 |
14 |
8 |
9 |
6 |
4 |
7 |
|
1 |
Вахрушев |
+ |
||||||||||||
|
2 |
Мамаев |
+ |
||||||||||||
|
3 |
Пермяков |
+ |
+ |
+ |
||||||||||
|
5 |
Бусыгина |
+ |
+ |
+ |
||||||||||
|
10 |
Макарова |
+ |
+ |
+ |
||||||||||
|
12 |
Рукавишникова |
+ |
+ |
+ |
||||||||||
|
13 |
Савельева |
+ |
+ |
|||||||||||
|
14 |
Хохолкова |
+ |
+ |
|||||||||||
|
8 |
Кабакова |
+ |
+ |
+ |
||||||||||
|
9 |
Кислицина |
+ |
+ |
|||||||||||
|
6 |
Дьяченко |
+ |
||||||||||||
|
4 |
Банина |
+ |
||||||||||||
|
7 |
Ермакова |
+ |
Таблица 3
|
№ п/п |
Фамилия |
Степень выраженности положительных качеств |
Степени выраженности отрицательных качеств(по модулю) |
|
|
1 |
Вахрушев |
7 |
= |
7 |
|
2 |
Мамаев |
7 |
< |
21 |
|
3 |
Пермяков |
14 |
> |
7 |
|
4 |
Банина |
12 |
> |
11 |
|
5 |
Бусыгина |
15 |
> |
7 |
|
6 |
Дьяченко |
14 |
> |
7 |
|
7 |
Ермакова |
15 |
> |
9 |
|
8 |
Кабакова |
14 |
> |
11 |
|
9 |
Кислицина |
8 |
< |
10 |
|
10 |
Макарова |
12 |
> |
11 |
|
11 |
Максютова |
17 |
> |
7 |
|
12 |
Рукавишникова |
11 |
> |
7 |
|
13 |
Савельева |
11 |
> |
8 |
|
14 |
Хохолкова |
13 |
> |
8 |
|
Общая сумма |
170 |
> |
120 |
Приложение 3
Результаты проверочных работ
Таблица 1
|
Ф. И. |
До комплексного анализа |
После комплексного анализа |
|
Вахрушев Роман |
5 |
5 |
|
Мамаев Матвей |
3 |
3 |
|
Пермяков Максим |
3 |
3 |
|
Банина Ольга |
5 |
5 |
|
Бусыгина Дарья |
4 |
5 |
|
Дьяченко Ольга |
3 |
4 |
|
Ермакова Анна |
5 |
5 |
|
Кабакова Мария |
3 |
4 |
|
Кислицина Ольга |
4 |
5 |
|
Макарова Анастасия |
4 |
5 |
|
Максютова Анастасия |
3 |
4 |
|
Рукавишникова Жанна |
4 |
4 |
|
Савельева Екатерина |
3 |
4 |
|
Хохолкова Анастасия |
4 |
4 |
|
Саранцева Екатерина |
3 |
4 |