Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Вятский государственный гуманитарный университет»
Физико-математический факультет
Кафедра дидактики физики и математики
Выпускная квалификационная работа
Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников
Выполнила студентка V курса
физико-математического факультета Коновалова Вера Сергеевна
Научный руководитель: к. пед. н.,
доцент кафедры дидактики физики и математики Шилова З.В.
Рецензент: к. пед. н., ст. преп.
кафедры дидактики физики и математики Зеленина Н.А.
Работа допущена к защите в ГАК
«___» _________2008 г. Зам. зав. кафедрой __________ М.В. Крутихина
«___» _________2008 г. Декан факультета ____________ Е.В. Кантор
Киров 2008
Содержание
Введение
1. Анализ учебной и учебно-методической литературы по геометрии
1.1. Анализ учебников по геометрии основной школы
1.2. Анализ учебно-методической литературы
2. Логическое мышление: основные понятия.Анализ психолого-педагогической литературы
2.1. Природа и виды мышления
2.2. Развитие мышления ребенка
2.3. Понятие логического мышления
2.4. Развитие логического мышления школьников в процессе обучения математике
3. Методика решения задач на построение
3.1. Анализ
3.2. Построение
3.3. Доказательство
3.4. Исследование
3.5. Методические рекомендации по обучению решению задач на построение
4. Методы решения задач на построение
4.1. Метод геометрических мест
4.2. Методы геометрических преобразований
4.2.1. Метод центральной симметрии
4.2.2. Метод осевой симметрии
4.2.3. Метод параллельного переноса
4.2.4. Метод поворота
4.2.5. Метод подобия
4.3. Алгебраический метод
5. Опытное преподавание
Заключение
Библиографический список
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Приложение 6
Введение
Геометрические задачи на построение, возможно, самые древние математические задачи. Кому-то они сейчас могут показаться не очень интересными и нужными, какими-то надуманными. И в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный семнадцатиугольник или треугольник по трем высотам, или даже просто сделать построение параллельной прямой. Современные технические устройства сделают все эти построения и быстрее, и точнее, чем любой человек, а заодно смогут выполнить и такие построения, которые просто невозможно выполнить при помощи циркуля и линейки.
И все же без задач на построение геометрия перестала бы быть геометрией. Геометрические построения являются весьма существенным элементом изучения геометрии. Однако, анализ содержания школьного математического образования позволил выявить ряд недостатков в обучении школьников:
1. Наметилась четкая тенденция к сокращению количества задач на построение в школьном курсе математики. Это объясняется тем, что значительно сужена роль задач на построение, которая соответствует целям обучения, таким как развитие мышления и воспитание учащихся, и проявляется в виде воздействия на мышление учеников, в первую очередь на логическое. В большинстве случаев, считается, что главная и единственная цель обучения решению таких задач – это формирование практических умений и навыков построения основных геометрических фигур: треугольников, перпендикуляров, биссектрис и т. п., то есть основное внимание уделяется практическому значению задач, при этом совершенно не рассматривается вопрос развития логического мышления учеников и возможности использования задач на построение при изучении геометрии.
2. Знания учащихся по данной теме нередко носят формальный характер, наблюдается отсутствие структурности. Так, при изучении задач на построение единственное, что требует учитель – это знание соответствующих алгоритмов построений. При этом не объясняется, как получен данный алгоритм. Поэтому ученик вынужден запоминать материал без понимания.
3. В настоящий момент в школе недостаточно уделяется внимания рассмотрению таких основных методов решения задач на построение как метод преобразований, алгебраический метод, метод геометрического места точек.
4. У учащихся нет четкого представления об этапах решения задач на построение: анализе, построении, доказательстве и исследовании, которые точно соответствуют этапам любого логического рассуждения. Практически не уделяется внимание одному из важных этапов – исследованию, в котором учащиеся зачастую не видят смысла, несмотря на то, что он, в свою очередь, является хорошим средством развития логического мышления.
Перечисленные выше недостатки и определили проблему исследования.
Проблема исследования заключается в рассмотрении на основе психологии, педагогики и методики преподавания математики возможности развития логического мышления учащихся при решении задач на построение в курсе основной школы.
Цель исследования: разработать методические рекомендации при решении задач на построение, способствующие развитию логического мышления учащихся.
Объект исследования: процесс обучения геометрии учащихся в курсе основной школы.
Предмет исследования: процесс обучения решению задач на построение.
Гипотеза: применение разработанных методических рекомендаций при решении задач на построение будут способствовать наиболее эффективному развитию логического мышления учащихся при обучении геометрии в курсе основной школы.
Задачи:
1) провести анализ учебных программ, учебной и учебно-методической литературы;
2) рассмотреть понятие логического мышления;
3) рассмотреть основные этапы решения задач на построение;
4) разработать методические рекомендации по обучению решению задач на построение;
5) рассмотреть методы решения задач на построение;
6) осуществить опытное преподавание.
Методы исследования:
анализ учебной, учебно-методической, психолого-педагогической литературы;
наблюдение;
анкетирование;
проведение психологических методик;
проведение опытного преподавания.
1. Анализ учебной и учебно-методической литературы по геометрии
Нами был предварительно проведен и анализ программы по математике (см. Приложение 1).
А также анализ учебников по математике для 5-6 классов.
1) Н.Я. Виленкин “Математика 5” [12]: в учебнике две главы “Натуральные числа” и “Дробные числа”, каждая содержит четыре параграфа. В нем первым из построений с помощью линейки (Глава 1,§1) является построение отрезка (далее уже многоугольника). А также изучается сравнение отрезков с помощью циркуля. Далее идет изучение прямой и луча. Следующие построения рассматриваются в начале второй главы в пункте окружность и круг. А именно построение окружности с помощью циркуля. В конце курса школьники учатся обращаться с чертежным треугольником (построения прямого угла).
Н.Я. Виленкин “Математика 6” [13]: в этом учебнике также две главы “Обыкновенные дроби” и “Рациональные числа”, каждая содержит четыре параграфа. В конце курса учащиеся знакомятся с перпендикулярными и параллельными прямыми и строят их с помощью чертежного треугольника и линейки.
2) Г.В. Дорофеев “Математика 5” [14]: в данном учебнике первым из построений с помощью линейки является построение прямой, проходящей через две данные точки, а также построение окружности с помощью циркуля. Далее следует изучение луча и сравнения отрезков с помощью циркуля. В следующей главе рассматривается понятие угла и его построение, в том числе с помощью угольника. Третья глава посвящена изучению многоугольников, в частности прямоугольников и треугольников.
Г.В. Дорофеев “Математика 6” [15]: в главе 2 ‘Прямые и окружности’ знакомит учащихся с перпендикулярными и параллельными прямыми, и их построением с помощью угольника и линейки. Далее определяются касательная к окружности, концентрические окружности, и рассматриваются варианты взаимного расположения прямой и окружности, двух прямых на плоскости. Предлагаются различные задачи на построение касательной к окружности; окружности, касающейся двух параллельных прямых; двух окружностей. Одна из глав учебника посвящена изучению симметрии: осевой и центральной. Предлагаются задачи на построение симметричных фигур, а также на нахождение кратчайшего пути. Также имеется глава, посвященная фигурам на плоскости, в частности треугольникам и параллелограммам. В ней рассматривается построение треугольника по трем сторонам и предлагаются задачи на построение различных треугольников (прямоугольных, равнобедренных, остроугольных, тупоугольных).
1.1 Анализ учебников по геометрии основной школы
Л.С. Атанасян, В.Ф. Бутузов [7]
а) 7 класс: содержит четыре главы. Тема “Задачи на построение” изучается в конце главы 2 “Треугольники”. В этом параграфе содержатся пункты “Окружность”, “Построения циркулем и линейкой” и “Примеры задач на построение”. Основываясь на том, что учащиеся умеют с 5 и 6 класса выполнять основные построения с помощью циркуля и линейки, в теме рассматриваются задачи на построение такие как: построение отрезка, равного данному; построение угла, равного данному; построение биссектрисы угла, перпендикулярных прямых и середины отрезка. Схема, по которой решаются задачи на построение, не вводится. Основная цель главы 2 – отработать навыки решения простейших задач на построение с помощью циркуля и линейки (см. Приложение 1).
В главе 3 “Параллельные прямые” рассматривается построение параллельных прямых с помощью чертежного треугольника и линейки, а также с помощью циркуля и линейки по заданной прямой и точке (в форме задачи).
В главе 4 “Соотношения между сторонами и углами треугольника” рассматривается задача о построении треугольника по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам и по трем сторонам. Данная глава содержит целый блок задач на построение для самостоятельного решения, который состоит в основном из задач на построение различных треугольников по различным элементам.
В конце 7 класса также имеется блок задач на построение, перед которым описывается схема, по которой решают задачи на построение: анализ, построение, доказательство, исследование. Приводится пример.
б) 8 класс: содержит пять глав. В главе 5 “Четырехугольники” после изучения многоугольника, параллелограмма и трапеции вводится блок задач на построение параллелограмма и трапеции по различным элементам. Перед этим еще раз идет повторение схемы решения задач на построение. В этой же главе после изучения прямоугольника, ромба и квадрата предлагается решить задачи на их построение.
В главе 7 “Подобные треугольники” рассматриваются задача на построение треугольника, при решении которой применяется метод подобия (в данном случае треугольников), в качестве практического приложения подобия треугольников. Также приводится ряд задач на построение треугольников по данным отношениям для самостоятельного решения. Основная цель главы 7 – сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольных треугольников (см. Приложение 1).
В начале главы 8 “Окружность” в пункте “Касательная к окружности” решается задача о проведении касательной к окружности через данную точку. Говорится о том, что решение подобных задач основано на теореме (признаке касательной). Также в главе изучаются четыре замечательные точки треугольника. Задачи на построение (касательной к окружности, серединного перпендикуляра к отрезку) содержит каждый пункт главы. Основная цель главы 8 – дать учащимся систематизированные сведения об окружности и ее свойствах, вписанной и описанной окружностях (см. Приложение 1).
В конце 8 класса в разделе задач повышенной трудности встречается задача на построение равнобедренной трапеции по основаниям и диагоналям. А также построения встречаются в задачах на повторение.
в) 9 класс: содержит четыре главы. В главе 12 “Длина окружности и площадь круга” в §1 “Правильные многоугольники” рассматривается построение правильных многоугольников. Предлагается с помощью циркуля и линейки вписать в окружность различные правильные многоугольники. Также построения встречаются в задачах не повторение. Основная цель главы 12 – расширить и систематизировать знания учащихся об окружностях и многоугольниках (см. Приложение 1).
В главе 13 “Движения” изучаются симметрии, поворот и параллельный перенос. В конце главы содержатся задачи на построение, решение которых основано на изученном материале. Основная цель главы 13 – познакомить с понятием движения на плоскости: симметриями, параллельным переносом, поворотом (см. Приложение 1).
2) А.В. Погорелов [5]
а) 7 класс: содержит пять параграфов. В §1 “Основные свойства простейших геометрических фигур” рассматривается, как построить параллельные прямые с помощью угольника и линейки. В §2 “Смежные и вертикальные углы” рассматривается, как построить перпендикулярные прямые с помощью угольника и линейки. §5 “Геометрические построения” содержит пункт “Что такое задачи на построение”, где рассказывается о чертежных инструментах и о том, что значит решить задачу на построение. Схема решения не вводится. В следующих пунктах рассматриваются задачи на построение треугольника с данными сторонами; угла, равного данному; биссектрисы угла; деление отрезка пополам; построение перпендикуляра к прямой. Далее идут пункты “Геометрическое место точек”, в котором вводится определение ГМТ и Теорема о ГМТ, равноудаленных от двух данных точек; а также “Метод геометрических мест”, который раскрывает сущность данного метода. В конце параграфа приводится ряд задач на построение для самостоятельного решения. В основном это задачи на построение треугольника и окружности по данным элементам и задачи на ГМТ. Основная цель §5 – решать простейшие задачи на построение с помощью циркуля и линейки (см. Приложение 1).
б) 8 класс: содержит пять параграфов. В конце §6 “Четырехугольники” содержится задача на построении четвертого пропорционального отрезка. Также содержится ряд задач на построение параллелограмма, ромба и трапеции по данным элементам. Основная цель §6 – дать учащимся систематизированные сведения о четырехугольниках и их свойствах (см. Приложение 1). В §9 “Движение” изучаются геометрические преобразования: центральная и осевая симметрии, поворот, параллельный перенос. В конце параграфа приведены задачи на построение, решение которых основано на методах данных преобразований. Основная цель §9 – познакомить учащихся с примерами геометрических преобразований (см. Приложение 1).
в) 9 класс: в §11 “Подобие фигур” изучаются геометрические преобразования: подобие и гомотетия. В конце параграфа приведены задачи на построение, решение которых основано на методах данных преобразований. Основная цель §11 – усвоить признаки подобия треугольников и отработать навыки их применения (см. Приложение 1). В §13 “Многоугольники” рассматриваются построения некоторых правильных многоугольников. В конце имеется пара задач: вписать в окружность n-угольник и описать около окружности правильный n-угольник. Основная цель §13 – расширить и систематизировать сведения о многоугольниках и окружностях (см. Приложение 1).
3) А.Д. Александров, А.Л. Вернер, В.И. Рыжик [6]
а) 7 класс: содержит три главы. В главе 1 “Начала геометрии” в §5 “Окружность и круг” содержится пункт “Построения циркулем и линейкой”, в котором рассказывается о чертежных инструментах, с помощью которых выполняются задачи на построение. Тут же приводится задача на построение треугольника, стороны которого равны сторонам данного треугольника. Приводится построение, доказательство и исследование, но на общей схеме внимание не заостряется. §6 “Углы” содержит пункт “Построение угла, равного данному, циркулем и линейкой”. Для самостоятельного решения задач нет. В §7 “Действия над углами” рассматривается задача на построение биссектрисы угла, которая решает еще две задачи: в данной точке прямой провести перпендикуляр к ней, построить прямой угол. Также параграф содержит пункт “Задача о делении угла на равные части циркулем и линейкой”, в котором рассказывается о неразрешимости задачи о трисекции угла. Основная цель главы 1 – рассказать о задачах систематического курса геометрии и заложить основу для его построения (см. Приложение 1).
В главе 2 “Треугольники” в §10 “Признаки равенства треугольников” рассматривается задача о построении треугольника по двум сторонам и углу между ними. В §11 “Серединный перпендикуляр” первыми пунктами идут задачи о делении отрезка пополам и о построении перпендикуляра к данной прямой через данную точку, не лежащую на данной прямой. В конце параграфа содержится несколько задач на построение. Основная цель главы 2 – развить навыки решения задач на построение с помощью циркуля и линейки, начать знакомство с симметриями фигур (см. Приложение 1).
В главе 3 “Параллельность” в §13 “Параллельные прямые” изучается, как строить параллельные прямые с помощью угольника и линейки. В §14 “Аксиома параллельности” рассматривается задача о построении треугольника по стороне и двум прилежащем к ней углам.
б) 8 класс: содержит три главы. В главе 5 “Метрические соотношения в треугольнике” в § “Применение теоремы Пифагора” содержится пункт “Геометрическое место точек”, где объясняется, что значит, когда про фигуру говорят, что она является ГМТ, обладающих данным свойством. Также приводятся примеры, каким ГМТ являются биссектриса и серединный перпендикуляр. Параграф содержит такие задачи как, например, найти ГМТ, равноудаленных от прямой на данное расстояние; найти ГМТ, равноудаленных от двух данных пересекающихся прямых.
в) 9 класс: содержит две главы. В главе 7 “Многоугольники и окружности” в задачах для самостоятельного решения к §31 “Хорды и касательные” содержатся задача на нахождение ГМТ, из которых данный отрезок виден под данным углом; задача на построение касательной к окружности из данной точки, общей касательной к двум окружностям. §33 “Правильные многоугольники” содержит пункт “Построение правильных многоугольников” с помощью циркуля и линейки. Также в нем рассказывается о том, что циркулем и линейкой могут быть построены не все правильные n-угольники, а только те, у которых n имеет определенное разложение. Предлагается решить задачи: вписать в окружность различные правильные n-угольники. В §35 “Площадь круга” рассказывается о неразрешимой задаче о квадратуре круга.
В главе 8 “Другие методы геометрии” в §36 “Метод координат” содержится пункт “Окружность Аполлония”, где решение задачи о ГМТ, отношение расстояний от которых до двух данных точек есть постоянная величина. В §40 “Виды движений” рассматриваются “Метод параллельного переноса”, “Метод симметрии” и “Метод поворота”. Приводятся примеры задач на построение, решение которых основано на данных методах. В задачах для самостоятельного решения к §40 содержатся задачи на отработку изученных методов, в том числе задачи на построение трапеции и треугольника по данным элементам. В §42 “Подобие” рассматривается “Метод подобия”. В качестве примера приводится задача на построение четвертого пропорционального отрезка. В задачах для самостоятельного решения к §42 содержатся задачи на отработку изученного метода, в том числе задачи на построение прямоугольного треугольника по отношению катетов к гипотенузе и по отношению катетов к периметру. А также задачи: построить квадрат, вписанный в треугольник, ромб, сегмент; построить сегмент, вписанный в равносторонний треугольник, квадрат, окружность. Основная цель главы 8 – познакомить учащихся с методами, отсутствовавшими в классической элементарной геометрии, но играющими в современной геометрии ведущую роль: методом координат, векторным методом, методом преобразований (см. Приложение 1).
4) А.П. Кисилев, Н.А. Рыбкин [8]
Учебник содержит пять глав и сборник задач по геометрии.
В главе 1 “Прямая линия” в §1 “Углы ” рассматривается построение перпендикулярных прямых с помощью угольника и линейки. §3 “Треугольники” содержит пункт “Геометрическое место”, где дается определение ГМТ, и приводятся примеры: что является ГМТ серединного перпендикуляра и биссектрисы. Далее следует § 4 “Основные задачи на построение”, где рассматриваются задачи на построение треугольника по трем его сторонам; угла, равного данному; биссектрисы угла; перпендикуляра к прямой из данной точки, лежащей и не лежащей на прямой; серединного перпендикуляра; задача о делении отрезка пополам; построение треугольника по основанию, углу, прилежащему к основанию, и сумме двух боковых сторон. После рассмотренных задач приводится схема решения задач на построение: анализ, построение, доказательство, исследование. В конце §4 имеется блок задач на построение для самостоятельного решения, который содержит задачи на построение суммы, разности углов; деление угла на n частей; построение различных треугольников по различным элементам; разделение данного отрезка на n равных частей; задачи на нахождение ГМТ, равноудаленных от двух данных точек, от трех вершин треугольника, от трех сторон треугольника и т.д. В §5 “Параллельные прямые” рассматривается построение параллельных прямых с помощью угольника и линейки. §6 “Параллелограммы и трапеции” содержит пункт “Задачи на построение”, в котором рассматриваются методы параллельного переноса, симметрии и примеры задач. Также учащимся предлагается самостоятельно решить задачи на построение трапеций, четырехугольников и треугольников по различным данным элементам, основываясь на изученных методах. В конце главы 1 имеется ряд задач на нахождение ГМТ и блок задач на построение.
В главе 3 “Подобные фигуры” в §4 “Подобие фигур произвольного вида” имеется пункт “Задачи на построение”, в котором рассматривается метод подобия, но задач на применение метода данный пункт не содержит. В §5 “Некоторые теоремы о пропорциональных отрезках” рассматривается задача о построении четвертого пропорционального отрезка. В §6 “Метрические соотношения между элементами треугольника и некоторых других фигур” рассматривается задача о построении отрезка, среднего пропорционального между двумя данными отрезками. §8 “Тригонометрические функции острого угла” содержит пункт “Построение угла по заданной величине одной из его тригонометрических функций”. В §9 “Понятие о приложении алгебры к геометрии” рассматривается задача о разделении отрезка в среднем и крайнем отношении, а затем следует пункт “Алгебраический способ решения геометрических задач”, который раскрывает алгебраический метод решения задач на построение. Следующим пунктом идет “Построение простейших формул” с помощью циркуля и линейки. В конце главы 3 содержится ряд задач на нахождение ГМТ и блок задач на построение.
В главе 4 “Правильные многоугольники” в §1 “Правильные многоугольники” рассматривается задача: вписать в данный круг правильный десятиугольник и определить его сторону в зависимости от радиуса. Также далее в пункте “На сколько равных частей можно делить окружность с помощью циркуля и линейки?”, в котором дается указание, как разделить окружность на определенное равное количество частей (и вписать в окружность правильные многоугольники с таким числом сторон).
В главе 5 “Измерение площадей” в §1 “Площади многоугольников” рассматриваются задачи на построение треугольника (квадрата), равновеликого данному; квадрата, площадь которого равна сумме (разности) площадей двух данных квадратов; площадь которого относится к площади данного квадрата, как m:n; разделить данный треугольник на m равновеликих частей прямыми, параллельными его стороне. В §2 “Площадь круга и его частей” приводится пункт, в котором рассказывается о неразрешимой задаче о квадратуре круга. В конце главы 5 содержится блок задач на построение.
В сборнике задач также имеются задачи на построение.
Вывод: В учебниках для 5-6 классов задачи на построение практически не рассматриваются как самостоятельные. Чаще всего это задания на построение фигур по заданным размерам. Процент заданий на построение из всех геометрических заданий: 5 класс – 39%, 6 класс – 34%. В целом картина кажется достаточно отрадной. Однако если учесть, что сам по себе геометрический материал в учебниках не превышает 13-16% от всего содержания учебника, то указанный процент заданий на построение падает до 4-6% [3].
Во всех учебниках по геометрии для 7-9 класса задачи на построение рассматриваются как самостоятельные в конце 7 класса. Осуществляются следующие элементарные построения: деление отрезка пополам; откладывание угла, равного данному; построение биссектрисы угла; построение перпендикуляра к прямой из данной точки, не лежащей на этой прямой. В качестве метода решения задач на построение в учебниках (кроме учебника [7]) рассматривается метод геометрического места точек. Схема решения приводится в учебниках [7], [8]. В учебнике [6] схема приводится без анализа. В учебнике [5] ее нет.
В 8-9 классах встречаются задания на построение фигур по некоторым заданным элементам. Произвольные треугольники и четырехугольники строятся по сторонам и углам. Четырехугольники особых видов (ромбы, квадраты, прямоугольники) – по сторонам и диагоналям. Рассматриваются приемы описывания и вписывания окружностей в треугольники и четырехугольники.
Алгебраический метод решения задач на построение приводится только в учебнике [8]. В учебнике [6] рассказывается о трисекции угла, квадратуре круга, окружности Аполлония.
В таблице приведен количественный анализ (процент заданий на построение) в учебниках:
|
Учебники |
Класс |
Всего задач в учебнике |
Из них на построение |
Процент от общего числа задач |
|
Александров А.Д. и др. “Геометрия 7-9” |
7 |
33 |
8 |
24 |
|
8 |
643 |
95 |
15 |
|
|
9 |
556 |
89 |
16 |
|
|
Атанасян Л.С. и др. “Геометрия 7-9” |
7 |
362 |
90 |
25 |
|
8 |
448 |
64 |
14 |
|
|
9 |
321 |
36 |
11 |
|
|
Погорелов А.В. “Геометрия 7-9” |
7 |
218 |
42 |
20 |
|
8 |
298 |
35 |
12 |
|
|
9 |
206 |
10 |
5 |
Рассматривая учебники, можно отметить, что в них достаточно высок процент заданий на построение в 7 классе, причем рассматриваются стандартные и элементарные задачи на построение. Однако к 9 классу процент геометрических заданий на построение резко падает. Быть может ситуация обусловлена тем, что к 9 классу у всех школьников уже развито логическое и пространственное мышление, сформированы графические умения и навыки, они легко и верно читают любой чертеж, не затрудняются с его интерпретацией, легко строят любой нужный чертеж по тексту задачи? Увы, ситуация совсем не такова. Так как задания на построение составляют базу для работы, развивающей навыки построения фигур, способствующей формированию умения читать и понимать чертеж, устанавливать связи между его частями, то недостаточность этой системы обусловливает плохое развитие пространственного и логического мышления ученика, низкий уровень его графической культуры. Эти недостатки не позволяют ученику эффективно изучать те разделы математики, где самостоятельно сделанная и хорошо понятая графическая интерпретация является тем самым “лучом света в темном царстве”, которого так иногда не хватает школьнику при изучении математики.
1.2 Анализ учебно-методической литературы
1) И.Ф. Шарыгин “Задачи по геометрии (Планиметрия)” [28]
Книга, состоящая из двух частей, включает более 600 задач по планиметрии. Вторая часть содержит параграф, посвященный теме геометрических мест точек. Задач предлагается немного, они достаточно сложные, предназначенные по большей мере для специализированных классов, для студентов. Задачи сопровождаются указаниями и подробными решениями. В некоторых других параграфах второй части, таких как, например, “Треугольник” и “Окружности и касательные”, также встречаются задачи на нахождение геометрического места точек.
2) В.В. Прасолов “Задачи по планиметрии (в двух частях)” [22] [23]
В этот сборник включены нестандартные геометрические задачи несколько повышенного по сравнению со школьными знаниями уровня. Для всех задач прилагаются решения. Книга состоит из двух частей. Первая содержит классические темы планиметрии, вторая – геометрические преобразования и задачи на олимпиадную и кружковую тематику.
Всего 29 глав. За основу классификации задач приняты методы решения геометрических задач. Одна из глав посвящена методу ГМТ, которая содержит достаточное количество задач на построение разного уровня сложности, в которых применяется данный метод. Применяются как основные ГМТ, так и более сложные.
Есть глава, посвященная геометрическим построениям треугольников, четырехугольников, окружностей с помощью различных методов, включает в себя разнообразный набор задач на построение. Кроме того, в этой главе рассматриваются построения с помощью одной линейки, одной двусторонней линейки, с помощью одного прямого угла. Также здесь приводятся необычные построения (например, деление угла на n равных частей).
Имеются отдельные главы, посвященные методам параллельного переноса, центральной симметрии, осевой симметрии, поворота, гомотетии, в которых также хорошо отражена суть методов и содержится хороший набор задач разного уровня на применение каждого метода. Даются основные понятия к каждой главе.
3) Я.П. Понарин “Элементарная геометрия (в двух томах)” [20] [21]
Книга предназначена для более углубленного изучения элементарной геометрии. Для учащихся школ, лицеев, гимназий с математической специализацией и студентов. Первый том посвящен планиметрии и преобразованиям плоскости, второй – стереометрии и преобразованиям пространства.
В данном пособии уделено много внимания методу геометрических преобразований, в связи с тем, что чисто геометрические методы в последнее время отходят на второй план и данный метод до сих пор не нашел своего места в школьном курсе геометрии. Как пишет автор, его пытались изучать с самого начала, растянув на всю восьмилетнюю школу. Теперь предполагается заняться им в конце изучения планиметрии. Но по-прежнему ученики не владеют им даже на начальном уровне. В книге расширен материал школьных учебников, добавлены многие геометрические факты. Теория геометрических построений вынесена за рамки пособия. В систематическом виде изложен теоретический и задачный материал по методу геометрических преобразований плоскости. Он позволяет оригинально и красиво решать многие геометрические задачи. Большую часть пособия составляют задачи различной степени трудности, к большинству из них даны ответы или краткие указания.
Первый том содержит две части. Вторая часть посвящена преобразованиям плоскости. В частности две первые ее главы описывают движения плоскости и методы решения задач на построение (центральная симметрия, осевая симметрия, параллельный перенос, поворот, подобие).
Второй том также содержит две части. В первой части четвертая глава посвящена ГМТ. Здесь рассматриваются различные ГМТ плоскости, а также ГМТ пространства: разность квадратов расстояний, сумма квадратов расстояний, сфера Аполлония. Применение метода ГМТ для решения стереометрических задач. Вторая часть посвящена преобразованиям пространства аналогично второй части первого тома. Две первые ее главы описывают движения пространства и методы решения задач на построение (центральная симметрия, осевая симметрия, параллельный перенос, поворот, подобие).
В книге отдельно не выделяется применение метода ГМТ для планиметрических задач, а также не рассмотрен алгебраический метод.
4) И.И. Александров “Сборник геометрических задач на построение с решениями” [1]
Книга насчитывает более 600 задач на построение, что представляет учащимся и преподавателям огромный выбор. В основном книга посвящена решению задач на построение при помощи циркуля и линейки, но последний раздел посвящен решению задач одним циркулем, двусторонней линейкой, прямого или острого угла, односторонней линейкой с применением вспомогательной окружности Штейнера.
Сборник можно разделить на три части, включающие: 1) основные построения; 2) задачи, приучающие к построениям; 3) задачи на различные методы решения (метод ГМТ, метод геометрических преобразований, алгебраический метод). Представлен очень хороший набор задач различной степени сложности, на применение различных методов, и приведены решения. Каждый метод подробно описан, приведены примеры. Также в книге рассмотрена тема: “Применение тригонометрии к решению геометрических задач на построение”.
Вывод: Во всех книгах достаточно хорошо рассмотрены те или иные методы решения задач на построение, приведены решения задач. В книге [28] представлены задачи только на метод ГМТ. Сборники [22], [23] содержат отдельные главы, посвященные различным методам (кроме алгебраического). Включенные в них задачи имеют несколько повышенный по сравнению со школьными знаниями уровень. Наиболее оптимальным из рассмотренных книг, по нашему мнению, является сборник [1], он содержит много задач на применение различных методов. Причем только в нем рассматривается алгебраический метод. Кроме того, достаточно хорошими книгами являются пособия [20], [21]. В них наилучшим образом представлена тема геометрических преобразований и только здесь рассматривается ГМТ пространства.
2. Логическое мышление: основные понятия. Анализ психолого-педагогической литературы
2.1 Природа и виды мышления
Существуют различные подходы к понятию “мышление”. Приведем некоторые из них.
Мышление – высшая форма активного отражения объективной реальности, состоящая в целенаправленном, опосредованном и обобщенном познании субъектом существующих связей и отношений предметов и явлений в творческом созидании новых идей, в прогнозировании событий и явлений [27].
Мышление – социально обусловленный, неразрывно связанный с речью психический процесс поисков и открытия существенно нового, процесс опосредованного и обобщенного отражения действительности в ходе ее анализа и синтеза. Мышление возникает на основе практической деятельности из чувственного познания и далеко выходит за его пределы [16].
Мышление отражает бытие в его связях и отношениях, в его многообразных опосредованиях.
Мышление — это обобщенное отражение объективной действительности в ее закономерных, наиболее существенных связях и отношениях. Оно характеризуется общностью и единством с речью. Другими словами, мышление есть психический процесс познания, связанный с открытием субъективно нового знания, с решением задач, с творческим преобразованием действительности.
Мышление – психический процесс обобщенного и опосредованного отражения устойчивых, закономерных свойств и отношений действительности, существенных для решения познавательных проблем, схематической ориентации в конкретной ситуациях.
Выделяют следующие виды мышления [26]:
1) Наглядно-действенное мышление. Основная характеристика этого мышления: решение задачи осуществляется с помощью реального преобразования ситуации, с помощью наблюдаемого двигательного акта.
2) Образное (или наглядно-образное) мышление. Функции образного мышления связаны с представлением ситуаций и изменений в них, которые человек хочет получить в результате своей деятельности, преобразующей ситуацию; с конкретизацией общих положений. С помощью образного мышления более полно воссоздается все многообразие различных фактических характеристик предмета. В образе может быть зафиксировано одновременное видение предмета с нескольких точек зрения. Очень важная особенность образного мышления — установление непривычных, “невероятных” сочетаний предметов и их свойств. В отличие от наглядно-действенного мышления при наглядно-образном мышлении ситуация преобразуется лишь в плане образа.
3) Теоретическое (или словесно-логическое) мышление. Это мышление характеризуется использованием понятий, логических конструкций, существующих, функционирующих на базе языка, языковых средств. Теоретическое мышление выявляет всеобщее отношение, исследует объект познания в системе его необходимых связей. Его результат – построение теоретических моделей, создание теорий, обобщение опыта, раскрытие закономерности развития различных явлений, знание которых обеспечивает преобразовательную деятельность человека. Теоретическое мышление неразрывно связано с практикой, но в своих конечных результатах имеет относительную самостоятельность.
Описанная классификация (тройка) не является единственной. В психологической литературе используется несколько “парных” классификаций [26]:
1) Теоретическое и практическое мышление по типу решаемых задач и вытекающих отсюда структурных и динамических особенностей. Теоретическое мышление — это познание законов, правил. Основная задача практического мышления — подготовка физического преобразования действительности: постановка цели, создание плана, проекта, схемы. Одна из важных особенностей практического мышления заключается в том, что оно развертывается в условиях жесткого дефицита времени. В практическом мышлении очень ограниченные возможности для проверки гипотез. Все это делает практическое мышление подчас еще более сложным, чем мышление теоретическое. Теоретическое мышление иногда сравнивают с мышлением эмпирическим. Здесь в качестве критерия используется характер обобщений, с которыми имеет дело мышление: в одном случае это научные понятия, а в другом — житейские, ситуативные обобщения.
2) Интуитивное и аналитическое (логическое) мышление. Обычно используются три признака: временной (время протекания процесса), структурный (членение на этапы), уровень протекания (осознанность или неосознанность). Аналитическое (логическое) мышление развернуто во времени, имеет четко выраженные этапы, в значительной степени представлено в сознании самого мыслящего человека. Интуитивное мышление характеризуется быстротой протекания, отсутствием четко выраженных этапов, является минимально осознанным.
3) Реалистическое и артистическое мышление. Реалистическое мышление направлено в основном на внешний мир, регулируется логическими законами. Артистическое мышление связано с реализацией желаний человека. Иногда используется термин эгоцентрическое мышление, оно характеризуется, прежде всего, невозможностью принять точку зрения другого человека.
4) Продуктивное и репродуктивное мышление. Различие основано на степени новизны получаемого в процессе мыслительной деятельности продукта по отношению к знаниям субъекта.
Сравнительная таблица основных видов мышления (см. Приложение 2).
2.2 Развитие мышления ребенка
В преддошкольном возрасте (до трех лет включительно) мышление в основном наглядно-действенное.
В возрасте четырех – семи лет возникает наглядно-образное мышление в простейшей форме преимущественно у дошкольников. Дошкольники мыслят лишь наглядными образами и еще не владеют понятиями (в строгом смысле) [17].
В школьном возрасте в процессе систематического мышление ребенка начинает перестраиваться и развивается теоретическое мышление.
По мере формирования теоретического мышления ребенок, подросток все больше учится осознавать обобщенные закономерности явлений. Ребенок не столько все глубже познает действительность, по мере того как развивается его мышление, сколько его мышление все более развивается, по мере того как углубляется его познавательное проникновение в действительность.
С 11 до 14 лет резко возрастает значимость причинных связей в мышлении ребенка, причем сначала сильно преобладает интерес к причинам явлений. Затем соотношение изменяется: подростка начинает больше интересовать будущее, его мышление начинает направляться на раскрытие следствий. Вместе с тем от установления единичных причинно-следственных зависимостей в частных наглядных ситуациях оно поднимается к пониманию общих закономерностей.
Новый уровень отвлеченной теоретической мысли сказывается также во взаимоотношениях мышления и речи, а также мышления и наглядно-образного содержания восприятия, представления.
В отношении между мышлением и речью новый уровень мышления находит себе выражение в том, что: а) значительную роль в речи начинают играть термины; б) другим выражением того же сдвига в мышлении является развивающееся в этот период понимание метафорического переносного значения слов; в) особенно заостренно сказываются особенности речевой формы отвлеченного мышления в умении оперировать формулами с буквенными обозначениями (алгебра, логика).
Развитие мышления ребенка происходит поэтапно, представляет собой некоторые ступени развития. При этом высшие ступени, развиваясь, не вытесняют низших, а преобразуют их. Когда развивается теоретическое мышление, то ни наглядно-действенное, ни наглядно-образное мышление, конечно, не исчезают, а преобразуются, совершенствуются, сами поднимаются на высшую ступень. Между ними создаются многообразнейшие, сложные, от случая к случаю индивидуально варьирующиеся взаимоотношения.
На различных этапах развития мышления разные области знания являются той базой, на которых формируются более высокие формы мышления, на которых оно раньше всего переходит на высшую ступень. В раннем возрасте такой областью является арифметика. При переходе из начальной в среднюю школу такую же роль в развитии отвлеченного мышления может играть алгебра. В разные периоды разные науки вносят каждая свой специфический вклад в развитие мышления и могут явиться тем плацдармом, на котором раньше формируются те или иные стороны более высоких ступеней мышления [24].
2.3 Понятие логического мышления
Логическое мышление как феномен изучается различными науками: философией, психологией, логикой. Каждая из них по-своему, что вполне справедливо, определяет его сущность.
Так, например, в одних источниках логическим мышлением называют процесс мышления, в котором умозаключения строго основываются на правильных суждениях. При таком мышлении явление получает убедительное объяснение, безошибочно устанавливаются причины и следствия, выявляются связи и отношения между понятиями, которые выражаются в суждениях, верность которых нельзя опровергнуть.
В других – определяют словесно-логическое мышление как один из видов мышления, характеризующийся использованием понятий, логических конструкций.
В свою очередь, в словаре психологических понятий К.К. Платонова логическое мышление определяется как “вид мышления, сущность которого в ориентировании понятиями, суждениями и умозаключениями с использованием законов логики” [19].
Отметим, что в психолого-педагогической литературе “логическое мышление” практически отождествляется с понятием “абстрактное”, “теоретическое”, “понятийное”, “категориальное”, “словесно-логическое (дискурсивное)” мышление, иногда они рассматриваются как синонимы.
Но при этом все сходятся в том, что логическое мышление – есть абстрактное, аналитическое, синтетическое мышление, функционирующее на базе языковых средств, активно развивающееся у человека, начиная с определенного возраста – с началом его обучения.
Цель развития логического мышления (определенность, последовательность, доказательность мысли) достигается решением следующих задач: овладение основными мыслительными операциями, структурой логических форм мышления, переносом приемов мыслительной деятельности из одной области знаний в другую. Организация логической подготовки базируется на принципах преемственности, учета возрастных особенностей, раскрытия общезначимости логических форм и отношений и др.; а содержание ее включает основные логические умения и соответствующие им мыслительные операции. Развитие логического мышления осуществляется посредством изучения процесса мышления, активного использования речи, соединения и взаимообогащения всех видов мышления.
2.4 Развитие логического мышления школьников в процессе обучения математике
Отметим, что развитие логического мышления непосредственно связано с процессом обучения математике. При этом многие исследователи отмечают, что одной из важнейших задач обучения, в том числе и математике, в школе является формирование у учащихся навыков осуществления логических операций, обучение их различным приемам логического мышления, вооружение знаниями логики и выработки у школьников умений и навыков использования этих знаний в учебной и практической деятельности.
В результате правильно организованного обучения математике школьники весьма быстро приобретают навыки логического мышления, в частности, умение обобщать, классифицировать и аргументированно обосновывать свои выводы.
Вместе с тем нет единого подхода к решению вопроса, как организовать такое обучение математике. Одни считают, что логические приемы являются неотъемлемой частью математики как науки, основы которой включены в содержание образования, поэтому у учащихся при изучении математики автоматически развивается логическое мышление на основе заданных образов (В.Г. Бейлинсон, Н.Н. Поспелов, М.Н. Скаткин).
Другой подход выражается во мнении части исследователей о том, что развитие логического мышления только через изучение учебных предметов, в том числе и математики, является малоэффективным, такой подход не обеспечивает полноценного усвоения приемов логического мышления и поэтому необходимы специальные учебные курсы по логике (Ю.И. Веринг, Н.И. Лифинцева, В.С. Нургалиев, В.Ф. Паламарчук).
Еще одна группа ученых (Д.Д. Зуев, В.В. Краевский) считают, что развитие логического мышления учащихся должно осуществляться на конкретном предметном содержании учебных дисциплин через акцентуацию, выявление и разъяснение встречающихся в них логических операций.
Но каков бы ни был подход к решению этого вопроса, большинство исследователей сходятся в том, что развивать логическое мышление в процессе обучения математике это значит: развивать у учащихся умение сравнивать наблюдаемые предметы, находить в них общие свойства и различия; вырабатывать умение выделять существенные свойства предметов и отвлекать (абстрагировать) их от второстепенных, несущественных; учить детей расчленять (анализировать) предмет на составные части в целях познания каждой составной части и соединять (синтезировать) расчлененные мысленно предметы в одно целое, познавая при этом взаимодействие частей и предмет как единое целое; учить школьников делать правильные выводы из наблюдений или фактов, уметь проверять эти выводы; прививать умение обобщать факты; развивать у учащихся умение убедительно доказывать истинность своих суждений и опровергать ложные умозаключения; следить за тем, чтобы мысли учащихся излагались определенно, последовательно, непротиворечиво, обоснованно.
Решение задач на построение, несомненно, развивает логическое и активное мышление учащихся. Ни одни задачи не содействуют так развитию в учениках наблюдательности и правильности мышления, представляя в то же время для них и наибольшую привлекательность, как геометрические (задачи) на построение.
Большое значение для развития логического мышления учащихся имеют и задачи на построение. Наличие анализа, доказательства и исследования при решении большинства таких задач показывает, что они представляют собой богатый материал для выработки у учащихся навыков правильно мыслить и логически рассуждать. При решении задач на построение они имеют дело не с конкретной, определенной фигурой, а должны создать необходимую фигуру, подвергающуюся различным изменениям в процессе решения. Вскрывая взаимосвязи между данными элементами, видим, как с изменением одних изменяются другие и даже вся фигура. Этим мы приучаем учащихся к диалектическому методу мышления и по возможности устраняем формализм в знаниях.
Трудно переоценить роль задач на построение в математическом развитии школьников. Они по своей постановке и методам решения не только наилучшим образом стимулируют накопление конкретных геометрических представлений, но и развивают способность отчетливо представлять себе ту или иную геометрическую фигуру и, более того, уметь мысленно оперировать элементами этой фигуры. Задачи на построение могут способствовать пониманию учащимися происхождения различных геометрических фигур, возможности их преобразования – все это является важной предпосылкой развития пространственного мышления школьников. Они сильно развивают логическое мышление, геометрическую интуицию.
Между тем заметим, что процесс формирования логического мышления, общелогических умений, как компонента общего образования, должен быть целенаправленным, непрерывным и связанным с процессом обучения математике на всех ее ступенях.
Вывод: Логическое мышление – есть абстрактное, аналитическое, синтетическое мышление, функционирующее на базе языковых средств, активно развивающееся у человека, начиная с определенного возраста – с началом его обучения. Развитие логического мышления – это формирование у учащихся навыков осуществления логических операций, обучение их различным приемам логического мышления, вооружение знаниями логики и выработка умений и навыков использования этих знаний в учебной и практической деятельности. Этот процесс непосредственно связан с процессом обучения математике, правильная организация которого обеспечивает наиболее эффективное развитие логического мышления, в том числе и при решении геометрических задач. При этом ни одни задачи не содействуют так развитию в учениках наблюдательности и логического мышления, представляя в то же время для них и наибольшую привлекательность, как задачи на построение.
3. Методика решения задач на построение
Суть решения задачи на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру, если дана некоторая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.
Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.
Найти решение задачи на построение – значит свести ее к конечному числу основных построений, то есть указать конечную последовательность основных построений, после выполнения которых, искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии.
Одной из основных проблем методики обучения решению задач на построение является методика введения и изучения этапов решения конструктивных задач. Еще в IV в. до н. э. древнегреческие геометры разработали общую схему решения задач на построение, которой мы пользуемся и теперь. Процесс решения задачи разбивают на 4 этапа: анализ, построение, доказательство и исследование. Рассмотрим каждый этап более подробно.
3.1 Анализ
Анализ — это важный этап решения задачи, который мы понимаем как поиск способа решения задачи на построение. На этом этапе должны быть подмечены такие зависимости между данными фигурами и искомой фигурой, которые позволили бы в дальнейшем построить эту искомую фигуру (если мы знаем, как строить искомую фигуру, то никакой анализ уже не нужен).
Анализ – подготовительный, предварительный этап решения задачи на построение.
Чтобы облегчить себе поиск связей между искомой фигурой и данными фигурами, обычно оказывается выгодным иметь перед глазами вспомогательный чертеж, чертеж-набросок, изображающий данные и искомые фигуры примерно в том расположении, которое предусмотрено условием задачи. Чертеж можно выполнить от руки, на глаз – это проект чертежа, который должен образоваться, когда задача уже решена.
На вспомогательном чертеже следует выделить данные элементы и важнейшие искомые элементы. Практически часто удобнее начинать построение вспомогательного чертежа не с данной фигуры, а с примерного изображения исходной фигуры, пристраивая к ней данные так, чтобы они находились в отношениях, указанны в условии задачи.
Если вспомогательный чертеж не подсказывает способа построения искомой фигуры, то пытаются обнаружить какую-либо часть искомой фигуры или вообще некоторую фигуру, которая может быть построена, и которой затем можно воспользоваться для построения искомой фигуры.
Также надо учитывать следующие моменты [2]:
1) если на вспомогательном чертеже не удается непосредственно заметить необходимые для решения связи между данными и искомыми элементами, то целесообразно ввести в чертеж вспомогательные фигуры: соединить уже имеющиеся точки прямыми, отметить точки пересечения имеющихся линий, продолжить некоторые отрезки и т. д. Иногда бывает полезно проводить параллели или перпендикуляры к уже имеющимся прямым;
2) если по условию задачи дана сумма или разность отрезков или углов, то эти величины следует ввести в чертеж, то есть следует изобразить их на чертеже-наброске, если их еще нет на нем;
3) в процессе проведения анализа бывает полезно вспомнить теоремы и ранее решенные задачи, в которых встречаются зависимости между элементами, о которых говорится в условии рассматриваемой задачи.
В Приложении 3 приведен анализ задачи на построение: “Построить треугольник, зная основание, меньший угол при основании и разность двух других сторон”.
Из данного примера видно, что при отыскании решения задачи на построение, как и для арифметических задач, применяется аналитико-синтетический метод. Следуя от вопроса задачи, учитываем, какие элементы нам известны, и, наоборот, исходные данные комбинируем так, чтобы построить искомую фигуру.
Название этапа “анализ” не означает, что для отыскания решения применяется только аналитический метод, подобно тому, как и при доказательстве, которое иногда называют “синтезом”, не всегда применяется синтетический метод рассуждения. При разборе задачи, при отыскании путей ее решения анализ и синтез находятся в постоянном взаимодействии, дополняют и проверяют друг друга.
3.2 Построение
Второй этап решения задач на построение состоит из двух частей:
1) перечисление в определенном порядке всех элементарных построений, которые нужно выполнить, согласно анализу, для решения задачи;
2) непосредственное выполнение этих построений на чертеже при помощи чертежных инструментов. Действительно, решить задачу с помощью тех или иных инструментов — значит указать конечную совокупность элементарных, допустимых для данных инструментов, построений, выполнение которых в определенной последовательности позволяет дать ответ на вопрос задачи.
Данный этап вводится при решении самой первой задачи на построение, которой обычно является задача о построении отрезка, равного данному, на данном луче с концом в начале этого луча. В беседе, сопровождающей введение этапа, необходимо отметить, в чем состоит решение любой задачи на построение и указать, что осуществление этого этапа как раз и состоит в перечислении конечного числа операций построения искомой фигуры.
Рис. 1
Рассмотрим решение задачи: “Построить квадрат по его диагонали”.
Анализ. Проведя диагональ А>1>С>1> (рис. 1), мы видим, что построение квадрата сводится к построению равнобедренного прямоугольного треугольника А>1>В>1>С>1> по его гипотенузе A>1>C>1>, который затем легко дополнить до квадрата.
Построение. Треугольник А>1>В>1>С>1> можно строить различными способами. Например:
1) Строим угол B>1>A>1>C>1>,
содержащий 45°, и на одной его стороне
откладываем отрезок А>1>С>1>>,
>и равный данной диагонали.
Проведя C>1>B>1>
A>1>B>1>,
получим треугольник А>1>В>1>С>1>,
который дополняем до квадрата A>1>B>1>C>1>D>1>,
что можно сделать различными способами.
2) Проведем через середину А>1>С>1>
перпендикуляр В>1>О>1>А>1>С>1>>
>и отложим B>1>O>1>=A>1>O>1>
и соединим В>1>
с А>1>
и С>1>;
получим треугольник A>1>B>1>C>1>.
3) На А>1>С>1>,
как на диаметре, строим окружность и из
точки О>1>
восставляем перпендикуляр О>1>В>1>А>1>С>1>
до пересечения с окружностью в точке
B>1>.
Соединив В>1>
с А>1>
и С>1>,
получим треугольник A>1>B>1>C>1>.
Проведя B>1>D>1>A>1>C>1>,
мы сразу можем получить точки B>1>
и D>1>,
как и в предыдущем случае. Очевидно, что
построение треугольника A>1>B>1>C>1>
возможно и другими способами [11].
Решение одной и той же задачи несколькими способами усиливает интерес учащихся к задачам на построение и сознательное отношение к решению таких задач. Если решать задачи на построение все время по заранее указанным методам, то этим самым сковывается изобретательность и инициатива учащихся в нахождении различных и оригинальных способов решения и им трудно научиться самостоятельно решать конструктивные задачи. Они применяют в первую очередь знания изучаемого материала и навыки, полученные при решении задач, предшествующих данной. Если решались задачи, требующие применения определенного метода, то и для предложенной задачи они изберут тот же знакомый им путь решения, даже если он нерационален. Указание учителя на существование более простого способа не дает должного эффекта, так как предложенное учителем решение кажется учащимся искусственным, которого они сами не смогли бы найти.
Конечно, если это делать до того как ученики приобретут прочные навыки в отыскании решений различными способами, то результаты окажутся отрицательными. Внимание учащихся каждый раз будет распыляться между всеми способами, и они ни одного из них не усвоят основательно, чтобы применять его достаточно сознательно.
Различными способами хорошо решать задачи в конце учебного года, при повторении курса геометрии, когда учащиеся уже имеют достаточные навыки в решении задач на построение. Задачу, допускающую различные способы решения, лучше задавать на дом, чтобы они не только решили, но и нашли наиболее простое решение.
3.3 Доказательство
После того как фигура построена, необходимо установить, удовлетворяет ли она условиям задачи, то есть показать, что фигура, полученная из данных элементов определенным построением, удовлетворяет всем условиям задачи. Значит, доказательство существенно зависит от способа построения. Одну и ту же задачу можно решать различными способами, в зависимости от намеченного при анализе плана построения, а поэтому, и доказательство в каждом случае будет свое. Доказательство представляет собой часть решения задачи, по своему логическому содержанию обратную анализу. Если в анализе устанавливается, что всякая фигура, удовлетворяющая поставленным условиям, может быть найдена таким-то и таким-то путем, то в этой, третьей части решения доказывается обратное положение. Это обратное положение в общем виде может быть сформулировано так: если некоторая фигура получена из данных элементов таким-то построением, то она действительно удовлетворяет поставленным условиям. В Приложении 3 приведено решение задачи: “Построить трапецию по четырем сторонам”.
При решении простейших задач, когда все условия задачи находят непосредственное отражение в плане построения, нет необходимости доказывать, что фигура, полученная из данных элементов таким построением, является искомой. Например: “Построить треугольник по двум сторонам и углу между ними”. Здесь доказательство сводится к простой проверке, такие ли взяли стороны, как данные, и будет ли построенный угол равен данному. В подобных задачах доказательство является излишним, ибо правильность решения обеспечивается соответствием построения анализу и данным условия задачи.
Доказательство не просто зависит от анализа и построения, между ними существует взаимосвязь и взаимообусловленность. Построение проводится по плану, составленному при анализе. Таких планов можно указать несколько. Построение и доказательство являются своеобразным критерием правильности и рациональности составленного плана. Если план не осуществим имеющимися инструментами или же построение оказывается нерациональным, мы вынуждены искать новый план решения. Аналогичным образом и доказательство, и исследование влияют на анализ, предопределяя нередко выбор плана решения.
Хотя доказательство при решении задач на построение проводится аналогично доказательству теорем, с использованием аксиом, теорем и свойств геометрических фигур, между ними имеется и некоторое различие. При доказательстве теорем в большинстве случаев без труда выделяют условие и заключение. При решении задач на построение уже труднее найти данные, на основании которых можно доказать, что построенная фигура является искомой. Поэтому при решении конструктивных задач в классе целесообразно иногда специально выделять, что дано, и что требуется доказать. Например, при решении задачи: “Построить ромб по двум его диагоналям” предлагаем ученику записать, что дано (диагонали взаимно перпендикулярны и, пересекаясь, делятся пополам) и что требуется доказать (стороны равны). В свою очередь при решении задач дома и в контрольных работах можно не требовать оформления доказательства с выделением отдельно условия и заключения. Нет надобности требовать проведения особого доказательства в задачах, где правильность решения очевидна [11].
3.4 Исследование
При построении обычно ограничиваются отысканием одного какого-либо решения, причем предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно еще выяснить следующие вопросы: 1) всегда ли (то есть при любом ли выборе данных) можно выполнить построение избранным способом; 2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить; 3) сколько решений имеет задача при каждом возможном выборе данных? Рассмотрение всех этих вопросов и составляет содержание исследования [2].
Таким образом, исследование имеет целью установить условия разрешимости и определить число решений. Нередко школьники и даже учителя проводят исследование, произвольно выбирая те или иные случаи, причем неясно, почему рассматриваются именно такие, а не какие-либо иные случаи. Остается неясным также, все ли возможные случаи рассмотрены. Практически в большинстве случаев удается достигнуть необходимой полноты исследования, если проводить это исследование по ходу построения, что является наиболее доступным и целесообразным способом. Сущность этого приема состоит в том, чтобы перебрать последовательно все шаги, из которых слагается построение, и относительно каждого шага установить, всегда ли указанное на этом шаге построение выполнимо, а если выполнимо, то однозначно ли.
Рассмотрим решение и исследование задачи: “Построить окружность, касающуюся данной прямой PQ и данной окружности (О; ОА) в заданной на ней точке А”.
Рис. 2
Решение. Решаем эту задачу методом геометрических мест. Проводим прямую ОА (рис. 2). В точке А строим касательную АВ к данной окружности, а затем — биссектрисы углов РВА и ABQ. Точки пересечения прямой ОА с прямыми ВМ и BN и будут центрами искомых окружностей.
Проводя исследование по построению,
легко обнаруживаем, что наше решение
не применимо, если OAPQ.
Для такого случая рассматриваем решение
задачи отдельно. В результате получим,
что если ОА
не перпендикулярна PQ,
то задача имеет два решения, за исключением
случая, когда окружность (О;
ОА) пересекает
PQ
в точке А, так
как тогда прямые ВМ,
ВN
и ОА пересекутся
в точке А, и
окружности не получим. Если же OAPQ,
но А не лежит
на PQ,
то получаем одну окружность с центром
на ОА и радиусом,
равным половине расстояния от точки А
до данной прямой PQ.
Если же при этом А
лежит на PQ,
то задача неопределенная.
Таким образом, для задачи имеются лишь 4 характерные конфигурации исходных данных:
1) ОА не перпендикулярна PQ и А не принадлежит PQ — 2 решения;
2) OA не перпендикулярна PQ и A принадлежит PQ — нет решений;
3) OAPQ,
но A
не принадлежит PQ
— 1 решение;
4) OAPQ
и А
принадлежит PQ
— бесконечное множество решений [11].
В итоге таких рассуждений решается вопрос о возможности и однозначности построения искомой фигуры данным способом. Но остается еще открытым вопрос: не возникнут ли новые решения, если изменить как-либо способ построения? Иногда удается доказать, что всякое решение данной задачи совпадает с одним из уже полученных решений. Если же это не удается, то можно предположить, что задача имеет другие решения, которые могут быть найдены другими способами. В этих случаях надо тщательно проверить, нет ли каких-либо иных возможных случаев расположения данных или искомых фигур, которые не были предусмотрены ранее проведенным анализом.
3.5 Методические рекомендации по обучению решению задач на построение
Как и в каком месте курса геометрии следует знакомить учащихся с общей схемой решения задач на построение? Здесь возникает два различных методических вопроса [10]. Первый из них — это вопрос о том>, >с какого времени в преподавании геометрии при решении задач должны фактически производиться анализ, построение, доказательство, исследование? Второй вопрос, отличный от первого, — это вопрос, когда учащийся должен быть ознакомлен с логической схемой решения задачи.
Обращаясь к первому вопросу, заметим, что первым по времени вводимым элементом лучше выбрать построение в смысле перечисления и описания тех или иных операций. Здесь имеется в виду самое описание процесса употребления инструмента (“прикладываем два острия ножек циркуля к точкам М и N, затем, не изменяя расстояния между остриями, помещаем одно из них в точку О” и т. п.). На более высокой ступени отдельные операции просто называются (“описываем из точки О окружность радиусом MN” или “опускаем из точки С перпендикуляр на прямую АВ”). Наконец, последней ступенью можно было бы считать ту, когда в качестве элементов построения могут называться и довольно сложные по своему выполнению, но хорошо известные учащимся задачи (“строим треугольник по гипотенузе и катету”, “проводим из точки М касательную к окружности” и т. п.).
Вторым моментом по времени появления в школьном курсе лучше выбрать исследование задачи. Первый элемент исследования появляется при решении задачи о построении треугольника по трем сторонам, в виде вопроса о том, можно ля выбрать все три стороны произвольно. К этому должно скоро прибавиться знакомство с возможностью существования нескольких решений одной задачи. Этому моменту нужно придавать весьма большую принципиальную значимость. Дело в том, что слова “найти точку” обозначают требование “найти все точки, которые...” (а не просто “какую-либо точку, которая...”). Аналогично “решить уравнение” значит “найти все числа, которые удовлетворяют уравнению” (а не просто “какое-либо число, которое...”). “Построить окружность” – это “построить, все окружности, которые...” (а не просто “построить какую-либо окружность, которая...”) и т. д.
Задачи на геометрические построения с двумя решениями (или более) – первый случай, когда учащийся встречается с такого рода выражениями в математике, и чрезвычайно важно, чтобы учащийся привыкал к ним с самого начала, с 7-8 класса. Иначе совершенно неизбежно возникновение в дальнейшем вопросов такого типа, как “зачем при извлечении корня брать оба знака”. Сам термин “исследование” должен появиться много раньше, чем, скажем, термин “анализ”.
Третьим моментом, появляющимся, примерно, в одно время с элементами исследования, является доказательство правильности выполнения построения. Уже такие задачи в 7 классе как построение угла, равного данному, построение перпендикуляров с помощью циркуля и линейки и т. д. ставят на очередь вопрос о том, будет ли построенный угол действительно равен данному, будет ли построенная прямая перпендикулярна к данной? Однако и на этой стадии работы и на последующих нет большой необходимости (только для соблюдения формального однообразия изложения) требовать проведения доказательства в тех задачах, где правильность построения усматривается непосредственно. Некоторые, даже сравнительно сложные, задачи на построение, могут, как кажется, оставляться без особого доказательства. Например, задача, решаемая методом геометрических мест: построить треугольник по основанию, противолежащему углу и медиане, проведенной к основанию.
Наконец, последним по времени элементом решения, на котором фиксируется внимание учащихся, является анализ. Началом этого вида работы следует считать обращение к ученикам, “придумавшим” то или иное решение задачи, с вопросом: “А как ты это решение нашел?”. Потом постепенно надо подвести учащихся к мысли о том, чтобы фиксировать свое внимание на самом процессе отыскания метода решения, этот процесс и получает название анализа.
Из выше сказанного следует, что в деле введения понятий анализа, построения, доказательства и исследования следует соблюдать с одной стороны, постепенность, а с другой стороны, – настойчивость в смысле многократного систематического обращения к одним и тем же вопросам.
Перейдем теперь ко второму вопросу – о введении в курсе геометрии схемы деления решения задач на построение на четыре части. Несомненно, что изучение этого вопроса на том месте, на котором он поставлен в учебниках, следует считать несвоевременным и не достигающим цели. Тем не менее, схема решения должна быть сообщена учащимся, но лишь значительно позднее. В течение учебного года, с начала систематическою курса геометрии в 7 классе до середины курса 8 класса, или даже несколько дольше, должна идти та систематическая, иногда даже незаметная для учащихся работа учителя по ознакомлению учеников с элементами общей схемы решения, о которой говорилось выше. Лишь в 8 классе учитель на примере специально подобранной задачи полностью излагает учащимся всю схему решения. Задачу следует, конечно, подобрать так, чтобы она допускала один наиболее естественный ход решения (при анализе задачи мысль учащихся должна легко пойти по вполне определенному пути), чтобы она требовала исследования, и в то же время, чтобы это исследование не было слишком сложным. Вместе с тем задача не должна быть слишком простой, так как в этом случае способ решения может оказаться очевидным для учащихся, и тогда анализ задачи покажется им чем-то искусственным. Наиболее подходящими для этой цели являются задачи, решаемые методом геометрических мест. Хорошим примером для иллюстрации общей схемы решения задач на построение является задача: “Построить треугольник по двум сторонам и острому углу, лежащему против одной из них”.
Сделав чертеж произвольного треугольника, учащиеся составляют план построения и при соответствующем выборе данных получают два решения. Они видят необходимость доказательства (проверки, какой из полученных треугольников является искомым), а также и необходимость исследования (всегда ли получим два решения?). Здесь естественно выделяются все этапы и очевидна их целесообразность. Если учащиеся хорошо владеют основными построениями, больших затруднений в оформлении решений они не испытывают.
Эта задача на построение является хорошим примером, показывающим связь между числом решений задачи на построение треугольника по определенным данным и признаками равенства треугольников.
При решении задач на построение параллелограммов хорошим примером для повторения общей схемы будет задача: “Построить параллелограмм по стороне и двум диагоналям”.
После того как схема решения задачи на построение объяснена учащимся, этой схемы следует придерживаться при решении всех дальнейших задач на построение.
Тем не менее, необязательно все задачи решать, строго придерживаясь схемы с подробным описанием всех этапов. Ученики проводят анализ лишь тогда, когда решение задачи не очевидно, доказательство – когда в нем есть необходимость.
Усвоение учащимися общей схемы имеет большое значение не только для решения задач на построение. С методической точки зрения и при решении арифметических задач, и при решении задач на составление уравнений мы пользуемся теми же четырьмя этапами, что и при решении задач на построение.
Остановимся более подробно на рассмотрении этапа “исследование”. Каждая задача на построение включает в себя требование построить геометрическую фигуру, удовлетворяющую определенным условиям, которые в большинстве своем задаются размерами или положением некоторых геометрических образов. Условия задач формулируются в самом общем виде, а поэтому исходные данные являются как бы параметрами, принимающими всевозможные допустимые значения. Необходимо учить школьников видеть эти допустимые значения.
Они определяются наиболее естественным образом. Например, в задаче: “Построить треугольник по двум сторонам а и b и углу С между ними” допустимыми значениями для а и b будут всевозможные отрезки, которые можно характеризовать положительными числами, их длинами, а угол С может принимать всевозможные значения от 0° до 180°.
Рассмотрим задачу: “Построить окружность, касающуюся данной окружности в данной на ней точке и данной прямой”. В ней прямая может занимать любое положение на плоскости. Окружностью также может быть любая окружность на плоскости. Но так как окружность характеризуется положением центра и величиной радиуса, то можно сказать, что центром данной окружности может быть любая точка плоскости, а радиусом – любой отрезок, длина которого 0<ℓ<∞.
Иногда рассматривают и направленные окружности, тогда уже радиус может быть и неположительным числом, но подобные случаи обычно оговариваются в условии задачи. Точка также может занимать произвольное положение, но уже не на плоскости, а на данной окружности, так как она обязательно должна принадлежать ей.
Решение задачи на построение считается законченным, если указаны необходимые и достаточные условия, при которых найденное решение является ответом на задачу. Значит, мы при всяком выборе данных должны устанавливать: имеет ли задача решение и если имеет, то сколько. Например: “Построить окружность, проходящую через три данные различные точки”. Если данные точки не лежат на одной прямой, то задача имеет решение и притом только одно; если же точки лежат на одной прямой, то задача решения не имеет.
Переходим теперь к одному из самых существенных, в методическом отношении, вопросов исследования задачи на построение. Как установить и перечислить все те случаи, которые имеют существенное значение для решения данной задачи? Известно, что очень часто учащиеся, решающие ту или иную задачу, особенно на первых порах, пытаются исследовать ее, исходя из вопроса: “А что будет, если…”, придумывая те или иные “если” более или менее произвольно. Необходимо приучать учащихся вести исследование по самому ходу построения. Желая исследовать задачу, надо в последовательном порядке перебрать еще раз те операции, из которых слагается построение, и для каждой из этих операций определить, всегда ли она возможна, какое число точек, отрезков и т. д. эта операция может давать. Таким путем удается сравнительно легко научиться исследованию задачи.
Исследование является составной частью решения. Решение задачи на построение можно считать законченным, если узнаем, сколько искомых фигур получим при определенных условиях, и, в частности, указано, когда получим искомый геометрический образ. Но исследование в задачах на построение, как и исследование при решении других задач по математике, имеет и общеобразовательное значение.
В процессе исследования учащиеся упражняются в практическом применении диалектического метода мышления. Они видят, что изменение данных задачи вызывает изменение искомой фигуры. Мы имеем дело не с “закостенелыми”, а с изменяющимися геометрическими образами, изменение одних величин обусловлено изменением других.
Для правильного проведения исследования нужно обладать хорошо развитым логическим мышлением. Значит, с другой стороны, исследование задач на построение является хорошим материалом для развития логического мышления учащихся.
Несмотря на необходимость и целесообразность исследования при решении задач на построение, этому этапу и в школе, и в методической литературе уделяется недостаточно внимания. Большое внимание уделяется обычно отысканию решения – анализу. Анализ – основной этап при решении задач на построение: не найдя решения, нельзя провести ни построения, ни доказательства, ни исследования. Но по трудности выполнения исследование является не менее сложным этапом. Наибольшее количество ошибок допускается именно при исследовании.
Вывод. Усвоение учащимися общей схемы решения задач на построение имеет большое значение. Анализ, построение, доказательство и исследование точно соответствуют этапам любого логического рассуждения. При введении данных понятий следует соблюдать с одной стороны, постепенность, а с другой стороны, – настойчивость в смысле многократного систематического обращения к одним и тем же вопросам.
4. Методы решения задач на построение
К основным методам решения задач на построение, изучаемых в средней школе, относятся:
1) Метод геометрических мест.
2) Методы геометрических преобразований:
а) метод центральной симметрии;
б) метод осевой симметрии;
в) метод параллельного переноса;
г) метод поворота;
д) метод подобия;
3) Алгебраический метод.
Перечисленные методы являются одним из видов применения на практике соответствующих геометрических понятий, которые составляют основу каждого из методов. Поэтому без хорошего знания этих понятий учениками не может быть никакой речи об успешном усвоении соответствующих методов. Но, с другой стороны, в силах учителя подобрать такую систему задач на построение и так построить обучение, чтобы решаемые задачи углубляли представление и увеличивали знания школьников о данном понятии, раскрывая его с разных сторон. Задачи при изучении конкретного метода должны подбираться так, чтобы в них как можно более ярко проявлялась суть изучаемого метода, особенно на первоначальном этапе его изучения. При этом если задача решается несколькими методами, то изучаемый метод должен позволять решить задачу наиболее экономно и красиво. Рассмотрим более подробно каждый метод.
4.1 Метод геометрических мест
Математическая сущность метода геометрических мест весьма проста. Она состоит в том, что искомая точка определяется как точка пересечения некоторых двух геометрических мест (или иногда как точка пересечения некоторого геометрического места с данной прямой или окружностью); при этом те условия задачи, которые определяют положение искомой точки, расчленяются мысленно на два условия, и каждое из них дает некоторое геометрическое место, построение которого оказывается возможным (иногда одно из этих геометрических мест заменяется непосредственно данной прямой или окружностью) [18].
Метод геометрических мест является одним из важнейших приемов решения геометрических задач на построение вообще и должен занимать большое место в решении задач на построение, по преимуществу в 8 классе.
При изложении этого метода в школе дело, конечно, заключается не в том, чтобы учащиеся умели описать суть метода словами, а в том, чтобы учащиеся умели сознательно пользоваться этим методом.
Основа данного метода – понятие геометрического места точек. Геометрическим местом точек (ГМТ) пространства, обладающих данным свойством, называется множество всех точек пространства, каждая из которых обладает этим свойством.
Все остальные точки пространства указанным свойством не обладают. ГМТ задается свойством точек, которое называется характеристическим свойством этого ГМТ (фигуры).
Каждая задача, в которой требуется найти ГМТ по его характеристическому свойству, предполагает требование описать это ГМТ наглядно через известные элементарные фигуры. Решение задачи на отыскание ГМТ неизбежно приводит к доказательству двух утверждений – прямого и ему противоположного; необходимо доказать, что: 1) каждая точка предполагаемого (искомого) ГМТ обладает заданным свойством; 2) любая точка, не принадлежащая этой фигуре, заданным свойством не обладает.
Набор изучаемых ГМТ может быть самым разнообразным. Традиционный школьный набор – это:
а) множество всех точек плоскости, удаленных от данной точки на данное расстояние;
б) множество всех точек плоскости, равноудаленных от двух данных точек;
в) множество всех точек плоскости, удаленных от данной прямой на данное расстояние;
г) множество всех точек плоскости, равноудаленных от двух данных прямых.
Кроме этого к списку по возможности могут быть добавлены следующие ГМТ:
а) множество всех точек плоскости, из которых данный отрезок виден под данным углом (частный случай – множество всех точек плоскости, из которых данный отрезок идеен под прямым углом);
б) множество всех точек плоскости, для каждой из которых разность квадратов расстояний до двух данных точек постоянна, равна квадрату данного отрезка;
в) множество вех точек плоскости, для каждой из которых отношение расстояний до двух данных точек постоянно (окружность Аполлония).
Рассматривать эти ГМТ целесообразно только в классах с углубленным изучением математики, а также на внеклассных занятиях по математике.
Сущность метода геометрических мест заключается в следующем:
а) задача сводится к построению некоторой точки;
б) выясняется, какими свойствами обладает данная точка;
в) рассматривается одно из свойств, строится множество всех точек, обладающих этим свойством;
г) берется следующее свойство и так далее;
д) поскольку искомая точка должна обладать всеми этими свойствами, то она должна принадлежать каждому из построенных множеств, то есть принадлежит пересечению этих множеств.
В Приложении 4 приведено решение задачи: “Построить треугольник АВС по двум высотам, проведенным из вершин В и С, и по медиане, проведенной из вершины А”.
Методические рекомендации по методу ГМТ [10]. Понятие ГМТ, обладающих некоторым свойством, лучше ввести на примере ГМТ, равноудаленных от двух данных точек. А затем, когда будут изучены признаки равенства прямоугольных треугольников, при решении задачи о нахождения точки, равноудаленной от двух данных точек А и В, необходимо дать определение ГМТ, обладающих некоторым свойством, как множество всех точек, обладающих этим свойством.
Уже в 7 классе встречаются некоторые задачи, решение которых можно было бы рассматривать как использование метода геометрических мест (например, задача на построение треугольника по трем сторонам). Однако само упоминание о методе и его изучение должно быть отнесено к 8 классу.
В каком же месте курса 8 класса следует знакомить учащихся с методом геометрических мест? Несомненно, что это должно быть сделано по возможности ранее. Наиболее подходящим для этого временем был бы тот момент, когда учащиеся в конце темы “Четырехугольники” ознакомились с достаточным числом геометрических мест.
Учитель начинает с того, что показывает учащимся, какое значение имеет идея геометрического места при решении хорошо известной им задачи, скажем при построении треугольника по трем сторонам. Пусть основание треугольника АВ уже построено; остается определить положение третей вершины С. Выясняется, что для определения положения точки С в задаче остаются два условия: длина сторон АС и ВС. Проводя дугу окружности с центром в точке А и радиусом В, мы строим геометрическое место точек, расстояние которых от точки А равно В; аналогично для второй дуги, и т. д. Вслед за этим может быть предложен как в классе, так и для решения дома, ряд других несложных задач, близких по содержанию к предыдущей, например:
1) построить треугольник по основанию, медиане, проведенной к основанию и боковой стороне;
2) построить треугольник по основанию, боковой стороне и высоте, опущенной на основание.
Целесообразно в качестве одной из первых задач на метод геометрических мест дать и такую задачу, где искомая фигура определялась бы не только по своей форме и размерам, но и по положению на плоскости. Примером может служить следующая задача:
3) построить равнобедренный треугольник, у которого основанием служит данный отрезок АВ, а вершина лежит на данной окружности [10].
В дальнейшей работе по геометрии в 8 классе задачи на метод геометрических мест должны предлагаться систематически до конца учебного года вместе с задачами на вычисление. Наряду с этим применение метода геометрических мест должно быть отчетливо выяснено учащимся и в тех вопросах теоретического курса, где это уместно. Сюда относятся такие вопросы, как проведение окружности через три точки, построение касательной к окружности из данной точки, построение вписанных и описанных окружностей (при решении этой задачи особенно полезным будет рассмотрение геометрического места точек, равноудаленных от двух пересекающихся прямых, вместо геометрического места точек, равноудаленных от сторон данного угла).
Задачи на построение, решаемые методом геометрических мест, могут быть весьма разнообразными. Не следует ставить себе целью дать какую-либо формальную их классификацию – она не имела бы большой ценности ни с научной, ни с методической стороны. Точно также не следует ставить цель указать некий стандартный список задач этого рода для средней школы. Это просто помощь преподавателю в подборе, а также и в составлении вновь задач такого рода, указав те точки зрения, которых при этом необходимо было бы придерживаться.
Различные задачи на построение, разрешаемые методом геометрических мест, отличаются одна от другой, прежде всего, характером тех геометрических мест, с помощью которых определяется положение искомой точки. Отбирая задачи на построение для решения с каждым классом, следует подумать о том, чтобы в этих задачах встречались, по возможности, разнообразные сочетания этих основных геометрических мест. Тем самым будет обеспечено достаточное разнообразие разрешаемых задач по существу, по той идее, которая лежит в их основе.
4.2 Методы геометрических преобразований
Методы этой группы имеют достаточно много общего. Каждый изучается, как правило, при рассмотрении соответствующего преобразования, при этом решаемые задачи служат для закрепления и более глубокого усвоения изучаемого понятия. Для повышения эффективности обучения необходимо, чтобы, кроме первоначальных представлений о самом преобразовании, учащиеся умели выполнять построение образов фигур при этом преобразовании, так как использование образа искомой фигуры при построении есть основа каждого из этих методов, их основная идея и суть.
Если искомую фигуру сразу построить затруднительно, то ее преобразуют в какую-нибудь другую фигуру, построение которой можно сделать легче или непосредственно.
При изучении этих методов целесообразно выделить наиболее характерные признаки с тем, чтобы в будущем, анализируя задачу, ученик мог выбрать соответствующий метод.
Действующая программа по геометрии не предполагает использовать идею геометрических преобразований в качестве руководящей идеи школьного курса геометрии, хотя использование геометрических преобразований при решении задач на построение имеет большое методическое значение [25].
4.2.1 Метод центральной симметрии
Симметрией относительно точки О (центральной симметрией) Z>0>> >пространства называется преобразование пространства, которое точку О отображает на себя, а любую другую точку М отображает на такую точку М>1>, что точка О является серединой отрезка ММ>1>.
Данный метод применим к тем задачам, в условии которых в той или иной форме указана точка, являющаяся центром симметрии искомой или вспомогательной фигуры.
Рассмотрим задачу: “Через данную точку А провести прямую так, чтобы ее отрезок с концами на данных прямой и окружности делился точкой пополам”.
Решение.
Пусть m
и α
— данные прямая и окружность, CD
—искомый отрезок, С
m,
Dа
(рис. 3). Тогда Z>A>(C)
=
D.
Если
Z>A>(m)
=
m>1>,
то Dm>1>
и, следовательно, Dа
m>1>.
Отсюда вытекает такое построение: строим
образ m>1>
прямой
m
при
симметрии Z>A>,
точки
D
и
Е
пересечения
прямой m>1>
с
данной окружностью α
определяют вместе с точкой А
искомые
прямые DA
и
ЕА
[20].
Рис. 3
4.2.2 Метод осевой симметрии
Симметрией пространства относительно данной прямой l (осевой симметрией) S>l> называется преобразование, которое каждую точку прямой l отображает на себя, а любую другую точку М пространства отображает на такую точку М>1>, что прямая l служит серединным перпендикуляром к отрезку ММ>1>. Прямая l называется осью симметрии.
Трудно указать общие признаки задач, решаемых методом осевой симметрии. В более сложных задачах метод осевой симметрии, нередко спрямляющий ломаные линии в прямые, может быть применим, если в условиях содержится сумма или разность частей некоторой ломаной линии. Можно ограничится указанием, что метод осевой симметрии применим для задач, в условии которых указана прямая, являющаяся осью симметрии части элементов фигуры. Такую прямую легко установить по свойствам фигур. Применение осевой симметрии целесообразно для задач, которые легко решаются, если часть данных расположена по одну сторону некоторой прямой, а остальные – по другую.
Рис. 4
Рассмотрим задачу: “Построить ромб так, чтобы одна из его диагоналей была равна данному отрезку r и лежала на данной прямой а, а остальные две вершины ромба лежали соответственно на данных прямых b и с”.
Анализ. Пусть (рис.4) ABDC — искомый ромб, AD = r. Замечаем, что задача о построении ромба сводится к построению одной какой-либо из его вершин, например вершины С. По свойствам ромба точки В и С симметричны относительно прямой а. Поэтому при осевой симметрии относительно прямой а точка В преобразуется в точку С, а, следовательно, прямая b — в некоторую прямую b', проходящую через точку С. Таким образом, точка С может быть построена как точка пересечения прямых с и b', из которых одна дана, а другая легко строится.
Построение. Строим
последовательно: прямую b',
симметричную с прямой b
относительно прямой а;
точку С, общую
для прямых с
и b';
прямую ВС;
точку О
ВС
а; точки А
и D
на прямой а,
отстоящие от точки О
на расстоянии
;
ABCD
— искомый ромб.
Доказательство ввиду его простоты опустим.
Исследование.
Возможны следующие случаи: 1) с
|| b',
решений нет; 2) с
b',
решений бесконечно много; 3) прямые с
и b'
пересекаются вне прямой а,
одно решение; 4) прямые с
и b'
пересекаются на прямой а,
решений нет [2].
4.2.3 Метод параллельного переноса
Параллельным
переносом на вектор
называется отображение плоскости на
себя, при котором каждая точка М
отображается в такую точку М>1>,
что вектор
равен вектору
.
Методом параллельного переноса решают задачи, при анализе которых трудно найти зависимость между данными элементами, позволяющую построить искомую фигуру (данные элементы удалены друг от друга); но если мы какую-нибудь часть или всю фигуру перенесем параллельно в некотором направлении на определенное расстояние, то получим вспомогательную фигуру, которую легко можно построить. Направление и величина переноса определяются так, чтобы во вспомогательную фигуру вошло большее число данных.
Рассмотрим задачу: “Построить выпуклый четырехугольник, зная три его угла и две противоположные стороны”.
Подробнее: даны два отрезка а
и b
и три угла α,
β, δ.
Требуется построить четырехугольник
ABCD
так, чтобы
А
= α,
В
= β,
D
= δ, AD
= a,
СВ = b.
Предполагается, что 0° < α
< 180°, 0° < β
< 180°, 0°< δ
< 180°.
Рис. 5
Анализ. Допустим,
что ABCD
(рис. 5) — искомый четырехугольник.
Перенесем сторону ВС
на вектор
,
и пусть отрезок ВС
займет после переноса положение АЕ.
Тогда в
AED
известны:
AD =
a, AE
=
b,
DAE
=
BAD
–BAE
=
=
A
– (180°
–
B)
= α
+ β
–
180°. По этим данным
AED
может быть построен.
Рис. 6
Построение. 1) На
произвольной прямой строим отрезок AD
= а
(рис. 6); 2) Через точку А
проводим луч AM
под углом α + β – 180°
к лучу AD;
3) Откладываем на луче AM
отрезок АЕ =
b;
4) Строим луч EN,
образующий с ЕА
угол β и
расположенный с точкой D
по разные стороны от прямой AM;
5) Строим луч DK
так, чтобы
ADK
был равен δ и
чтобы луч DK
располагался по ту же сторону прямой
DE,
что и луч EN;
6) Отмечаем точку С
пересечения лучей EN
и DK
— третью вершину
четырехугольника; 7) Четвертая вершина
В получается
в пересечении прямой AF,
параллельной СЕ,
с прямой CL,
параллельной АЕ.
Доказательство.
BAD
=
ВАЕ+DAE
= (180°
– β)
+ (α + β
– 180°) = α.
ABC
=
СЕА,
как углы, стороны которых соответственно
параллельны и противоположно направлены.
СЕА
= β
по построению.
ADC
= δ
по построению. Отрезок AD
= а
по построению. ВС =
АЕ, как отрезки параллельных
между параллельными. Но АЕ
= b,
а значит, и ВС
= b
[2].
4.2.4 Метод поворота
Поворотом плоскости вокруг точки
О на угол
называется отображение плоскости на
себя, при котором каждая точка М
отображается в такую точку М>1>,
что ОМ = ОМ>1>
и угол МОМ>1>
=
.
Данный метод применяется к тем задачам, где либо части фигур сближаются в положение, удобное для построения, либо при заданных явно или косвенно центре и угле поворота требуется отыскать две соответственные точки, лежащие на данных или искомых фигурах.
Рассмотрим задачу: “Земельный участок квадратной формы был огорожен. От изгороди сохранились два столба на параллельных сторонах квадрата. Кроме того, остался столб в центре квадрата. Требуется восстановить границу участка”.
Анализ. Пусть ABCD — искомый квадрат, О — его центр, М и N— данные точки соответственно на сторонах АВ и CD (рис. 7). Если повернуть квадрат на 180° около его центра О, то он преобразуется сам в себя. Точка М займет некоторое положение М' на стороне CD, а точка N — некоторое положение N' на стороне АВ. После этого нетрудно уже построить прямые АВ и CD и восстановить искомый квадрат.
Рис. 7
Построение. 1) Строим точку М', симметричную М относительно 0, и точку N', симметричную N относительно О. 2) Строим прямые MN' и NM'. 3) Повернем построенные прямые около точки О на 90°. Четыре построенные прямые ограничивают искомый квадрат.
Доказательство опускаем.
Исследование. По смыслу задачи невозможен случай, когда точки М и N располагаются с точкой О на одной прямой, но не симметричны относительно О. Если точки М и N симметричны относительно О, то задача становится неопределенной. В остальных случаях задача имеет единственное решение [2].
4.2.5 Метод подобия
Метод подобия состоит в том, что сначала строится некоторая фигура, подобная искомой, но удовлетворяющая не всем поставленным в задаче условиям. Затем построенную вспомогательную фигуру заменяем фигурой, ей подобной и удовлетворяющей уже всем требуемым условиям [18].
Задача решается методом подобия, если ее условие можно разделить на две части, одна из которых определяет форму фигуры с точностью до подобия, а вторая – размеры фигуры. При решении задач в классе или разборе задач из домашнего задания на этот метод следует задавать учащимся вопросы: Что (какая часть) в условии задачи определяет фигуру с точностью до подобия? Что определяет размеры искомой фигуры?
Методические рекомендации по методу подобия [10]. При разработке метода подобия целесообразно классифицировать решаемые задачи по способу задания размеров искомой фигуры:
задачи, в которых размеры искомой фигуры определяются заданием некоторого отрезка;
задачи, в которых размеры искомой фигуры определяются заданием суммы или разности некоторых ее отрезков;
задачи, в которых размеры искомой фигуры определяются положением ее относительно данных фигур.
Такая классификация удобна, главным образом, потому, что для каждой из трех групп задач способы выбора центра подобия различны.
В задачах из первой группы за центр подобия лучше всего выбирать один из концов отрезка вспомогательной фигуры, соответствующего данному отрезку, через который проходит наибольшее число прямолинейных отрезков искомой фигуры, так как при гомотетии лишь прямые, проходящие через центр подобия, преобразуются сами в себя. При таком выборе легко находить одну точку (второй конец данного отрезка) искомой фигуры, что в большинстве случаев значительно облегчает выполнение дальнейшего построения.
И для задач второй группы за центр подобия можно выбирать один из концов построенной суммы или разности отрезков, соответствующей данной. Целесообразно расчленить подобное преобразование: отдельно найти один из отрезков, сумма или разность которых дана, а затем выполнить построение искомой фигуры.
При решении задач третьей группы центр подобия уже определяется, и в большинстве случаев однозначно, расположением фигуры, подобной искомой, относительно данных фигур.
В Приложении 4 приведено решение задачи на метод подобия: “Построить трапецию ABCD по углу А и основанию ВС, если известно, что AB:CD:AD = 1:2:3”.
4.3 Алгебраический метод
Алгебраический метод решения задач на построении – один из важнейших методов теории конструктивных задач. Именно с помощью этого метода решаются вопросы, связанные с разрешимостью задач тем или иным набором инструментов.
Кроме того, это один из самых мощных методов, позволяющий решать многие задачи, решение которых обычными способами затруднительно. Метод прекрасно демонстрирует тесную взаимосвязь алгебры и геометрии.
Но, к сожалению, в школьном курсе геометрии алгебраическому методу практически не уделяется внимания, хотя с методической точки зрения изучение этого метода не представляет особых сложностей.
Суть метода состоит в следующем:
а) задача сводится к построению некоторого отрезка;
б) используя известные геометрические соотношения между искомыми и данными, составляют уравнение (систему уравнений), связывающее искомые и данные;
в) решая уравнение или систему уравнений, выражают формулой длину искомого отрезка через длины данных;
г) по формуле строится искомый отрезок (если это возможно);
д) с помощью найденного отрезка строится искомая фигура.
Подготовительную работу составляет изучение основных формул и способов построения, где также отрабатываются некоторые элементы схемы решения задач алгебраическим методом, и усваивается сама идея такого подхода к решению задач на построение.
В школьном курсе геометрии обычно рассматривают построения циркулем и линейкой отрезков, заданных следующими некоторыми простейшими формулами [2]:
1) х = а + b (рис. 8).
2) х = а — b(а > b) (рис. 9).
Рис. 8 Рис.9
3) х = nа, где n — натуральное число. Сводится к построению 1). На рис. 10 построен отрезок х, такой, что х = 6а.
Рис. 10 Рис. 11
4) х =
.
Строим луч, выходящий из какого-либо конца О данного отрезка а под произвольным углом к нему. Откладываем на этом луче n раз произвольный отрезок b, так что OB = nb (см. рис. 11). Соединяем точку В со вторым концом А отрезка а. Через точку В>1>, определяемую условием 0В>1> = b, проводим прямую, параллельную АВ, и отмечаем точку A>1>, в которой она пересечет отрезок а.
5) х =
а (n
и m
— данные натуральные числа).
Разделим отрезок а на m равных частей и увеличим полученный отрезок в п раз.
6) х =
(построение отрезка, четвертого
пропорционального трем данным отрезкам).
Запишем условие в виде пропорции с : а = b : х. Пусть (рис. 12) ОА = а, ОС = с, так что члены одного из отношений отложены на одном луче, исходящем из точки О. На другом луче, исходящем из той же точки, откладываем известный член другого отношения ОB = b. Через точку А проводим прямую, параллельную ВС, и отмечаем точку X ее пересечения с прямой ОВ. Отрезок ОХ искомый, то есть ОХ = х.
Рис. 12 Рис. 13 Рис. 14
7) x
=
.
Можно воспользоваться построением 6), полагая b = а.
8) х =
(построение среднего пропорционального
двух данных отрезков).
Строим отрезки АС = а, ВС = b, так что АВ = а + b. На АВ как на диаметре строим полуокружность (см. рис. 13). В точке С восставим перпендикуляр к АВ и отметим точку D его пересечения с окружностью. Тогда х = CD.
9) х =
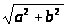Отрезок x
строится как гипотенуза прямоугольного
треугольника с катетами а
и b
(см. рис. 14).
10) х =
(a
> b).
Отрезок x
строится как катет
прямоугольного треугольника с гипотенузой
а и катетом
b.
К рассмотренным построениям можно свести построение отрезков, заданных более сложными формулами.
Желательно постепенное изучение этих формул, когда каждая из них разбирается при рассмотрении теории, необходимой для осуществления соответствующего построения.
На этом месте целесообразно также введение простейших задач на алгебраический метод (например, задача о восстановлении отрезков по их сумме и разности) с тем, чтобы формулы рассматривались во взаимосвязи. В дальнейшем, перед серьезным изучением метода, формулы следует повторить.
В Приложении 4 приведена задача на алгебраический метод: “Из вершин данного треугольника как из центров описать три окружности, касающиеся попарно внешним образом”.
Вывод. Описанные методы рекомендуется использовать для решения геометрических задач на построение. При этом необходимо обращать внимание в том числе и на развитие инициативы учащихся, привитие им вкуса и навыков к решению конструктивных задач.
Было бы неправильно думать, что методы решения задач на построение могут служить основой для классификации самих задач. Существенным, а не случайным следует признавать то обстоятельство, что целый ряд задач на построение может одинаково успешно решаться различными методами. С другой стороны, существуют задачи, которые решаются просто комбинацией основных построений без явного применения какого-либо метода.
С методической точки зрения наиболее приемлемым является применение при обучении решению задач на построение следующего принципа. Необходимо осуществлять последовательный подбор задач в соответствии с целями курса геометрии и постепенное ознакомление учащихся с методами решения задач на построение.
В свою очередь, необходимо ознакомить учащихся с самими методами и научить определять, каким из них можно решить предложенную задачу. Для этого, прежде всего, учащихся необходимо научить выделять наиболее характерные признаки задач, решаемых тем или иным методом. Эти признаки определяются самим содержанием метода.
5. Опытное преподавание
Опытное преподавание применяется для объективной и достоверной проверки гипотезы и предполагает одновременное использование целого ряда методов, например, наблюдение, диагностирующие контрольные работы, беседа и другие.
Одной из задач опытного преподавания являлась проверка эффективности разработанного факультативного курса по решению задач на построение, как предусмотренных школьной программой, так и не встречающихся в школьном курсе математики. Курс рассчитан на учащихся 8 классов.
Цели факультативного курса:
Сформировать у учащихся представление о методах ГМТ и подобия, используемых при решении задач на построение, и научить их применять.
Сформировать четкое представление об этапах решения задач на построение.
Способствовать развитию логического мышления учащихся.
Сформировать настойчивость, целеустремленность, трудолюбие через решение задач.
Развить математическую речь с присущей ей краткостью, точностью и лаконичностью.
Знания и умения, которыми должны владеть учащиеся перед изучением факультативного курса по теме “Задачи на построение и методы их решения”:
Владеть основными понятиями, относящимися к теме.
Уметь пользоваться чертежными инструментами.
Уметь выполнять основные геометрические построения.
Иметь представление об этапах решения задач на построения.
Этапы курса:
Разработка программы факультативных занятий “Задачи на построение и методы их решения” для учащихся 8 класса.
Проведение анкетирования среди учителей и учащихся.
Проведение психологических методик на определение уровня развития логического мышления №1.
Проведение диагностирующей контрольной работы №1.
Проведение разработанной программы факультативных занятий.
Проведение диагностирующей контрольной работы №2.
Проведение психологических методик на определение уровня развития логического мышления №2.
Анализ полученных результатов опытной работы.
Этап №1
Разработка программы факультативных занятий “Задачи на построение и методы их решения” для учащихся 8 класса.
Факультативные занятия были разработаны на основе анализа математической, методической и учебной литературы с использованием методических рекомендаций (см. §2, стр. 31; §3, стр. 39, стр. 45).
Этап №2
В ходе опытного преподавания было проведено анкетирование среди 6 учителей г. Кирова и г. Кирово-Чепецка. Проанализируем результаты полученных данных.
Какие трудности встречаются при изучении задач на построение?
Большинство учителей на этот вопрос ответили, что чаще всего учащиеся не видят с чего начинать строить (поэтапно), отсюда возникает еще одна проблема – на анализ уходит много времени.
Возвращаетесь ли Вы к задачам на построение при изучении других тем?
Учителя стараются на протяжении всего курса обучения возвращаться к задачам на построение. Но чаще всего учителя не видят в этом необходимости из-за нехватки времени.
Достаточно ли внимания уделяется задачам на построение в школьных учебниках?
Большинство учителей считают, что в школьных учебниках мало уделяется внимания задачам на построение.
Считаете ли вы нужным проводить курсы или факультативные занятия, направленные на решение задач на построение? Если да, то на сколько часов они должны быть рассчитаны и для каких классов?
Большинство учителей считают факультативные занятия и элективные курсы по данной теме необходимыми или по крайней мере желательными. Особенно это касается 8-9 классов. Оптимальное количество занятий составляет 17 часов.
На что необходимо обращать внимание (сделать упор) при обучении решению задач на построение?
Учителя считают, что в первую очередь необходимо обращать внимание на первый этап решения задач на построение – анализ, а также на исследование и, конечно, особенно в 7-8 классе нужно обращать внимание учащихся на построение чертежа с помощью чертежных инструментов.
Опытное преподавание осуществлялось в восьмых классах гимназии №2 г. Кирово-Чепецка. Первоначально среди учащихся было проведено анкетирование. Проанализируем результаты полученных данных.
1. Какие трудности вы испытываете при решении задач на построение
У большинства учащихся вызывает затруднение построение чертежа, нахождение пути решения задачи.
2. Какие этапы решения задач на построение вы используете?
Учащиеся не могут назвать конкретные этапы решения задач на построение. Чаще всего они описывают такой алгоритм: 1) построение рисунка; 2) запись условия (что дано в задаче, что нужно найти); 3) решение задачи; или же просто описывают как строить чертеж (построить угол, затем стороны и т.д.); некоторые учащиеся поставили прочерк в этом пункте.
3. Какие методы решения задач на построение вы знаете (отметить):
а) метод геометрических мест точек;
б) метод подобия;
в) метод осевой симметрии;
г) метод центральной симметрии;
д) метод поворота;
е) метод параллельного переноса;
ж) алгебраический метод.
В анкете учащихся указывали практически все представленные методы, что свидетельствует о том, что они не имеют четкого представления, четкой системы в данной области.
По результатам данного анкетирования можно сказать, что учащиеся плохо представляют как решать задачи на построение, не знают этапов, не имеют четкого представления о методах, решение подобных задач представляет для них трудность.
Этап №3
Были проведены психологические методики, которые выявляют уровень развития логического мышления учащихся (см. Приложение 5). В первую очередь нам необходимо выяснить как изменится уровень логического мышления учащихся, поэтому мы ограничимся лишь показателями количества правильных ответов по каждой методике. Затем данные результаты сравним с результатами, полученными после проведения факультативных занятий.
Получены следующие данные (по каждой методике указано количество правильных ответов):
Табл.1
|
Образование простых аналогий (из 16) |
Логичность (из 20) |
Исключение понятий (из 17) |
|
|
1.Балыбердина |
8 |
11 |
13 |
|
2.Ворсин |
15 |
15 |
17 |
|
3.Вострикова |
15 |
16 |
14 |
|
4.Гаврилина |
14 |
16 |
14 |
|
5.Двоеглазова |
8 |
14 |
15 |
|
6.Егошин |
16 |
15 |
15 |
|
7.Захаров |
12 |
13 |
14 |
|
8.Ладыгина |
16 |
18 |
16 |
|
9.Лысенко |
16 |
15 |
15 |
|
10.Медянцев |
12 |
15 |
15 |
|
11.Муралева |
14 |
18 |
14 |
|
12.Садаков |
16 |
15 |
15 |
|
13.Симонова |
14 |
17 |
17 |
|
14.Солодянкина |
3 |
11 |
16 |
|
15.Чупракова |
16 |
17 |
17 |
Этап №4
Проведение диагностирующей контрольной работы №1.
На контрольной работе учащимся было предложено 3 задания, которые было необходимо выполнить в течение 1 часа. Содержание диагностирующей контрольной работы №1 представлено в Приложении 6.
Результаты диагностирующей контрольной работы №1 отображены в таблице 2.
Табл.2
|
№ задания |
1 |
2 |
3 |
|
Кол-во человек, решивших задание |
5 |
3 |
7 |
|
Доля человек, решивших задание в процентах |
33% |
20% |
47% |
Этап №5
Проведение разработанной программы факультативных занятий.
Занятия проводились 1 раз в неделю по два часа. Всего было проведено 6 занятий.
Основные задачи проведения факультативных занятий:
выявить тот материал, который вызывает у учащихся наибольшие затруднения;
определить эффективность усвоения материала посредством текущей проверки;
выявить заинтересованность учащихся в изучении данной темы (программу факультативного курса с подробным конспектом одного из занятий см. в Приложении 6).
Этап №6
Проведение диагностирующей контрольной работы №2.
Контрольная работа была проведена после проведения факультативных занятий разработанной программы. Задача: выявление знаний и умений решать задачи на построение методом ГМТ и подобия.
Учащимся было предложено 3 задания, которые было необходимо выполнить в течение 1 часа. Содержание диагностирующей контрольной работы №2 представлено в Приложении 6.
Результаты диагностирующей контрольной работы №2 отображены в таблице 3.
Табл.3
|
№ задания |
1 |
2 |
3 |
|
Кол-во человек, решивших задание |
11 |
7 |
13 |
|
Доля человек, решивших задание в процентах |
73% |
47% |
87% |
Этап №7
Были проведены те же психологические методики, что и перед началом эксперимента.
Получены следующие данные (по каждой методике указано количество правильных ответов):
Табл.4
|
Образование простых аналогий (из 16) |
Логичность (из 20) |
Исключение понятий (из 17) |
|
|
1.Балыбердина |
11 |
14 |
15 |
|
2.Ворсин |
15 |
17 |
17 |
|
3.Вострикова |
16 |
18 |
16 |
|
4.Гаврилина |
15 |
17 |
15 |
|
5.Двоеглазова |
9 |
14 |
16 |
|
6.Егошин |
16 |
16 |
16 |
|
7.Захаров |
13 |
15 |
16 |
|
8.Ладыгина |
16 |
18 |
17 |
|
9.Лысенко |
16 |
16 |
17 |
|
10.Медянцев |
14 |
16 |
15 |
|
11.Муралева |
16 |
18 |
15 |
|
12.Садаков |
16 |
17 |
16 |
|
13.Симонова |
15 |
19 |
17 |
|
14.Солодянкина |
10 |
15 |
16 |
|
15.Чупракова |
16 |
18 |
17 |
Этап №8
Анализ полученных результатов опытной работы.
На основании таблиц №2 и №3 можно построить диаграмму, отображающую сравнение результатов контрольных работ, проведенных перед посещением учащимися факультативных занятий и после их посещения.
Как видно из диаграммы, перед проведением факультативных занятий уровень знаний учащихся был ниже, чем средний, а после проведения занятий он значительно повысился. Положительная тенденция заметна: учащиеся научились решать задачи на построение методом ГМТ и методом подобия, и большинство справились с заданиями 1,3; значительно улучшилось умение решать более сложные задачи. Многие учащиеся овладели методом ГМТ и методом подобия при решении задач на построение.
Кроме того, на основании таблиц 1,4 можно построить диаграмму, отображающую сравнение результатов психологических методик, проведенных перед посещением учащимися факультативных занятий и после их посещения.
Методика “Образование простых аналогий”
Методика “Логичность”
3) Методика “Исключение понятий”
Как видно из диаграмм, уровень развития логического мышления учащихся после проведения факультативных занятий увеличился. Таким образом, можно утверждать, что решение задач на построение положительно влияют на развитие логического мышления учащихся.
Вывод. Опытное преподавание показало, что более глубокое и объемное изучение задач на построение и методов их решения дает возможность учащимся лучше ориентироваться в данной теме, творчески подходить к каждой задаче, применять наиболее рациональный метод решения, а также повысить уровень своего логического мышления.
Заключение
Выполнен анализ учебных программ, учебной и учебно-методической литературы по геометрии, в ходе которого найдены сходства и различия по данной теме. Рассматривая учебники, можно отметить, что в них достаточно высок процент заданий на построение в 7 классе, причем рассматриваются стандартные и элементарные задачи на построение. Однако к 9 классу процент геометрических заданий на построение резко падает. Так как задания на построение составляют базу для работы, развивающей навыки построения фигур, способствующей формированию умения читать и понимать чертеж, устанавливать связи между его частями, то недостаточность этой системы обусловливает плохое развитие пространственного и логического мышления ученика, низкий уровень его графической культуры. Эти недостатки не позволяют ученику эффективно изучать многие разделы математики.
Рассмотрено понятие логического мышления, сделан анализ психолого-педагогический литературы по теме исследования, показаны возможности развития логического мышления учеников при решении задач на построение.
Рассмотрены основные этапы решения задач на построение: анализ, построение, доказательство, исследование, которые точно соответствуют этапам любого логического рассуждения, каждый из которых является важным и требует должного внимания при решении задач.
Разработаны методические рекомендации по обучению решения задач на построение.
Рассмотрены основные методы решения задач на построение. Отметим, что необходимо знакомить учащихся с самими методами и учить определять, каким из них можно решить предложенную задачу.
Проведено опытное преподавание.
Таким образом, задачи данной работы были выполнены, в ходе их выполнения подтвердилась гипотеза исследования. Цель работы была достигнута.
Кроме того, отметим, что:
необходимо уделять больше внимания изучению задач на построение, так как при грамотном использовании они являются мощным средством развития логического мышления учащихся;
геометрические задачи на построение не нужно рассматривать как что-то отдельное, независимое от остального курса геометрии. Процессы обучения решению задач и изучение геометрии неразрывно связаны. Причем связь эта должна быть двусторонней, то есть необходимо не только обучать решению задач на построение, используя ранее полученные знания, но и, наоборот, использовать конструктивные задачи при изучении геометрии.
Библиографический список
Александров, И.И. Сборник геометрических задач на построение с решениями / И.И.Александров. – М.: Учпедгиз,1954.
Аргунов, Б.И. Элементарная геометрия: учеб. пособие для пед. ин-тов / Б.И. Аргунов, М.Б. Балк. – М.: Просвещение, 1966.
Белошистая, А.В. Задачи на построение в школьном курсе геометрии / А. В. Белошистая // Математика в школе. – 2002. – №9. – С. 47-50.
Геометрия: доп.главы к шк.учеб.8 кл.: учеб.пособие для учащихся шк.и классов с углубл.изуч.математики / Л.С.Атанасян, В.Ф. Бутузов, С.Д. Кадомцев и др. – М.: Просвещение, 1996.
Геометрия: учеб. для 7-9 кл. общеобразовательных учреждений / А. В. Погорелов. – М.: Просвещение, 2004.
Геометрия: учеб. для 7-9 кл. сред. шк. / А. Д. Александров, А. Л. Вернер, В.И. Рыжик. – М.: Просвещение, 1992.
Геометрия: учеб. для 7-9 кл. сред. шк / Л. С. Атанасян. – М.: Просвещение, 1991.
Геометрия: Планиметрия: 7-9 кл.: учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995.
Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991.
Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ВятГГУ, 2008. – С. 59-69.
Мазаник, А.А. Задачи на построение по геометрии в восьмилетней школе. Пособие для учителей / А.А.Мазаник. – Минск: Народная асвета, 1967.
Математика: учеб. для 5 кл. общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Сайтком, 2000.
Математика: учеб. для 6 кл. общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Сайтком, 2000.
Математика: учеб. для 5 кл. общеобразовательных учреждений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др. – М.: Просвещение, 1994.
Математика: учеб. для 6 кл. общеобразовательных учреждений / Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др. – М.: Дрофа, 1998.
Мисюркеев, И.В. Геометрические построения. Пособие для учителей / И.В.Мисюркеев. – М: Учпедгиз, 1950.
Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. – М.: Просвещение, 1986.
Перепелкин, Д.И. Геометрические построения в средней школе / Д.И. Перепелкин. – М.: Издательство академии педагогических наук РСФСР,1947.
Платонов, К.К. Краткий словарь системы психологических понятий / К.К. Платонов. – М.: Высш. шк., 1984.
Понарин, Я.П. Элементарная геометрия: В 2 т. – Т.1: Планиметрия, преобразования плоскости / Я.П.Понарин. – М.: МЦНМО, 2004.
Понарин, Я.П. Элементарная геометрия: В 2 т. – Т.2: Стереометрия, преобразования пространства / Я.П.Понарин – М.: МЦНМО, 2006.
Прасолов, В.В. Задачи по планиметрии. Ч.1 / В.В. Прасолов. – М.: Наука, 1991.
Прасолов, В.В. Задачи по планиметрии. Ч.2 / В.В. Прасолов. – М.: Наука, 1991.
Рубинштейн, С.Л. Основы общей психологии / С.Л. Рубинштейн. – СПб.: Питер, 1989.
Саранцев, Г.И. Обучение математическим доказательствам и опровержениям в школе / Г.И. Саранцев. – М.: ВЛАДОС, 2005.
Тихомиров, О.К. Психология мышления / О.К. Тихомиров. – М.: Академия, 2002.
Философский энциклопедический словарь. – М.: Советская энциклопедия, 1983.
Шарыгин, И.Ф. Задачи по геометрии (Планиметрия) / И.Ф. Шарыгин. – М.: Наука, 1986.
Приложение 1
Анализ программ
Учебники “Геометрия 7-9”
Л.С. Атанасян, В.Ф. Бутузов [7]
а) 7 класс. Глава 2 “Треугольники” (14 ч): Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Основные задачи на построение с помощью циркуля и линейки. Основная цель – отработать навыки решения простейших задач на построение с помощью циркуля и линейки. На начальном этапе изучения темы полезно больше внимания уделять использованию средств наглядности, решению задач по готовым чертежам.
Глава 4 “Соотношения между сторонами и углами треугольника” (16 ч): Сумма углов треугольника. Соотношения между сторонами и углами треугольника. Неравенство треугольника. Некоторые свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Задачи на построение. Основная цель – расширить знания учащихся о треугольниках. При решении задач на построение в 7 классе рекомендуется ограничиваться только выполнением построения искомой фигуры циркулем и линейкой. В отдельных случаях можно проводить устно анализ и доказательство, а элементы исследования могут присутствовать лишь тогда, когда это оговорено условием задачи.
б) 8 класс. Глава 7 “Подобные треугольники” (19 ч): подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника. Основная цель – сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольных треугольников. Решение задач на построение методом подобия можно рассмотреть с учащимися, интересующимся математикой.
В главе 8 “Окружность” (17 ч): Касательная к окружности и ее свойства. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Основная цель – дать учащимся систематизированные сведения об окружности и ее свойствах, вписанной и описанной окружностях. В этой же теме имеется ряд задач на построение вписанных и описанных окружностей с помощью циркуля.
в) 9 класс. Глава 12 “Длина окружности и площадь круга” (16 ч): Правильные многогранники. Длина окружности и площадь круга. Основная цель – расширить и систематизировать знания учащихся об окружностях и многоугольниках. Построение правильных многоугольников с помощью циркуля и линейки ограничивается построением квадрата, правильных треугольника, шестиугольника и 2n-угольника.
Глава 13 “Движение” (12 ч): Понятие движения. Параллельный перенос и поворот. Основная цель – познакомить с понятием движения на плоскости: симметриями, параллельным переносом, поворотом. При изучении темы основное внимание следует уделить выработке навыков построения образов точек, отрезков, треугольников при симметриях, параллельном переносе, повороте.
А.В. Погорелов [5]
а) 7 класс. §5 “Геометрические построения”. Основная цель – решать простейшие задачи на построение с помощью циркуля и линейки. Решение задач на построение с помощью циркуля и линейки: треугольника по трем сторонам; угла, равного данному; биссектрисы угла; перпендикулярной прямой; деление отрезка пополам.
б) 8 класс. §6 “Четырехугольники (20 ч): Определение четырехугольника. Параллелограмм, его признаки и свойства. Прямоугольник, ромб, квадрат и их свойства. Основная цель – дать учащимся систематизированные сведения о четырехугольниках и их свойствах.
§9 “Движение” (8 ч): Движение и его свойства. Симметрия относительно точки и прямой поворот. Параллельный перенос и его свойства. Понятие о равенстве фигур. Основная цель – познакомить учащихся с примерами геометрических преобразований. Симметрия относительно точки и прямой, параллельный перенос учащиеся должны усвоить на уровне практических применений.
§11 “Подобие фигур” (17 ч): Понятие о гомотетии и подобии фигур. Подобие треугольников. Признаки подобия треугольников. Подобие прямоугольных треугольников. Центральные и вписанные углы и их свойства. Основная цель – усвоить признаки подобия треугольников и отработать навыки их применения.
§13 “Многоугольники” (12 ч): Ломаная. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники. Окружность, вписанная в правильный многоугольник. Окружность, описанная около правильного многоугольника. Длина окружности. Длина дуги окружности. Радианная мера угла. Основная цель – расширить и систематизировать сведения о многоугольниках и окружностях.
3) А.Д. Александров, А.Л. Вернер, В.И. Рыжик [6]
а) 7 класс. Глава 1 “Начала геометрии” (15 ч): Геометрические фигуры. Первые задачи геометрии. Построения. Отрезки. Луч и прямая. Действия над отрезками. Длина отрезка. Расстояние. Окружность и круг. Угол. Действия над углами. Величина угла. Основная цель – рассказать о задачах систематического курса геометрии и заложить основу для его построения. Особую роль в 7 классе играют геометрические построения. Первые аксиомы появляются как утверждения о возможности выполнения простейших построений, а первые доказательства дают обоснование того, что построенные фигуры обладают требуемыми свойствами. Изложение как этой темы, так и последующих должно сочетать наглядность и логичность, а также быть связано с практическими применениями.
Глава 2 “Треугольники” (20 ч): Треугольник и его элементы. Равенство треугольников. Два признака равенства треугольников. Деление отрезка пополам и построение перпендикуляра. Серединный перпендикуляр отрезка. Построение биссектрис, высот и медиан треугольника. Свойства равнобедренного треугольника. Понятие об осевой симметрии. Признак равнобедренного треугольника. Основная цель – развить навыки решения задач на построение с помощью циркуля и линейки, начать знакомство с симметриями фигур.
б) 8 класс. Глава 5 “Метрические соотношения в треугольнике” (34 ч): Теорема Пифагора. Применение теоремы Пифагора: равенство прямоугольных треугольников, сравнение перпендикуляра и наклонной, неравенство треугольника, характерное свойство биссектрисы угла. Синус. Свойства синуса и его график. Применения синуса: решение прямоугольных треугольников, вычисление площади треугольника, теорема синусов, решение треугольников. Косинус, его свойства и график. Применения косинуса: теорем косинусов, решение треугольников, средняя линия треугольника, сравнение сторон и углов треугольника. Тангенс и его свойства. Основная цель – изучить основы тригонометрии, доказать три важнейшие теоремы и продемонстрировать богатство возможных применений этих теорем в теории и в практике, в частности при решении треугольников.
в) 9 класс. Глава 7 “Многоугольники и окружности” (18 ч): Хорды и касательные. Градусная мера дуги окружности. Вписанные углы. Вписанные и описанные окружности. Правильные многоугольники. Центр правильного многоугольника. Длина окружности площадь круга. Основная цель – измерение длины окружности и площади круга. Остальные результаты этой темы имеют второстепенный характер.
Глава 8 “Другие методы геометрии” (34 ч): Метод координат: расстояние между точками, понятие об уравнении фигуры, уравнение окружности. Векторы и координаты: разложение вектора по осям координат, координаты векторов и их связь с координатами точек, уравнение прямой. Скалярное умножение и его свойства. Преобразование фигур. Движение фигур и его свойства. Преобразования фигур. Движение фигур и его свойства. Виды движений: перенос, симметрии, поворот. Симметрия фигур. Подобие. Гомотетия. Свойства подобия. Подобие треугольников. Основная цель – познакомить учащихся с методами. Отсутствовавшими в классической элементарной геометрии, но играющими в современной геометрии ведущую роль: методом координат, векторным методом, методом преобразований.
Основная цель всех учебников при введении задач на построение – это развить и отработать навыки решения простейших задач на построение с помощью циркуля и линейки.
Приложение 2
Сравнительная таблица основных видов мышления
|
Практическое мышление |
Теоретическое мышление |
|
— совершается в ходе практической деятельности и направлено на решение практических задач; — начинается с возникновения проблемной ситуации, которую нужно решить; — протекает в условиях дефицита времени, опасности или высокой ответственности за принимаемое решение; — направлено на преобразование реальной действительности |
— направлено на познание и объяснение явлений действительности; — процесс мышления предполагает создание гипотезы, новой идеи или образа, а также проверку гипотезы на соответствие реальности
|
|
Интуитивное мышление |
Логическое мышление |
|
— при интуитивном мышлении переход к новому знанию происходит через озарение; — процесс мышления неосознаваем и слит с самим действием; — объектами мышления являются объекты — оригиналы, с которыми взаимодействует человек; — интуитивное мышление выполняет функцию получения нового знания |
— при логическом мышлении происходит плавный логический переход от данного к новому; — процесс мышления осознан, отделен от своего продукта, а способы действия выделены и превращены в операции, применимые ко многим подобным объектам; — объектами логического мышления выступают знаковые системы; — логическое мышление выполняет функцию трансляции уже полученного знания другому |
Приложение 3
Задачи к §3 “Методика решения задач на построение”
3.1. Анализ
Анализ задачи на построение: “Построить треугольник, зная основание, меньший угол при основании и разность двух других сторон”.
Рис. 1
Чтобы найти решение, нужно вначале изучить условие задачи, посмотреть, какие элементы искомого треугольника даны. Для этого начертим произвольный треугольник A>1>B>1>C>1> (рис.1) и отметим элементы, соответствующие данным по условию. Пусть это будет сторона A>1>C>1> и угол C>1>A>1>B>1>. Но на чертеже нет разности двух других сторон. А так как для решения задачи мы должны учесть все данные, то нужно показать и разность. Это можно сделать четырьмя способами: на меньшей стороне отложить большую от точки C>1 >или от точки B>1> либо на большей отложить меньшую и вновь откладывать как от точки B>1>, так и от точки A>1>. Если разность будет около точки В>1>, то тогда данные не связаны между собой, и нельзя наметить план решения. Если же В>1>А>1> отложим от точки В>1> на В>1>С>1>, то данные: основание, угол при основании и разность двух других сторон — будут связаны между собой, но и эта связь не дает возможности наметить план решения, она недостаточно жестка, чтобы построить, восстановить фигуру D>2>C>1>A>1>B>1>. Лучше всего ввести разность, откладывая B>1>D>1> = B>1>C>1>, так как в этом случае мы уже сможем восстановить фигуру C>1>A>1>D>1>. Конкретизировав таким образом данные задачи, приступаем к составлению плана решения.
Построив на произвольной прямой отрезок, равный основанию, получим две вершины треугольника: А>1> и С>1>. Зная угол С>1>А>1>В>1>, мы можем найти и положение точки D>1>, где D>1>A>1> = B>1>A>1> — В>1>С>1>. Остается рассмотреть, как построить точку В>1>, зная положение точки D>1>. Так как C>1>B>1> = B>1>D>1>, то точка B>1> равноудалена от точек C>1> и D>1>, поэтому она должна лежать на перпендикуляре P>1>Q>1>, проведенном к отрезку C>1>D>1> через его середину. Точка пересечения прямой P>1>Q>1> и луча A>1>D>1> и будет точкой В>1>. Следовательно, приходим к следующему построению. На произвольной прямой откладываем отрезок, равный основанию, и строим угол, равный данному, одна из сторон которого содержит построенный отрезок, а вершина совпадает с концом этого отрезка. На второй стороне угла откладываем отрезок, равный разности двух других сторон треугольника, и строим геометрическое место точек, равноудаленных от соответствующих концов основания и построенного отрезка. Точку пересечения этого геометрического места со стороной угла, содержащей разность, соединяем с концом основания и получаем, искомый треугольник [11].
3.3. Доказательство
Задача. Построить трапецию по четырем сторонам (рис. 2).
Решение. Проведя CK||BA, решение задачи сводим к построению треугольника KCD по трем сторонам: две равны боковым сторонам трапеции (АВ = КС), a KD = AD — BC. Построим треугольник КCD, и, считая сторону AD построенной, дополним его до трапеции различными способами:
1) Проведем BC||AD и, отложив меньшее основание, соединим полученную точку В с А.
Доказательство сведется к установлению равенства: АВ = КС.
2) Если провести АВ||КС и BC||AD, то тогда уже надо доказать, что АВ = КС и ВС = АК.
Рис. 2
3) Если провести прямую CB||DA и на ней найти точки В и В>1> отстоящие от А на расстоянии, равном боковой стороне, то в этом случае точка В>1> будет посторонней и лишь точка В будет искомой, причем доказательство (ВС = АК) уже усложняется.
4) Если отыскивать точку В, как точку пересечения окружностей (А; АВ) и (С; СВ), то из двух точек В и В>2> (рис. 2) только точка В будет искомой.
Третий и четвертый случаи подчеркивают необходимость доказательства. В анализе мы находим необходимые условия, которым должно подчиняться построение, чтобы получить искомую фигуру. Надо еще установить, что найденные необходимые условия являются и достаточными, то есть, что построенная фигура удовлетворяет всем требованиям задачи [11].
Приложение 4
Задачи к §4 “Методы решения задач на построение”
4.1 Метод геометрических мест точек
Задача. Построить треугольник АВС по двум высотам, проведенным из вершин В и С, и по медиане, проведенной из вершины А.
Рис. 3
Решение.
Предположим, что треугольник АВС построен.
Опустим из середины А>1> стороны ВС перпендикуляры А>1>В' и А>1>С' на прямые АС и АВ соответственно.
Ясно, что АА>1> = m>a>, А>1>В' = h>b>/2 и А>1>С' = h>с>/2. Из этого вытекает следующее построение.
Строим отрезок АА>1> длиной m>a>. Затем строим прямоугольные треугольники АА>1>В' и АА>1>С' по известным катетам и гипотенузе так, чтобы они лежали по разные стороны от прямой АА>1>. Остается построить точки В и С на сторонах АС' и АВ' угла С'АВ' так, чтобы отрезок ВС делился точкой А>1> пополам.
Для этого отложим на луче АА>1> отрезок AD = 2АА>1>, а затем проведем через точку D прямые, параллельные сторонам угла С'АВ'.
Точки пересечения этих прямых со сторонами угла С'АВ' являются вершинами искомого треугольника (рис.3) [22].
4.2 Метод геометрических преобразований
4.2.5 Метод подобия
Задача. Построить трапецию ABCD по углу А и основанию ВС, если известно, что AB:CD:AD = 1:2:3.
Рис. 4
Рис. 5
Решение.
Задачу надо понимать так: даны угол hk
и
отрезок PQ
(рис.
4).
Требуется
построить с помощью циркуля и линейки
трапецию ABCD,
у
которой
A
=
hk,
BC
=
PQ,
а
остальные три стороны АВ,
CD
и AD
относятся
как 1:2:3. Построим сначала какую-нибудь
трапецию AB>1>C>1>D>1>,
у
которой
А
=
hk
и
AB>1>:C>1>D>1>:AD>1>
=
1:2:3. Это сделать совсем не трудно. Строим
угол А,
равный
данному углу, и на его сторонах откладываем
произвольный отрезок АВ>1>
и
отрезок AD>1>
= 3AB>1>>
>(рис.
5).
После
этого через точку В>1>,
проводим прямую l,
параллельную AD>1>
и
строим окружность радиуса 2АВ>1>,
с центром в точке D>1>,.
Эта окружность пересекает прямую l
в двух точках С>1>
и C>1>'.
Итак,
мы построили две трапеции AB>1>C>1>D>l>
и
АВ>1>С>1>'D>1>,
у которых
A
=
hk
и
стороны АВ>1>,
ВС>1>
(В>1>С>1>')
и
C>1>D>l>
(С>1>'D>1>)
относятся как 1:2:3.
Возьмем
одну из этих трапеций, например, AB>1>C>1>D>l>,
проведем прямую АС>1>,
и построим отрезок ВС
с
концами на сторонах угла В>1>АС>1>,
который параллелен B>1>C>1>
и равен PQ.
Это
можно сделать так: на луче AD>1>
откладываем
отрезок AE
= PQ
и
через точку Е
проводим
прямую, параллельную AB>1>.
Она пересекается с прямой АС>1>
в точке С
(рис. 6).
Через
точку С
проводим прямую, параллельную B>1>C>1>,
и получаем точку В.
Очевидно,
отрезок ВС
равен
PQ.
Остается
провести
через точку С
прямую, параллельную C>1>D>l>.
Она пересекает луч AD>1>,
в точке D.
Трапеция
ABCD
искомая.
В самом деле,
А
=
hk,
BC
= PQ
и
(это следует из подобия треугольников
ABC
и
AB>1>C>1>,
ACD
и
AС>1>D>1>).
Отсюда получаем, что AB:СD:AD
= AB>1>:C>1>D>1>:AD>1>
= 1:2:3.
Рис. 6
Построенная трапеция ABCD удовлетворяет всем условиям задачи. Если вместо трапеции AB>1>C>1>D>l> взять трапецию АВ>1>С>1>'D>1> и проделать такие же построения, то получим второе решение задачи (рис. 7). Итак, данная задача имеет два решения [4].
Рис. 7
4.3. Алгебраический метод
Пример. Из вершин данного треугольника как из центров описать три окружности, касающиеся попарно внешним образом.
Пусть ABC (рис. 8) — данный треугольник, а, b, с — его стороны, х, у и z — радиусы искомых окружностей.
Рис. 8
Выразим длины отрезков х,
у, z
через длины известных отрезков а,
b,
с. Тогда х+у=с,
y+z=a,
z+x=b.
Поэтому 2х+2у+2z
= a+b+c,
x+y+z=
(a+b+c),
откуда
.
Строим теперь один из найденных
отрезков, например х,
по формуле
и проводим окружность (A,
х). Две другие окружности
проводим из центров В
и С радиусами
соответственно с — х
и b
— х.
Для доказательства достаточно заметить теперь, что две последние окружности касаются между собой, так как сумма их радиусов (с — х) + (b — х) = с + b — 2х = (с + b) — (с + b — а) = а = ВС, то есть равна расстоянию между их центрами.
Задача всегда однозначно разрешима, так как:
1) в треугольнике ABC b+c>a, и поэтому отрезок x может быть построен;
2) с>х,
потому что с — х
=
(так
как а+с>b);
3) b>х,
потому что b
– х =
>0
[2].
Приложение 5
Психологические методики
МЕТОДИКА “ОБРАЗОВАНИЕ ПРОСТЫХ АНАЛОГИЙ” [9]
Под №1 слева написано два слова: сверху лошадь, внизу жеребенок. Какая между ними связь? Жеребенок – детеныш лошади. А справа под №1 тоже одно слово корова, а снизу 5 слов на выбор. Из них нужно выбрать только одно, которое будет так же относиться к слову корова, как жеребенок к лошади, т.е. чтобы оно обозначало детеныша коровы. Это будет теленок. Подчеркиваем слово теленок. Итак, нужно сначала установить, как связаны между собой слова, написанные слева, и затем установить такую же связь справа. Так же решаются все задачи.
|
1. Лошадь |
Корова |
|
|
Жеребенок 2. Школа |
Пастбище, рога, молоко, теленок, бык Больница |
|
|
Обучение 3. Яйцо |
Доктор, ученик, учреждение, лечение, больной Картофель |
|
|
Скорлупа 4. Ложка |
Курица, огород, капуста, суп, шелуха Вилка |
|
|
Каша 5. Коньки |
Масло, нож, тарелка, мясо, посуда Лодка |
|
|
Зима 6. Ухо |
Лед, каток, весна, лето, река Зубы |
|
|
Слышать 7. Собака |
Видеть, лечить, рот, щетка, жевать Щука |
|
|
Шерсть 8. Пробка |
Овца, ловкость, рыба, удочки, чешуя Камень |
|
|
Плавать 9. Чай |
Пловец, тонуть, гранит, возить, каменщик Суп |
|
|
Сахар 10. Дерево |
Вода, тарелка, крупа, соль, ложка Рука |
|
|
Сук 11 Дождь |
Топор, перчатка, нога, палец, работа Мороз |
|
|
Зонтик 12. Песня |
Палка, холод, сани, зима, шуба Картина |
|
|
Глухой 13. Нож |
Хромой, слепой, художник, рисунок, больной Стол |
|
|
Сталь 14. Рыба |
Вилка, дерево, стул, пища, скатерть Муха |
|
|
Сеть 15. Утро |
Решето, комар комната, жужжать, паутина Зима |
|
|
Ночь 16. Птица |
Мороз, день, январь, осень, сани Человек |
|
|
Гнездо |
Люди, птенец, рабочий, зверь, дом |
КЛЮЧ К МЕТОДИКЕ “ОБРАЗОВАНИЕ ПРОСТЫХ АНАЛОГИИ”
Теленок 2. Лечение 3. Шелуха 4. Мясо 5. Лето 6. Жевать 7. Чешуя 8. Тонуть 9 Соль 10. Палец 11. Шуба 12. Слепой 13. Дерево 14. Паутина 15. Осень 16. Дом.
МЕТОДИКА “ЛОГИЧНОСТЬ” [9]
Вы получили бланк с 20-ю заданиями. Каждое из заданий представляет собой умозаключение, состоящее из 2-х взаимосвязанных суждений и вытекающего из них вывода. Требуется определить, какие выводы правильные, а какие ошибочные.
БЛАНК ЗАДАНИЙ К МЕТОДИКЕ “ЛОГИЧНОСТЬ”
Все металлы проводят электричество. Ртуть – металл. Следовательно, ртуть проводит электричество.
Все арабы смуглы. Ахмед смугл. Следовательно, Ахмед – араб.
Некоторые капиталистические страны – члены НАТО. Япония – капиталистическая страна. Следовательно, Япония – член НАТО.
Все Герои России награждаются Золотой звездой Героя. Иванов награжден Золотой звездой Героя. Следовательно, Иванов – Герой России.
Все сочинения Пушкина нельзя прочесть за одну ночь. “Медный всадник” - сочинение Пушкина. Следовательно, “Медный всадник” нельзя прочесть за одну ночь.
Лица, занимающиеся мошенничеством, привлекаются к уголовной ответственности. Л. мошенничеством не занимался. Следовательно, Л. не привлечен к уголовной ответственности.
Все студенты высшей школы изучают логику. Смирнова изучает логику. Следовательно, Смирнова – слушатель высшей школы.
Некоторые студенты МГУ – бывшие военнослужащие. Петров – студент МГУ. Следовательно, Петров – бывший военнослужащий.
Все хлебопекарни г. Кирова выполнили дневной план производства. Хлебопекарня ЧП Сидорова не является хлебопекарней г. Кирова. Следовательно, хлебопекарня ЧП Сидорова не выполнила дневной план производства.
Некоторые работники 2-го управления – юристы. Фомин – юрист. Следовательно, он работник 2-го управления.
Все граждане России имеют право на труд. Иванов – гражданин России. Следовательно, Иванов имеет право на труд.
Все металлы куются. Золото – металл. Следовательно, золото куется.
Все коренные жители Конго – негры. Мухаммед – негр. Следовательно, Мухаммед – житель Конго.
Все студенты Ленинградского университета изучают историю России. Н. Изучает историю России. Следовательно, Н. – студент Ленинградского университета.
Когда идет дождь, крыши домов мокрые. Крыши домов мокрые. Следовательно, идет дождь.
Некоторые капиталисты стремятся к развязыванию войны. Рассел – капиталист. Следовательно, Рассел стремится к развязыванию войны.
Все студенты 3-го курса написали курсовые работы по специальности. В. написал курсовую работу по специальности. Следовательно, В. – студент 3-го курса.
Комитет солдатских матерей выступает против войны. Джонс выступает против войны. Следовательно, Джонс входит в комитет солдатских матерей.
Некоторые капиталистические страны входят в состав Общего рынка. Австрия – капиталистическая страна. Следовательно, Австрия входит в состав Общего рынка.
Все ученики 3 “б” класса отличники. Петя Смирнов – отличник. Следовательно, Петя Смирнов – ученик 3 “б” класса.
КЛЮЧ К МЕТОДИКЕ “ЛОГИЧНОСТЬ”
Ответы “верно”: 1,11,12.
Ответы “неверно”: все остальные.
МЕТОДИКА “ИСКЛЮЧЕНИЕ ПОНЯТИЙ” [9]
Вы получили бланк, на котором написаны серии слов. Каждая серия состоит из пяти слов. Четыре из них являются в некоторой степени однородными понятиями и могут быть объединены по общему для них признаку, а одно слово не соответствует этим требованиям и должно быть исключено. Вы должны просмотреть каждую серию, найти слово, подлежащее исключению и выписать его на листочке под соответствующим номером. Например, даны пять слов: “кирпич, глина, известь, камень, дом”. Первые четыре слова можно объединить одном понятием “строительные материалы”, а последнее слово лишнее. Нужно записать “1.дом”. И так по порядку нужно решить все 17 серий.
БЛАНК ЗАДАНИЙ К МЕТОДИКЕ “ИСКЛЮЧЕНИЕ ПОНЯТИЙ”
1. дряхлый, старый, изношенный, маленький, ветхий
2. смелый, храбрый, отважный, злой, решительный
3. Василий, Федор, Семен, Иванов, Порфирий
3. молоко, сливки, сыр, сало, сметана
4. скоро, быстро, поспешно, постепенно, торопливо
5. глубокий, высокий, светлый, низкий, мелкий
6. лист, почка, кора, дерево, сук
7. дом, сарай, изба, хижина, здание
8. береза, сосна, дерево, дуб, ель
9. ненавидеть, презирать, негодовать, возмущаться, наказывать
10. темный, светлый, голубой, яркий, тусклый
11. гнездо, нора, курятник, берлога, сторожка
12. неудача, крах, провал, поражение, волнение
13. молоток, клещи, топор, гвоздь, долото
14. минута, секунда, час, вечер, сутки
15. грабеж, кража, землетрясение, поджог, нападение
16. успех, победа, удача, спокойствие, выигрыш.
КЛЮЧ К МЕТОДИКЕ “ИСКЛЮЧЕНИЕ ПОНЯТИЙ”
|
1. маленький |
2. злой |
3. Иванов |
|
4. сало |
5. постепенно |
6. светлый |
|
7. дерево |
8. сарай |
9. дерево |
|
10. наказывать |
11. голубой |
12. сторожка |
|
13. волнение |
14. гвоздь |
15. вечер |
|
16. землетрясение |
17. спокойствие |
Приложение 6
Диагностирующая контрольная работа №1
Найти точку, равноудаленную от трех данных точек.
Построить треугольник по данному основанию, боковой стороне и высоте, опущенной на основание.
Построить треугольник по двум углам и медиане.
Диагностирующая контрольная работа №2
Даны 3 точки: А, В, С. Постройте точку Х, которая равноудалена от точек А и В и находится на данном расстоянии от точки С.
Построить параллелограмм, зная одну из сторон, опущенную на эту сторону высоту и одну из диагоналей.
Построить треугольник, зная отношение трех его сторон и биссектрису угла
Программа факультативного курса занятий для 8 класса по теме “Задачи на построение и методы их решения”
Программа рассчитана на 6 часов. Занятия проводятся по 1 часу.
Занятие №1
Тема: ГМТ. Метод ГМТ.
Тип: урок изучения нового материала
Цели:
1) образовательные: повторить ранее изученный геометрический материал по теме решение задач на построение, сформировать у учащихся понятие геометрического места точек, сформировать представление о методе ГМТ, научить применять метод ГМТ при решении задач на построение, сформировать четкое представление об этапах решения задач на построение;
2) воспитательные: воспитать умение проводить анализ, исследование задачи, умение видеть решение, формировать грамотность речи;
3) развивающие: развить умение применять метод ГМТ для других задач.
Этапы:
1. Организационный момент
2. Актуализация знаний
3. Изучение нового материала
4. Решение задач
5. Подведение итогов.
Ход факультативного занятия:
Организационный момент
Как вы уже поняли из анкеты, задачи на построение можно решать различными методами: методом геометрических мест точек, подобия, осевой симметрии, центральной симметрии, поворота, параллельного переноса, алгебраическим методом. Сегодня на уроке мы введем понятие ГМТ и рассмотрим в чем заключается метод ГМТ. Запишите тему урока: “ГМТ. Метод ГМТ”.
Актуализация знаний
Вы изучали геометрические построения на протяжении 7 и 8 классов. Вспомните, какие построения вы выполняли? Таким образом, вы знаете как выполнить построение:
отрезка, равного данному;
угла, равного данному;
биссектрисы угла;
перпендикулярных прямых;
середины отрезка;
треугольника по трем сторонам;
деление отрезка на n равных частей.
3. Изучение нового материала
Также вы строили серединный перпендикуляр к данному отрезку. Как вы это делали? (чертеж на доске)
Наверняка вы говорили о том, что на серединном перпендикуляре к данному отрезку находятся все точки, которые равноудалены от концов отрезка.
Говорят, что серединный перпендикуляр – это геометрическое место точек, равноудаленных от двух данных точек.
Геометрическим местом точек плоскости, обладающих данным свойством, называется множество всех точек плоскости, каждая из которых обладает этим свойством (запись определения в тетради).
Рассмотрим еще некоторые основные геометрические построения (раздаточный материал):
I. Геометрическое место точек, одинаково удаленных от данной точки (окружность).
II. Геометрическое место точек, одинаково удаленных от данной прямой (пара параллельных прямых).
III. Геометрическое место точек, равноудаленных от двух данных точек (серединный перпендикуляр к отрезку)
IV. Геометрическое место точек, равноудаленных от двух данных а) пересекающихся, б) параллельных прямых (пара перпендикулярных прямых в первом случае, прямая линия — во втором).
Существуют также более сложные ГМТ, которые используются при решении задач (раздаточный материал):
1) Геометрическое место вершин С треугольников, имеющих общее основание АВ, у которых боковая сторона АС равна данному отрезку.
2) Геометрическое место вершин С треугольников с общим основанием АВ, у которых медиана, проведенная к основанию, равна данному отрезку.
3) Геометрическое место центров окружностей данного радиуса, проходящих через данную точку.
4) Геометрическое место центров окружностей данного радиуса, касающихся данной окружности (внешним образом, внутренним образом).
5) Геометрическое место вершин треугольников с общим основанием, у которых высота, опущенная на это основание, равна данному отрезку.
6) Геометрическое место центров окружностей данного радиуса, касающихся данной прямой.
7) Геометрическое место центров окружностей данного радиуса, отсекающих на данной прямой хорду данной длины.
8) Геометрическое место середин отрезков, соединяющих данную точку со всеми точками данной прямой.
9) Геометрическое место вершин равнобедренных треугольников с общим основанием.
10) Геометрическое место центров окружностей, проходящих через две данные точки.
11) Геометрическое место центров окружностей, описанных около всех треугольников с общим основанием.
12) Геометрическое место центров окружностей, касающихся внешним образом (внутренним образом) двух равных окружностей.
13) Геометрическое место центров окружностей, касающихся двух данных (пересекающихся, параллельных) прямых.
14) Геометрическое место вершин прямоугольных треугольников с общей гипотенузой.
Теперь вспомните, как вы строили треугольник по трем сторонам (чертеж на доске).
Какие ГМТ здесь используются? Их пересечение дает нам третью вершину искомого треугольника. Оказывается, что при решении данной задачи вы использовали метод ГМТ.
Суть метода ГМТ заключается в следующем: сводят задачу к нахождению некоторой точки, которая определяется двумя условиями, вытекающими из требования задачи.
Допустим, геометрическим местом точек, удовлетворяющих первому условию, есть фигура F>1>, а геометрическим местом точек, удовлетворяющих второму условию, есть фигура F>2>. Тогда каждая точка пересечения этих двух геометрических мест удовлетворяет требованиям задачи. Например, построение треугольника по трем сторонам.
Таким образом, задача не будет иметь решений, если эти ГМТ не пересекаются. И будет иметь столько решений, сколько имеющихся точек пересечения указанных мест (показать на том же примере).
4. Решение задач
1) Построить треугольник по основанию, боковой стороне и медиане, проведенной к основанию (пересечение ГМТ №1 и №2).
2) Постройте равнобедренный треугольник по основанию и радиусу описанной окружности (пересечение ГМТ №9 и описанной окружности, центр которой – ГМТ №11).
3) Построить окружность данного радиуса, проходящую через две данные точки (пересечение ГМТ №3 и №3).
5. Подведение итогов
Итак, что вы узнали на сегодняшнем занятии? Сформулируйте понятие ГМТ. В чем заключается метод ГМТ? Какие существуют этапы решения задач на построение? Раскройте суть каждого из этапов.
Домашнее задание: 1) Построить равнобедренный треугольник по основанию и боковой стороне. 2) Постройте ромб так, чтобы две противолежащие его вершины были в двух данных точках А и В и третья на данной окружности О. 3) Постройте окружность, которая касается сторон данного угла, причем одной из них – в данной точке.
Рекомендуемая литература: [11], [16], [18], [22].
Занятие №2
Тема: Применение метода ГМТ к решению задач на построение.
Цели: Научить применять метод ГМТ к решению задач на построение.
Краткое содержание: Повторение изученного материала, решение задач на построение, в которых используется более сложные геометрические места точек.
Рекомендуемая литература: [11], [16], [18], [22].
Занятие №3
Тема: Подобие. Метод подобия.
Цели: Повторить тему подобия фигур, сформировать понятие о методе подобия при решении задач на построение.
Краткое содержание: рассмотрение случаев, когда задача на построение решается методом подобия, суть метода подобия, решение задач, в которых размеры фигуры определяются заданием некоторого отрезка, различные случаи выбора центра подобия.
Рекомендуемая литература: [4], [11], [16].
Занятие №4
Тема: Применение метода подобия к решению задач на построение.
Цели: Научить применять метод подобия к решению задач на построение.
Краткое содержание: Повторение изученного материала, решение задач на построение, в которых размеры фигуры определяются заданием некоторого отрезка, суммы или разности отрезков.
Рекомендуемая литература: [4], [11], [16].
Занятие №5
Тема: Решение задач на построение методами ГМТ и подобия.
Цели: Научить видеть какой из методов следует применять к той или иной задаче.
Краткое содержание: Решение задач на применение различных методов: ГМТ и подобия.
Рекомендуемая литература: [4], [11], [16], [18], [20], [21], [22].
Занятие №6
Тема: Решение задач на построение методами ГМТ и подобия.
Цели: Научить применять методы ГМТ и подобия к решению более сложных задач на построение, научить видеть какой из методов следует применять к той или иной задаче.
Краткое содержание: Решение более сложных задач на построение на применение различных методов: ГМТ и подобия.
Рекомендуемая литература: [4], [11], [16], [18], [20], [21], [22].