Графические работы на уроках стереометрии в средней школе

Оглавление

Введение 3

Глава 1. Проявление пространственного мышления в учебной деятельности 5

1.1. Модель формирования пространственного образа 7

1.1.1. Внимание 8

1.1.2. Психологические особенности пространственного мышления 9

1.2. Особенности пространственного образа 11

Глава 2. Основные показатели и условия развития пространственного мышления, формируемого на графической основе 14

2.1. Типы оперирования пространственными образами 15

2.2. Широта оперирования геометрическим образом и полнота образа 17

2.3. Использование разных систем отсчета при оперировании пространственными образами 21

Глава 3. Зависимость структуры пространственного образа от его функций в решении графических задач 23

Глава 4. Методика работы с геометрическими образами 27

4.1. Задания на создание геометрических образов 27

4.1.1. Задания на перевод словесных данных задачи в графический образ 27

4.1.2. Задания на выделение существенных признаков геометрических понятий, их актуализацию 28

4.1.3. Задания на вычленение фигуры из состава других фигур чертежа 29

4.1.4. Задания на сравнение фигур чертежа 30

4.1.5. Задания на построение недостающих фигур чертежа в ходе решения задачи 32

4.1.6. Задания на рассмотрение фигур чертежа с разных точек зрения 33

4.2. Задания на оперирование геометрическими образами 36

4.2.1. Задания на мысленное видоизменение пространственного положения исходного образа 37

4.2.2. Задания на мысленное видоизменение структуры геометрического образа 38

4.2.3. Задания на мысленное изменение пространственного положения и структуры геометрического образа 39

Глава 5. Дидактические материалы по теме «Параллельность в пространстве» 41

5.1. Уроки изучения нового материала 43

5.2. Уроки применения знаний, умений и навыков 47

5.3. Уроки проверки знаний, умений и навыков 57

Заключение 60

Библиографический список 61

Введение

Очень многие «беды» начинающих изучать стереометрию про­исходят от неумения сделать правильный и удобный («конст­руктивный» для решения задачи) рисунок, или чертеж (мы не различаем эти понятия). Часто учащиеся не понимают, как пространственные фигуры изобразить на плоскости, правильно оперировать ими, так как чертеж несет в себе смысловую нагрузку, не понятную школьникам. Наглядные и правильно выполненные чертежи обладают определенной спецификой изображения на них пространственных фигур, и очень важно овладеть этой спецификой изображать верно и наглядно пространственные фигуры. Поэтому изучение проблемы изображения геометрических фигур актуально и необходимо для развития образного мышления школьников.

Образное мышление в математике реализуется через создание (построение) образов геометрических объектов, оперирование ими при усвоении знаний, решении задач. В этом процессе особое значение имеет ориентация в пространстве. Поэтому в математике образное мышление выступает прежде всего, как пространственное, интегрирующее в себе проективные и метрические представления о геометрических объектах (их свойствах и отношениях). Пространственное мышление обеспечивает взаимопереход от двух- к трехмерным образам и обратно, а также произвольное изменение точки отсчета.

Целью работы является изучение влияния графических работ на развитие образного мышления школьника.

Для реализации цели поставлены следующие задачи:

изучить теоретический материал, освещающий психологические закономерности создания образов, оперирования ими при решении задач;

изучить типы оперирования образами, отражающие разные уровни развития математического мышления;

составить типологию заданий на чтение (восприятие) геометрического чертежа, его преобразование, свободное конструирование;

разработать дидактический материал по одной из тем курса стереометрии, направленный на формирование различных способов создания образов и оперирования ими.

Глава 1. Проявление пространственного мышления в учебной деятельности

Пространственное мышление – вид умственной деятельности, обеспечивающий создание пространственных образов и оперирование ими в процессе решения различных практических и теоретических задач.

Особенности пространственного мышления ярко выступают в процессе решения графических задач, где вычленение пространственных соотношений, их преобразование осуществляется на основе условных изображений (рисунков, чертежей и т.п.). В процессе деятельности человек выделяет пространственные соотношения в воспринимаемом пространстве, отражает их в представлениях или понятиях. Но ему нередко приходится не только их фиксировать и соответственно регулировать свою деятельность, но и прогнозировать новые соотношения, ранее невоспринимаемые. На основе чувственного познания заданных пространственных соотношений с помощью сложной системы умственных действий человек создает новые пространственные образы и выражает их в словесной или графической форме. Это достигается специальной деятельностью представливания¹, обеспечивающей восприятие заданных пространственных соотношений, их мысленную переработку и создание на основе новых пространственных образов.

Деятельность представливания есть основной механизм пространственного мышления. Его содержанием является оперирование образами, их преобразование, причем нередко длительное и многократное. В этот процесс вовлекаются образы, возникающие на различной графической основе, поэтому в пространственном мышлении происходит постоянное перекодирование образов, т.е. переход от пространственных образов реальных объектов к их условно-графическим изображениям; от трехмерных изображений к двухмерным и обратно.

Пространственное мышление в своей наиболее развитой форме оперирует образами, содержанием которых является воспроизведение и преобразование пространственных свойств и отношений объектов: их формы, величины, взаимного расположения частей. Под пространственными соотношениями понимаются соотношения между объектами пространства или между пространственными признаками этих объектов. Они выражаются понятиями о направлении (вперед-назад, вверх-вниз, налево-направо), о расстояниях (близко-далеко), об их отношениях (ближе-дальше), о местоположении (в середине), о протяженности объектов пространства (высокий-низкий, длинный-короткий) и т.п.

Пространственное мышление в своих наиболее развитых формах проявляется в процессе решения графических задач, где происходит создание образов и оперирование ими.

При чтении и построении чертежа необходимо менять единую зрительную позицию и рассматривать объект с разных точек зрения. Здесь происходит «преобразование» образов сразу и одновременно в трех разных направлениях при переходе:

от реального объекта к его условно – графическому изображению;

от трехмерных изображений к двумерным и обратно;

от фиксированной «в себе» точки отсчета к другим системам отсчета, произвольной их смене.

Пространственное мышление, обладая всеми характерными особенностями образного мышления, имеет свои специфические черты, что связано с содержанием самих образов, условиями их создания и оперирования ими. Основной оперативной единицей пространственного мышления являются пространственные образы, в которых отражаются пространственные образы и отношения. Пространственное мышление в своих наиболее развитых формах формируется на графической основе, поэтому ведущими образами являются для него зрительные образы. Переход от одних зрительных образов к другим постоянно наблюдается при решении тех задач, где используются разнотипные графические изображения. На их основе возникают не только отдельные образы, адекватные каждому изображению, но и их целостная система. Умение мыслить в системе этих образов и характеризует пространственное мышление.

1.1. Модель формирования пространственного образа

Первым шагом на любом этапе познания, в том числе и при формировании представлений, является восприятие, «живое созерцание» определённой визуальной информации, например, чертежа, схемы, модели, рисунка и т.п. Для того чтобы сделать его действенным, необходимо не просто смотреть на предлагаемые для восприятия зрительные образы, а видеть заложенную в них информацию, то есть осуществлять анализ визуальной информации.

Анализ визуальной информации начинается с создания общей структуры информационного сообщения, заложенного в данном зрительном образе (модели, рисунке, чертеже, схеме и пр.) и выделения его элементов. Учебная математическая информация, задаваемая наглядным образом, довольно четко подразделяется на элементы. Например, при изображении пространственных или плоских геометрических конфигураций, в одних случаях к элементам можно отнести сами эти фигуры, в других - выделенные на чертеже их составляющие (высоты, углы, стороны, вершины и пр.). Таким образом, происходит расчленение, в котором важную роль играет опознание отдельных ее фрагментов (узнавание), отождествление одинаковых, сходных по форме или по смыслу ее элементов. Система связей выделенных элементов будет составлять структуру данной визуальной информации. Осознание структуры исходной визуальной информации заключается в определении связей между ее элементами.

В ходе активного зрительного восприятия визуальной информации учащийся отождествляет отдельные ее фрагменты с известными ему достаточно простыми объектами и понятиями. Распознавание стандартной ситуации, стандарта может происходить как при постановке задачи (применить признак параллельности для построения сечения куба), так и неявно, в процессе выделения знакомого представления в новых условиях (стороны треугольника - отрезки, вершины - точки), уяснения частного вида более общего знакомого понятия (треугольник - равносторонний треугольник).

Таким образом, в посильном для изучения материале обучаемый находит некоторые известные ему объекты в виде элементов чертежа, схемы, графика, модели; выделяет их, дифференцирует по степени сходства, определяет известный ему структурный стандарт по отношению ко всей представленной визуальной информации. Получение начальных, явным способом предлагаемых данных информации приводит к вычленению признаков геометрического объекта, которые являются основой для формирования его первичного образа.

Далее учащийся приступает к уточнению и детализации исходной визуальной информации, сравнивает ее с некоторым обобщенным образом (стандартом, эталоном). Таким образом, в памяти учащегося происходит окончательное закрепление - образование содержательных образов (пространственных представлений).

Вся деятельность пространственного мышления при работе с наглядным материалом направлена на формирование обобщенных пространственных представлений.

Для обобщения и систематизации всего вышесказанного, нами выработана общая схема формирования пространственного образа. Не последнюю роль в формировании пространственного мышления играет внимание, пространственное мышление и пространственные представления. Остановимся подробнее на этих понятиях.

1.1.1. Внимание

Для восприятия любого явления необходимо, чтобы оно смогло вызвать ориентировочную реакцию, которая и позволит нам «настроить» на него свои органы чувств. Подобная произвольная или непроизвольная направленность и сосредоточенность психической деятельности на каком-либо объекте восприятия и называется вниманием. Без него восприятие невозможно.

Внимание обусловливает избирательность, сознательный или полусознательный отбор информации, поступающей через органы чувств.

Внимание обладает определёнными параметрами и особенностями, которые во многом являются характеристикой человеческих способностей и возможностей. К основным свойствам внимания обычно относят следующие: концентрированность, интенсивность, устойчивость, объем, переключение внимания, распределение внимания.

Особый интерес всегда привлекало произвольное внимание, требующее сознательного самоконтроля и сопровождаемое чувством усилия над собой, в некотором смысле самопринуждением индивида, который в этом случае подавляет свои непроизвольные реакции во имя долга, разумной необходимости.

1.1.2. Психологические особенности пространственного мышления

Пространственное мышление - вид умственной деятельности, обеспечивающей создание пространственных образов и оперирование ими в процессе решения различных практических и теоретических задач. Пространственное мышление есть такое психологическое образование, которое формируется в различных видах деятельности (практической и теоретической). Для его развития большое значение имеют продуктивные формы деятельности: конструирование, изобразительное (графическое). В ходе овладения ими, целенаправленно формируются умения представлять в пространстве результаты своих действий и воплощать их в рисунке, чертеже, постройке, поделке. Мысленно видоизменять их и создавать на этой основе новые, в соответствии с созданным образом, планировать результаты своего труда, а также основные этапы его осуществления, учитывая не только временную, но и пространственную последовательность их выполнения.

Пространственное мышление в своей развитой форме оперирует образами, содержанием которых является воспроизведение и преобразование пространственных свойств и отношений объектов: их формы, величины, взаимного положения частей. Оперирование пространственными образами в видимом или воображаемом пространстве, является содержанием пространственного мышления. Выделение пространственных зависимостей из объекта восприятия часто затруднено ввиду сложности его конструкции. Многие особенности (например, внутреннее строение) скрыты от непосредственного наблюдения. Поэтому выделять пространственные зависимости, присущие объекту, нередко приходится опосредствованно, через сравнение, сопоставление различных частей и элементов конструкции. Общее, что характеризует любой пространственный образ - это отражение в нём объективных законов пространства. Однако это отражение определяется деятельностным отношением субъекта к окружающему его пространству, разнообразием условий, форм и способов отражения, что определяет различия в конкретном содержании пространственного образа. Пространственные свойства и отношения неотделимы от конкретных вещей и предметов - их носителей, но наиболее отчётливо они выступают в геометрических объектах (объёмных телах, плоскостных моделях, чертежах, схемах и т.п.), которые являются своеобразными абстракциями от реальных предметов. Не случайно, поэтому геометрические объекты (их различные сочетания) служат тем основным материалом, на котором создаются пространственные образы и происходит оперирование ими.

В современной психологии понятие пространственных представлений связывается с понятием образа объекта или явления, который возникает в результате восприятия. При этом большое внимание уделяется зрительным образам, так как их информационная ёмкость особенно велика. Они позволяют мгновенно схватывать отношения между реальной и представляемой ситуацией. Пространственные представления являются целостными субъективными образами пространственных объектов или явлений, которые отражены и закреплены в памяти на основе восприятия наглядного материала в процессе деятельности. Тогда формирование и развитие пространственных представлений можно рассматривать как процесс создания образов и оперирование ими.

Познавательная природа представлений раскрывается в том, что они являются промежуточным звеном при переходе от ощущения к мысли. Ясные и отчётливые представления о геометрических объектах, последовательно образованные в сознании обучаемых, являются прочной основой для усвоения научных знаний. Представление, как важный элемент познания, призвано связывать образы предметов и явлений со смыслом и содержанием понятия о них. Но, в свою очередь, формирование представлений требует овладения понятием, поскольку понятие определяет содержание образа. Пространственные представления по отношению к мышлению являются исходной базой, условием развития, но, в то же время, и формирование представлений требует предварительного овладения понятиями и фактами. Можно сказать, что процесс формирования пространственных представлений о геометрических объектах проходит на основе знаний о них.

На основе вышесказанного можно сделать вывод, что содержание пространственных представлений следует рассматривать как образ отраженного объекта или явления, в совокупности со знаниями об объекте, извлеченные в процессе его восприятия. Это результат визуального мышления, сочетающего в себе взаимосвязанные пространственный и логический компоненты мышления.

Итак, под пространственным представлением, формируемым в процессе обучения геометрии, будем понимать обобщенный образ геометрического объекта, складывающийся в результате переработки (анализа) информации о нем, поступающей через органы чувств.

1.2. Особенности пространственного образа

Содержанием пространственного мышления является оперирование пространственными образами в видимом или воображаемом пространстве на основе различных графических изображений, что связано с необходимостью «перекодирования» образов, создаваемых на разной наглядной основе.

Выделение пространственных зависимостей из объекта восприятия часто затруднено ввиду сложности его конструкции. Многие особенности (например, внутреннее строение) скрыты от непосредственного наблюдения. Поэтому выделять пространственные зависимости, присущие объекту, нередко приходится опосредствованно, через сравнение, сопоставление различных частей и элементов конструкции.

Пространственные свойства и отношения выявляются как путем восприятия реальных объектов, так и их заменителей, причем графическое изображение реального объекта может значительно расходиться с обозначаемым объектом, создавая специфические сложности для возникновения на этой основе адекватных пространственных образов.

Пространственные свойства и отношения неотделимы от конкретных вещей и предметов — их носителей, но наиболее отчет­ливо они выступают в геометрических объектах (объемных телах, плоскостных моделях, чертежах, схемах и т.п.), которые являются своеобразными абстракциями от реальных предметов. Не случайно, поэтому геометрические объекты (их различные сочетания) служат тем основным материалом, на котором создаются пространственные образы и происходит оперирование ими.

Предметную очерченность любого объекта создает его контур, что позволяет отличать один предмет от другого, сравнивать их между собой путем применения общественно выработанных сенсорных эталонов.

Пространственные свойства характеризуют не только внешний вид (конфигурацию) предмета, но и его структуру (строение), что во многом определяет функциональную значимость этого предмета (его назначение, область применения). В ряду других свойств (цвет, масса, фактура поверхности и т. п.) пространственные свойства занимают ведущее место в характеристике предмета. Опираясь на эти свойства, человек распознает различные предметы, классифицирует их, широко использует геометрические знания в различных видах как теоретической, так и практической деятельности.

Положение объекта по отношению к другим объектам определяется его размещенностью в пространстве. Определить его положение — это и значит указать его место в совокупности мест, занимаемых другими, окружающими его объектами. Пространственные соотношения характеризуют не столько сам объект, сколько его положение в системе других объектов (если объект сложный по структуре, то внутри этой структуры устанавливаются пространственные соотношения его частей, части и целого). Пространственные соотношения нередко имеют сложную структуру, оперирование ими опосредствуется специальными знаниями и умениями. Особенности пространственного образа определяются не только его содержанием и условиями возникновения. Как уже отмечалось, важной характеристикой пространственного мышления является перекодирование образов, возникающих на различной наглядной основе. В ходе усвоения знаний в качестве наглядной основы может выступать и реальный (конкретный) предмет, и теоретическая модель, воспроизводящая его строение (конструкцию), происходящие в нем, скрытые от непосредственного наблюдения процессы и графическое изображение отдельного объекта или целой совокупности объектов.

Условные графические изображения способствуют передаче более скрытых от непосредственного восприятия свойств изучаемого объекта. Освобожденные от конкретных «телесных» особенностей объекта, они передают главным образом конструкцию (строение) объекта, его геометрическую форму, пропорции, пространственное положение его отдельных частей.

Условные графические изображения объектов дают возможность выявить скрытые пространственные связи и отношения, как бы перейти от явления к сущности.

Пространственные образы, создаваемые на различной графической основе, являются сложными по своей природе. В них фиксируются пространственные зависимости, присущие как отдельным предметам, так и целому классу предметов, имеющих общие геометрические конструктивно-технические особенности.

Геометрический чертеж может выступать как

специальный предмет изучения;

просто наглядная опора для отвлеченного хода мысли, своеобразный образ-схема;

условие для воспроизведения по нему различных наглядных образов конкретного объекта.

Во всех рассмотренных случаях происходит перекодирование образов, различающихся содержанием и уровнем обобщенности пространственных свойств и отношений. Все это указывает на то, что использование в учебных целях различной наглядности, на основе которой создаются пространственные образы и осуществляется оперирование ими, требует анализа ее психологического содержания. К сожалению, в школе учебная наглядность классифицируется лишь по ее предметному (графическому) содержанию и часто используется только в качестве иллюстративного материала, ее функции в развитии пространственного мышления учащихся исследованы недостаточно.

Глава 2. Основные показатели и условия развития пространственного мышления, формируемого на графической основе

При характеристике уровня развития пространственного мышления в качестве основного показателя развития пространственного мышления, осуществляемого в условиях графической деятельности, принят тип оперирования образом. Для того чтобы этот показатель был надежным, используются еще два тесно связанных с ним показателя - широта оперирования образом и полнота образа.

2.1. Типы оперирования пространственными образами

При создании любого образа, в том числе и пространственного, мысленному преобразованию подвергается наглядная основа, на базе которой образ возникает. При оперировании образом мысленно видоизменяется уже созданный на этой образ, нередко в условиях полного отвлечения от нее.

Выделяя оперирование образами в особый вид деятельности представливания, не совпадающий ни по своему содержанию, ни по условиям осуществления, ни по результатам с процессом создания образа, тем самым получаем возможность определить основную функцию пространственного мышления. Под пространственным мышлением подразумевается свободное оперирование пространственными образами, созданными на различной наглядной основе, их преобразование с учетом требований задачи.

Все многообразие случаев оперирования пространственными образами можно свести к трем основным: приводящим к изменению положения воображаемого объекта (I тип), изменению его структуры (II тип) и к комбинации этих преобразований (III тип). Остановимся на описании каждого типа оперирования.

Первый тип оперирования характеризуется тем, что исходный образ, уже созданный на графической наглядной основе, в процессе решения задачи мысленно видоизменяется в соответствии с условиями задачи. Эти изменения касаются в основном пространственного положения и не затрагивают структурных особенностей образа. Типичными случаями такого оперирования являются различные мысленные вращения, перемещения уже созданного образа как в пределах одной плоскости, так и с выходом из нее, что приводит к существенному видоизменению исходного образа, созданного на графической основе, которая объективно остается при этом неизменной. Следует отметить, что приемы мысленного вращения (смещения) применяются при создании пространственного образа. Но в этом случае они используются применительно к изображению (например, чертежу) или отдельным его элементам. В процессе оперирования изменению подлежат не столько элементы воспринимаемого изображения, сколько уже созданный на их основе образ. Мысленное вращение осуществляется при этом без непосредственной опоры на наглядность.

Второй тип оперирования характеризуется тем, что исходный образ под влиянием задачи преобразуется в основном по структуре. Это достигается благодаря различным трансформациям исходного образа путем мысленной перегруппировки его составных элементов с помощью применения различных приемов наложения, совмещения, добавления (усечения) и т.п. При втором типе оперирования образ изменяется настолько, что становится мало похожим на исходный. Степень новизны создаваемого образа в этом случае намного выше той, которая наблюдалась при первом типе оперирования, так как исходный образ подвергается здесь более радикальному преобразованию. Намного выше также и умственная активность, поскольку все преобразования образа осуществляются, как правило, в уме, без непосредственной опоры на изображение. Все производимые преобразования и их результаты приходится удерживать в памяти, как бы видеть их мысленным взором.

Третий тип оперирования характеризуется тем, что преобразования исходного образа выполняются длительно и неоднократно. Они представляют собой целую серию умственных действий, последовательно сменяющих друг друга и направленных на преобразования исходного образа одновременно и по пространственному положению, и по структуре.

Сравнительный анализ трех типов оперирования пространственными образами показывает, что оперирование может осуществляться применительно к разным элементам в структуре образа: его форме, положению, их сочетаниям. Выделенные типы оперирования пространственными образами, их доступность учащимся рассматриваются как один из важных и весьма надежных показателей, характеризующих уровень развития пространственного мышления.

В соответствии с тремя типами оперирования выделены три уровня развития пространственного мышления (низкий, средний, высокий). Этот показатель положительно коррелирует с другими показателями, такими, как широта оперирования пространственным образом, полнота образа, его динамичность, обобщенность, обратимость и т.п.

Итак, рассмотрены основные типы оперирования пространственными образами, встречающиеся в процессе решения графических задач, различных по своему предметному содержанию. Исследование реальных механизмов, обеспечивающих возможность оперировать образами, поможет понять психологическую природу затруднений, разработать надежные критерии для определения уровня развития пространственного мышления.

2.2. Широта оперирования геометрическим образом и полнота образа

Представим, что учащийся хорошо выполняет преобразования по тому или иному типу. Чтобы убедиться в том, что данный тип оперирования для него не случаен, необходимо проверить его устойчивость, т. е. возможность выполнять данные преобразования на различном графическом материале. В этих целях используется такой показатель, как широта оперирования. Кроме того, оперирование пространственным образом предполагает, что учащиеся мысленно преобразуют заданную графическую наглядность в трех тесно взаимосвязанных направлениях: по форме, величине, пространственному положению. Отражение этих признаков в образе, мысленно преобразуемом, и характеризует полноту образа. Если эти признаки не теряются человеком в процессе преобразования образа, то можно наняться на успешность его преобразования.

Вот почему тип, широта оперирования и полнота образа приняты в качестве основных показателей развития пространственного мышления.

Тип оперирования образом есть доступный ученику способ преобразования созданного образа. С помощью данного показателя удается не только выявлять намеченный тип оперирования образом, сложившийся испытуемого к моменту проверки, но и следить за динамикой его изменений в процессе обучения.

Широта оперирования есть степень свободы манипулирования образом с учетом той графической основы, на которой образ первоначально создавался. Данный показатель дает возможность выявить степень устойчивости в оперировании образом по тому или иному типу, независимо от характера изображения. Свобода такого оперирования, проявляющаяся в легкости и быстроте перехода от одного графического изображения к другому, своеобразное «перекодирование» их содержания типичны для развитого мышления. На основании этого показателя легко установить, является ли данный тип оперирования образом, результатом непосредственного обучения или же это есть проявление индивидуальной способности ученика, который самостоятельно, по собственной инициативе осуществляет подобные преобразования на разнотипных изображениях. Важным здесь является умение создавать образы и оперировать ими, используя для этого разные виды графических изображений.

Оценивая уровень развития пространственного мышления учитывается также содержание пространственного образа, который создается на различной графической основе, а затем преобразуется. Ведь от того, каков образ по содержанию (насколько в нем полно отражены все пространственные характеристики объекта), во многом зависит успешность оперирования им. Для выявления структуры образа использовалась такая его характеристика, как полнота.

Полнота образа характеризует его структуру, т.е. набор элементов, связи между ними, их динамическое соотношение. В образе отражается не только состав входящих в его структуру элементов (форма, величина), но и их пространственная размещенность (относительно заданной плоскости или взаимного расположения элементов).

Умение вычленять пространственные соотношения и оперировать ими прямо не зависит от усвоения знаний, в то время как умение вычленять форму и размеры изображенного объекта опосредствуется целой системой усвоенных знаний, приемов и способов действий.

Относительная «независимость» умения к вычленению пространственных свойств и отношений от специальных знаний выступает в качестве показателя, характеризующего наиболее устойчивую индивидуально-психологическую особенность людей, связанную с ориентацией в пространстве. Эта способность носит устойчивый характер и проявляется при работе с разным учебным материалом. Под влиянием специального обучения она может успешно развиваться, но темпы и характер ее развития во многом определяются исходной основой, выявление которой очень важно для правильной индивидуализации обучения, что особенно существенно при обучении графическим дисциплинам в школе.

Важной характеристикой полноты образа является его динамичность, выражающаяся в умении:

мысленно фиксировать изменения в содержании образа;

произвольно изменять точку отсчета.

Выделенные показатели: широта и тип оперирования образом, отражающиеся в его полноте и динамичности, характеризуют уровень развития пространственного мышления.

Овладение специальной системой графических знаний, умений и навыков является важнейшим условием, вне которого не может быть развития пространственного мышления. Однако последнее зависит не только от усвоения специальных знаний, но и от структуры пространственных образов.

Создание соответствующих упражнений на основе классификации различных видов изображений и типов их преобразований не только способствовало правильному и более раннему усвоению учащимися основополагающих понятий о пространстве и его элементах (таких, например, как пространственное тело, плоскость и т.п.), но играло бы большую роль в развитии пространственного мышления школьников.

Для формирования пространственного мышления важно не только уметь абстрагировать признаки пространственных объектов, но и понимать относительность границ между отдельными группами объектов, возможность использования для их анализа различных критериев, тесно взаимосвязанных. Относительность пространственных характеристик объектов обусловлена динамикой объектов, их постоянным движением, перемещением, преобразованием. К сожалению, развитию этой важной особенности пространственного мышления не уделяется пока должного внимания. А между тем понимание учащимися не только способа существования, но и происхождения различных геометрических форм, возможность их преобразования является важной предпосылкой для формирования динамичности (обратимости, взаимозаменяемости) пространственных образов.

Ориентация по схеме тела оказывает существенное влияние на формирование и развитие всей системы пространственных образов. Будучи прочно закрепленной, она переносится с практических действий с предметами на анализ геометрического пространства, что вызывает значительные трудности, которые проявляются у школьников при усвоении геометрии.

Итак, создание и оперирование пространственными образами опирается на сложную систему знаний о пространственных свойствах и отношениях, на формирование специальных приемов их восприятия и представливания. Но этого оказывается недостаточно. Нужна сложная, кропотливая и систематическая работа по формированию умений использовать различные графические изображения, произвольно изменять систему отсчета (см. ниже).

Это требует существенного изменения содержания и методов обучения. По-видимому, отсутствием в должной мере этих изменений можно объяснить психологическую природу многих трудностей, связанных, в частности, с овладением графической деятельностью. Так, становится, например, понятной причина массовой ошибки, которую допускают учащиеся, когда вид слева называют видом справа. При ориентировке по схеме тела вид сбоку располагается на чертеже справа, если плоскость чертежа представить в прямоугольной системе координат. Но при составлении проекций чертежа за основную систему отсчета принимается не позиция наблюдателя, а фиксированная позиция объекта (выбирается его главный вид). По отношению к нему строится вид сверху и слева.

Отсутствие у учащихся динамической смены точек отсчета и порождает многие трудности, встречающиеся при овладении графической деятельностью.

Развитие пространственного мышления в процессе обучения идет по следующим основным направлениям:

овладение произвольностью в использовании систем отсчета;

формирование обобщенных способов создания пространственных образов и оперирования ими, т.е. совершенствование деятельности представливания;

усвоение графической культуры, что обеспечивает возможность оперирования пространственными образами разной меры конкретности, наглядности, перекодирование этих образов в соответствии с требованиями графической деятельности.

2.3. Использование разных систем отсчета при оперировании пространственными образами

Одной из особенностей пространственного мышления является использование разных систем ориентации в пространстве (видимом или воображаемом). Наиболее естественной, закрепленной всем опытом человека системой ориентации является схема тела (исходная позиция наблюдателя), которая лежит в основе практической ориентации в системе предметов и явлений. Ее изменение нередко влечет за собой перестройку всей системы пространственных отношений. Пространственная размещенность предметов объективно остается неизменной, но их мысленное отражение в образе будет меняться при изменении точки отсчета.

То же самое можно наблюдать при создании образов на графической основе. Чертеж будет различным, если изменяется позиция наблюдателя относительно одного и того же объекта. По своей структуре объект не изменяется, но в зависимости от того, какой вид его принимается за главный, изменяются изображения его проекций на плоскость, а вместе с тем и образы этих проекций.

При переходе к геометрическому пространству учащиеся наряду с опорой на схему тела вынуждены часто абстрагироваться от нее. Так, при определении пространственной размещенности геометрических объектов за исходную точку отсчета часто принимается не наблюдатель, а любой, абстрактный, произвольно выбранный элемент (точка, отрезок, угол и т.п.), по отношению к которому пространственно размещаются все другие элементы. Это особенно четко обнаруживается, когда образы геометрических объектов формируются на основе условно – графических изображений (чертежей, схем, графиков и т.п.).

При усвоении курса начертательной геометрии основные трудности возникают при необходимости изменить базу отсчета, выйти мысленно за пределы трехгранного угла, обращенного к наблюдателю, и представить расположение геометрических фигур в других октантах. Оставаясь в пределах эмпирической системы отсчета, человек не сможет овладеть геометрическим пространством в его теоретическом содержании. В ходе решения графических задач учащиеся постоянно изменяют базу отсчета, принимая за исходные не только реальные объекты, но и абстрактные геометрические фигуры.

Переход от реального пространства к системе его условно – графических заменителей связан с формированием адекватных средств, направленных на произвольное создание образов и оперирование ими. Этот переход не осуществляется автоматически. Он обеспечивается в процессе усвоения специального понятийного аппарата, использованием систем отсчета, способов представливания.

Для более эффективного развития пространственного мышления необходима классификация разных типов пространственных задач с учетом всех требований, предъявляемых к использованию различных систем отсчета на основе анализа каждой из них.

Глава 3. Зависимость структуры пространственного образа от его функций в решении графических задач

Выше были рассмотрены условия, в которых осуществляется возникновение образа и оперирование им. Среди этих условий можно выделить следующие:

характер наглядной основы, на которой образ впервые воз­никает;

особенности графической задачи, определяющей требования к созданию образа и оперированию им.

В процессе решения задач часто используется не один, а несколько видов графических изображений (рисунок, чертеж и др.), что требует не только создания образов, адекватных заданным изображениям, но и перекодирования их.

В процессе решения задачи необходимо, опираясь на разные графические изображения, увидеть объект многопланово, причем образы, возникающие на основе изображений, должны сливаться в единый, целостный образ. Единичные образы, полученные от восприятия каждого изображения, различаются уровнем наглядности, обобщенности, схематичности. Они не просто рядоположно существуют, а видоизме­няются, преобразуются в процессе решения. Поэтому в конечном образе — образе-результате — отражается в снятом виде вся логика преобразований исходных образов. Структура этих образов зависит от содержания исходной наглядности, на которой они возникают.

Структура пространственного образа существенно зави­сит от характера наглядной основы, на которой образ возникает. В процессе решения графических задач используются не одно, а несколько изображений разного типа, требуется переход от одно­го к другому, что обусловливает изменения в структуре образа. В каждом графическом образе отражаются по преимуществу те свойства объекта, которые фиксируются графическим изображением. Однако структура пространственного образа определяется не только характером наглядной основы. Она определяется также той функцией, которую образ выполняет в процессе решения графической задачи. В зависимости от функции в образе фиксируются не все свойства и признаки отображаемого объекта, а лишь те, которые необходимы для реализации деятельности, ее успешного осуществления. Избирательность психического отражения — фундаментальная закономерность, выражающаяся в за­висимости структуры образа от его функции в деятельности. Эта закономерность в специфическом виде проявляется и при созда­нии пространственных образов.

Образ «рождается» под влиянием двух тесно взаимосвязанных детерминант: наглядной основы и требований деятельности, обусловленных конкретными условиями задачи. Это важно иметь в виду при использовании принципа наглядности в обучении. Нередко выбор наглядного графического изображения диктуется только его иллюстративной функцией. Но важно учитывать также требования учебной задачи и, исходя из этого, выбирать адекватное графическое изображение.

Выбор графической иллюстрации должен опираться на анализ содержания учебной деятельности, с учетом той реальной задачи, которую выполняет ученик. Необходимо предоставлять ученикам свободу выбора в использовании графических изображений с учетом их функции в усвоении заданного учебного материала, легкости оперирования ими.

После рассмотрения сложных зависимостей, которые имеют место в процессе создания образа с учетом исходной графической основы и содержания задачи, проанализируем, как проявляются эти зависимости при решении графических задач, где создание пространственных образов и оперирование ими являются основной целью.

Следует подчеркнуть, что в задачах начертательной геометрии образ, возникающий первоначально на заданной графической основе, является лишь исходной моделью, обладающей различным набором пространственных и проекционных признаков. Какие из них будут использованы — это зависит от конкретного условия задачи, где фиксируется направление мысленного преобразования исходного образа — модели.

Все выполняемые преобразования, требующие деятельности представливания, непосредственно не заданы исходным изобра­жением. Конечный образ, фиксирующий результат решения, конструируется (строится) с учетом требований задачи. Поэтому структура образа (набор отображаемых им элементов, признаков, свойств) зависит от функции образа в системе задачи. Причем в процессе решения задачи может происходить переориентация на различные признаки и свойства.

Таким образом, в задачах по начертательной геометрии имеет место динамическое соотношение пространственных признаков и свойств, которые непосредственно фиксируются в ходе решения задачи. Здесь также наблюдается своеобразное перекодирование, но выражается оно не только в переходе от одного графического образа к другому, но и в переходе от одних пространственных признаков к другим.

Структура пространственного образа, создаваемого на различной графической основе, определяется конкретными условиями и требованиями деятельности. Она динамически меняется в зависимости от содержания графической задачи, по­скольку имеет место постоянный переход:

от наглядных изображений к условно-схематическим;

от трехмерных (объемных) к двухмерным (плоскостным);

от одной системы ориентации к другой, используя различные свойства изображенного объекта (его форму, величину, пространственные соотношения).

Необходимость изменения структуры пространственных образов определяется их функцией в деятельности (в процессе решения задачи). Первоначально возникший образ (на основе чтения исходного изображения) может только тогда выполнять функцию контроля, коррекции, прогнозирования деятельности (т.е. регулирующую функцию), когда он в процессе решения задачи по­стоянно преобразуется.

Во многих графических задачах логика движения образов (их видоизменение, взаимопревращение) и есть по существу основной механизм решения.

С одной стороны, образ не может быть инвариантным по отношению к той наглядной (графической) основе, на которой он создается. Он должен быть адекватен этой основе. С другой — образ не может быть чем-то неподвижным, статичным, застывшим. Он должен быть динамичным, подвижным, оперативным. В противном случае он не сможет выполнять свою функцию в процессе решения задачи, где требуется не просто зафиксировать наличную, исходную ситуацию, а ее преобразовать.

Если исходная графическая наглядность в условии задачи зада­ется, как правило, стабильной, неизмененной, то функция образа постоянно меняется, что требует непрерывного переструктурирования образов. Статичность и динамичность образа выступают здесь в единстве. Там, где они рассогласованы, возникают трудности в решении графических задач.

Исходная наглядность является лишь первичной основой со­здания образа. В процессе решения задачи образ неоднократно преобразуется. Его преобразования тесно связаны не только с со­хранением образа в памяти, но и с использованием понятийного аппарата, определяющего способы преобразования образа в логике задачи.

В основе решения графических задач лежит деятельность представливания, приобретающая сложную структуру. Процесс решения графических задач складывается из своеобразного сочетания исходных образов, возникающих на заданной наглядной основе, выбора способов их преобразования (графического моделирования) и образов, представляющих собой графические схемы движений, воспроизводящих логику мысленного построения изображения. Единство и взаимопроникновение этих образов на основе широкого использования знаний, понятий о видах изображений, способов их построений обеспечивают нахождение правильных стратегий решения графических задач, где образные и понятийные компоненты сливаются в единое целое.

Глава 4. Методика работы с геометрическими образами

Работа с геометрическими образами при усвоении математики предполагает значительную нагрузку на интеллект, поэтому «насыщение» урока учебным материалом, требующим работы с образом, должно опираться на четкое осознание учителем того, какой тип заданий он предлагает ученику.

Таких заданий в геометрии используется много. Они содержатся в учебниках, анализируются учителем на уроке, задаются в виде контрольных (самостоятельных) работ, как домашние задания. Они различаются своим математическим содержанием. Они неоднородны и по составу той реальной деятельности, которая обеспечивает создание по чертежу образов. Но именно с этой точки зрения задания в учебниках недостаточно систематизированы ни в пределах одной темы, ни курса в целом. Задавая их ученикам, учитель не всегда отдает себе отчет в том, какие требования они предъявляют к созданию образа. Конечно, образ возникает у ученика по чертежу (в большинстве случаев) адекватный, но как именно он возникает, этого, как правило, не знают ни авторы учебников, ни учителя. Констатируя конечный результат — созданный образ (правильный или неправильный), учитель не располагает набором заданий, который позволил бы ему «зондировать» сам процесс создания геометрического образа. Целесообразно различать две системы заданий (см. 4.1 и 4.2).

4.1. Задания на создание геометрических образов

1. Задания на перевод словесных данных задачи в графический

образ

Эти задания широко используются в школьной геометрии. Они предполагают выполнение чертежа в соответствии с условием задачи, заданным в словесной или символьной форме. Есть такие задачи, которые задаются словами и не содержат ни букв, ни символов в тексте («Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится в этой точке пополам»).

Пример1: Сделайте чертежи по условиям задач, используя данные в них обозначения:

Прямая АВ пересекает плоскость α в точке М (рис. 1).

Плоскости α и β пересекаются по прямой МР, а плоскости α и γ пересекаются по другой прямой МТ (рис. 2).

2. Задания на выделение существенных признаков

геометрических понятий, их актуализацию

Выделение существенных признаков может осуществляться:

а) по словесному описанию условий задачи;

б) по графическому изображению фигуры.

Ученик по словесному описанию задачи должен выделить (подчеркнуть) те слова, в которых заключены существенные признаки понятий, опознать их; уметь дифференцировать словесно те условия (их совокупность), которые определяют, что «дано», а что «требуется найти» (доказать, вычислить и т.п.). Это необходимо, чтобы ученик мог сознательно отчленять известное от искомого. Вычленение существенных признаков понятий можно организовать и по чертежу.

Пример 2: На рисунке изображены три попарно пересекающиеся прямые, которые пересекают плоскость α. Верно ли сделан рисунок? (рис. 3)

Решение: При внимательном изучении рисунка видно, что прямые а, b и c лежат в одной плоскости (используется аксиома задания плоскости).

Прямые а, b и c пересекают плоскость α по прямой, на которой лежат точки А, В и С (аксиома пересечения плоскостей). Но по чертежу видно, что через точки А, В и С невозможно провести единственной прямой. Следовательно, рисунок сделан неверно.

4.1.3. Задания на вычленение фигуры из состава других фигур

чертежа

Очень часто чертеж представляет собой не одну (однородную) фигуру, а их совокупность. Для решения задачи не все фигуры одинаково значимы. Необходимо зрительно выделить эту фигуру из состава других, мысленно ее «подчеркнуть»; удержать в образе, чтобы работать с ней. Для этого необходимо фиксировать внимание не на всех, а лишь на отдельных фигурах; причем на разных этапах решения задачи может происходить как бы смена «фигуры и фона»: те фигуры, которые рассматривались как значимые для решения задачи, должны сменяться другими. Для этого ученику нужно от них отвлечься, чтобы перейти к другим. Необходимы специальные упражнения, обеспечивающие возможность не только продуктивного выделения фигуры из фона, но и динамической смены их (то, что было «фоном» становится «фигурой», и наоборот). Такие задания полезны как в целях дифференциации учащихся, так и для развития у них умения последовательно, логично, обоснованно переходить в образах от одной фигуры к другой, подобно тому, как они учатся строго, логично, последовательно словесно излагать свои мысли. Переход от одной фигуры к другой в образах должен быть аргументирован опознаванием существенных признаков, детерминирован требованиями задачи.

Такие задания можно составить на любом материале, используя различные геометрические фигуры как двух-, так и трехмерные. Они предполагают смену анализа фигур: переход от одних к другим, отвлечение от остальных.

Пример 3: Назовите по рисунку (рис. 4):

Плоскости, в которых лежат прямые РЕ, МК, DВ, АВ, АС;

Точки пересечения прямой DК с плоскостью АВС, прямой СЕ с плоскостью АDВ.

Решение:

4.1.4. Задания на сравнение фигур чертежа

Эти задания также требуют произвольного внимания, обеспечивающего гибкий переход от одних элементов к другим, с целью их сравнения по заданным признакам.

Такие задания требуют знания существенных признаков; фиксации внимания на двух или более фигурах; мысленного сопоставления их элементов; опознания на них существенных признаков, объединение фигур на основе их сходства и различия с целью вычленения общего признака, т.е. установления в образах определенной логической связи.

Сравнение элементов чертежа может осуществляться двумя путями. Первый путь — установление того, является ли данный объект элементом определенного множества объектов или нет (задача подведения под «понятие», осуществляемая в образной форме). Второй путь — установление принадлежности данного объекта одному из классов заданного множества объектов (задача на классификацию). И в том, и в другом случае выявляются, а также развиваются определенные логические операции, но осуществляются они над образами, ведь при этом имеет место мысленное воссоздание или видоизменение элементов чертежа, хотя исходный чертеж не изменяется. Происходит зрительная актуализация существенных признаков, выявление их логической структуры, мысленная проверка наличия этих признаков у рассматриваемой фигуры, их опознание.

Пример 4 (задача на классификацию): Сумма всех ребер параллелепипеда АВСDА_>1>В_>1>С_>1>D_>1> равна 120 см. Найдите каждое ребро параллелепипеда, если известно, что ; (рис. 5).

Решение: Используется свойство равенства противолежащих сторон граней – параллелограммов. Тогда см. Найдем искомое в задаче:

;

Отсюда .

4.1.5. Задания на построение недостающих фигур чертежа в ходе

решения задачи

В геометрии очень много заданий, требующих дополнительных построений. Они основаны на тщательном анализе исходных элементов чертежа, определении их существенных (по условию задачи) признаков, причем этот анализ идет в мысленном плане (элементы чертежа сравниваются зрительно). На этой основе возникает догадка о необходимости введения нового элемента и только после этого осуществляется его построение. Такие задания развивают у ученика «образную» логику. Ведь решение о дополнительном построении возникает не сразу, а после тщательного анализа элементов исходного чертежа, сопоставления их со словесными условиями задачи, выработки некоторой стратегии решения и как результат — выполнение построения на основе вычленения и обоснования недостающего данного (или их совокупности), что открывает путь к решению задачи, позволяет переосмыслить исходный чертеж.

Рассмотрев все элементы чертежа, определив их существенные (понятийные) признаки, ученик должен «расширить» круг необходимых данных, для чего и делается дополнительное построение. Оно может быть результатом «слепых» проб, когда ученик без достаточного анализа задачи делает те или иные построения — легко отказывается от одних и переходит к другим. Но построение может быть строго логически обосновано результатом решения задачи (ее отдельного этапа). Это нетрудно установить, наблюдая за работой ученика над задачей.

Задания на расширение данных чертежа путем:

а) дополнительных построений;

б) «переосмысливания», т.е. мысленного «включения» в другую фигуру, имеют большую диагностическую ценность.

Они проявляют возможность ученика выйти за пределы наличной наглядной ситуации, расширить ее, руководствуясь логикой решения задачи.

Эти задания имеют особую ценность в стереометрии, где поиск и нахождение нового элемента нередко представляет собой целую цепь мысленных преобразований, осуществляемых над образом исходной фигуры, когда требуется не только выделение понятийных признаков («ребро куба», «диагональ параллелепипеда», «сечение конуса» и т.п.), но и подлинное создание нового геометрического образа (мысленное «выделение» нового элемента чертежа; «помещение» его в определенной плоскости, выделение среди других). Конечно, все эти умения не формируются сами собой. Они должны быть обеспечены системой заданий. Должны быть разработаны соответствующие правила (образцы, рекомендации), их решения, которые бы раскрывали ученику «технологию» создания образа: возможность мысленно прослеживать его изменения, удерживать в образе его основные элементы, вводить новые — необходимые и достаточные для решения задачи.

Пример 5: Найдите образующую усеченного конуса, если радиусы оснований равны 3 см и 6 см, а высота равна 4 см (рис. 6).

Решение: Достроим усеченный конус до полного и рассмотрим его диагональное сечение. Заметим, что радиус нижнего основания усеченного конуса вдвое больше радиуса верхнего основания. Следовательно, высота и образующая конуса увеличатся в два раза (по подобию треугольников). По теореме Пифагора: образующая усеченного конуса равна 5 см.

4.1.6. Задания на рассмотрение фигур чертежа с разных точек

зрения

Эти задания используются в тех случаях, когда некоторые фигуры чертежа надо рассмотреть в плане разных понятий, т. е. переосмыслить их. Это достигается вычленением отдельной фигуры, выделением ее из остальных и включением в новые фигуры, путем их сочетания. Все это должно осуществляться мысленно, что требует, во-первых, абстрагирования отдельных фигур (углов, отрезков, их комбинаций) и, во-вторых, объединения с новыми, т.е. своеобразного мысленного синтеза этих фигур. Заметим, что такое видоизменение чертежа осуществляется «в уме» (ведь исходный чертеж остается при этом неизменным), поэтому вся работа ученика протекает «во внутреннем плане», скрыта от непосредственного наблюдения со стороны учителя. Необходимо обучать вычленению отдельной фигуры, включению ее в другие. Для этого важно сформировать у ученика в определенном порядке следующие мыслительные операции: сосредоточение своего внимания на отдельной фигуре, отвлечения от остальных; актуализация существенных признаков геометрических понятий, характеризующих данную фигуру; актуализация геометрических понятий, отражающих свойства других фигур чертежа; сопоставление данной фигуры с другими, включение ее в состав этих фигур; объединение на основе новых геометрических понятий (признаков, свойств, отношений), что дает возможность рассмотреть их по-новому, т.е. переосмыслить.

Вся эта система мыслительных действий (их содержание, последовательность осуществления) должна быть выявлена, описана и задана для усвоения учащимся. Иначе их взор будет лишь «скользить» по чертежу, не решая никаких конкретных задач. Ведь недаром говорится, что «смотреть не значит видеть». Чтобы видеть, надо уметь осуществлять определенные мыслительные действия, с содержанием которых ученики должны быть знакомы. Это умение обеспечивает основную логическую операцию — произвольное включение одной и той же фигуры в состав различных элементов чертежа, что формирует такие важные качества ума, как внимательность, наблюдательность, сообразительность. Это включение осуществляется в процессе решения задачи неоднократно, подчинено логике решения задачи.

Пример 6: Точка Е – середина ребра РВ правильного тетраэдра РАВС. Опустите перпендикуляры из точки Е на прямые а) АР, ВС и АВ (рис. 7а); б) АС (рис. 7б).

Найдите длину каждого перпендикуляра, если ребро тетраэдра равно а.

Решение: Необходимо выделять грани (сечение) из состава тетраэдра, чтобы опустить из заданной точки перпендикуляры на заданные ребра.

а) Найдем длину перпендикуляра: Δ РАВ – равносторонний и т.Е – середина ребра РВ. ΔВМР ~ ΔЕКР с коэффициентом подобия (по определению преобразования подобия). Зная длины сторон ΔЕКР: , применим теорему Пифагора и получим: . Остальные длины перпендикуляров равны этому же значению.

б) Заметим, что перпендикуляр МЕ будет лежать в плоскости, перпендикулярной ребру АС. Чтобы построить эту плоскость, опустим из вершин В и Р перпендикуляры РМ и ВМ, тогда любая прямая, лежащая в ней будет перпендикулярна АС.

Найдем длину МЕ: В ΔАВС перпендикуляр МВ является медианой, следовательно, по теореме Пифагора . РМ = МВ. Тогда в равнобедренном ΔРМВ медиана МЕ является высотой. По теореме Пифагора: .

Итак, выделено шесть видов заданий на создание геометрических образов (внутренне взаимосвязанных). Они предполагают:

перевод текста задачи в графический образ (его построение по условию задачи, выраженного словесно, с использованием символических обозначений);

актуализацию существенных признаков;

вычленение различных элементов чертежа, их сравнение, выделение, опознание;

видоизменение чертежа (мысленное или практическое) путем его переосмысливания, дополнительных построений, расширения исходных данных.

При выполнении этих заданий от ученика требуется воссоздание образа по словесному описанию или чертежу и его мысленное видоизменение (без изменения самого чертежа), что предполагает развитие произвольности восприятия, хорошей зрительной памяти; точной фиксации образа чертежа, го мысленного, причем, неоднократного преобразования в указанном направлении.

4.2. Задания на оперирование геометрическими образами

Эти задания отличаются тем, что их выполнение не предполагает опору на чертеж (данный в готовом виде или сделанный учеником по условию задачи). Вся работа с исходным образом осуществляется в основном «в воображении». Эти задания вызывают наибольшие трудности у тех учащихся, которые не могут «удержать» образ (он как бы расплывается, размывается, исчезает, а не имея четкого исходного образа, нельзя им мысленно «манипулировать»).

Есть здесь и другая трудность. Ученики, создающие отчетливые исходные образы, тоже затрудняются их мысленно видоизменять. Но эти затруднения отличны от тех, при которых образ, наоборот, не сохраняется, а расплывается. По условию задачи надо образ не столько «удержать», сколько его видоизменить (преобразовать в новый), т. е. отвлечься от него, а это как раз и трудно для тех учеников, у которых возникают яркие образы. Таким образом, трудность в оперировании геометрическими образами по своему психологическому содержанию различна, что требует использования разных методических приемов (дидактических материалов) в целях ее выявления, индивидуальной коррекции.

Использование заданий на оперирование геометрическими образами должно, поэтому предваряться заданиями на их создание, поскольку механизм создания образа во многом определяет и механизм оперирования образом.

Традиционно в методике обучения геометрии чертеж считается основой такого механизма. Однако опора на него полезна не всегда и не всем ученикам. Используя его как костыли, ученики перестают работать методом «в воображении». И, кроме того, сам чертеж (в ходе решения задачи) выполняет далеко не однородную функцию. Недостаточно его иметь. Необходимо выполнять разнообразные действия по его переосмысливанию, мысленному видоизменению исходных данных, что является важным этапом на пути к переходу на оперирование образом по представлению, т.е. без зрительной опоры на чертеж.

4.2.1. Задания на мысленное видоизменение пространственного

положения исходного образа

Эти задания могут быть составлены на разном геометрическом материале (как планиметрии, так и стереометрии). Наиболее удобен для их разработки материал, излагающий знания о различных пространственных перемещениях: симметрия, параллельный перенос, повороты разных видов, гомотетия и др. Они широко используются в школьном курсе геометрии.

Эти задания характеризуются тем, что образ, уже созданный на чувственной основе (при опоре на словесное описание задачи, ее чертеж) подвергается преобразованиям, касающимся изменения только его пространственного положения.

Примеры таких заданий показывают, что при их выполнении необходимо сначала создать исходный пространственный образ, а затем мысленно его преобразовать по положению относительно исходного образа.

Пример 7: Четыре параллельные прямые пересекают параллельные плоскости в вершинах параллелограммов ABCD и A_>1>B_>1>C_>1>D_>1> соответственно. Докажите, что параллелограммы ABCD и A_>1>B_>1>C_>1>D_>1> совмещаются параллельным переносом (рис. 8).

Решение: Так как плоскости параллельны и прямые параллельны, то АА_>1 >= ВВ_>1 >= СС_>1 >= DD_>1>. A_>1>D_>1>DA, B_>1>C_>1>CB, A_>1>B_>1>BC, C_>1>D_>1>DC – параллелограммы (для того, чтобы четырехугольник был параллелограммом, достаточно равенства и параллельности одной пары его сторон). Тем самым выполняются свойства параллельного переноса: точки смещаются по параллельным прямым на одно и тоже расстояние; каждая прямая переходит в параллельную ей прямую. Следовательно, параллелограммы ABCD и A_>1>B_>1>C_>1>D_>1> совмещаются параллельным переносом.

4.2.2. Задания на мысленное видоизменение структуры

геометрического образа

Эти задания в отличие от предыдущих (см. 4.2.1) предполагают более сложные мыслительные преобразования исходного геометрического образа, затрагивающие его структурные изменения. Следить в «уме» за этими изменениями довольно трудно. К сожалению, в практике обучения, чтобы снять эту трудность ученикам рекомендуется использовать бумажные модели, позволяющие путем реальных манипуляций с ними, найти новую структурную конфигурацию. Конечно, такой методический прием облегчает многим ученикам выполнение этих заданий. Но использовать его как обязательный, по-видимому, не следует, так как он тормозит деятельность воображения.

Такие задания могут быть составлены на разном учебном материале, важно, чтобы они включали геометрические преобразования (поворот, осевую симметрию, параллельный перенос и т.п.).

Такие задачи можно решать в уме, по словесному описанию, а можно сначала сделать исходный чертеж, а затем уже мысленно выполнять требуемые преобразования.

Пример 8: Дан ∆АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А_>1>, а сторону ВС – в точке В_>1>. Найдите длину отрезка А_>1>В_>1>, если АВ = 15 см, и АА_>1>:АС = 2:3 (рис. 9).

Решение: Для построения используется признак параллельности прямой и плоскости.

АВ || А_>1>В_>1>, тогда ∆АВС ~ ∆А_>1>В_>1>С_>1>.

(по свойству преобразования подобия). Найдем искомое:

. Следовательно, А_>1>В_>1> = 5 см.

4.2.3. Задания на мысленное изменение пространственного

положения и структуры геометрического образа

Эти задания наиболее сложные. Они предполагают неоднократные преобразования образа фигуры и по положению, и по структуре одновременно, что приводит к созданию нового геометрического образа. Подобные задания хорошо развивают пространственное мышление, подготавливают учащихся к решению целого ряда конструктивно-технических (технологических) задач, что особенно важно для обеспечения единой линии развития пространственное мышления в системе непрерывного образования (особенно технического).

К сожалению, эти задания используются на уроках очень мало, учителя их относят к заданиям повышенной трудности. С их помощью проверяется возможность ученика последовательно осуществлять мысленные преобразования образа, изменяющие его пространственное положение и структуру. Эти преобразования могут осуществляться по отношению к структуре замкнутой фигуры (ее внутреннего пространства), а могут изменять ее положение и структуру по отношению к другим фигурам (ее внешнее пространство).

Описанные задания на все три типа оперирования геометрическими образами отличаются тем, что в них и создаваемый исходный образ, и его видоизменения осуществляются в уме, без опоры на чертеж, что придает им диагностическую ценность. С помощью таких заданий можно установить, как ученик оперирует образом, что его особенно затрудняет. При этом удается оценить не только, какой образ возникает, но и как он создается и преобразуется каждым учеником. Использование этих заданий в практике экспериментального обучения показало, в частности, что при создании образа (оперировании им) ученики используют различные способы:

отображение фигуры по отдельным элементам (точкам, отрезкам) и их последующее объединение;

отображение сначала одного, целостного элемента (прямая, луч, полуплоскость) и последовательное «достраивание» в уме остальных элементов;

оперирование целостным образом фигуры и экстраполяция искомого результата.

Если тот или иной способ (его использование) носит устойчивый характер (что легко проверить при предъявлении серии заданий), можно говорить об индивидуальных проявлениях способов работы с образом и по ним судить об уровне развития пространственное мышления. Отметим, что при использовании каждого способа можно правильно решить задачу, но с точки зрения оценки пространственное мышления эти способы не равнозначны.

Для выявления тех способов создания образов, которыми фактически пользуются ученики, можно (особенно в старших классах) использовать такой прием: после того, как задача решена, предложить рассказать о том, какие действия по преобразованию образа геометрической фигуры были использованы. Ученики с удивлением узнают, что, решая одну и ту же задачу, они применяли разные способы мысленного «видения» геометрической фигуры. Такой методический прием имеет большое не только диагностическое, но и развивающее значение.

Пример 9: Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма (рис. 10).

Решение: Целесообразно рассматривать фигуру с разных сторон: каждые две пересекающиеся прямые задают плоскость (аксиома задания плоскости) → треугольник → параллельность и равенство противолежащих сторон параллелограмма из свойства средней линии треугольника → A_>1>B_>1>C_>1>D_>1> – параллелограмм (по определению).

Глава 5. Дидактические материалы по теме «Параллельность в пространстве»

Эффективность учебно-воспитательного процесса во многом зависит от умения учащихся самостоятельно получать и применять знания. Проблема методики формирования умений самостоятельной работы учащихся является актуальной для каждого преподавателя математики. Преподавание геометрии дает возможность в наибольшей степени развить у учащихся умение самостоятельной работы, особенно при решении задач. У учащихся необходимо формировать различные способы создания образов и оперирования ими.

Задания на создание геометрических образов используются в трех видах:

создание наглядного образа;

изменение чертежа, заданного в готовом виде, в ходе решения задачи;

мысленное видоизменение чертежа (по воображению) без изменения его исходного вида.

Для того, чтобы развивать у учащихся умение самостоятельно решать геометрические задачи, необходимо иметь дидактические материалы (задачи, упражнения), в которых бы учитывались особенности создания пространственных образов и оперирование ими.

Знание учителем конкретных особенностей создания учеником геометрических образов позволяет ему успешно проводить коррекционную работу, развивать пространственное мышление ученика в нужном направлении.

Далее разработана серия дидактических задач на разновидности «создания образа» по чертежу по теме: «Параллельность в пространстве». Задачи разбиты по типам урока: изучение нового материала; применение знаний, умений и навыков; проверка знаний, умений и навыков. Серия задач содержит задания на перевод словесных данных задачи в графический образ; выделение существенных признаков геометрических понятий; вычленение фигуры из состава чертежа; сравнение фигур (преобразование подобия); рассмотрение фигур чертежа с разных точек зрения; видоизменение пространственного положения, структуры исходного образа.

Все задачи даются в словесной формулировке для того, чтобы выявить у учащихся умение создавать пространственный образ по словесному описанию, уравнивания при этом исходные условия создания образа. К каждой задаче указаны применяемые определения, признаки, свойства геометрических понятий.

Изучение темы «Параллельность в пространстве» можно разделить на 3 части:

параллельность прямых;

параллельность прямой и плоскости;

параллельность плоскостей.

5.1. Уроки изучения нового материала

1.01. Сделайте чертеж: Прямая MP параллельна плоскости α, а прямая МТ пересекает эту плоскость в точке Т (рис. 11).

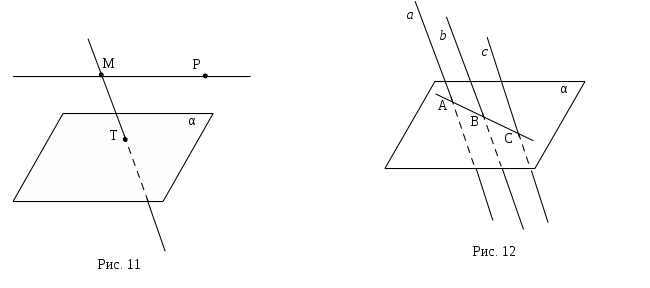
1.02. Сделайте чертеж: Плоскость α пересекает три параллельные прямые a, b и c соответственно в точках А, В и С, принадлежащих одной прямой (рис. 12).

1.03. Сделайте чертеж: Плоскость α пересекает три параллельные прямые a, b и c соответственно в вершинах ∆АВС (рис. 13).

1.04. Нарисуйте куб ABCDA_>1>B_>1>C_>1>D_>1> (рис. 14). 1) Выделите в нем ребро ВВ_>1> и назовите все ребра куба: а) параллельные ему; б) пересекающие его; в) скрещивающиеся с ним. 2) Выделите диагональ AD_>1> грани ADA_>1>D_>1> куба и назовите диагонали граней: а) параллельные AD_>1>; б) пересекающие ее; в) скрещивающиеся с ней. Ответ обоснуйте.

2.01. Сделайте чертеж: Плоскость α проходит через середины сторон АВ и АС треугольника АВС и не содержит вершины А (рис. 15).

2.02. Сделайте чертеж: Прямая MP параллельна плоскости α, а плоскость РМТ пересекает эту плоскость по прямой КТ (рис. 16).

2.03. Сделайте чертеж: Прямая а параллельна каждой из параллельных плоскостей α и β (рис. 17).

2.04. Известно, что прямая m параллельна плоскости α. Параллельна ли эта прямая любой прямой, лежащей в этой плоскости α (рис. 18)? Ответ обоснуйте.

Решение: Пусть прямая а принадлежит плоскости α. Выберем на прямой m произвольно точку М и проведем через нее и прямую а плоскость β (аксиома задания плоскости). Прямые m и а не пересекаются (по условию), тогда они либо параллельны (), либо скрещиваются (). Следовательно, прямыми, параллельными прямой m, будут только те, с помощью которых можно задать плоскость (при участии m).

2.06. Даны две скрещивающиеся прямые а и b (рис. 19). Через каждую точку прямой а проводится прямая, параллельная прямой b. Докажите, что все такие прямые лежат в одной плоскости. Как расположена эта плоскость по отношению к прямой b? Ответ обоснуйте.

Решение: Пусть m || b , , тогда m и а задают плоскость α. Возьмем в плоскости α прямую с || b. По признаку параллельности прямых: с || m, тогда они задают некоторую плоскость β. По условию , значит, они тоже задают плоскость, которая совпадает с α. Следовательно, все прямые, параллельные b и пересекающие а лежат в плоскости, которая в свою очередь параллельна b (по признаку параллельности прямой и плоскости).

2.07. В тетраэдре ABCD точки K, F, N и M – середины ребер соответственно AD, BD, BC и AC (рис. 20). Заполните таблицу, выбрав (обведя в кружок) определенное вами расположение указанных прямой и плоскости: А – пересекаются, Б – параллельны, В – прямая лежит в плоскости, Г – невозможно определить:

	Прямая и плоскость	Взаимное расположение
1	BD и AMN	А Б В Г
2	MN и ABC	А Б В Г
3	KC и DMN	А Б В Г
4	MN и ABD	А Б В Г
5	KF и DMN	А Б В Г
6	FN и KMF	А Б В Г
7	CF и AND	А Б В Г
8	FN и DMK	А Б В Г

3.01. Сделайте чертеж: Плоскости α и β имеют общую прямую а, плоскости α и γ – общую прямую b, а плоскости β и γ – общую прямую с. Прямые а и b параллельны (рис. 21).

3.02. Сделайте чертеж: Плоскости α и β имеют общую прямую а, плоскости α и γ – общую прямую b, а плоскости β и γ параллельны (рис. 22).

3.03. Сделайте чертеж: Сторона ВС треугольника АВС лежит на плоскости α. Через вершину А и точку М – середину стороны АС – проведены соответственно плоскости β и γ, пересекающие плоскость ∆АВС по прямым АК и МТ (рис. 23).

3.04. В тетраэдре РАВС проведено сечение А_>1>В_>1>Р_>1>, параллельное грани АВР. Определите взаимное расположение медиан РЕ и Р_>1>Е_>1> треугольников соответственно АВР и А_>1>В_>1>Р_>1 >(рис. 24).

Решение: Рассмотреть 3 случая взаимного расположения прямых в пространстве: параллельность, пересечение, скрещивание. Итог: РЕ || Р_>1>Е_>1>.

3.05. Постройте сечение треугольной пирамиды РАВС плоскостью, которая проходит через внутреннюю точку К основания АВС и параллельна грани РАВ (рис.25).

Решение: Плоскость сечения проходит через точку К, пересекает грани АРС, СРВ и АВС пирамиды и параллельна АРВ. Следовательно, прямые пересечения с гранями параллельны соответствующим ребрам грани АРВ. Построение следует начать с нижнего основания через известную точку К. Далее через полученные точки пересечения с ребрами АС и ВС провести параллельные прямые АР и ВР соответственно.

5.2. Уроки применения знаний, умений и навыков

1.05. Докажите, что середины ребер АР, СР, ВС и АВ тетраэдра РАВС лежат в одной плоскости. Определите вид фигуры, вершинами которой служат эти точки (модификация задачи, приведенной в пункте 4.2.3).

1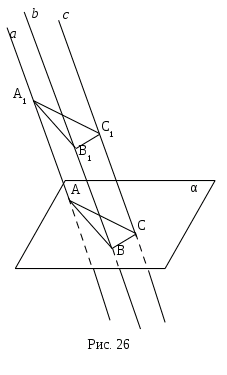.06. Треугольник АВС лежит в плоскости α. Через его вершины проведены параллельные прямые, не лежащие в плоскости α. На них отложены равные отрезки АА_>1>, ВВ_>1> и СС_>1> по одну сторону от α. Докажите, что ∆АВС и ∆А_>1>В_>1>С_>1> равны (рис. 26).

Решение: Используется: способ задания плоскости через параллельные прямые (попарное рассмотрение заданных параллельных прямых); определение параллелограмма (достаточно равенства и параллельности одной пары противолежащих сторон (по условию)); условие равенства треугольников по трем сторонам.

1.07. Прямая АВ пересекает плоскость α. Через концы отрезка АВ и его середину С проведены параллельные прямые, пересекающие плоскость α в точках А_>1>, В_>1> и С_>1>. Рассмотрите случаи: 1) отрезок АВ не пересекает плоскость α (рис. 27а); 2) отрезок АВ пересекает α (рис. 27б). В каждом случае найдите: а) длину отрезка СС_>1>, если: АА_>1> = 7, ВВ_>1> = 5; б) длину отрезка АА_>1>, если ВВ_>1> = 7, СС_>1>= 11.

Решение: а) Точки А, В и С лежат на одной прямой (из пересечения параллельных прямых с прямой АВ и плоскостью α). В_>1>С_>1> = С_>1>А_>1> (по теореме Фалеса). СС_>1> – средняя линия трапеции АА_>1>ВВ_>1>.

б) Сделаем выносной рисунок пересечения АВ и А_>1>В_>1> и проведем через точку В прямую, параллельную прямой А_>1>В_>1 >(рис. 27в).

A_>1>L = 5 (т.к. BL ‌|| A_>1>B_>1>)

CL_>1> – средняя линия в ∆АLВ

1.08. Через вершины А, В, С и D параллелограмма ABCD, расположенного в одном полупространстве относительно плоскости α, точку О пересечения его диагоналей и центроид М треугольника BCD проведены параллельные прямые, которые пересекают данную плоскость α соответственно в точках А_>1>, В_>1>, С_>1>, D_>1>, О_>1>, М_>1>. Найдите ММ_>1>, ОО_>1> и DD_>1>, если АА_>1> = 17, СС_>1> = 5, ВВ_>1> = 15 (рис. 28).

Решение: В задаче используется выделение фигуры из состава чертежа, чертеж рассматривается с разных точек.

АСС_>1>А_>1> – трапеция (параллельные прямые АА_>1> и ВВ_>1> задают плоскость). ОО_>1> – средняя линия трапеции: .

BDD_>1>B_>1> – трапеция: .

ОСС_>1>О_>1> – трапеция.

ОМ = ОС (свойство пересечения медиан треугольника), О_>1>М_>1> = О_>1>С_>1> (аналогично). Следовательно, .

1.09. Докажите, что отрезки, соединяющие середины противолежащих ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам (рис. 29).

Решение: ML || DB, NK || DB (как средние линии треугольников ADB и CDB соответственно), ML = NK. NMLK – параллелограмм (параллельные прямые задают плоскость). Из свойства диагоналей треугольника следует, что отрезки, соединяющие середины противолежащих ребер тетраэдра пересекаются и точкой пересечения делятся пополам. Доказательства для ОР аналогично.

2.08. В правильном тетраэдре DABC, все ребра которого равны 6, точка К лежит на ребре BD так, что DК = 2; точка М лежит на ребре ВС так, что ВМ = 4; точка Р – середина ребра АВ. а) Докажите, что КМ параллельна плоскости ADC. б) Докажите, что РМ не параллельна плоскости ADC. в) Проведите через точку Р прямую, параллельную плоскости ADC и пересекающую ребро DB в точке L. Найдите длину LK. г) Постройте сечение тетраэдра плоскостью, проходящей через точки Р и К параллельно АС (рис.30).

Решение: а) По теореме Фалеса: DC ||КМ. По признаку параллельности прямой и плоскости: (АDC) ||КМ.

б) РМ не параллельна АС (СМ≠АР), следовательно, они пересекаются, так как лежат в одной плоскости. Тогда, РМ не параллельна плоскости ADC.

в) По теореме Фалеса: DL = 3. Тогда, LK = 1.

г) (PKS) – искомое сечение, где PS – средняя линия треугольника АВС.

2.09. Основанием правильной четырехугольной пирамиды PABCD является параллелограмм ABCD. Постройте ее сечение плоскостью, проходящей через АВ и точку К, лежащую в грани: а) ВСР (рис. 31а); б) DCP (рис. 31б). Какая фигура получается в сечении?

В обоих случаях – равнобокая трапеция.

2.10. Даны три попарно скрещивающиеся прямые а, b и с. Всегда ли существует плоскость: а) параллельная каждой из этих прямых (рис. 32а); б) пересекающая каждую из них (рис. 32б)? Ответ обоснуйте и выполните соответствующий рисунок.

Решение: а) Плоскость, параллельная каждой из скрещивающихся прямых существует, если данные прямые лежат в параллельных плоскостях.

б) Плоскость, пересекающая каждую из скрещивающихся прямых, существует, если существует прямая, принадлежащая этой плоскости, которая пересекает каждую из данных прямых.

2.11. Дан куб ABCDA_>1>B_>1>C_>1>D_>1>. Пусть Р_>1>, Р_>2>, Р_>3>, Р_>4>, Р_>5>, Р_>6>, Р_>7>, Р_>8> – середины ребер соответственно АВ, ВВ_>1>, В_>1>А_>1, >А_>1>А, CD, СС_>1>, С_>1>D_>1>, DD_>1>. Каково взаимное положение таких прямых и плоскостей, как: а) Р_>3>Р_>4>_> >и Р_>1>Р_>2>Р_>6> (рис. 33а); б) Р_>7>Р_>8> и Р_>1>Р_>2>Р_>6> (рис. 33б); в) Р_>4>Р_>7> и Р_>1>Р_>2>Р_>5> (рис. 33в); г) Р_>1>Р_>6> и АВ_>1>D (рис. 33г); д) АС и Р_>3>Р_>4>Р_>5> (рис. 33д); е) BD и Р_>3>Р_>4>Р_>5> (рис. 33е)?_> >

Решение: а) Р_>3>Р_>4>_> >|| (Р_>1>Р_>2>Р_>6>) (признак параллельности прямой и плоскости);

б) Р_>7>Р_>8> || (Р_>1>Р_>2>Р_>6>) (признак параллельности прямой и плоскости);

в) Р_>4>Р_>7> (Р_>1>Р_>2>Р_>5>) (при параллельном проектировании Р_>4>Р_>7> на вектор прямая пересечет плоскость Р_>1>Р_>2>Р_>5>);

г) Р_>1>Р_>6> || (АВ_>1>D) (дополним плоскость АВ_>1>D до плоскости АВ_>1>С_>1>D; при параллельном проектировании Р_>1>Р_>6> на вектор прямая будет лежать в плоскости АВ_>1>С_>1>D, следовательно, в этой плоскости существует прямая, параллельная Р_>1>Р_>6>);

д) АС || (Р_>3>Р_>4>Р_>5>) (дополним плоскость Р_>3>Р_>4>Р_>5> до Р_>3>Р_>4>Р_>6>Р_>5>; при параллельном проектировании АС на вектор прямая перейдет в диагональ параллелограмма Р_>3>Р_>4>Р_>6>Р_>5>, следовательно, в этой плоскости существует прямая, параллельная АС);

е) BD Р_>3>Р_>4>Р_>5> (при параллельном проектировании BD на вектор прямая пересечет плоскость Р_>3>Р_>4>Р_>5>).

Дан параллелепипед ABCDA_>1>B_>1>C_>1>D_>1>, P и Q – внутренние точки граней соответственно ABCD и A_>1>B_>1>C_>1>D_>1>. Постройте сечение параллелепипеда плоскостью, проходящей через точки P и Q и параллельной прямой СС_>1> (рис. 34).

Решение: Проведем прямые PР_>1> и QQ_>1>, параллельные СС_>1>. Они задают плоскость, параллельную СС_>1> и проходящую через точки P и Q.

2.13. Дан куб ABCDA_>1>B_>1>C_>1>D_>1>; точка Р – середина ребра АА_>1>. Постройте сечение куба плоскостью, проходящей через точки Р и D_>1> параллельно диагонали АС грани ABCD куба (рис. 35). Найдите периметр сечения, если ребро куба равно 10.

Решение: АС_>1> || (РВ_>1>D_>1>) (в этом можно убедиться, применив свойство диагоналей в параллелограмме A_>1>B_>1>C_>1>D_>1> и теорему Фалеса к треугольнику АА_>1>С_>1>). По теореме Пифагора: . По формуле Герона: .

2.14. Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36).

Решение: Пусть прямые а и b скрещиваются. Выберем на прямой а произвольно точку А и проведем прямую с, параллельную b (через точку, не лежащую на данной прямой можно провести единственную прямую, параллельную данной). Прямые а и с задают плоскость β. По признаку параллельности прямой и плоскости: b || β. Аналогично, проведем прямую d в плоскости α.

α || β (если две пересекающиеся прямые плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны).

3.06. Постройте сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку М основания ABCDE параллельно грани РAB (рис. 37).

Р

Рис. 37

ешение: Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани РАВ, то: а) прямая пересечения плоскости α с плоскостью основания пирамиды должна быть параллельна АВ; б) прямая пересечения α с плоскостью грани РВС – параллельна АР; в) прямая пересечения α с плоскостью РАD – параллельна РА, поэтому проводим: 1) через точку М прямую KF || AB; 2) FH || PA; 3) KR || PB; 4) ML || AP. Пятиугольник HLRKF – искомое сечение. В доказательстве используется признак параллельности прямой и плоскости, признак параллельности плоскостей.

3.07. Точки А, В и С лежат в плоскости α и не лежат на одной прямой. Равные и параллельные отрезки АА_>1>, ВВ_>1> и СС_>1> расположены по одну сторону от плоскости α. Докажите, что (А_>1>В_>1>С_>1>) || (АВС) (рис. 38).

Решение: ВВ_>1>С_>1>С – параллелограмм (из параллельности и равенства ВВ_>1> и СС_>1>), следовательно ВС || В_>1>С_>1>. АВ || А_>1>В_>1> (аналогично). По теореме о параллельности плоскостей (по двум пересекающимся прямым): (А_>1>В_>1>С_>1>) || (АВС).

3.08. Точка В не лежит в плоскости ΔAEC, точки М, К и Р – середины отрезков соответственно АВ, ВС и ВЕ (рис.39). а) Докажите, что плоскости МКР и АЕС параллельны. б) Найдите площадь ΔМКР, если площадь ΔAEC равна 48 см².

Решение: а)Заметим, что ΔAEC и не лежащая в нем точка В образуют тетраэдр ВАСЕ. МК || АС (МК – средняя линия ΔAВC). КР || СЕ (КР – средняя линия ΔВCЕ). По теореме о параллельности плоскостей (через пересекающиеся прямые): (МКР)||(АСЕ).

б) По формуле Герона:

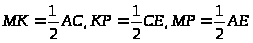, как средние линии соответствующих треугольников. Подставим данные значения в формулу: . Отсюда .

3.09. Три отрезка А_>1>А_>2>, В_>1>В_>2> и С_>1>С_>2>, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А_>1>В_>1>С_>1> и А_>2>В_>2>С_>2> параллельны (рис. 40).

Решение: Каждые две пересекающиеся прямые задают плоскость (через любые две пересекающиеся прямые можно провести плоскость, и притом только одну). Так как точка пересечения делит прямые пополам, то по теореме Фалеса: А_>1>В_>1> || В_>2>А_>2>. Аналогично доказывается параллельность С_>1>В_>1> и С_>2>В_>2>, А_>1>В_>1> и А_>2>В_>2>. По теореме о параллельности плоскостей (через пересекающиеся прямые): (А_>1>В_>1>С_>1>)||(А_>2>В_>2>С_>2>).

3.10. Прямая DF пересекает параллельные плоскости α, β и γ соответственно в точках D, Е и F, при этом DF = 3, ЕF = 9 (рис. 41). Прямая EG пересекает плоскости α и γ соответственно в точках G и Н, при этом EG = 12. Найдите длину GН.

Решение: Прямые EF и ЕH задают плоскость EFH, которая пересекает плоскости α и γ по прямым GD и FH соответственно. ∆GED ~∆HEF (так как GD || FH, ). По свойству преобразования подобия: . Тогда .

3.11. Плоскости α и β пересекаются по прямой с (рис. 42). Через точки А и В, расположенные вне этих плоскостей, проводятся параллельно плоскости β и параллельные между собой прямые АС и BD (), а также – параллельно плоскости α и параллельные между собой прямые АЕ и BF (). Докажите: а) плоскости АСЕ и BDF параллельны; б) плоскости АСЕ и BDF пересекают плоскости α и β по параллельным прямым.

Решение: а) GА || DB, АЕ || FВ по условию. По теореме о параллельности плоскостей (через пересекающиеся прямые): (АСЕ) || (DBF).

б) BF и АЕ задают плоскость, параллельную плоскости α. По свойству параллельных плоскостей: EF || с. Аналогично CD || c. По признаку параллельности прямых: CD || EF.

5.3. Уроки проверки знаний, умений и навыков

Для проверки знаний, умений и навыков разработаны три задачи на выявление типов оперирования пространственными образами: изменение пространственного положения образа (I тип); преобразование структуры образа (II тип); изменение положения и структуры образа одновременно (III тип).

I вариант

1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А_>1>, В_>1>, С_>1> и D_>1>. Докажите, что четырехугольник А_>1>В_>1>С_>1>D_>1 >тоже параллелограмм (рис. 43).

Решение: АА_>1> = DD_>1> = СС_>1> = ВВ_>1> (отрезки параллельных прямых, заключенные между параллельными плоскостями, равны). Попарно параллельные прямые задают параллелограммы (задание плоскости через параллельные прямые), следовательно D_>1>А_>1> || DА || СВ || С_>1>В_>1>. По определению А_>1>В_>1>С_>1>D_>1 >параллелограмм.

2. Докажите, что через любую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой (модификация задачи 2.14).

3. Даны две параллельные плоскости, точка вне этих плоскостей и окружность в одной из этих плоскостей (рис. 44). Через каждую точку Х окружности и данную точку проводится прямая, пересекающая вторую плоскость в некоторой точке Х_>1>. Что представляет собой геометрическое место точек Х_>1>?

Решение: Заметим, что при данном преобразовании расстояние между точками изменяется в одно и тоже число раз (рассмотрение двух пересекающихся прямых и обобщение на множество прямых, обладающих данным свойством). Данный факт и указанный способ преобразования дает основание считать, что геометрическим местом точек Х_>1> является окружность, гомотетичная данной, с коэффициентом гомотетии .

II вариант

1. Докажите, что если четыре прямые, проходящие через точку А, пересекает плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через А, тоже в вершинах параллелограмма (рис. 45).

Решение: Используется метод, подобный задаче 1 I варианта. Указание: Две пересекающиеся прямые задают плоскость – параллелограмм, в котором они являются диагоналями.

2. Точки А, В, С и D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD (пример 9).

3. Даны две параллельные плоскости, пересекающая их прямая и окружность в одной из плоскостей (рис. 46). Через каждую точку Х окружности проводится прямая, параллельная данной прямой и пересекающая вторую плоскость в некоторой точке Х_>1>. Что представляет собой геометрическое место точек Х_>1>?

Решение: Аналогично задаче 3 I варианта, но с применением подобия фигур.

Заключение

Дидактические материалы разрабатывались в соответствии с показателями, характеризующими пространственное мышление. По своему содержанию:

Обеспечивали выявление не только конечного результата выполнения задания, но и процесса его достижения; при этом были довольно краткими, не требовали для своего решения больших временных затрат;

Составлялись на различном графическом материале и предполагали в основном оперирование формой, величиной изображаемых объектов, их пространственным положением.

Использование этого материала позволяет наиболее адекватно характеризовать пространственное мышление по интересующим показателям и вместе с тем сделать эти задания учебными по содержанию. Задания включают все основные типы оперирования, описанные в работе, и составляют определенный ряд, восходящий от простых преобразований с опорой на восприятие ко все более сложным, осуществляемым в уме, что определяло и порядок их предъявления. При этом учитывался характер графической основы, степень ее обобщенности, условности.

Приведенные в курсовой работе материалы показывают, что графические работы в стереометрии играют большую роль в формировании пространственного (образного) мышления учащихся, как компонента сложного интеллектуального образования.

В работе раскрывается содержание, структура и функции пространственного мышления, формируемого на графической основе; описываются дидактические условия составления заданий на выявление наличных возможностей учащихся в создании геометрических образов, их коррекции и развитии в нужном направлении.

Считаю, что поставленные цели и задаче в работе достигнуты.

Библиографический список

Бакин, Р. А. Методика формирования пространственного образа при помощи компьютерной анимации [Текст]: диплом / Р. А. Бакин. – Киров: 2005.

Геометрия [Текст]: учеб. для 10 – 11 кл. сред. шк. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев [и др.]. – 2-ое изд. – М.: Просвещение, 1993. – 207 с.: ил.

Геометрия. 10 кл. [Текст]: учеб. для общеобразоват. Учреждений с углубл. И профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. – М.: Дрофа, 2003. – 224 с.: ил.

Геометрия. 10 кл. [Текст]: задачник для общеобразоват. Учреждений с углубл. И профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. – М.: Дрофа, 2003. – 256 с.: ил.

Зеленина, Н. А. Заключительный этап решения геометрических задач в основной школе [Текст]: диссертация на соискание ученой степени кандидата пед. наук / Н. А. Зеленина. – Киров: 2004. – 158 с.

Повышение эффективности обучения математике в школе [Текст]: кн. Для учителя: из опыта работы / Г. Д, Глейзер. – М.: Просвещение, 1989. – 240 с.

Погорелов, А. В. Геометрия [Текст]: учеб. для 7 – 11 кл. сред. шк. / А. В. Погорелов. – 2-ое изд. - М.: Просвещение, 1991. – 384 с.: ил.

Фридман, Л. М. Наглядность и моделирование в обучения [Текст]: кн. для учителя / Л. М. Фридман. – М.: Знание, 1984. – 80 с.: ил.

Якиманская, И.С. Психологические основы математического образования [Текст]: учебное пособие / И.С. Якиманская. – М.: Издательский центр «Академия», 2004. – 320 с.

1 Термин «представливание» был введен Б. М. Тепловым для описания сложной интеллектуальной деятельности по созданию образов и оперированию ими. В дальнейшем он стал широко использоваться для обозначения процесса преднамеренного, произвольного воспроизведения образа и мысленного оперирования им при решении графических задач.