Разработка управляющей части автомата для сложения двух чисел с плавающей запятой в дополнительном коде с помощью модели Мура
Содержание
Стр.
Задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3
1й раздел. Разработка машинного алгоритма выполнения операций . . . . . . . . . . . . . . . 3
Построение алгоритма операций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Пример выполнения сложения, оценка погрешности . . . . . . . . . . . . . . . . . . . . . . . 5
2й раздел. Разработка ГСА и функциональной схемы ОА . . . . . . . . . . . . . . . . . . . . . . . . 5
2.1. Разработка ГСА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5
2.2. Построение функциональной схемы ОА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3й раздел. Разработка логической схемы управляющей части автомата . . . . . . . . . . . . .8
3.1. Составление таблицы переходов-выходов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8
3.2. Граф автомата Мура . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3. Построение функций возбуждения входов триггеров и логической схемы . . . .10
4й раздел. Оценка времени выполнения микропрограммы . . . . . . . . . . . . . . . . . . . . . . .12
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Задание
Разработать управляющую часть автомата для сложения двух чисел с плавающей запятой в дополнительном коде с помощью модели Мура. Логическую схему реализовать в базисе «И-НЕ» на D-триггерах.
Раздел 1. Разработка машинного алгоритма выполнения операции.
Шаг 1. Сравнить порядки чисел A и B. Вычислить разность порядков чисел. Если p 14, то выдать число A и закончить выполнение. Если p -14, то выдать число B и закончить выполнение. Если 0 p <,то сдвинуть мантиссу числа B на pразрядов вправо. Если 0 >p >,то сдвинуть мантиссу числа А на pразрядов вправо. Порядок ответа равен большему порядку.
Шаг 2. Сложить мантиссы по правилам ДК.
Шаг 3. Проверить условие нормализации Если оно не выполняется, сдвинуть сумму на один разряд вправо, к порядку результата прибавить единицу и перейти к п. 5.
Шаг 4. Циклически проверять условие нормализации Если оно не выполняется, сдвинуть сумму на один разряд влево, от порядка результата отнять единицу.
Шаг 5. Проверить сумматор порядков на переполнением. Если возникло переполнение, установить флаг №1. Если возникла ошибка типа «машинный ноль», установить флаг №2.
Блок-схема имеет следующий вид.
























1

1
1
0
0
0








































































0
1
1

0
1
0
1
1
1
0
0
0
Р
ассмотрим
пример выполнения операции.
П
ри
сдвиге мантиссы числа В получается
погрешность, равная:
Раздел 2. Разработка ГСА и функциональной схемы ОА.
Регистры РгА и РгВ имеют 22 разряда: биты 0-1 – знак числа, биты 2-15 – мантисса, бит 16 – знак порядка, бит 17-21 – порядок. Сумматор мантисс СММ имеет следующую структуру: биты 0-1 – знак, биты 2-15 – мантисса. Сумматор порядков СМП имеет следующую структуру: бит 0 – знак, биты 1-5 – порядок. Используются два одноразрядных регистра в качестве флагов переполнения F1 и машинного нуля F2. Типы слов, используемых в микропрограмме, представлены в таблице.
-
Тип
Слово
Пояснение
I
A(0:21)
Первое слагаемое
I
B(0:21)
Второе слагаемое
L
PrA(0:21)
Регистр А
L
PrB(0:21)
Регистр В
LO
CMM(0:15)
Сумматор мантисс
LO
CMП(0:5)
Сумматор порядков
LO
F1(0)
Флаг переполнения
LO
F2(0)
Флаг машинного нуля
Список микроопераций и логических условий представлен в таблице.
|
Y1 |
РгА:=А |
X1 |
T0&T2&T3&T4 T0&T1 РгА(16)&РгВ(16)&T0 |
Y2 |
РгВ:=В |
X2 |
T0&T2&T3&(T4 T5) T0&T1 РгА(16)&РгВ(16)&T0 |
|
Y3 |
СММ:=0 |
X3 |
T0=0 |
|
Y4 |
F1:=0 |
X4 |
СМП=0 |
|
Y5 |
F2:=0 |
X5 |
Z0&Z1 Z0&Z1 |
|
Y6 |
СМП:=РгА(16:21)+РгВ(16:21)+1 |
X6 |
Z0&Z1 Z0&Z1 |
|
Y7 |
СММ:=РгА(0:15) |
X7 |
F1&T0 |
|
Y8 |
СМП:=РгА(16:21) |
X8 |
F1&T0 |
|
Y9 |
СММ:=РгВ(0:15) |
||
|
Y10 |
СМП:=РгВ(16:21) |
||
|
Y11 |
РгА(0:15):=R1(РгА(0).РгА(0:15)) |
||
|
Y12 |
СМП:=СМП+1 |
||
|
Y13 |
РгВ(0:15):=R1(РгВ(0).РгВ(0:15)) |
||
|
Y14 |
СМП:=СМП-1 |
||
|
Y15 |
СММ:=РгА(0:15)+РгВ(0:15) |
||
|
Y16 |
F1:=СМП(0) |
||
|
Y17 |
СММ:=R1(СММ(0).СММ(0:15)) |
||
|
Y18 |
СММ:=L1(СММ(0:15).0) |
||
|
Y19 |
F1:=1 |
||
|
Y20 |
F2:=1 |
Ti – разряды СМП, Zi – разряды СММ. Условия X5 и X6 соответствуют условиям ив блок-схеме.
ГСА имеет вид:

b0



















1
1
0
0
b1
b2
b3
b4

0
1






1
1


0
0




b5
b6

b7
b8


b9
0
1




0


b10


1


























0
0
1
1
b11
b12
b13
b14
b0
Функциональная схема ОА имеет вид:

0 1

2

15
16

17
21
РгА

0 1

2

15
16

17
21
РгВ

0

1
5
СМП

0 1

2
15
СММ
F1
F2
X4

X3

Y13
Y2


Y10
Y4
Y19
Y20
Y5


Y8

Y11
Y1



Y7



Y9
Y3

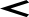

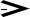
Y18
Y17
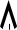
Y12
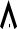
Y14





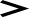
Y16
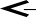
X5, X6
Раздел 3. Разработка логической схемы управляющей части автомата.
Каждое состояния автомата кодируется двоичным числом, равным индексу данного состояния. Например, b12 = 1100. Таблица переходов-выходов имеет вид:
|
Код ABCD |
Исх. сост. |
Входной набор |
Выходной набор |
След. сост. |
|
0000 |
B0 |
-- |
-- |
B1 |
|
0001 |
B1 |
-- |
Y1…Y5 |
B2 |
|
0010 |
B2 |
X1 |
Y6 |
B3 |
|
0010 |
B2 |
X1&X2 |
Y6 |
B4 |
|
0010 |
B2 |
X1&X2&X3&X4 |
Y6 |
B5 |
|
0010 |
B2 |
X1&X2&X3&X4 |
Y6 |
B7 |
|
0010 |
B2 |
X1&X2&X3&X4 |
Y6 |
B6 |
|
0010 |
B2 |
X1&X2&X3&X4 |
Y6 |
B8 |
|
0011 |
B3 |
-- |
Y7 Y8 |
B0 |
|
0100 |
B4 |
-- |
Y9 Y10 |
B0 |
|
0101 |
B5 |
X4 |
Y11 Y12 |
B5 |
|
0101 |
B5 |
X4 |
Y11 Y12 |
B7 |
|
0110 |
B6 |
X4 |
Y13 Y14 |
B6 |
|
0110 |
B6 |
X4 |
Y13 Y14 |
B8 |
|
0111 |
B7 |
-- |
Y10 |
B9 |
|
1000 |
B8 |
-- |
Y8 |
B9 |
|
1001 |
B9 |
X5 |
Y15 Y16 |
B10 |
|
1001 |
B9 |
X5&X6 |
Y15 Y16 |
B11 |
|
1001 |
B9 |
X5&X6&X8 |
Y15 Y16 |
B14 |
|
1001 |
B9 |
X5&X6&X8 |
Y15 Y16 |
B13 |
|
1010 |
B10 |
X7 |
Y17 Y12 |
B12 |
|
1010 |
B10 |
X7 |
Y17 Y12 |
B13 |
|
1011 |
B11 |
X6 |
Y18 Y14 |
B11 |
|
1011 |
B11 |
X6&X8 |
Y18 Y14 |
B13 |
|
1011 |
B11 |
X6&X8 |
Y18 Y14 |
B14 |
|
1100 |
B12 |
-- |
Y19 |
B0 |
|
1101 |
B13 |
-- |
Y4 |
B0 |
|
1110 |
B14 |
-- |
Y4 Y20 |
B0 |
Граф автомата Мура имеет вид:
И
з
таблицы переходов-выходов можно вывести
выражения для выходных сигналов:
И
з
графа автомата Мура выводятся выражения
для сигналов возбуждения триггеров:
Заменим
комбинации ABCD на Bi (например, B12 = A&B&C&D)
и будем минимизировать выражения в
скобках.






Теперь осуществим переход в базис «И-НЕ».
Раздел 4. Оценка времени выполнения микропрограммы.
Временной граф имеет следующий вид.

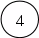
104/256


152/256


108/256

148/256

1/2
1/2



1/5
1/5







4/5
4/5

1/2
1/2





2/3


1/3


1/4



1/4
3/4
3/4
В
графе имеются три цикла: 8-9, 11-12, 17-21. Будем
считать, что количество итераций циклов
8-9 и 11-12 равно 5, а цикла 17-21 – 3. Таким
образом, время выполнения циклов 8-9 и
11-12, имеющих по две вершины, равно 10, а
цикла 17-21 – 6. Теперь рассчитаем вероятности
выполнения каждой вершины, заменив
циклы вершинами: 8-9 – Ц1, 11-12 – Ц2, 17-21 –
Ц3.
Заключение.
В результате проделанной работы построена управляющая часть операционного автомата, который умеет складывать числа с плавающей запятой. В ходе работы приобретены навыки практического решения задач логического проектирования узлов и блоков ЭВМ. Логическая схема автомата, построенная в базисе «И-НЕ», содержит 52 элемента «И-НЕ», один дешифратор и 4 D-триггера. В ходе вычисления оценки времени выполнения микропрограммы было определено, что операция сложения двух чисел с плавающей запятой выполняется в среднем в течение 11 тактов.