Методичні вказівки до виконання розрахунко роботи дослідження за допомогою еом коливань системи з одним ступенем вільності

Міністерство транспорту України

Дніпропетровський державний технічний університет

залізничного транспорту

Кафедра “ Теоретична механіка “

МЕТОДИЧНІ ВКАЗІВКИ

ДО ВИКОНАННЯ РОЗРАХУНКОВОЇ

РОБОТИ “ДОСЛІДЖЕННЯ ЗА ДОПОМОГОЮ

ЕОМ КОЛИВАНЬ СИСТЕМИ З ОДНИМ

СТУПЕНЕМ ВІЛЬНОСТІ ”

Вільні коливання та вимушені коливання точки

при не гармонічному збуренні

Частина ІІ

Укладачі: Л. А. Манашкін

Л. Г. Маслєєва

Д. Б. Астраханцев

А.Ю. Журавльов

Для студентів других курсів

спеціальностей : 7.092107,

7.100501 , 7.092202 , 7.090603,

7.092203 , 7.100502

Дніпропетровськ 2001

Зміст.

Вступ.......................................................................................................

Постановка задачі

Складання диференціального рівняння вимушених коливань механічної системи

Визначення амплітудно- та фозово- частотних характеристик системи

Розкладання функції в ряд Фур’є та визначення параметрів гармонік збурюючої сили

Дослідження вимушених коливань механічної системи.

Визначення (за допомогою ЕОМ) “точного” рішення диференціального рівняння. Аналіз рішення.

Підбір (за допомогою ЕОМ) раціональної кількості гармонік в розкладенні функції .

Побудова аналітичного рішення диференціального рівняння. Підбір раціональної кількості гармонік в розкладенні функції .

Стисла характеристика програми .

Порядок підготовки вихідних даних для виконання розрахунку на ЕОМ.

Схеми механічних систем та розрахункові дані до них.

Перелік літератури.

Вступ.

Друга частина розрахункової роботи по дослідженню коливань системи з одним ступенем вільності включає задачу про дослідження малих вимушених коливань системи тіл з пружними елементами (пружинами) при дії на одне з тіл системи періодичної збурюючої сили негармонічного типу. Рішення задачі зводиться до визначення закону руху системи (в узагальнених координатах) при нульових початкових умовах. При цьому використовується як аналітичний метод рішення задачі, так і метод численного інтегрування диференціального рівняння руху системи з використанням персональної ЕОМ.

Методичні вказівки містять приклад виконання розрахункової роботи. Тут приведені також стисла характеристика програми , що розроблена для рішення вище вказаної задачі за допомогою ЕОМ (автори програми – студенти ф-ту УПП Астраханцев Д. Б., Журавльов А. Ю.), порядок підготовки вихідних даних для виконання на ЕОМ, схеми механічних систем та розрахункові данні до них.

Виконання розрахункової роботи складається із слідуючи етапів:

складання диференціального рівняння руху механічної системи (в узагальнених координатах);

виконання розрахунку на ЕОМ;

визначення аналітичного рішення;

зіставлення результатів розрахунків на ЕОМ і аналітичного рішення.

Постановка задачі

Методику дослідження малих коливань системи при дії негармонічної періодичної сили розглянемо на наступному прикладі.

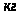Механічна система, що зображена на рис.1, складається з трьох тіл масою = 200, = 0, = 800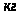, та двох пружин жорсткістю та . Тіло 2 представляє собою суцільній однорідний диск радіуса , а тіло 3 – ступінчатий диск (м; м) з радіусом інерцій м.

Така механічна система має один ступінь вільності.

Нехай рух системи викликається періодичною збурюючи силою , що прикладена до тіла 1 і відноситься до сил “прямокутного” типу (рис. ) з параметрами кН, , де - амплітуда збурюючой сили, і – відповідно її частота та період.

Будемо вважати, що рух системи починається із положення статичної рівноваги.

Розрахунки проведемо у наступному порядку:

За допомогою рівняння Лагранжа ІІ-го роду складемо рівняння руху механічної системи. За узагальнену приймемо координату , яка визначає положення тіла 1 відносно його положення статичної рівноваги: . При цьому коефіцієнт в’язкого опору руху підберемо із умови [ ], щоб вільні коливання системи згасали до 0,1 початкової амплітуди за час , де Т – період власних коливань системи.

Початкові умови задачі візьмемо нульовими, так як рух системи починається із положення статичної рівноваги:

Визначимо (за допомогою ЕОМ) амплітудно-частотну (АЧХ) та фазово-частотну (ФЧХ) характеристики системи.

Розкладемо функцію в ряд Фур’є і визначимо (за допомогою ЕОМ) параметри гармонік в розкладенні.

Визначимо (за допомогою ЕОМ) рішення диференціального рівняння руху механичної системи для випадку, коли збурююча сила задається кусочно-лінійною функцією (“точне” рішення).

Розглянемо також випадок, коли сила задається сумою гармонік. При цьому встановимо, при якому раціональному значенні = функція визначається з 5% точністю (по відношенню до “точного рішення”).

Проаналізуємо характер коливального процесу при різних значеннях <.

Користуючись АЧХ и ФЧХ системи та знайденими параметрами гармонік у розкладенні сили , побудуємо (за принципом суперпозиції) аналітичне рішення диференціального рівняння, руху механічної системи.

При цьому встановимо, при якому раціональне значені аналітичне рішення визначається з 5% точністю по відношенню до “точного” рішення.

Співставлення рішень будемо проводити для контрольного моменту часу , який рекомендується вибирати із умови: .

Складання диференціального рівняння вимушених коливань механічної системи.

Рівняння вимушених коливань заданої механічної системи (рис.1) складемо за допомогою рівняння Лагранжа ІІ-го роду:

, ( )

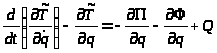де і - узагальнена координата та швидкість, і - кінетична і потенціальна енергії системи відповідно, - функція розсіювання, - узагальнена непотенціальна сила.

Складемо вираз кінетичної енергії системи в її довільному положенні, враховуючи, що тіло 1 виконує поступальний рух, а тіла 2 і 3 – обертальний рух; при цьому швидкості усіх тіл виразимо через узагальнену швидкість :

;

; ; ; ;

= .

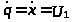У виразі та - моменти інерції тіл 2 і 3 відносно центральної осі.

Позначимо коефіцієнт =, де - зведена маса системи. Тоді:

. ( )

Складемо вираз потенціальної енергії системи: , де - потенціальна енергія сил ваги, а - потенціальна енергія сил пружності, що діють на тіла системи.

Обчислемо потенціальну енергію системи в її довільному положенні як роботу потенціальних сил на переміщенні системи із довільного положення в положення статичної рівноваги:

;

,

де ; ;

тут , - статичні подовження пружин; , - зміна довжини відповідної пружини при відхиленні системи від стану статичної рівноваги; , - подовження пружини в довільному положенні системи.

Врахуємо, що , =, а в стані статичної рівноваги .

Вираз потенціальної енергії системи та її похідної мають вигляд:

;

.

При рівновазі системи () маємо:

, тобто .

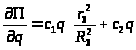Тоді вираз потенціальної енергії системи приймає вигляд:

=, ( )

де =.

Функцію розсіювання будемо вважати залежною від узагальненої швидкості , а її похідну представимо у вигляді:

,

де - коефіцієнт в’язкості (дисипативний коефіцієнт).

До непотенціальних сил, що діють на систему, відноситься тільки збурююча сила , можлива робота якої ; тоді

.

Візьмемо відповідні похідні і складемо рівняння Лагранжа для заданої системи:

; ; 0; ;

=;

;

;

;

, ( )

де і .

Диференціальне рівняння ( ) представляє собою неоднорідне диференціальне рівняння другого порядку відносно узагальненої координати зі сталими коефіцієнтами.

Рішення задачі про дослідження вимушених коливань системи зводиться до рішення цього диференціального рівняння при заданих початкових умовах задачі. Оскільки у розглянутому випадку рух системи починається із стану статичної рівноваги, то початкові умови будуть нульовими:

при : ; . ( )

Як відомо, аналітичне рішення рівняння ( ) складається із суми двох рішень , де - загальне рішення однорідного рівняння, - частинне рішення неоднорідного диференціального рівняння.

Слід зауважити, що рішення в даному випадку (при відповідному підборі коефіцієнта ) практично згасає через . Тоді получається, що при .

Визначимо чисельні значення параметрів системи та коефіцієнтів в рівнянні ( ):

== 0,2 + 0 += 0,2 + 0,056 = 0,256т;

== + 10 = 3,56 + 10 = 13,6кН^.м ^–1;

=7,29с ^–1; =0,861с;

= 0,456кН^.с^.м ^–1;

==0,891с ^–1.

Для перевірки вірності визначення коефіцієнту рекомендується підрахувати значення співмножника в рішенні при =5^.0,861 = 4,31с:

.

Таке значення співмножника (наближене до нуля) в рішенні підтверджує факт, що вільні коливання системи на цей момент часу практично згасають; значить коефіцієнт знайдено вірно.

Визначення амплітудних- та фазово-частотних характеристик системи.

Шляхом виведення, за допомогою ЕОМ, для заданої механічної системи з параметрами = 0,256т; = 13,6кН^.м ^–1; = 0,456кН^.с^.м^–1 получимо (шляхом введення на друкарський пристрій – принтер) амплітудно- та фазово-частотніх характеристики системи та приведемо їх на рис.2 і рис.3 (відповідно).

Розкладання функції F(t) в ряд Фур’є та визначення параметрів гармонік збурюючої сили.

Розкладемо функцію в ряд Фур’є:

, ( )

де - номер гармоніки, а - число гармонік в розкладенні.

Визначимо (за допомогою ЕОМ) параметри гармонік: амплітуди , частоти та початкової фази .

Для заданої сили “прямокутного” типу з параметрами кН, значення параметрів гармонік наведені у табл.1.

Таблиця 1.

Номер гармоніки,	, кН	,	, рад.
1	0,764	2	0
2	0,255	6	0
3	0,153	10	0
4	0,109	14	0
5	0,085	18	0

Дослідження вимушених коливань механічної системи.

Визначення (за допомогою ЕОМ) “точного” рішення диференціального рівняння. Аналіз рішення.

Визначимо за допомогою ЕОМ “точне” рішення диференціального рівняння для випадку, коли сила представлена однією гармонікою (=1). Два графіка функцій для відповідних випадків виводяться на екран ЕОМ. Перед виводом графіків на друкарський пристрій їх треба “промасштабувати”, тобто получити рішення на заданому відрізку інтегрування 0, де рекомендується задавати рівним 810. На рис.4 приведені вказані графіки функцій для заданої механічної системи. Лінія 1 відображає “точне” рішення, а лінія 2 – рішення у випадку = 1 (тобто, коли ).

Із графіків видно, що функції получаються періодичними, тобто рух механічної системи получається періодичним-коливальним. І в першому, і в другому випадку при с процеси получилися явно усталеними, тобто без вільних коливань. Але в “точному” рішенні навіть при явно виражені дві частоти – одна дорівнює (див. лінію 2 для випадку = 1; це частота першої гармоніки), а друга частота – втричі більша (це частота другої гармоніки, див. табл. 1). Рішення, що відповідають лініям 1 і 2, значно відрізняються одне від одного. Наприклад, в момент часу с (=4,31с) значення м (точне рішення) і м (випадок = 1).

Підбір (за допомогою ЕОМ) раціональної кількості гармонік в розкладанні функції .

Визначимо (за допомогою ЕОМ) функції для випадків = 2, 3. На рис. 5, а, б лініями 1 показані графіки для “точного” рішення, а лініями 2 – графіки тих же функцій для випадків = 2; = 3 (відповідно). Із рисунків випливає, що при = 2 графік відрізняється від “точного” рішення, але в значно меншій степені, ніж при = 1. А у випадку = 3 графік практично не відрізняється від “точного” рішення.

Значення відповідних функції при с становлять м (= 2) і м (= 3), тобто при = 2 різниця в значеннях відповідає  = 5,7%, а при = 3 -  = 3,7%.

За одержаним результатам можна зробити висновок, що для отримання рішення з 5% точністю достатньо взяти кількість гармонік = 3 в розкладенні збурюючої сили в ряд Фур’є.

Побудова аналітичного рішення диференціального рівняння. Підбірраціональної кількості гармонік в розкладанні функції .

Побудуємо аналітичне рішення диференціального рівняння ( ), представивши збурюючу силу розкладенням в ряд Фур’є:

.

Врахуемо, що при рішення практично згасає. Тоді для цих моментів часу:

=. ( ).

Відмітимо, що рішення змінюється з частотою , яка є частотою відповідної гармоніки збурюючої сили.

Користуючись даними табл. 1 та графіками АЧХ і ФЧХ системи, визначимо значення коефіцієнта динамічності та зсуву фаз для

гармонік (), а також амплітуди коливань механічної системи , що відповідають цим гармонікам.

Значення знайдених величин зведемо у табл. 2.

Таблиця 2.

Номер гармоніки,	, с-1			, м	, м	, рад
1	2	0,274	1,08	0,0562	0,0607	0,088
2	6	0,823	2,63	0,0188	0,0497	0,076
3	10	1,37	1,06	0,0113	0,012	3,09
4	14	1,92	0,366	0,008	0,0029	3,09
5	18	2,47	0,195	0,006	0,0012	3,09

Із табл. 2 випливає, що визначальними є амплітуди коливань першої () та другої () гармоніки в рішенні , значення цих амплітуд одного порядку; амплітуди третьої гармоніки () майже в 6 разів менша, а четверта () – в 20 разів менша, ніж амплітуди перших двох гармонік. Цим пояснюється факт виділення частот перших двох гармонік функції в рішенні .

Обмежимося значенням = 3 і побудуємо рішення для випадку усталених вимушених коливань (). Оскільки (табл. 1), рішення має вигляд:

=

= (м).

Знайдемо значення узагальненої координати в момент часу с:

 = 4,2%.

Із розрахунків випливає, що визначальними є значення рішення для перших двох гармонік. При = 3 аналітичне рішення добре збігається з “точним” рішенням на ЕОМ (відхилення рішення не перевищує  = 5%).

Стисла характеристика програми .

Если надо – gardemarin@rambler.ru