К некоторым вопросам возникновения вселенной: флуктуации - механизм образования

К некоторым вопросам возникновения вселенной: флуктуации - механизм образования

Проняев Вадим Викторович

"Познайте истину и истина сделает вас свободным".

И. Кант

Аннотация

В работе, в свете последних представлений о возникновении Вселенной, приводятся некоторые математические выкладки, касающиеся механизма образования флуктуаций, которые в представлении автора должны объединить сторонников официальной концепции "Большого Взрыва" и альтернативной концепции "Нулевой Вселенной" с законом У. Кэри.

I. Введение

В данной работе представляется к рассмотрению некоторые абстрактные математические модели, опирающиеся на известные разделы математики и призваны, с единственной целью, - это объединить сторонников официальной концепции "Большого Взрыва" со сторонниками альтернативной концепции "Нулевой Вселенной" с законом У. Кэри. А общее у них одно - это наличие при рассмотрении обеих концепций флуктуаций. Напомним, что по А.Д. Линде утверждающим, что существует множество вселенных, т.е. было множество "Больших Взрывов", а наполняющая вакуум энергия при "содрогании" ("встряхивании"), проявляющаяся в возрастающих флуктуациях и вызывает "Большой Взрыв". Также в концепции "Нулевой Вселенной" с законом У. Кэри рассматриваются случайные флуктуации вакуума, как предвестники будущей материи и энергии. Здесь работа не будет носить спорный или полемический характер, поскольку журналы такие статьи не рассматривают; в данной работе мы "встанем" над "всем этим", т.е. их спорами, а начнем решать несколько другую, но общую для всех проблему, каков же этот механизм образования флуктуаций и вообще из-за чего они появляются (были ли неизбежны они ?) Возможно, эта работа создаст определенное продвижение к конструктивному диалогу представителей той и другой концепций. Здесь несколько отвлечемся и автор постарается ответить на вопрос (по-своему): а почему этот диалог уже давно не носил и не носит конструктивный характер? Уже давно не секрет для многих читателей, что открытое таинственное явление (микроволновое фоновое излучение) американскими исследователями А. Пензиасом и Р. Вильсоном, приписанно к концепции "Большого Взрыва", так вот, это "приписывание" опровергается, если рассматривать модель вращающейся Вселенной [1], предложенную профессором В.П. Селезневым и другими учеными. Кстати, в модели "Нулевой Вселенной" с законами У. Кэри нет тех изъянов, которые присущи концепции "Большого Взрыва". По концепции "Нулевой Вселенной" - материя и энергия - взаимно уничтожающиеся противоположности, при этом 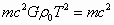, т.е. потенциальная энергия "познаваемой Вселенной" в поле массы m равна ее инертной массе, здесь - гравитационная постоянная, Т - величина с размеренностью времени, обратная постоянная Хаббла, c - скорость света, - средняя плотность вещества во Вселенной. С другими основными положениями концепции "Нулевой Вселенной" можно подробнее ознакомиться в статье профессора М.Л. Арушанова на сайте http://www.sciteclibrary.ru/rus/avtors-p.html (искать по фамилии автора - профессора М.Л. Арушанова). Судя по сообщениям некоторых СМИ, и также интернета, сторонникам альтернативных подходов чрезвычайно трудно получить финансовую поддержку, а опубликовать в научном издании альтернативную статью практически невозможно (в отличии от релятивистов). Напомним, что по сообщениям в интернете, известному астроному Х. Арпу было отказано в наблюдениях крупнейшими американскими обсерваториями, поскольку целью его исследований были поиски фактов против релятивистской космологической модели. Примерно такое положение во всех странах, где научная интелегенция предметно занимается данной проблемой. В России, например, создан научный совет, призванный бороться с лженаукой, в т.ч. с астрологическими бессмыслицами, при этом, неплохо было бы вспомнить, что в стенах самих "храмов науки" порой культивируется еще худшая бессмыслица. Это все к тому, что официальная наука у нас и за границей в той или иной мере монополизировала истину, в том смысле, что существует только концепция "Большого Взрыва", а остальные концепции лженаучны (ошибочные). При такой монополизации в этих "храмах" отсутствует вообще всякая мысль. Зададимся вопросом, а почему во всем официальном научном мире резкое негативное отношение к альтернативным концепциям возникновения Вселенной? Ответ, возможно, удивит многих читателей… говорить… не надо… все-таки скажу. Он сам собой вытекает из следующих источников. Вспомним весьма известную книгу о времени С. Хокинга, разошедшуюся большими тиражами по всем странам мира: вспомните, по ходу чтения С. Хокинг не раз обращается к Богу (божьему промыслу), при этом он пишет, что встречался и не раз с папой И. Павлом II; разговор велся о сотворении мира. А теперь обратимся, к вышеупомянутой, статье М.Л. Арушанова, где сторонники "Большого Взрыва", не имея оснований для выбора между гипергиперсфероидом и гиперболоидом, апеллируют к божественному промыслу (см. стр. 5 этой статьи). Вот и ответ получается сам собой: в концепции "Большого Взрыва" есть "лазейка" для божественного промысла, понятно, другие альтернативные концепции, например, "Нулевая Вселенная" с законом У. Кэри такой "лазейки" не представляет. Но к этим рассуждениям еще вернемся в заключительной части статьи, чтобы не усугублять далее отношений…

Все-таки каков механизм образования флуктуации? В своей статье М. Л. Арушанов приводит высказывания известных ученых о проблеме "больших чисел", т.е. любые два очень больших безразмерных числа встречающиеся в Природе, связаны между собой простым математическим соотношением, в котором коэффициенты определяются порядком величины и далее профессор М.Л. Арушанов приводит несколько соотношений, одно из них , где - энергия, т.е. о том, о чем мы говорили ранее (см. вышеупомянутое соотношение), в смысле масса и потенциальная энергия равны между собой, т.е.

Так вот для этого выражения представим следующий математический аппарат наиболее адекватно отражающий суть процесса, т.е. у нас получится нечто абстрактной математической модели. Эта теория чисел - с числами Бернулли уходящими в бесконечность, для которых справедлива следующая рекуррентная формула, или имеем для нашего случая следующее сравнение, т.е. масса и потенциальная энергия равны между собой.

Также пространства Соболева бесконечного порядка прекрасно подходят для нашего случая, ведь они являются энергетическими пространствами. Напомним, что для этих пространств характерно две задачи - это когда энергетическое пространство задачи Дирихле бесконечного порядка тривиально, т.е. состоит из одного нуля и когда энергетическое пространство уже периодической задачи бесконечного порядка нетривиально, т.е. можно произвести сравнение для вышеуказанного случая, когда масса и потенциальная энергия равны между собой, но об этом более подробно см. следующий раздел. Для удобства чтения в дальнейшем, то состояние, предшествующее началу появления материи для концепции "Нулевой Вселенной" с законом У. Кэри, или концепции "Большого взрыва" - назовем Х - субстанцией.

II Содержание

Здесь, наиболее для проверки Х- субстанции на предмет появления флуктуации - подходит время, или для нашего случая простые числа, которые вместе с временем "уходят" в бесконечность, т.к. они связаны с числами Бернулли.

Начнем с теории чисел. [2] Известно, что числа Бернулли можно представить как , где - простое число; - число классов дивизоров - кругового поля, h0 - множитель числа классов дивизоров - кругового поля. Значит упрощенно выразим для удобства как , где - некоторое соответствующее число.

Далее внесем в эти рассуждения "фактор" регулярности и иррегулярности простых чисел (pc - простое регулярное число, pi - простое иррегулярное число, a- составное число). Запишем соотношения простых чисел (их "формирование") в виде (1), (2), (3), (4),…

Ввиду того, что для pc числители никакого числа Бернулли не делятся на , то например в выражении (2) для "достижения" равенства, введем соответсвующие "остатки" от деления, - это числа b, f и d, т.е. . Понятно, что здесь числа Бернулли могут выбираться достаточно в широком "диапазоне", ведь все их числители не могут делиться на pc, соответсвенно k,b, f и d - тоже будут различны, т.е. имеем осуществления действия принципов гипотезы подстановки- (на конкретном i не будем останавливаться, - это не столь важно), - все эти рассуждения относятся к нестандартному анализу [3]. Другими словами, возможно наблюдать определенное количество случаев подстановки, чего не скажешь о выражении (4), где вообще подобного ничего не имеем, ведь в (4) все числители соответсвующих чисел Бернулли делятся на pi и статистические данные свидетельствуют об этом: выражения (1), (2) и (3) - довольно часто "выполняются", а (4) на известном промежутке нет, т.е. в вероятностном аспекте (1), (2) и (3) предпочтительнее (4). Поэтому при сравнении выражений (2) и (4) между собой и если учесть, что они "участвуют" в дальнейшем "формировании" pc и pi на бесконечность, то имеем подтверждение (очевидное), что количество pc больше количества pi, т.е. q>t (5), или имеем ослабленное предположение гипотезы Зигеля (отношение числа pc ко всем простым числам стремиться к пределу , где e - основание натурального логарифма). Далее произведем своеобразное моделирование; q -пусть будет показатель накопления pc, определяющий динамический фактор ("стремление" к флуктуации), t - показатель накопления pi, определяющий фактор "покоя" ("сдерживающий" фактор), Вn - постоянно меняющийся по определенному закону определяющий фактор средних величин состояния энергии, вокруг которых и происходит флуктуации в Х- субстанции. Потом pc и pi могут быть представлены как показатели определяющие структуру состояния Х- субстанции в смысле каких-то объединенных метрик, вакуумной силы и т.п. b, f, d - "компенсационные" показатели "инертности" процессов в Х - субстанции. Дальнейшие рассуждения будут укладываться в материалистический принцип: единство и борьба противоположностей. В самом деле, в Х- субстанции известные вакуумные силы были "подчинены" одной единой цели - сохранение "покоя" достаточно "хрупкой" Х- субстанции. "Компенсационные" элементы адекватно "реагировали" на динамичное изменение Bn, но с другой стороны в выражении (4) - нет (оно не выполнялось, или выполнялось крайне редко), поэтому-то и постепенно накапливалась эта "погрешность", т.е. (5), проявляющаяся в флуктуациях. Правильность (подтверждение) (5) продемонстрируем на пространствах Соболева бесконечного порядка (б.п.), имеющие особенность, а именно две конкретные задачи - это задача Дирихле, когда (6) и периодическая задача, когда (7), т.е. можно записать , m*=0,1,… где [a,b] некоторый отрезок [4]. Здесь имеем один и тот же интеграл энергии, т.е. , откуда и следует факториальные оценки производных , с вещественными переменными x1,…,xn, также с нормой производной в пространстве Лебега . Такие пространства и есть пространства Соболева б.п. , где - мультииндексы. Далее, если - ограниченная область с гладкой границей, то такие пространства соответствуют задаче Дирихле б.п., обозначают их - 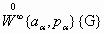, т.е. для них справедливо выражение (6), - вакуумное состояние или состояние, в нашем случае как Х- субстанция, а для перехода в состояние, скажем, флуктуаций, т.е. процессов необходимых для поддержания условного равновесия "покоя" Х- субстанции - это нетривиальное состояние (7), нужно выполнение условий: , Здесь последовательность MN определяет неквазианалитический класс Адамара C{MN}, где MN, N=0,1,…,-числовые последовательности, - выпуклая регуляризация последовательности MN посредством логарифмов. Если 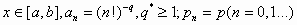где числа и порождают неквазианалитический класс Адамара, если q*>p или см. выражение (5), т.е. то что и нужно в данных представлениях. Также известным гомеоморфизмом , можно моделировать в Х- субстанции появление флуктуаций, так и переход из Х- субстанции к Вселенной с материей и энергией. Понятно, что здесь "покоящаяся" условно Х- субстанция с потенциальной вакуумной энергией и "динамичное" энергетическое пространство образовавшейся Вселенной или флуктуаций "Нулевой Вселенной", причем как отмечалось выше с одним и тем же интегралом энергии, до и после, уже с уточненной работой вакуумных сил, т.е. закон сохранения энергии не нарушается. Вообще в какой-то момент "динамичность выражения (2) по сравнению с "инертностью" выражения (4) оказалась решающей (дошла до критического состояния), т.е. q условно на много стало превышать t с разницей v ,- они стали противоположными (хотя это, понятно, наблюдалось всегда). Просто это стало решающим фактором, например, перед "Большим взрывом" (q-t=vmax); стоит заметить, что отрезок [a,b] может распространяться как на ничтожный размер, так и на астрономический размер. Здесь также vmax можно рассматривать как фактор появления материи и энергии при случайных флуктуациях вблизи квазинулевых энергетических барьеров, где имеется, именно значительный, градиент потенциальной энергии (для "Нулевой Вселенной").

III. Выводы

Причина флуктуаций предположительно кроется в неком неизбежном не всегда "компенсирующем" факторе, направленном на устранение неточности действия некоторой составляющей известной вакуумной силы по "поддержанию" очень "хрупкого" энергетического состояния Х- субстанции, проявляющегося в флуктуациях и как следствие накапливаемой "погрешности", - дальнейшего усиления действия вакуумных сил, флуктуаций и достижения критического состояния с последовавшим взрывом или появлением материи для "Нулевой Вселенной".

Возможно в данных представлениях прообразами материи-антиматерии, частицы-античастицы могут служить показатели q-t; pc-pi в Х- субстанции соответственно (или наоборот).

В общем получается, что Вселенная с материей возникла из "погрешностей", в смысле беспорядка, причем заметим, неизбежного или, как говорит официальная наука, из некого квантового шума в результате просачивания через потенциальный барьер и, кстати, приведенные здесь разделы математики "поддерживают" это.

И последнее, если вернуться к диалогу начатому в I разделе, то заметим, что вопрос сотворения Вселенной - есть и будет самым главным вопросом современности как для науки, так и для религии. При этом трудно себе представить, что будет, если вдруг божественное начало останется ни при чем, а вот этого кто-то очень и очень не хочет.

Автор благодарен профессору Арушанову М.Л. за внимание проявленное к моей работе.

Список литературы

Демин В.Н., Селезнев В.П. Мироздание постигая: М., 1989, с.241-244.

Боревич З.И., Шафаревич И.Р. Теория чисел. М., "Наука", 1964, с.479, 484.

Кановей В.Г. Неразрешимые гипотезы в теории внутренних множеств Э. Нельсона. Ж.//Успехи математических наук, т. 46, вып. 6 (282), 1991, с. 3-47.

Дубинский Ю.А. Пространства Соболева бесконечного порядка. Ж//Успехи математических наук, т.46, вып. 6 (282), 1991, с. 97-128.

Для подготовки данной применялись материалы сети Интернет из общего доступа