Анализ нагруженности рычажного механизма

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ ХАРЬКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ

Кафедра ИКГ

Пояснительная записка

к курсовой работе по

курсу: “Техническая механика”

на тему: "Анализ нагруженности рычажного механизма”

Выполнил:

Ст . группы ПЕА-98-2

Почепцов П.А.

Харьков 1999

СОДЕРЖАНИЕ

Введение…………………………………………………………………..

Задание на курсовую работу…………………………………………

1. Динамический анализ механизма…………………………………..

1.1. Структурный анализ механизма……………………….………

1.2. Кинематический анализ механизма…………………………….

1.3. Силовой анализ механизма……………………………………...

2. Расчёт элементов кинематических пар на прочность….………..

Выводы……………………………………………………………………

Введение

Механикой называется область науки, цель которой – изучение движения и напряжённого состояния элементов машин, строительных конструкций под действием приложенных к ним сил. Принцип работы большинства приборов заключается в том, что реакция элемента на изменение измеряемой величины выражается в механическом перемещении. Непосредственное измерение этих малых перемещений с высокой точностью невозможно без передаточного механизма, увеличивающего неравномерные перемещения чувствительного элемента в равномерное движение и передающего их на устройство.

Механику принято делить на теоретическую и прикладную. В теоретической механике устанавливаются общие закономерности изучаемых объектов вне связи с их конкретными приложениями. Под термином прикладная механика понимают область механики, посвящённую изучению движения и напряжённого состояния реальных технических объектов - конструкций, машин и т. п. С учётом основных закономерностей, установленных в теоретической механике.

Проектирование, изготовление и правильная эксплуатация механизмов предполагают знание физических процессов, положенных в основу работы устройств, применяемых способов расчёта, принципа конструирования узлов и деталей.

Каждый механизм состоит из большого количества деталей, определенным способом соединённых между собой. Длительность их функционирования зависит от конструктивной формы, точности изготовления, материала и других факторов. При создании любых механизмов нужно уделять внимание вопросам технологичности и экономичности.

Исходные данные:

= 40.82 рад./с.

= 45 мм.

= 90 мм.

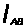= 30 мм.

= 115 мм.

Момент инерции звена: =

Сила полезного сопротивления : Р=5 Н

Масса звена: =, = 2.4 кг. / м.

Масса подзуна С = 1.8 кг

Масса подзуна С = 1.2 кг

1. Динамический анализ механизма.

1.1. Структурный анализ механизма.

Подвижно соединенные между собой части механизма называются звеньями. В механизме различают неподвижное звено и подвижные звенья, которые могут совершать поступательное и вращательное движения.

Структурно-кинематической схемой механизма называется условное изображение взаимосвязанных неподвижных звеньев, выполненное в принятом стандартном масштабе длин с принятием условных обозначений кинематических пар.

На рисунке представлен механизм шарнирного четырехзвенника, тип которого определяется количеством, формой и взаимным расположением звеньев.

Перечень звеньев механизма:

1. – стояк; 2. – шатун; 3,5 – ползун; 4. – коромысло

Перечень кинематических пар:

1–2 – кинематическая пара 5-го класса, вращающаяся;

2–4 – кинематическая пара 5-го класса, вращающаяся;

2–3 – кинематическая пара 5-го класса, вращающаяся;

4-5 - кинематическая пара 5-го класса, вращающаяся;

Перечень структурных групп:

Механизм, что исследуется, засчитывают к механизмам 2-го

класса.

Определение ступени движения механизма:

Ступень движения механизма определим по уравнению Чебышева

W= - -

где – количество движущихся звеньев механизма;

, – количество кинематических пар 4-го та 5-го классов.

Для механизма, что исследуется, количество движущихся звеньев =5, кинематических пар 5-го класса =7, кинематические пары 4-го класса отсутствуют. Имеем:

W=35–27=1

Для работы механизму необходима только одно ведущее звено, так как ступень движимости равна единице.

1.2. Кинематический анализ механизма.

1.2.1. Определение скоростей точек и звеньев механизма.

Планом скоростей называется диаграмма, на которой изображены векторы скоростей точек плоского механизма.

Для определения скоростей точек и звеньев механизма воспользуемся методом планов скоростей. Построение планов скоростей начинаем с скорости точки B ведущего звена АB. Учитывая, что скорость ведущего звена  известна, скорость точки B определим из уравнения

V=LAB

где LAB – длина звена АB, м.

VB= 40,820,03м. = 1,22 м/с

Вектор VB направлен перпендикулярно звену АB.

От произвольно взятой точки P ( полюса плану скоростей) отложим вектор произвольной длины, что численно равен вектору скорости. VB

Масштабный коэффициент скорости  определим из уравнения

V=VB/PVB

где VB – скорость точки, м / с;

PVB – длина вектора, мм.

= 1,22/100= 0,01 м/с.мм.

Для определения скорости точки C воспользуемся условием её принадлежности звену – ВС.Скорость точки С определяется из векторного уравнения:

VC=VB+VCB

В этой векторной сумме неизвестно второе слагаемое. Известно, только ,что линия действия этого вектора перпендикулярна к звену BC. Проводим соответствующую линию на плане скоростей через точку в. Второе ур-ние для скорости точки С составляем с учётом неподвижной опоры-1:

VC=V1+VC1

Скорость V1 равна нулю. Скорость VC1 направлена вдоль направления движения ползуна. На плане этой скорости соответствует линия ,параллельная направляющей. На пересечении этой линии и линии перпендикулярной звену BC находится точка с. Численно скорость VC равняется

VC=PVCV

где PVC – длина вектора, мм.

VC = 120 0,01 = 1,2 м./с.

Для нахождения скорости точки Е воспользуемся тем ,что она принадлежит звену ВС и делит звено на равные отрезки. Для векторов скоростей справедливо :

LBC/LEC=bc/ec ,

где LEC-длина звена EC,

ec-длина вектора на плане скоростей.

На плане скоростей точка е находится на отрезке вс деля его в соотношении LBC/LEC. Вектор ,соединяющий полюс с точкой е,соответствует скорости VE ,численное значение которой равно

VE=PvEV=97,50,01=0,97 м./с.

Определим скорость точки D. Точка D принадлежит звену DE.

Это даёт векторное ур-ние

VD=VE+VDE

В этой векторной сумме неизвестно второе слагаемое.Известно только ,что линия действия этого вектора перпендикулярна звену ED. Проводим соответствующую линию на плане скоростей через точку е. Второе ур-ние составляем относительно неподвижнойопоры:

VD=V1+VD1

V1=0.

VD1-направлена вдоль движения ползуна. На плане этой скорости соответствует линия ,параллельная направляющей. На пересечении это линии и линии перпендикулярной звену DE находится точка d. Численно скорость VD равна :

VD = PVDV=790,01=0,79 м/с

Построеный план скоростей позволяет определять не только скорости всех точек механизма, а так же величину и направление скоростей звеньев.Определяем угловые скорости звена ЕD и ВС.

CB=VCB/LCB

где CB – угловая скорость движения звена CB

VCB-скорость движения точки С относительно В

VCB=cbV=540,01 = 0,54 м./с.

CB=0,54/0,09=6 рад/с

Аналогично для звена DE :

DE=VDE/LDE=Vde/LDE

DE=1070,01/0,115=9,3 рад/с

Направление угловой скорости CB определяем путём перенесения вектора VCB в точку c на схеме механизма. Направление этого вектора указывает на направление движения звена СВ около точки В. Аналогично и для звена DE.

1.2.2. Определение ускорений точек и звеньев механизма.

Для определения ускорений точек и звеньев механизма воспользуемся методом планов ускорений.

Построение планов ускорений начинаем с ведущего звена механизма. Поскольку AB = const , то :

aB=²LAB=40,82²0,03=49,98 м/с²

Ускорение точки B направлено вдоль звена АB к центру её вращения. С любой произвольной точки PA отложим вектор произвольной длины, что численно равен вектору ускорения точки B.Масштабный коэффициент ускорений найдём таким образом:

_>A>=a_>B>/P_>AB>=49,98/99=0,5 м/ммс²

где P_>AB> – длина вектора, мм.

Для определения ускорения точки C запишем ур-ние плоско-параллельного движения звена ВС :

a_>E>=a_>B>+aⁿ_>CB>+a^_>CB>

где aⁿ_>CB> – центростремительная составляющая ускорения относительно движения точки С около точки В;

a^_>CB> – касательная составляющая ускорения точки С относительно точки В.

aⁿ_>CB>=V²_>CB>/L_>CB>=(_>V>cb)²/ L_>CB>=(0,0154)²/0,09=3,24 м/с²

Длина соответствующего вектора на плане :

n_>CB>=aⁿ_>CB>/_>A>=3,24/0,5=6,48 мм

На плане ускорений из точки b` проводим вектор n_>CB> , параллельный звену BC и направленный от С к В , а из конца этого вектора - перпендикуляр в обе стороны , который соответствует направлению касательного ускорения a^_>CB>.Для исследования движения ползуна необходимо использовать точку 1 на неподвижной направляющей. Тогда ур-ние движения точки С :

a_>C>=a_>1>+a_>C1>

На плане ускорений точка 1 находится в полюсе т.к. она неподвижная

Про a_>C1> известно , что оно параллельно направляющей. Поэтому на плане через полюс проводится горизонтальная линия.На пересечении этой линии и линии перпендикулярной звену ВС находится точка с`.

Численное значение ускорения :

a_>C>=_>A>P_>a>_>c`>

где P_>a>_>c`>_>>- длина вектора , соединяющего полюс с точкой с`.

a_>C>=320,5=16 м/с²

Точку е` можно найти на отрезке b`c` соответственно с соотношением :

b`e`/b`c`=L_>BE>/L_>BC>

из которого b`e`=b`c`L_>BE>/L_>BC>=86,5/2=43,2 мм

Значение ускорения a_>E> определяется по формуле :

a_>E>=_>A>P_>Ae>=0,559=29,5 м/с²

Для нахождения ускорения точки D запишем :

a_>D>=a_>E>+aⁿ_>DE>+a^_>DE>

Центростремительное ускорение aⁿ_>DE> найдём таким образом :

aⁿ_>DE>=V²_>DE>/L_>DE>=(_>V>de)²/L_>DE>=(1070,01)²/0,115=9,9 м/с²

Длина соответствующего вектора на плане ускорений :

n_>DE>=aⁿ_>DE>/_>A>=9,9/0,5=19,8 мм

На плане ускорений из точки е` проводим вектор n_>DE> ,параллельный звену DE и направленный от D к E , а из конца этого вектора перпендикуляр в обе стороны , который соответствует направлению касательного ускорения a^_>DE> .

Ур-ние движения точки D :

a_>D>=a_>1>+a_>D1>

Т.к. точка 1-неподвижна ,то на плане скоростей точка находится в полюсе. Ускорение a_>D1> направлено параллельно направляющей , поэтому на плане проводится вертикальная линия . На пересечении её илинии перпендикулярной звену DE НАХОДИТСЯ ТОЧКА d`.Численно ускорение d` равно :

a_>D>=_>A>P_>Ad`>=410,5=20,5 м/с²

Ускорения середины звеньев равны :

a_>S1>=49,90,5=24,75 м/с²

a_>S2>=29,5 м/с²

a_>S4>=23 м/с²

Угловое ускорение звена BC определяем из соотношения :

=a^_>CB>/L_>CB>=_>A>_>BC>/L_>CB>

где _>BC> -длина вектора a^_>CB> на плане ускорений

_>CB>=86,50,5/0,09=480 1/с²

Если вектор _>BC> условно перенести в точку С ,можно найти направление _>CB>,они направлены в одну сторону.

Для звена DE имеем :

_>DE>= a^_>DE>/L_>DE>=_>A>_>DE>/L_>DE>=360,5/0,115=156 1/c²

Его направление находим условным переносомвектора _>DE> в точку D.

1.3 Силовой анализ механизма

Метод силового анализа механизма с использованием сил инерции и установления динамического уравнения носит название кинестатического расчета. Этот расчет основан на принципе д'Аламбера, который предполагает, что в общем случае все силы инерции звена, совершающие сложное движение, могут быть сведены к главной векторной силе инерции и к паре сил инерции , которая определяется по формулам

;

где m – масса звена;

– ускорение центра масс;

– момент инерции звена относительно оси проходящей через центр масс звена;

E – угловое ускорение звена.

Сила инерции звена направлена противоположно ускорению, а момент инерции в сторону обратную направлению углового ускорения.

Делим механизм на группы Ассура.

Нам дано: g = 2,4 кг/м; а масса звена равна m = gl, тогда:

m_>AB>= 0,032,4 =0,072 кг. P_>1>=0,0729,8=0,705 H

m_>BC>= 0,092,4 = 0,216 кг. P_>2>=0,2169,8=2,116 H

m_>DE>= 0,1152,4 = 0,276 кг. P_>3>=1,89,8=17,64 H

P_>4>=0,2769,8=2,704 H

P_>5>=1,29,8=11,76 H

Момент инерции стержня определяется по формуле

;

I_>BC>=0,2160,09²/12=0,00014 кгм²

I_>ED>=0,2760,115²/12=0,0003 кгм²

Сила инерции определяется:

F_>u1>=0,07224,75=1,78 H

F_>u2>=29,50,216=6,37 H

F_>u4>=230,276=6,348 H

Момент инерции определяем как

M_>u2>=I_>BC>_>BC>=0,00014480=0,067 H

M_>u4>=I_>ED>_>ED>=0,0003156=0,046 H

Для нахождения реакций в кинематических парах разбиваем механизм на группы Ассура. Начнем с группы звеньев наиболеее удаленной от ведущего звена.Это группа 4-5.Шарнирные связи заменяем реакциями R_>E> и R_>5>. Ракция в шарнире Е неизвестна ни по модулю ни по направлению, поэтому раскладываем её на составляющие :R_>E>ⁿ-по направлению оси и R_>E>^-перпендикулярно ей. Реакция в шарнире D неизвестна по модулю и направлена перпендикулярно оси OY.

M_>D>=M_>4>+F_>i4>h_>i4>-P_>4>H_>4>-R_>E>^L_>DE>=0

Отсюда :

R_>E>^= M_>4>+F_>i4>h_>i4>-P_>4>H4/L_>DE>=0,046+6,3480,047-2,7040,029/0,115=2,313 Н

Для определения R_>E>ⁿ и R_>5> рассмотрим ур-ние равновесия 2-х поводковой группы :

R_>E>ⁿ+R_>E>^+F_>i4>+F_>i5>+R_>5>+P_>4>+P_>5>+Pпс=0

Согласно с этим векторным ур-нием строится замкнутый силовой многоугольник. На чертеже выбирается полюс и от него проводим вектор произвольной длины согласно направлению одной из сил. Масштабный коэффицент вычисляется по формуле :

_>F>=F_>i5>/P_>F>F_>i5>=24,6/120=0,2

где P_>F>F_>i5>-длина соответствующего вектора на плане сил.

После этого к вектору F_>i5> в произвольном порядке достраиваем остальные слагаемые векторного ур-ния, пересчитывая длины векторов через масштабный коэффицент. Используя план сил определим модули сил R_>E> и R_>5>.

R_>E>=1220,2=24,4 H

R_>5>=530,2=10,6

Для определения реакций в шарнирах B и C рассмотрим группу 2-3.

Шарнирные связи заменяются реакциями R_>B> и R_>3>. Реакция в шарнире Е известна из рассматриваемойй ранее кинематической пары и берется с противоположным направлением. Реакция в шарнире В неизвестна, поэтому раскладываем её на составляющие R_>B>^ и R_>B>ⁿ.

Реакция в шарнире С направлена перпендикулярно оси OX.

Сумма моментов относительно С равна нулю , отсюда

R_>B>^=(R_>E>h_>R>+F_>i2>-M_>2>-P_>2>H_>2>)/L_>BC>=6,015 H

Для определения R_>B>ⁿ и R_>3> рассмотрим ур-ние :

R_>B>^+R_>B>ⁿ+R_>E>+F_>i2>+F_>i3>+R_>3>+P_>2>+P_>1>=0

_>F>= F_>i3>/P_>F> F_>i3>=28,8/144=0,2 Н/мм

Используя план сил определим модули сил R_>B>_>>и R_>3>:

R_>B>=1210,2=24,2 H

R_>3>=590,2=11,8 H

Ведущее звено.

Запишем ур-ние моментов относительно точки В :

M=-R_>A>^L_>AB>+P_>1>H_>1>=0 R_>A>^=P_>1>H_>1>/L_>AB>=0,19 H

Для определения R_>A>ⁿ и P_>ур> запишем векторное ур-ние равновесия сил

R_>A>ⁿ+ R_>A>^+ R_>B>+ F_>i1>+ P_>1>+ P_>ур>=0

Согласно с этим векторным ур-нием строится замкнутый силовой многоугольник. Масштабный коэффицент вычисляется по формуле :

_>F>= R_>B>/ P_>F> R_>B>=46,4/90=0,5 Н/мм

Используя план сил определим модули сил R_>A>_>>и P_>ур>:

R_>A>=280,5=14 H

P_>ур>=420,5=21 H

Результаты измерений сведены в таблицах

точка \ пар-тр	B	C	E	D	S_>1>	S_>2>	S_>4>	CB	DE
V,м/с	1,22	1,2	0,97	0,79	0,61	0,71	0,99
a,м/с²	49,98	16	29,5	20,5	24,75	29,5	23
,1/С²								480	156

ЗВЕНЬЯ \ ПАРАМЕТР	1	2	3	4	5
m, кг	0,072	0,216	1,8	0,276	1,2
I, кгм²		0,00014		0,0003
F_>u>, Н	1,78	6,37		6,348
M_>u>, Нм		0,067		0,046

точки \ реакции	A	B	C	D	E
R^, H	0,19	6,015			2,313
Rⁿ, H	14	23,4			22
R, H	14	24,2	11,8	1	22,2

2. Расчет элементов кинематических пар на прочность.

2.1. Определение внешних сил, действующих на звенья.

В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции кинематических пар R, силы веса и полезного сопротивления.

Под действием внешних сил звенья плоского механизма испытывают сложные деформации. Для заданного механизма преобладающим видом совместных деформаций является изгиб с растяжением – сжатием. Рассмотрим группу 4-5 как груз на двух опорах , нагруженных соответствующими силами, т.е. выбираем расчетную схему.

Расчетная схема.

Из ур-ния суммы моментов относительно точки Е найдем опорную реакцию К_>Д> :

M_>E>=M_>4>+(P_>4>^-F_>i4>^)L_>DE>/2 + (-P_>пс>^-F_>i5>^+R_>5>^+P_>5>^)L_>DE>-K_>D>L_>DE>=0

Отсюда найдем K_>D>:

K_>D>=(0,046+(2,704-5,383)0,057+(-2,5-12,3+10,392+5,88)0,115)/0,115=

= -0,083 H

Из ур-ния суммы моментов относительно D найдем опорную реакцию К_>E>:

M_>D>=(K_>E>R_>E>^)L_>DE>-M_>4>+(P_>4>^-F_>i4>^)L_>DE>/2

Отсюда найдем К_>E>:

К_>E>=(-0,1152,313+0,046+(5,383-1,473)0,0575)/0,115=0,043 H

Из ур-ния N_>Z>=0 найдём опорную реакцию Н_>Е>:

H_>E>=R_>E>ⁿ+P_>1>ⁿ-F_>i4>ⁿ+P_>5>ⁿ-F_>i5>ⁿ-P_>пс>ⁿ-R_>5>ⁿ=

=22+2,268-3,364+10,184-21,304-4,33-6= -0,546

Построение эпюры N_>Z>.

Используя метод сечений для нормальной суммы N_>Z>_>>получаем такие ур-ния :

N_>Z>¹=R_>5>ⁿ+P_>пс>ⁿ+F_>i5>ⁿ-P_>5>ⁿ=6+4,33+21,304-10,18=21,454 H

N_>Z>²=H_>E>+R_>e>ⁿ=22,546 H

По этим ур-ниям строим эпюру N_>Z>

2.4. Построение эпюры Q_>y>.

Для поперечной силы Q_>y> ,используя метод сечений записываются такие аналитические ур-ния :

Q_>y>¹=-K_>D>+F_>i5>^+P_>пс>^-P_>5>^-R_>5>^=-0,083+12,3+2,5-5,88-10,392=-1,56 H

Q_>y>²=R_>E>^-K_>E>=2,313-0,043=2,27 H

По этим ур-ниям строим эпюру Q_>y>.

Построение эпюры M_>x>.

На участках 1 и 2 записываем ур-ния для изгибающего момента :

M_>x>¹=(F_>i5>^+P_>пс>-P_>5>^-R_>5>^-K_>D>)z_>1> 0Z_>1>0,0575

M_>x>¹=0;-0,089

M_>x>²=-(R_>E>^+K_>E>)Z_>2> 0Z_>2>0,0575

M_>x>²={0;-0,135}

По этим ур-ниям строим эпюру M_>x>, из неё видно ,что опасное сечение проходит через точку S_>4> , потомучто в ней изгибающий момент M_>x> и нормальная сила-максимальны :

M_>max>=0,135 Нм N_>max>=22,5 H

2.6.Подбор сечения.

Из условия _>max>=M_>x>^max/W_>x>[] находим

W_>x>=0,1351000/1200=0,1125 см

Находим по сортаменту размер двутавра

Круглое сечение W_>x>=d³0,1d³

d=1,125 см

Прямоугольное сечение W_>x>=bh²/6=4b³/6

b=0,41 см

h=0,82 см

Материал звеньев СТ 3 []=120 МПа

ВЫВОДЫ.

Цель курсового проектирования – закрепление теоретических знаний, что были получены во время изучения курса “Техническая механика”, ознакомление с методами проектирования механизмов. Первый этап конструирования любого механизма – это составление его кинематической схемы, расчет кинематических параметров, определение нагрузки различных деталей и энергетических характеристик механизма в целом.

Выполняя курсовой проект по технической механике, овладел методами определения кинематических параметров механизмов, оценки сил, что действуют на отдельные звенья механизма, научился творчески оценивать сконструированный механизм с точки зрения его назначения – обеспечивать необходимые параметры движения звена.