Разработка управленческих решений (работа 6)
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Контрольно-курсовая работа по дисциплине
«РАЗРАБОТКА УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ»
Содержание
1. Метод экспертных оценок
2. Принятие решения по нескольким критериальным показателям
3. Определение оптимальной очередности расстановки оборудования на серийном участке производства
4. Оптимизация календарного планирования серийно-поточных линий и предметно-замкнутых участков
5. Оптимизация обработки разномаршрутных партий деталей при последовательном их виде движения
1. Метод экспертных оценок
Задание. На основе двух модификаций метода экспертных оценок (простого ранжирования и попарного сравнения), требуется принять управленческое решение по определению важнейших факторов, влияющих на уровень успеваемости группы.
Решить эту задачу мы можем двумя методами: методом простого ранжирования и методом попарного сравнения.
1.1. Метод простого ранжирования
Этот метод используется в условиях неопределенности принятия решений, базируется на опросе мнений специалистов. Суть метода заключается в том, что группе специалистов предлагается высказать свое мнение по значимости предложенных показателей, свойств, проблем. Высказанные мнения подвергаются соответствующей обработке, в результате чего они ранжируются по степени важности. Полученный результат принимается за основу принятия управленческого решения, либо используется для последующих исследований.
Алгоритм решения задачи включает следующие этапы:
Разработка критерия решения задачи.
Обработка мнений экспертов и определение коэффициента значимости.
Определение коэффициента конкордации W, характеризующего степень согласованности экспертов.
Исходные данные для решения задачи приведены в таблице 1.
Таблица 1
Исходные данные:
|
№№ |
№№ экспертов, ранги значимости рассмотренных факторов |
|||||
|
факторов |
1 |
7 |
8 |
9 |
10 |
11 |
|
X>1> |
1 |
3 |
5 |
6 |
7 |
4 |
|
X>2> |
1 |
5 |
8 |
1 |
2 |
3 |
|
X>3> |
2 |
3 |
3 |
6 |
5 |
4 |
|
X>4> |
4 |
1 |
1 |
2 |
2 |
1 |
|
X>5> |
4 |
4 |
3 |
1 |
6 |
3 |
|
X>6> |
4 |
4 |
5 |
3 |
4 |
7 |
|
X>7> |
3 |
5 |
3 |
4 |
7 |
1 |
|
X>8> |
5 |
6 |
3 |
4 |
8 |
7 |
Этап 1. В качестве критерия управленческого решения выступает успеваемость, которую можно оценить показателем среднего балла за сессию.
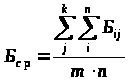
Б>ij> - оценка, полученная i-м студентом на i-м экзамене
m - число студентов в группе
n - количество экзаменов за сессию
Для того чтобы улучшить значение рассматриваемого критерия, необходимо определить факторы, влияющие на его величину
Б>ср> = f (x>1 >, x>2 , >, х>n>)
Можно выделить следующие факторы (их значения приведены в табл.2):
уровень преподавания;
уровень организации учебного процесса;
дисциплинированность студента;
качество школьной подготовки;
бытовые условия;
семейное положение;
материальное положение;
возраст;
Таблица 2
|
№№ факторов |
№№ экспертов |
|||||
|
1 |
7 |
8 |
9 |
10 |
11 |
|
|
X>1> |
1 |
3 |
5 |
6 |
7 |
4 |
|
X>2> |
1 |
5 |
8 |
1 |
2 |
3 |
|
X>3> |
2 |
3 |
3 |
6 |
5 |
4 |
|
X>4> |
4 |
1 |
1 |
2 |
2 |
1 |
|
X>5> |
4 |
4 |
3 |
1 |
6 |
3 |
|
X>6> |
4 |
4 |
5 |
3 |
4 |
7 |
|
X>7> |
3 |
5 |
3 |
4 |
7 |
1 |
|
X>8> |
5 |
6 |
3 |
4 |
8 |
7 |
|
|
24 |
31 |
31 |
27 |
41 |
30 |
Метод экспертных оценок позволяет проранжировать факторы по степени важности и выбрать важнейшие из них.
Каждый эксперт, используя свой опыт, проставляет ранги значимости рассмотренных факторов. Наиболее значимым присваивается ранг 1, менее значимому ранг 2 и т.д. Если же, по мнению эксперта, факторы имеют одинаковую значимость, им присваивается одинаковый ранг, при этом эти ранги называются связанными рангами.
Этап 2. Производится обработка мнений экспертов. Если были введены связанные ранги, то необходимо, для обеспечения условий сопоставимости оценки, произвести их пересчет, который выполняется таким образом, чтобы пересчитанных связанных рангов равнялась натурального ряда числа чисел, равных числу рассмотренных факторов (см. табл. 3).
Таблица 3
Матрица пересчитанных рангов
|
1 |
7 |
8 |
9 |
10 |
11 |
Б |
k>t> |
|
|
х>1> |
1,5 |
2,5 |
6,5 |
7,5 |
6,5 |
5,5 |
30 |
0,138 |
|
х>2> |
1,5 |
6,5 |
8 |
1,5 |
1,5 |
3,5 |
22,5 |
0,104 |
|
х>3> |
3 |
2,5 |
3,75 |
7,5 |
4 |
5,5 |
26,25 |
0,121 |
|
х>4> |
6 |
1 |
1 |
3 |
1,5 |
1,5 |
14,2 |
0,065 |
|
х>5> |
6 |
4,5 |
3,75 |
1,5 |
5 |
3,5 |
24,25 |
0,112 |
|
х>6> |
6 |
4,5 |
6,5 |
4 |
3 |
7,5 |
31,5 |
0,145 |
|
х>7> |
4 |
6,5 |
3,75 |
5,5 |
6,5 |
1,5 |
27,75 |
0,128 |
|
х>8> |
8 |
8 |
3,75 |
5,5 |
8 |
7,5 |
40,75 |
0,188 |
|
|
36 |
36 |
36 |
36 |
36 |
36 |
217,2 |
- |
После пересчета связанных рангов определяется сумма баллов по строкам матрицы и определяется коэффициент значимости.
Исходя из суммы баллов и
коэффициента значимости можно
проранжировать рассмотренные факторы
по степени важности: чем меньше сумма
баллов (больше коэффициент значимости),
тем важнее фактор. Средний балл за сессию
будут выступать как функция: Б>ср>
=
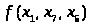 .
.
Итак, мы получили следующую последовательность:
х>4 >
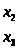
х>8>
х>6>
х>5>
х>7>
х>1>
х>8>
х>6>
х>5>
х>7>
х>1>
Вывод: в данном примере наиболее существенными являются факторы х>1>, х>7>, х>5>.
Полученный результат можно принять за основу и использовать в дальнейших исследованиях, исходя из уровня величины коэффициента конкордации W.
Этап 3. Величина этого коэффициента изменяется в пределах от 0 до 1, при чем, если коэффициент приобретает значение 0, то мнение всех экспертов совершенно различно, если 1 - то мнения абсолютно одинаковы.
Обычно считается, что если величина коэффициента конкордации превышает 0,5, то полученный результат можно взять за основу и использовать для последующих решений (приемлемая согласованность).
Если его значение менее 0,5, то необходимо повторить процесс, улучшить состав экспертов.
Коэффициент конкордации рассчитывается по следующей зависимости:
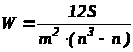 ;
;
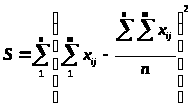
При наличии связанных рангов коэффициент W рассчитывается по формуле:
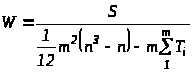 ;
;
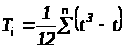
S – отклонение среднего ранга j-го признака;
n – количество экспертов;
m – число экспертов;
t - число связанных рангов, введенных i-м экспертом;
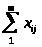 - сумма рангов значимости,
введенных i-м
экспертом (из исходных данных);
- сумма рангов значимости,
введенных i-м
экспертом (из исходных данных);
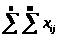 - общая сумма рангов,
введенных экспертами.
- общая сумма рангов,
введенных экспертами.
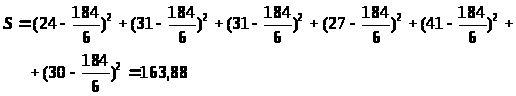
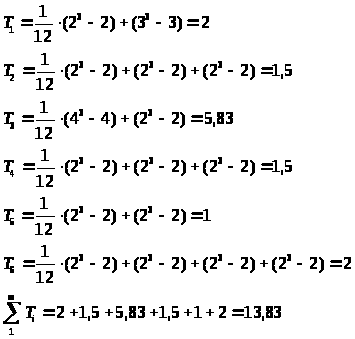
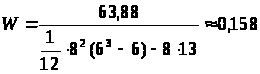
Вывод: коэффициент конкордации W<0,5, а следовательно, согласованность в оценках экспертов отсутствует.
Недостаток рассмотренного метода заключается в том, что эксперту при ранжировании факторов достаточно сложно ориентироваться в общей их совокупности. Эти недостатки исключает другая модификация метода экспертных оценок - это метод попарного сравнения.
1.2. Метод попарного сравнения
Суть метода состоит в том, что экспертам предлагается сравнить факторы между собой, при этом используется следующая шкала:
1. если фактор x>i> более значим, чем фактор x>j> , то это обозначается 1.
x>i>> >> >x>j> [1]
2. если фактор x>i> менее значим, чем фактор x>j> , то это обозначается 0.
x>i>> >> >x>j> [0]
3. если фактор x>i> имеет одинаковую значимость с фактором x>j> , то это обозначается 0,5. x>i>> >x>j> [0,5]
Суть метода состоит в том, что экспертам предлагается произвести попарную оценку факторов в форме матриц (таблица 4).
Таблица 4
Матрица попарного сравнения факторов, выполненная каждым экспертом
|
Эксперт № 1 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
0,5 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>2> |
0,5 |
0,5 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>3> |
0 |
0 |
0,5 |
1 |
1 |
1 |
1 |
1 |
|
x>4> |
0 |
0 |
0 |
0,5 |
0,5 |
0,5 |
0 |
1 |
|
x>5> |
0 |
0 |
0 |
0 |
0,5 |
0,5 |
0 |
1 |
|
x>6> |
0 |
0 |
0 |
0 |
0,5 |
0,5 |
0 |
1 |
|
x>7> |
0 |
0 |
0 |
1 |
1 |
1 |
0,5 |
1 |
|
x>8> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
|
Эксперт № 2 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
1 |
0,5 |
0 |
1 |
1 |
1 |
1 |
|
x>2> |
0 |
0,5 |
0 |
0 |
0 |
0 |
0,5 |
1 |
|
x>3> |
0,5 |
1 |
0,5 |
0 |
1 |
1 |
1 |
1 |
|
x>4> |
1 |
1 |
1 |
0,5 |
1 |
1 |
1 |
1 |
|
x>5> |
0 |
1 |
0 |
0 |
0,5 |
0,5 |
1 |
1 |
|
x>6> |
0 |
1 |
0 |
0 |
0 |
0,5 |
1 |
1 |
|
x>7> |
0 |
0,5 |
0 |
0 |
0 |
0 |
0,5 |
1 |
|
x>8> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
|
Эксперт № 3 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
1 |
1 |
0 |
0 |
0,5 |
0 |
0 |
|
x>2> |
0 |
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x>3> |
0 |
1 |
0,5 |
0 |
0,5 |
1 |
0,5 |
0,5 |
|
x>4> |
1 |
1 |
1 |
0,5 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
1 |
0,5 |
0 |
0,5 |
1 |
0,5 |
0,5 |
|
x>6> |
0,5 |
1 |
0 |
0 |
0 |
0,5 |
0 |
0 |
|
x>7> |
1 |
1 |
0,5 |
0 |
0,5 |
1 |
0,5 |
0,5 |
|
x>8> |
1 |
1 |
0,5 |
0 |
0,5 |
1 |
0,5 |
0,5 |
|
Эксперт № 4 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
0 |
0,5 |
0 |
0 |
0 |
0 |
0 |
|
x>2> |
1 |
0,5 |
1 |
1 |
0,5 |
1 |
1 |
1 |
|
x>3> |
0,5 |
0 |
0,5 |
0 |
0 |
0 |
0 |
0 |
|
x>4> |
1 |
0 |
1 |
0,5 |
0 |
1 |
1 |
1 |
|
x>5> |
1 |
0,5 |
1 |
1 |
0,5 |
1 |
1 |
1 |
|
x>6> |
1 |
0 |
1 |
0 |
0 |
0,5 |
1 |
1 |
|
x>7> |
1 |
0 |
1 |
0 |
0 |
0 |
0,5 |
0,5 |
|
x>8> |
1 |
0 |
1 |
0 |
0 |
0 |
0,5 |
0,5 |
|
Эксперт № 5 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
0 |
0 |
0 |
0 |
0 |
0,5 |
1 |
|
x>2> |
1 |
0,5 |
1 |
0,5 |
1 |
1 |
1 |
1 |
|
x>3> |
1 |
0 |
0,5 |
0 |
1 |
0 |
1 |
1 |
|
x>4> |
1 |
0,5 |
1 |
0,5 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
0 |
0 |
0 |
0,5 |
0 |
1 |
1 |
|
x>6> |
1 |
0 |
1 |
0 |
1 |
0,5 |
1 |
1 |
|
x>7> |
0,5 |
0 |
0 |
0 |
0 |
0 |
0,5 |
1 |
|
x>8> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
|
Эксперт № 6 |
||||||||
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
|
|
x>1> |
0,5 |
0 |
0,5 |
0 |
0 |
1 |
0 |
1 |
|
x>2> |
1 |
0,5 |
1 |
0 |
0,5 |
1 |
0 |
1 |
|
x>3> |
0,5 |
0 |
0,5 |
0 |
0 |
1 |
0 |
1 |
|
x>4> |
1 |
1 |
1 |
0,5 |
1 |
1 |
0,5 |
1 |
|
x>5> |
1 |
0,5 |
1 |
0 |
0,5 |
1 |
0 |
1 |
|
x>6> |
0 |
0 |
0 |
0 |
0 |
0,5 |
0 |
0,5 |
|
x>7> |
1 |
1 |
1 |
0,5 |
1 |
1 |
0,5 |
1 |
|
x>8> |
0 |
0 |
0 |
0 |
0 |
0,5 |
0 |
0,5 |
Математическое ожидание оценки попарного сравнения факторов определяется по формуле:
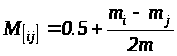
где: m>i> - число предпочтений отданных i-му фактору в рассматриваемых сочетаниях пар факторов (количество единиц).
m>j> - число предпочтений отданных j-му фактору в рассматриваемых сочетаниях пар факторов (количество нулей).
m - число опрошенных экспертов.
Отмеченная выше шкала сравнений используется для по парного сравнения факторов и для дальнейшего заполнения матрицы математических ожиданий оценок по парного сравнения факторов, при чем, в каждой клеточке матрицы записывается значимость фактора, отмеченного в столбце матрицы по отношению к фактору строки матрицы шапки.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После определения математических ожиданий заполняется матрица математических ожиданий оценок попарного сравнения факторов (таблица 5).
Таблица 5
Матрица математических ожиданий оценок попарного сравнения факторов
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
x>8> |
Б>i> |
|
|
x>1> |
0,5 |
0,17 |
0,335 |
0,165 |
0,335 |
0,585 |
0,415 |
0,665 |
3,17 |
|
x>2> |
0,83 |
0,5 |
0,665 |
0,415 |
0,5 |
0,665 |
0,585 |
0,835 |
4,995 |
|
x>3> |
0,665 |
0,335 |
0,5 |
0,165 |
0,585 |
0,665 |
0,585 |
0,75 |
4,25 |
|
x>4> |
0,835 |
0,595 |
0,835 |
0,5 |
0,75 |
0,915 |
0,75 |
1 |
6,18 |
|
x>5> |
0,665 |
0,5 |
0,415 |
0,25 |
0,5 |
0,665 |
0,585 |
0,915 |
4,495 |
|
x>6> |
0,415 |
0,335 |
0,335 |
0,085 |
0,335 |
0,5 |
0,5 |
0,75 |
3,255 |
|
x>7> |
0,585 |
0,415 |
0,415 |
0,25 |
0,415 |
0,5 |
0,5 |
0,335 |
3,415 |
|
x>8> |
0,335 |
0,165 |
0,25 |
0 |
0,085 |
0,25 |
0,665 |
0,5 |
2,25 |
|
|
32 |
Ранжирование рассмотренных факторов по важности осуществляется по рассчитанных баллов в порядке убывания , либо по коэффициенту значимости k>t> , который рассчитывается по формуле:
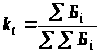 .
.
Вывод. Рассмотренная модификация метода экспертных оценок дает тождественный результат, что и при использовании метода простого ранжирования. При этом от исходных данных простого ранжирования достаточно просто перейти к оценке попарного сравнения и наоборот.
В результате проведенных расчетов было выявлено, что наиболее значимыми факторами являются факторы 4, 3, 2, 8, проранжированные в порядке убывания суммы баллов, т. е.:
х>4 >
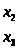
х>8>
х>6>
х>5>
х>7>
х>1>
.
х>8>
х>6>
х>5>
х>7>
х>1>
.
Следует также отметить, что согласованности у экспертов нет (о чем свидетельствует коэффициент конкордации меньше 0,05), поэтому надо улучшить их состав, т.к. они не в состоянии дать адекватную оценку и средний балл не будет вычислен правильно.
2. Принятие решения по нескольким критериальным показателям
На практике обычно приходится принимать решения не по одному критерию, а по нескольким, поэтому их значения при сравнительной оценке имеют разнонаправленный характер. В этих условиях необходимо рассматриваемую систему оценок показателей свести к одному комплексному, на основе которого и будет приниматься решение.
Для построения комплексной оценки необходимо решить 2 проблемы:
рассматриваемые критериальные показатели имеют неодинаковую значимость;
показатели оцениваются в различных единицах измерения; для построения комплексной оценки необходимо перейти к единому измерению.
Первая проблема чаще всего решается за счет применения метода попарного сравнения.
Для решения второй проблемы используется единый измеритель для частных показателей. Чаще всего в качестве такого измерителя применяется балльная оценка. При этом оценка выполняется с использованием 2-х подходов:
I-й подход используется при отсутствии статистических данных в значениях рассматриваемых показателей (пределов изменения);
II-й подход используется при наличии статистических данных (пределов изменения) о значениях рассматриваемых показателей.
При использовании I-го подхода для перевода в баллы поступают следующим образом: лучшее значение рассматриваемого показателя приравнивается к 1 баллу, а остальные значения определяются в долях от этого балла. Данный подход прост, дает объективную оценку, но не учитывает лучшие достижения, которые лежат за пределами рассматриваемых вариантов.
Для исключения этого недостатка необходима информация о пределах изменения рассматриваемого показателя. При его наличии используется II-й подход. В этом случае для перевода значений в баллы строится шкала перевода. При этом система балльной оценки выбирается с использованием теории статистики.
n = 1 + 3,332 lg N
N – число статистических наблюдений;
n – принятая система балльной оценки, полученная с использованием правильного округления.
Перевод в баллы осуществляется на основе шкалы перевода с применением процедуры интерполяции табличных данных.
Задание. Из 6-ти вариантов альтернативных решений, каждое из которых оценивается 5-ю критериальными показателями, выбрать лучший вариант. Оценку выполнить, используя 2 подхода:
при отсутствии статистических данных о пределах изменения рассматриваемых показателей;
при их наличии.
Пределы изменения устанавливаются по следующим количествам измерений: N = 8.
Оценку значимости выполнить на основе попарной оценки по мнению исполнителя.
Таблица 6
Исходные данные
|
№№ показателя |
Альтернативы |
|||||
|
А>1> |
А>2> |
А>3> |
А>4> |
А>5> |
А>6> |
|
|
x>1> |
5 |
7 |
14 |
18 |
20 |
19 |
|
x>2> |
10 |
4 |
9 |
5 |
8 |
7 |
|
x>3> |
4 |
11 |
7 |
7 |
9 |
8 |
|
x>4> |
1 |
2 |
1 |
1 |
3 |
4 |
|
x>5> |
10 |
21 |
23 |
17 |
18 |
19 |
Таблица 7
Пределы изменения и значимость рассматриваемых показателей
|
№ п/п |
Наименование показателя |
Единицы измерения |
Пределы изменений |
Значимость Kз>i> |
|
1 |
Прирост объема производства |
% |
5 – 25 |
0,25 |
|
2 |
Рентабельность продукции |
% |
2 – 10 |
0,1 |
|
3 |
Срок освоения проекта |
Мес. |
3 – 15 |
0,15 |
|
4 |
Срок возврата капвложений |
Мес. |
1 – 4 |
0,3 |
|
5 |
Снижение себестоимости |
% |
5 – 30 |
0,2 |
I подход. Итак, имеются 6-ть вариантов альтернативных решений и отсутствуют статистические данные о значении рассматриваемых показателей. Значимость каждого варианта известна и приведена в таблице 7.
Приравняем к 1 лучшее значение показателя среди всех рассматриваемых, а остальные значения определим в долях от этого балла. Результаты сведем в таблицу 8. Далее путем перемножения и суммирования всех альтернатив x>i>A>i>> >на Kз>i> получим комплексную оценку показателей.
Таблица 8
Комплексная оценка показателей по первому подходу
|
№ |
Оценка в баллах |
Kз>i> |
Оценка в баллах с учетом Kз>i> |
||||||||||
|
А>1> |
А>2> |
А>3> |
А>4> |
А>5> |
А>6> |
А>1> |
А>2> |
А>3> |
А>4> |
А>5> |
А>6> |
||
|
x>1> |
0,25 |
0,35 |
0,7 |
0,9 |
1 |
0,95 |
0,0667 |
0,017 |
0,023 |
0,047 |
0,063 |
1,067 |
0,064 |
|
x>2> |
1 |
0,4 |
0,9 |
0,5 |
0,8 |
0,7 |
0,267 |
0,267 |
0,107 |
0,204 |
0,134 |
0,214 |
0,187 |
|
x>3> |
0,36 |
1 |
0,64 |
0,64 |
0,82 |
0,73 |
0,133 |
0,133 |
0,133 |
0,085 |
0,081 |
0,109 |
0,097 |
|
x>4> |
1 |
0,5 |
1 |
1 |
0,33 |
0,25 |
0,333 |
0,333 |
0,167 |
0,333 |
0,333 |
0,11 |
0,083 |
|
x>5> |
1 |
0,48 |
0,43 |
0,588 |
0,78 |
0,83 |
0,2 |
0,2 |
0,096 |
0,118 |
0,118 |
0,156 |
0,166 |
|
Комплексная оценка |
0,95 |
0,526 |
0,787 |
0,729 |
0,656 |
0,597 |
|||||||
|
№ 1 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
№ 2 |
Вывод: используя первый подход, определили, что лучшим вариантом из альтернативных будет вариант А>2> , т.к. он имеет наибольшую комплексную оценку. Далее идут варианты: А>2 >→ А>4 >→ А>3> → А>1> → А>6> → А>5 >.
II подход.
N = 8; n = 1 + 3,332 lg 8 = 4,009 = 4
Исходя из расчетов, оценка показателей будет производиться по 4-х балльной шкале.
Далее определяется размах варьирования и шаг изменения значения показателя в расчете на баллы по каждому критериальному показателю.
R = R >max>> >- R >min>> >
где R>i> – размах варьирования показателя x>i>> >.
Шаг изменения значения показателя рассчитывается по формуле:
h
=
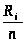
h – шаг изменения значения показателя.
Определим пределы изменения для каждого показателя:
-
x>1> :
R>1> = 25 – 5 = 20,
h>1> = 4
x>2>> >:
R>2> = 10 – 2 = 8,
h>2> = 1,6
x>3>> >:
R>3> = 15 – 3 = 12,
h>3> = 2,4
x>4>> >:
R>4> = 4 – 1 = 3,
h>4> = 0,6
x>5>> >:
R>5> = 30 – 5 = 25,
h>5> = 5
Далее нужно определить оценку x>i>A>i>> >по каждому показателю. Для этого воспользуемся шкалой перевода в баллы (табл. 9)
Таблица 9
Шкала перевода в баллы
|
№ показателя |
Оценка в баллах |
||||
|
0 ÷ 1 |
1÷2 |
2÷3 |
3÷4 |
4÷5 |
|
|
x>1> |
5 ÷ 9 |
9 ÷ 13 |
13 ÷ 17 |
17 ÷ 21 |
21÷25 |
|
x>2> |
2 ÷ 3,6 |
3,6 ÷ 5,2 |
5,2 ÷ 6,8 |
6,8 ÷ 8,4 |
8,4÷10 |
|
x>3> |
3 ÷ 5,4 |
5,4 ÷ 7,8 |
7,8 ÷ 10,2 |
10,2 ÷ 12,6 |
12,6÷15 |
|
x>4> |
4 ÷ 3,4 |
3,4÷ 2,8 |
2,8÷ 2,2 |
2,2 ÷ 1,6 |
1,6÷1 |
|
x>5> |
30 ÷ 25 |
25 ÷ 20 |
20 ÷ 15 |
15 ÷10 |
10÷5 |
Для того, чтобы определить оценку x>i>A>i>> >,> >нужно из численного значения показателя вычесть нижний интервал, разделить на шаг и прибавить предыдущий интервал. Результаты оценки сведем в таблицу 10.
Таблица 10
Комплексная оценка показателей по второму подходу
|
№ |
Оценка в баллах |
Kз>i> |
Оценка в баллах с учетом Kз>i> |
||||||||||
|
А>1> |
А>2> |
А>3> |
А>4> |
А>5> |
А>6> |
А>1> |
А>2> |
А>3> |
А>4> |
А>5> |
А>6> |
||
|
x>1> |
0 |
0,5 |
2,25 |
3 |
3,5 |
3,25 |
0,0667 |
0 |
0,0335 |
0,15 |
0,201 |
0,235 |
0,218 |
|
x>2> |
5 |
1,25 |
4,375 |
1,875 |
3,75 |
3,125 |
0,267 |
1,335 |
0,334 |
0,168 |
0,5 |
0,1 |
0,83 |
|
x>3> |
0,42 |
3,33 |
1,667 |
1,667 |
2,58 |
2,083 |
0,133 |
0,055 |
0,443 |
0,22 |
0,22 |
0,34 |
0,287 |
|
x>4> |
5 |
3,33 |
5 |
5 |
1,67 |
2,4 |
0,333 |
1,605 |
1,105 |
1,665 |
1,605 |
0,55 |
0,799 |
|
x>5> |
4 |
3,8 |
1,4 |
1,6 |
2,4 |
2,2 |
0,2 |
0,8 |
0,76 |
0,28 |
0,32 |
0,48 |
0,44 |
|
Комплексная оценка |
3,79 |
2,54 |
2,148 |
2,85 |
2,6 |
2,565 |
|||||||
|
№ 1 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
№ 2 |
Вывод: используя второй подход, определили, что лучшим вариантом из альтернативных будет вариант А>2> , т.к. он имеет наибольшую комплексную оценку. Далее идут варианты: А>2 >→ А>4 >→ А>3> → А>1> → А>6> → А>5 >. Результаты по второму подходу, полученные в ходе вычислений, совпадают с результатами, полученными при применении первого подхода.
3. Определение оптимальной очередности расстановки оборудования на серийном участке производства
В серийном производстве в условиях петляющих технологических маршрутов обработки деталей стоит задача оптимизации размещения оборудования, позволяющая повысить уровень прямоточности производственного процесса.
Рассмотрим алгоритм решения задачи по методу, основанному на элементах теории упорядочения множеств без доказательства основных положений, заложенных в этом методе.
Задание. На серийном участке производства обрабатываются петлеобразномаршрутные детали. Деталеоперации закреплены за станками в соответствии с их допустимой объемной годовой загрузкой (таблица ). Необходимо найти такое размещение станков по площадкам, которое соответствует наименьшему грузопотоку деталей:
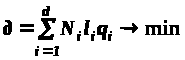 ,
,
где N>i> - годовая программа выпуска детали i-го наименования;
l>i> - путь, проходимый i-ой деталью по всем операциям технологического процесса;
q>i> - средняя масса детали;
d>i> - число наименований обрабатываемых на участке деталей.
Постановка и решение задачи предполагает наличие поперечного и продольного грузооборота деталей на участке. Поперечный грузооборот - это движение деталей от станков, размещенных в один или несколько рядов, к оси главного прохода участка и обратно. Продольный грузооборот - это движение деталей вдоль этой оси. При изменении очередности расстановки станков меняется только продольный грузооборот, поперечный остается постоянным. Поэтому при решении задачи учитывается только продольный грузооборот.
Обычно на участке используется оборудование одного типоразмера. В этих условиях расстояния между станками, как правило, имеет одну и ту же величину. Это обстоятельство позволяет принять еще одно допущение, не оказывающее влияние на результат решения задачи - принять расстояние между станками равное единице длины.
Алгоритм решения задачи включает следующие этапы:
- расчет исходного суммарного грузооборота;
- построение матрицы грузооборота и ее уравновешивание;
- расчет оптимальной очередности расстановки оборудования;
оценка полученного результата: расчет процента снижения суммарного грузооборота.
Таблица 11
Исходные данные:
|
№№ станков |
||||||
|
1 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
3;10 |
1;13 |
7 |
8 |
8;13 |
3;10 |
|
2 |
6 |
6;11 |
3;12 |
7;12 |
7 |
9 |
|
3 |
9;13 |
1;5 |
8 |
1 |
1;9 |
1;4 |
|
4 |
1;5 |
3 |
4;9 |
6;11 |
6;14 |
8;12 |
|
5 |
2 |
2;1 |
6 |
2;5 |
3;11 |
11 |
|
6 |
9 |
10 |
10 |
4 |
2;10 |
2;6 |
|
7 |
4;8 |
8;12 |
1;5 |
3;10 |
5 |
5 |
|
8 |
7;12 |
9 |
2;11 |
9 |
4;12 |
7 |
|
Q>i>>(>>T>>)> |
20 |
16 |
17 |
19 |
20 |
21 |
Q>i>>(>>T>>)> - масса годовой производственной программы в тоннах.
Итак, за серийным участком производства, состоящим из 8 станков, закреплена обработка 6-ти деталей, имеющих сложные петляющие технологические маршруты. Закрепление деталеопераций за станками и масса годовой производственной программы по деталям приведены в табл.12.
Таблица 12
Закрепление деталей за станками
|
Номер детали |
Номер станка |
Масса годовой производственной программы, т |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
1 |
3;10 |
6 |
9;13 |
1;5 |
2 |
4;8 |
7;12 |
11 |
20 |
|
7 |
1;13 |
6;11 |
1;5 |
3 |
2;1 |
10 |
8;12 |
9 |
16 |
|
8 |
7 |
3;12 |
8 |
4;9 |
6 |
10 |
1;5 |
2;11 |
17 |
|
9 |
8 |
7; 12 |
1 |
6; 11 |
2; 5 |
4 |
3; 10 |
9 |
19 |
|
10 |
8;13 |
7 |
1;9 |
6;14 |
3;11 |
2;10 |
5 |
4;12 |
20 |
|
11 |
3;10 |
9 |
1;4 |
8;12 |
11 |
2;6 |
5 |
7 |
21 |
Этап 1. Расчет исходного суммарного грузооборота.
Обозначим место складирования заготовок буквой А, расположим его слева на участке, место складирования готовых деталей - буквой В - и разместим его справа. Тогда при расположении станков в один ряд в порядке их нумерации суммарный грузооборот определяется с помощью табл.13.
Таблица 13
Исходный грузооборот
|
№ дет. |
А |
Номер операций, закрепленных за станками |
В |
Масса годовой программы |
Путь, проход. деталью, L>i> |
Грузооборот по детали, Г>i> |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||||
|
1 |
3;10 |
6 |
9;13 |
1;5 |
2 |
4;8 |
7;12 |
3;10 |
20 |
47 |
940 |
||
|
7 |
1;13 |
6;11 |
1;5 |
3 |
2;1 |
10 |
8;12 |
1;13 |
16 |
43 |
688 |
||
|
8 |
7 |
3;12 |
8 |
4;9 |
6 |
10 |
1;5 |
7 |
17 |
43 |
731 |
||
|
9 |
8 |
7; 12 |
1 |
6; 11 |
2; 5 |
4 |
3; 10 |
8 |
19 |
33 |
627 |
||
|
10 |
8;13 |
7 |
1;9 |
6;14 |
3;11 |
2;10 |
5 |
8;13 |
20 |
43 |
860 |
||
|
11 |
3;10 |
9 |
1;4 |
8;12 |
11 |
2;6 |
5 |
3;10 |
21 |
37 |
777 |
||
Суммарный
грузооборот,
|
4 623 |
Этап 2. Построение матрицы грузооборота и ее уравновешивание.
Матрица грузооборота представляет собой таблицу (табл. ), на пересечении строк и столбцов которой указываются грузовые связи соответствующих номерам строки и столбца станков. Грузовая связь между станками будет тогда, когда на них выполняются две соседние операции. Аналогично учитывается грузовая связь станка со складом заготовок, при этом на нем должна выполняться первая операция, и со складом готовых деталей при условии выполнения на станке последней операции.
Следует отметить, что матрица (табл. 14) симметрична относительно диагонали таким образом, что для ее заполнения достаточно рассчитать клетки над диагональю, а затем переписать заполненные строчки в соответствующий столбец.
Таблица 14
Матрица грузооборота
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
В |
|
А |
0 |
0+10 |
0+33 |
76+18 |
20 |
0+48 |
0+25.5 |
17+4.5 |
0+48 |
— |
|
1 |
0+10 |
0 |
60 |
73 |
36 |
58 |
41 |
16 |
59 |
16+10 |
|
2 |
0+33 |
60 |
0 |
16 |
116 |
16 |
16 |
36 |
17 |
36+33 |
|
3 |
76+18 |
73 |
16 |
0 |
17 |
19 |
81 |
41 |
0 |
20+18 |
|
4 |
20 |
36 |
116 |
17 |
0 |
55 |
17 |
56 |
21 |
41 |
|
5 |
0+48 |
58 |
16 |
19 |
55 |
0 |
59 |
36 |
40 |
0+48 |
|
6 |
0+25.5 |
41 |
16 |
81 |
17 |
59 |
0 |
60 |
54 |
0+25.5 |
|
7 |
17+4.5 |
16 |
36 |
41 |
56 |
36 |
60 |
0 |
92 |
16+4.5 |
|
8 |
0+48 |
59 |
17 |
0 |
21 |
40 |
54 |
92 |
0 |
0+48 |
|
В |
— |
16+10 |
36+33 |
20+18 |
41 |
0+48 |
0+25.5 |
16+4.5 |
0+48 |
— |
|
Q>i> |
— |
359 |
313 |
343 |
379 |
283 |
328 |
370 |
283 |
— |
|
|
— |
10 |
33 |
18 |
0 |
48 |
25,5 |
4,5 |
48 |
— |
После заполнения грузовых связей между всеми станками подсчитываются суммы грузовых связей по столбцам Q>i> , исключая столбцы А и В. В нашем примере эти суммы соответственно равны 284; 275; 290; 306; 278; 320; 328, 239 что говорит о том, что полученная матрица не уравновешена.
Уравновешенной матрицей считается такая, для которой суммы по строкам и столбцам равны одной и той же величине. Для расчета оптимальной очередности расположения станков необходимо иметь уравновешенную матрицу.
Процесс уравновешивания осуществляется следующим образом:
- выбирается максимальная сумма из полученных значений Q>i> , в нашем примере она равна 328;
- определяется для каждого
столбца (исключая А и В) поправки ,
рассчитываемые по формуле:
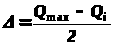
- найденные значения добавляются в клетки А и В соответствующего столбца, а так как матрица симметрична, эти значения необходимо добавить в зеркально-отражаемые клетки А и В того же номера строки. Эта операция позволяет уравновесить матрицу, т.е. добиться, чтобы сумма грузооборотов по каждой строке и столбцу равнялась в нашем случае 328.
Полученная уравновешенная матрица (табл. 15) используется для расчета оптимальной очередности расстановки станков.
Таблица 15
Уравновешенная матрица грузооборота
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
В |
|
А |
0 |
10 |
33 |
94 |
20 |
48 |
25,5 |
21,5 |
48 |
— |
|
1 |
10 |
0 |
60 |
73 |
36 |
58 |
41 |
16 |
59 |
26 |
|
2 |
33 |
60 |
0 |
16 |
116 |
16 |
16 |
36 |
17 |
69 |
|
3 |
94 |
73 |
16 |
0 |
17 |
19 |
81 |
41 |
0 |
38 |
|
4 |
20 |
36 |
116 |
17 |
0 |
55 |
17 |
56 |
21 |
41 |
|
5 |
48 |
58 |
16 |
19 |
55 |
0 |
59 |
36 |
40 |
48 |
|
6 |
25,5 |
41 |
16 |
81 |
17 |
59 |
0 |
60 |
54 |
25,5 |
|
7 |
21,5 |
16 |
36 |
41 |
56 |
36 |
60 |
0 |
92 |
20,5 |
|
8 |
48 |
59 |
17 |
0 |
21 |
40 |
54 |
92 |
0 |
48 |
|
В |
— |
26 |
69 |
38 |
41 |
48 |
25,5 |
20,5 |
48 |
- |
Этап 3. Расчет оптимальной очередности расстановки оборудования.
Расчет ведется по форме расчетной таблицы (табл. 16). Из уравновешенной матрицы грузооборота в расчетной таблице указываются грузовые связи кладовой заготовок А и кладовой заготовок В с каждым из станков.
Расстановка оборудования осуществляется путем выполнения последовательных шагов. За каждый шаг устанавливается два станка - слева около кладовой заготовок и справа рядом с кладовой готовых деталей. Станки выбираются по максимальному значению грузовой связи с кладовой заготовок и кладовой готовых деталей. В рассматриваемом примере 3-й станок имеет максимальную грузовую связь с кладовой заготовок, равную 55 кг., а 8-й станок имеет наибольшую связь с кладовой готовых деталей – 62,5 кг. Устанавливаем слева 3-й станок, а справа – 8-й.
Затем из матрицы грузооборота выделяют грузовые связи еще неустановленных станков 1, 2, 4, 5, 6, 7, записывают их в таблицу и суммируют с предыдущей грузовой связью этих станков со складом заготовок.
Далее выбираются максимальные значения из грузовых связей неустановленных станков. Слева эти максимальные значения равны 70 т. на 5-м станке, справа – 72,5 т на 2-м станке, соответственно, устанавливаем эти станки слева и справа. Затем процесс повторяется, выбираются максимумы из грузовых связей неустановленных станков. Эти максимумы равны 138 т. слева по 7-му станку и 109 т. справа по 6-му станку. Второй шаг позволяет установить слева седьмой станок, справа - шестой. Затем выписываются из матрицы грузооборота грузовые связи установленных станков; грузовые связи 2-го и 4-го с не установленными. Нарастающим итогом рассчитывается сумма грузооборотов по неустановленным станкам и выбираются максимальные значения: слева максимум приходится на 1-й станок, справа на 4-й станок.
Таблица 16
Расчёт оптимальной очередности расстановки оборудования
|
Номер станка |
А |
Шаг 1 |
Шаг 2 |
Шаг 3 |
Шаг 4 |
Шаг 3 |
Шаг 2 |
Шаг 1 |
В |
Номер станка |
||||||
|
3 |
|
6 |
|
8 |
|
7 |
5 |
|
1 |
|
4 |
|
2 |
|||
|
1 |
10 |
73 |
83 |
41 |
124 |
122 |
36 |
86 |
60 |
26 |
1 |
|||||
|
2 |
83 |
69 |
2 |
|||||||||||||
|
3 |
94 |
38 |
3 |
|||||||||||||
|
4 |
20 |
17 |
37 |
155 |
116 |
41 |
4 |
|||||||||
|
5 |
48 |
19 |
67 |
59 |
126 |
40 |
166 |
177 |
58 |
119 |
55 |
64 |
16 |
48 |
5 |
|
|
6 |
25,5 |
81 |
106 |
41,5 |
16 |
25,5 |
6 |
|||||||||
|
7 |
21,5 |
41 |
62,5 |
60 |
22,5 |
92 |
214,5 |
128,5 |
16 |
112,5 |
56 |
56,5 |
36 |
20,5 |
7 |
|
|
8 |
48 |
0 |
48 |
92 |
140 |
86 |
21 |
65 |
17 |
48 |
8 |
|||||
Таким образом, рассчитана оптимальная очередность расстановки станков:
А — 3 —6 — 8— 7 — 5 — 1 — 4 — 2 — В.
Этап 4. Оценка полученного результата.
Рассчитаем суммарный грузооборот при рассчитанной оптимальной очередности расстановки станков (табл. 17).
Таблица 17
Результирующий грузооборот
|
№ дет. |
А |
Номер операций, закрепленных за станками |
В |
Массагодовойпроизвод. программыQ>i> |
l>i> |
Г>i> |
|||||||
|
3 |
6 |
8 |
7 |
5 |
1 |
4 |
2 |
||||||
|
6 |
9;13 |
4;8 |
3;10 |
7;12 |
2 |
3;10 |
1;5 |
6 |
20 |
46 |
920 |
||
|
9 |
1;5 |
10 |
1;13 |
8;12 |
2;1 |
1;13 |
3 |
6;11 |
16 |
40 |
640 |
||
|
12 |
8 |
10 |
7 |
1;5 |
6 |
7 |
4;9 |
3;12 |
17 |
38 |
646 |
||
|
13 |
1 |
4 |
8 |
3; 10 |
2; 5 |
8 |
6; 11 |
7; 12 |
19 |
24 |
456 |
||
|
14 |
1;9 |
2;10 |
8;13 |
5 |
3;11 |
8;13 |
6;14 |
7 |
20 |
30 |
600 |
||
|
15 |
1;4 |
2;6 |
3;10 |
5 |
11 |
3;10 |
8;12 |
9 |
21 |
28 |
588 |
||
|
Суммарный грузооборот |
3850 |
Вывод: поставленная задача достигнута, суммарный грузооборот при оптимальной расстановке станков снижен на 773 т или на 16,72 %.
4. Оптимизация календарного планирования серийно-поточных линий и предметно-замкнутых участков
В организации производства оптимизация календарного планирования является довольно сложной задачей, решение которой оказывает значительное влияние на уровень эффективности производства. Обычно в качестве критерия этой задачи принимается совокупный производственный цикл обработки. Сокращение длительности производственного цикла обработки деталей ведет к снижению потребности в оборотных средствах.
Рассмотрим оптимизацию календарного планирования на основе использования метода проф. А.С. Валькова.
Приведем методику решения задач оптимального календарного планирования для следующих условий:
- оптимизация обработки одно маршрутных партий деталей при последовательном их виде движения;
- оптимизация обработки разно маршрутных партий деталей при последовательном их виде движения.
4.1. Оптимизация обработки одно маршрутных партий деталей при последовательном их виде движения
Задание. На основе заданного технологического процесса обработки партий деталей и заданной длительности операционных циклов требуется определить оптимальную очередность обработки деталей, обеспечивающую минимальный производственный цикл обработки партий деталей, рассчитываемый по формуле:
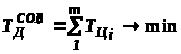 ,
(1)
,
(1)
где Т>Ц>>i> - длительность производственного цикла обработки партий деталей i-го наименования; m - число обрабатываемых на участке партий деталей. Алгоритм решения задачи включает следующие этапы:
- расчет исходных календарных параметров;
- рассмотрение всех возможных сочетаний пар партий деталей и определение оптимальной очередности обработки в рассматриваемом сочетании;
- определение общей оптимальной очередности обработки деталей;
- построение графика, сравнение его с исходной очередностью по принятому критерию.
Исходные данные приведены в таблице 18.
Таблица 18
Исходные данные
Номероперации |
Длительность операционных циклов, ч |
|||||
|
Номер детали |
||||||
|
1 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
1,8 |
0,7 |
2,9 |
2,5 |
1,5 |
0,9 |
|
2 |
2,5 |
0,9 |
2,7 |
0,8 |
1,6 |
2,6 |
|
3 |
0,4 |
2,6 |
0,7 |
1,9 |
3,4 |
2,5 |
|
4 |
2,1 |
2,9 |
2,5 |
1,5 |
0,9 |
2,7 |
|
5 |
0,9 |
1,7 |
0,4 |
1,7 |
0,9 |
2,7 |
|
6 |
1,5 |
0,9 |
1,3 |
1,6 |
0,7 |
2,9 |
|
7 |
2,9 |
2,5 |
0,5 |
2,5 |
1,5 |
1,7 |
|
8 |
0,7 |
3,5 |
2,5 |
0,8 |
1,6 |
2,6 |
На участке обрабатываются шесть партий одномаршрутных деталей, технологический процесс состоит из пяти операций.
На основе исходных данных составляется таблица календарных параметров. Каждая операция оценивается следующими параметрами:
|
j |
t>ij> |
S>ij> |
|
B>ij> |
A>ij> |
R>ij> |
|
- |
T>kij> |
- |
где j - номер операции;
t>ij> - длительность операционного цикла;
S>ij> - нормированное время межоперационного перерыва;
B>ij> - последующий цикл обработки;
A>ij> - предыдущий цикл обработки;
R>ij> - разность последующего и предыдущего циклов;
T>kij>- время окончания обработки партии на операции.
Расчет исходных календарных параметров ведется по следующим зависимостям:
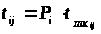 ,
,
где P>i>> >- размер партии деталей i-го наименования;
t>ш>>kij> - норма штучно-калькуляционного времени на выполнение j-й операции по партии i-го наименования;
A>ij >= A>i,j-1 >+ t>i,j-1 >+ S>i,j-1>;
B>ij >= B>i,j-1 >+ t>i,j-1 >+ S>i,j-1>;
R>ij >= B>ij >- A>ij>;
T>kij> = A>ij> + t>ij> .
Для рассматриваемого примера исходные календарные параметры принимают вид табл. 19.
Таблица 19. Исходные календарные параметры
|
1 |
7 |
8 |
8 |
10 |
11 |
|||||||||||||
|
1 |
1 |
1,8 |
0 |
1 |
0,7 |
0 |
1 |
2,9 |
0 |
1 |
2,5 |
0 |
1 |
1,5 |
0 |
1 |
0,9 |
0 |
|
11 |
0 |
11 |
15 |
0 |
15 |
10,6 |
0 |
10,6 |
10,8 |
0 |
10,8 |
10,6 |
0 |
10,6 |
17,7 |
0 |
17,7 |
|
|
- |
1,8 |
- |
- |
0,7 |
- |
- |
2,9 |
- |
- |
2,5 |
- |
- |
1,5 |
- |
- |
0,9 |
- |
|
|
2 |
2 |
2,5 |
0 |
2 |
0,9 |
0 |
2 |
2,7 |
0 |
2 |
0,8 |
0 |
2 |
1,6 |
0 |
2 |
2,6 |
0 |
|
8,5 |
1,8 |
6,7 |
14,1 |
0,7 |
13,4 |
7,9 |
2,9 |
5 |
10 |
2,5 |
7,5 |
9 |
1,5 |
7,5 |
15,1 |
0,9 |
14,2 |
|
|
- |
4,3 |
- |
- |
1,6 |
- |
- |
5,6 |
- |
- |
3,3 |
- |
- |
3,1 |
- |
- |
3,5 |
- |
|
|
3 |
3 |
0,4 |
0 |
3 |
2,6 |
0 |
3 |
0,7 |
0 |
3 |
1,9 |
0 |
3 |
3,4 |
0 |
3 |
2,5 |
0 |
|
8,1 |
4,3 |
3,8 |
11,5 |
1,6 |
9,9 |
7,2 |
5,6 |
1,6 |
8,1 |
3,3 |
4,8 |
5,6 |
3,1 |
2,5 |
12,6 |
3,5 |
9,1 |
|
|
- |
4,7 |
- |
- |
4,2 |
- |
- |
6,3 |
- |
- |
5,2 |
- |
- |
6,5 |
- |
- |
6 |
- |
|
|
4 |
4 |
2,1 |
0 |
4 |
2,9 |
0 |
4 |
2,5 |
0 |
4 |
1,5 |
0 |
4 |
0,9 |
0 |
4 |
2,7 |
0 |
|
6 |
4,7 |
1,3 |
8,6 |
4,2 |
4,4 |
4,7 |
6,3 |
-1,6 |
6,6 |
5,2 |
1,4 |
4,7 |
6,5 |
-1,8 |
9,9 |
6 |
3,9 |
|
|
- |
6,8 |
- |
- |
7,1 |
- |
- |
8,8 |
- |
- |
6,7 |
- |
- |
7,4 |
- |
- |
8,7 |
- |
|
|
5 |
5 |
0,9 |
0 |
5 |
1,7 |
0 |
5 |
0,4 |
0 |
5 |
1,7 |
0 |
5 |
0,9 |
0 |
5 |
2,7 |
0 |
|
5,1 |
6,8 |
-1,7 |
6,9 |
7,1 |
-0,2 |
4,3 |
8,8 |
-4,5 |
4,9 |
6,7 |
-1,8 |
3,8 |
7,4 |
-3,6 |
7,2 |
8,7 |
-1,5 |
|
|
- |
7,7 |
- |
- |
8,8 |
- |
- |
9,2 |
- |
- |
8,4 |
- |
- |
8,3 |
- |
- |
11,4 |
- |
|
|
6 |
6 |
1,5 |
0 |
6 |
0,9 |
0 |
6 |
1,3 |
0 |
6 |
1,6 |
0 |
6 |
0,7 |
0 |
6 |
2,9 |
0 |
|
3,6 |
7,7 |
-4,1 |
6 |
8,8 |
-2,8 |
3 |
9,2 |
-6,2 |
3,3 |
8,4 |
-5,1 |
3,1 |
8,3 |
-5,2 |
4,3 |
11,4 |
-7,1 |
|
|
- |
9,2 |
- |
- |
9,7 |
- |
- |
10,5 |
- |
- |
10 |
- |
- |
9 |
- |
- |
14,3 |
- |
|
|
7 |
7 |
2,9 |
0 |
7 |
2,5 |
0 |
7 |
0,5 |
0 |
7 |
2,5 |
0 |
7 |
1,5 |
0 |
7 |
1,7 |
0 |
|
0,7 |
9,2 |
-8,5 |
3,5 |
9,7 |
-6,2 |
2,5 |
10,5 |
-8 |
0,8 |
10 |
-9,2 |
1,6 |
9 |
-7,4 |
2,6 |
14,3 |
-11,7 |
|
|
- |
12,1 |
- |
- |
12,2 |
- |
- |
11 |
- |
- |
12,5 |
- |
- |
10,5 |
- |
- |
16 |
- |
|
|
8 |
8 |
0,7 |
0 |
8 |
3,5 |
0 |
8 |
2,5 |
0 |
8 |
0,8 |
0 |
8 |
1,6 |
0 |
8 |
2,6 |
0 |
|
0 |
12,1 |
-12,1 |
0 |
12,2 |
-12,2 |
0 |
11 |
-11 |
0 |
12,5 |
-12,5 |
0 |
10,5 |
-10,5 |
0 |
16 |
-16 |
|
|
- |
12,8 |
- |
- |
15,7 |
- |
- |
13,5 |
- |
- |
13,3 |
- |
- |
12,1 |
- |
- |
18,6 |
- |
На следующем этапе методики решения задачи рассматриваются возможные сочетания пар партий деталей и в каждом из этих сочетаний определяется оптимальная очередность их обработки.
Для каждого сочетания пар деталей составляется расчетная таблица.
|
q |
, |
R>> |
R>> |
>> |
>> |
f |
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
||||||
|
5 |
, - номера рассматриваемых партий деталей;
R>> - разность разностей последующего и предыдущего циклов,
R>>=R>>-R>>, (2)
>>, >> - нормативные совмещения операционных циклов на станке при сроке начала первых операций для обеих партий деталей, равном нулю, рассчитываются по формулам:
>>=Т>К>>>-Т>Н>>>; (3)
>>=Т>К>>>-Т>Н>>>. (4)
Оптимальная очередность для рассматриваемого сочетания пары деталей определяются следующим образом:
1) определяются критические пары операций, которые соответствуют max>> и max>> . Эти пары могут быть следующих разновидностей:
1.1.) одноименные (ОИ), если max>> и max>> попадают на один станок;
1.2.) разноименные однонаправленные (ОН), если у этих максимумов знаки R>>> >и R>> одинаковые;
1.3.) разноименные разнонаправленные (РН), если у этих максимумов знаки R>>> >и R>> противоположные;
2) для одноименных критических пар операций оптимальная очередность соответствует положительному знаку R>>> >и R>> ;
3) для разноименных критических пар операций очередность определяется по знаку оценки Sab. Если знак отрицательный (или 0), то оптимальная очередность равна ab, если знак положительный - соответственно ba. При этом под ab понимаются номера партий деталей, записанные через по следующему правилу: если R>> на первой критической операции имеет знак плюс, то =a; =b; если минус, наоборот, =b; =a. Оценка Sab определяется по следующим зависимостям:
а) для равнонаправленных
SPH>ab>> >= b>2 >- b>1 >+ Bb>2 >- Ab>1 >- Ba>2 >+ Aa>1> ; (5)
б) для однонаправленных
при ab>2>ab>1> - по формуле (5);
при ab>2>ab>1> - по формуле (6);
SOH>ab >= a>1 >- a>2 >- Aa>1 >- Ba>2 >- Ab>1 >+ Bb>2> ; (6)
где a>1>, a>2>, b>1>, b>2> - длительности операционных циклов обработки данных партий деталей соответственно на первой или критической паре операций,
Aa>1>, Ab>1>, Ba>2>, Bb>2> - соответственно последующие и предыдущие циклы обработки партий деталей для обозначенных партий и пар критических операций. Проиллюстрируем данный этап:
Таблица 20
|
1-7 |
|||||||
|
q |
1-7 |
R>1-7> |
R>7-1> |
>1-7> |
>7-1> |
f>опт> |
q>K>> >= 2,8- (PH); R>1;7 >= - 6,7 < 0 = b = 1; = a = 7; S>ab> определяется по формуле (5); S>7;1>=0,7-2,5+0-1,8-0+0,7=-2,9; f>ОПТ>> >= a-b = 1-7; |
|
1 |
11 |
-4 |
4 |
1,8 |
0,7 |
7-1 |
|
|
2 |
2:2 |
-6,7 |
6,7 |
3,6 |
-0,2 |
||
|
3 |
3:3 |
-6,1 |
6,1 |
3,1 |
-0,1 |
||
|
4 |
4:4 |
-3,1 |
3,1 |
2,6 |
2,4 |
||
|
5 |
5:5 |
-1,5 |
1,5 |
0,6 |
2 |
||
|
6 |
6:6 |
-1,3 |
1,3 |
0,4 |
2 |
||
|
7 |
7:7 |
-2,3 |
2,3 |
2,4 |
3 |
||
|
8 |
8:8 |
0,1 |
-0,1 |
0,6 |
3,6 |
||
|
1-8 |
|||||||
|
q |
1-8 |
R>1>>;>>8> |
R>8>>;>>1> |
>1>>;>>8> |
>8>>;>>1> |
f>опт> |
q>K>> >= 1,4 - (OH); R>1;8 >= 0.4 > 0 = a= 1; = b = 8; S>ab> определяется по формуле (5); S>1>>;>>8>=2.1-1.8+0-6-0+9.9=4.2; f>ОПТ>> >= b-a =8-1; |
|
1 |
11 |
0,4 |
-0,4 |
1,8 |
2,9 |
8-1 |
|
|
2 |
2:2 |
1,7 |
-2 |
1,4 |
3,8 |
||
|
3 |
3:3 |
2,2 |
-2 |
-1 |
2 |
||
|
4 |
4:4 |
2,9 |
-3 |
0,5 |
4,1 |
||
|
5 |
5:5 |
2,8 |
-3 |
-1 |
2,4 |
||
|
6 |
6:6 |
2,1 |
-2 |
0 |
2,8 |
||
|
7 |
7:7 |
-0,5 |
0,5 |
1,6 |
1,8 |
||
|
8 |
8:8 |
-1,1 |
1,1 |
1,8 |
1,4 |
||
|
1-9 |
|||||||
|
q |
1-9 |
R>1>>;>>9> |
R>9>>;>>1> |
>1>>;>>9> |
>9>>;>>1> |
f>опт> |
q>K >= 2,7 - (ОИ); т.к. R>91><0 => f>ОПТ>> >=9-1 |
|
1 |
11 |
0,2 |
-0,2 |
1,8 |
2,5 |
9-1 |
|
|
2 |
2:2 |
-0,8 |
0,8 |
1,8 |
1,5 |
||
|
3 |
3:3 |
-1 |
1 |
1,4 |
0,9 |
||
|
4 |
4:4 |
-0,1 |
0,1 |
1,6 |
2 |
||
|
5 |
5:5 |
0,1 |
-0,1 |
1 |
1,6 |
||
|
6 |
6:6 |
1 |
-1 |
0,8 |
2,3 |
||
|
7 |
7:7 |
0,7 |
-0,7 |
2,1 |
3,3 |
||
|
8 |
8:8 |
0,4 |
-0,4 |
0,3 |
1,2 |
||
|
1-10 |
|||||||
|
q |
1-10 |
R>1>>;>>10> |
R>10>>;>>1> |
>1>>;1>>0> |
>10>>;>>1> |
f>опт> |
q>K>> >= 4,7 - (PH); R>1>>,10>> >= 3,1 > 0 = a = 1; = b = 10; S>ab> определяется по формуле (5); S>1>>;>>10>=1.5-0.9+1.6-6.5-0.7+4.7= -0.3; f>ОПТ >= ab = 1-10; |
|
1 |
11 |
0,4 |
-0,4 |
1,8 |
1,5 |
1-10 |
|
|
2 |
2:2 |
-0,8 |
0,8 |
2,8 |
1,3 |
||
|
3 |
3:3 |
1,3 |
-1,3 |
1,6 |
2,2 |
||
|
4 |
4:4 |
3,1 |
-3,1 |
0,3 |
2,7 |
||
|
5 |
5:5 |
1,9 |
-1,9 |
0,3 |
1,5 |
||
|
6 |
6:6 |
1,1 |
-1,1 |
0,9 |
1,3 |
||
|
7 |
7:7 |
-1,1 |
1,1 |
3,1 |
1,3 |
||
|
8 |
8:8 |
-1,6 |
1,6 |
2,3 |
0 |
||
|
1-11 |
|||||||
|
q |
1-11 |
R>1>>;1>>1> |
R>1>>1>>;>>1> |
>1>>;1>>1> |
>1>>1>>;>>1> |
f>опт> |
q>K>> >= 2,7 - (PH); R>6;15 >= - 7,5 < 0 = b = 1; = a = 11; S>ab> определяется по формуле (5); S>1>>1>>;>>1>> >=2.9-2.5+0.7-1.8-2.6+0.9= -2.4; f>ОПТ >= ab = 11-1; |
|
1 |
11 |
-6,7 |
6,7 |
1,8 |
0,9 |
11-1 |
|
|
2 |
2:2 |
-7,5 |
7,5 |
3,4 |
1,7 |
||
|
3 |
3:3 |
-5,3 |
5,3 |
1,2 |
1,7 |
||
|
4 |
4:4 |
-2,6 |
2,6 |
0,8 |
4 |
||
|
5 |
5:5 |
-0,2 |
0,2 |
-1 |
4,6 |
||
|
6 |
6:6 |
3 |
-3 |
-2,2 |
6,6 |
||
|
7 |
7:7 |
3,2 |
-3,2 |
-2,2 |
6,8 |
||
|
8 |
8:8 |
3,9 |
-3,9 |
-3,2 |
6,5 |
||
|
7-8 |
|||||||
|
q |
7-8 |
R>7>>;>>8> |
R>8>>;>>7> |
>7>>;>>8> |
>8>>;>>7> |
f>опт> |
q>K>> >= 2,8 - (PH); R>9;12 >= 8,4>0 = a = 7; = b = 8; S>ab> определяется по формуле (5); S>7>>;>>8>=2.5-2.7+0-2.9-0+0.7= -2.4; f>ОПТ>> >= ab = 7-8; |
|
1 |
11 |
4,4 |
-4,4 |
0,7 |
2,9 |
7-8 |
|
|
2 |
2:2 |
8,4 |
-8,4 |
-1,3 |
4,9 |
||
|
3 |
3:3 |
8,3 |
-8,3 |
-1,4 |
4,7 |
||
|
4 |
4:4 |
6 |
-6 |
0,8 |
4,6 |
||
|
5 |
5:5 |
4,3 |
-4,3 |
0 |
2,1 |
||
|
6 |
6:6 |
3,4 |
-3,4 |
0,5 |
1,7 |
||
|
7 |
7:7 |
1,8 |
-1,8 |
1,7 |
1,3 |
||
|
8 |
8:8 |
-1,2 |
1,2 |
4,7 |
1,3 |
||
|
7-9 |
|||||||
|
q |
7-9 |
R>7>>;>>9> |
R>9>>;>>7> |
>7>>;>>9> |
>9>>;>>7> |
f>опт> |
q>K>> >= 3,8 - (OH); R>7;9 >= 5,1>0 = a = 7; = b = 9; S>ab> определяется по формуле (5); S>7;9>=0.8-1.9+0-3.3-0+1.6= -2.8; f>ОПТ >= ab = 7-9; |
|
1 |
11 |
4,2 |
-4,2 |
0,7 |
2,5 |
7-9 |
|
|
2 |
2:2 |
5,9 |
-5,9 |
-0,9 |
2,6 |
||
|
3 |
3:3 |
5,1 |
-5,1 |
0,9 |
3,6 |
||
|
4 |
4:4 |
3 |
-3 |
1,9 |
2,5 |
||
|
5 |
5:5 |
1,6 |
-1,6 |
2,1 |
1,3 |
||
|
6 |
6:6 |
2,3 |
-2,3 |
1,3 |
1,2 |
||
|
7 |
7:7 |
3 |
-3 |
2,2 |
2,8 |
||
|
8 |
8:8 |
0,3 |
-0,3 |
3,2 |
1,1 |
||
|
7-10 |
|||||||
|
q |
7-10 |
R>7>>;1>>0> |
R>10>>;>>7> |
>7>>;1>>0> |
>1>>0>>;>>7> |
f>опт> |
q>K>> >= 3,8 - (PH); R>7>>;1>>0>> >= 7,4> 0 = a= 7; = b = 10; S>ab> определяется по формуле (5); S>7>>;>>10>> >=1.6-3.4+0-3.1-0+0.7=-4.2; f>ОПТ >= ab = 7-10; |
|
1 |
11 |
4,4 |
-4,4 |
0,7 |
1,5 |
7-10 |
|
|
2 |
2:2 |
5,9 |
-5,9 |
0,1 |
2,4 |
||
|
3 |
3:3 |
7,4 |
-7,4 |
1,1 |
4,9 |
||
|
4 |
4:4 |
6,2 |
-6,2 |
0,6 |
3,2 |
||
|
5 |
5:5 |
3,4 |
-3,4 |
1,4 |
1,2 |
||
|
6 |
6:6 |
2,4 |
-2,4 |
1,4 |
0,2 |
||
|
7 |
7:7 |
1,2 |
-1,2 |
3,2 |
0,8 |
||
|
8 |
8:8 |
-1,7 |
1,7 |
5,2 |
-0,1 |
||
|
7-11 |
|||||||
|
q |
7-11 |
R>7>>;1>>1> |
R>1>>1>>;>>7> |
>7>>;1>>1> |
>1>>1>>;>>7> |
f>опт> |
q>K>> >= 4,8 - (ОH); R>9;15 >= 0,5 > 0 = a = 7; = b = 11; S>ab> определяется по формуле (5); S>7>>;>>11>> >=2.6-2.7+0-6-0+4.2=-1.9; f>ОПТ >= ab = 7-11; |
|
1 |
11 |
-2,7 |
2,7 |
0,7 |
0,9 |
7-11 |
|
|
2 |
2:2 |
-0,8 |
0,8 |
0,7 |
2,8 |
||
|
3 |
3:3 |
0,8 |
-0,8 |
0,7 |
4,4 |
||
|
4 |
4:4 |
0,5 |
-0,5 |
1,1 |
4,5 |
||
|
5 |
5:5 |
1,3 |
-1,3 |
0,1 |
4,3 |
||
|
6 |
6:6 |
4,3 |
-4,3 |
-1,7 |
5,5 |
||
|
7 |
7:7 |
5,5 |
-5,5 |
-2,1 |
6,3 |
||
|
8 |
8:8 |
3,8 |
-3,8 |
-0,3 |
6,4 |
||
|
8-9 |
|||||||
|
q |
8-9 |
R>8>>;>>9> |
R>9>>;>>8> |
>8>>;>>9> |
>9>>;>>8> |
f>опт> |
q>K>> >= 1,2 - (ОH); R>8;9 >= -0.2 < 0 = b = 8; = a = 9; S>ab> определяется по формуле (5); S>9>>;>>8>=2.7-2.9+7.9-0-10+0=-2.3; f>ОПТ >= ab = 9-8; |
|
1 |
11 |
-0,2 |
0,2 |
2,9 |
2,5 |
9-8 |
|
|
2 |
2:2 |
-2,5 |
2,5 |
4,1 |
0,4 |
||
|
3 |
3:3 |
-3,6 |
3,6 |
1,6 |
1,1 |
||
|
4 |
4:4 |
-3 |
3 |
2,3 |
0,4 |
||
|
5 |
5:5 |
-2,7 |
2,7 |
1,8 |
-0,4 |
||
|
6 |
6:6 |
-1,1 |
1,1 |
2,2 |
0,8 |
||
|
7 |
7:7 |
1,2 |
-1,2 |
2 |
2 |
||
|
8 |
8:8 |
1,5 |
-1,5 |
3 |
2,3 |
||
|
8-10 |
|||||||
|
q |
8-10 |
R>8>>;1>>0> |
R>10>>;>>8> |
>8>>;1>>0> |
>1>>0>>;>>8> |
f>опт> |
q>K>> >= 1,2 - (PH); R>8>>;1>>0>> >= 0 = a = 8; = b = 10; S>ab> определяется по формуле (5); S>8>>;1>>0>=1.6-1.5+9-0-7.9+0= 1.2; f>ОПТ>> >= ba = 10-8; |
|
1 |
11 |
0 |
0 |
2,9 |
1,5 |
10-8 |
|
|
2 |
2:2 |
-2,5 |
2,5 |
4,1 |
0,2 |
||
|
3 |
3:3 |
-0,9 |
0,9 |
3,2 |
0,9 |
||
|
4 |
4:4 |
0,2 |
-0,2 |
2,3 |
1,1 |
||
|
5 |
5:5 |
-0,9 |
0,9 |
1,8 |
-0,5 |
||
|
6 |
6:6 |
-1 |
1 |
2,2 |
-0,2 |
||
|
7 |
7:7 |
-0,6 |
0,6 |
2 |
0 |
||
|
8 |
8:8 |
-0,5 |
0,5 |
3 |
1,1 |
||
|
8-11 |
|||||||
|
q |
8-11 |
R>8>>;1>>1> |
R>1>>1>>;>>8> |
>8>>;1>>1> |
>1>>1>>;>>8> |
f>опт> |
q>K>> >= 2,8 - (PH); R>8;11 >= -9,2 < 0 = b = 8; = a = 11; S>ab> определяется по формуле (5); S>11>>;>>8>> >=2.5-2.7+0-2.9-0+0.9=-2,2; f>ОПТ >= ab = 11-8; |
|
1 |
11 |
-7,1 |
7,1 |
2,9 |
0,9 |
11-8 |
|
|
2 |
2:2 |
-9,2 |
9,2 |
4,7 |
0,6 |
||
|
3 |
3:3 |
-7,5 |
7,5 |
2,8 |
0,4 |
||
|
4 |
4:4 |
-5,5 |
5,5 |
2,8 |
2,4 |
||
|
5 |
5:5 |
-3 |
3 |
0,5 |
2,6 |
||
|
6 |
6:6 |
0,9 |
-0,9 |
-0,9 |
5,1 |
||
|
7 |
7:7 |
3,7 |
-3,7 |
-3,3 |
5,5 |
||
|
8 |
8:8 |
5 |
-5 |
-2,5 |
7,6 |
||
|
9-10 |
|||||||
|
q |
9-10 |
R>9>>;1>>0> |
R>1>>0>>;>>9> |
>9>>;1>>0> |
>1>>0>>;>>9> |
f>опт> |
q>K>> >= 1,8 - (PH); R>9>>;1>>0>> >= 2,3 > 0 = a = 9; = b = 10; S>ab> определяется по формуле (5); S>9>>;1>>0>> >=1.5-3.4+1.6-3.1-0.8+3.3=-0.9; f>ОПТ >= ab = 9-10; |
|
1 |
11 |
0,2 |
-0,2 |
2,5 |
1,5 |
9-10 |
|
|
2 |
2:2 |
0 |
0 |
1,8 |
0,6 |
||
|
3 |
3:3 |
2,3 |
-2,3 |
2,1 |
3,2 |
||
|
4 |
4:4 |
3,2 |
-3,2 |
0,2 |
2,2 |
||
|
5 |
5:5 |
1,8 |
-1,8 |
1 |
1,6 |
||
|
6 |
6:6 |
0,1 |
-0,1 |
1,7 |
0,6 |
||
|
7 |
7:7 |
-1,8 |
1,8 |
3,5 |
0,5 |
||
|
8 |
8:8 |
-2 |
2 |
2,8 |
-0,4 |
||
|
9-11 |
|||||||
|
q |
9-11 |
R>9>>;1>>1> |
R>1>>1>>;>>9> |
>9>>;1>>1> |
>1>>1>>;>>9> |
f>опт> |
q>K>> >= 1,8 - (PH); R>15;13 >= -6,9 < 0 = b = 9; = a = 11; S>ab> определяется по формуле (5); S>1>>1>>;>>9>=0.8-2.5+0-0-0+0=-1.7; f>ОПТ >= ab = 11-9; |
|
1 |
11 |
-6,9 |
6,9 |
2,5 |
0,9 |
11-9 |
|
|
2 |
2:2 |
-6,7 |
6,7 |
2,4 |
1 |
||
|
3 |
3:3 |
-4,3 |
4,3 |
1,7 |
2,7 |
||
|
4 |
4:4 |
-2,5 |
2,5 |
0,7 |
3,5 |
||
|
5 |
5:5 |
-0,3 |
0,3 |
-0,3 |
4,7 |
||
|
6 |
6:6 |
2 |
-2 |
-1,4 |
5,9 |
||
|
7 |
7:7 |
2,5 |
-2,5 |
-1,8 |
6 |
||
|
8 |
8:8 |
3,5 |
-3,5 |
-2,7 |
6,1 |
||
|
10-11 |
|||||||
|
q |
10-11 |
R>1>>0>>;1>>1> |
R>1>>1>>;1>>0> |
>1>>0>>;1>>1> |
>1>>1>>;1>>0> |
f>опт> |
q>K>> >= 2,8 - (PH); R>1>>0>>;1>>1>> >= -6.7 < 0 = b = 10; = a = 11; S>ab> определяется по формуле (5); S>1>>1>>;1>>0>=1.6-1.6+0-1.5-0+0.9 =-0,6; f>ОПТ >= ab = 11-10; |
|
1 |
11 |
-7,1 |
7,1 |
1,5 |
0,9 |
11-10 |
|
|
2 |
2:2 |
-6,7 |
6,7 |
2,2 |
2 |
||
|
3 |
3:3 |
-6,6 |
6,6 |
3 |
2,9 |
||
|
4 |
4:4 |
-5,7 |
5,7 |
1,4 |
2,2 |
||
|
5 |
5:5 |
-2,1 |
2,1 |
-0,4 |
4 |
||
|
6 |
6:6 |
1,9 |
-1,9 |
-2,4 |
6 |
||
|
7 |
7:7 |
4,3 |
-4,3 |
-3,8 |
7 |
||
|
8 |
8:8 |
5,5 |
-5,5 |
-3,9 |
8,1 |
Общая очередность определяется методом пометок, учитывающая приоритет в обработке на основе выполненных вычислений (табл. 21).
Таблица 21
Расчет оптимальной очередности расстановки станков
|
Сочетание партий |
Оптимальная очередность в сочетании |
|
1-7 |
7-1 |
|
1-8 |
8-1 |
|
1-9 |
9-1 |
|
1-10 |
1-10 |
|
1-11 |
11-1 |
|
7-8 |
7-8 |
|
7-9 |
7-9 |
|
7-10 |
7-10 |
|
7-11 |
7-11 |
|
8-9 |
9-8 |
|
8-10 |
10-8 |
|
8-11 |
11-8 |
|
9-10 |
9-10 |
|
9-11 |
11-9 |
|
10-11 |
11-10 |
Вывод: общая оптимальная очередность обработки деталей на поточной линии f>ОПТ >= 7 – 11 – 9 – 10 – 1 – 8.
5. Оптимизация обработки разно маршрутных партий деталей при последовательном их виде движения
Методика решения задачи для разно маршрутных деталей характеризуется тем, что рассмотренный алгоритм дополняется следующим этапом: после определения оптимальной параллельной очередности обработки партий деталей выделяются опорные станки, для которых разность разностей последующего и предыдущего циклов в полученной оптимальной очередности 0. Для этих станков оптимальная очередность определяется по поправке: R>>> >= T>g>>>> >- T>g>>> .
Если R 0, то оптимальная очередность совпадает с оптимальной очередностью групповой обработки, если R 0 - очередность обратная.
Общая оптимальная очередность обработки партий деталей по каждому станку принимается на основе приоритетов, рассчитываемых по полученным результатам.
Пример: на участке обрабатываются пять разномаршрутных деталей. Длительности операционных циклов и закрепления детале-операций за станками задана и приведена в табл. 22. Требуется определить оптимальную очередность обработки партий деталей на каждом станке.
Таблица 22
Исходные данные
|
№ станков |
№№ деталей, длительность операционного цикла в часах |
|||||
|
1 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
5 ;1,8 |
7 ;0,7 |
8 ;2,9 |
7 ;2,5 |
6; 1,5 |
8; 0,9 |
|
2 |
6 ;2,5 |
6 ;0,9 |
2 ;2,7 |
8 ;0,8 |
3; 1,6 |
7; 2,6 |
|
3 |
1 ;0,4 |
5 ;2,6 |
1 ;0,7 |
2 ;1,9 |
4; 3,4 |
1; 2,5 |
|
4 |
7 ;2,1 |
4 ;2,9 |
6 ;2,5 |
3 ;1,5 |
5; 0,9 |
6; 2,7 |
|
5 |
8 ;0,9 |
3 ;1,7 |
3 ;0,4 |
1 ;1,7 |
7; 0,9 |
5; 2,7 |
|
6 |
2 ;1,5 |
8 ;0,9 |
4 ;1,3 |
6 ;1,6 |
2; 0,7 |
2; 2,9 |
|
7 |
3 ;2,9 |
1 ;2,5 |
5 ;0,5 |
5 ;2,5 |
1; 1,5 |
3; 1,7 |
|
8 |
4 ;0,7 |
2 ;3,5 |
7 ;2,5 |
4 ;0,8 |
8;1,6 |
4; 2,6 |
Таблица 23. Исходные календарные параметры
|
6 |
9 |
12 |
13 |
14 |
15 |
|||||||||||||
|
1 |
5 |
1,8 |
0 |
7 |
0,7 |
0 |
8 |
2,9 |
0 |
7 |
2,5 |
0 |
6 |
1,5 |
0 |
8 |
0,9 |
0 |
|
5,5 |
5,5 |
0 |
0,9 |
14,1 |
-13,2 |
0 |
10,6 |
-10,6 |
0,8 |
10 |
-9,2 |
2,5 |
8,1 |
-5,6 |
0 |
17,7 |
-17,7 |
|
|
- |
7,3 |
- |
- |
14,8 |
- |
- |
13,5 |
- |
- |
12,5 |
- |
- |
9,6 |
- |
- |
18,6 |
- |
|
|
2 |
6 |
2,5 |
0 |
6 |
0,9 |
0 |
2 |
2,7 |
0 |
8 |
0,8 |
0 |
3 |
1,6 |
0 |
7 |
2,6 |
0 |
|
3 |
7,3 |
-4,3 |
1,6 |
13,2 |
-11,6 |
10,1 |
0,7 |
9,4 |
0 |
12,5 |
-12,5 |
8,3 |
2,2 |
6,1 |
0,9 |
15,1 |
-14,2 |
|
|
- |
9,8 |
- |
- |
14,1 |
- |
- |
3,4 |
- |
- |
13,3 |
- |
- |
3,8 |
- |
- |
17,7 |
- |
|
|
3 |
1 |
0,4 |
0 |
5 |
2,6 |
0 |
1 |
0,7 |
0 |
2 |
1,9 |
0 |
4 |
3,4 |
0 |
1 |
2,5 |
0 |
|
12,4 |
0 |
12,4 |
2,5 |
10,6 |
-8,1 |
12,8 |
0 |
12,8 |
9,7 |
1,7 |
8 |
4,9 |
3,8 |
1,1 |
16,1 |
0 |
16,1 |
|
|
- |
0,4 |
- |
- |
13,2 |
- |
- |
0,7 |
- |
- |
3,6 |
- |
- |
7,2 |
- |
- |
2,5 |
- |
|
|
4 |
7 |
2,1 |
0 |
4 |
2,9 |
0 |
6 |
2,5 |
0 |
3 |
1,5 |
0 |
5 |
0,9 |
0 |
6 |
2,7 |
0 |
|
0,9 |
9,8 |
-8,9 |
5,1 |
7,7 |
-2,6 |
5,4 |
5,6 |
-0,2 |
8,2 |
3,6 |
4,6 |
4 |
7,2 |
-3,2 |
3,5 |
12,4 |
-8,9 |
|
|
- |
11,9 |
- |
- |
10,6 |
- |
- |
8,1 |
- |
- |
5,1 |
- |
- |
8,1 |
- |
- |
15,1 |
- |
|
|
5 |
8 |
0,9 |
0 |
3 |
1,7 |
0 |
3 |
0,4 |
0 |
1 |
1,7 |
0 |
7 |
0,9 |
0 |
5 |
2,7 |
0 |
|
0 |
11,9 |
-11,9 |
8 |
6 |
2 |
9,7 |
3,4 |
6,3 |
11,6 |
0 |
11,6 |
1,6 |
9,6 |
-8 |
6,2 |
9,7 |
-3,5 |
|
|
- |
12,8 |
- |
- |
7,7 |
- |
- |
3,8 |
- |
- |
1,7 |
- |
- |
10,5 |
- |
- |
12,4 |
- |
|
|
6 |
2 |
1,5 |
0 |
8 |
0,9 |
0 |
4 |
1,3 |
0 |
6 |
1,6 |
0 |
2 |
0,7 |
0 |
2 |
2,9 |
0 |
|
10,9 |
0,4 |
10,5 |
0 |
14,8 |
-14,8 |
8,4 |
3,8 |
4,6 |
3,3 |
8,4 |
5,1 |
9,9 |
1,5 |
8,4 |
13,2 |
2,5 |
10,7 |
|
|
- |
1,9 |
- |
- |
15,7 |
- |
- |
5,1 |
- |
- |
10 |
- |
- |
2,2 |
- |
- |
5,4 |
- |
|
|
7 |
3 |
2,9 |
0 |
1 |
2,5 |
0 |
5 |
0,5 |
0 |
5 |
2,5 |
0 |
1 |
1,5 |
0 |
3 |
1,7 |
0 |
|
8 |
1,9 |
6,1 |
13,2 |
0 |
13,2 |
7,9 |
5,1 |
2,8 |
4,9 |
5,9 |
-1 |
10,6 |
0 |
10,6 |
11,5 |
5,4 |
6,1 |
|
|
- |
4,8 |
- |
- |
2,5 |
- |
- |
5,6 |
- |
- |
8,4 |
- |
- |
1,5 |
- |
- |
7,1 |
- |
|
|
8 |
4 |
0,7 |
0 |
2 |
3,5 |
0 |
7 |
2,5 |
0 |
4 |
0,8 |
0 |
8 |
1,6 |
0 |
4 |
2,6 |
0 |
|
7,3 |
4,8 |
2,5 |
9,7 |
2,5 |
7,2 |
2,9 |
8,1 |
-5,2 |
7,4 |
5,1 |
2,3 |
0 |
10,5 |
-10,5 |
8,9 |
7,1 |
1,8 |
|
|
- |
5,5 |
- |
- |
6 |
- |
- |
10,6 |
- |
- |
5,9 |
- |
- |
12,1 |
- |
- |
9,7 |
- |
На основании исходных данных составляется таблица исходных календарных параметров (табл. 23).
Далее рассматриваются возможные сочетания пар партий деталей 2-5, 2-7, 2-9, 2-10, 2-11, 5-7, 5-9, 5-10, 5-11, 4-9, 7-10, 7-11, 9-10, 9-11, 10-11. Для каждого из сочетаний рассчитываются оптимальная очередность обработки партий по каждому из станков. Проиллюстрируем данный этап (табл.24).
Таблица 24
|
1-7 |
|||||||
|
q |
1 - 7 |
R>1;7> |
R>7;1> |
>1;7> |
>7;1> |
f>опт> |
q>K>> >= 5,6 - (PH); R>1;7 >= -13,9 < 0 = b = 1; = a = 7; S>ab> определяется по формуле (5); S>7;1>=1.5-0.9+10.9-11.9-0+1.7=1.3; f>ОПТ>> >= ba = 1-7; q>оп>= 1,2,3,6; Δ R>1-7>=12,8-15,7= - 2,9 < 0 |
|
1 |
5:7 |
13,2 |
-13,2 |
-6,8 |
9,3 |
1-7 |
|
|
2 |
6:6 |
7,3 |
-7,3 |
-3,4 |
6,8 |
1-7 |
|
|
3 |
1:5 |
20,5 |
-20,5 |
-10,2 |
13,2 |
1-7 |
|
|
4 |
7:4 |
-6,3 |
6,3 |
4,2 |
0,8 |
7-1 |
|
|
5 |
8:3 |
-13,9 |
13,9 |
6,8 |
-4,2 |
7-1 |
|
|
6 |
2:8 |
25,3 |
-25,3 |
-12,9 |
15,3 |
1-7 |
|
|
7 |
3:1 |
-7,1 |
7,1 |
4,8 |
0,6 |
7-1 |
|
|
8 |
4:2 |
-4,7 |
4,7 |
3 |
1,2 |
7-1 |
|
|
1-8 |
|||||||
|
q |
1,8 |
R>1>>;>>8> |
R>8>>;>>1> |
>1>>;>>8> |
>8>>;>>1> |
f>опт> |
q>K>> >= 1,5 - (PH); R>1>>;>>8>> >= 10,6 > 0 = a = 1; = b = 8; S>ab> определяется по формуле (5); S>1;8>=0.4-2.9+9.7-10.6-0+5.5= 2.1; f>ОПТ>> >= ba = 8-1; q>оп>= 2,3,4,5; Δ R>1;8>=12,8-13,5= - 0.7 < 0 |
|
1 |
5:8 |
10,6 |
-10,6 |
-3,3 |
8 |
1-8 |
|
|
2 |
6:2 |
-13,7 |
13,7 |
9,1 |
-3,9 |
8-1 |
|
|
3 |
1:1 |
-0,4 |
0,4 |
0,4 |
0,7 |
8-1 |
|
|
4 |
7:6 |
-8,7 |
8,7 |
6,3 |
-1,7 |
8-1 |
|
|
5 |
8:3 |
-18,2 |
18,2 |
9,4 |
-8,1 |
8-1 |
|
|
6 |
2:4 |
5,9 |
-5,9 |
-1,9 |
4,7 |
1-8 |
|
|
7 |
3:5 |
3,3 |
-3,3 |
-0,3 |
3,7 |
1-8 |
|
|
8 |
4:7 |
7,7 |
-7,7 |
-2,6 |
5,8 |
1-8 |
|
|
1-9 |
|||||||
|
q |
1,9 |
R>1>>;>>9> |
R>9>>;>>1> |
>1>>;>>9> |
>9>>;>>1> |
f>опт> |
q>K>> >= 5,6 - (РН); R>1>>;>>9>> >= -23,5 < 0 = b = 1; = a = 9; S>ab> определяется по формуле (5); S>12>=1.5-0.9+10.9-11.9-3.3+0=-3.7; f>ОПТ>> >= ab = 9-1; q>оп>= 4,5; Δ R>1;9>=12,8-13,3= - 0.5 < 0 |
|
1 |
5:7 |
9,2 |
-9,2 |
-2,7 |
7 |
1-9 |
|
|
2 |
6:8 |
8,2 |
-8,2 |
-2,7 |
6 |
1-9 |
|
|
3 |
1:2 |
4,4 |
-4,4 |
-1,3 |
3,6 |
1-9 |
|
|
4 |
7:3 |
-13,5 |
13,5 |
8,3 |
-4,7 |
9-1 |
|
|
5 |
8:1 |
-23,5 |
23,5 |
12,8 |
-10,2 |
9-1 |
|
|
6 |
2:6 |
5,4 |
-5,4 |
-6,5 |
9,6 |
1-9 |
|
|
7 |
3:5 |
7,1 |
-7,1 |
-1,1 |
6,5 |
1-9 |
|
|
8 |
4:4 |
0,2 |
-0,2 |
0,4 |
1,1 |
1-9 |
|
|
1-10 |
|||||||
|
q |
1,10 |
R>1>>;1>>0> |
R>1>>0>>;>>1> |
>1>>;1>>0> |
>1>>0>>;>>1> |
f>опт> |
q>K>> >= 2,8 - (PH); R>1>>;1>>0>> >= -10,4< 0 = b = 1; = a = 10; S>ab> определяется по формуле (5); S>10;1>=0.7-2.5+7.3-7.3-0+2.2=0.4; f>ОПТ>> >= ba = 1-10; q>оп>= 1,3,6,8; Δ R>1;10>=12,8-12,1= 0.7 > 0 |
|
1 |
5:6 |
5,6 |
-5,6 |
-0,8 |
4,1 |
1-10 |
|
|
2 |
6:3 |
-10,4 |
10,4 |
7,6 |
-3,5 |
1-10 |
|
|
3 |
1:4 |
11,3 |
-11,3 |
-3,4 |
7,2 |
1-10 |
|
|
4 |
7:5 |
-5,7 |
5,7 |
4,7 |
-1,7 |
1-10 |
|
|
5 |
8:7 |
-3,9 |
3,9 |
3,2 |
-1,4 |
1-10 |
|
|
6 |
2:2 |
2,1 |
-2,1 |
0,4 |
1,8 |
1-10 |
|
|
7 |
3:1 |
-4,5 |
4,5 |
4,8 |
-0,4 |
1-10 |
|
|
8 |
4:8 |
13 |
-13 |
-5 |
7,3 |
1-10 |
|
|
1-11 |
|||||||
|
q |
1,11 |
R>1>>;1>>1> |
R>1>>1>>;>>1> |
>1>>;1>>1> |
>1>>1>>;>>1> |
f>опт> |
q>K>> >= 1,5 - (PH); R>1>>;>>5>> >= 17,7 > 0 = a = 1; = b = 11; S>ab> определяется по формуле (5); S>1;11 >=2.7-0.9+6.2-17.7-0+5.5= -4.2; f>ОПТ>> >= ab = 1-11; q>оп>= 1,2,4,7,8; Δ R>1;11>=12,8-18,6= - 5,8 < 0 |
|
1 |
5:8 |
17,7 |
-17,7 |
-10,4 |
13,1 |
1-11 |
|
|
2 |
6:7 |
9,9 |
-9,9 |
-5,3 |
10,4 |
1-11 |
|
|
3 |
1:1 |
-3,7 |
3,7 |
0,4 |
2,5 |
11-1 |
|
|
4 |
7:6 |
0 |
0 |
-0,5 |
5,3 |
1-11 |
|
|
5 |
8:5 |
-8,4 |
8,4 |
3,1 |
0,5 |
11-1 |
|
|
6 |
2:2 |
-0,2 |
0,2 |
-0,6 |
5 |
11-1 |
|
|
7 |
3:3 |
0 |
0 |
-0,6 |
5,2 |
1-11 |
|
|
8 |
4:4 |
0,7 |
-0,7 |
-1,6 |
4,9 |
1-11 |
|
|
7-8 |
|||||||
|
q |
7,8 |
R>7>>;>> 8> |
R>8>>;>>7> |
>7>>;>>8> |
>8>>;>>7> |
f>опт> |
q>K>> >= 2,8 - (PH); R>7>>;>>8>> >= -21<0 = b = 7; = a = 8; S>ab> определяется по формуле (5); S>8;7>=3.5-0.9+9.7-13.2-2.9+0.7=-3.1; f>ОПТ>> >= ab = 8-7; q>оп>=1,2,3,4,5,6; Δ R>7;8>=15,7-13,5= 2,2 > 0 |
|
1 |
7:8 |
-2,6 |
2,6 |
4,2 |
-0,6 |
8-7 |
|
|
2 |
6:2 |
-21 |
21 |
13,4 |
-9,8 |
8-7 |
|
|
3 |
5:1 |
-20,9 |
20,9 |
13,2 |
-9,9 |
8-7 |
|
|
4 |
4:6 |
-2,4 |
2,4 |
5 |
0,4 |
8-7 |
|
|
5 |
3:3 |
-4,3 |
4,3 |
4,3 |
-2,2 |
8-7 |
|
|
6 |
8:4 |
-19,4 |
19,4 |
11,9 |
-9,7 |
8-7 |
|
|
7 |
1:5 |
10,4 |
-10,4 |
-2,6 |
5,6 |
8-7 |
|
|
8 |
2:7 |
12,4 |
-12,4 |
-2,1 |
8,1 |
8-7 |
|
|
7-9 |
|||||||
|
q |
7,9 |
R>7>>;>>9> |
R>9>>;>>7> |
>7>>;>>9> |
>9>>;>>7> |
f>опт> |
q>K>> >= 3,7 - (PH); R>7>>;>>9>> >= -16,1 < 0 = b = 7; = a = 9; S>ab> определяется по формуле (5); S>9;7>=2.5-2.6+13.2-10.6-4.9+1.7= -0.7; f>ОПТ >= ab = 9-7; q>оп>= 1,3,4,5,6; Δ R>7;9>=15,7-13,3 = 2.4 |
|
1 |
7:7 |
-4 |
4 |
4,8 |
-1,6 |
9-7 |
|
|
2 |
6:8 |
0,9 |
-0,9 |
1,6 |
0,1 |
9-7 |
|
|
3 |
5:2 |
-16,1 |
16,1 |
11,5 |
-7 |
9-7 |
|
|
4 |
4:3 |
-7,2 |
7,2 |
7 |
-2,6 |
9-7 |
|
|
5 |
3:1 |
-9,6 |
9,6 |
7,7 |
-4,3 |
9-7 |
|
|
6 |
8:6 |
-19,9 |
19,9 |
7,3 |
-4,8 |
9-7 |
|
|
7 |
1:5 |
14,2 |
-14,2 |
-3,4 |
8,4 |
9-7 |
|
|
8 |
2:4 |
4,9 |
-4,9 |
0,9 |
3,4 |
9-7 |
|
|
7-10 |
|||||||
|
q |
7,10 |
R>7>>;1>>0> |
R>1>>0>>;>>7> |
>7>>;1>>0> |
>1>>0>>;>>7> |
f>опт> |
q>K>> >= 6,8 - (PH); R>7>>;1>>0>> >= - 23,2 < 0 = b = 7; = a = 10; S>ab> определяется по формуле (5); S>10;7 >=3.5-0.9+9.7-14.8-0+1.5=-1; f>ОПТ>> >= ab = 10-7; q>оп>= 1,2,3,6; Δ R>7;10>=15.7-12.1=3.6>0 |
|
1 |
7:6 |
-7,6 |
7,6 |
6,7 |
-4,5 |
10-7 |
|
|
2 |
6:3 |
-17,7 |
17,7 |
11,9 |
-9,4 |
10-7 |
|
|
3 |
5:4 |
-9,2 |
9,2 |
9,4 |
-3,4 |
10-7 |
|
|
4 |
4:5 |
0,6 |
-0,6 |
3,4 |
0,4 |
10-7 |
|
|
5 |
3:7 |
10 |
-10 |
-1,9 |
4,5 |
10-7 |
|
|
6 |
8:2 |
-23,2 |
23,2 |
14,2 |
-12,6 |
10-7 |
|
|
7 |
1:1 |
2,6 |
-2,6 |
2,5 |
1,5 |
10-7 |
|
|
8 |
2:8 |
17,7 |
-17,7 |
-4,5 |
9,6 |
10-7 |
|
|
7-11 |
|||||||
|
q |
7,11 |
R>7>>;1>>1> |
R>1>>1>>;>>7> |
>7>>;1>>1> |
>1>>1>>;>>7> |
f>опт> |
q>K>> >= 3,4 - (PH); R>7>>;1>>1>> >= -24,2 < 0 = b = 7; = a = 11; S>ab> определяется по формуле (5); S>11;7 >=2.9-2.6+5.1-10.6-3.5+0=-8.7; f>ОПТ>> >= ab = 11-7; q>оп>= 3,6; Δ R>7;11>=15,7-18,6= -2,9 < 0 |
|
1 |
7:8 |
4,5 |
-4,5 |
-2,9 |
4,5 |
7-11 |
|
|
2 |
6:7 |
2,6 |
-2,6 |
-1 |
4,5 |
7-11 |
|
|
3 |
5:1 |
-24,2 |
24,2 |
13,2 |
-8,1 |
11-7 |
|
|
4 |
4:6 |
6,3 |
-6,3 |
-1,8 |
7,4 |
7-11 |
|
|
5 |
3:5 |
5,5 |
-5,5 |
-2 |
6,4 |
7-11 |
|
|
6 |
8:2 |
-25,5 |
25,5 |
13,2 |
-9,4 |
11-7 |
|
|
7 |
1:3 |
7,1 |
-7,1 |
-2,9 |
7,1 |
7-11 |
|
|
8 |
2:4 |
5,4 |
-5,4 |
-1,1 |
7,2 |
7-11 |
|
|
8-9 |
|||||||
|
q |
8,9 |
R>8>>;>>9> |
R>9>>;>>8> |
>8>>;>>9> |
>9>>;>>8> |
f>опт> |
q>K>> >= 2,7 - (ОH); R>8>>;>>9>> >= 21,9 > 0 = a = 8; = b = 9; S>ab> определяется по формуле (5); S>8;9>=2.5-0.8+4.9-12.5-7.9+0.7= -13.1; f>ОПТ>> >= ab = 8-9; q>оп>=2,3,7; Δ R>8;9>=13,5-13,3= 0,2 >0 |
|
1 |
8:7 |
-1,4 |
1,4 |
5,4 |
1,9 |
8-9 |
|
|
2 |
2:8 |
21,9 |
-21,9 |
1,2 |
12,6 |
8-9 |
|
|
3 |
1:2 |
4,8 |
-4,8 |
-3,1 |
3,6 |
8-9 |
|
|
4 |
6:3 |
-4,8 |
4,8 |
0,9 |
-0,5 |
8-9 |
|
|
5 |
3:1 |
-5,3 |
5,3 |
-5,8 |
-1,7 |
8-9 |
|
|
6 |
4:6 |
-0,5 |
0,5 |
3,6 |
6,2 |
8-9 |
|
|
7 |
5:5 |
3,8 |
-3,8 |
5,6 |
3,3 |
8-9 |
|
|
8 |
7:4 |
-7,5 |
7,5 |
0,1 |
-2,2 |
8-9 |
|
|
8-10 |
|||||||
|
q |
8,10 |
R>8>>;1>>0> |
R>1>>0>>;>>8> |
>8>>;1>>0> |
>1>>0>>;>>8> |
f>опт> |
q>K>> >= 3,7 - (PH); R>8>>;1>>0>> >= 11,7 > 0 = a = 8; = b = 10; S>ab> определяется по формуле (5); S>8;10>=1.5-3.4+10.6-3.8-7.9+0=-3; f>ОПТ>> >= ab = 8-10; q>оп>= 2,3,4,5,8; Δ R>8;10>=13,5-12,1= 1,4 > 0 |
|
1 |
8:6 |
-5 |
5 |
5,4 |
-1 |
8-10 |
|
|
2 |
2:3 |
3,3 |
-3,3 |
1,2 |
3,1 |
8-10 |
|
|
3 |
1:4 |
11,7 |
-11,7 |
-3,1 |
7,2 |
8-10 |
|
|
4 |
6:5 |
3 |
-3 |
0,9 |
2,5 |
8-10 |
|
|
5 |
3:7 |
14,3 |
-14,3 |
-5,8 |
7,1 |
8-10 |
|
|
6 |
4:2 |
-3,8 |
3,8 |
3,6 |
-1,6 |
8-10 |
|
|
7 |
5:1 |
-7,8 |
7,8 |
5,6 |
-3,6 |
8-10 |
|
|
8 |
7:8 |
5,3 |
-5,3 |
0,1 |
4 |
8-10 |
|
|
8-11 |
|||||||
|
q |
8,11 |
R>8>>;1>>1> |
R>1>>1>>;>>8> |
>8>>;1>>1> |
>1>>1>>;>>8> |
f>опт> |
q>K>> >= 2,8 - (PH); R>8>>;1>>1>> >= 23,6 > 0 = a = 8; = b= 11; S>ab> определяется по формуле (5); S>8;11 >=2.6-2.6+8.9-15.1-2.9+0.7=-8.4; f>ОПТ>> >= ab = 8-11; q>оп>= 1,2,4,5; Δ R>8;11>=13,5-18,6= - 5,1 < 0 |
|
1 |
8:8 |
7,1 |
-7,1 |
-4,2 |
8 |
8-11 |
|
|
2 |
2:7 |
23,6 |
-23,6 |
-11,7 |
17 |
8-11 |
|
|
3 |
1:1 |
-3,3 |
3,3 |
0,7 |
2,5 |
11-8 |
|
|
4 |
6:6 |
8,7 |
-8,7 |
-4,3 |
9,5 |
8-11 |
|
|
5 |
3:5 |
9,8 |
-9,8 |
-5,9 |
9 |
8-11 |
|
|
6 |
4:2 |
-6,1 |
6,1 |
2,6 |
1,6 |
11-8 |
|
|
7 |
5:3 |
-3,3 |
3,3 |
0,2 |
2 |
11-8 |
|
|
8 |
7:4 |
-7 |
7 |
3,5 |
1,6 |
11-8 |
|
|
9-10 |
|||||||
|
q |
9,10 |
R>9>>;1>>0> |
R>1>>0>>;>>9> |
>9>>;1>>0> |
>1>>0>>;>>9> |
f>опт> |
q>K>> >= 2,5 - (PH); R>9>>;1>>0>> >= -18,6 < 0 = b = 9; = a = 10; S>ab> определяется по формуле (5); S>10;9 >=1.7-0.8+11.6-12.5-1.6+2.2=0.6; f>ОПТ>> >= ba = 9-10; q>оп>= 3,4,5,8; Δ R>9;10>=13,3-12,1= 1,2 > 0 |
|
1 |
7:6 |
-3,6 |
3,6 |
4,4 |
-0,4 |
9-10 |
|
|
2 |
8:3 |
-18,6 |
18,6 |
11,1 |
-8,7 |
9-10 |
|
|
3 |
2:4 |
6,9 |
-6,9 |
-0,2 |
5,5 |
9-10 |
|
|
4 |
3:5 |
7,8 |
-7,8 |
-2,1 |
4,5 |
9-10 |
|
|
5 |
1:7 |
19,6 |
-19,6 |
-7,9 |
10,5 |
9-10 |
|
|
6 |
6:2 |
-3,3 |
3,3 |
8,5 |
-6,2 |
9-10 |
|
|
7 |
5:1 |
-11,6 |
11,6 |
8,4 |
-4,4 |
9-10 |
|
|
8 |
4:8 |
12,8 |
-12,8 |
-4,6 |
7 |
9-10 |
|
|
9-11 |
|||||||
|
q |
9,11 |
R>9>>;1>>1> |
R>1>>1>>;>>9> |
>9>>;1>>1> |
>1>>1>>;>>9> |
f>опт> |
q>K>> >= 5,6 - (PH); R>9>>;1>>1>> >= 15,1 > 0 = a = 9; = b = 11; S>ab> определяется по формуле (5); S>9;11>=2.9-2.7+13.2-9.7-3.3+0=0.4; f>ОПТ>> >= ba = 11-9; q>оп>= 3,6,7; Δ R>9;11>=13,3-18,6= 5,3 > 0 |
|
1 |
7:8 |
8,5 |
-8,5 |
-5,2 |
8,6 |
11-9 |
|
|
2 |
8:7 |
1,7 |
-1,7 |
-1,8 |
5,2 |
11-9 |
|
|
3 |
2:1 |
-8,1 |
8,1 |
3,6 |
0,8 |
11-9 |
|
|
4 |
3:6 |
13,5 |
-13,5 |
-7,3 |
11,5 |
11-9 |
|
|
5 |
1:5 |
15,1 |
-15,1 |
-8 |
12,4 |
11-9 |
|
|
6 |
6:2 |
-5,6 |
5,6 |
7,5 |
-3 |
11-9 |
|
|
7 |
5:3 |
-7,1 |
7,1 |
3 |
1,2 |
11-9 |
|
|
8 |
4:4 |
0,5 |
-0,5 |
-1,2 |
4,6 |
11-9 |
|
|
10-11 |
|||||||
|
q |
10,11 |
R>1>>0>>;1>>1> |
R>1>>1>>;1>>0> |
>1>>0>>;1>>1> |
>1>>1>>;1>>0> |
f>опт> |
q>K>> >= 2,3 - (PH); R>10;11 >= 20.3 > 0 = a = 10; = b = 11; S>ab> определяется по формуле (5); S>1>>0>>;1>>1>=2.5-2.6+16.1-15.1-4.9+2.2= -1.8; f>ОПТ >= ab = 10-11; q>оп>= 1,2,4,6,8; Δ R>1>>0>>;1>>1>=12,1-18,6= - 5,1 < 0 |
|
1 |
6:8 |
12,1 |
-12,1 |
-8,1 |
10,5 |
10-11 |
|
|
2 |
3:7 |
20,3 |
-20,3 |
-11,3 |
15,5 |
10-11 |
|
|
3 |
4:1 |
-15 |
15 |
7,2 |
-1,3 |
11-10 |
|
|
4 |
5:6 |
5,7 |
-5,7 |
-4,3 |
7,9 |
10-11 |
|
|
5 |
7:5 |
-4,5 |
4,5 |
0,8 |
2,8 |
11-10 |
|
|
6 |
2:2 |
-2,3 |
2,3 |
-0,3 |
3,9 |
11-10 |
|
|
7 |
1:3 |
4,5 |
-4,5 |
-3,9 |
7,1 |
10-11 |
|
|
8 |
8:4 |
-12,3 |
12,3 |
5 |
-0,8 |
11-10 |
На основе рассчитанных оптимальных очередностей обработки пар партий деталей методом приоритетов определяется общая оптимальная очередность обработки партий деталей по каждому из станков (табл. 25).
Таблица 25. Определение общей очередности деталей
|
Номер станка |
Оптимальная очередность в сочетаниях пар партий деталей |
Общая оптимальная Очередность обрабатываемых партий деталей |
||||||||||||||
|
1-7 |
1-8 |
1-9 |
1-10 |
1-11 |
7-8 |
7-9 |
7-10 |
7-11 |
8-9 |
8-10 |
8-11 |
9-10 |
9-11 |
10-11 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
1 |
1-7 |
1-8 |
1-9 |
1-10 |
1-11 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
8-11 |
9-10 |
11-9 |
10-11 |
1
– 8 – |
|
2 |
1-7 |
8-1 |
1-9 |
1-10 |
1-11 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
8-11 |
9-10 |
11-9 |
10-11 |
8
-
|
|
3 |
1-7 |
8-1 |
1-9 |
1-10 |
11-1 |
8-7 |
9-7 |
10-7 |
11-7 |
8-9 |
8-10 |
11-8 |
9-10 |
11-9 |
11-10 |
11
– 8 – 9 -
|
|
4 |
7-1 |
8-1 |
9-1 |
1-10 |
1-11 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
8-11 |
9-10 |
11-9 |
10-11 |
8
– 9 -
|
|
5 |
7-1 |
8-1 |
9-1 |
1-10 |
11-1 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
8-11 |
9-10 |
11-9 |
11-10 |
8
-
|
|
6 |
1-7 |
1-8 |
1-9 |
1-10 |
11-1 |
8-7 |
9-7 |
10-7 |
11-7 |
8-9 |
8-10 |
11-8 |
9-10 |
11-9 |
11-10 |
11 – 1 – 8 – 9 – 10 - 7 |
|
7 |
7-1 |
1-8 |
1-9 |
1-10 |
1-11 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
11-8 |
9-10 |
11-9 |
10-11 |
1
– 8 -
|
|
8 |
7-1 |
1-8 |
1-9 |
1-10 |
1-11 |
8-7 |
9-7 |
10-7 |
7-11 |
8-9 |
8-10 |
11-8 |
9-10 |
11-9 |
11-10 |
1
-
|
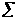
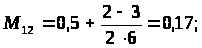
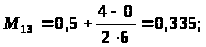
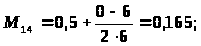
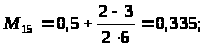
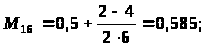
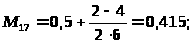
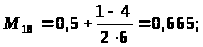
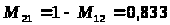 ;
;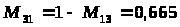 ;
;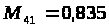 ;
;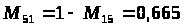 ;
;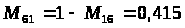 ;
;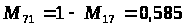 ;
;
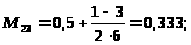
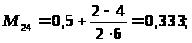
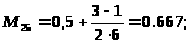

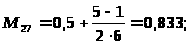
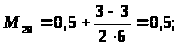
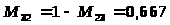 ;
;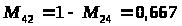 ;
;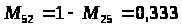 ;
;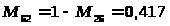 ;
;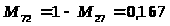 ;
;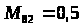
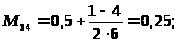
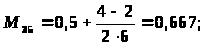
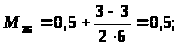
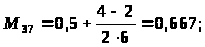
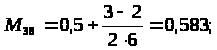
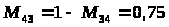 ;
;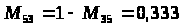 ;
;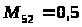 ;
;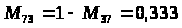 ;
;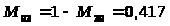
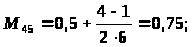
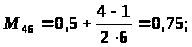
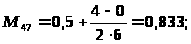
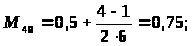
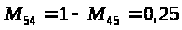 ;
;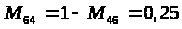 ;
;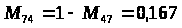 ;
;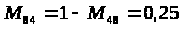
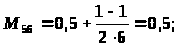
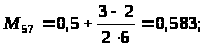
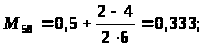
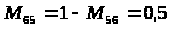 ;
;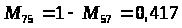 ;
;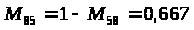
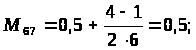
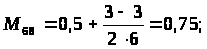
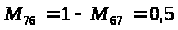 ;
;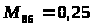 ;
;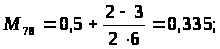
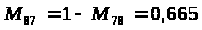 ;
;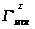
 –
–

 - 7 - 11
- 7 - 11 - 7
- 7 -
-
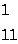
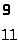 - 7 -
- 7 -
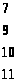
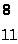 -
-
 - 10
- 10