Від стародавніх до сучасних теорій руху планет

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ім. Т.Г. Шевченка

Фізичний факультет, кафедра астрономії

ДИПЛОМНИЙ ПРОЕКТ

ТЕМА:

Від стародавніх до сучасних теорій руху планет

Виконав: студент ІІІ курсу

Група 112 ФА

Колосов Сергій

Київ 2010

Зміст

Вступ

Перші кроки завжди важкі

Трохи теорії

Сучасні теорії руху небесних тіл

Висновок

Література

Вступ

Ще здавна серед "нерухомих зір" мешканці Землі помітили "блукаючі зорі", які грецькою мовою називаються планетами. Тоді були відомі 7 "блукаючих зір": зореподібні - Меркурій, Венера, Марс, Юпітер і Сатурн, а також дископодібні - Сонце та Місяць. Згодом, коли з'ясувалось, що Сонце є найближчою до нас зорею, а Місяць є супутником нашої планети Земля, назва "планети" закріпилась лише за тими космічними об'єктами, які обертаються навколо Сонця. Ще пізніше, крім згаданих планет, були відкриті планети Уран, Нептун і Плутон, декілька десятків супутників планет, а також декілька тисяч так званих малих планет (астероїдів).

Найпростіше помітити "блукання" Місяця серед зір, бо він швидко рухається із заходу на схід і за 27.3 доби "пробігає" всю небесну сферу, тобто здійснює повний оберт. Якщо в якусь ніч примітити його положення по відношенню до найближчих зір, то вже наступної ночі Місяць знаходитиметься в оточенні інших зір, бо за добу переміститься по небу на 13.2".

Переміщення Сонця серед зір не можна спостерігати безпосередньо, бо зорі вдень невидимі. Проте, якщо замітити якусь зорю поблизу горизонту в західній частині неба невдовзі після заходу Сонця і спробувати її відшукати через декілька днів в той же час, то можна помітити, що вона знизилась і ніби наблизилась до Сонця. Ще через декілька днів зоря зникне за горизонтом, а її місце займе інша зоря, яка раніше знаходилась на схід від першої. Надалі і ця зоря теж наближатиметься до Сонця. Саме за такими спостереженнями можна зробити висновок про зміну положення Сонця серед зір.

В давні часи спостереження за положеннями зір та планет проводились регулярно, що надало можливість визначити видимий шлях Сонця по небу. Виявилось, що Сонце, як і Місяць, рухається із заходу на схід і за 365.25 доби його видимий шлях набуде вигляду кола на небесній сфері, тобто через цей інтервал часу воно повертається до тих же самих зір. Річний шлях Сонця серед зір назвали екліптикою, яка за уявленнями древніх не змінює свого положення по відношенню до зір. За добу Сонце зміщується вздовж екліптики на схід приблизно на 1º.

Більш складним виявився рух зореподібних планет, які завжди розташовані поблизу екліптики. Нижні планети Меркурій і Венера ніби коливаються відносно Сонця. Спочатку планета рухається серед зір швидше за Сонце і обганяє його. Потім на певній кутовій відстані на схід від Сонця планета сповільнює свій рух, а Сонце наздоганяє та випереджає планету. Через деякий час, досягнувши максимального кутового віддалення на захід від Сонця, планета знову починає рухатися швидше і наздоганяє його. Надалі увесь цикл повторюється. Найбільше віддалення від Сонця сягає 40º для Венери і в середньому 23° (від 18 до 28°) для Меркурія. Ось тому Меркурій і Венера видимі тільки або вранці на сході, незадовго до сходу Сонця, або увечері на заході, після заходу Сонця.

Для верхніх планет - Марса, Юпітера, Сатурна, Урана і Нептуна - характерні "петлі" на небі. В основному ці планети переміщуються серед зір із заходу на схід. Проте в певні періоди кожна з них сповільнює свій рух, зупиняється серед зір, а згодом починає рухатись у зворотному напрямку, тобто зі сходу на захід. Ще через деякий час планета знову зупиняється і починає рухатись у звичайному для неї напрямку. Таким чином, спостерігач має можливість зафіксувати в рухові планет "петлі". Марс здійснює їх через кожні 780, Юпітер - 399, а Сатурн - 378 діб.

Перші кроки завжди важкі

Перші спроби пояснити видимі переміщення планет на небі, а заодно створити теорії руху з метою передбачення їхніх положень в будь-який наступний чи минулий момент належать стародавнім грекам і вавілонянам. Зокрема відомо, що одна з перших астрономічних доктрин для пояснення руху планет була запропонована Евдоксом Кнідським (біля 410-350 р. до н. е) і базувалась па системі концентричних сфер, в центрі яких знаходиться Земля. Згідно Евдоксу видимий рух кожної планети можна відтворити за допомогою чотирьох сфер, кожна з яких обертається рівномірно навколо своєї осі. Осі всіх сфер перетинаються в одній точці, але мають різні нахили. За цією концепцією дві сфери обертаються із заходу на схід, а дві інші в протилежному напрямку, до того ж періоди обертання сфер приймаються різними. Кожна із сфер, незалежно від її власного обертання, "сприймає" рух інших зовнішніх по відношенню до неї сфер. На екваторі внутрішної четвертої сфери знаходиться точка, яка зображає певну планету. Складний рух точки з урахуванням напрямку обертання всіх чотирьох сфер, періодів їхнього обертання і нахилу осей відтворює видимий рух планет з тими особливостями, про які згадувалось вище. Подальше вдосконалення системи Евдокса запропонував Каліпп, який збільшив число сфер до п'яти для Сонця, Місяця, Меркурія. Венери і Марса. Загалом, в теорії Каліппа нараховувалось 33 сфери для всіх планет. Згодом Аристотель ускладнив ще більше моделі Евдокса і Каліппа. Нагадаємо ще, що з праць Архімеда відомо про запропоновану ще в III ст. до н.е. Арістархом Самосським завершену модель геліоцентричної системи світу, в якій Земля разом з Олімпом і помешканням богів оберталась навколо своєї осі. На жаль, це вчення не було сприйняте позитивно, а перемогло уявлення про геоцентричну будову світу, яким користувались аж до XVI ст. До нас дійшли й інші свідчення про погляди на будову світу та про пояснення особливостей руху планет. Проте, на нашу думку, на цьому більш детально зупинятись не варто. Зауважимо лише, що матеріали цих вчених древності не збереглись у письмовому вигляді. Ми маємо лише свідчення так званих коментаторів їхніх вчень, тому неможливо проаналізувати математичні основи згаданих теорій, результати і точність обчислень для передбачення руху планет.

Трохи теорії

Стародавня наука про теорії руху планет починається для нас від Гіппарха (II ст. до н.е.) і Птолемея (II ст. н.е.). Останній у широковідомому трактаті "Альмагест" подав геоцентричну картину світу і теорії руху планет, а також прокоментував погляди та розрахунки щодо руху світил свого попередника Гіппарха. У короткому нарисі немає змоги зосередити увагу навіть на основних положеннях теорій руху відомих на той час планет, а тому зупинимось лише на викладенні підходу, яким користувались Гіппарх та Птолемей для дослідження руху планет. З цією метою розглянемо один з простих випадків руху в площині - а саме обертання паралелограма навколо однієї з його сторін.

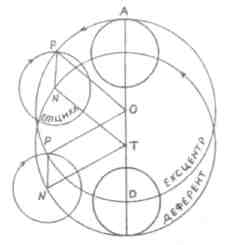
Нехай в паралелограмі TNPO сторони-стержні мають змогу обертатись в площині навколо кожної з вершин завдяки наявності в них шарнірів. Закріпимо на площині сторону ТО паралелограма і повернемо його на 360° проти годинникової стрілки. Неважко збагнути і довести, що вершини N і Р, які лежать на одній із сторін паралелограма, опишуть два кола однакового діаметра з центрами в точках Т і О. При обертанні сторони TN проти годинникової стрілки сторона NP буде обертатись за годинниковою стрілкою. Причому за повний оберт сторони TN відрізок NP зробить теж повний оберт навколо точки N. Отже, точка Р опише коло радіусом NP з центром в точці N. Така сукупність рухів дістала в кінематиці назву пари обертань: одне з них зводиться до переносного обертання відрізка NP разом із NT, а інше є відносним обертанням NP навколо шарніра N. Абсолютний рух NP, тобто його рух відносно нерухомих осей в площині рисунка, зводиться до поступального переміщення. Крім того, в даному випадку поступальний рух є коловим. Розглянута схема руху шарнірного паралелограма надає можливість зрозуміти вчення про теорії руху стародавніх вчених.

Нагадаємо, що коло радіуса TN в "Альмагесті" названо деферентом (основне коло), коло радіуса ОР - ексцентром (ексцентричне коло), а коло радіуса NP - епіциклом. Точка N зображає так знану середню (фіктивну) планету, точка Р - реальну планету, а точка Т збігається з оком спостерігача і разом з тим, за уявленнями древніх, з центром світу. Відмітимо два особливі положення шарнірного паралелограма. В першому з них планета Р збігається з точкою А і знаходиться на найбільшій відстані від Т (паралелограм витягується в одну лінію), в другому положенні планета Р збігається з точкою D і віддалена від ока спостерігача Т на найменшу відстань. За грецькою термінологією ці точки дістали назви апогей і перигей. Якщо позначимо радіус деферента або ексцентра через а, радіус епіцикла - b (приймається, що b < а), r_>1> = ТА і r_>2> = TD, то

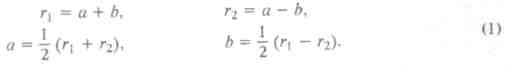
Відношення

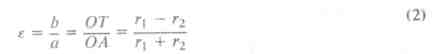
одержало назву ексцентриситет ексцентра. Саме від t: залежить відхилення реального нерівномірного руху планет від рівномірного.

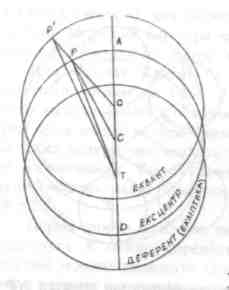
Наведена геометрична модель деферентів, ексцентрів і епіциклів та співвідношення (1) і (2) надають можливість вивести всі необхідні формули для розрахунку широти і довготи планети. Такий геометричний, а по своїй суті кінематичний підхід використовувався для створення перш за все теорій руху Сонця і Місяця, а потім вже планет і одержав назву гіпотези простого ексцентриситету. Саме завдяки цій гіпотезі вдалось пояснити та врахувати відмінність швидкостей Сонця і Місяця поблизу апогею і перигею, тобто так звану першу нерівність в рухові планет. З наявністю цієї нерівності пов'язане виникнення таких фундаментальних понять, як середній рух Сонця, тропічний рік й інших. Проте Гіппарху і Птолемею була відома також нерівність руху і зореподібних планет по підношенню до Сонця, яка дістала назву другої нерівності. Задачу про врахування другої нерівності Птолемей вирішив тим же методом деферентів і епіциклів, як і для випадку першої нерівності. Але з метою уточнення теорії руху цих планет ним було здійснене бісектування ексцентриситету. Суть його можна пояснити за допомогою рисунка.

Нехай через Ρ позначена планета, Τ - око спостерігача або центр екліптики, О - центр рівномірного обертання. Тому, як і раніше, ОТ = аг (г - повний ексцентриситет, а - радіус ексцентра). Поділимо ОТ пополам і з'єднаємо планету Ρ із середньою точкою відрізка ОТ, яку позначимо через С. Нехай планета Р рухається по колу радіуса PC, яке є ексцентром, але так, що рівномірно обертається не радіус PC, а пряма РО. До цього і зводиться Птолемеєве бісектування ексцентриситету. За теорією, побудованою на основі такої геометричної моделі, рух планети є нерівномірним, бо точка О обумовлює нерівність руху планети по ексцентру. Отже, поруч з ексцентром і деферентом з'являється ще одне коло рівномірного обертання точки Р' - проекції точки Ρ на коло, яке дістало назву еквант в Альфонсійських таблицях (у Птолемея ця назва відсутня). Порівняно з гіпотезою простого ексцентриситету, яка відповідає врахуванню членів першого порядку, його бісектування уточнює теорії руху до рівня збереження деяких членів другого порядку відносно ексцентриситету.

Необхідно звернути увагу ще на дві обставини, які можна кваліфікувати як визначне досягнення древніх астрономів. Одна з них стосується відліку напрямків кутів при астрономічних спостереженнях. Справа в тому, що положення світил проектуються на небесну сферу, радіус якої, за уявленням древніх, вважався безмежно великим в порівнянні з відстаннями до Сонця, Місяця і планет. Отже, два паралельні напрямки ΝΡ - радіус епіцикла і ТА - лінія абсид (див. рис. на с 206) практично "збігаються" в одній точці небесної сфери. Положення цієї точки серед "нерухомих" зір наперед невідоме, тому неможливо проводити відлік кутів від неї. Гіппарх прийняв за початок відліку кутів точку весняного рівнодення, положення якої визначалось з певною точністю по рівності тривалості дня і ночі весною. Інша обставина свідчить про факт відкриття ще Гіппархом поступального руху рівнодення вздовж екліптики, або так званої прецесії, яка становить лише біля 50" за рік. Останнє підтверджує досить високий рівень по точності теорій руху планет стародавніх вчених бо на гой час точність спостережень не перевищувала 10'.

Загалом, теорії руху планет Птолемея, подані в "Альмагесті". є унікальним досягненням. Точність обчислених положень окремих планет сягає 2' на інтервалі в декілька десятиріч. Крім того, уже в постньютонівський період з'ясувалось, що три із чотирьох визначуваних Птолемеєм елементів орбіти, а саме ексцентриситет в, довгота перигею π і середня довгота, по своїй суті є геліоцентричними. Лише радіус епіцикла 6 має геоцентричну суть. Залишається нерозгаданою одна з найбільших таємниць в історії астрономічної науки: як могло статися гак, що стародавні вчені фактично користувались геліоцентричними параметрами руху планет, і чому Птолемей не зміг перейти до геліоцентричної моделі побудови Сонячної системи. Деякі відомі вчені навіть висувають припущення про те, що система Птолемея є переробкою і відлунням ще раніше детально розробленої геліоцентричної моделі про будову планетної системи, але залишеної потім в зв'язку з протиріччям її релігійній схоластиці та догмам верховних жерців.

Геометричний, а по суті кінематичний підхід до створення теорій руху планет зберігався аж до XVI століття і був "похований" видатними досягненнями середньовічних вчених Коперника (1473-1543), Тихо Браге (1546-1601), Галілея (1564 - 1642), Кеплера (1571 - 1630), Ньютона (1643-1727) та інших. Спочатку Коперник намагався уточнити теорії руху Сонця і планет на основі геометричного підходу і замінив паралелограм Птолемея подвійним паралелограмом. Проте він не зміг впоратись з відомими на той час нерівностями в рухові Сонця, Місяця і планет в рамках геоцентричної будови планетної системи, тому відмовився від неї і кінець кінцем дійшов висновку, що Земля обертається навколо Сонця. Потім Тихо Браге на основі спостережень Місяця з небувалою до того часу точністю 0.5' знайшов третю нерівність, суть якої полягає у відхиленні на 40.5' спостереженого положення Місяця від розрахованого за теорією Птолемея-Коперника між сизигіями і квадратурами. Ця нерівність дістала назву варіації Місяця. Надалі Тихо Браге знайшов четверту нерівність - річну нерівність руху Місяця з амплітудою 4.5', згідно з якою довгота Місяця зменшується в період руху Землі від перигелію до афелію її орбіти, а потім збільшується в наступні шість місяців. Із спостережень Тихо Браге випливає також п'ята нерівність - евекція по широті, перша з відкритих в широті Місяця. Аналізуючи теорію Птолемея, Кеплер дійшов висновку, що рух планет відбувається по овальній кривій. Згодом він зрозумів, а потім і довів, що така крива є еліпсом. Ця геометрична крива була відома ще стародавнім математикам. Надалі Кеплер усвідомив, що Сонце розташоване в одному з фокусів сімейства еліпсів, а кожна планета рухається по своєму еліпсові. Це надало змогу сформулювати три знамениті закони Кеплера. Відомий астроном Галілей, сучасник Кеплера, винайшов оптичну трубу-телескоп і відкрив чотири супутники Юпітера та фази Венери. Після цього не лишилося сумніву відносно геліоцентричної будови планетної системи. Нарешті, геніальний Ньютон відкрив закон всесвітнього тяжіння

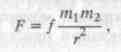
де F - стала тяжіння, т_>1 >і m_>2> - маси матеріальних частинок, r - відстань між ними. Отже, був виявлений механізм взаємодії окремих членів планетної системи, що надало змогу відмежуватися назавжди від кінематичного підходу і перейти до динамічного при створенні теорій руху планет.

Такою була сукупність найбільш вагомих факторів перед початком створення динамічних теорій руху планет. Проте понад 150 років пройшло ще до того часу, як закон Ньютона набув повного визнання і разом із законами Кеплера став теоретичною основою для побудови сучасних теорій руху планет, їхніх супутників, комет, астероїдів і інших космічних тіл. Утвердженню закона Ньютона сприяли створення нових методів вищої математики та розробка способів визначення збурень планет видатними математиками і механіками Клеро (1713-1765), Д'Аламбером (1717-1783), Ейлером (1707-1783), Лагранжем (1736-1813), Лапласом (1749 - 1827) та іншими. Під збуреннями розуміється відхилення реального руху небесних тіл від руху по еліпсу, параболі чи гіперболі. В епоху Кеплера спостереження велись неозброєним оком і збурення були мало помітними, а коли положення почали визначати за допомогою телескопів і різних вимірювальних пристроїв в десятки і сотні разів точніше, збурення набули реальних фактів і їх необхідно було враховувати при дослідженні руху планет і супутників. В цей період і була започаткована сучасна небесна механіка. На той час її розвиток обумовлювався двома основними факторами: потребами практичної астрономії та необхідністю перевірки закону Ньютона.

Практичний аспект небесної механіки зводився у XVIII ст. (перед винайденням хронометра) до розробки точної теорії руху Місяця, бо саме за його спостереженнями визначались довготи пунктів на Землі. Невдовзі небесні механіки опанували загальний підхід до задачі про рух тіл Сонячної системи. Оскільки наймасивнішим тілом є Сонце, то, безперечно, на рух окремої планети його вплив буде незрівнянно більшим, піж вплив від інших членів планетної системи. Це надає: змогу обмежитися іноді взаємним притяганням тільки Сонця і планети або планети та її супутника. Так виникла задача двох тіл. Врахування збурень від третього тіла або η тіл призводить до так званих задач трьох тіл та η тіл. До цього часу в аналітичному вигляді не знайдені повні розв'язки про рух трьох і більшого числа тіл. Ось тому рух небесних тіл досліджувався здебільшого методами кількісної небесної механіки, зокрема способом послідовних наближень. Оскільки цим способом побудовані аналітичні теорії всіх великих планет, зупинимось на його суті.

При використанні способу послідовних наближень враховують ту обставину, що планети рухаються наближено по незбурених еліптичних орбітах, тому за законами Кеплера можна обраховувати їхні наближені положення на будь-який момент. Враховуючи приблизне взаємне розташування всіх чи окремих планет, можна знайти сили взаємного тяжіння і обумовлені ними прискорення планет для кожного моменту. Ці додаткові прискорення від Сонця будуть збурюючими прискореннями. Вони визначають не самі траєкторії руху, а їхні відхилення від еліптичних орбіт. За цими збурюючими прискореннями можна знайти і збурення для кожного моменту часу. Це будуть збурення, знайдені в першому наближенні, або збурення першого порядку. Врахування збурень першого порядку надає можливість обчислити для кожної планети на будь-який момент нові положення в просторі (перше наближення). Ці нові наближені положення будуть більш точними в порівнянні з обчисленими за формулами еліптичного руху. Надалі, враховуючи більш точне взаємне розташування планет на кожний момент із першого наближення, знову знаходять взаємне притягання і збурюючі прискорення, а потім і самі збурення. Знайдені збурення в другому наближенні будуть точнішими за збурення першого порядку. Після врахування останніх знаходять положення планет ще точніше (друге наближення). В такий спосіб можна обчислити збурення третього порядку і т.д. Практична цінність аналітичних теорій руху зводиться не тільки до обчислення видимих положень небесних тіл, а й до можливості дослідити характер взаємного впливу планет та інших небесних об'єктів, а також до можливості обрахувати їхні маси.

З 50-х років XX ст. почали інтенсивно розвиватися так звані чисельні теорії руху планет. Цьому сприяло створення та нарощування потужності сучасних електронно-обчислювальних машин. Основна відмінність чисельних теорій полягає в тому, що за їхньою допомогою одержують не формули для визначення збурень в залежності від часу, а лише певні числа, які фіксують положення небесного тіла в просторі на вибрані моменти часу. Пояснимо суть використання чисельних методів для створення теорій руху небесних тіл.

Якщо небесні тіла притягаються за законом Ньютона і якщо для кожного тіла відомі в початковий момент to положення і швидкість, то легко знайти сили, з якими тіла діють одне на друге, а також прискорення, які вони надають одне другому в початковий момент. Тепер виберімо момент ty, близький до t_>0>, і приймемо, що за інтервал часу At - t\ - ί$ прискорення не змінюється. Тоді за формулами рівноприскореного руху для кожного тіла розраховують відхилення від рівномірного і прямолінійного руху за час Δ/, а також положення і швидкість в момент t\. За новими положеннями тіл знову можна обрахувати діючі сили між ними і прискорення в t\. Надалі визначаються положення і швидкості для наступного близького моменту t_>2> і т.д. В такий спосіб послідовно, крок за кроком, можна обчислити і скласти таблицю положень тіл на моменти t\, t_>2>, t$,..., тобто побудувати чисельну теорію руху на певному інтервалі часу.

Основним недоліком чисельних теорій руху є те, що для їхнього створення уже необхідно знати точні маси досліджуваних небесних тіл і повні відомості про величини і характер їхнього притягання.

Крім того, при чисельних розрахунках одержують безпосередньо збурення, а не залежності між цими збуреннями і величинами, які пов'язані з масами, елементами орбіт і іншими властивостями збурюючих тіл і їхніх рухів.

Тому без наявності аналітичних теорій руху, можливо, не знали б маси Венери і Меркурія, не змогли б відкрити "па кінчику пера" планети Нептун, Плутон і т.д. Чисельні методи не дозволяють ефективно вивчати також загальні властивості руху небесних тіл. Ось тому зараз чисельні й аналітичні теорії руху поєднуються і створюються чисельно-аналітичні теорії руху. Загалом, чисельні теорії не можуть замінити аналітичні, проте вони широко розповсюджені і мають велику практичну цінність.

Сучасні теорії руху небесних тіл

Серед найбільш досконалих аналітичних теорій руху необхідно згадати планетні теорії Левер'є, створені в 50-60-х pp. минулого століття. Вони мають вигляд таблиць, в яких положення Сонця і семи великих планет (крім Плутона) відносно Землі подані в залежності від часу. Згодом з'ясувалося, що розбіжність положень, обчислених за теоріями Левер'є і нових спостережень почала збільшуватись, зокрема це найбільше стосувалось Юпітера і Сатурна. В зв'язку з цим американський астроном Хілл в 1895 р. побудував також аналітичні теорії руху Юпітера і Сатурна, проте і вони не усунули розбіжності теорій і спостережень. Тому Гайо в 1913 р. здійснив уточнення теорії і довів розбіжність до розмірів похибок спостережень. Поліпшені теорії Левер'є були основними в астрономії до початку XX ст., а для зовнішніх планет використовувались ще тривалий час в першій половині XX ст. В 1895-1898 pp. Нюкомом були опубліковані нові аналітичні теорії руху Меркурія, Венери, Землі, Марса, Урана і Нептуна теж у вигляді таблиць. Вони базувались на положеннях, спостережених на всіх обсерваторіях світу з 1750 р. по 1892 p.: 40000 положень для Сонця, 5400 положень і 4 проходження по диску Сонця для Меркурія, 12000 положень і 2 проходження по диску Сонця для Венери, 4000 положень для Марса. Проте і тут не обійшлось без несподіванок. Спостереження Марса в опозицію 1902-1903 pp. розбігались з теорією на 3", а в опозицію 1905 р. - вже на 6". Як згодом з'ясував Росе, причиною розбіжності теорії і спостережень було помилкове на 0.7" значення ексцентриситету, прийняте Нюкомом для обчислень. Тому Росе ввів поправки до Нюкомової теорії для Марса. Пізніше ще вносились деякі уточнення в теорії Нюкома, з якими вони і використовувались для внутрішніх планет аж до 80-х років XX ст. Що стосується теорій руху зовнішніх планет, то вони були менш точними. Ось тому вже в 50-х роках XX ст. теорії Нюкома для Юпітера, Сатурна, Урана, Нептуна були замінені чисельними теоріями, побудованими Еккертом, Брауером і Клеменсом шляхом чисельного інтегрування диференціальних рівнянь руху. У 80-х роках астрономи перейшли на використання чисельної теорії руху планет DE200, а в 1997 р. Міжнародним астрономічним союзом рекомендовані ще більш досконалі чисельні теорії руху планет DE403.

Першу наближену теорію руху Місяця створив Ейлер ще в 1722 р. Через 100 років Хілл розвинув ідеї Ейлера, і були закладені найбільш точні, теоретичні основи для обчислення положень Місяця. Найдосконаліша аналітична теорія руху Місяця створена Брауном і опублікована в 1919 р. Це був результат майже 30-річної праці Брауна, який, по суті, продовжив та розвинув надбання Хілла. Відтоді теорія руху Місяця неодноразово уточнювалась. Спочатку в 1960 р. теорія Брауна була поліпшена за рахунок введення в середню довготу Місяця емпіричної нерівності 8.72" - 26.74"Г - 11.227", пояснення якої до цього часу було проблематичним. Надалі після 1971 р. була виправлена помилка в 182 членові місячної теорії Брауна і був здійснений перехід на систему астрономічних сталих МАС 1964 р. Нарешті, було здійснене ще одне поліпшення теорії, яке зводиться до заміни співвідношень Брауна для збурень від Сонця співвідношеннями Еккерта. Загалом, теорія руху Місяця за Брауном подається у вигляді тригонометричних рядів із складним аргументом, який залежить від часу, вікових і періодичних збурень. Ряди налічують понад 1650 членів. Щоб обчислити, наприклад, довготу Місяця з точністю до 0.1", необхідно скласти 655 членів. Проте необхідно зауважити, що точність 0 1" є лише точністю обчислень, а справжня розбіжність обчислених і спостережених положень Місяця в багато разів більша. В останні десятиріччя замість теорії Брауна набули поширення чисельні теорії руху Місяця DL200 і DL403, кожна з яких вводилась одночасно з DE200 і DE403.

Як же оцінюється сучасний стан теорій руху планет і Місяця? Найбільш оптимальним критерієм досконалості теорій руху планет, їхніх супутників, астероїдів і комет вважається узгодженість обчислених і спостережених положень на коротких (десятки і сотні років) та історично тривалих (тисячі і сотні тисяч років) інтервалах часу. Перш за все, ця узгодженість залежить від точності врахування періодичних і вікових збурень.

Періодичні збурення характеризують відхилення від руху по еліптичних орбітах в одну або іншу сторону. Для планет періодичні збурення порівняно невеликі. Зокрема, найбільші видимі відхилення на небі від еліптичного руху становлять для Меркурія біля 15", Венери - 30", Землі - Г, Марса - 2', Урана - З', Нептуна - 1.5', а для масивних планет Юпітера і Сатурна відхилення сягають 28' і 48'. При порівнянні сучасних аналітичних і чисельних теорій руху планет з даними спостережень з 1800 р. по теперішній час мають місце розходження періодичного характеру не більше декількох секунд. Це свідчить про те, що наявні теорії руху придатні для користування на інтервалі 100-200 років. За цей час елементи орбіт будуть змінюватись у відповідності з тими формулами, які покладені в основу теорій. Чи будуть елементи змінюватись надалі так - невідомо.

Вікові збурення регулярно збільшують відхилення від незбуреного руху. З їхнього аналізу можна впевнитись в зміні деяких елементів орбіт планет до таких величин, які є нереальними. Наприклад, для Венери розрахований ексцентриситет орбіти за теорією Левер'є через 20 тисяч років набуде від'ємного значення. Проте він не може бути меншим нуля. На коротких інтервалах часу теж відомі факти неузгодженості аналітичних теорій руху планет і спостережень до 1". Зокрема, час від часу в публікаціях з'являються повідомлення про додаткові вікові зміни довгот перигеліїв і вузлів орбіт деяких планет, не знайдено пояснення так званого непрецесійного руху рівнодення біля 1" в століття та інше. Це невеликі відхилення, але вони є свідченням про необхідність уточнення теорій руху тіл Сонячної системи.

Найбільші ускладнення виникають при створенні теорій руху супутників планет, зокрема Місяця. Це пояснюється необхідністю досконалого знання гравітаційної фігури та внутрішньої будови планет, які мало вивчені. Для Місяця проблема створення теорії руху ускладнюється ще й близьким розташуванням його відносно Сонця, яке є масивним тілом і суттєво збурює рух в орбіті. Саме тому, ще в 60-70-х роках XX ст. три рази уточнювалась остання аналітична теорія руху Місяця, створена Брауном. Зокрема, лише в 60-х роках знайшла пояснення і була виключена з розряду емпіричних нерівність понад 9". Для низки супутників інших планет теорії руху є ще досить наближеними.

Висновок

Загалом, можна стверджувати, що сучасні аналітичні і чисельні теорії руху небесних тіл є досить високоточними і задовольняють потребам вирішення наукових і прикладних завдань, проте їх не можна вважати завершеними. За точністю обчислень, прийнятих мас планет і інших констант теорії забезпечують формальну точність на рівні сотих часток дугових секунд, але неузгодженість обчислених і спостережених положень збільшується на 1-2 порядки на інтервалі декількох десятків років. Ось тому астрономи, "наділені працелюбністю та любов'ю до істини", як говорив Птолемей, мають перед собою одне з найважливіших завдань: продовжувати, примножувати та уточнювати ряди спостережень і їхню методичну обробку до тих пір, поки не будуть з'ясовані існуючі загадки в цій проблемі. Отже, дослідження руху тіл Сонячної системи і створення їхніх теорій руху залишиться і надалі однією з найважливіших проблем в астрономії.

Література

А. Алексеев. Древние и современные теории движения небесных тел.М., 1989.

Астрономічний календар на 1999 рік. ГАО АН України, 1998.