Прогнозирование емкости и коньюктуры рынка

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Московский Государственный Текстильный Университет

имени А. Н. Косыгина

кафедра экономики

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ (вариант №23, 1 и 2 часть)

По курсу:

«Прогнозирование емкости и коньюктуры рынка».

Выполнил: студент группы 47-03

Котляр Владимир

Проверил:

Станкевич А.В.

Москва – 2007

Задание № 1

Период

1

2

3

4

5

6

7

8

9

10

Уровень ряда

16,7

17,2

17,5

19,4

16,8

19,3

16,5

19,4

18,1

16,1

На основании данных о еженедельном спросе на текстильную продукцию:

    построить график (рис. 1) и визуально оценить наличие в нем тенденции;

    проверить наличие или отсутствие в исходном временном ряде тенденции с помощью коэффициента Кендэла;

    если исходный ряд является стационарным, то рассчитать точечный и интервальный прогноз с периодом упреждения прогноза, равным 1.

Рис. 1. Еженедельный спрос на текстильную продукцию

При визуальной оценке наличия в графике тенденции можно отметить сильную его приближенность к полиному высокого порядка (шестой степени), использование которого нецелесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения, что противоречит смыслу тенденции.

Таким образом, в результате визуальной оценки можно сделать вывод об отсутствии в графике тенденции.

2).

 

t

Yt

Pt

 

1

16,7

-

 

2

17,2

1

 

3

17,5

2

 

4

19,4

3

 

5

16,8

1

 

6

19,3

4

 

7

16,5

0

 

8

19,4

6

 

9

18,1

5

 

10

16,1

0

итого

 

177

22

Определим расчетное значение коэффициента Кендэла (>р>):

>р> =

4  р

– 1,

n  (n – 1)

где n – количество уровней во временном ряде.

>р> =

4  22

– 1 = -0,0222

10  (10 – 1)

Коэффициент Кендэла является случайной величиной, соответствует нормальному распределению и изменяется от -1 до +1. Теоретическими характеристиками коэффициента Кендэла являются математическое ожидание, которое равно нулю (М>> = 0) и дисперсия, рассчитываемая по формуле:

>>2 =

2  (2  n + 5)

.

9  n  (n – 1)

>>2 =

2  (2  10 + 5)

=

50

= 0,062

9  10  (10 – 1)

810

Если сопоставить расчетное и теоретическое значение коэффициента Кендэла, то может возникнуть три ситуации.

1) (0 – t>d> ) < >р> < (0 + t>d> ),

где t>d> – коэффициент доверия.

Данный вариант означает, что с вероятностью t>d> во временном ряде нет тренда.

2) >р> < (0 – t>d> )

Данный вариант означает, что с выбранной вероятностью в ряде имеет место убывающая тенденция.

3) >р> > (0 + t>d> )

Данный вариант означает, что с выбранной вероятностью в ряде имеет место возрастающая тенденция.

При выбранной вероятности 0,95 (95%) коэффициент доверия t>d> = 1,96.

(0 – 1,9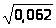6  ) < >р> < (0 + 1,96  )

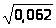- 0,488 < - 0,0222 < + 0,488

Таким образом, с вероятностью 95% можно говорить об отсутствии тенденции среднего уровня (тренда) во временном ряде.

3)

t

Yt

Yt-Yсреднее

(Yt-Yсреднее)^2

1

16,7

-1

1

2

17,2

-0,5

0,25

3

17,5

-0,2

0,04

4

19,4

1,7

2,89

5

16,8

-0,9

0,81

6

19,3

1,6

2,56

7

16,5

-1,2

1,44

8

19,4

1,7

2,89

9

18,1

0,4

0,16

10

16,1

-1,6

2,56

 

177

 

14,6

Так как во временном ряде нет тенденции, то данный временной ряд является стационарным процессом.

Поскольку в ряде отсутствует тенденция, то точечный прогноз определяется как средняя арифметическая простая:

==

y>t>

,

n

где n – количество уровней ряда.

==

177

= 17,7

10

Интервальный прогноз:

=+ t>> ,

где t>> – табличное значение по распределению Стьюдента с числом степеней свободы

К = n – 1 и уровнем значимости а; – дисперсия временного ряда.

=

(y>t> –)2

=

14,6

= 1,46

n

10

При заданном уровне значимости a = 0,05 ( = 1 – а = 1 – 0,05 = 0,95) и числе степеней свободы К = 10 – 1 = 9, определим табличное значение t-критерия Стьюдента (см. Приложение 1). Табличное значение критерия Стьюдента t>> = 2,262.

Определим интервальный прогноз.

=17,7 – 2,262 = + 14,8

=24,16 + 2,262 = + 20,6

Таким образом, с вероятностью 0,95 (95%) можно говорить о том, что на 11-ю неделю уровень ряда будет находиться в промежутке между 14,8 и 20,6.

Задание № 2

Период

1

2

3

4

5

6

7

8

9

10

11

12

Уровень ряда

11,0

10,8

10,7

10,5

11,7

12,2

12,5

12,1

13,0

13,7

13,0

14,0

По данным о ежедневном обороте магазина «Ткани для дома»:

    построить график исходного временного ряда и визуально оценить наличие в нем тенденции и возможный ее тип. Сгладить исходный временной ряд с помощью скользящей средней (шаг сглаживания равен 3). Построить график сглаженного ряда и визуально оценить возможный в нем тип тенденции. Оба графика построить на одном чертеже (рис. 2). Результаты обеих визуальных оценок отметить в отчете;

    оценить с помощью метода Фостера – Стюарта и коэффициента Кендела наличие тенденции (в среднем и дисперсии) в исходном временном ряде. Сравнить полученные оценки с оценками, полученными при выполнении пункта 1, и сделать окончательный свой вывод. Результаты вывода отметить в отчете;

    по исходным данным методом усреднения по левой и правой половине определить параметры линейного тренда = а>0> + а>1>t. Построить график исходного временного ряда и полученного линейного тренда на одном чертеже (рис. 3). Оценить визуально, отражает ли линейный тренд тенденцию временного ряда? Свой вывод отразить в отчете;

    по исходным данным методом МНК рассчитать параметры линейного тренда = а>0> + а>1>t. Кроме того, выбрать нелинейную модель, которая, по вашему мнению, может хорошо описать тенденцию исходного временного ряда. Рассчитать параметры выбранной вами нелинейной трендовой модели. Построить три графика (исходный временной ряд, линейная и выбранная вами нелинейная трендовая модели) на одном чертеже (рис. 4). Определить аналитическим способом, какая из двух трендовых моделей (линейная и нелинейная) наилучшим образом аппроксимирует исходный временной ряд;

    построить график ряда отклонений е>t> (рис. 5) и визуально оценить отсутствие в нем тенденции. Оценить адекватность выбранной модели тренда исходному ряду на основе анализа данных ряда отклонений;

    рассчитать точечную и интервальную прогнозную оценку с периодом упреждения, равным  = 1.

1)

t

y>t>

Скользящая сумма 3 уровней

Скользящая средняя из 3 уровней

1

11,9

-

2

12,6

36,7

18,35

3

12,2

38,7

19,35

4

13,9

40,4

20,2

5

14,3

42,8

21,4

6

14,6

44,2

22,1

7

15,3

44,3

22,15

8

14,4

45,5

22,75

9

15,8

46,9

23,45

10

16,7

49,9

24,95

11

17,4

50,2

25,1

12

16,1

-

-

Рис. 2. Еженедельный оборот магазина «Ткани для дома» (исходный и сглаженный ряд)

После построения графика (рис. 2) можно сделать вывод о наличии возрастающей тенденции. После построения сглаженного ряда стало более наглядно видно наличие возрастающей тенденции.

2). а) Метод Фостера – Стюарта

t

Yt

Ut

lt

S

D

Pt

1

11,9

-

-

-

-

-

2

12,6

1

0

1

1

1

3

12,2

0

0

0

0

1

4

13,9

1

0

1

1

3

5

14,3

1

0

1

1

4

6

14,6

1

0

1

1

5

7

15,3

1

0

1

1

6

8

14,4

0

0

0

0

5

9

15,8

1

0

1

1

8

10

16,7

1

0

1

1

9

11

17,4

1

0

1

1

10

12

16,1

0

0

0

0

9

 

175,2

 

 

8

8

61

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выдвинем нулевую гипотезу: во временном ряде (данные графы 2) нет тенденции среднего уровня и нет тенденции дисперсии. Для проверки выдвинутой нулевой гипотезы необходимо рассчитать по формулам и значения t>1> и t>2>. Но для этого надо знать значения μ, σ>1>,> >σ>2 >. В приложении 1 приведены данные для n=10 и для n=15, а нам надо найти данные для n=12.

Для нахождения данных при n=12 используем принцип интерполяции, предположив, что эти данные в интервале от n=10 до n=15 изменяются линейно, т.е. равномерно. Поэтому нам нужно к значениям данных при n=10 прибавить их изменения за два (2=12–10) шага и получить искомые данных.

Найдем μ для n=12 следующим образом. Значение μ для n=10, согласно приложению 1, равно 3,858. Увеличение μ при изменении n на 2 шага найдем следующим образом

.

Отсюда μ(12)=μ(10)+Δμ=3,858+0,311=4,169. Аналогичным образом найдем значения для σ>1>(12)=1,381 и для σ>2>(12)=2,040. По формулам (2.7) найдем значения t>1 >и t>2>

= (8 – 4,169)/1,381 = 3,326; = (8-0)/2,040 = 3,92

Случайные величины t>1> и t>2> имеют распределение Стьюдента с числом степеней свободы К = n – 1 = 12 – 1 = 11 и уровнем значимости a, который может принимать значения 0,01; 0,05 и т.д. Примем уровень значимости (вероятность, с которой исследователь может ошибиться), равный 0,05 (5%). На основе выбранного уровня значимости а = 0,05 рассчитаем доверительную вероятность:  = 1 – а = 1 – 0,05 = 0,95.

По числу степеней свободы К = 11 и величине доверительной вероятности  = 0,95 по таблице «Значение t-критерия Стьюдента» (Приложение 1)определим табличное значение случайной величины (t>>): t>> = 2,201.

Расчетные значения t>1> и t>2> сопоставим с табличным t>>.

Если сопоставить расчетные значения t>1> и t>2> с табличным t>>, то может возникнуть четыре ситуации.

1) |t>1>| > |t>>|.

Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью  во временном ряде имеет место тенденция дисперсии.

2) |t>1>| < |t>>|.

Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции принимается и с вероятностью  во временном ряде нет тенденции дисперсии.

3) |t>2>| > |t>>|.

Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью  во временном ряде имеет место тенденция в среднем.

4) |t>2>| < |t>>|.

Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции принимается и с вероятностью  во временном ряде нет тенденции в среднем.

1) 3,326 > 2,201; 3,92 > 2,201 нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью  = 0,95 можно говорить, что во временном ряде имеет место тенденция дисперсии

б) Метод коэффициента Кенделла

Определим расчетное значение коэффициента Кендэла (>р>):

>р> =

4  р

– 1,

n  (n – 1)

где n – количество уровней во временном ряде.

>р> =

4  61

– 1 = 0,85

12  (12 – 1)

Коэффициент Кендэла является случайной величиной, соответствует нормальному распределению и изменяется от -1 до +1. Теоретическими характеристиками коэффициента Кендэла являются математическое ожидание, которое равно нулю (М>> = 0) и дисперсия, рассчитываемая по формуле:

>>2 =

2  (2  n + 5)

.

9  n  (n – 1)

>>2 =

2  (2  12 + 5)

=

58

= 0,049

9  12  (12 – 1)

1188

Если сопоставить расчетное и теоретическое значение коэффициента Кендэла, то может возникнуть три ситуации.

1) (0 – t>d> ) < >р> < (0 + t>d> ),

где t>d> – коэффициент доверия.

Данный вариант означает, что с вероятностью t>d> во временном ряде нет тренда.

2) >р> < (0 – t>d> )

Данный вариант означает, что с выбранной вероятностью в ряде имеет место убывающая тенденция.

3) >р> > (0 + t>d> )

Данный вариант означает, что с выбранной вероятностью в ряде имеет место возрастающая тенденция.

При выбранной вероятности 0,95 (95%) коэффициент доверия t>d> = 1,96.

>р> > (0 + 1,96  )

0,85 > + 0,434

Таким образом, с вероятностью 0,95 (95%) можно говорить о наличии в ряде возрастающей тенденции в среднем (тренда).

В ходе анализа временного ряда на наличие в нем тенденции среднего уровня (тренда) по методу Фостера – Стюарта и методу коэффициента Кенделла получены аналогичные результаты. Следовательно, в ряде отмечается возрастающая тенденция в среднем.

Таким образом, визуальная оценка нашла свое подтверждение в ходе аналитических расчетов с использованием соответствующих методов оценки временного ряда на наличие в нем тенденции.

3). Метод усреднения по левой и правой половине

Метод усреднения по левой и правой половине - графический метод, используется для нахождения параметров линейного тренда.

Для нахождения параметров а>0> и а>1> разделим исходные данные пополам и по каждой половине рассчитаем средние значения фактора и уровня ряда.

>1 >=

1 + 2 + 3 + 4 + 5 + 6

= 3,5

6

>1 >=

11,9 + 12,6 + 12,2 + 13,9 + 14,3 + 14,6

= 13,25

6

>2 >=

7 + 8 + 9 + 10 + 11 + 12

= 9,5

6

>2 >=

15,3 + 14,4 + 15,8 + 16,7 + 17,4 + 16,1

= 15,95

6

В результате расчетов получили две точки: А (3,5; 13,25), В (9,5; 15,95).

Построим графическую модель исходного временного ряда и найдя точки А и В, проведем через них прямую, которая будет отображать тенденцию исходного временного ряда (рис. 3).

y>t>

Рис. 3. Еженедельный оборот магазина «Ткани для дома» (исходный ряд и линейный тренд)

Из графика видно, что построенный линейный тренд отражает тенденцию исходного ряда: возрастающий тренд.

Для нахождения параметра а>0> продолжим линию до пересечения с осью ординат. Чтобы найти параметр а>1>, преобразуем уравнение тренда:

а>1>t = – а>0> | :t

а>1> =

– а>0>

t

Зададимся произвольным значение параметра t (например, t = 3,5). По графику модели найдем значение параметра а>0> (а>0> = 13,45). Рассчитаем значение параметра а>1>.

а>1> =

13,25 – 11,8

= 0,41

3,5

Таким образом, уравнение линейного тренда будет иметь следующий конкретный вид:

= 11,8+ 0,41t.

4). Расчет параметров линейного тренда >t>> >= а>0> + а>1>t по исходным данным методом МНК.

t

y

t2

y>t>

1

11,9

1

11,9

2

12,6

4

25,2

3

12,2

9

36,6

4

13,9

16

55,6

5

14,3

25

71,5

6

14,6

36

87,6

7

15,3

49

107,1

8

14,4

64

115,2

9

15,8

81

142,2

10

16,7

100

167

11

17,4

121

191,4

12

16,1

144

193,2
78

175,2

650

1204,5

Для нахождения параметров строится система нормальных уравнений.

=(175,2*650-78*1204,5)/(12*650-78*78)=11,614;

=(12*1204,5-175,2*78)/(12*650-78*78)=-0,459

Расчет параметров параболического тренда >t>> >= а>0> + а>1>t + a>2>t2 по исходным данным методом МНК.

t

y

t2

y>t>

t4

yt2

t3

1

11,9

1

11,9

1

11,9

1

2

12,6

4

25,2

16

50,4

8

3

12,2

9

36,6

81

109,8

27

4

13,9

16

55,6

256

222,4

64

5

14,3

25

71,5

625

357,5

125

6

14,6

36

87,6

1296

525,6

216

7

15,3

49

107,1

2401

749,7

343

8

14,4

64

115,2

4096

921,6

512

9

15,8

81

142,2

6561

1279,8

729

10

16,7

100

167

10000

1670

1000

11

17,4

121

191,4

14641

2105,4

1331

12

16,1

144

193,2

20736

2318,4

1728

78

175,2

650

1204,5

60710

10322,5

6084

Для нахождения параметров строится система нормальных уравнений.

na>0> + a>1>t + a>2>t2 = y;

a>0>t + a>1>t2 + a>2>t3 = yt;

a>0>t2 + a>1>t3 + a>2>t4 = yt2.

а>0> =

y t2 t4 + t t3 yt2 + yt t3 t2 – t yt t4 – t3 t3 y – t2 t2 yt2

.

n t2 t4 + t t3 t2 + t t3 t2 – t2 t2 t2 – t3 t3 n – t t t4

а>0> =

175,2  650  60710 + 78  6084  10322,5 + 1204,5  6084  650 – 78  1204,5  60710 –

12  650  60710 + 78  6084  650 + 78  6084  650 – 650  650  650 –

– 6084  6084  175,2 – 650  650  10322,5

= 11,12.

– 6084  6084  12 – 78  78  60710

а>1> =

n yt t4 + t yt2 t2 + y t3 t2 – t2 yt t2 – yt2 t3 n – y t t4

.

n t2 t4 + t t3 t2 + t t3 t2 – t2 t2 t2 – t3 t3 n – t t t4

а>1> =

12  1204,5  60710 + 78  10322,5  650 + 175,2  6084  650 – 650  1204,5  650 –

12  650  60710 + 78  6084  650 + 78  6084  650 – 650  650  650 –

– 10322,5  6084  12 – 175,2  78  60710

= 0,67.

– 6084  6084  12 – 78  78  60710

а>2> =

n t2 yt2 + t t3 y + t yt t2 – y t2 t2 – yt t3 n – t t yt2

.

n t2 t4 + t t3 t2 + t t3 t2 – t2 t2 t2 – t3 t3 n – t t t4

а>2> =

12  650  10322,5 + 78  6084  175,2 + 78  1204,5  650 – 175,2  650  650 –

12  650  60710 + 78  6084  650 + 78  6084  650 – 650  650  650 –

– 1204,5  6084  12 – 78  78  10322,5

= -0,016.

– 6084  6084  12 – 78  78  60710

Таким образом, параболический тренд имеет следующий вид:

>t>> >= 11,12 + 0,67  t - 0,016  t2.

Рис. 4. Еженедельный оборот магазина «Ткани для дома» (исходный ряд, линейный и параболический тренд)

Проведем оценку аппроксимации линейного тренда и выбранной параболической трендовой модели с помощью критерия наименьшей суммы квадратов отклонений, который имеет следующий вид:

S =

(y>t> – )2

 min

n – m

где n – количество уровней ряда; m – число параметров трендовой модели.

t

y>t>

Линейный
тренд

Параболический
тренд

>t>

(y>t> – >t>)2

>t>

(y>t> – >t>)2

1

11,9

12,21

0,0961

11,774

0,015876

2

12,6

12,62

0,0004

12,396

0,041616

3

12,2

13,03

0,6889

12,986

0,617796

4

13,9

13,44

0,2116

13,544

0,126736

5

14,3

13,85

0,2025

14,07

0,0529

6

14,6

14,26

0,1156

14,564

0,001296

7

15,3

14,67

0,3969

15,026

0,075076

8

14,4

15,08

0,4624

15,456

1,115136

9

15,8

15,49

0,0961

15,854

0,002916

10

16,7

15,9

0,64

16,22

0,2304

11

17,4

16,31

1,1881

16,554

0,715716

12

16,1

16,72

0,3844

16,856

0,571536
-

-

173,58

4,483

175,3

3,567

Для линейного тренда

S =

4,483

= 0,4483.

12 – 2

Для параболического тренда

S =

3,567

= 0,396.

12 – 3

0,4483 > 0,396;  параболическая модель наилучшим образом аппроксимирует исходный временной ряд.

5)

t

y>t>

e>t>

P>t>

e>t>2

(e>t> –>t>) 2

(e>t> – e>t-1>) 2

1

11,9

12,21

-0,31

–

0,0961

0,198025

–

2

12,6

12,62

-0,02

1

0,0004

0,024025

0,166

3

12,2

13,03

-0,83

1

0,6889

0,931225

0,107

4

13,9

13,44

0,46

1

0,2116

0,105625

0,200

5

14,3

13,85

0,45

0

0,2025

0,099225

0,870

6

14,6

14,26

0,34

1

0,1156

0,042025

0,045

7

15,3

14,67

0,63

1

0,3969

0,245025

0,000

8

14,4

15,08

-0,68

1

0,4624

0,664225

0,529

9

15,8

15,49

0,31

0

0,0961

0,030625

0,306

10

16,7

15,9

0,8

0

0,64

0,442225

0,111

11

17,4

16,31

1,09

1

1,1881

0,912025

1,182

12

16,1

16,72

-0,62

–

0,3844

0,570025

0,352

175,2

173,58

1,62

7

4,483

4,2643

3,868

Найдем величины случайных отклонений для исходного ряда по формуле: e>t> = y>t> – >t>.

Построим график ряда отклонений e>t> (рис. 5).

t

Рис. 5. График ряда отклонений e>t>

Из графика видно, что в ряде отклонений e>t> отсутствует тенденция.

Оценим адекватность выбранной трендовой модели (параболы) исходному ряду на основе анализа ряда отклонений e>t>.

1) Колебание величины e>t> носит случайный характер. Выполнение этого условия означает, что величина e>t> не содержит элементов тренда. Проверим это условие с помощью критерия поворотных точек. Точка считается поворотной, если выполняется одно из следующих условий:

e>t-1> < e>t> > e>t+1>

e>t-1> > e>t> < e>t+1>

Обозначим поворотные точки как Р>t> = 1. В противном случае P>t> = 0. Найдем сумму всех поворотных точек P = P>t>.

Выдвинем нулевую гипотезу – Н>0>: колебание величины et носит случайный характер. Для проверки нулевой гипотезы рассчитаем математическое ожидание и дисперсию поворотных точек.

М(Р) =

2 (n – 2)

=

2  (12 – 2)

= 6,667.

3

3

D(Р) =

16 n – 29

=

16  12 – 29

= 1,811.

90

90

При вероятности 0,95 (95%) коэффициент доверия t>d> = 1,96.

Если расчетное значение числа поворотных точек попадает в интервал
(М(Р) – t>d> ) < P < (М(Р) + t>d> ), то с выбранной вероятностью можно утверждать, что колебания величины e>t> носит случайный характер.

(6,667 – 1,96 ) < 7 < (6,667 + 1,96 )

4,029 < 7 < 9.305

Таким образом, с вероятностью 95% можно утверждать, что колебания величины e>t> носит случайный характер.

2) Распределение величины e>t>соответствует нормальному распределению. Для этого используем RS-критерий.

S= == 0,706

RS>р> =

e>max> – e>min>

=

1.09– (- 0,83)

= 2,777.

S

0,706

Определим табличное значение RS-критерия по таблице «Значения RS-критерия для n от 10 до 30» (Приложение 3).

RS>12Н> = 2,67 + 2 

3,18 – 2,67

= 2,772

20 – 10

RS>12В> = 3,85 + 2 

4,49 – 3,85

= 3,978

20 – 10

Выдвинем нулевую гипотезу: величина e>t> соответствует нормальному распределению. Для этого должно выполняться условие: RS>12Н> < RS>р> < RS>12В>.

Поскольку это условие выполняется (2,772 < 2,777 < 3,978), то с вероятность 0,95 (95%) можно утверждать, что распределение величины e>t> соответствует нормальному распределению.

3) Математическое ожидание величины e>t> равно нулю. Для проверки этого условия выдвинем нулевую гипотезу – Н>0>: М(e>t>) = 0, после чего определим расчетное значение величины t>р>:

t>р> =

– 0

,

S>e>

где – средняя арифметическая простая величины e>t>; S>e> – среднее квадратическое отклонение величины e>t>.

e>t>

=

1.62

= 0,135

n

12

S>e>= == 0,623

t>р> =

0,135 – 0

= 0,75.

0,623

Найдем табличное значение t>т> (Приложение 1) по распределению Стьюдента при доверительной вероятности  = 1 – а = 1 – 0,05 = 0,95 и числе степеней свободы К = n – 1 = 12 – 1 = 11. В данном случае t>т> = 2,201.

Сопоставим табличное и расчетное значения. Если t>h> < t>т>, то нулевая гипотеза принимается, и наоборот.

0,75 < 2,201,  с вероятностью 0,95 (95%) принимается нулевая гипотеза, т.е. М(e>t>) = 0.

4) Независимость членов ряда между собой (проверка временного ряда на отсутствие автокорреляции). Для проверки данного условия используется критерий Дарбина – Уотсона, расчетное значение которого определяется следующим образом:

d>р> =

(e>t> – e>t-1>) 2

=

8,4451

= 1,88.

 e>t>2

4,483

d>р> = 4 – 1,88 = 2,12.

По таблице «Распределение критерия Дарбина – Уотсона» для положительной автокорреляции (для 5% уровня значимости)» находим табличное значение d­­>т>. При n = 12 и V = 1 нижнее и верхнее значения распределения будут соответственно равны d>1> = 1,08 и d>2> = 1,36.

Сравним расчетное и табличное значения: d>р> > d>2> (2,12 > 1,36). Таким образом, с вероятностью 95% можно говорить об отсутствии в ряде автокорреляции.

6). Рассчитаем точечную прогнозную оценку с периодом упреждения  = 1 для линейного тренда (>t>> >= 11,614+ 0,459 t):

>(>>n>>+>>>>)> = а>0> + а>1>  (n+);

>(12+1)> = 11,614+ 0,459 (12 + 1) = 17,581.

Интервальный прогноз для линейного тренда:

>(n+>>>>)> =>(n+>>>>)> + t>т>  S,

где n – число уровней ряда в периоде основания прогноза;  - период упреждения прогноза; t>т>­ – табличное значение по Стьюденту с уровнем значимости (а) и числом степеней свободы (К = n - 2); S– стандартная ошибка тренда.

t>т>  = К;  >(>>n>>+>>>>)> =>(>>n>>+>>>>)> + S К.

При  = 1 и n = 12 по таблице «Значение К для оценки доверительных интервалов прогноза при вероятности  = 0,9 (линейный тренд)» (Приложение 6) К = 2,1274.

S= == 0,67.

Интервальный прогноз для линейного тренда

>(12+1)> = 17,581 + 0,67  2,1274=19,0064

>(12+1)> = 17,581 - 0,67  2,1274=16,1556

16,1556 < >13> < 19,0064, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 16,1556 до 19,0064 д.е.

>t>> >= 11,12 + 0,67  t - 0,016  t2.

Рассчитаем точечную прогнозную оценку с периодом упреждения  = 1 для параболического тренда (>t>> >= 11,12 + 0,67  t - 0,016  t2):

>(>>n>>+>>>>)> = а>0> + а>1>  (n+) + а>2>  (n+)2;

>13> = 11,12 + 0,67  13 - 0,016  132 = 17,126.

Интервальный прогноз для нелинейного (параболического) тренда:

>(n+>>>>)> =>(n+>>>>)> + S К.

При  = 1 и n = 12 по таблице «Значение К для оценки доверительных интервалов прогноза при вероятности  = 0,9 (параболический тренд)» (Приложение 7) К = 2,636.

S= == 0,63.

Интервальный прогноз для нелинейного (параболического) тренда

>13> = 17,126 + 0,63  2,636=18,7867

>13> = 17,126 - 0,63  2,636=15,4653

15,4653 < >13> < 18,7867, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 15,4653 до 18,7867 д.е.